Hydrological Early Warning System Based on a Deep Learning Runoff Model Coupled with a Meteorological Forecast
Abstract
1. Introduction
2. Materials and Methods
2.1. Data-Driven Techniques
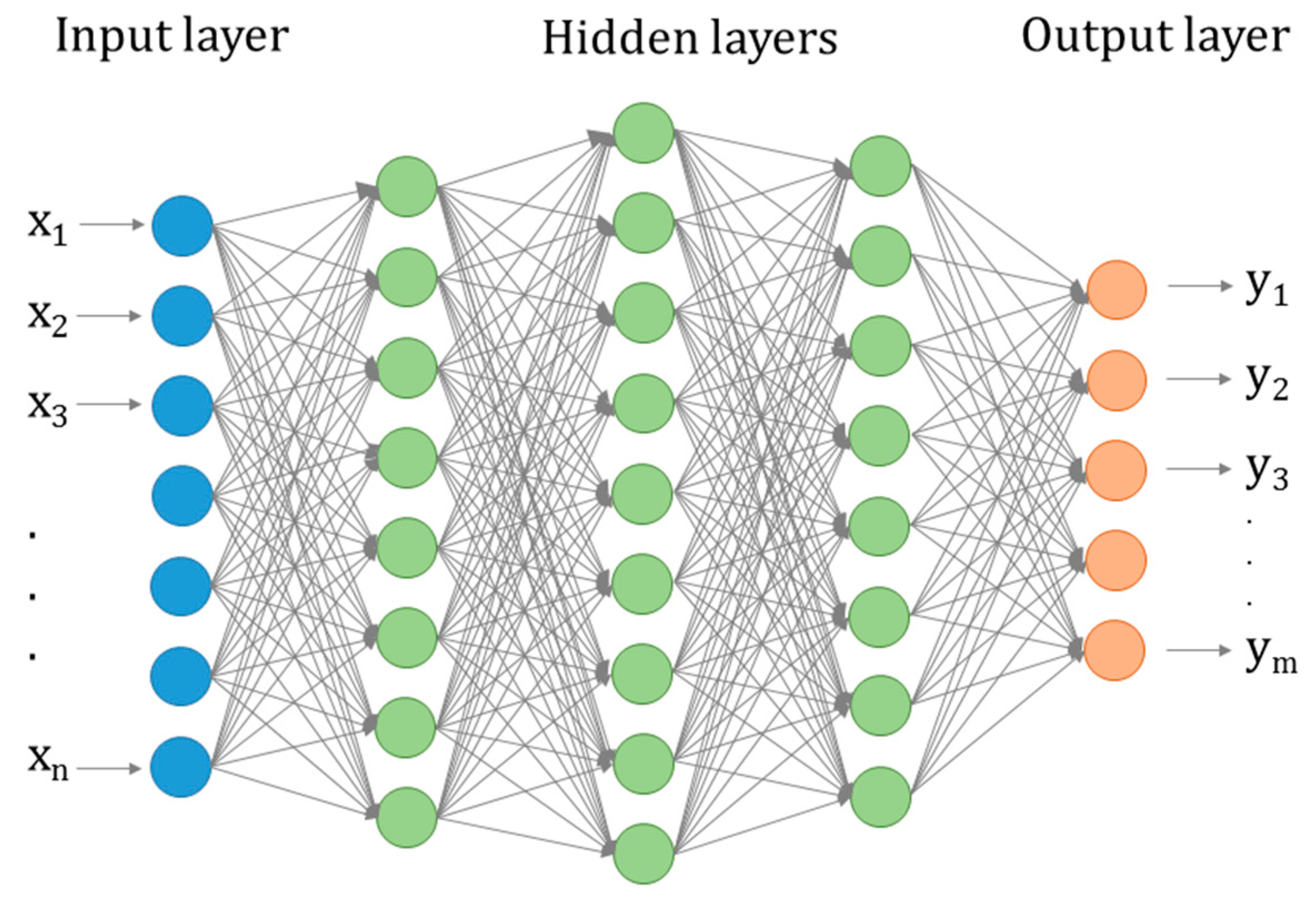
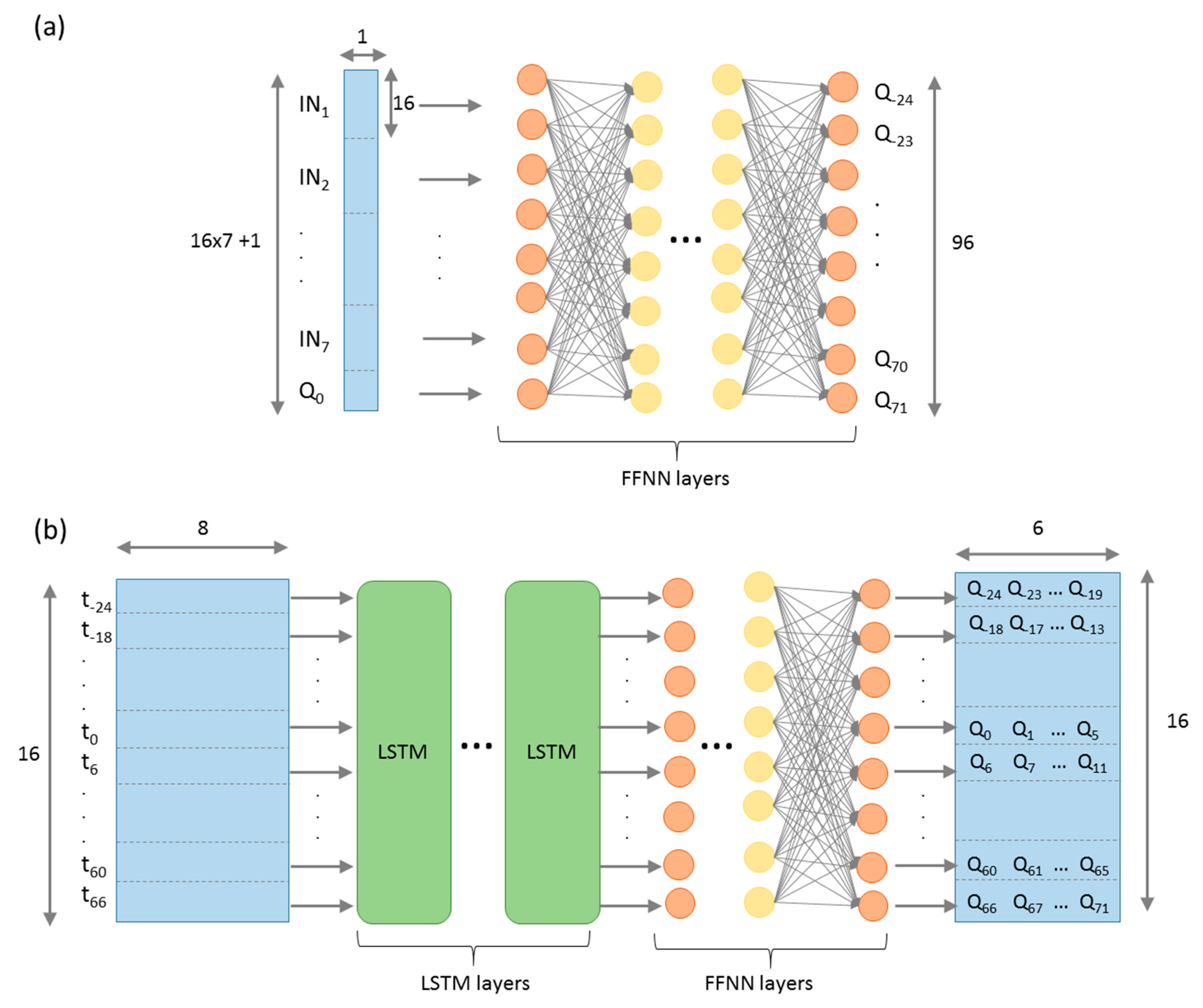
2.1.1. Artificial Neural Networks
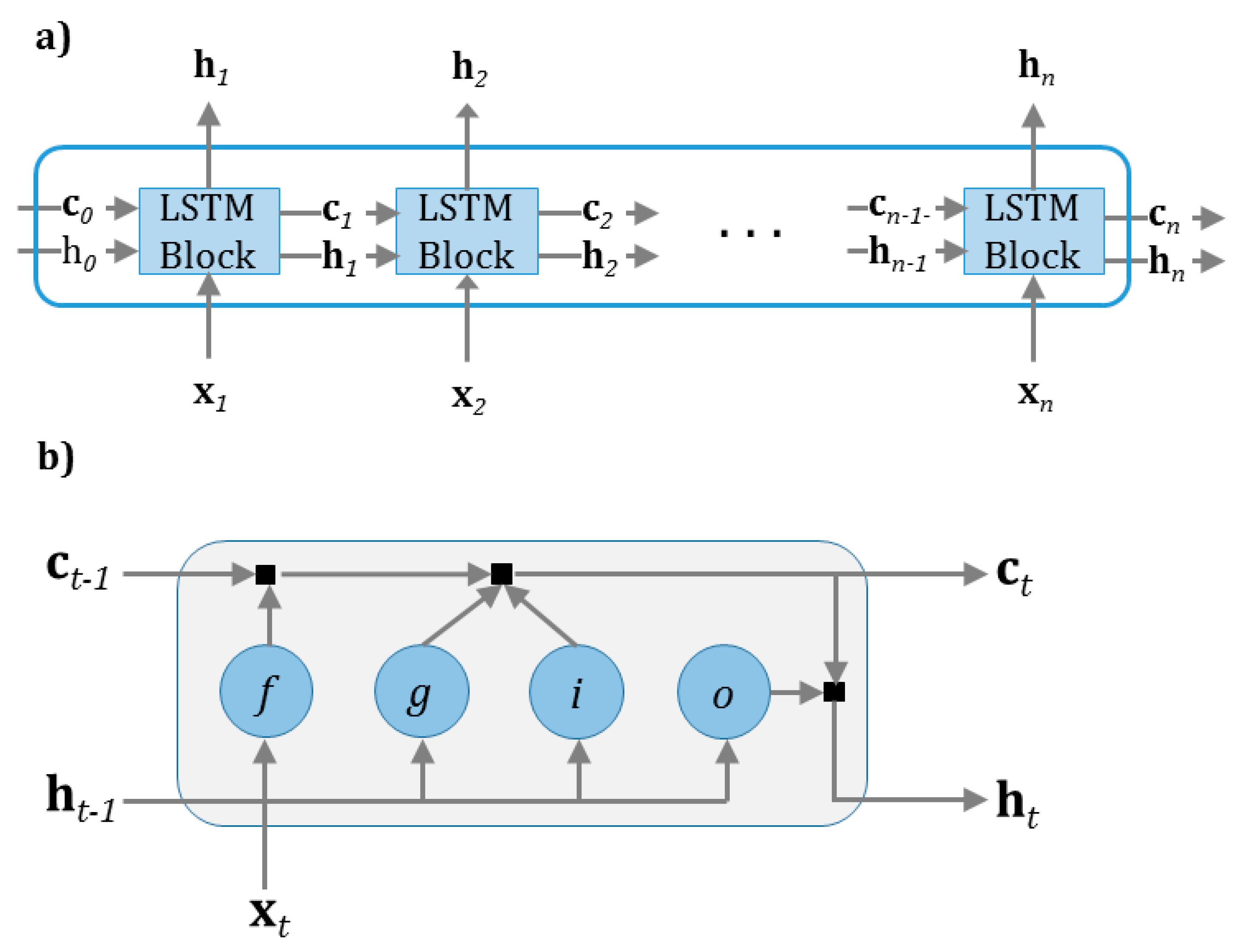
2.1.2. Deep Learning Based on LSTM Neural Networks
2.2. Hydrological Description of the Study Area
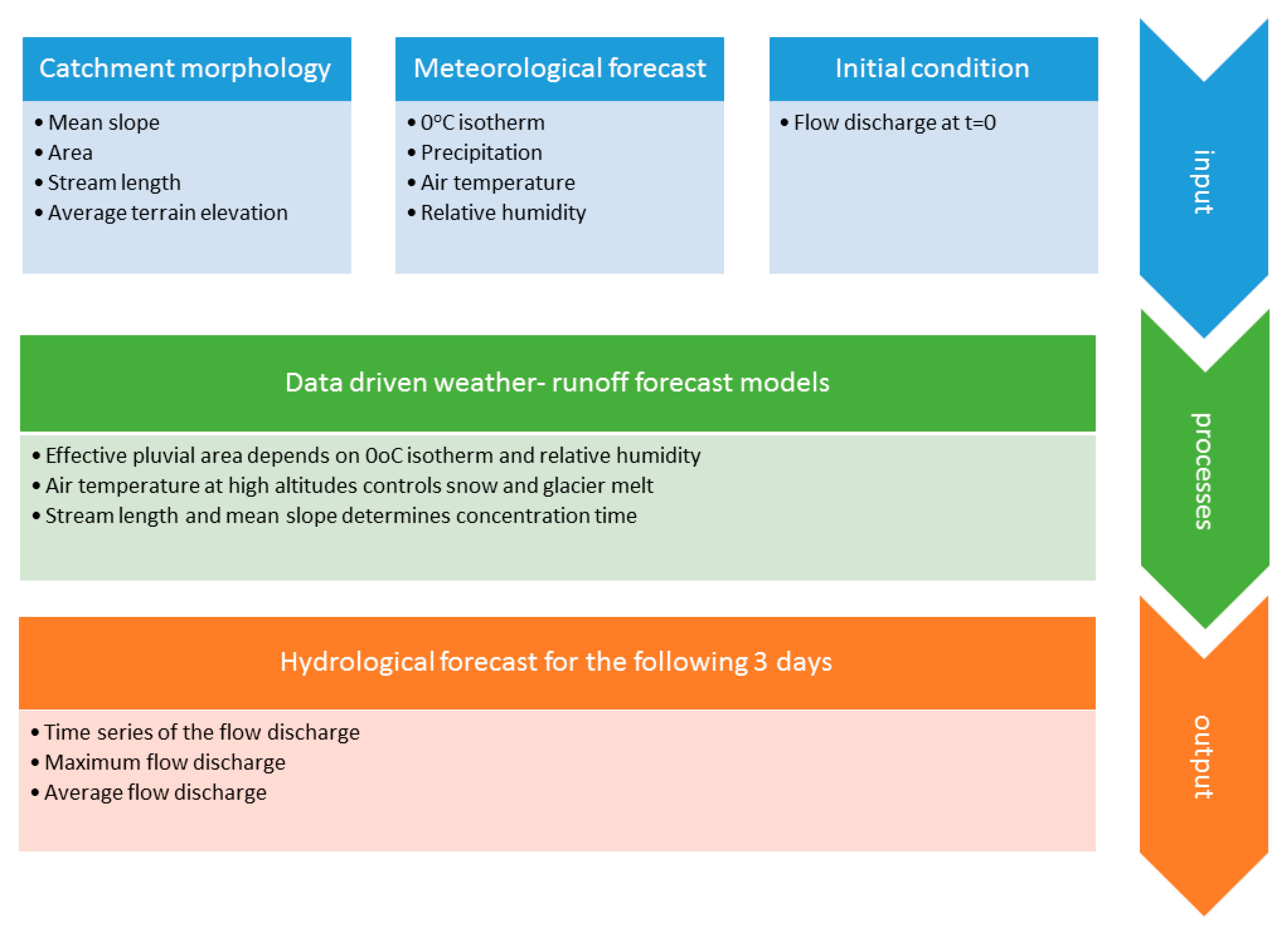
2.3. Coupled Model of a Meteorological Forecast with a Short-Range Runoff Forecast
2.3.1. Input Data
- Watershed geomorphology: The geomorphological characteristics were calculated from NASA Shuttle Radar Topography Mission (SRTM) version 3.0 global 1 arc second. For this aim, the watershed associated to each one of the flow stations was defined, and the information was summarized in one single table that list as a function of the elevation, the following information: Watershed area (km2); length of the mainstream (km); maximum, minimum and average elevation of the watershed; and the average slope. This table is read at each time to create time series of the geomorphological information as a function of the 0 °C isotherm elevation that splits the watershed into solid and liquid precipitation areas. Besides the watershed area, the time-series of the length of the mainstream, and the average slope and maximum elevation of the watershed were used as inputs of the data-driven weather-runoff models, as they are associated with the computation of the concentration time of the watershed [40]. The average elevation of the watershed was used to vertically interpolate the precipitation time-series from the GFS-NCEP meteorological model.
- Meteorological forecast: The weather forecast was obtained from a statistical scaling of gridded data of the GFS provided by NCEP, from which we obtained precipitation and air relative humidity at the average elevation of the watershed below the 0 °C isotherm, and air temperature at 2 m above the terrain in 3500 m a.s.l, and this reference terrain elevation was the same for all of the nine catchments. This last variable was chosen based on preliminary trial and error tests that showed that it gave better results in the representation of diurnal flow pulses during snow melt. We tested for other constant reference elevations (2000 and 4000 m a.s.l), and the results were not sensitive to this value. Furthermore, without good results, we also tested as reference temperature, the temperature at the average elevation of the catchment below the 0 °C isotherm that varies in time. We used the forecast datasets with a horizontal resolution of 0.5 × 0.5 degree, available from 2004 to present, and with a horizontal resolution of 0.25 × 0.25 degree, available from 2007 to present. Vertical scaling of the GFS information was made by linearly interpolating the meteorological variables as a function of the terrain elevation, using the GFS grid points located in a 0.5 degree of radius, regardless of the horizontal resolution of the GFS model, following the vertical scaling methodology described in [41]. Furthermore, each forecast starts with the weather forecast and is updated every 6 h, at 0:00, 6:00, 12:00 and 18:00 h UTC-time.
- Initial condition: The present flow conditions of all nine flow stations were obtained from real-time hour measurements of the General Direction of Water of the Chilean government; so that, the observed flow was used as an initial condition (t = 0).
2.3.2. Data-Driven Weather-Runoff Forecast Models
2.4. Evaluation Metrics for Model Skills
2.5. Structure of the Data-Driven Weather-Runoff Forecasts Models
3. Results
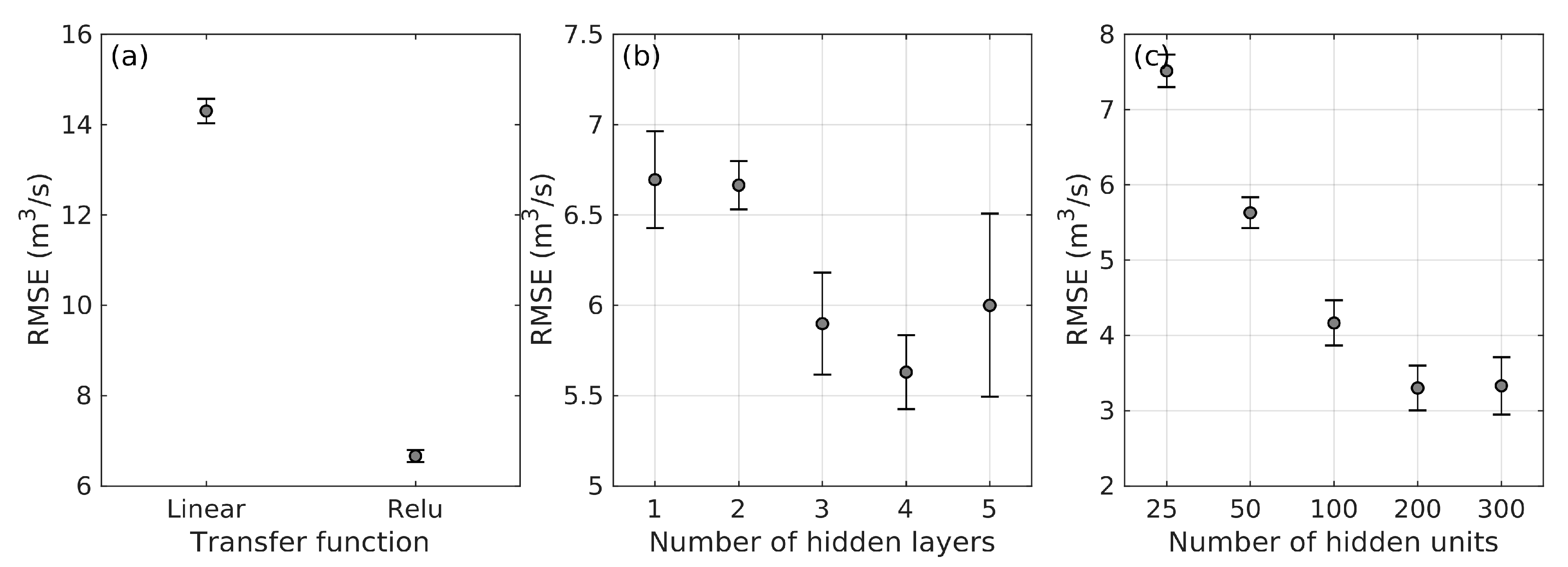
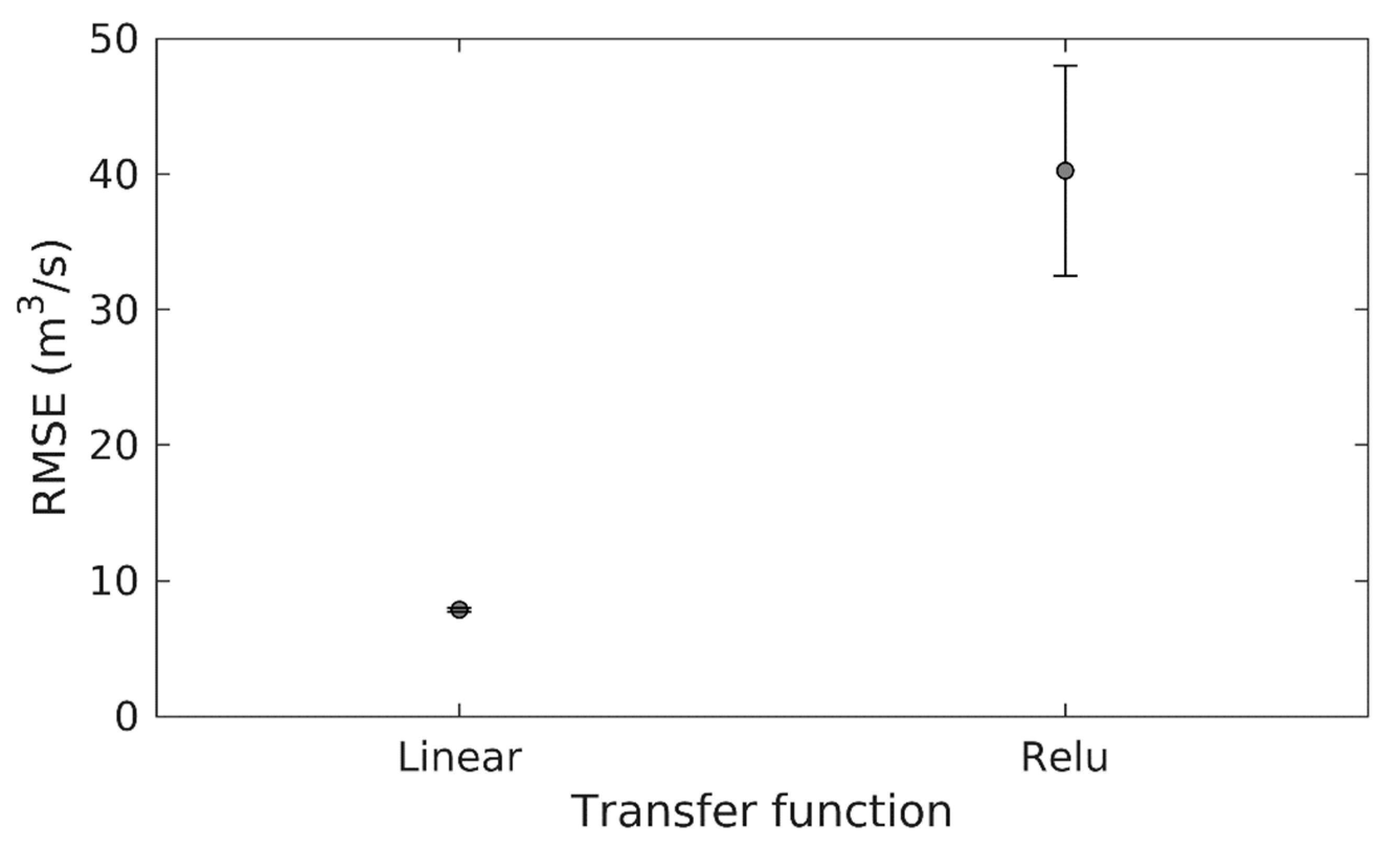
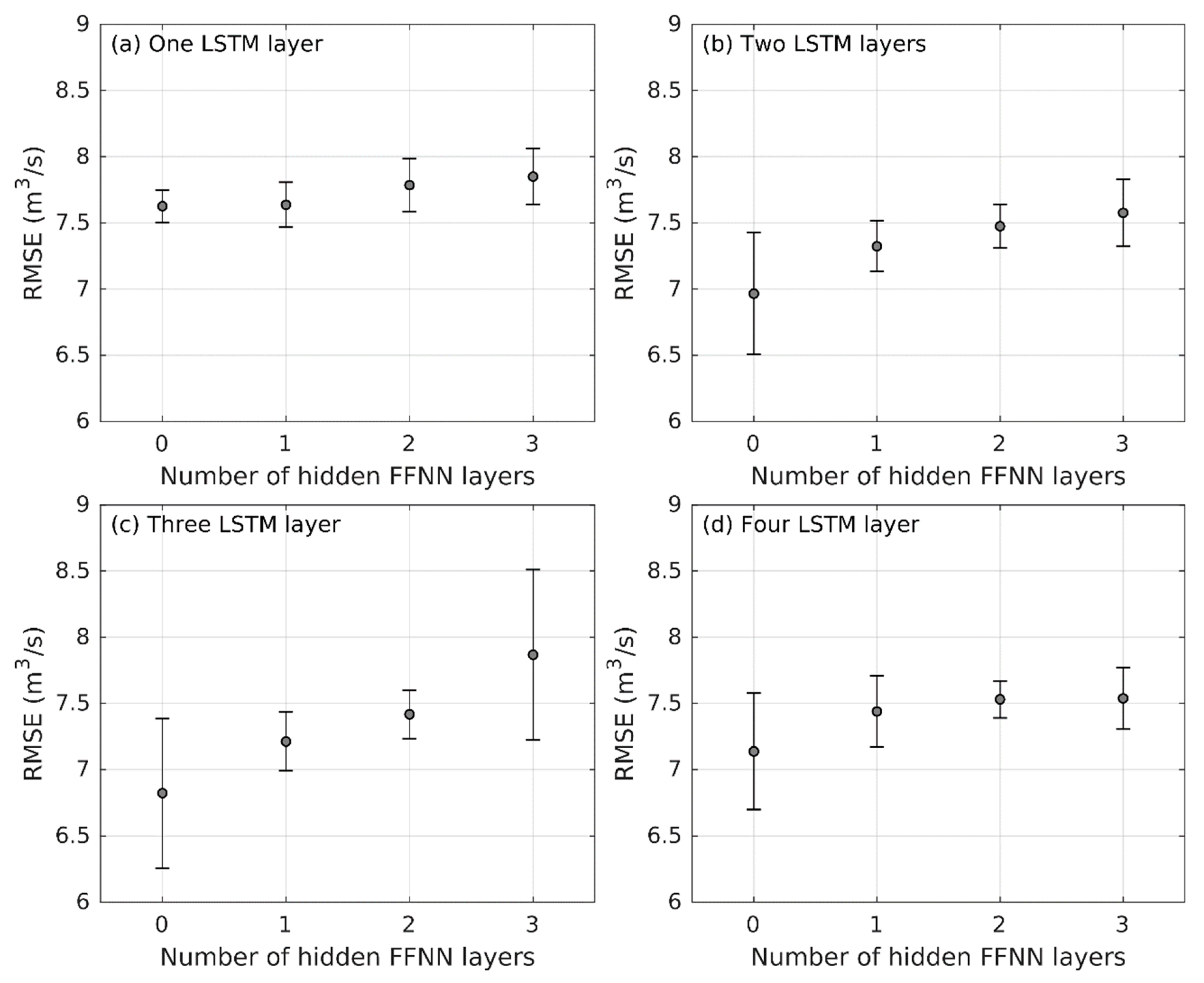
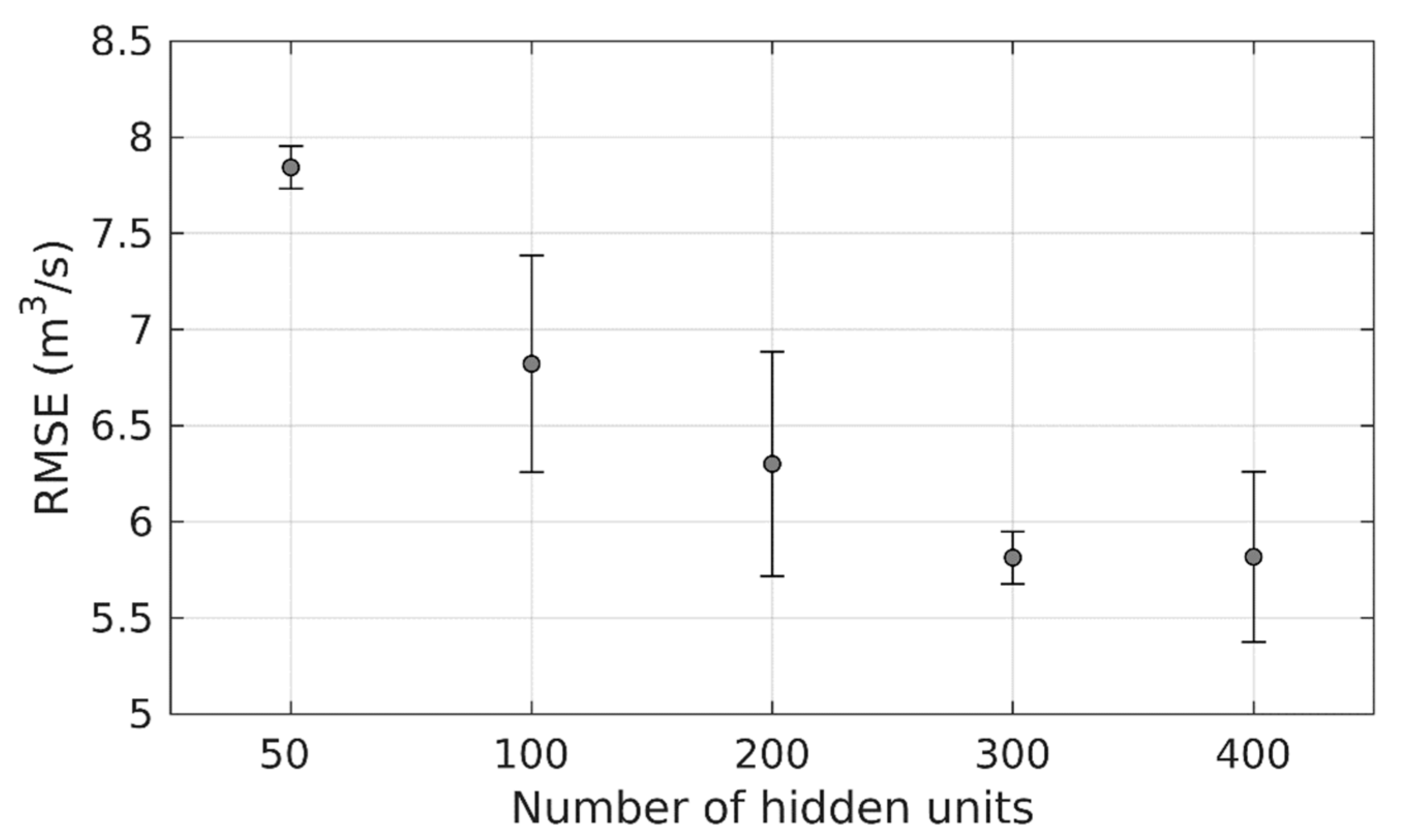
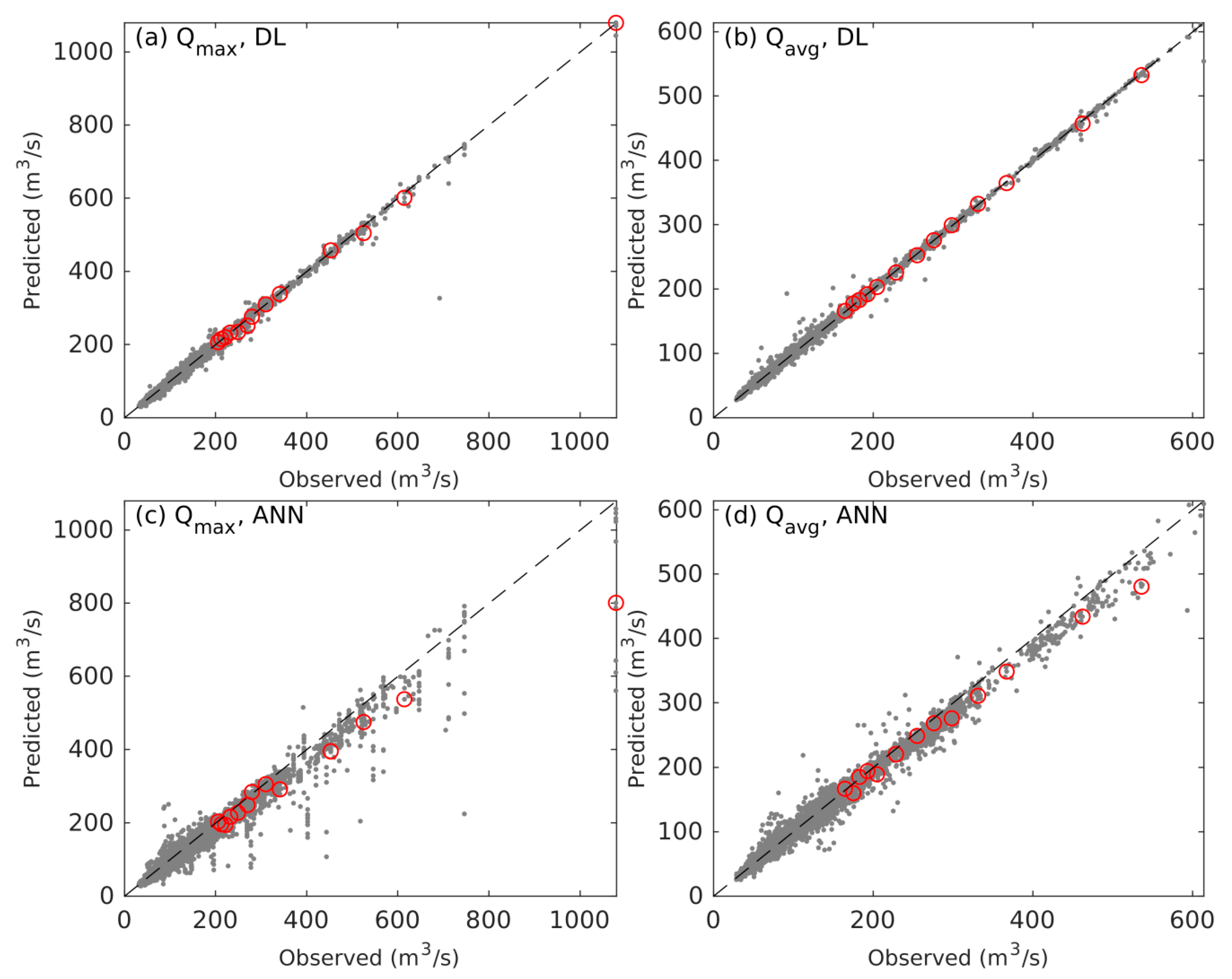
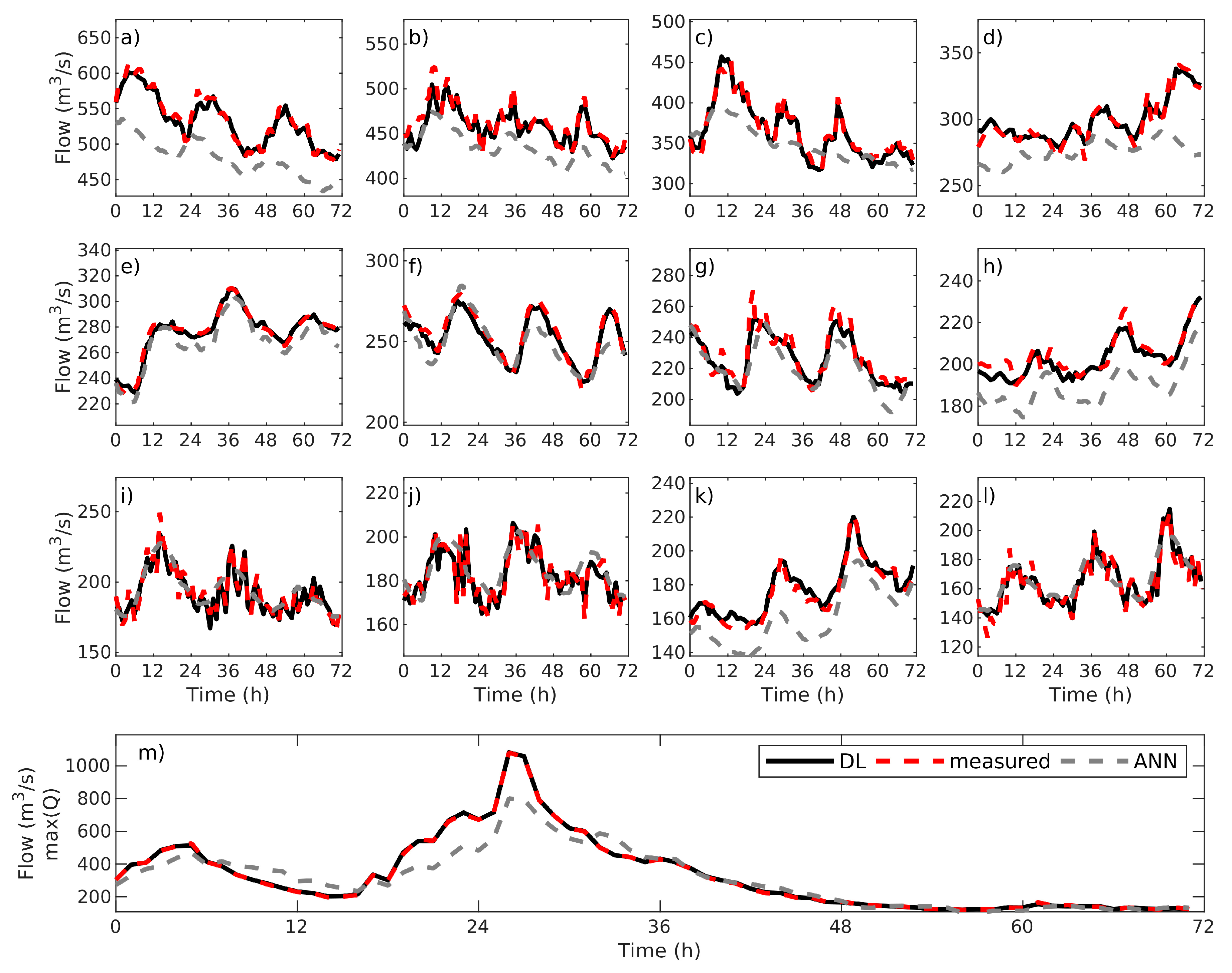
3.1. Performance of ANN versus DL Weather-Runoff Forecast Models
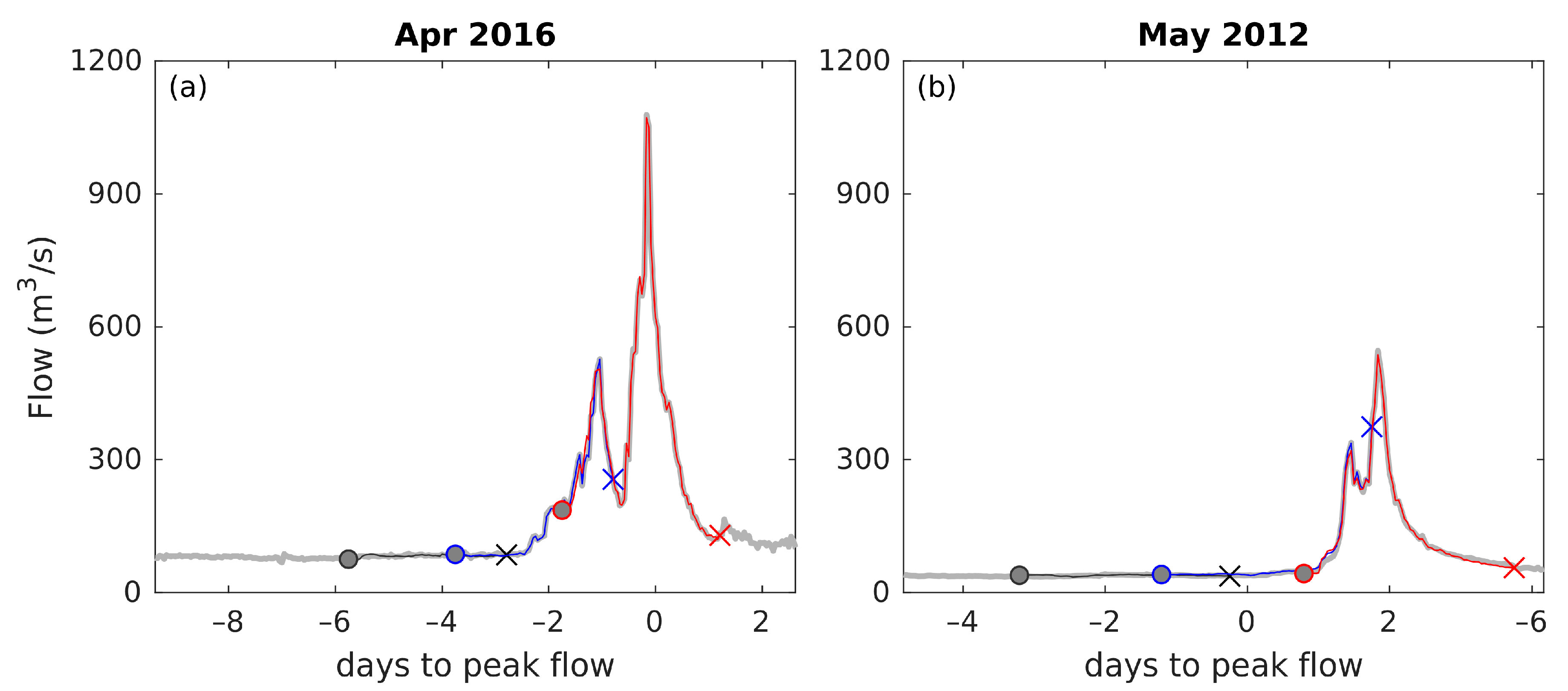
3.2. Performance of the Early Warning System
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
- -
- Online flow measurements: http://dgasatel.mop.cl/
- -
- GFS-NCEP meteorological analysis and forecast: https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs
- -
- NASA Shuttle Radar Topography Mission (SRTM) version 3.0: https://search.earthdata.nasa.gov/.
Acknowledgments
Conflicts of Interest
References
- Coumou, D.; Rahmstorf, S. A decade of weather extremes. Nat. Clim. Chang. 2012, 2, 491–496. [Google Scholar] [CrossRef]
- Alfieri, L.; Bisselink, B.; Dottori, F.; Naumann, G.; De Roo, A.; Salamon, P.; Wyser, K.; Feyen, L.; Roo, A. Global projections of river flood risk in a warmer world. Earth’s Futur. 2017, 5, 171–182. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- United Nations Office for Disaster Risk Reduction. Global Assessment Report on Disaster Risk Reduction; United Nations Office for Disaster Risk Reduction: Geneva, Switzerland, 2015; p. 2015. [Google Scholar]
- Srinivasulu, S.; Jain, A. Rainfall-Runoff Modelling: Integrating Available Data and Modern Techniques. Water Sci. Technol. Libr. 2008, 68, 59–70. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Tata McGraw−Hill Education: New York, NY, USA, 1988. [Google Scholar]
- Ay, M.; Özyıldırım, S. Artificial Intelligence (AI) Studies in Water Resources. Nat. Eng. Sci. 2018, 3, 187–195. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 1: Concepts and methodology. Hydrol. Earth Syst. Sci. 2010, 14, 1931–1941. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gupta, H.V.; Sorooshian, S. Artificial Neural Network Modeling of the Rainfall-Runoff Process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Toth, E. Data−Driven Streamflow Simulation: The Influence of Exogenous Variables and Temporal Resolution. In Practical Hydroinformatics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 113–125. [Google Scholar]
- Fischer, E.M.; Beyerle, U.; Knutti, R. Robust spatially aggregated projections of climate extremes. Nat. Clim. Chang. 2013, 3, 1033–1038. [Google Scholar] [CrossRef]
- Ganguly, A.R.; Kodra, E.A.; Banerjee, A.; Boriah, S.; Chatterjee, S.; Choudhary, A.; Das, D.; Faghmous, J.; Ganguli, P.; Ghosh, S.; et al. Toward enhanced understanding and projections of climate extremes using physics-guided data mining techniques. Nonlinear Process. Geophys. 2014, 21, 777–795. [Google Scholar] [CrossRef]
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water 2019, 11, 977. [Google Scholar] [CrossRef]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.W.; Mount, N.J.; See, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Prog. Phys. Geogr. Earth Environ. 2012, 36, 480–513. [Google Scholar] [CrossRef]
- Chen, L.; Ye, L.; Singh, V.; Zhou, J.; Guo, S. Determination of input for artificial neural networks for flood forecasting using the copula entropy method. J. Hydrol. Eng. 2013, 19, 04014021. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Sudheer, K.P. Comparison of methods used for quantifying prediction interval in artificial neural network hydrologic models. Model. Earth Syst. Environ. 2016, 2, 22. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Sudheer, K.P. Methods used for quantifying the prediction uncertainty of artificial neural network based hydrologic models. Stoch. Environ. Res. Risk Assess. 2017, 31, 1659–1670. [Google Scholar] [CrossRef]
- Nayak, P.; Sudheer, K.; Rangan, D.; Ramasastri, K. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Firat, M.; Güngör, M. Hydrological time-series modelling using an adaptive neuro-fuzzy inference system. Hydrol. Process. 2008, 22, 2122–2132. [Google Scholar] [CrossRef]
- Chang, T.K.; Talei, A.; Chua, L.H.C.; Alaghmand, S. The Impact of Training Data Sequence on the Performance of Neuro-Fuzzy Rainfall-Runoff Models with Online Learning. Water 2018, 11, 52. [Google Scholar] [CrossRef]
- Graves, A.; Liwicki, M.; Bunke, H.; Schmidhuber, J.; Fernández, S. Unconstrained On-Line Handwriting Recognition with Recurrent Neural Networks. In Advances in Neural Information Processing Systems 20 (NIPS 2007); Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2008; pp. 577–584. [Google Scholar]
- Graves, A.; Schmidhuber, J. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. In Advances in Neural Information Processing Systems 221 (NIPS 2008); Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2009; pp. 545–552. [Google Scholar]
- Graves, A.; Mohamed, A.R.; Hinton, G.; Graves, A. Speech Recognition with Deep Recurrent Neural Networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Gers, F.A.; Eck, D.; Schmidhuber, J. Applying LSTM to Time Series Predictable through Time-Window Approaches. In Neural Nets WIRN Vietri-01; Springer: London, UK, 2002; pp. 193–200. [Google Scholar]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to Spatiotemporally Seamless Coverage of Continental U.S. Using a Deep Learning Neural Network. Geophys. Res. Lett. 2017, 44, 11030–11039. [Google Scholar] [CrossRef]
- Mayer, H.; Gomez, F.; Wierstra, D.; Nagy, I.; Knoll, A.; Schmidhuber, J. A System for Robotic Heart Surgery that Learns to Tie Knots Using Recurrent Neural Networks. Adv. Robot. 2008, 22, 1521–1537. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.J.; Ganguly, S.; Hsu, K.L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating deep−learning−powered hydrologic science advances as a community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.P.; Yang, Z.; Wang, G.; Zhu, Q. Integration of a Parsimonious Hydrological Model with Recurrent Neural Networks for Improved Streamflow Forecasting. Water 2018, 10, 1655. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short−term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Brenning, A. Geomorphological, hydrological and climatic significance of rock glaciers in the Andes of Central Chile (33–35° S). Permafr. Periglac. Process. 2005, 16, 231–240. [Google Scholar] [CrossRef]
- Rutllant, J.; Fuenzalida, H. Synoptic aspects of the central chile rainfall variability associated with the southern oscillation. Int. J. Clim. 2007, 11, 63–76. [Google Scholar] [CrossRef]
- Degré, A.; Beckers, E.; Becquervort, S. Applied Hydrology; Tata McGraw−Hill Education: New York, NY, USA, 2013. [Google Scholar]
- De La Fuente, A.; Meruane, C. Spectral model for long-term computation of thermodynamics and potential evaporation in shallow wetlands. Water Resour. Res. 2017, 53, 7696–7715. [Google Scholar] [CrossRef]
- DeWalle, D.R.; Rango, A. Principles of Snow Hydrology; Cambridge University Press: London, UK, 2008. [Google Scholar]
- Chang, T.K.; Talei, A.; Quek, C.; Pauwels, V.R. Rainfall-runoff modelling using a self-reliant fuzzy inference network with flexible structure. J. Hydrol. 2018, 564, 1179–1193. [Google Scholar] [CrossRef]
| River | ID | Flow Station Name | Area (km2) | Zmin (m a.s.l) | Zmax (m a.s.l) | Zavg (m a.s.l) | Slope (%) | Stream Length (km) | Glacier Area (km2) | % Glacier in Watershed | First Data |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Maipo River | 1 | Maipo en El Manzano | 4839 | 882 | 6550 | 3180 | 63.8 | 118.7 | 370.7 | 7.7 | March 2004 |
| 2 | Río Volcan en Queltehues | 523 | 1353 | 5967 | 3364 | 64.6 | 41.3 | 63.8 | 12.2 | March 2014 | |
| 3 | Río Olivares antes Junta Río Colorado | 783 | 1525 | 6500 | 3364 | 68.7 | 48.7 | 94.1 | 12.0 | March 2013 | |
| 4 | Río Colorado antes Junta Río Olivares | 543 | 2369 | 6047 | 3689 | 67.6 | 29.5 | 81.2 | 15.0 | August 2008 | |
| Mapocho River | 5 | Mapocho Los Almendros | 637 | 968 | 5417 | 2778 | 56.8 | 39.5 | 20.1 | 3.2 | April 2016 |
| 6 | Estero Arrayán Montosa | 217 | 1227 | 3829 | 2509 | 53.1 | 24.8 | 0.3 | 0.1 | March 2004 | |
| 7 | Río Molina antes Junta San Francisco | 300 | 1335 | 5417 | 2647 | 50.9 | 25.5 | 5.3 | 1.8 | January 2012 | |
| 8 | Estero Yerba Loca antes Junta San Francisco’ | 109 | 1630 | 5350 | 3416 | 68.2 | 18.1 | 8.9 | 8.1 | January 2012 | |
| 9 | Río San Francisco antes Junta Estero Yerba Loca | 136 | 1586 | 4853 | 3126 | 60.6 | 23.0 | 6.0 | 4.4 | January 2012 |
| River | ID | Subset | Number of Data Block | Flow (m3/s) | ||||
|---|---|---|---|---|---|---|---|---|
| Max | Average | Min | Percentile (90%) | Percentile (99%) | ||||
| Maipo River | 1 | Train | 74,780 | 1078.6 | 121.1 | 32.8 | 209.6 | 517.8 |
| Validation | 21,366 | 1078.6 | 119.8 | 33.6 | 207.5 | 459.3 | ||
| Test | 10,683 | 1078.6 | 124.6 | 33.6 | 222.1 | 525.0 | ||
| 2 | Train | 72,282 | 61.6 | 9.1 | 0.1 | 22.8 | 48.1 | |
| Validation | 20,652 | 61.6 | 9.6 | 0.1 | 24.5 | 50.2 | ||
| Test | 10,326 | 61.6 | 9.2 | 0.1 | 23.1 | 49.9 | ||
| 3 | Train | 68,258 | 124.1 | 9.7 | 0.4 | 25.9 | 75.2 | |
| Validation | 19,502 | 88.5 | 9.7 | 0.4 | 27.2 | 74.3 | ||
| Test | 9751 | 124.1 | 10.2 | 0.4 | 26.7 | 75.2 | ||
| 4 | Train | 76,946 | 165.0 | 7.6 | 0.4 | 27.1 | 56.2 | |
| Validation | 21,985 | 165.0 | 7.9 | 0.4 | 27.5 | 58.6 | ||
| Test | 10,992 | 165.0 | 8.1 | 0.4 | 28.6 | 58.6 | ||
| Mapocho River | 5 | Train | 66,317 | 26.8 | 1.5 | 0.1 | 2.7 | 9.3 |
| Validation | 18,948 | 26.8 | 1.4 | 0.1 | 2.6 | 7.6 | ||
| Test | 9474 | 26.8 | 1.5 | 0.1 | 2.6 | 8.1 | ||
| 6 | Train | 39,768 | 20.4 | 1.5 | 0.1 | 2.6 | 12.9 | |
| Validation | 11,362 | 20.4 | 1.6 | 0.4 | 3.0 | 11.3 | ||
| Test | 5681 | 20.4 | 1.5 | 0.3 | 2.7 | 12.8 | ||
| 7 | Train | 48,610 | 256.6 | 4.3 | 0.4 | 7.8 | 27.3 | |
| Validation | 13,889 | 256.6 | 4.2 | 0.4 | 7.8 | 29.3 | ||
| Test | 6944 | 256.6 | 4.2 | 0.4 | 7.4 | 28.9 | ||
| 8 | Train | 78,629 | 8.5 | 1.2 | 0.1 | 2.8 | 5.9 | |
| Validation | 22,465 | 8.5 | 1.2 | 0.1 | 2.8 | 5.5 | ||
| Test | 11,233 | 8.5 | 1.2 | 0.1 | 2.7 | 5.5 | ||
| 9 | Train | 41,520 | 3.3 | 0.3 | 0.1 | 0.5 | 2.5 | |
| Validation | 11,863 | 3.1 | 0.3 | 0.1 | 0.5 | 2.1 | ||
| Test | 5931 | 3.3 | 0.3 | 0.1 | 0.5 | 2.6 | ||
| Parameters and Functions | Value |
|---|---|
| Transfer function | Linear/Relu |
| Number of hidden layers | 1–5 |
| Number of hidden neurons | 25–400 |
| Parameters and Functions | Value |
|---|---|
| Transfer function (FFNN) | Linear/Relu |
| Number of LSTM layers | 1–4 |
| Number of hidden FFNN layers | 0–3 |
| Number of neurons in the LSTM layers | 50–400 |
| Number of neurons in the FFNN layers | 50–400 |
| River | ID | Variable | DL Model | ANN Model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| % Glacier in Watershed | |||||||||||
| Maipo | 1 | 0.049 | 0.996 | 5.829 | 0.998 | 0.155 | 0.955 | 18.344 | 0.982 | 7.7 | |
| 0.028 | 0.998 | 2.705 | 0.999 | 0.074 | 0.988 | 7.199 | 0.995 | ||||
| 2 | 0.146 | 0.983 | 1.285 | 0.992 | 0.255 | 0.949 | 2.248 | 0.977 | 12.2 | ||
| 0.206 | 0.973 | 0.485 | 0.987 | 0.582 | 0.784 | 1.370 | 0.885 | ||||
| 3 | 0.143 | 0.990 | 1.326 | 0.995 | 0.583 | 0.840 | 5.412 | 0.939 | 12.0 | ||
| 0.109 | 0.993 | 0.629 | 0.997 | 0.180 | 0.980 | 1.037 | 0.994 | ||||
| 4 | 0.214 | 0.986 | 1.519 | 0.993 | 0.823 | 0.799 | 5.836 | 0.919 | 15.0 | ||
| 0.103 | 0.993 | 0.484 | 0.996 | 0.229 | 0.964 | 1.076 | 0.983 | ||||
| Mapocho | 5 | 0.082 | 0.995 | 0.115 | 0.998 | 0.261 | 0.952 | 0.366 | 0.977 | 3.2 | |
| 0.072 | 0.992 | 0.082 | 0.996 | 0.127 | 0.974 | 0.144 | 0.988 | ||||
| 6 | 0.097 | 0.994 | 0.142 | 0.997 | 0.319 | 0.932 | 0.464 | 0.968 | 0.1 | ||
| 0.055 | 0.995 | 0.062 | 0.998 | 0.105 | 0.983 | 0.118 | 0.992 | ||||
| 7 | 0.355 | 0.984 | 1.385 | 0.992 | 1.279 | 0.797 | 4.991 | 0.895 | 1.8 | ||
| 0.055 | 0.998 | 0.012 | 0.999 | 0.144 | 0.986 | 0.032 | 0.993 | ||||
| 8 | 0.075 | 0.994 | 0.086 | 0.997 | 0.199 | 0.958 | 0.229 | 0.981 | 8.1 | ||
| 0.048 | 0.997 | 0.043 | 0.999 | 0.119 | 0.983 | 0.107 | 0.993 | ||||
| 9 | 0.093 | 0.996 | 0.026 | 0.998 | 0.277 | 0.964 | 0.077 | 0.982 | 4.4 | ||
| 0.147 | 0.994 | 0.348 | 0.997 | 0.529 | 0.921 | 1.250 | 0.960 | ||||
| April 2016 | May 2012 | ||||||
|---|---|---|---|---|---|---|---|
| Starting Time of Simulation | Qmax | EQp | ETp | Starting Time of Simulation | Qmax | EQp | ETp |
| (m3/s) | (%) | (h) | (m3/s) | (%) | (h) | ||
| −3 days 15 h | 527.1 | 0.1 | 0 | −3 days 2 h | 386.2 | 3.1 | 0 |
| −3 days 3 h | 705.1 | −0.5 | 0 | −2 days 14 h | 546.1 | 0.6 | 0 |
| −2 days 15 h | 1078.6 | 0.5 | 0 | −2 days 2 h | 546.1 | 0.5 | 0 |
| −2 days 3 h | 1078.6 | 0.6 | 0 | −1 day 14 h | 546.1 | 0.5 | 0 |
| −1 day 15 h | 1078.6 | 0.6 | 0 | −1 day 2 h | 546.1 | 1.7 | 0 |
| −1 day 3 h | 1078.6 | −0.1 | 0 | 0 day 14 h | 546.1 | −0.3 | 0 |
| 0 day 15 h | 1078.6 | 0.4 | 0 | 0 day 2 h | 546.1 | 13.2 | 0 |
| 0 day 3 h | 1078.6 | 3.2 | 0 | 0 day 1 h | 144.4 | 5.4 | 0 |
| 0 day 9 h | 429.1 | −1.0 | 0 | 0 day 1 h | 88.3 | 2.0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de la Fuente, A.; Meruane, V.; Meruane, C. Hydrological Early Warning System Based on a Deep Learning Runoff Model Coupled with a Meteorological Forecast. Water 2019, 11, 1808. https://doi.org/10.3390/w11091808
de la Fuente A, Meruane V, Meruane C. Hydrological Early Warning System Based on a Deep Learning Runoff Model Coupled with a Meteorological Forecast. Water. 2019; 11(9):1808. https://doi.org/10.3390/w11091808
Chicago/Turabian Stylede la Fuente, Alberto, Viviana Meruane, and Carolina Meruane. 2019. "Hydrological Early Warning System Based on a Deep Learning Runoff Model Coupled with a Meteorological Forecast" Water 11, no. 9: 1808. https://doi.org/10.3390/w11091808
APA Stylede la Fuente, A., Meruane, V., & Meruane, C. (2019). Hydrological Early Warning System Based on a Deep Learning Runoff Model Coupled with a Meteorological Forecast. Water, 11(9), 1808. https://doi.org/10.3390/w11091808






