Validation of the 3D-MOHID Hydrodynamic Model for the Tagus Coastal Area
Abstract
1. Introduction
2. Materials and Methods
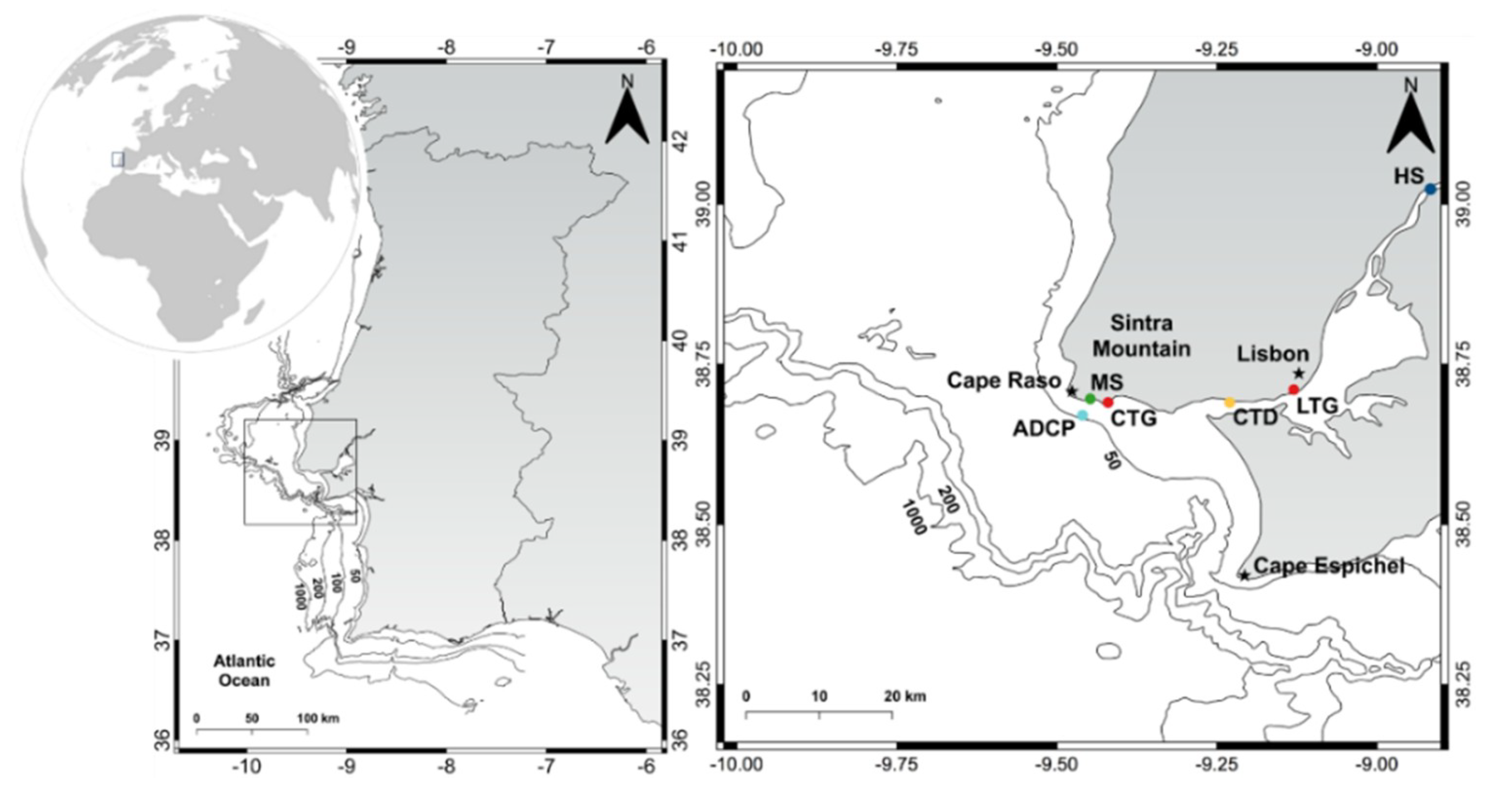
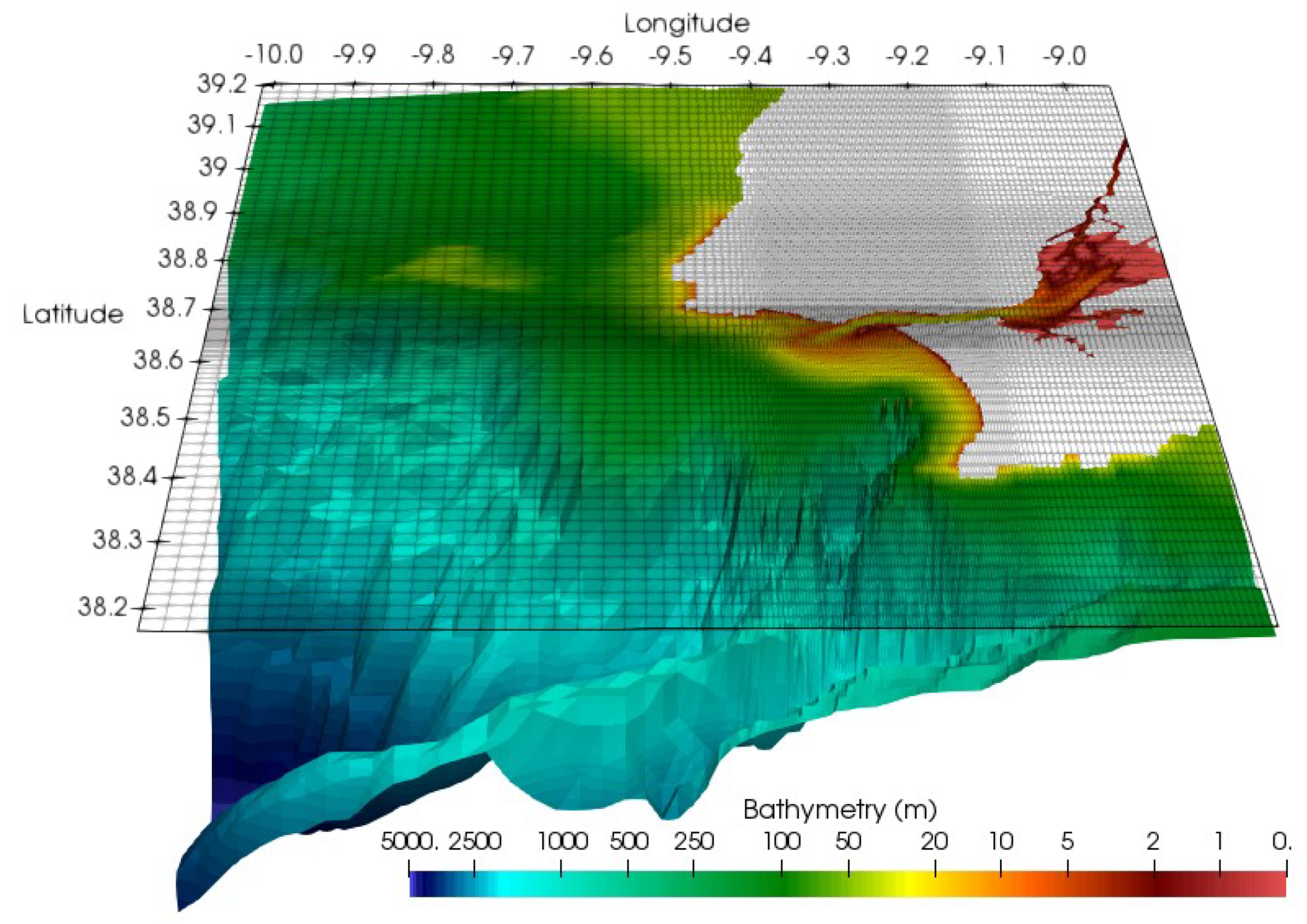
2.1. Study Area
2.2. Model
2.3. Available Observations Data
2.3.1. Water Level
2.3.2. Seawater Temperature and Salinity
2.3.3. Current Velocity
2.3.4. Seawater Temperature Based on Satellite Images
2.4. Statistics
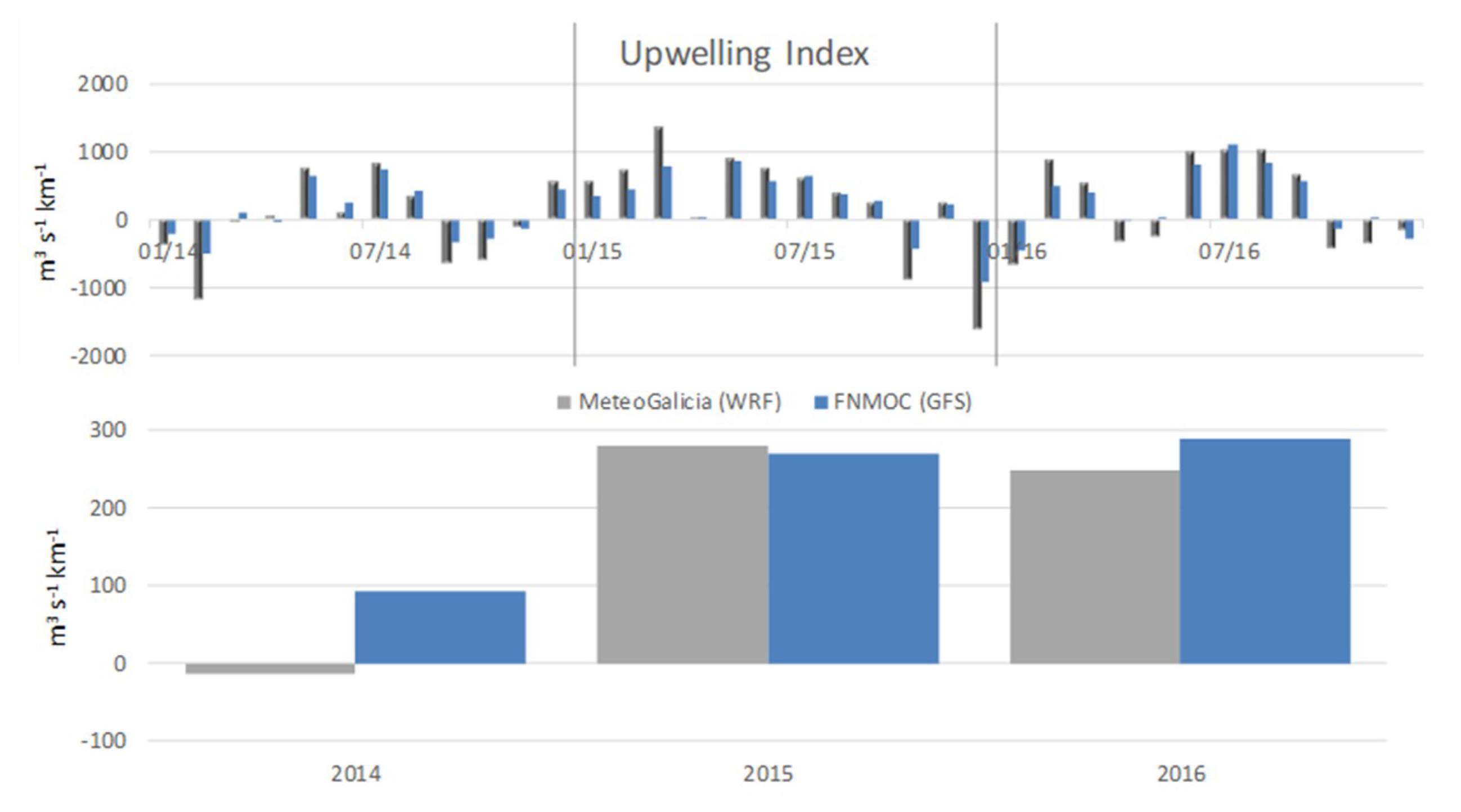
3. Results and Discussion
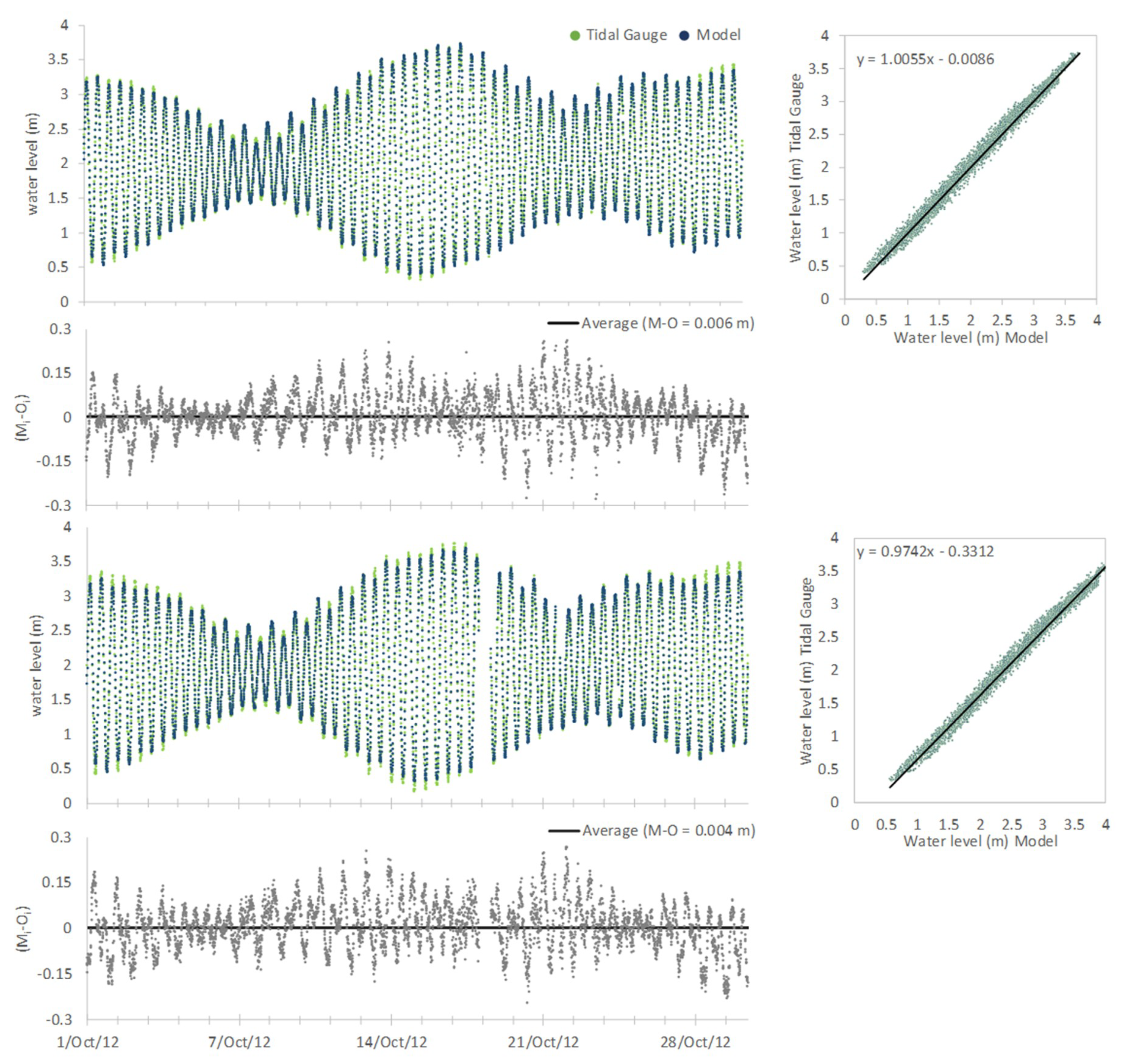
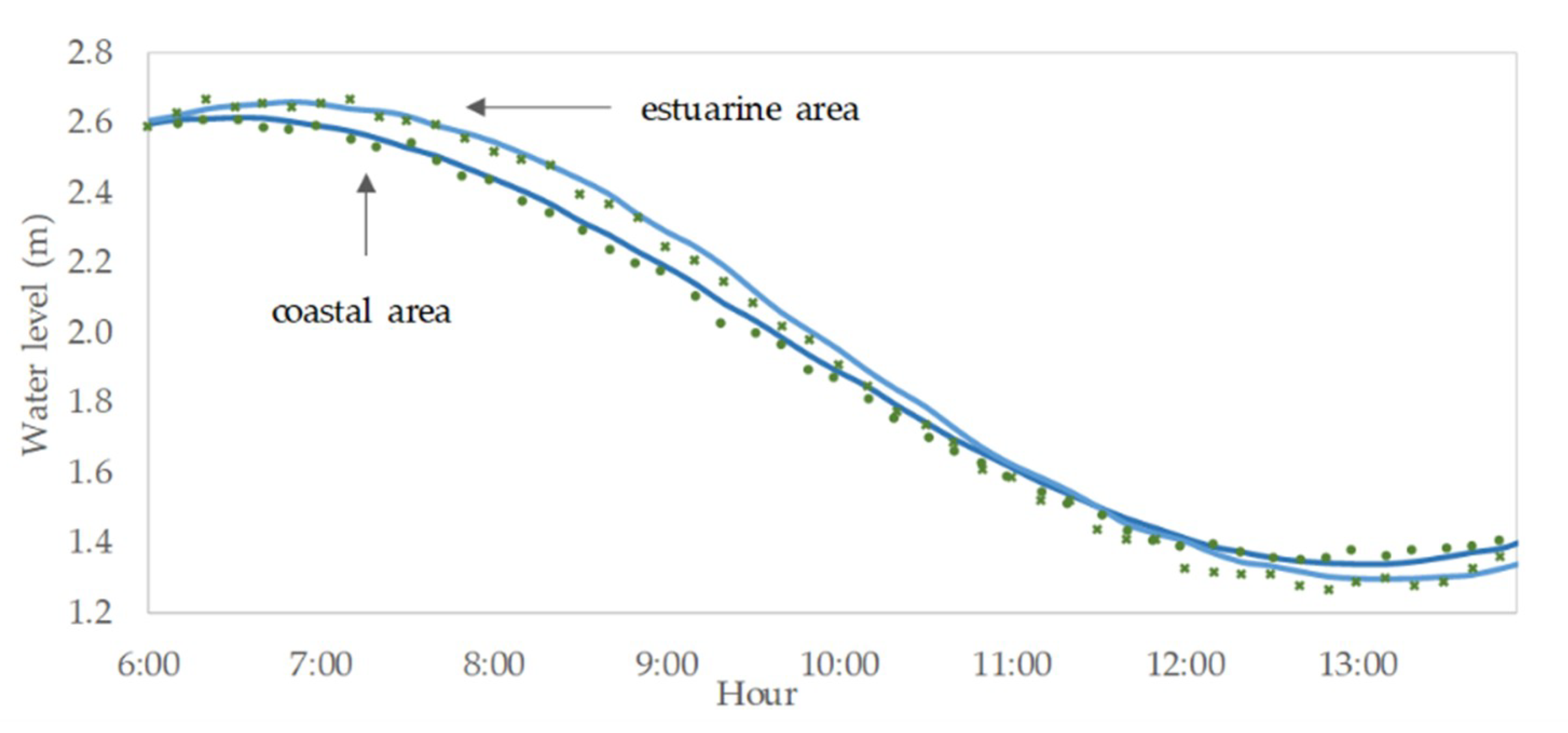
3.1. Water Level–Time Series Data
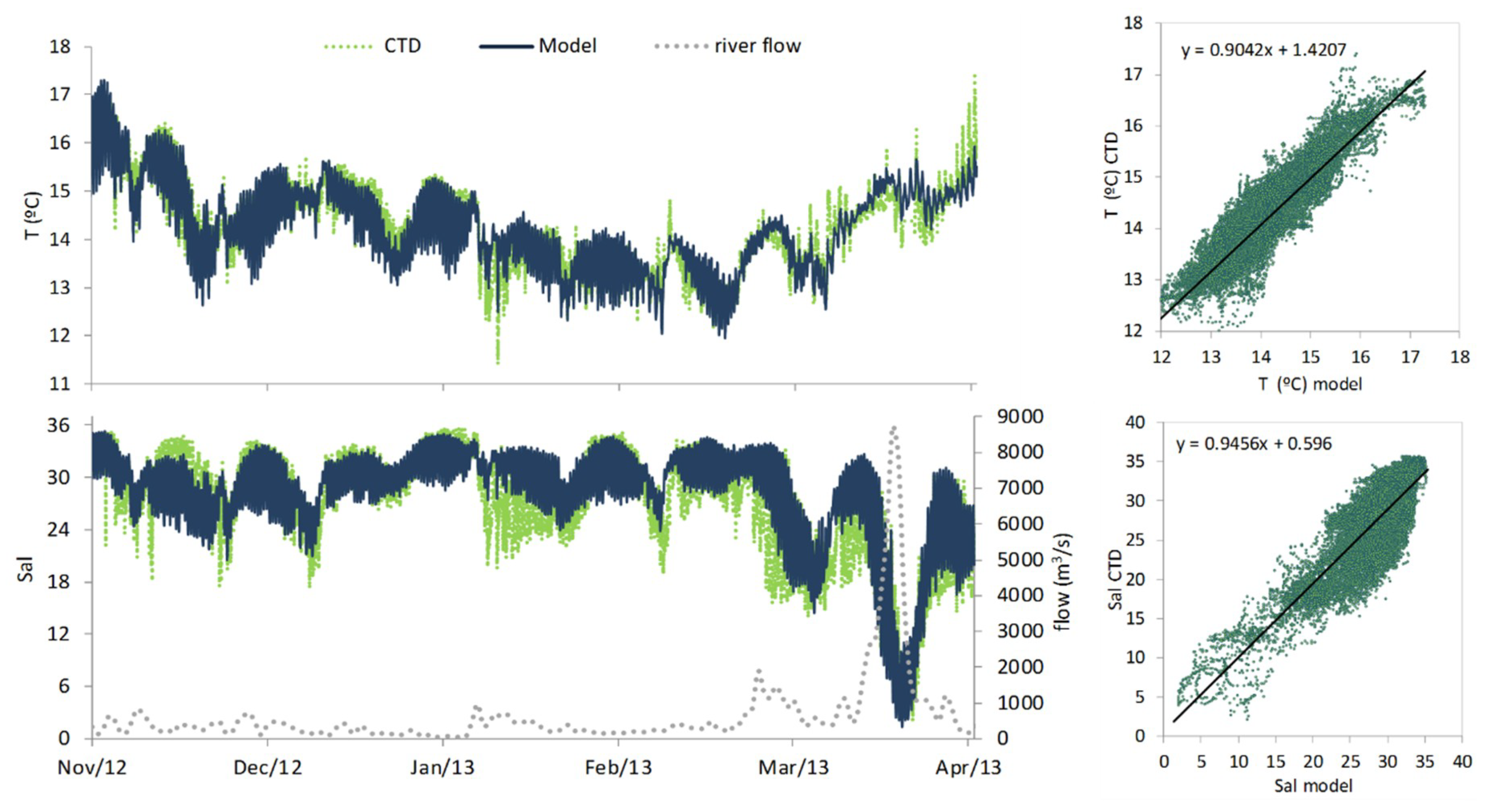
3.2. Seawater Temperature and Salinity–Time Series Data
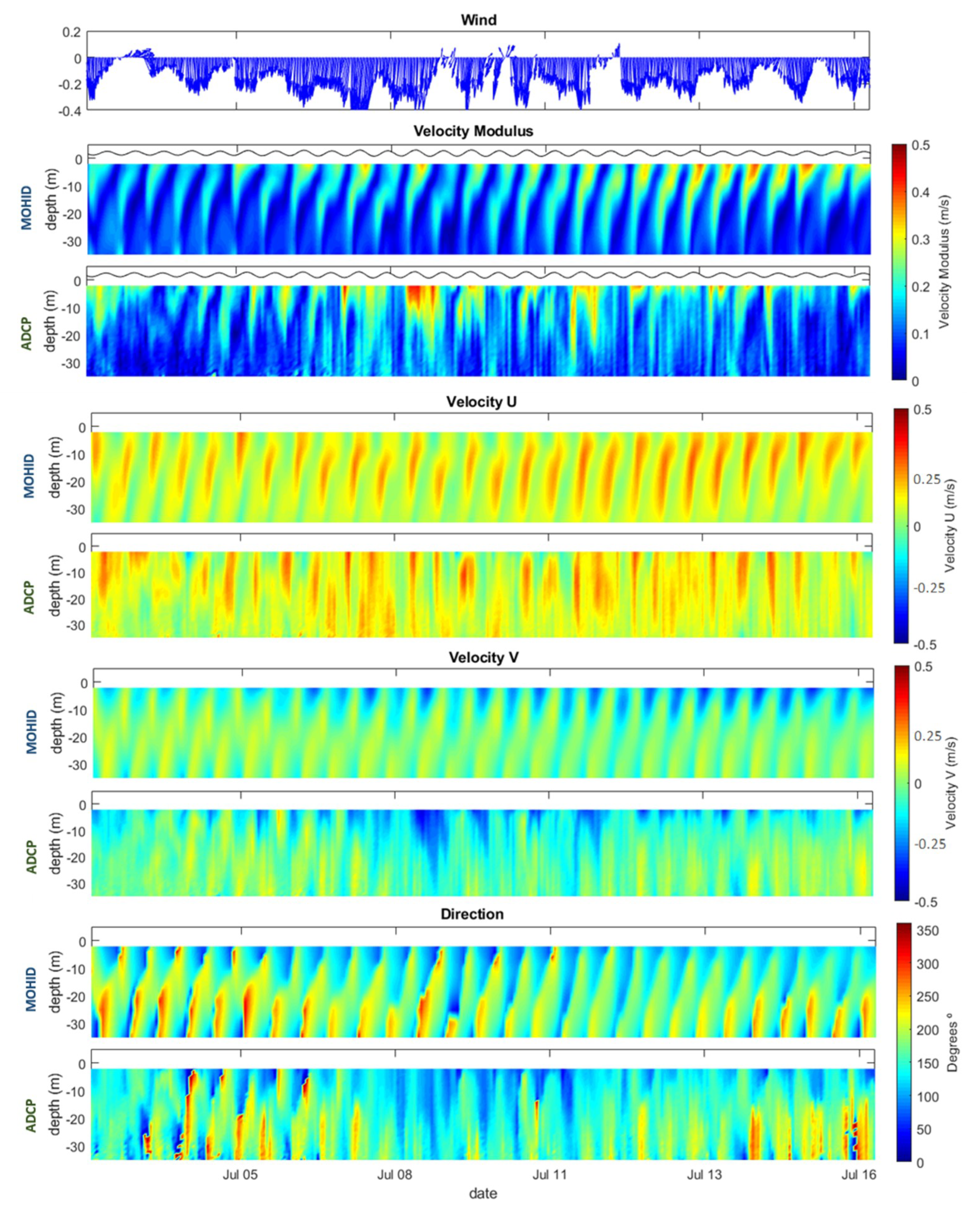
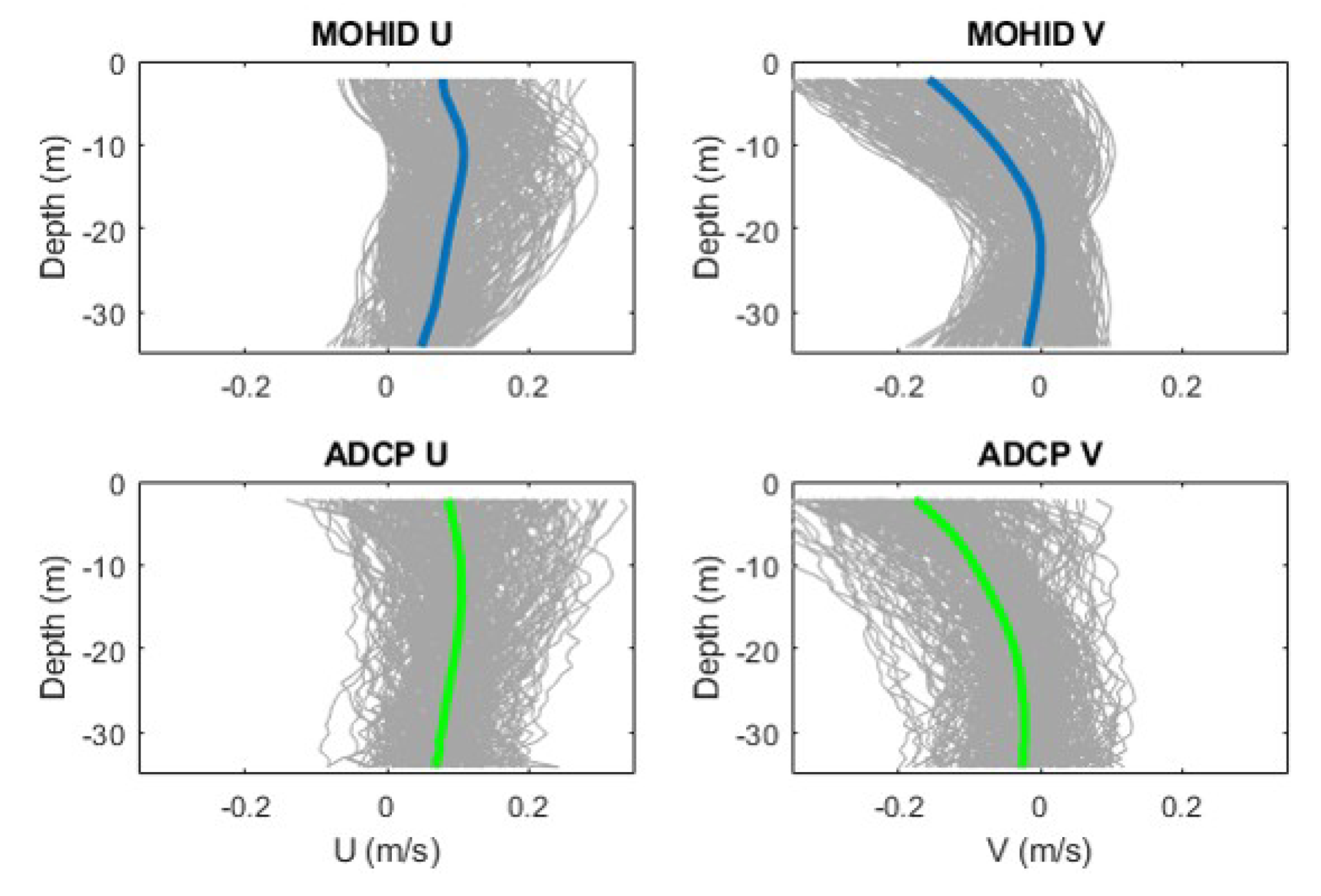
3.3. Currents–ADCP Analysis
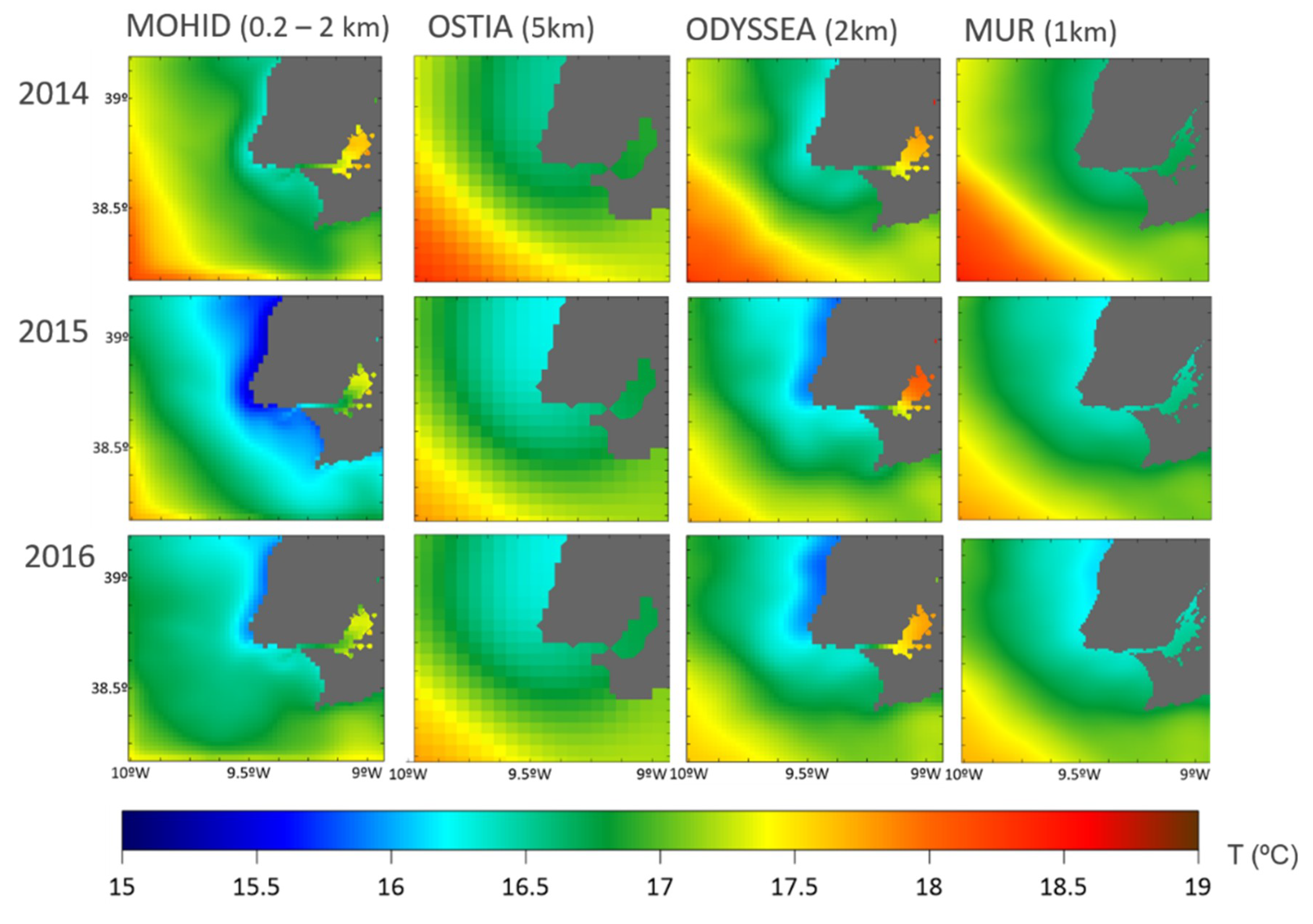
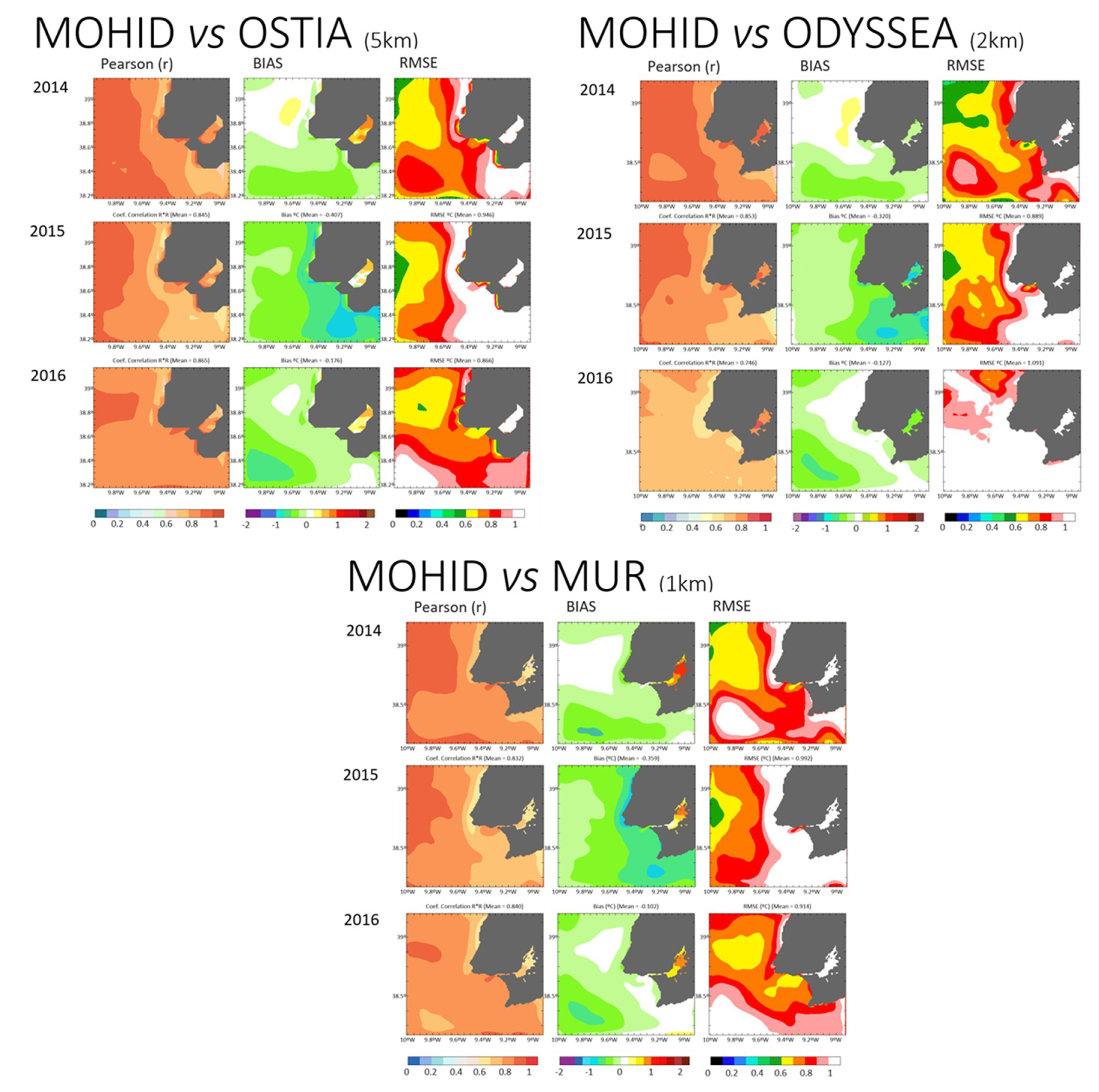
3.4. Seawater Temperature–Validation with Satellite
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lakhan, V.C.; Trenhaile, A.S. Models and the Coastal System. In Elsevier Oceanography Series; Lakhan, A.S., Trenhaile, V.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; Volume 49, pp. 1–16. [Google Scholar]
- Murthy, C.R.; Sinha, P.C.; Rao, Y.R. Modelling and monitoring of coastal marine processes. In Modelling and Monitoring of Coastal Marine Processes; Capital Publishing Company: New Delhi, India, 2008; pp. 1–246. [Google Scholar]
- Iglesias, I.; Avilez-Valente, P.; Luís Pinho, J.; Bio, A.; Manuel Vieira, J.; Bastos, L.; Veloso-Gomes, F. Numerical Modeling Tools Applied to Estuarine and Coastal Hydrodynamics: A User Perspective. In Coastal and Marine Environments—Physical Processes and Numerical Modelling; Intechopen: London, UK, 2019; p. 20. [Google Scholar]
- Petihakis, G.; Triantafyllou, G.; Korres, G.; Tsiaras, K.; Theodorou, A. Ecosystem modelling: Towards the development of a management tool for a marine coastal system part-II, ecosystem processes and biogeochemical fluxes. J. Mar. Syst. 2012, 94, S49–S64. [Google Scholar] [CrossRef]
- Lazure, P.; Garnier, V.; Dumas, F.; Herry, C.; Chifflet, M. Development of a hydrodynamic model of the Bay of Biscay. Validation of hydrology. Cont. Shelf Res. 2009, 29, 985–997. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. On validating numerical hydrodynamic models of complex tidal flow. Int. J. Mar. Energy 2013, 3, e82–e97. [Google Scholar] [CrossRef]
- Guerreiro, M.; Fortunato, A.B.; Freire, P.; Rilo, A.; Taborda, R.; Freitas, M.C.; Andrade, C.; Silva, T.; Rodrigues, M.; Bertin, X.; et al. Evolution of the hydrodynamics of the Tagus estuary (Portugal) in the 21st century. Revista de Gestão Costeira Integrada-Journal of Integrated Coastal Zone Management 2014, 15, 65–80. [Google Scholar] [CrossRef]
- Cucco, A.; Quattrocchi, G.; Olita, A.; Fazioli, L.; Ribotti, A.; Sinerchia, M.; Tedesco, C.; Sorgente, R. Hydrodynamic modelling of coastal seas: The role of tidal dynamics in the Messina Strait, Western Mediterranean Sea. Nat. Hazards Earth Syst. Sci. 2016, 16, 1553–1569. [Google Scholar] [CrossRef]
- Gaeta, M.G.; Samaras, A.G.; Federico, I.; Archetti, R.; Maicu, F.; Lorenzetti, G. A coupled wave-3-D hydrodynamics model of the Taranto Sea (Italy): A multiple-nesting approach. Nat. Hazards Earth Syst. Sci. 2016, 16, 2071–2083. [Google Scholar] [CrossRef]
- Sedigh, M.; Tomlinson, R.; Cartwright, N.; Etemad-Shahidi, A. Numerical modelling of the Gold Coast Seaway area hydrodynamics and littoral drift. Ocean Eng. 2016, 121, 47–61. [Google Scholar] [CrossRef]
- Wild-allen, K.; Andrewartha, J. Connectivity between estuaries in fl uences nutrient transport, cycling and water quality. Mar. Chem. 2016, 185, 12–26. [Google Scholar] [CrossRef]
- Yin, Y.; Karunarathna, H.; Reeve, D.E. Numerical modelling of hydrodynamic and morphodynamic response of a meso-tidal estuary inlet to the impacts of global climate variabilities. Mar. Geol. 2019, 407, 229–247. [Google Scholar] [CrossRef]
- Garneau, C.; Duchesne, S.; St-Hilaire, A. Comparison of modelling approaches to estimate trapping efficiency of sedimentation basins on peatlands used for peat extraction. Ecol. Eng. 2019, 133, 60–68. [Google Scholar] [CrossRef]
- Restrepo, J.C.; Escobar, J.; Otero, L.; Franco, D.; Pierini, J.; Correa, I. Factors Influencing the Distribution and Characteristics of Surface Sediment in the Bay of Cartagena, Colombia. J. Coast. Res. 2016, 331, 135–148. [Google Scholar] [CrossRef]
- Ospino, S.; Restrepo, J.C.; Otero, L.; Pierini, J.; Alvarez-Silva, O. Saltwater Intrusion into a River with High Fluvial Discharge: A Microtidal Estuary of the Magdalena River, Colombia. J. Coast. Res. 2018, 34, 1273–1288. [Google Scholar] [CrossRef]
- Franz, G.A.S.; Leitão, P.; dos Santos, A.; Juliano, M.; Neves, R. From regional to local scale modelling on the south-eastern Brazilian shelf: Case study of Paranaguá estuarine system. Braz. J. Oceanogr. 2016, 64, 277–294. [Google Scholar] [CrossRef]
- Angeletti, S.; Pierini, J.O.; Cervellini, P.M. Suspended sediment contribution resulting from bioturbation in intertidal sites of a SW Atlantic mesotidal estuary: Data analysis and numerical modelling. Sci. Mar. 2019, 82, 245–256. [Google Scholar] [CrossRef]
- Pierini, J.O.; Campuzano, F.J.; Leitão, P.C.; Gómez, E.A.; Neves, R.J. Atmospheric Influence Over the Residence Time in the Bahia Blanca Estuary, Argentina. Thalassas 2019, 35, 275–286. [Google Scholar] [CrossRef]
- Alonso, R.; Jackson, M.; Santoro, P.; Fossati, M.; Solari, S.; Teixeira, L. Wave and tidal energy resource assessment in Uruguayan shelf seas. Renew. Energy 2017, 114, 18–31. [Google Scholar] [CrossRef]
- Saraiva, S.; Fernandes, L.; van der Meer, J.; Neves, R.; Kooijman, S.A.L.M. The role of bivalves in the Balgzand: First steps on an integrated modelling approach. Ecol. Mod. 2017, 359, 34–48. [Google Scholar] [CrossRef]
- Ascione Kenov, I.; Muttin, F.; Campbell, R.; Fernandes, R.; Campuzano, F.; Machado, F.; Franz, G.; Neves, R. Water fluxes and renewal rates at Pertuis d’Antioche/Marennes-Oléron Bay, France. Estuar. Coast. Shelf Sci. 2015, 167, 32–44. [Google Scholar] [CrossRef]
- Muttin, F.; Campbell, R.; Ouansafi, A.; Benelmostafa, Y. Numerical modelling and full-scale exercise of oil-spill containment boom on Galician coast. Int. J. Comput. Methods Exp. Meas. 2017, 5, 760–770. [Google Scholar] [CrossRef]
- Galesic, M.; Andricevic, R.; Gotovac, H.; Srzic, V. Concentration statistics of solute transport for the near field zone of an estuary. Adv. Water Resour. 2016, 94, 424–440. [Google Scholar] [CrossRef]
- Salamena, G.G.; Martins, F.; Ridd, P.V. The density-driven circulation of the coastal hypersaline system of the Great Barrier Reef, Australia. Mar. Pollut. Bull. 2016, 105, 277–285. [Google Scholar] [CrossRef]
- Li, Y.; Martins, F.; Wolanski, E. Sensitivity analysis of the physical dynamics of the Fly River plume in Torres Strait. Estuar. Coast. Shelf Sci. 2017, 194, 84–91. [Google Scholar] [CrossRef]
- Bartolomeu, S.; Malhadas, M.S.; Ribeiro, J.; Leitão, P.C.; Dias, J.M. Influence of MeteOcean processes on MSYM sea level predictions in the Malacca Straits. Mod. Manag. Forum 2018, 2, 1–17. [Google Scholar] [CrossRef][Green Version]
- Lee, J.-H.; Lim, B.-J.; Kim, D.-Y.; Park, S.-H.; Chang, Y.-S. The Validation of MOHID Regional Ocean Circulation Model around the East Asian Seas in 2016. J. Korean Earth Sci. Soc. 2018, 39, 436–457. [Google Scholar] [CrossRef]
- Campuzano, F.; Brito, D.; Juliano, M.; Fernandes, R.; de Pablo, H.; Neves, R. Coupling watersheds, estuaries and regional ocean through numerical modelling for Western Iberia: A novel methodology. Ocean Dyn. 2016, 66, 1745–1756. [Google Scholar] [CrossRef]
- Silva, A.; Pinto, L.; Rodrigues, S.M.; de Pablo, H.; Santos, M.; Moita, T.; Mateus, M. A HAB warning system for shellfish harvesting in Portugal. Harmful Algae 2016, 53, 33–39. [Google Scholar] [CrossRef]
- Janeiro, J.; Neves, A.; Martins, F.; Relvas, P. Integrating technologies for oil spill response in the SW Iberian coast. J. Mar. Syst. 2017, 173, 31–42. [Google Scholar] [CrossRef]
- Valentim, J.M.; Vaz, N.; Silva, H.; Duarte, B.; Caçador, I.; Dias, J.M. Tagus estuary and Ria de Aveiro salt marsh dynamics and the impact of sea level rise. Estuar. Coast. Shelf Sci. 2013, 130, 138–151. [Google Scholar] [CrossRef]
- Fernandes, R.; Braunschweig, F.; Lourenço, F.; Neves, R. Combining operational models and data into a dynamic vessel risk assessment tool for coastal regions. Ocean Sci. 2016, 12, 285–317. [Google Scholar] [CrossRef]
- Gaspar, R.; Marques, L.; Pinto, L.; Baeta, A.; Pereira, L.; Martins, I.; Marques, J.C.; Neto, J.M. Origin here, impact there—The need of integrated management for river basins and coastal areas. Ecol. Indic. 2017, 72, 794–802. [Google Scholar] [CrossRef]
- Vargas, C.I.C.; Vaz, N.; Dias, J.M. An evaluation of climate change effects in estuarine salinity patterns: Application to Ria de Aveiro shallow water system. Estuar. Coast. Shelf Sci. 2017, 189, 33–45. [Google Scholar] [CrossRef]
- Martins, I.; Dias, E.; Ilarri, M.I.; Campuzano, F.J.; Pinto, L.; Santos, M.M.; Antunes, C. Antagonistic effects of multiple stressors on macroinvertebrate biomass from a temperate estuary (Minho estuary, NW Iberian Peninsula). Ecol. Indic. 2019, 101, 792–803. [Google Scholar] [CrossRef]
- Portela, L.I.; Neves, R. Numerical modelling of suspended sediment transport in tidal estuaries: A comparison between the Tagus (Portugal) and the Scheldt (Belgium-the Netherlands). Neth. J. Aquat. Ecol. 1994, 28, 329–335. [Google Scholar] [CrossRef]
- Franz, G.; Pinto, L.; Ascione, I.; Mateus, M.; Fernandes, R.; Leitão, P.; Neves, R. Modelling of cohesive sediment dynamics in tidal estuarine systems: Case study of Tagus estuary, Portugal. Estuar. Coast. Shelf Sci. 2014, 151, 34–44. [Google Scholar] [CrossRef]
- Franz, G.; Leitão, P.; Pinto, L.; Jauch, E.; Fernandes, L.; Neves, R. Development and validation of a morphological model for multiple sediment classes. Int. J. Sediment Res. 2017, 32, 585–596. [Google Scholar] [CrossRef]
- Mateus, M.; Neves, R. Evaluating light and nutrient limitation in the Tagus estuary using a process-oriented ecological model. Proc. Inst. Mar. Eng. Sci. Technol. Part A J. Mar. Eng. Technol. 2008, 32, 585–592. [Google Scholar] [CrossRef]
- Mateus, M.; Riflet, G.; Chambel, P.; Fernandes, L.; Fernandes, R.; Juliano, M.; Campuzano, F.; de Pablo, H.; Neves, R. An operational model for the West Iberian coast: Products and services. Ocean Sci. 2012, 8, 713–732. [Google Scholar] [CrossRef]
- Viegas, C.; Neves, R.; Fernandes, R.; Mateus, M. Modelling tools to support an early alert system for bathing water quality. Environ. Eng. Manag. J. 2012, 11, 907–918. [Google Scholar] [CrossRef]
- Viegas, C.; Nunes, S.; Fernandes, R.; Neves, R. Streams contribution on bathing water quality after rainfall events in Costa do Estoril- a tool to implement an alert system for bathing water quality. J. Coast. Res. 2015, 56, 1961–1965. [Google Scholar]
- Canas, A.; Santos, A.; Leitao, P. Effect of large scale atmospheric pressure changes on water level in the tagus estuary. J. Coast. Res. 2009, 56, 1627–1631. [Google Scholar]
- Braunschweig, F.; Martins, F.; Chambel, P.; Neves, R. A methodology to estimate renewal time scales in estuaries: The Tagus Estuary case. Ocean Dyn. 2003, 53, 137–145. [Google Scholar] [CrossRef]
- Oliveira, A.P.; Mateus, M.D.; Cabeçadas, G.; Neves, R. Water-air CO2 fluxes in the Tagus estuary plume (Portugal) during two distinct winter episodes. Carbon Balance Manag. 2015, 10, 1–15. [Google Scholar] [CrossRef]
- Vaz, N.; Fernandes, L.; Leitão, P.C.; Dias, J.M.; Neves, R.; Manuel, A. The Tagus estuarine plume induced by wind and river runoff: Winter 2007 case study. J. Coast. Res. 2009, 56, 1090–1094. [Google Scholar]
- Vaz, N.; Rodrigues, J.G.; Mateus, M.; Franz, G.; Campuzano, F.; Neves, R.; Dias, J.M. Subtidal variability of the Tagus river plume in winter 2013. Sci. Total Environ. 2018, 627, 1353–1362. [Google Scholar] [CrossRef]
- Otero, P.; Ruiz-Villarreal, M.; Peliz, A. Variability of river plumes off Northwest Iberia in response to wind events. J. Mar. Syst. 2008, 72, 238–255. [Google Scholar] [CrossRef]
- Oliveira, P.B.; Nolasco, R.; Dubert, J.; Moita, T.; Peliz, Á. Surface temperature, chlorophyll and advection patterns during a summer upwelling event off central Portugal. Cont. Shelf Res. 2009, 29, 759–774. [Google Scholar] [CrossRef]
- Stansby, P.K. Coastal hydrodynamics—Present and future. J. Hydraul. Res. 2013, 51, 341–350. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuacy in Watershed Simulation. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Rosen, S.D. Recommended methodology and considerations for acceptance of the calibration and validation of a hydrodynamic model. In Proceedings of the 40th CIESM Congress, Marseille, France, 28 October–1 November 2013. [Google Scholar]
- Williams, J.J.; Esteves, L.S. Guidance on Setup, Calibration, and Validation of Hydrodynamic, Wave, and Sediment Models for Shelf Seas and Estuaries. Adv. Civ. Eng. 2017, 2017, 1–25. [Google Scholar] [CrossRef]
- Valente, A.S.; da Silva, J.C.B. On the observability of the fortnightly cycle of the Tagus estuary turbid plume using MODIS ocean colour images. J. Mar. Syst. 2009, 75, 131–137. [Google Scholar] [CrossRef]
- Fortunato, A.B.; Baptista, A.M.; Luettich, R.A. A three-dimensional model of tidal currents in the mouth of the Tagus estuary. Cont. Shelf Res. 1997, 17, 1689–1714. [Google Scholar] [CrossRef]
- Fernández-Nóvoa, D.; Gómez-Gesteira, M.; Mendes, R.; DeCastro, M.; Vaz, N.; Dias, J.M. Influence of main forcing affecting the Tagus turbid plume under high river discharges using MODIS imagery. PLoS ONE 2017, 12, 1–27. [Google Scholar] [CrossRef]
- Fortunato, A.B.; Oliveira, A.; Baptista, A.M. On the effect of tidal flats on the hydrodynamics of the Tagus estuary. Oceanol. Acta 1999, 22, 31–44. [Google Scholar] [CrossRef]
- Fortunato, A.B.; Freire, P.; Bertin, X.; Rodrigues, M.; Ferreira, J.; Liberato, M.L.R. A numerical study of the February 15, 1941 storm in the Tagus estuary. Cont. Shelf Res. 2017, 144, 50–64. [Google Scholar] [CrossRef]
- Jouanneau, J.M.; Garcia, C.; Oliveira, A.; Rodrigues, A.; Dias, J.A.; Weber, O. Dispersal and deposition of suspended sediment on the shelf off the Tagus and Sado estuaries, S.W. Portugal. Prog. Oceanogr. 1998, 42, 233–257. [Google Scholar] [CrossRef]
- Stanley, D.J. La plate-forme continentale du Portugal et les provinces adjacentes: Analyse géomorphologique. Geo Mar. Lett. 1982, 2, 109. [Google Scholar] [CrossRef]
- Gameiro, C.; Cartaxana, P.; Brotas, V. Environmental drivers of phytoplankton distribution and composition in Tagus Estuary, Portugal. Estuar. Coast. Shelf Sci. 2007, 75, 21–34. [Google Scholar] [CrossRef]
- Neves, F. Dynamics and Hydrology of the Tagus estuary: Results from In Situ Observations. Ph.D. Thesis, Universidade de Lisboa, Lisbon, Portugal, 2010. [Google Scholar]
- Rodrigues, R. The Tagus Estuarine Plume Variability: Impact in Coastal Circulation and Hydrography. Master’s Thesis, University of Aveiro, Aveiro, Portugal, 2015. [Google Scholar]
- Rusu, L.; Bernardino, M.; Guedes Soares, C. Modelling the influence of currents on wave propagation at the entrance of the Tagus estuary. Ocean Eng. 2011, 38, 1174–1183. [Google Scholar] [CrossRef]
- Vaz, N.; Mateus, M.; Plecha, S.; Sousa, M.C.; Leitão, P.C.; Neves, R.; Dias, J.M. Modeling SST and chlorophyll patterns in a coupled estuary-coastal system of Portugal: The Tagus case study. J. Mar. Syst. 2015, 147, 123–137. [Google Scholar] [CrossRef]
- Fiúza, A.F.G.; Macedo, M.E.; Guerreiro, M.R. Climatological space and time variation of the Portuguese coastal upwelling. Oceanol. Acta 1982, 5, 31–40. [Google Scholar]
- Ambar, I.; Fiúza, A. Some Features of the Portugal Current System: A poleward slope undercurrent, an upwelling-related summer southward flow and an autumn-winter poleward coastal surface current. In Proceedings of the 2nd International Conference on Air-Sea Interaction and on Meteorology and Oceanography, Boston, MA, USA, 18–22 September 1994. [Google Scholar]
- Fiúza, A.F.G. Upwelling patterns off Portugal. In Coastal Upwelling Its Sediment Record; Springer: New York, NY, USA, 1983; pp. 85–98. [Google Scholar] [CrossRef]
- Ruiz-Villarreal, M. Hydrodynamic Model Study of the Ria de Pontevedra Under Estuarine Conditions. Estuar. Coast. Shelf Sci. 2002, 54, 101–113. [Google Scholar] [CrossRef]
- Moita, M.T.; Oliveira, P.B.; Mendes, J.C.; Palma, A.S. Distribution of chlorophyll a and Gymnodinium catenatum associated with coastal upwelling plumes off central Portugal. Acta Oecol. 2003, 24, 125–132. [Google Scholar] [CrossRef]
- Blazek, J. Principles of Solution of the Governing Equations. In Computational Fluid Dynamics: Principles and Applications, 3rd ed.; Blazek, J., Ed.; Elsevier Science: San Diego, CA, USA, 2015; pp. 121–166. [Google Scholar]
- Millero, F.J.; Poisson, A. International one-atmosphere equation of state of seawater. Deep Sea Res. Part A Oceanogr. Res. Pap. 1981, 28, 625–629. [Google Scholar] [CrossRef]
- Leitão, P.; Mateus, M.; Braunschweig, F.; Fernandes, L.; Neves, R. Modelling coastal systems: The MOHID Water numerical lab. In Perspectives on Integrated Coastal Zone Management in South America; Neves, R., Baretta, J., Mateus, M., Eds.; IST Press: Lisbon, Portugal, 2008; pp. 77–88. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Campuzano, F.J.; Fernandes, R.; Leitão, P.C.; Viegas, C.; de Pablo, H.; Neves, R. Implementing local operational models based on an offline downscaling technique: The Tagus estuary case. In Proceedings of the 2.as Jornadas de Engenharia Hidrográfica, Lisbon, Portugal, 20–22 June 2012. [Google Scholar]
- Flather, R.A. A Tidal Model of the North-West European Continental Shelf. Mem. Soc. R. Sci. Liège 1976, 10, 141–164. [Google Scholar]
- Burchard, H.; Bolding, K.; Villarreal, M.R. GOTM, A General Ocean Turbulence Model; Report EUR18745 EN; Space Applications Institute: Athens, Greece, 1999. [Google Scholar]
- Trancoso, A.R. Operational Modelling as a Tool in Wind Power Forecasts and Meteorological Warnings. PhD Thesis, Universidade de Lisboa, Lisboa, Portugal, 2012. [Google Scholar]
- Carrere, L.; Lyard, F.; Cancet, M.; Roblou, L.; Guillot, A.; Roblou, L. FES 2012: A new global tidal model taking advantage of nearly 20 years of altimetry. In Proceedings of the 20 Years of Progress in Radar Altimetry, Venice, Italy, 24–29 September 2012. [Google Scholar]
- Drillet, Y.; Bourdallé-Badie, R.; Siefridt, L.; Le Provost, C. Meddies in the Mercator North Atlantic and Mediterranean Sea eddy-resolving model. J. Geophys. Res. C Ocean. 2005, 110, 1–16. [Google Scholar] [CrossRef]
- Grell, G.A.; Dudhia, J.S.D. A description of the fifth-generation Penn State/NCAR Mesoscale Model (MM5). NCAR Technical Note NCAR/TN-398+STR 1994. [Google Scholar] [CrossRef]
- Stark, J.D.; Donlon, C.J.; Martin, M.J.; McCulloch, M.E. OSTIA: An operational, high resolution, real time, global sea surface temperature analysis system. In Proceedings of the Oceans MTS/IEEE Conference, Vancouver, BC, Canada, 18–21 June 2007. [Google Scholar]
- Autret, E.; Paul, F.; Tandéo, P.; Hackett, B. For Level 3 and 4 ODYSSEA SST products over the global ocean and north western shelves—SST _ GLO _ SST _ L3 _ NRT _ OBSERVATIONS _ 010 _ 010—SST _ NWS _ SST _ L4 _ NRT _ OBSERVATIONS _ 010 _ 003, 2017; EU Copernicus Marine Service–Public: Brussels, Belgium.
- Martin, M.; Dash, P.; Ignatov, A.; Banzon, V.; Beggs, H.; Brasnett, B.; Cayula, J.F.; Cummings, J.; Donlon, C.; Gentemann, C.; et al. Group for High Resolution Sea Surface temperature (GHRSST) analysis fields inter-comparisons. Part 1: A GHRSST multi-product ensemble (GMPE). Deep. Res. Part II Top. Stud. Oceanogr. 2012, 77–80, 21–30. [Google Scholar] [CrossRef]
- Parkinson, C.L.; Ward, A.; King, M.D. Earth Science Reference Handbook; National Aeronautics and Space Administration: Washington, DC, USA, 2006. [Google Scholar]
- Glock, K.; Tritthart, M.; Habersack, H.; Hauer, C. Comparison of hydrodynamics simulated by 1D, 2D and 3D models focusing on bed shear stresses. Water 2019, 11, 226. [Google Scholar] [CrossRef]
- García-Alba, J.; Bárcena, J.F.; Ugarteburu, C.; García, A. Artificial neural networks as emulators of process-based models to analyse bathing water quality in estuaries. Water Res. 2019, 150, 283–295. [Google Scholar] [CrossRef]
| Settings | Level 1 –WestIberia | Level2–PCOMS | Level 3-TagusROFI |
|---|---|---|---|
| Model characterization | 2D-Barotropic | 3D–Baroclinic | 3D-Baroclinic |
| Grid corners | 33.50° N–49.90° N 1.00° W–13.50° W | 34.38° N–45.00° N 12.60° W–5.50° W | 38.16° N–39.21° N 10.02° W–8.90° W |
| Cells dimension | 208 × 156 | 177 × 125 | 121 × 146 |
| Bathymetry | EMODneta Hydrography portal | EMODneta Hydrography portal | Delaunay triangulation with IH Data and GEBCO |
| Horizontal Grid | Regular: (≈5.7 km) | Regular: (≈5.7 km) | Irregular: 200 m to 2 km |
| Vertical Grid | 1 layer | 7 Sigma Layer (0 m–8.68 m) 43 Cartesian layers | 7 Sigma Layer (0 m–8.68 m) 43 Cartesian layers |
| Δt | 60 seconds | 60 seconds | 6 seconds |
| Tides | FES2004b & FES2012c | From Level1 | From Level2 |
| OBC Water | From MercatorOcéan PSY2V4 (Releases 1–4)d | From Level2 | |
| Assimilation | Flow relaxation scheme of 10 cells with a time decay of 1 week at the open boundary and 0 inside the domain | Flow relaxation scheme of 10 cells with a time decay of 1 week at the open boundary and 0 inside the domain | |
| OBC Atmosphere | MM5e (9 km) | MM5e (9 km) | WRFf (3 km) |
| Discharges | No | No | Tagus (hourly), Sorraia, Trancão and WWTP (monthly) |
| Turbulence | GOTMg | GOTMg | |
| Bottom | Rugosity of 0.0025 m2 s−1 | Rugosity of 0. 0025 m2 s−1 | Rugosity of 0. 0025 m2 s−1 |
| Tide Gauge | Average (min–max) MOHID | Average (min-max) Tide Gauge | n | Pearson (r) | BIAS | RMSE |
|---|---|---|---|---|---|---|
| CTG | 2.02 (0.39–3.73) | 2.02 (0.31–3.69) | 4445 | 0.995 | 0.003 | 0.17 |
| LTG | 2.01 (0.32–3.70) | 2.00 (0-17–3.77) | 4341 | 0.994 | 0.005 | 0.45 |
| Parameter | Average (min-max) MOHID | Average (min-max) CTD | n | Pearson (r) | BIAS | RMSE |
|---|---|---|---|---|---|---|
| Temperature | 14.2 (11.4–17.4) | 14.3 (11.9–17.3) | 21436 | 0.91 | 0.1 | 0.4 |
| Salinity | 28.0 (2.1–35.6) | 27.4 (1.3–35.3) | 21436 | 0.86 | –0.9 | 2.9 |
| Average (min-max) MOHID | Average (min-max) ADCP | n | Pearson (r) | BIAS | RMSE | |
|---|---|---|---|---|---|---|
| Depth (2.5 m–15 m) | ||||||
| Vel. Modulus (m s−1) | 0.16 (0.0087–0.41) | 0.17 (0.0054–0.43) | 1440 | 0.68 | 0.014 | 0.10 |
| Direction (rad) | 151 (0.2–360) | 134 (2.4–359) | 0.63 | –9.8 | 45 | |
| Velocity u (m s−1) | 0.097 (−0.069–0.30) | 0.099 (−0.14–0.34) | 0.63 | 0.0019 | 0.092 | |
| Velocity v (m s−1) | −0.089 (−0.38–0.11) | −0.11 (−0.43–0.11) | 0.73 | −0.025 | 0.11 | |
| Depth (15 m–30 m) | ||||||
| Vel. Modulus (m s−1) | 0.10 (0.0039–0.30) | 0.12 (0.0025–0.34) | 1440 | 0.62 | 0.018 | 0.065 |
| Direction (rad) | 151 (0.2–360) | 164 (2–358) | 0.66 | –14 | 50 | |
| Velocity u (m s−1) | 0.084 (−0.046–0.30) | 0.092 (−0.086–0.29) | 0.63 | 0.0082 | 0.066 | |
| Velocity v (m s−1) | −0.052 (−0.15–0.098) | −0.035 (−0.26–0.13) | 0.71 | –0.029 | 0.071 |
| Year | Satellite | Average MOHID | Average L4 products | n (per day) | Pearson (r) | BIAS | RMSE |
|---|---|---|---|---|---|---|---|
| 2014 | OSTIA | 17.11 | 17.18 | 355 | 0.937 | −0.064 | 0.846 |
| ODYSSEA | 17.11 | 17.17 | 2095 | 0.948 | −0.059 | 0.773 | |
| MUR | 17.12 | 17.20 | 8356 | 0.934 | −0.078 | 0.894 | |
| 2015 | OSTIA | 16.50 | 16.91 | 255 | 0.919 | −0.407 | 0.946 |
| ODYSSEA | 16.51 | 16.83 | 2095 | 0.924 | −0.320 | 0.889 | |
| MUR | 16.56 | 16.87 | 8356 | 0.912 | −0.359 | 0.992 | |
| 2016 | OSTIA | 16.74 | 16.19 | 355 | 0.930 | −0.176 | 0.866 |
| ODYSSEA | 16.71 | 16.83 | 2095 | 0.864 | −0.127 | 0.978 | |
| MUR | 16.73 | 16.83 | 8356 | 0.916 | −0.102 | 0.914 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Pablo, H.; Sobrinho, J.; Garcia, M.; Campuzano, F.; Juliano, M.; Neves, R. Validation of the 3D-MOHID Hydrodynamic Model for the Tagus Coastal Area. Water 2019, 11, 1713. https://doi.org/10.3390/w11081713
de Pablo H, Sobrinho J, Garcia M, Campuzano F, Juliano M, Neves R. Validation of the 3D-MOHID Hydrodynamic Model for the Tagus Coastal Area. Water. 2019; 11(8):1713. https://doi.org/10.3390/w11081713
Chicago/Turabian Stylede Pablo, Hilda, João Sobrinho, Mariangel Garcia, Francisco Campuzano, Manuela Juliano, and Ramiro Neves. 2019. "Validation of the 3D-MOHID Hydrodynamic Model for the Tagus Coastal Area" Water 11, no. 8: 1713. https://doi.org/10.3390/w11081713
APA Stylede Pablo, H., Sobrinho, J., Garcia, M., Campuzano, F., Juliano, M., & Neves, R. (2019). Validation of the 3D-MOHID Hydrodynamic Model for the Tagus Coastal Area. Water, 11(8), 1713. https://doi.org/10.3390/w11081713






