The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan
Abstract
1. Introduction
2. Materials and Methods
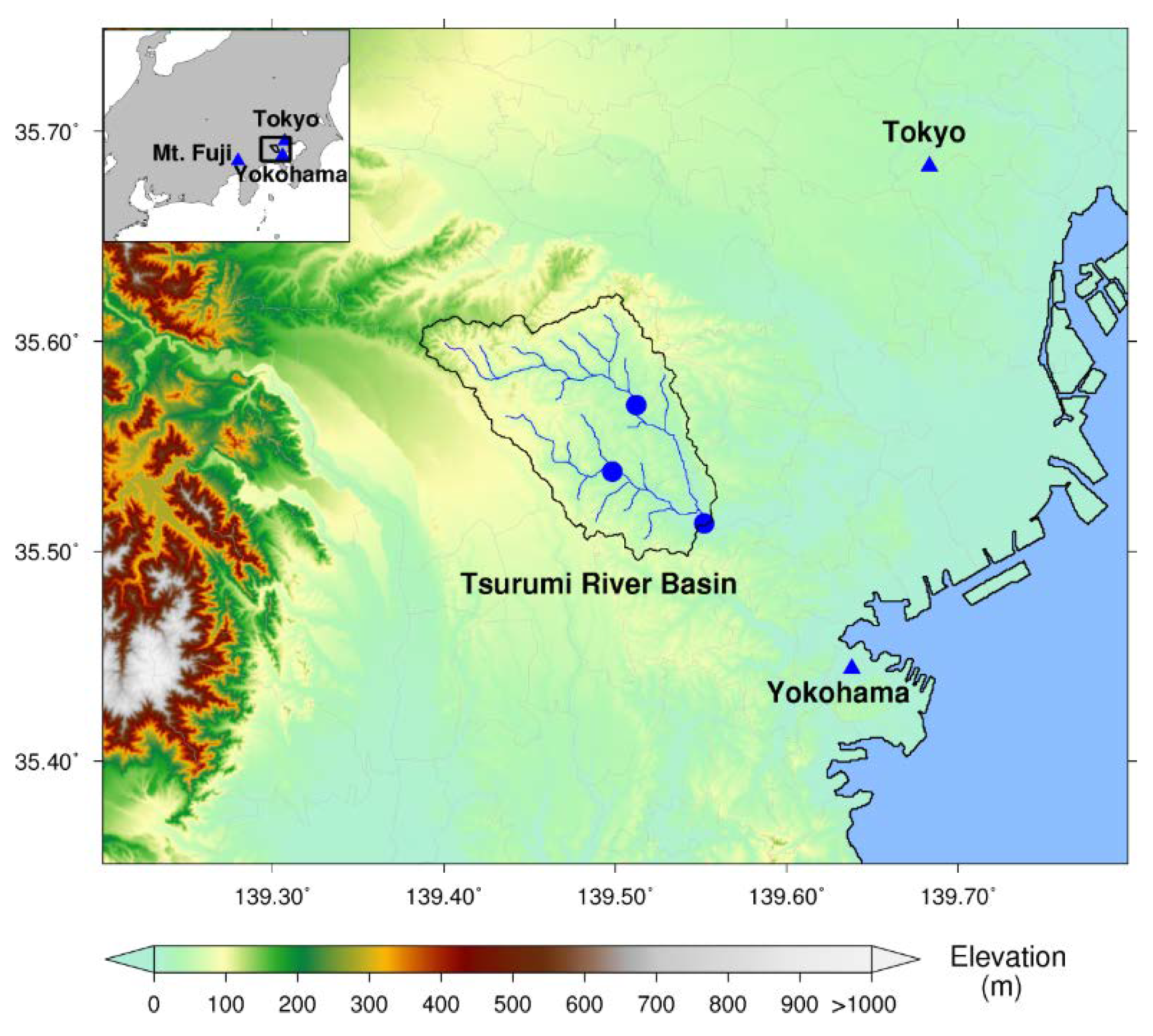
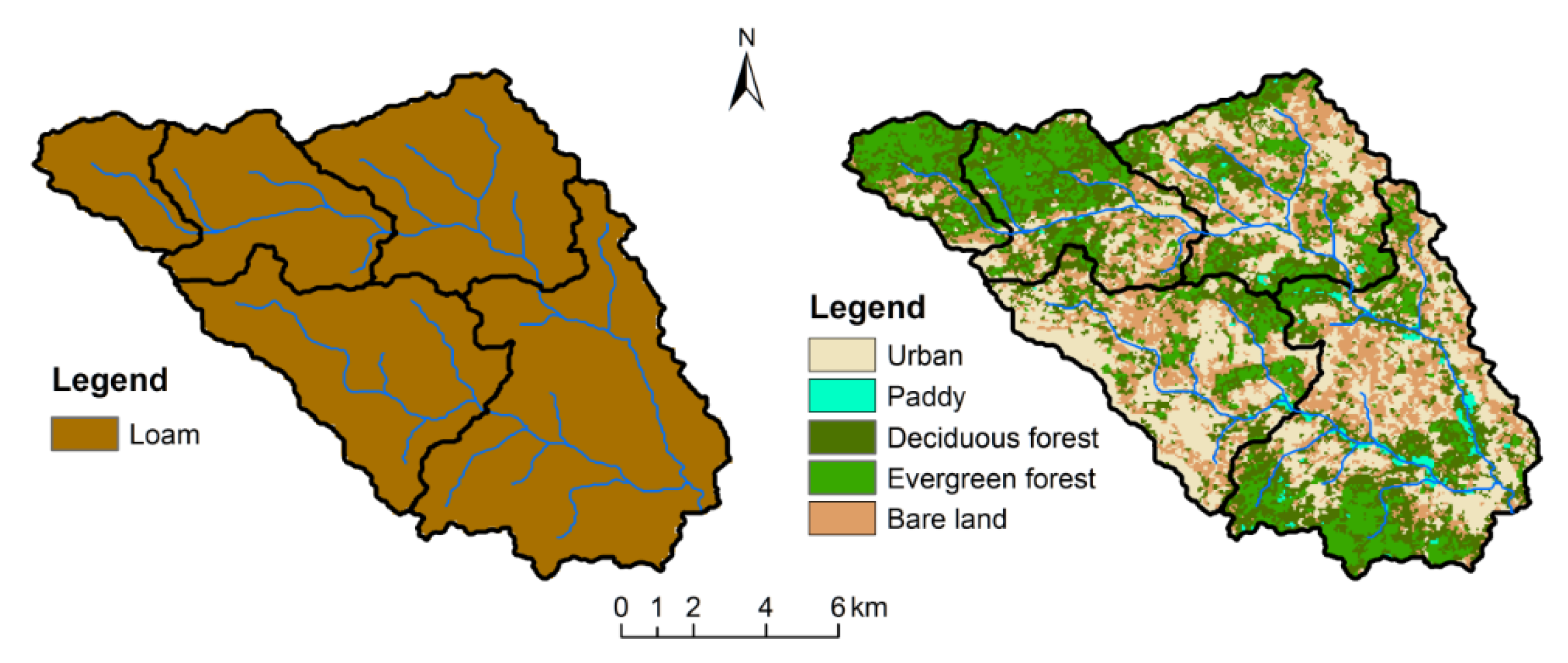
2.1. Study Area and Rainfall Events
2.2. Hydrological Model
2.2.1. Model Set-Up
2.2.2. Optimization of Model Parameters
2.3. Assessment Tools
3. Results
3.1. Evaluation of the Model Performance
3.2. Spatial Resolution of Radar Rainfall Data
3.2.1. Rescaling of Radar Rainfall Data
3.2.2. Inter-Comparison of Simulated Discharge Data
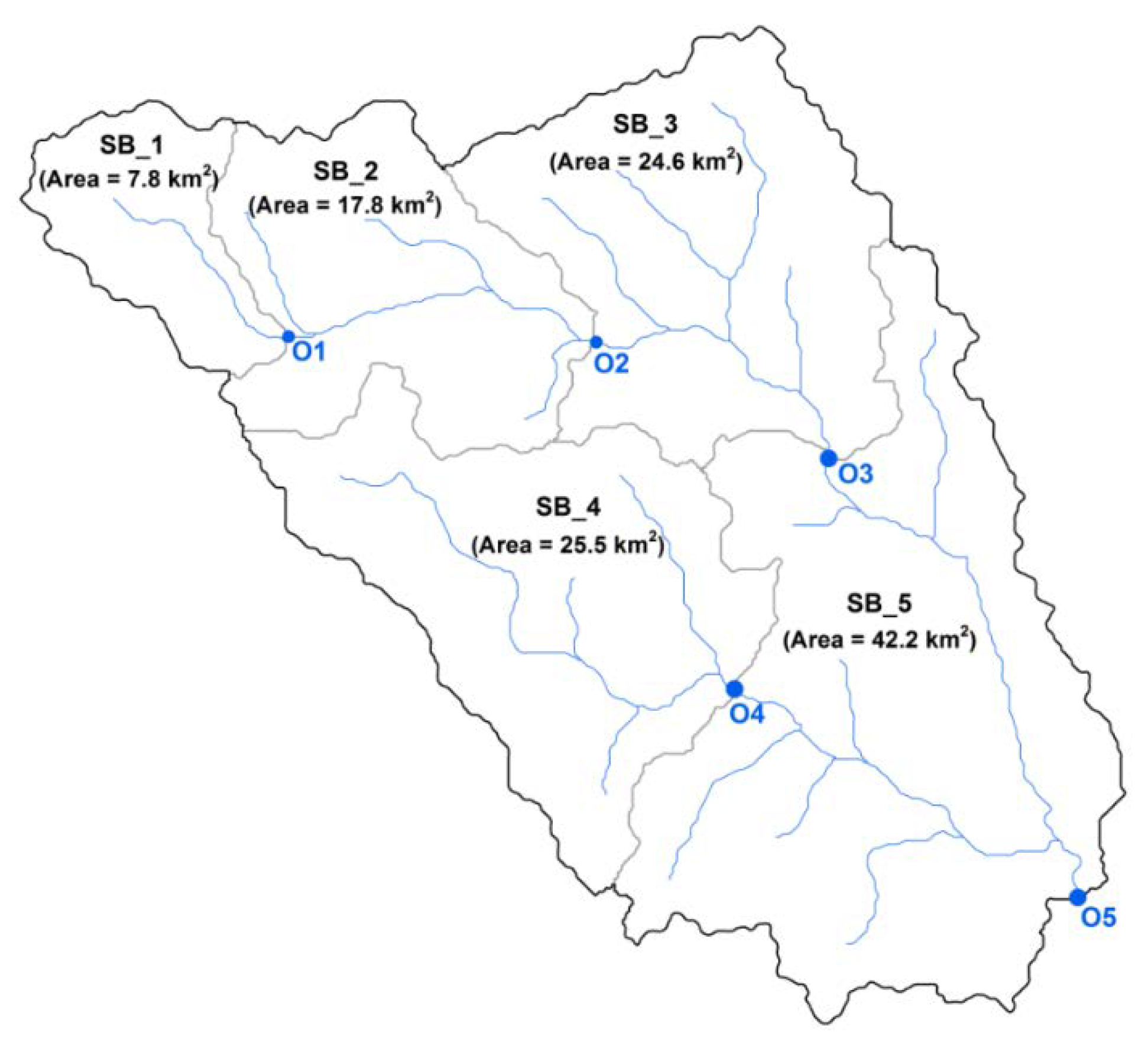
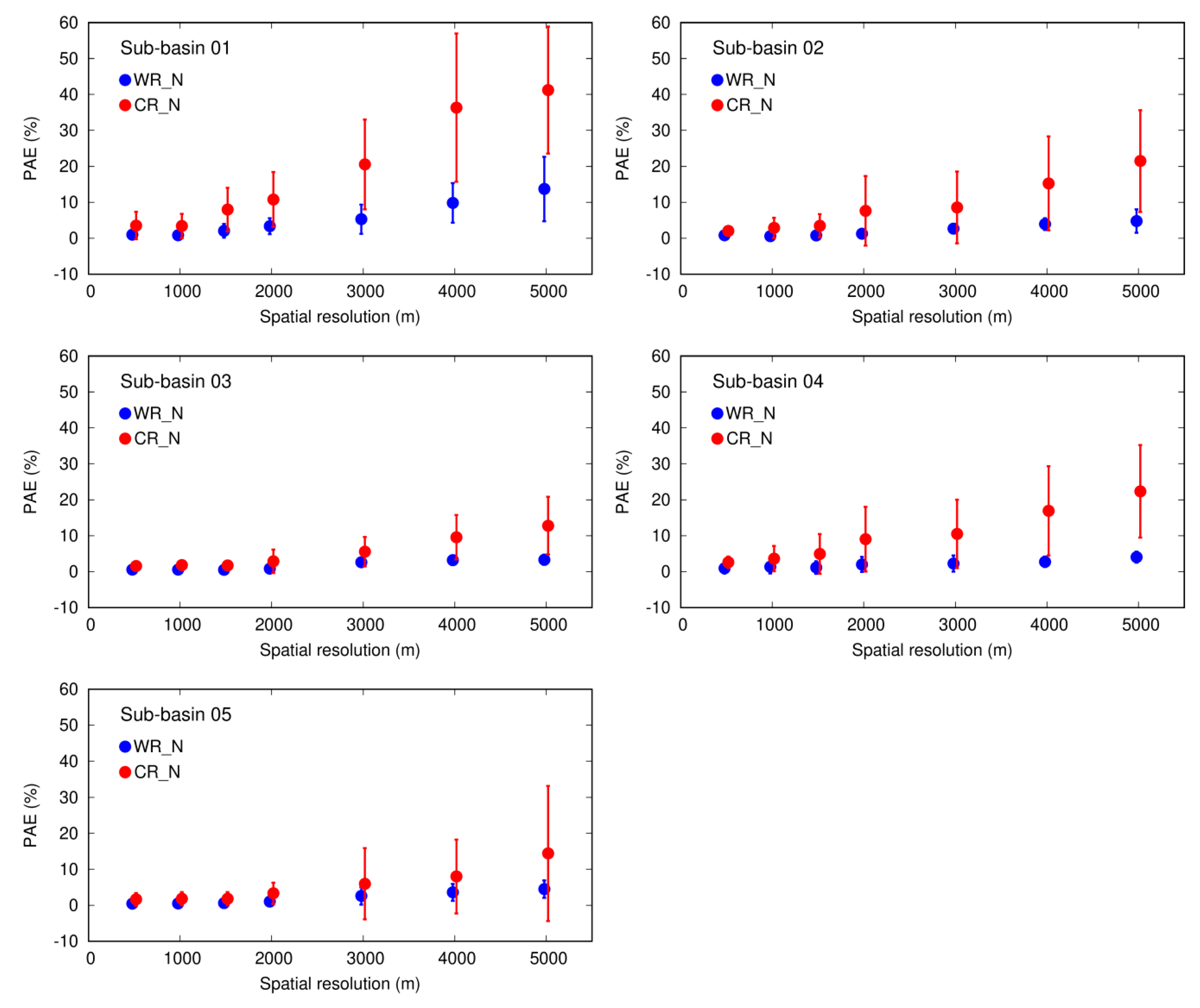
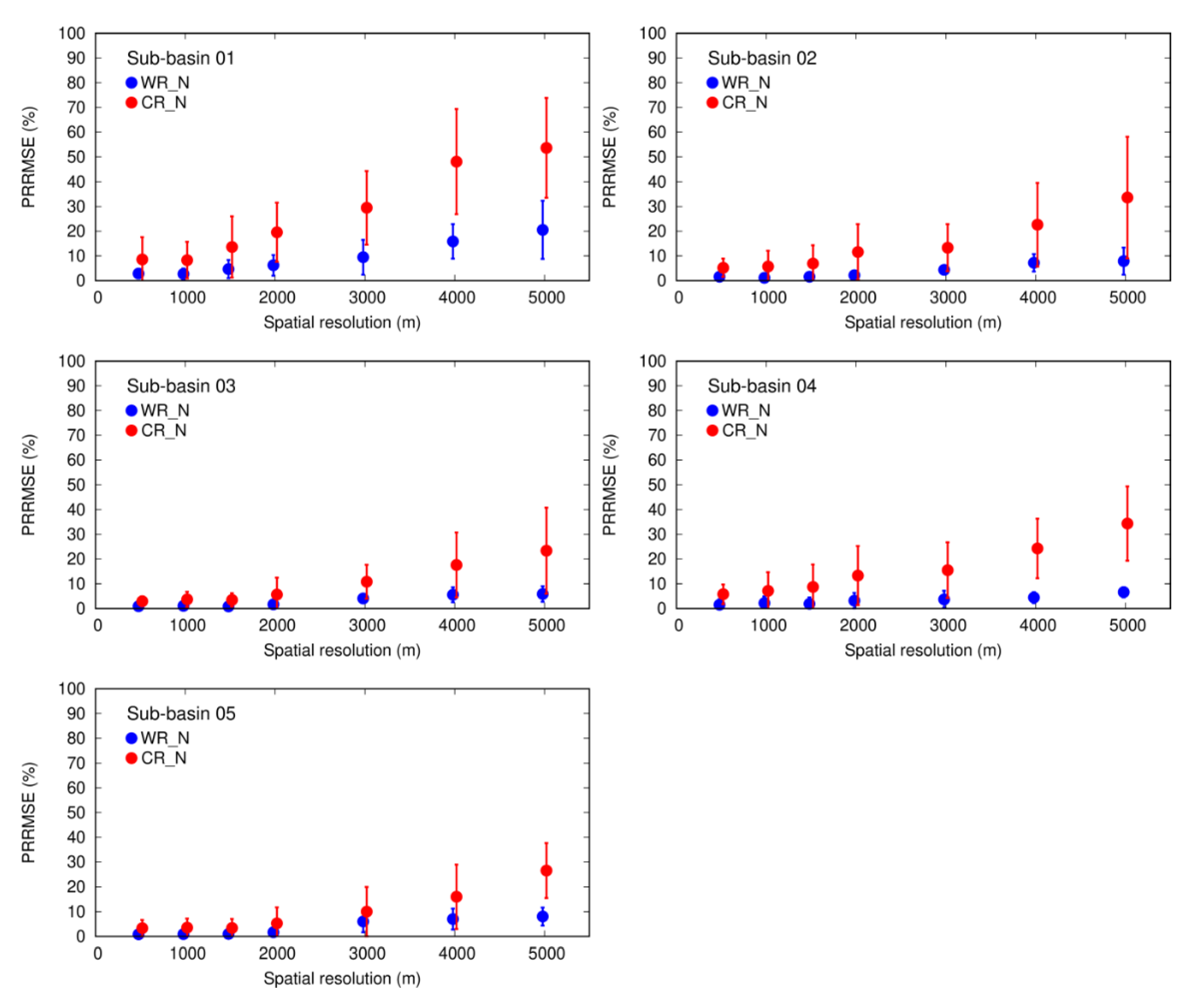
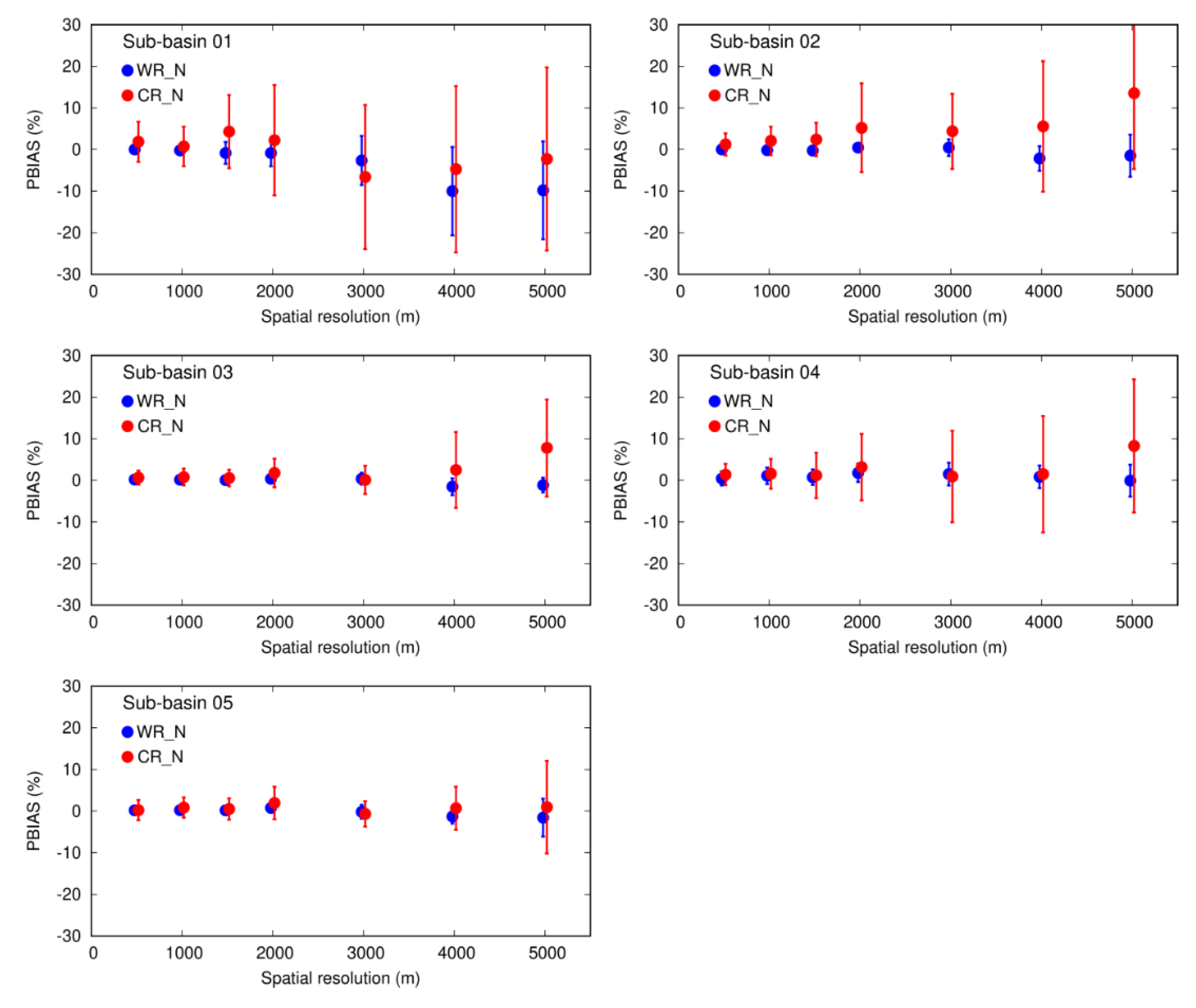
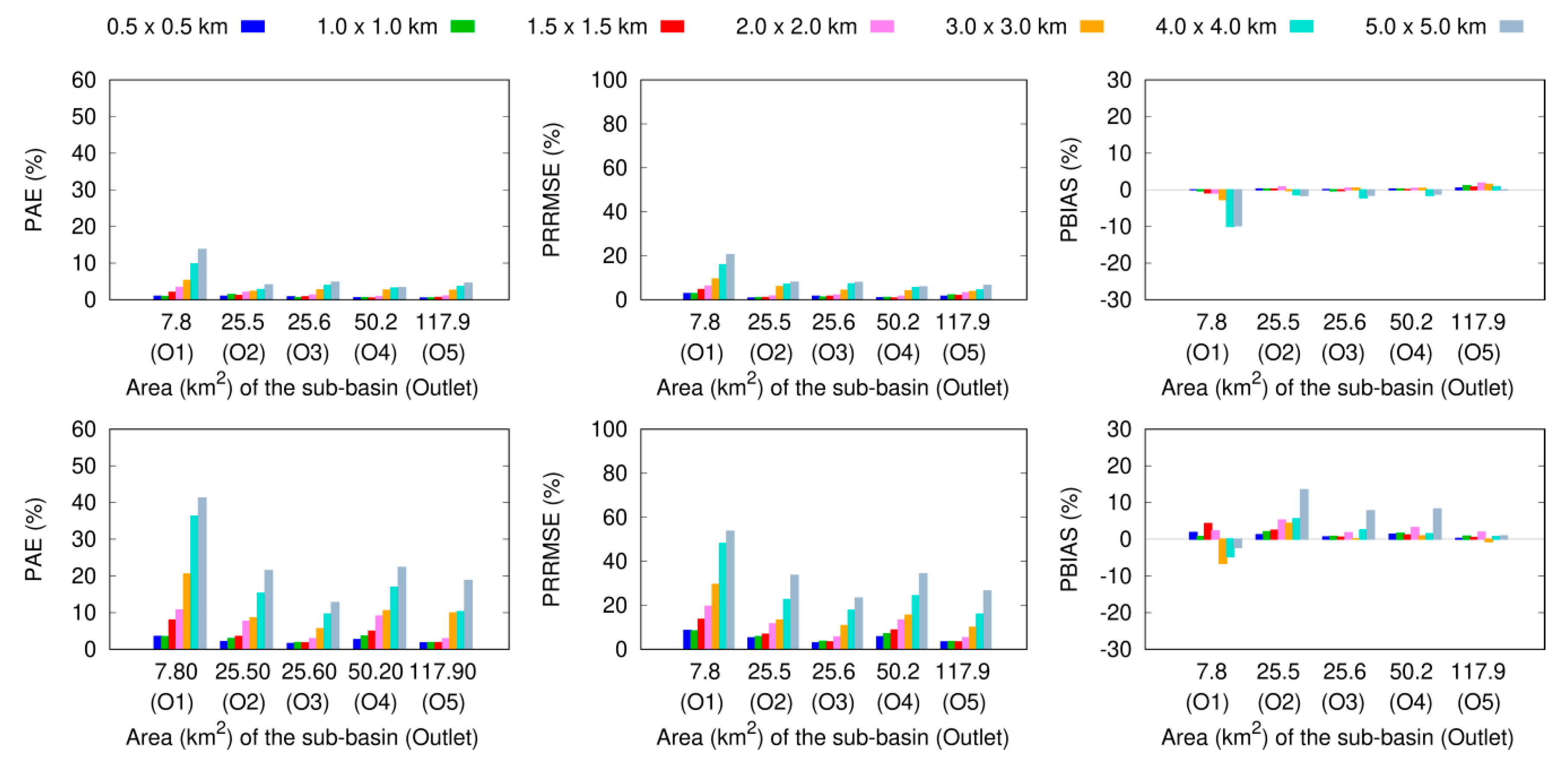
3.2.3. Uncertainties at the Sub-Basin Scale
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilson, C.B.; Valdés, J.B.; Rodriguez-Iturbe, I. On the influence of the spatial distribution of rainfall on storm runoff. Water Resour. Res. 1979, 15, 321–328. [Google Scholar] [CrossRef]
- Dong, X.; Dohmen-Janssen, M.; Booij, M.J. Appropriate spatial sampling of rainfall for flow simulation. Hydrol. Sci. J. 2005, 50, 279–298. [Google Scholar] [CrossRef]
- Cole, S.J.; Moore, R.J. Hydrological modelling using raingauge- and radar-based estimators of areal rainfall. J. Hydrol. 2008, 358, 159–181. [Google Scholar] [CrossRef]
- Yoon, S.S.; Lee, B. Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses. Water 2017, 9, 931. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degre, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Muthusamy, M.; Schellart, A.; Tait, S.; Heuvelink, G.B.M. Geostatistical upscaling of rain gauge data to support uncertainty analysis of lumped urban hydrological models. Hydrol. Earth Syst. Sci. 2017, 21, 1077–1091. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; Veldhuis, M.C.T.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F. Determining the Optimal Spatial Distribution of Weather Station Networks for Hydrological Modeling Purposes Using RCM Datasets: An Experimental Approach. J. Hydrometeorol. 2014, 15, 517–526. [Google Scholar] [CrossRef]
- Allegretti, M.; Bertoldo, S.; Prato, A.; Lucianaz, C.; Rorato, O.; Notarpietro, R.; Gabella, M. X-Band Mini Radar for Observing and Monitoring Rainfall Events. Atmos. Clim. Sci. 2012, 2, 290–297. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Book Company: New York, NY, USA, 1988; p. 572. [Google Scholar]
- Xie, P.; Arkin, P.A. An Intercomparison of Gauge Observations and Satellite Estimates of Monthly Precipitation. J. Appl. Meteorol. 1995, 34, 1143–1160. [Google Scholar] [CrossRef]
- Kubota, T.; Ushio, T.; Shige, S.; Kida, S.; Kachi, M.; Okamoto, K. Verification of High-Resolution Satellite-Based Rainfall Estimates around Japan Using a Gauge-Calibrated Ground-Radar Dataset. J. Meteorol. Soc. Jpn. 2009, 87, 203–222. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Qamer, F.M.; Pedreros, D.; Murthy, M.; Wahid, S.M.; Shrestha, M. Evaluating the accuracy of Climate Hazard Group (CHG) satellite rainfall estimates for precipitation based drought monitoring in Koshi basin, Nepal. J. Hydrol. Reg. Stud. 2017, 13, 138–151. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.-E.; Quirmbachd, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar]
- Gao, Y.; Chen, Y.; Zhang, L.; Peng, T. Radar-Rainfall Estimation from S-band Radar and its Impact on the Runoff Simulation of a Heavy Rainfall Event in the Huaihe River Basin. J. Meteorol. Soc. Jpn. 2016, 94, 75–89. [Google Scholar] [CrossRef][Green Version]
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of Spatial Interpolation Schemes for Rainfall Data and Application in Hydrological Modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- P.C., S.; Nakatani, T.; Misumi, R. Hydrological simulation of small river basin in northern Kyushu, Japan during the extreme rainfall event of July 5–6 2017. J. Disaster Res. 2018, 13, 396–409. [Google Scholar] [CrossRef]
- P.C., S.; Nakatani, T.; Misumi, R. Analysis of Flood Inundation in Ungauged Mountainous River Basins: A Case Study of an Extreme Rain Event on 5–6 July 2017 in Northern Kyushu, Japan. J. Disaster Res. 2018, 13, 860–872. [Google Scholar] [CrossRef]
- Chintalapudi, S.; Sharif, H.O.; Xie, H. Sensitivity of Distributed Hydrologic Simulations to Ground and Satellite Based Rainfall Products. Water 2014, 6, 1221–1245. [Google Scholar] [CrossRef]
- Neary, V.S.; Habib, E.; Fleming, M. Hydrologic Modeling with NEXRAD Precipitation in Middle Tennessee. J. Hydrol. Eng. 2004, 9, 339–349. [Google Scholar] [CrossRef]
- Paudel, M.; Nelson, E.J.; Scharffenberg, W. Comparison of Lumped and Quasi-Distributed Clark Runoff Models Using the SCS Curve Number Equation. J. Hydrol. Eng. 2009, 14, 1098–1106. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; Van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Goormans, T.; Willems, P. Evaluating the accuracy of C- and X-band weather radars and their application for stream flow simulation. J. Hydroinform. 2013, 15, 1121–1136. [Google Scholar] [CrossRef]
- Goormans, T.; Willems, P. Using Local Weather Radar Data for Sewer System Modeling: Case Study in Flanders, Belgium. J. Hydrol. Eng. 2013, 18, 269–278. [Google Scholar] [CrossRef]
- Gurung, P. Integration of gauge and radar rainfall to enable best simulation of hydrological parameters. Hydrol. Sci. J. 2017, 62, 114–123. [Google Scholar] [CrossRef]
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2014, 28, 3505–3520. [Google Scholar] [CrossRef]
- Fabry, F.; Bellon, A.; Duncan, M.R.; Austin, G.L. High resolution rainfall measurements by radar for very small basins: The sampling problem reexamined. J. Hydrol. 1994, 161, 415–428. [Google Scholar] [CrossRef]
- Maesaka, T.; Maki, M.; Iwanami, K. Operational Rainfall Estimation by X-band MP Radar Network in MLIT, Japan. In Proceedings of the 35th Conference on Radar Meteorology, Pittsburgh, PA, USA, 26–30 September 2011. [Google Scholar]
- Maki, M.; Iwanami, K.; Misumi, R.; Park, S.G.; Moriwaki, H.; Maruyama, K.I.; Watabe, I.; Lee, D.I.; Jang, M.; Kim, H.K.; et al. Semi-operational rainfall observations with X-band multi-parameter radar. Atmos. Sci. Lett. 2005, 6, 12–18. [Google Scholar] [CrossRef]
- P.C., S.; Misumi, R.; Nakatani, T.; Iwanami, K.; Maki, M.; Maesaka, T.; Hirano, K. Accuracy of quantitative precipitation estimation using operational weather radars: A case study of heavy rainfall on 9–10 September 2015 in the East Kanto region, Japan. J. Disaster Res. 2011, 11, 1003–1016. [Google Scholar] [CrossRef]
- P.C., S.; Maki, M. Application of a modified digital elevation model method to correct radar reflectivity of X-band dual-polarization radars in mountainous regions. Hydrol. Res. Lett. 2014, 8, 77–83. [Google Scholar]
- US Army Corps of Engineers (USACE). Hydrologic Modeling System HEC-HMS: Technical Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2000. [Google Scholar]
- US Army Corps of Engineers (USACE). Hydrologic Modeling System HEC-HMS: Application Guide; Hydrologic Engineering Center: Davis, CA, USA, 2015. [Google Scholar]
- US Army Corps of Engineers (USACE). Hydrologic Modeling System HEC-HMS: Quick Start Guide: Version 4.2; Hydrologic Engineering Center: Davis, CA, USA, 2016. [Google Scholar]
- Ghavidelfar, S.; Alvankar, S.R.; Razmkhah, A. Comparison of the Lumped and Quasi-distributed Clark Runoff Models in Simulating Flood Hydrographs on a Semi-arid Watershed. Water Resour. Manag. 2011, 25, 1775–1790. [Google Scholar] [CrossRef]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical Note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar]
- Montesarchio, V.; Lombardo, F.; Napolitano, F. Rainfall thresholds and flood warning: An operative case study. Nat. Hazards Earth Syst. Sci. 2009, 9, 135–144. [Google Scholar] [CrossRef]
- Woodward, D.E.; Hawkins, R.H.; Jiang, R.; Hjelmfelt, A.T.; Van Mullem, J.A.; Quan, Q.D. Runoff Curve Number Method: Examination of the Initial Abstraction Ratio. In Proceedings of the 2003 World Water & Environmental Resources Congress, Philadelphia, PA, USA, 23–26 June 2003. [Google Scholar]
- Jin, H.; Liang, R.; Wang, Y.; Tumula, P. Flood-Runoff in Semi-Arid and Sub-Humid Regions, a Case Study: A Simulation of Jianghe Watershed in Northern China. Water 2015, 7, 5155–5172. [Google Scholar] [CrossRef]
- Fang, G.; Yuan, Y.; Gao, Y.; Huang, X.; Guo, Y. Assessing the effects of urbanization on flood events with urban agglomeration polders type of flood control pattern using the HEC-HMS model in the Qinhuai River basin, China. Water 2018, 10, 1003. [Google Scholar] [CrossRef]
- Tassew, B.G.; Belete, M.A.; Miegel, K. Application of HEC-HMS model for flow simulation in the Lake Tana basin: The case of Gilgel Abay catchment, upper Blue Nile basin, Ethiopia. Hydrology 2019, 6, 21. [Google Scholar] [CrossRef]
- Kauffeldt, A.; Wetterhall, F.; Pappenberger, F.; Salamon, P.; Thielen, J. Technical review of large-scale hydrological models for implementation in operational flood forecasting schemes on continental level. Environ. Model. Softw. 2016, 75, 68–76. [Google Scholar] [CrossRef]
- Rafee, S.A.A.; Uvo, C.B.; Martins, J.A.; Domingues, L.M.; Rudke, A.P.; Fujita, T.; Freitas, E.D. Large-Scale Hydrological Modelling of the Upper Paraná River Basin. Water 2019, 11, 882. [Google Scholar] [CrossRef]
- López, P.L.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef]
- Szcześniak, M.; Piniewski, M. Improvement of Hydrological Simulations by Applying Daily Precipitation Interpolation Schemes in Meso-Scale Catchments. Water 2015, 7, 747–779. [Google Scholar] [CrossRef]
- Shekhar, S.; Xiong, H. Inverse Distance Weighting; Springer: New York, NY, USA, 2008; p. 600. [Google Scholar]
- Dirks, K.N.; Hay, J.E.; Stow, C.D.; Harris, D. High resolution studies of rainfall on Norfolk Island. Part 2: Interpolation of rainfall data. J. Hydrol. 1989, 208, 187–193. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.; Jun, H. A Study of the Influence of the Spatial Distribution of Rain Gauge Networks on Areal Average Rainfall Calculation. Water 2018, 10, 1635. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, Y.; Engel, B.; Zhang, W.; Peng, H.; Chen, X.; Xia, H. Performance Assessment of Spatial Interpolation of Precipitation for Hydrological Process Simulation in the Three Gorges Basin. Water 2017, 9, 838. [Google Scholar] [CrossRef]
- Avila, F.B.; Dong, S.; Menang, K.P.; Rajczak, J.; Renom, M.; Donat, M.G.; Alexander, L.V. Systematic investigation of gridding-related scaling effects on annual statistics of daily temperature and precipitation maxima: A case study for south-east Australia. Weather Clim. Extrem. 2015, 9, 6–16. [Google Scholar] [CrossRef]
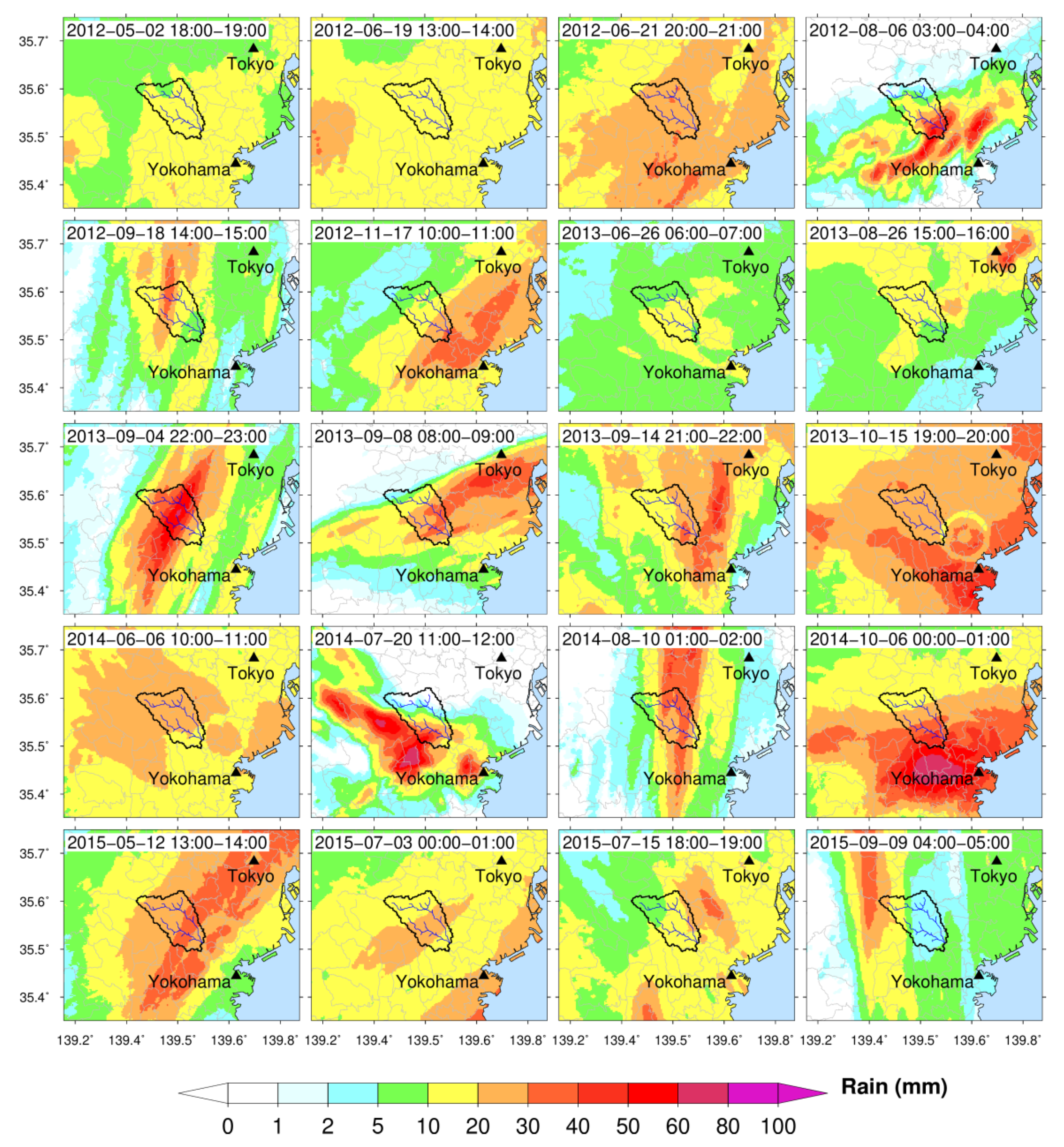
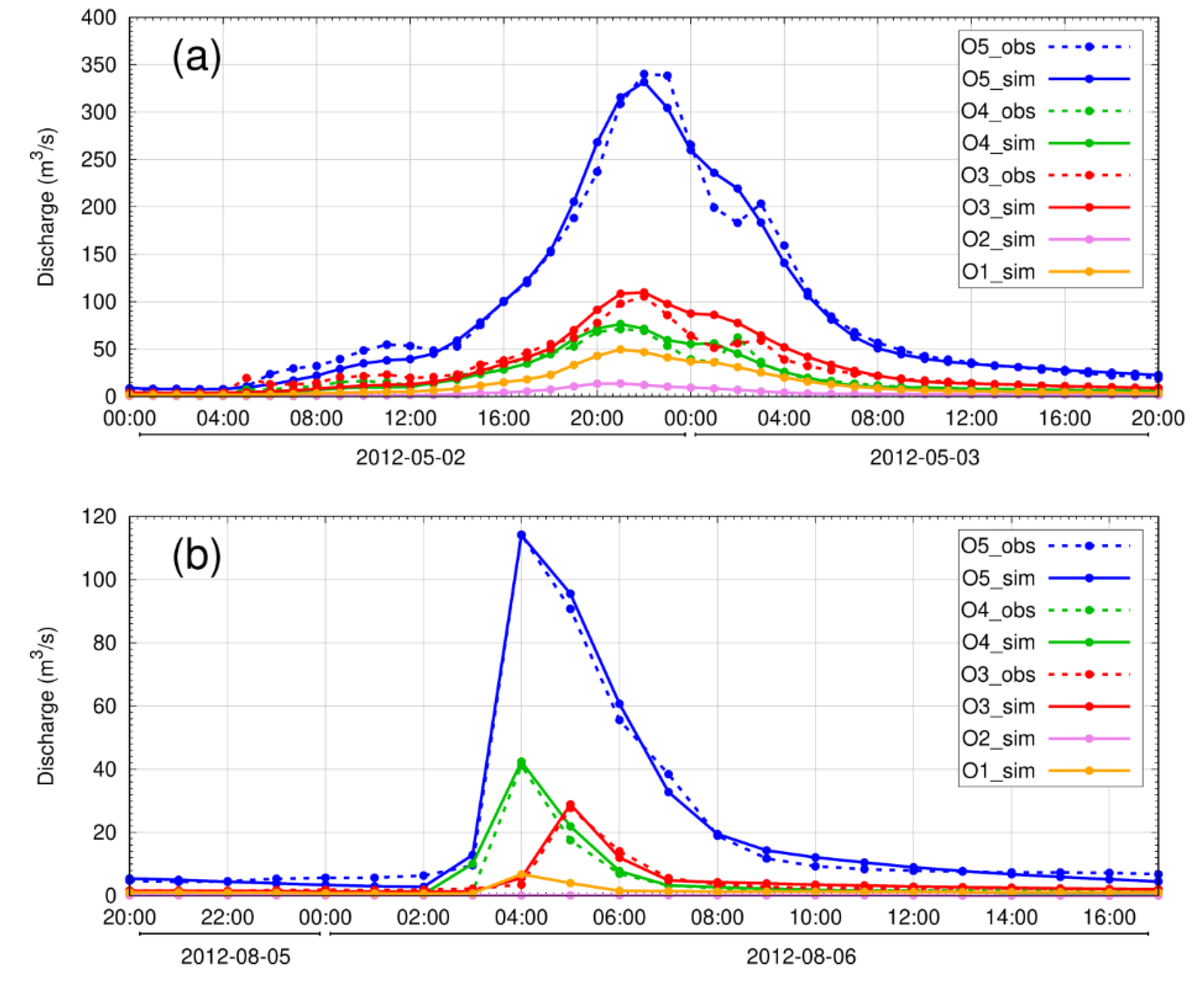
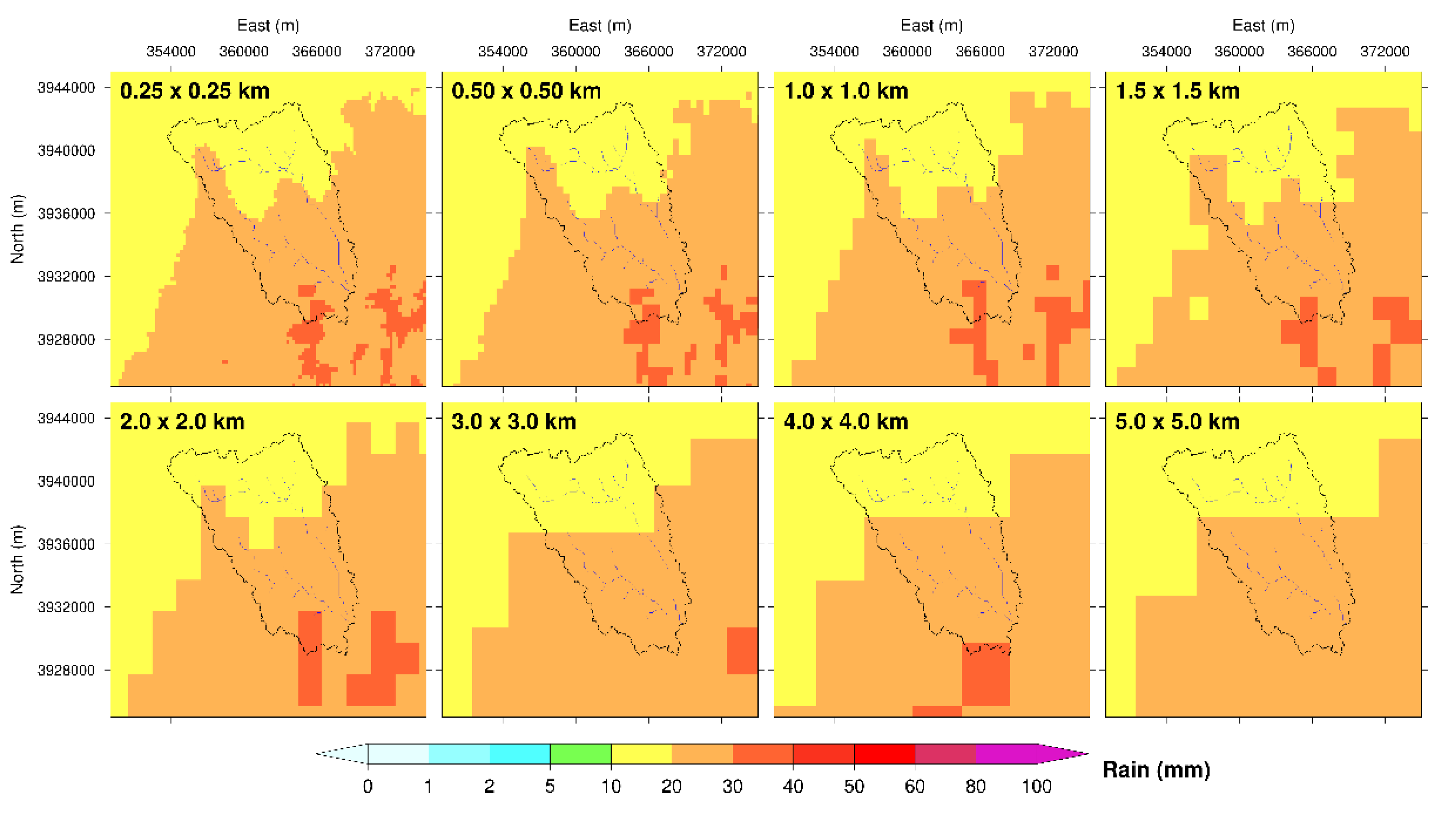
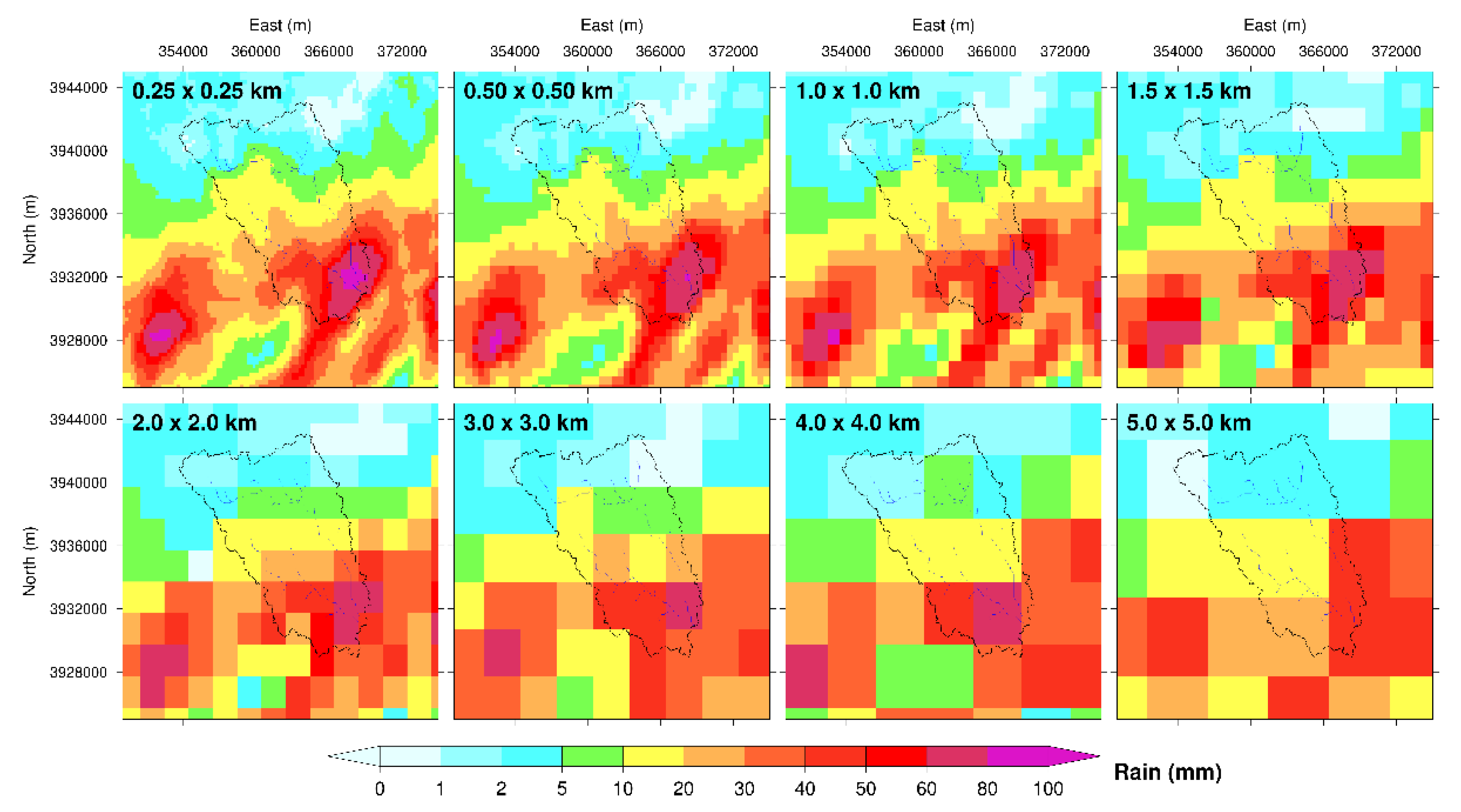
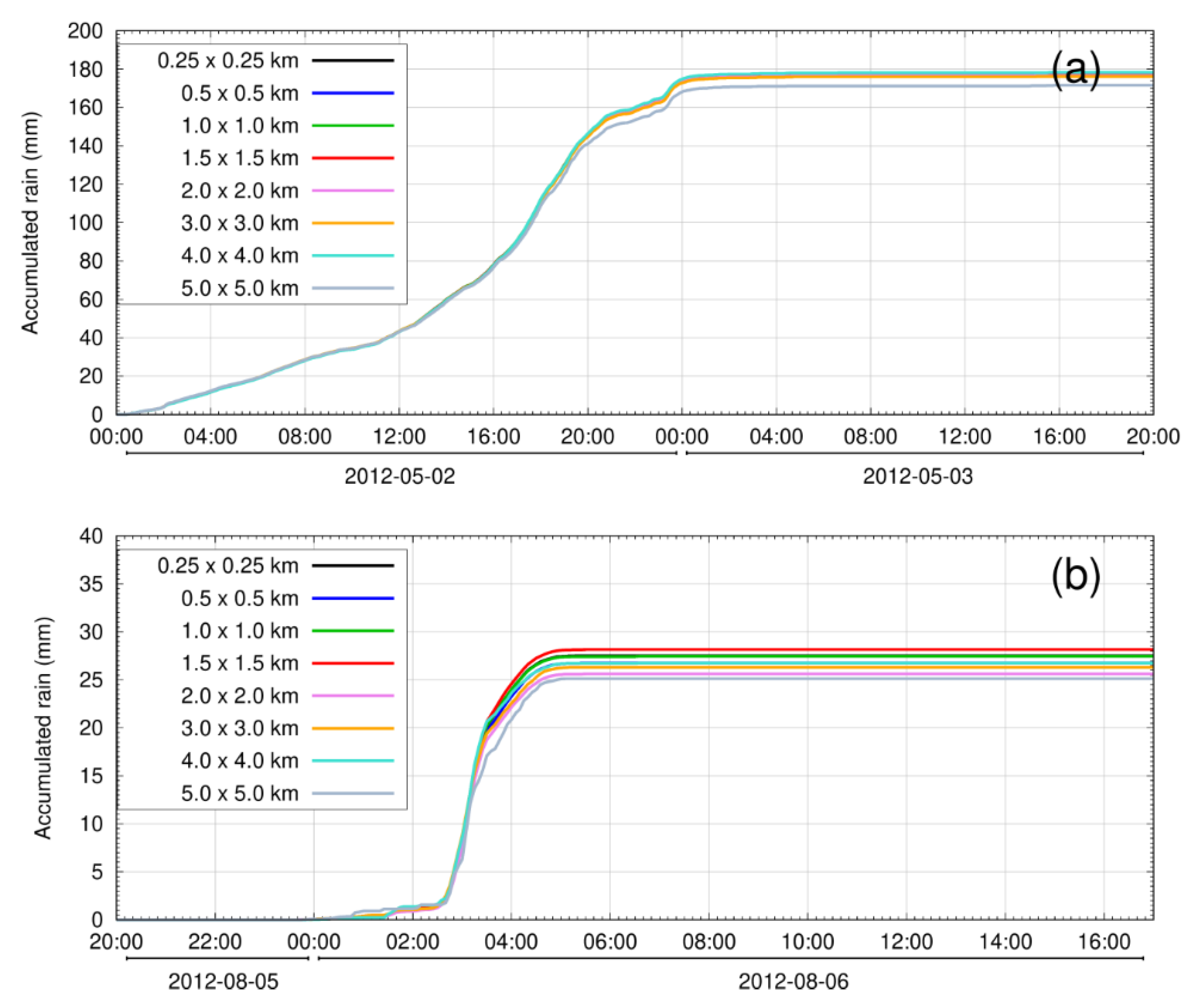



| SN | Date | Considered Time Period (UTC) | Total Hours | * Peak Q (m3/s) | Summary of Rainfall Event | Name Given | |
|---|---|---|---|---|---|---|---|
| Start Time | End Time | ||||||
| 1 | 2–3 May 2012 | 02:00 02-May | 20:00 03-May | 43 | 340 | Widespread, typhoon-affected, rainfall, long time period | WR_N1 |
| 2 | 19–20 June 2012 | 03:00 19-June | 13:00 20-May | 36 | 273 | Widespread, typhoon-affected, heavy rainfall, long time period | WR_N2 |
| 3 | 21–22 June 2012 | 18:00 21-June | 15:00 22-June | 22 | 239 | Widespread, typhoon-affected, heavy rainfall, short time period | WR_N3 |
| 4 | 05–06 August 2012 | 20:00 05-August | 15:00 06-August | 20 | 114 | Convective, scattered heavy rainfall, short time period | CR_N1 |
| 5 | 18–19 September 2012 | 22:00 18-September | 07:00 19-September | 22 | 107 | Convective, scattered rainfall and widespread rainfall, short time period | CR_N2 |
| 6 | 17–18 November 2012 | 04:00 17-November | 23:00 17-November | 20 | 144 | Convective, scattered rain, long echo type, heavy rainfall, short time period | CR_N3 |
| 7 | 26–26 June 2013 | 00:00 26-June | 23:00 26-June | 24 | 101 | Widespread, moderate rainfall, short time period | WR_N4 |
| 8 | 26–27 August 2013 | 10:00 26-August | 07:00 27-August | 22 | 101 | Widespread, moderate rainfall, short time period | WR_N5 |
| 9 | 04–06 September 2013 | 11:00 04-September | 10:00 05-September | 24 | 332 | Convective, scattered rain, long echo type, heavy rainfall, short time period | CR_N4 |
| 10 | 08–09 September 2013 | 04:00 08-September | 00:00 09-September | 21 | 185 | Convective, scattered rain, long echo type, heavy rainfall, short time period | CR_N5 |
| 11 | 14–15 September 2013 | 15:00 14-September | 16:00 15-September | 26 | 407 | Scattered rain, typhoon affected, heavy rainfall, long time period | CR_N6 |
| 12 | 15–16 October 2013 | 02:00 15-October | 11:00 16-October | 34 | 503 | Widespread, typhoon affected, heavy rainfall, long time period | WR_N6 |
| 13 | 05–07 June 2014 | 21:00 05-June | 23:00 07-June | 51 | 288 | Widespread, moderate rainfall, long time period | WR_N7 |
| 14 | 20–21 July 2014 | 05:00 20-July | 00:00 21-July | 20 | 221 | Convective, scattered heavy rainfall, short time period | CR_N7 |
| 15 | 09–10 August 2014 | 16:00 09-August | 20:00 10-August | 29 | 236 | Convective, scattered rain, long echo type, heavy rainfall, long time period | CR_N8 |
| 16 | 04–06 October 2014 | 19:00 04-October | 02:00 07-October | 56 | 557 | Widespread, typhoon affected, heavy rainfall, long time period | WR_N8 |
| 17 | 12–13 May 2015 | 07:00 12-May | 08:00 13-May | 26 | 265 | Widespread, typhoon affected, heavy rainfall, long time period | WR_N9 |
| 18 | 02–04 July 2015 | 15:00 02-July | 06:00 04-July | 43 | 154 | Widespread, typhoon affected, heavy rainfall, long time period | WR_N10 |
| 19 | 15–17 July 2015 | 13:00 15-July | 10:00 17-July | 46 | 114 | Convective, scattered heavy rainfall, long time period | CR_N9 |
| 20 | 07–09 September 2015 | 15:00 07-September | 20:00 09-September | 54 | 279 | Long echo type, typhoon affected, heavy rainfall, long time period | CR_N10 |
| Basin Model | Meteorological Model | Control | Time Series Data | ||
|---|---|---|---|---|---|
| Parameter | Method | Parameter | Method | Time Period | Time Period |
| Loss | SCS CN | Radar rainfall | Gridded data | Selected hours (Table 1) | Discharge data (Table 1) |
| Transform | ModClarck | ||||
| Baseflow | Recession | ||||
| Routing | Muskingum–Cunge | ||||
| Sub-Basin Outlet | NSE (%) | PAE (%) | PRRMSE (%) | PBIAS (%) |
|---|---|---|---|---|
| O3 | 86 (±14) | 23.5 (±9.9) | 40.3 (±17.1) | −5.7 (±12.2) |
| O4 | 88 (±8) | 23.6 (±8.0) | 40.5 (±14.7) | 3.1 (±9.7) |
| O5 | 95 (±5) | 14.9 (±5.9) | 21.9 (±7.5) | 0.6 (±4.8) |
| Average | 90 (±10) | 20.6 (±7.9) | 34.2 (±13.1) | −0.7 (±8.9) |
| Sub-Basin Outlet | NSE (%) | PAE (%) | PRRMSE (%) | PBIAS (%) |
|---|---|---|---|---|
| O3 | 90 (±5) | 29.2 (±8.8) | 44.1 (±9.7) | −13.9 (±10.4) |
| O4 | 89 (±10) | 28.4 (±12.1) | 50.9 (±30.7) | −2.2 (±7.5) |
| O5 | 91 (±8) | 20.4 (±7.9) | 30.5 (±12.1) | −4.5 (±9.7) |
| Average | 90 (±8) | 26.0 (±9.6) | 41.8 (±17.5) | −6.9 (±9.2) |
| Sub-Basin | Loss—Gridded SCS Curve Number | Transform—ModClark | Base Flow—Recession | |||
|---|---|---|---|---|---|---|
| AR (-) | SF (-) | TC (h) | SC (h) | RC (-) | RP (-) | |
| SB_1 | 0.12 (±0.01) | 0.59 (±0.18) | 0.18 (±0.18) | 1.51 (±0.77) | 0.10 (±0.02) | 0.10 (±0.03) |
| SB_2 | 0.12 (±0.01) | 0.60 (±0.19) | 0.40 (±0.41) | 1.39 (±0.82) | 0.10 (±0.02) | 0.10 (±0.03) |
| SB_3 | 0.12 (±0.01) | 0.57 (±0.20) | 0.40 (±0.40) | 1.48 (±0.77) | 0.11 (±0.02) | 0.11 (±0.04) |
| SB_4 | 0.11 (±0.01) | 0.50 (±0.16) | 0.53 (±0.50) | 1.19 (±0.59) | 0.15 (±0.20) | 0.11 (±0.03) |
| SB_5 | 0.12 (±0.03) | 0.65 (±0.17) | 0.78 (±0.61) | 2.52 (±0.96) | 0.18 (±0.25) | 0.10 (±0.03) |
| Event | Coefficient of Variation (%) for Sub-Basins | ||||
|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | |
| WR_N1 | 1.0 | 1.0 | 0.6 | 1.1 | 1.9 |
| WR_N2 | 3.4 | 0.7 | 0.7 | 1.7 | 1.0 |
| WR_N3 | 3.8 | 2.3 | 4.6 | 2.4 | 2.4 |
| WR_N4 | 4.4 | 3.4 | 1.9 | 1.1 | 0.6 |
| WR_N5 | 9.1 | 3.7 | 1.9 | 1.3 | 2.4 |
| WR_N6 | 3.2 | 1.5 | 1.4 | 1.8 | 1.6 |
| WR_N7 | 2.7 | 0.9 | 0.7 | 2.9 | 2.3 |
| WR_N8 | 2.5 | 0.8 | 1.0 | 0.5 | 1.4 |
| WR_N9 | 12.4 | 3.4 | 3.6 | 1.4 | 3.7 |
| WR_N10 | 1.2 | 2.8 | 2.8 | 3.0 | 2.9 |
| Mean | 4.4 | 2.0 | 1.9 | 1.7 | 2.0 |
| CR_N1 | – | 44.0 | 14.7 | 11.2 | 5.8 |
| CR_N2 | 43.0 | 26.4 | 13.2 | 9.9 | 10.6 |
| CR_N3 | 16.2 | 2.0 | 2.4 | 2.3 | 2.2 |
| CR_N4 | 47.0 | 10.9 | 6.4 | 3.9 | 6.8 |
| CR_N5 | – | 8.7 | 7.9 | 3.5 | 3.6 |
| CR_N6 | 7.4 | 2.5 | 1.3 | 4.4 | 2.0 |
| CR_N7 | – | 48.2 | 9.0 | 44.6 | 3.5 |
| CR_N8 | 23.7 | 12.1 | 3.3 | 9.6 | 3.3 |
| CR_N9 | 37.3 | 4.4 | 2.1 | 2.6 | 1.4 |
| CR_N10 | 18.8 | 5.0 | 4.0 | 3.7 | 3.6 |
| Mean | 27.6 | 16.4 | 6.4 | 9.6 | 4.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
P. C., S.; Nakatani, T.; Misumi, R. The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan. Water 2019, 11, 1703. https://doi.org/10.3390/w11081703
P. C. S, Nakatani T, Misumi R. The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan. Water. 2019; 11(8):1703. https://doi.org/10.3390/w11081703
Chicago/Turabian StyleP. C., Shakti, Tsuyoshi Nakatani, and Ryohei Misumi. 2019. "The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan" Water 11, no. 8: 1703. https://doi.org/10.3390/w11081703
APA StyleP. C., S., Nakatani, T., & Misumi, R. (2019). The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan. Water, 11(8), 1703. https://doi.org/10.3390/w11081703






