Change in the Extent of Glaciers and Glacier Runoff in the Chinese Sector of the Ile River Basin between 1962 and 2012
Abstract
1. Introduction
2. Study Area
Climate
3. Data and Methods
3.1. Meteorological and Streamflow Data and Calculation of Trends
3.2. Assessment of Changes in Glacier Area
3.3. Calculation of Runoff from Glacier Surface
3.3.1. Calculation of Runoff from Glacier Surface Using Degree-Day Model
3.3.2. Calculation of Glacier Runoff Using Temperature-Index Method
3.3.3. Calculation of Glacier Runoff from Changes in Ice Volume
3.3.4. Separation of Runoff Components
4. Results
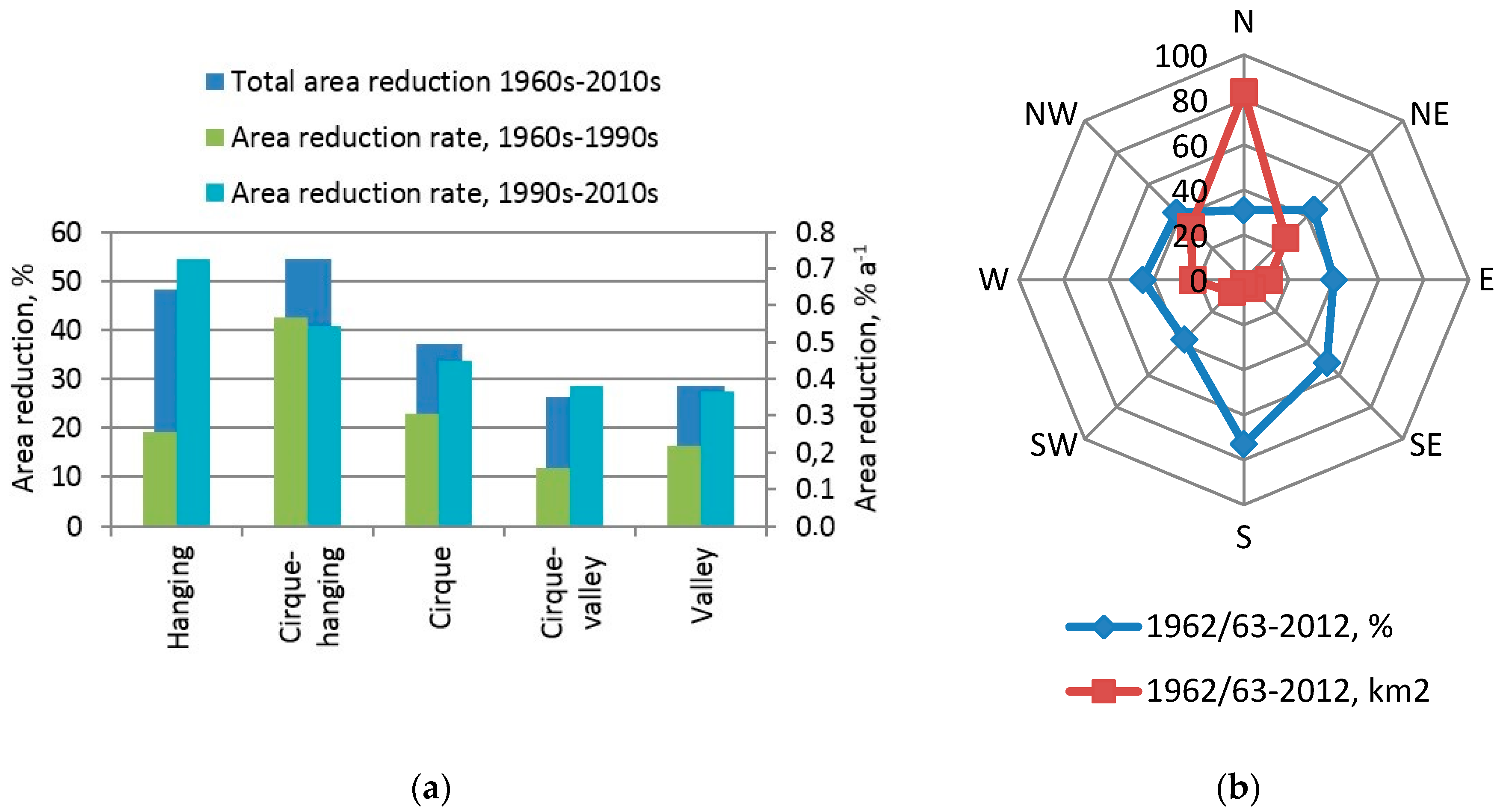
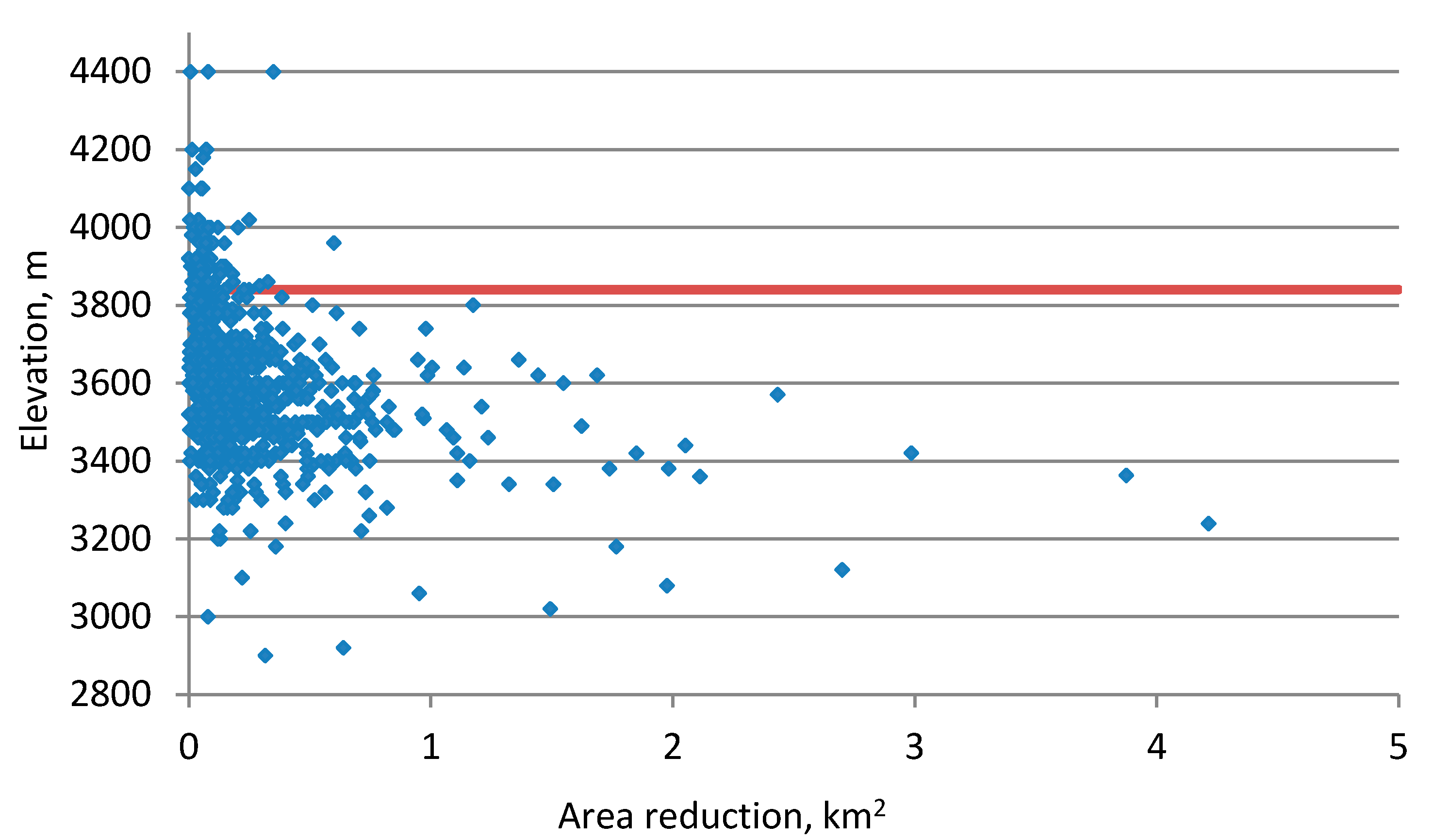
4.1. Changes in Glacier Area in the Kuksu, Kunes, and Qiedeke River Basins
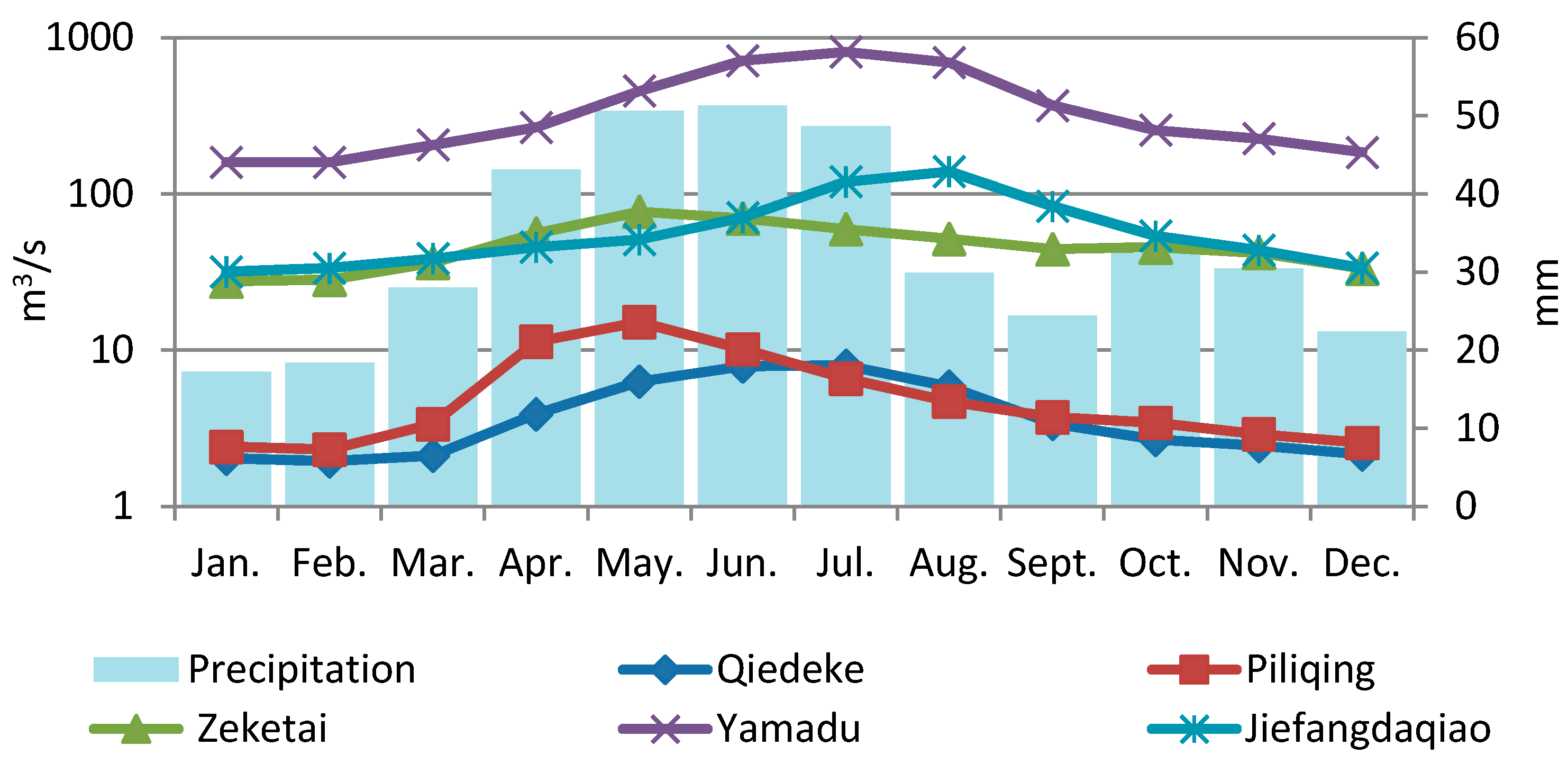
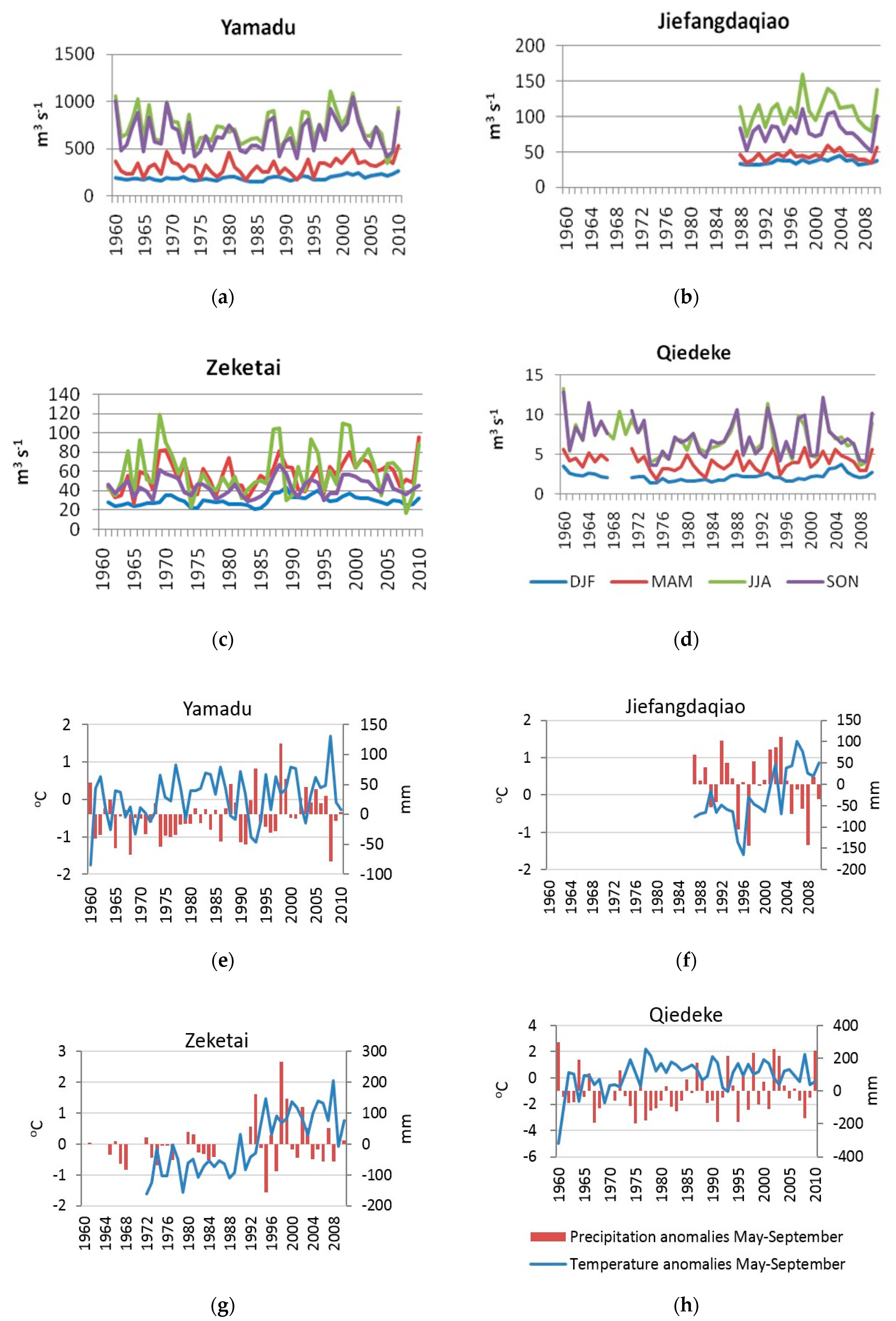
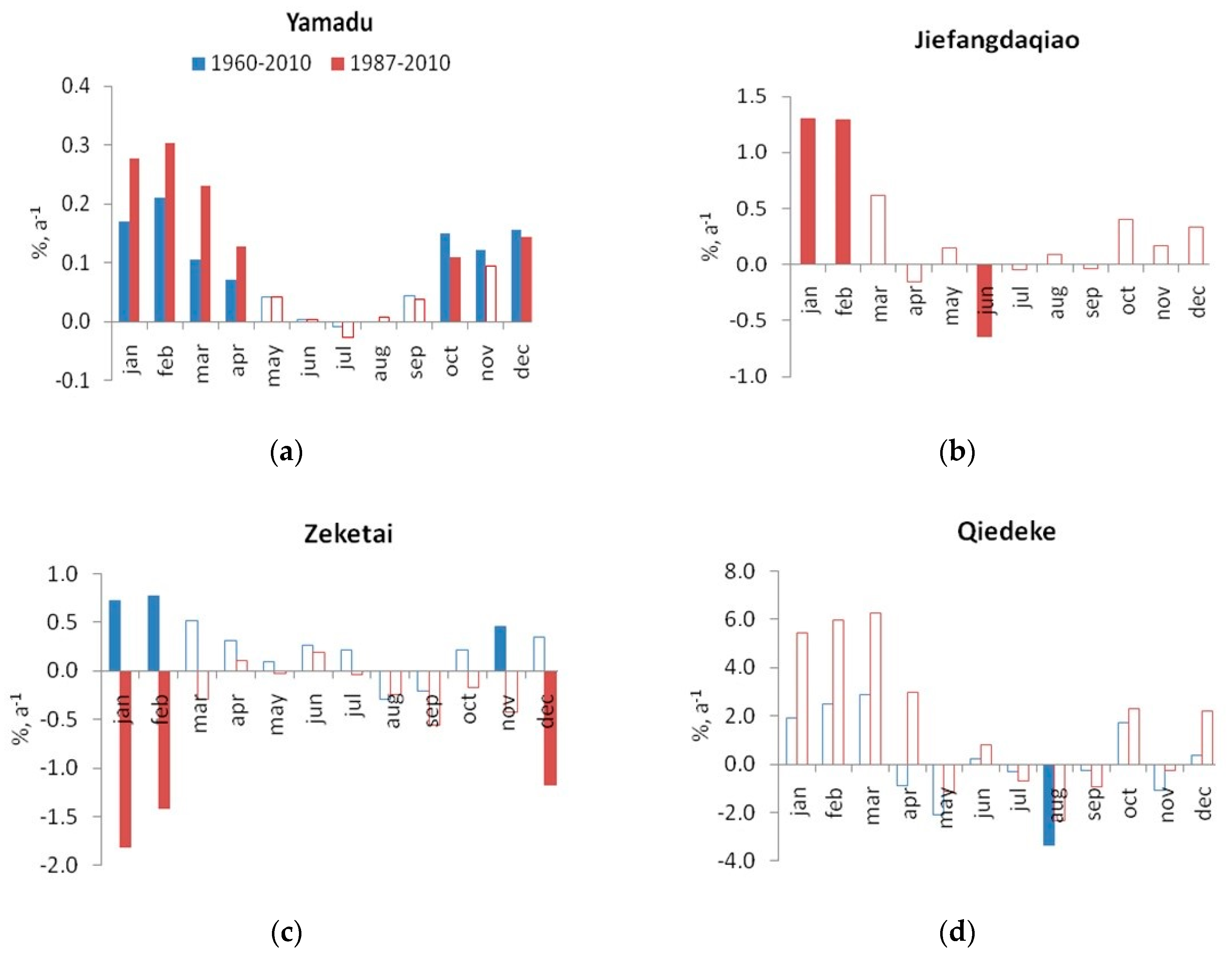
4.2. Changes in Streamflow
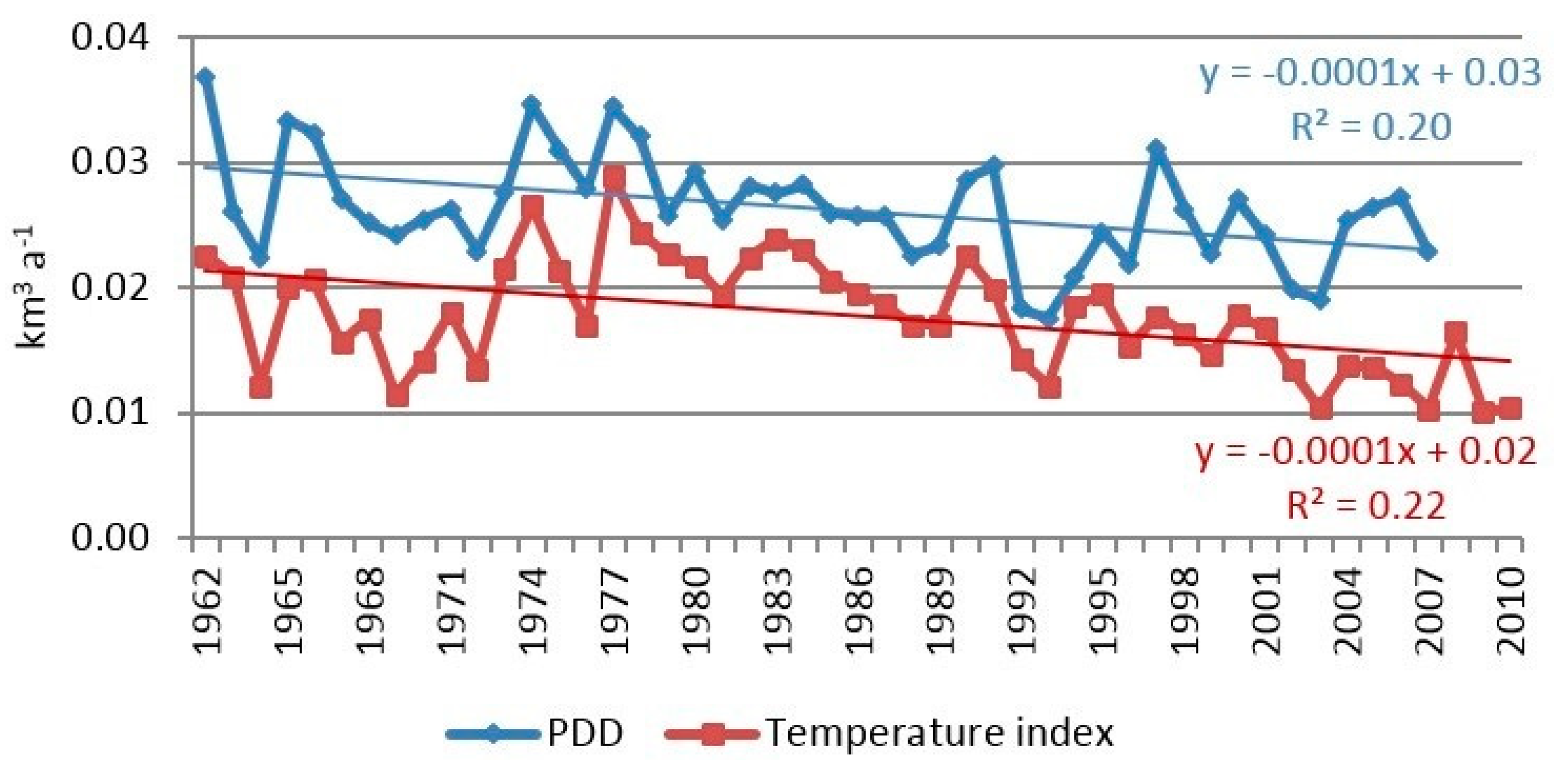
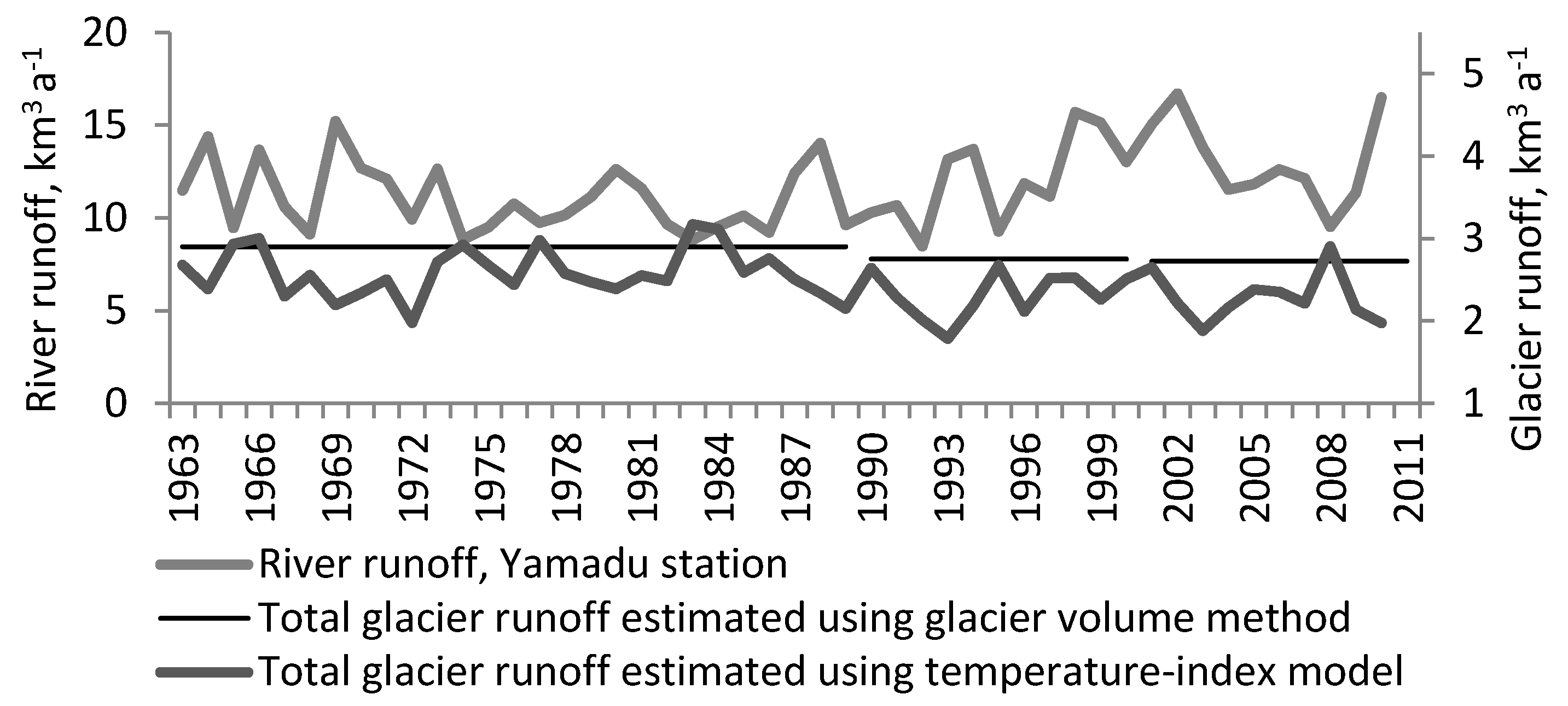
4.3. Runoff from Glacier Surfaces Calculated by PDD and Temperature-Index Methods
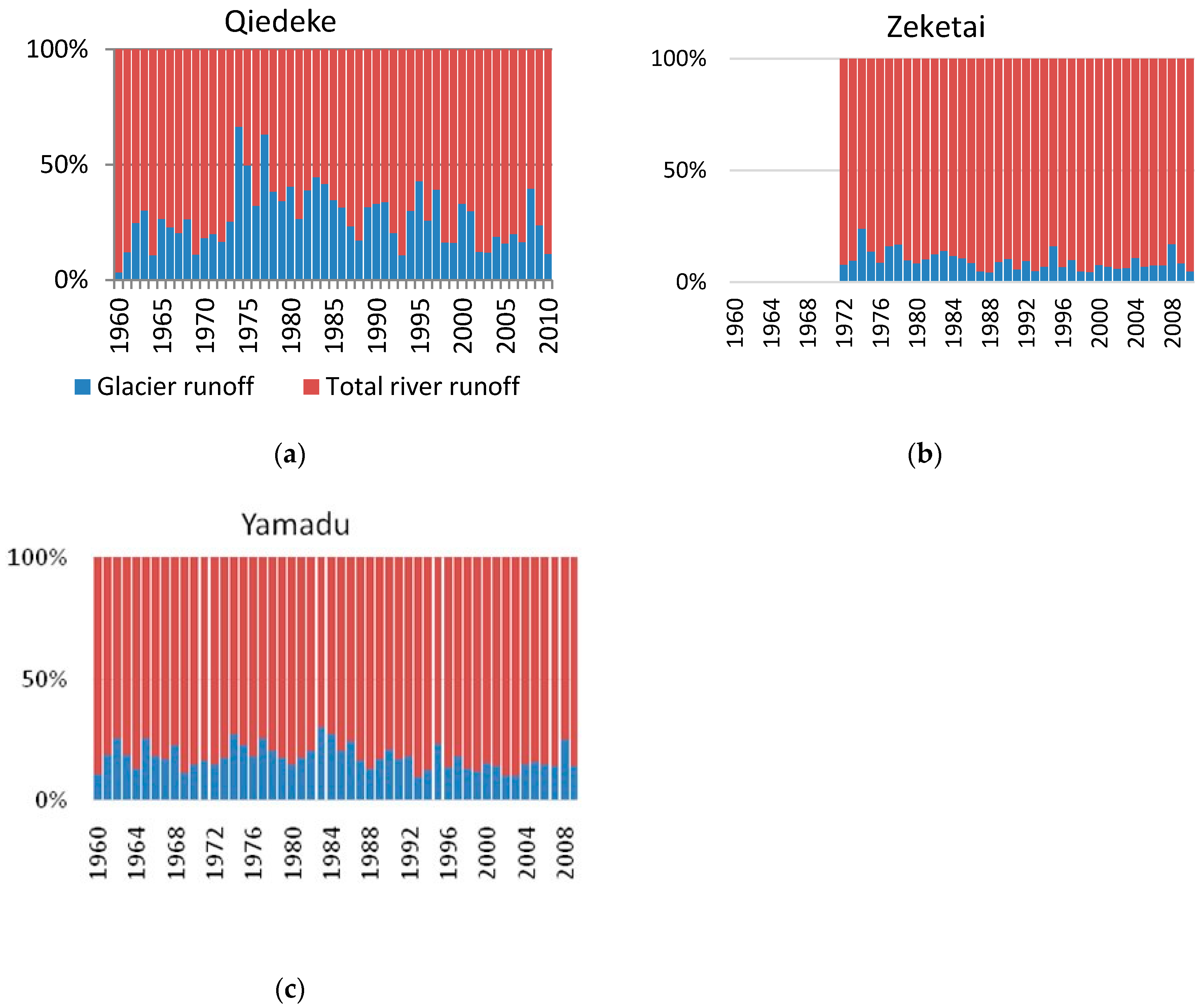
4.4. Calculation of Runoff from Melting of Muli-Year Ice from Changes in Ice Volume
5. Discussion
6. Conclusions
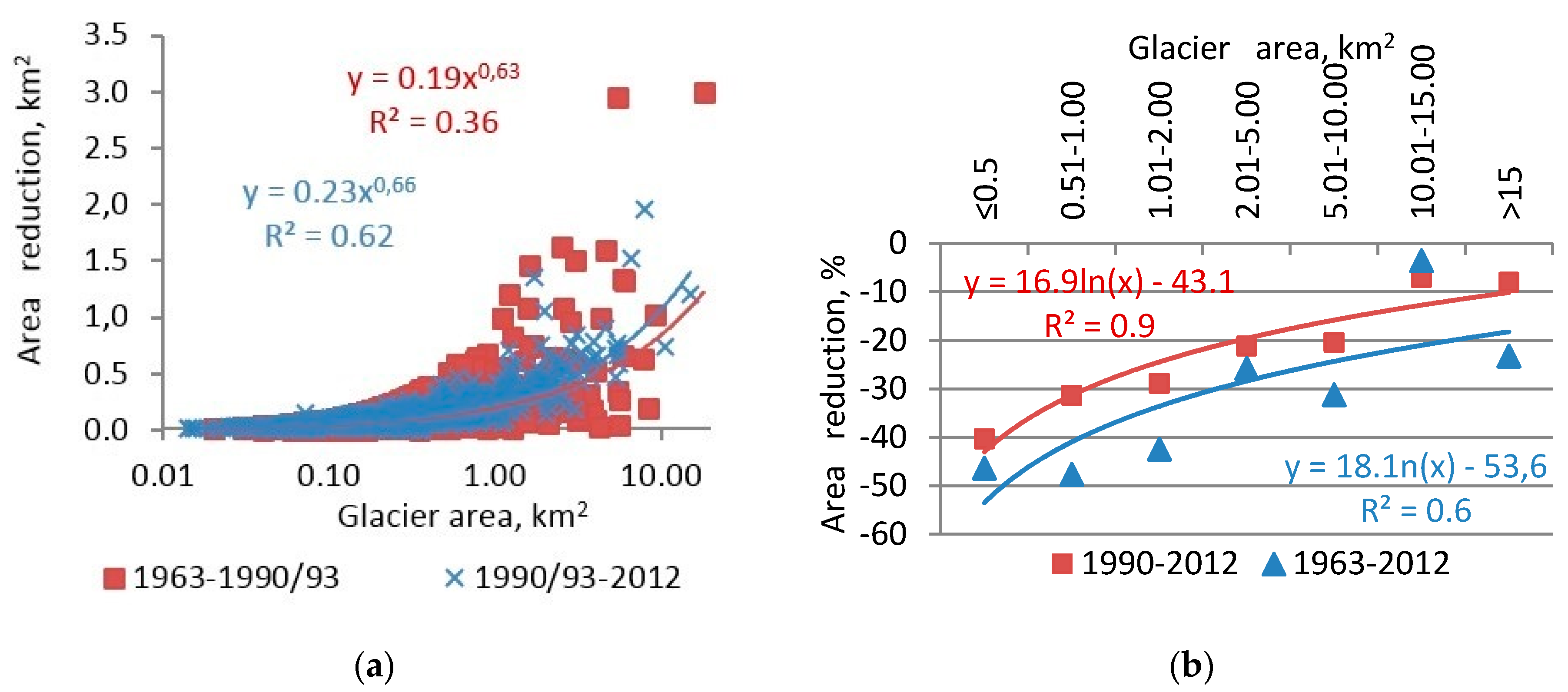
- In the Kuksu, Kunes, and Qiedeke basins of the C-IRB region, glaciers lost 191.3 km2 or 36.9% of their initial area between the 1960s and 2010s;
- Glacier wastage intensified from 0.5% to 1.2% a−1 in the 1962/63–1990/93 and 1990/93–2012 periods, respectively;
- There were no statistically significant trends in the streamflow of the Ile and its tributaries during the warm season to date, although negative trends were registered in the Qiedeke streamflow in August and, more recently, in the Tekes flow at Jiefangdaqiao in June;
- Positive trends were registered in the Tekes flow at Jiefangdaqiao in winter and in the Ile flow at Yamadu in autumn, winter, and early spring, in line with similar trends observed in other regions of the Tien Shan; and
- The estimations of total glacier runoff and runoff formed through the loss of multiyear ice in the Ile basin showed a reduction in both absolute values and its share in total river runoff since the 1980s in contrast to total river runoff.
Author Contributions
Funding
Conflicts of Interest
References
- Sorg, A.; Bolch, T.; Stoffel, M.; Solomina, O.; Beniston, M. Climate change impacts on glaciers and runoff in Tien Shan (Central Asia). Nat. Clim. Chang. 2012, 2, 725–731. [Google Scholar] [CrossRef]
- Unger-Shayesteh, K.; Vorogushyn, S.; Farinotti, D.; Gafurov, A.; Duethmanna, D.; Mandychevc, A.; Merza, B. What do we know about past changes in the water cycle of Central Asian headwaters? A review. Glob. Planet. Chang. 2013, 110, 4–25. [Google Scholar] [CrossRef]
- Groisman, P.; Shugat, H.; Kicklinghter, D.; Henerby, G.; Tchebakova, N.; Maksyutov, S.; Monier, E.; Gutman, G.; Gulev, S.; Qi, J.; et al. Northern Eurasia Future Initiative (NEFI): Facing the challenges and pathways of global change in the twenty-first century. Prog. Earth Planet. Sci. 2017, 4, 41. [Google Scholar] [CrossRef]
- Shchetinnikov, S.A. The Morphology and Regime of Pamir-Alai Glaciers; Central Asia Hydro-Meteorological Institute: Tashken, Uzbekistan, 1998; p. 219. (In Russian) [Google Scholar]
- Aizen, V.B.; Aizen, E.M.; Surazakov, A.B.; Kuzmichenok, V. Assessment of Glacial Area and Volume Change in Tien Shan (Central Asia) During the Last 150 years Using Geodetic, Aerial Photo, ASTER and SRTM Data. Ann. Glaciol. 2006, 43, 202–213. [Google Scholar] [CrossRef]
- Li, B.; Zhu, A.X.; Zhang, Y.; Pei, T.; Qin, C.; Zhou, C. Glacier change over the past four decades in the middle Chinese Tien Shan. J. Glaciol. 2006, 52, 425–432. [Google Scholar] [CrossRef]
- Shangguan, D.; Liu, S.; Ding, Y.; Ding, L.; Xu, J.; Li, J. Glacier changes during the last forty years in the Tarim Interior River basin, northwest China. Prog. Nat. Sci. 2006, 19, 727–732. [Google Scholar] [CrossRef]
- Shi, Y. Concise Glacier Inventory of China; Popular Science Press: Shanghai, China, 2008; pp. 0–205. [Google Scholar]
- Kotlyakov, V.; Severskiy, I. Glaciers of central Asia: Current situation, changes and possible impact on water resources. In Assessment of Snow, Glacier and Water Resources in Asia; Braun, L., Hagg, W., Severskiy, I., Young, G., Eds.; International Hydrological Program–Hydrology and Water Resources Programme: Koblenz, Germany, 2009; pp. 151–159. [Google Scholar]
- Kutuzov, S.; Shahgedanova, M. Glacier retreat and climatic variability in the eastern Terskey-Alatoo, inner Tien Shan between the middle of the 19th century and beginning of the 21st century. Global Planet. Chang. 2009, 69, 59–70. [Google Scholar] [CrossRef]
- Narama, C.; Kääb, A.; Duishonakunov, M.; Abdrakhmanov, K. Spatial variability of recent glacier area changes in the Tien Shan Mountains, Central Asia, using Corona (~1970), Landsat (~2000), and ALOS (~2007) satellite data. Global Planet. Chang. 2010, 71, 42–54. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Wang, F.; Edwards, R. Glacier shrinkage in the Ebinur lake basin, Tien Shan, China, during the past 40 years. J. Glaciol. 2014, 60, 245–254. [Google Scholar] [CrossRef]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Molg, T.; Bolch, T.; Vorogushin, S.; Guntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Pieczonka, T.; Bolch, T. Region-wide glacier mass budgets and area changes for the Central Tien Shan between 1975 and 1999 using Hexagon KH-9 imagery. Global Planet. Chang. 2015, 128, 1–13. [Google Scholar] [CrossRef]
- Cogley, J.G. Glacier shrinkage across High Mountain Asia. Ann. Glaciol. 2016, 57, 41–49. [Google Scholar] [CrossRef]
- Severskiy, I.; Vilesov, E.; Armstrong, R.; Kokarev, A.; Kogutenko, L.; Usmanova, Z.; Morozova, V.; Raup, H.B. Changes in glaciers of the Balkhash-Alakol basin, Central Asia, over recent decades. Ann. Glaciol. 2016, 57, 382–394. [Google Scholar] [CrossRef]
- WGMS. Global Glacier Change Bulletin No. 2 (2014–2015), Based on database version; Zemp, M., Nussbaumer, S.U., GärtnerRoer, I., Huber, J., Machguth, H., Paul, F., Hoelzle, M., Eds.; ICSU(WDS)/IUGG(IACS)/UNEP/UNESCO/WMO, World Glacier Monitoring Service: Zurich, Switzerland, 2015; p. 244. [Google Scholar] [CrossRef]
- Cao, M.S. Detection of abrupt changes in glacier mass balance in the Tien Shan Mountains. J. Glaciol. 1998, 44, 352–358. [Google Scholar] [CrossRef][Green Version]
- Vilesov, E.; Uvarov, V. Evolution of the Recent Glaciation in the Zailyskiy Alatau in the 20th Century; Kazakh State University: Almaty, Kazakhstan, 2001; pp. 0–252. (In Russian) [Google Scholar]
- Severskiy, I.V.; Kokarev, A.L.; Severskiy, S.I.; Tokmagambetov, T.; Shesterova, I.; Shagalova, L. Contemporary and Prognostic Changes of Glaciation in Balkhash Lake Basin; VAC Publishing House: Almaty, Kazakhstan, 2006; p. 68. [Google Scholar]
- Aizen, V.B.; Aizen, E.M.; Kuzmichenok, V.A. Glaciers and hydrological changes in the Tien Shan: Simulation and prediction. Environ. Res. Lett. 2007, 2, 045019. [Google Scholar] [CrossRef]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Global Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
- Yao, T.; Wang, Y.; Liu, S.; Pu, J.; Shen, Y.; Lu, A. Recent glacial retreat in the Chinese part of High Asia and its impact on water resources of Northwest China. In Assessment of Snow, Glacier and Water Resources in Asia; Braun, L., Hagg, W., Severskiy, I., Young, G., Eds.; International Hydrological Program–Hydrology and Water Resources Programme: Koblenz, Germany, 2009; pp. 26–35. [Google Scholar]
- Barandun, M.; Huss, M.; Usubaliev, R.; Azisov, E.; Berthier, E.; Kääb, A.; Bolch, T.; Hoelzle, M. Multi-decadal mass balance series of three Kyrgyz glaciers inferred from modelling constrained with repeated snow line observations. Cryosphere 2018, 12, 1899–1919. [Google Scholar] [CrossRef]
- Osmonov, A.; Bolch, T.; Xi, C.; Kurban, A.; Guo, W. Glacier characteristics and changes in the Sary-Jaz River Basin (Central Tien Shan, Kyrgyzstan)—1990–2010. Remote Sens. Lett. 2013, 4, 725–734. [Google Scholar] [CrossRef]
- Niederer, P.; Bilenko, V.; Ershove, N.; Hurni, H.; Yerokin, S.; Maselli, D. Tracing glacier wastage in the Northern Tien Shan (Kyrgyzstan/Central Asia) over the last 40 years. Clim. Chang. 2008, 86, 227–234. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Li, Z.; Wang, F.; Li, H.; Li, Y.; Huang, X. Glacier area variation and climate change in the Chinese Tianshan Mountains since 1960. J. Geogr. Sci. 2011, 21, 263–273. [Google Scholar] [CrossRef]
- Severskiy, I.V. Current and projected changes of glaciation in Central Asia and their probable impact on water resources. In Assessment of Snow, Glacier and Water Resources in Asia; UNESCO-IH and German IHP/HWRP National Committee: Koblenz, Germany, 2009; pp. 99–111. [Google Scholar]
- Kriegel, D.C.; Mayer, W.; Hagg, S.; Vorogushin, S.; Duethmann, D.; Gafurov, A.; Farinotti, D. Changes in glacierisation, climate and runoff in the second half of the 20th century in the Naryn basin, Central Asia. Global Planet. Chang. 2013, 110, 51–61. [Google Scholar] [CrossRef]
- Duethmann, D.; Menz, C.; Jiang, T.; Vorogushin, S. Projections for headwater catchments of the Tarim River reveal glacier retreat and decreasing surface water availability but uncertainties are large. Environ. Res. Lett. 2016, 11, 054024. [Google Scholar] [CrossRef]
- Shahgedanova, M.; Afzal, M.; Severskiy, I.; Usmanova, Z.; Saidaliyeva, Z.; Kapitsa, V.; Kasatkin, N.; Dolgikh, S. Changes in the mountain river discharge in the northern Tien Shan since the mid-20th Century: Results from the analysis of a homogeneous daily streamflow data set from seven catchments. J. Hydrol. 2018, 564, 1133–1152. [Google Scholar] [CrossRef]
- Hagg, W.; Hoelzle, M.; Wagner, S.; Mayr, E.; Klose, Z. Glacier and runoff changes in the Rukhk catchment, upper Amu-Darya basin until 2050. Global Planet. Chang. 2013, 110, 62–73. [Google Scholar] [CrossRef]
- Ma, C.; Sun, L.; Liu, S.; Shao, M.; Luo, Y. Impact of climate change on the streamflow in the glacierized Chu River Basin, Central Asia. J. Arid Land 2015, 7, 501–513. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Bierkens, M.F.P.; Lutz, A.F.; Immerzeel, W. Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 2017, 549, 257. [Google Scholar] [CrossRef]
- Zhupankhan, A.; Tussupova, K.; Berndtsson, R. Could changing power relationships lead to better water sharing in Central Asia? Water 2017, 9, 139. [Google Scholar] [CrossRef]
- Kezer, K.; Matsuyama, H. Decrease of river runoff in the Lake Balkhash basin in Central Asia. Hydrol. Process. 2006, 20, 1407–1423. [Google Scholar] [CrossRef]
- Yapiyev, V.; Sagintayev, Z.; Verhoef, A.; Kassymbekova, A.; Baigaliyeva, M.; Zhumabayev, D.; Abudanash, D.; Ongdas, N.; Jumassultanova, S. The changing water cycle: Burabay National Nature Park, Northern Kazakhstan. Water 2017, 4, e1227. [Google Scholar] [CrossRef]
- Ding, L.; Xie, W.; Liu, C.; Wang, C.; Wang, Z. Glacier Inventory of China III. Tienshan Mountains (Ile River Drainage Basin); Science Press, Academia Sinica, Lanzhou Institute of Glaciology and Geocryology, Chinese Academy of Sciences: Beijing, China, 1986. (In Chinese) [Google Scholar]
- Guo, W.; Liu, S.; Xu, J.; Wu, L.; Shangguan, D.; Yao, X.; Wei, J.; Bao, W.; Yu, P.; Liu, Q.; et al. The second Chinese glacier inventory: Data, methods and results. J. Glaciol. 2015, 61, 357–372. [Google Scholar] [CrossRef]
- Xu, J.; Liu, S.; Guo, W.; Zhang, Z.; Wei, J.; Feng, T. Glacial Area Changes in the Ili River Catchment (Northeastern Tian Shan) in Xinjiang, China, from the 1960s to 2009. Adv. Meteorol. 2015, 12. [Google Scholar] [CrossRef]
- CMWR (China’s Ministry of Water Resources). Evaluation of Chinese Water Resources; Water Resources Publisher: Beijing, China, 1987; p. 194. (In Chinese)
- Severskiy, I.V.; Xie, Z. Snow Cover and Avalanches in Tien Shan Mountains; VAC Publishing House: Almaty, Kazakhstan, 2000; p. 179. [Google Scholar]
- Severskiy, I.; Blagoveshenskiy, V. Estimation of Avalanches Hazards of Mountain Area; Science: Almaty, Kazakhstan, 1983; p. 215. (In Russian) [Google Scholar]
- Schroder, H.; Severskiy, I. Water Resources in the Basin of the Ili River (Republic of Kazakhstan): Final Report; Mensch and Buch Verlag: Berlin, Germany, 2004; p. 310. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters. Environ. Process. 2015, 2, 729–749. [Google Scholar] [CrossRef]
- GLOVIS. Available online: http://glovis.usgs.gov/ (accessed on 23 June 2019).
- GLIMS: Global Land Ice Measurements from Space. Available online: http://www.glims.org/ (accessed on 23 June 2019).
- Arendt, A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Huss, M.; Kaser, G.; Kienholz, C.; et al. Randolph Glacier Inventory—A Dataset of Global Glacier Outlines: Version 4.0. In Global Land Ice Measurements from Space; Digital Media: Boulder, CO, USA, 2014. [Google Scholar]
- Arendt, A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Huss, M.; Kaser, G.; Kienholz, C.; et al. Randolph Glacier Inventory—A Dataset of Global Glacier Outlines: Version 5.0. In Global Land Ice Measurements from Space; Digital Media: Boulder, CO, USA, 2015. [Google Scholar]
- Global Land Survey 2000. Available online: http://landsat.usgs.gov/GLS2000_Accuracy.php (accessed on 23 June 2019).
- ASTER Global Digital Elevation Map. Available online: https://asterweb.jpl.nasa.gov/gdem.asp (accessed on 23 June 2019).
- Kapitsa, V.; Shahgedanova, M.; Machguth, H.; Severskiy, I.; Medeu, A. Assessment of evolution and risks of glacier lake outbursts in the Djungarskiy Alatau, Central Asia, using Landsat imagery and glacier bed topography modelling. Nat. Hazards Earth Syst. Sci. 2017, 17, 1837–1856. [Google Scholar] [CrossRef]
- Bolch, T.; Kamp, U. Glacier mapping in high mountains using DEMs, Landsat and ASTER data. Grazer Schr. Geogr. Raumforsch. 2006, 41, 13–24. [Google Scholar]
- Paul, F.; Barry, R.G.; Cogley, J.G.; Frey, H.; Haeberli, W.; Ohmura, A.; Ommanney, C.S.L.; Raup, B.; Rivera, A.; Zemp, M. Recommendations for the compilation of glacier inventory data from digital sources. Ann. Glaciol. 2009, 50, 119–126. [Google Scholar] [CrossRef]
- Kokarev, A.; Shesterova, I. Change of the glacier systems on the northern slope of Zailiyskiy Alatau for the second half of XX and the beginning of XXI centuries. Ice Snow 2011, 4, 39–46. (In Russian) [Google Scholar]
- Bolch, T.; Menounos, B.; Wheate, R. Landsat-based inventory of glaciers in western Canada, 1985–2005. Remote Sens. Environ. 2010, 114, 127–137. [Google Scholar] [CrossRef]
- Cogley, J.G.; Hock, R.; Rasmussen, L.A.; Arendt, A.A.; Bauder, A.; Braithwaite, R.J.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L.; et al. Glossary of Glacier Mass Balance and Related Terms; IHP-VII Technical Documents in Hydrology No. 86, IACS Contribution No. 2; UNESCO-IHP: Paris, France, 2011. [Google Scholar]
- Braithwaite, R. Temperature and precipitation climate at the equilibrium-line altitude of glaciers expressed by the degree-day factor for melting snow. J. Glaciol. 2008, 54, 437–444. [Google Scholar] [CrossRef]
- Hock, R. Temperature Index Melt Modelling in Mountain Areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Lang, H.; Braun, L. On the information content of air temperature in the context of snow melt estimation. In Hydrology of Mountainous Areas, Proceedings of the Strbské Pleso Workshop, Czechoslovakia, Strbské Pleso 1 June 1988; Molnar, L., Ed.; International Association of Hydrological Sciences Publication: Wallingford, UK, 1990; pp. 347–354. [Google Scholar]
- Yatagai, A.O.; Arakawa, K.; Kamiguchi, H.; Kawamoto, H.; Nodzu, M.I.; Hamada, A. A 44-year daily gridded precipitation dataset for Asia based on a dense network of rain gauges. SOLA 2009, 5, 137–140. [Google Scholar] [CrossRef]
- Yatagai, A.K.; Kamiguchi, O.; Arakawa, A.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a Long-term Daily Gridded Precipitation Dataset for Asia based on a Dense Network of Rain Gauges. Bull. Am. Meteorol. Soc. 2012. [Google Scholar] [CrossRef]
- Krenke, A. Mass Transfer in Glacial Systems in the USSR; Gydrometeoizdat: Leningrad, Russia, 1982; p. 288. (In Russian) [Google Scholar]
- Bahr, D.; Pfeffer, W.; Kaser, G. A review of volume-area scaling of glaciers. Rev. Geophys. 2014, 53, 95–140. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Ohmura, A. Estimation of Alpine glacier water resources and their change since the 1870s. Hydrology in mountainous regions. In I–Hydrological Measurements; the Water Cycle, Proceedings of Two Lausanne Symposia, August 1990; International Association of Hydrological Sciences Publication: Wallingford, UK, 1990; Volume 193, pp. 127–135. [Google Scholar]
- Raper, S.C.; Braithwaite, R.J. Low sea level rise projections from mountain glaciers and icecaps under global warming. Nature 2006, 439, 311–313. [Google Scholar] [CrossRef] [PubMed]
- Farinotti, D.; Huss, M.; Bauder, A.; Funk, M.; Truffer, M. A method to estimate ice volume and ice thickness distribution of alpine glaciers. J. Glaciol. 2009, 55, 422–430. [Google Scholar] [CrossRef]
- Radic, V.; Hock, R. Regionally differentiated contribution of mountain glaciers and ice caps to future sea-level rise. Nat. Geosci. 2011, 4, 91–94. [Google Scholar] [CrossRef]
- Sosedov, I. Methods of Territorial Water Balance Generalizations in the Mountains; Nauka: Almaty, Kazakhstan, 1976; p. 154. (In Russian) [Google Scholar]
- Armstrong, R.L. The Glaciers of the Hindu Kush-Himalayan Region: A Summary of the Science Regarding glacier Melt/Retreat in the Himalayanm, Hindu Kush, Karakorum, Pamir, and Tien Shan mountain ranges; Technical Report; International Centre for Integrated Mountain Development (ICIMOD): Kathmandu, Nepal, 2010; pp. 0–16. [Google Scholar]
- Kotlyakov, V. Glaciologycal Dictionary; Hydrometeoizdat: Leningra, Russia, 1984; p. 564. (In Rusian) [Google Scholar]
- Kemmerikh, A.O. Rol’lednikov v stoke rek Sredney Azii; (The role of glaciers for river runoff in Central Asia), Materialy Glaciologicheskikh Issledovanii (Data of Glaciological Studies); Nauka Publisher: Moscow, Russia, 1972; Volume 20, pp. 82–94. (In Russian) [Google Scholar]
- He, Y.; Pang, H.; Theakstone, W.; Zhang, D.; Lu, A.; Song, B.; Yuan, L.; Ning, B. Spatial and temporal variations of oxygen isotopes in snowpacks and glacial runoff in different types of glacial area in western China. Ann. Glaciol. 2006, 43, 269–274. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, S.; He, J.; Pu, J.; Wu, X.B.; Xi, J. Tracing the major source area of the mountainous runoff generation of the Heihe River in northwest China using stable isotope technique Chin. Sci. Bull. 2009, 54, 2751–2757. [Google Scholar] [CrossRef]
- Oberhänsli, H.; Weise, S.; Stanichny, S. Oxygen and hydrogen isotopic water characteristics of the Aral Sea, Central Asia. J. Mar. Syst. 2009, 76, 310–321. [Google Scholar] [CrossRef]
- Dahlke, H.E.; Lyon, S.W.; Jansson, P.; Karlin, T.; Rosqvist, G. Isotopic investigation of runoff generation in a glacierized catchment in northern Sweden. Hydrol. Process. 2016, 28, 1383–1398. [Google Scholar] [CrossRef]
- Dyurgerov, M.B.; Liu, C.; Xie, Z. Tien Shan Glaciers; BINITI: Moscow, Russia, 1995; p. 233. (In Russian) [Google Scholar]
- Glazirin, G.E. Distribution and Regime of Mountain Glaciers; Hydrometeoizdat: Leningrad, Russia, 1985; p. 180. (In Russian) [Google Scholar]
- Makarevich, K.G.; Vilesov, E.N.; Golovkova, R.G.; Denisova, T.J.; Shabanov, P.F. The Tuyuksu Glaciers (North Tien Shan); Gidrometeoizdat: Leningrad, Russia, 1984; p. 170. (In Russian) [Google Scholar]
- Wang, P.; Li, Z.; Huai, B.; Wang, W.; Li, H.; Wang, L. Spatial variability of glacial changes and their effects on water resources in the Chinese Tianshan Mountains during the last five decades. J. Arid Land 2015, 7, 717–727. [Google Scholar] [CrossRef]
- Vilesov, E.; Morozova, V.; Severskiy, I. Glaciation Jungar (Zhetysu) Alatau: Past, Present, Future; PH KazNU: Almaty, Kazakhstan, 2013; p. 244. (In Russian) [Google Scholar]
- Kaldybaev, A.; Chen, Y.; Vilesov, E. Glacier change in the Karatal river basin, Zhetysu (Dzhungar) Alatau, Kazakhstan. Ann. Glaciol. 2016, 57, 11–19. [Google Scholar] [CrossRef]
- Liu, S.; Su, Z.; Zhao, J.; Dong, D. Chinese Glacier Illustrations; Chinese Edition.; Popular Science Press: Shanghai, China, 2014; p. 150. [Google Scholar]
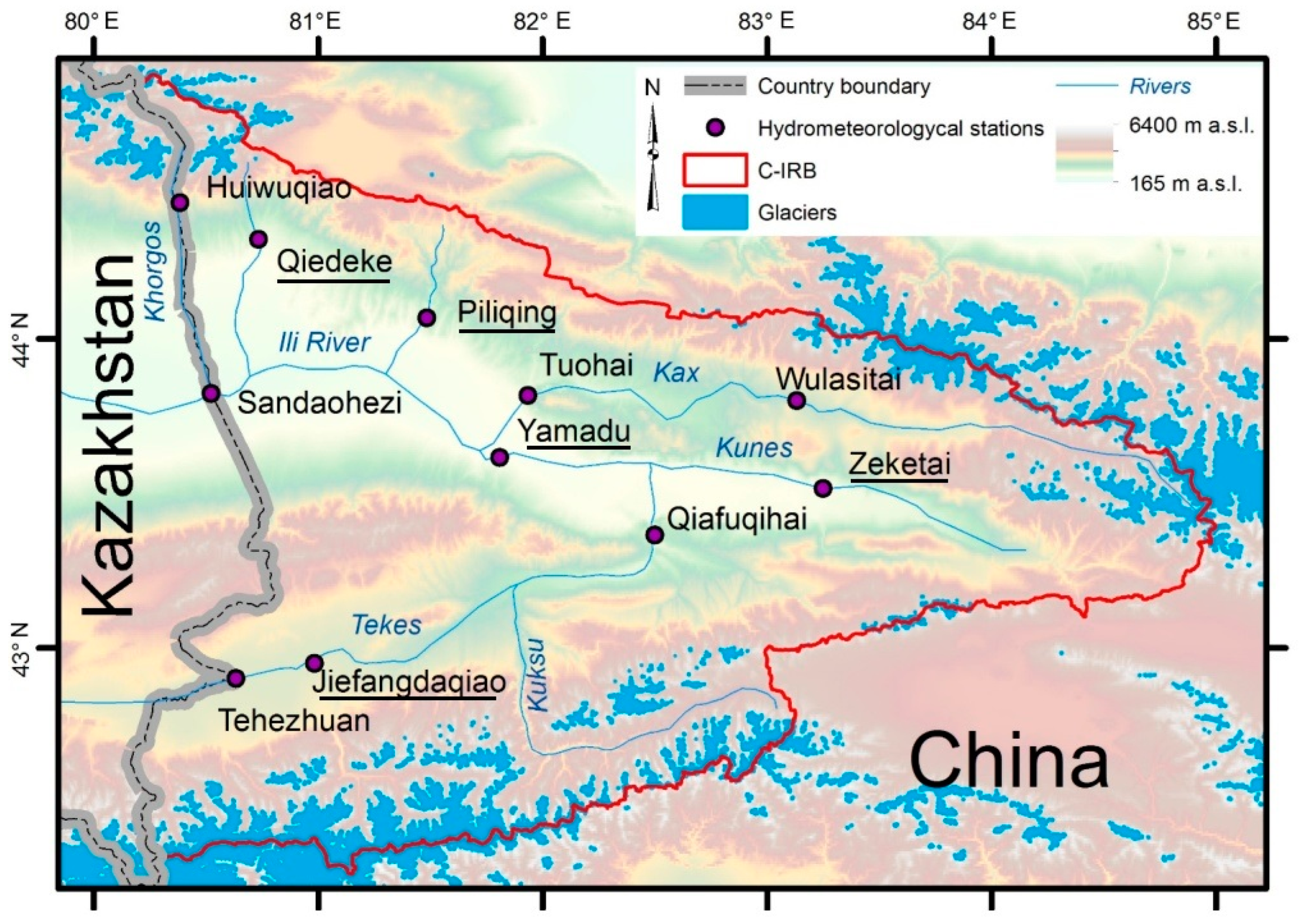
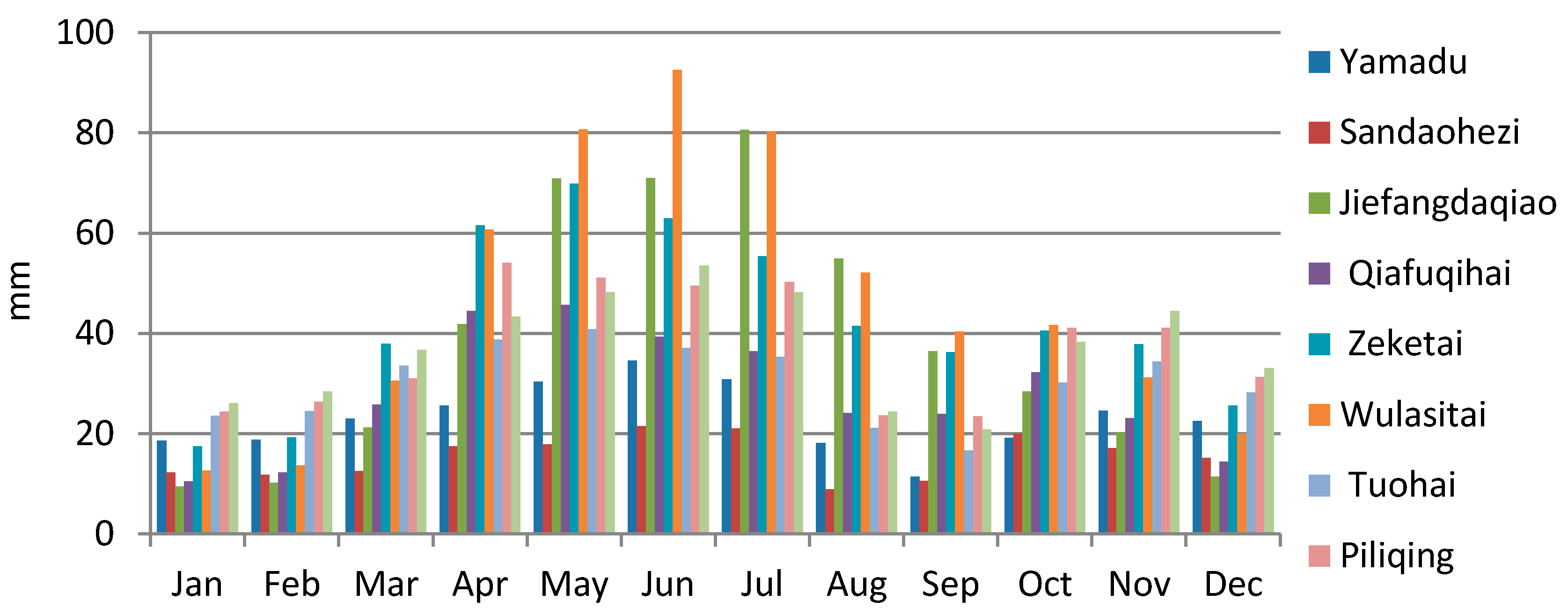
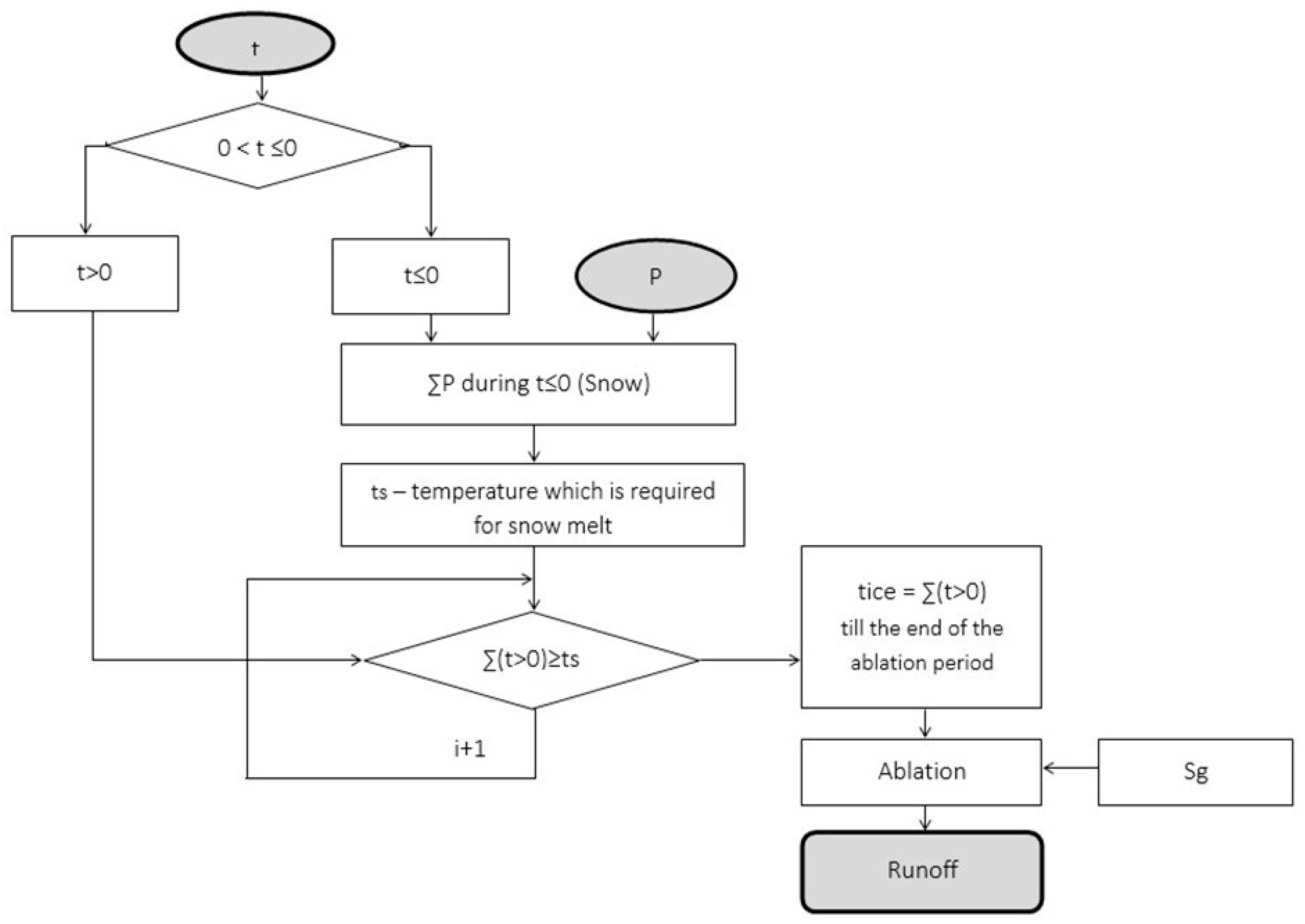
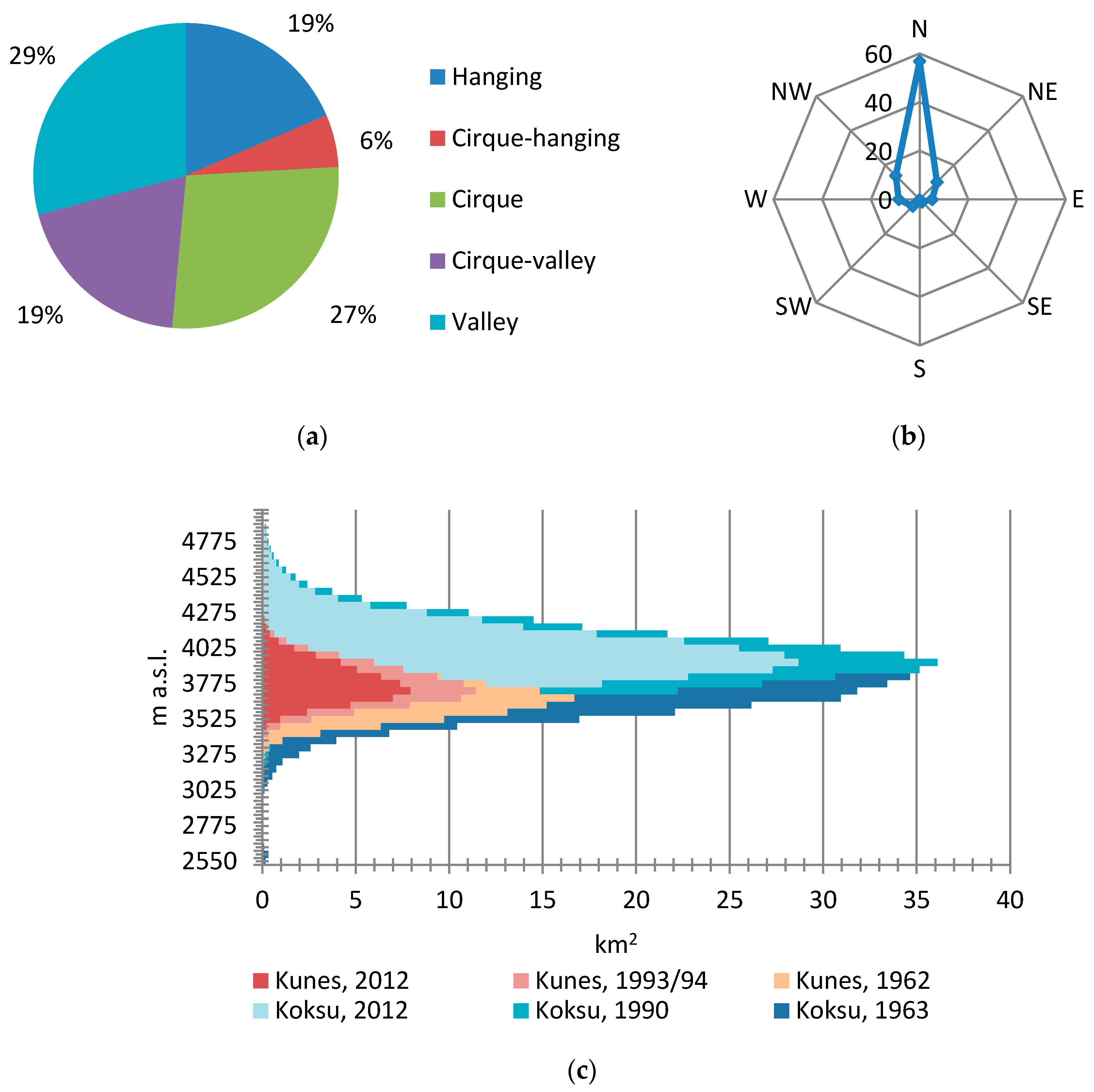
| Name | River | Altitude, m a.s.l. | Start Year | Missing Data | Area, km2 | Glacierized Area, % |
|---|---|---|---|---|---|---|
| Yamadu | Ile | 700 | 1953 | 1954–1956 | 49,186 | 2.8 |
| Sandaohezi | Ile | 530 | 1989 | 1988–1990, 1992, 1994–2001 | 61,640 | 2.2 |
| Jiefangdaqiao | Tekes | 1640 | 1985 | 1985, 1986 | 8635 | 8.0 |
| Qiafuqihai | Tekes | 900 | 1956 | 1956 | 27,402 | 3.6 |
| Tehezhuan | Tekes | 1700 | 2002 | 2002–2004 | 6293 | |
| Zeketai | Kunes | 870 | 1960 | 1969–1971, 1974 | 4123 | 1.0 |
| Wulasitai | Kax | 1440 | 1957 | 2005–2010 | 5081 | 6.0 |
| Tuohai | Kax | 830 | 1953 | 1953–1954, 1993–1994 | 8656 | 3.6 |
| Piliqing | Piliqing | 860 | 1956 | 1994 | 794 | 0.0 |
| Qiedeke | Qiedeke | 940 | 1956 | 1968–1970 | 291 | 3.0 |
| Huiwuqiao | Khorgos | 1290 | 2003 | 2003 | 1160 |
| River Basin | Date | Satellite and Sensor | Resolution |
|---|---|---|---|
| Koksu | 2 August 1990 | Landsat 5TM | 30 m/15 m (multi-spectral/panchromatic) |
| 22 August 1994 | |||
| 31 August 2012 | Landsat 7 ETM+ | ||
| 7 September 2012 | |||
| 1 August 2013 | Landsat 8 OLI TIRS | ||
| Kunes | 2 August 1990 | Landsat 5TM | 30 m/15 m |
| 28 August 1993 | |||
| 22 August 1994 | |||
| 31 August 2012 | Landsat 7 ETM+ | ||
| 7 September 2012 | |||
| 29 August 2014 | Landsat 8 OLI TIRS | ||
| Qiedeke | 20 September 1991 | Landsat 5TM | 30 m/15 m |
| 13 August 2012 | Landsat 7 ETM+ | ||
| 11 August 2014 | Landsat 8 OLI TIRS |
| Glacier Runoff Components | Index | Runoff Volume | |
|---|---|---|---|
| 109 m3 | % | ||
| Snow melting at the firn area | f | 41.8 | 16.1 |
| Snow melting at the terminus | s | 114.5 | 44 |
| Ice melting at the terminus | g | 101.9 | 39.1 |
| Ice melting under the moraine | j | 2.2 | 0.8 |
| Total | 260.4 | 100 | |
| Year | Number | Area, km2 | H min, m | Number | Area, km2 | H min, m |
|---|---|---|---|---|---|---|
| Kuksu | Kunes | |||||
| 1962/63 | 625 | 421.6 | 3680 | 250 | 96.7 | 3554 |
| 1990 | 648 | 376.8 ± 11.3 | - | - | - | - |
| 1993 | - | - | 240 | 81.5 ± 2.4 | - | |
| 2007/09 | 493 | 293.5 ± 14.1 | 3761 | 193 | 51.8 ± 2.5 | 3615 |
| 2011/12 | 638 | 279.2 ± 8.4 | 3746 | 193 | 52.4 ± 1.6 | 3615 |
| Year | 1960s | 1990s | 2010s |
| Area, km2 | 518, 3 | 450, 4 | 326, 9 |
| Period | 1960s–1990s | 1990s–2010s | 1960s–2010s |
| Area change, km2 | 67.8 ± 5.9 | 123.5 ± 10.9 | 191.3 ± 16.8 |
| Rate, km2 a−1 | 2.4 ± 0.2 | 5.6 ± 0.5 | 3.9 ± 0.3 |
| Area change, % | 13.1 ± 8.8 | 27.4 ± 8.4 | 36.9 ± 6.5 |
| Rate, % a−1 | 0.5 ± 0.003 | 1.2 ± 0.003 | 0.8 ± 0.001 |
| Size Class, km2 | Number 1962/63 | Total Clear Ice Area, km2 | Area Loss, %/(% a−1) | |||||
|---|---|---|---|---|---|---|---|---|
| 1962/63 | 1990/93 | 2007/09 | 2012/13 | 1960s–1990s | 1990s–2010s | 1960s–2010s | ||
| ≤0.5 | 634 | 116.8 ± 8.9 | 105.1 ± 4.7 | 52.7 ± 2.5 | 62.7 ± 3.0 | 10 (0.4) | 40 (3.3) | 46 (0.9) |
| 0.51–1.0 | 118 | 83.1 ± 6.3 | 63.4 ± 2.9 | 46.3 ± 2.2 | 43.5 ± 2.1 | 24 (0.9) | 31 (2.6) | 48 (1.0) |
| 1.01–2.0 | 65 | 87.9 ± 6.7 | 71.1 ± 3.2 | 54.1 ± 2.6 | 50.6 ± 2.4 | 19 (0.7) | 29 (2.4) | 42 (0.9) |
| 2.01–5.0 | 46 | 136.7 ± 10.4 | 128.7 ± 5.8 | 111.1 ± 5.3 | 101.5 ± 4.9 | 6 (0.2) | 21 (1.8) | 26 (0.5) |
| 5.01–10.0 | 10 | 65.3 ± 5.0 | 56.4 ± 2.5 | 51.9 ± 2.5 | 44.9 ± 2.2 | 14 (0.5) | 20 (1.7) | 31 (0.6) |
| 10.01–15.0 | 1 | 10.2 ± 0.8 | 10.6 ± 0.5 | 9.8 ± 0.5 | 9.9 ± 0.5 | +4 (+0.1) | 7 (0.6) | 3 (0.1) |
| >15 | 1 | 18.2 ± 1.4 | 15.2 ± 0.7 | 17.1 ± 0.8 | 13.9 ± 0.7 | 17 (0.6) | 8 (0.7) | 23 (0.5) |
| Total | 875 | 518.3 | 450.4 | 343.1 | 326.9 | 13.1 (0.5) | 27.4 (1.2) | 36.9 (0.8) |
| Station | Streamflow, m3 s−1 | Precipitation, mm | Correlation of Streamflow and Precipitation | Correlation of Streamflow and Temperature |
|---|---|---|---|---|
| Qiedeke | 4.1 | 445 | 0.57 | 0.87 |
| Piliqing | 5.7 | 447 | 0.77 | 0.57 |
| Zeketai | 47.6 | 506 | 0.96 | 0.84 |
| Yamadu | 374.8 | 278 | 0.49 | 0.87 |
| Jiefangdaqiao | 62.0 | 457 | 0.68 | 0.77 |
| Basin | 1962/63 | 1990 | 2000 | 2007 | 2008 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|
| Khorgos | 55.2 | 45.3 | 41.7 | 30.7 | 32.2 | 31.6 | 31.4 |
| Kax | 421.6 | 359.2 | 336.9 | 314.1 | 316.8 | 311.5 | 309.7 |
| Kunes | 96.7 | 82.9 | 69.0 | 51. 8 | 57.5 | 56.6 | 52.4 |
| Kuksu | 421.6 | 376.8 | 342.0 | 293.5 | 314.3 | 309.1 | 279.2 |
| Tekes | 1027.6 | 852.4 | 789.9 | 847.8 | 709.3 | 697.4 | 693.5 |
| Basin | Area Loss | Ice Volume, km3 | Ice Volume Loss | |||
|---|---|---|---|---|---|---|
| km2 | % | 1963 | 2011 г. | km3 | % | |
| Kax | −104.8 | −25 | 28.17 | 19.55 | −8.62 | −31 |
| Kunes | −40.1 | −41 | 3.45 | 1.76 | −1.68 | −49 |
| Kuksu | −112.5 | −27 | 23.08 | 14.15 | −8.94 | −39 |
| Tekes | −330.2 | −32 | 85.35 | 46.19 | −39.15 | −46 |
| Total | −611.0 | −30 | 142.18 | 82.69 | −59.49 | −42 |
| Time Period | Measured River Runoff | Qice km3 a−1 | % of Qice in Qriver | Liquid Precipitation km3 a−1 | Qglacial km3 a−1 | % of Qglacial in Qriver | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | Veg. Period | Year | Veg. Period | Year | Veg. Period | ||||||
| Qriver m3 s−1 | V km3 | Qriver m3 s−1 | V km3 | ||||||||
| 1963–1991 | 347.9 | 11.0 | 511.4 | 8.1 | 1.5 | 13.6 | 18.5 | 0.18 | 2.4 | 21.8 | 29.6 |
| 1992–2000 | 391.1 | 12.4 | 579.3 | 9.2 | 1.4 | 11.3 | 15.2 | 0.15 | 2.3 | 18.1 | 24.3 |
| 2001–2007 | 422.6 | 13.4 | 608.6 | 9.6 | 2.2 | 16.4 | 22.9 | 0.22 | 3.5 | 26.2 | 36.5 |
| 2008–2011 | 399.1 | 12.6 | 531.1 | 8.4 | 0.6 | 4.8 | 7.1 | 0.06 | 0.95 | 7.5 | 11.3 |
| Mean | 391.5 | 12.4 | 567.4 | 8.9 | 1.4 | 11.6 | 15.9 | 0.16 | 2.31 | 18.5 | 25.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kogutenko, L.; Severskiy, I.; Shahgedanova, M.; Lin, B. Change in the Extent of Glaciers and Glacier Runoff in the Chinese Sector of the Ile River Basin between 1962 and 2012. Water 2019, 11, 1668. https://doi.org/10.3390/w11081668
Kogutenko L, Severskiy I, Shahgedanova M, Lin B. Change in the Extent of Glaciers and Glacier Runoff in the Chinese Sector of the Ile River Basin between 1962 and 2012. Water. 2019; 11(8):1668. https://doi.org/10.3390/w11081668
Chicago/Turabian StyleKogutenko, Larissa, Igor Severskiy, Maria Shahgedanova, and Bigzhang Lin. 2019. "Change in the Extent of Glaciers and Glacier Runoff in the Chinese Sector of the Ile River Basin between 1962 and 2012" Water 11, no. 8: 1668. https://doi.org/10.3390/w11081668
APA StyleKogutenko, L., Severskiy, I., Shahgedanova, M., & Lin, B. (2019). Change in the Extent of Glaciers and Glacier Runoff in the Chinese Sector of the Ile River Basin between 1962 and 2012. Water, 11(8), 1668. https://doi.org/10.3390/w11081668




