MRT-Lattice Boltzmann Model for Multilayer Shallow Water Flow
Abstract
1. Introduction
1.1. Lattice Boltzmann Model
1.2. LBM on HPC Environments
1.3. Objective of the Study
2. Multilayer Shallow Water Equations
3. MRT-Lattice Boltzmann Modeling
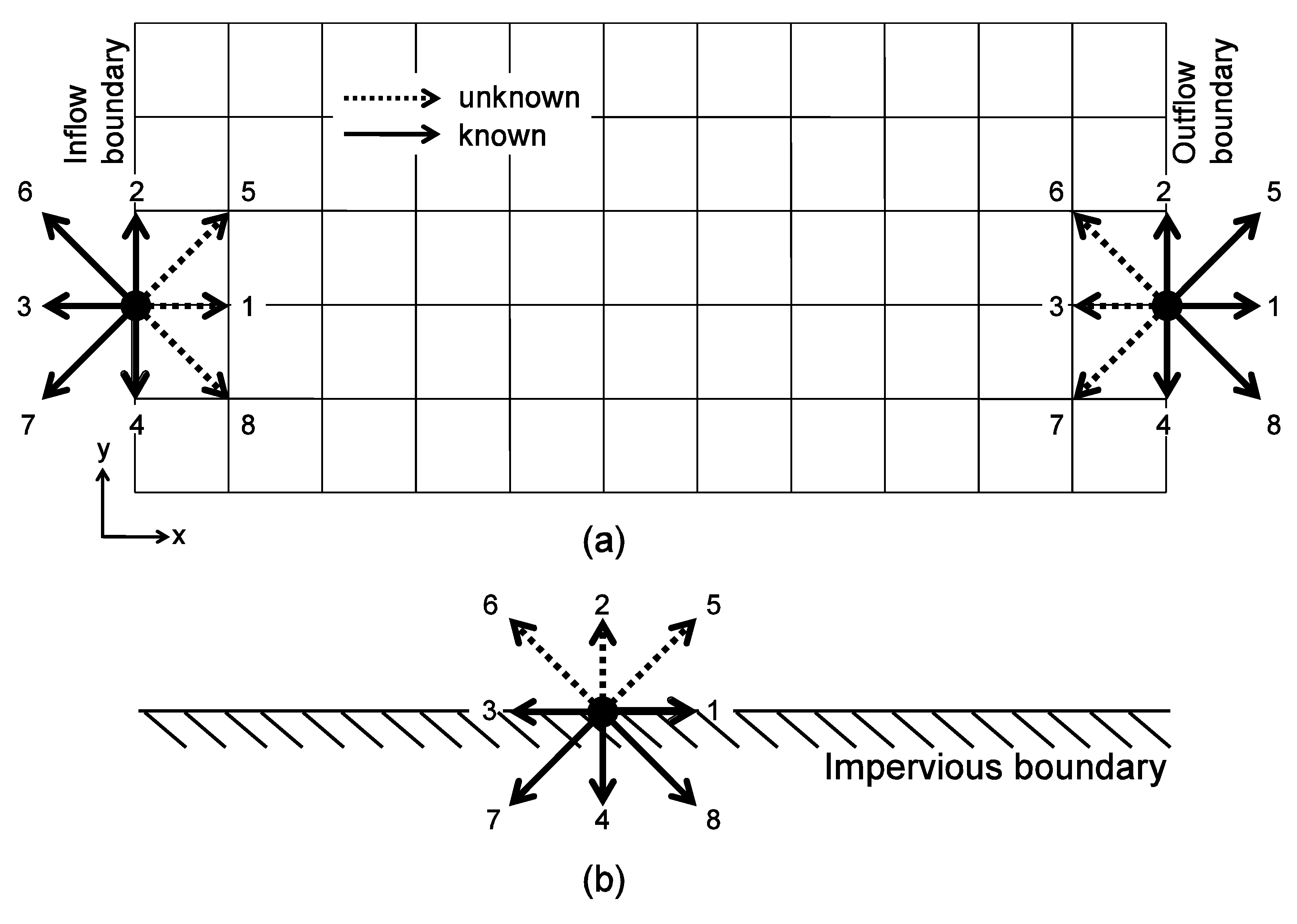
4. Multilayer Initial and Boundary Conditions
4.1. Initial Conditions
4.2. Periodic Boundary Conditions
4.3. Solid Boundary Conditions
4.4. Open Boundary Conditions
5. GPU Accelerated LBM
5.1. Jacket’s GPU Engine
5.2. Optimizing MATLAB GPU Performance
5.3. Computational Aspects
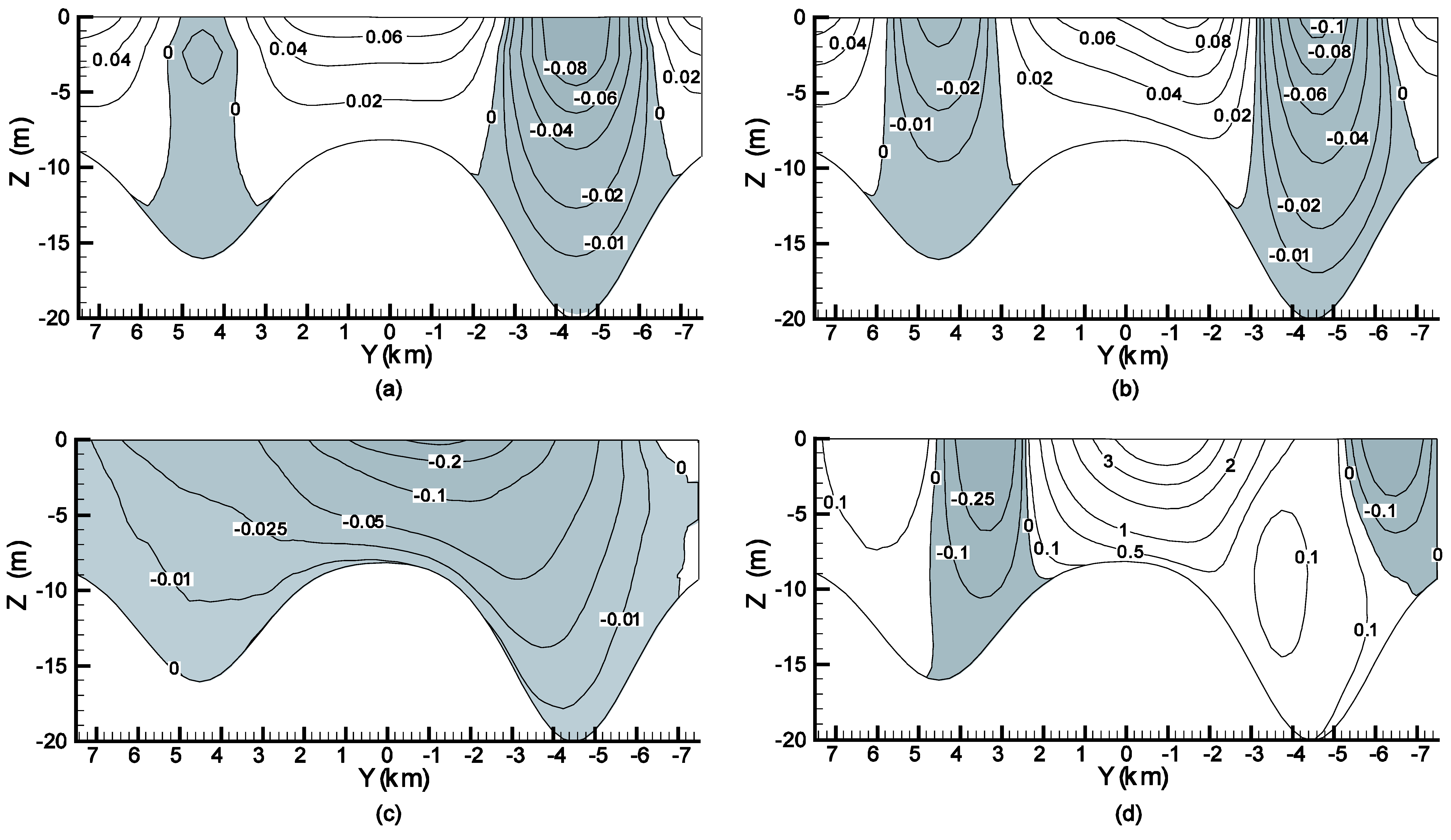
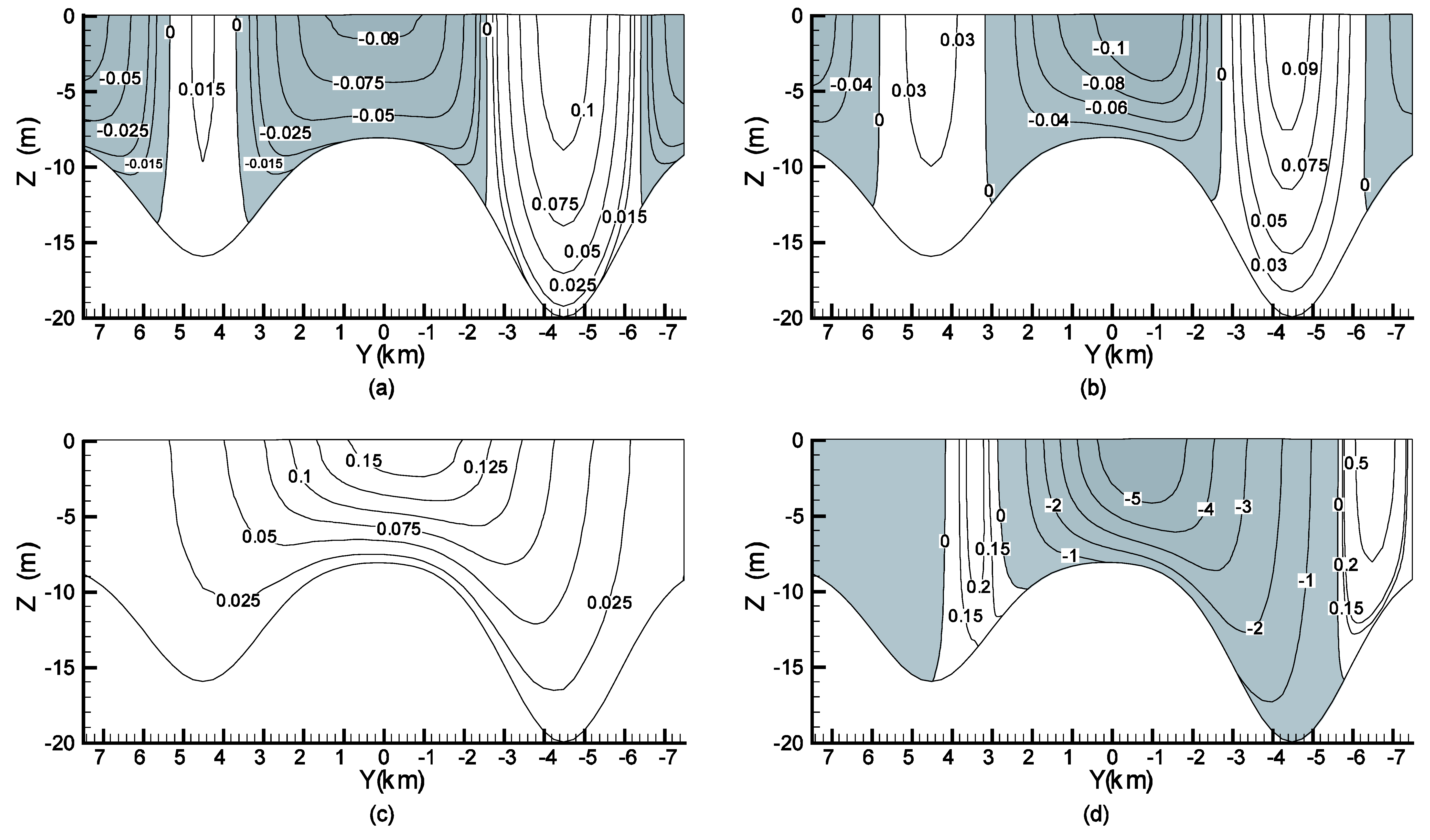
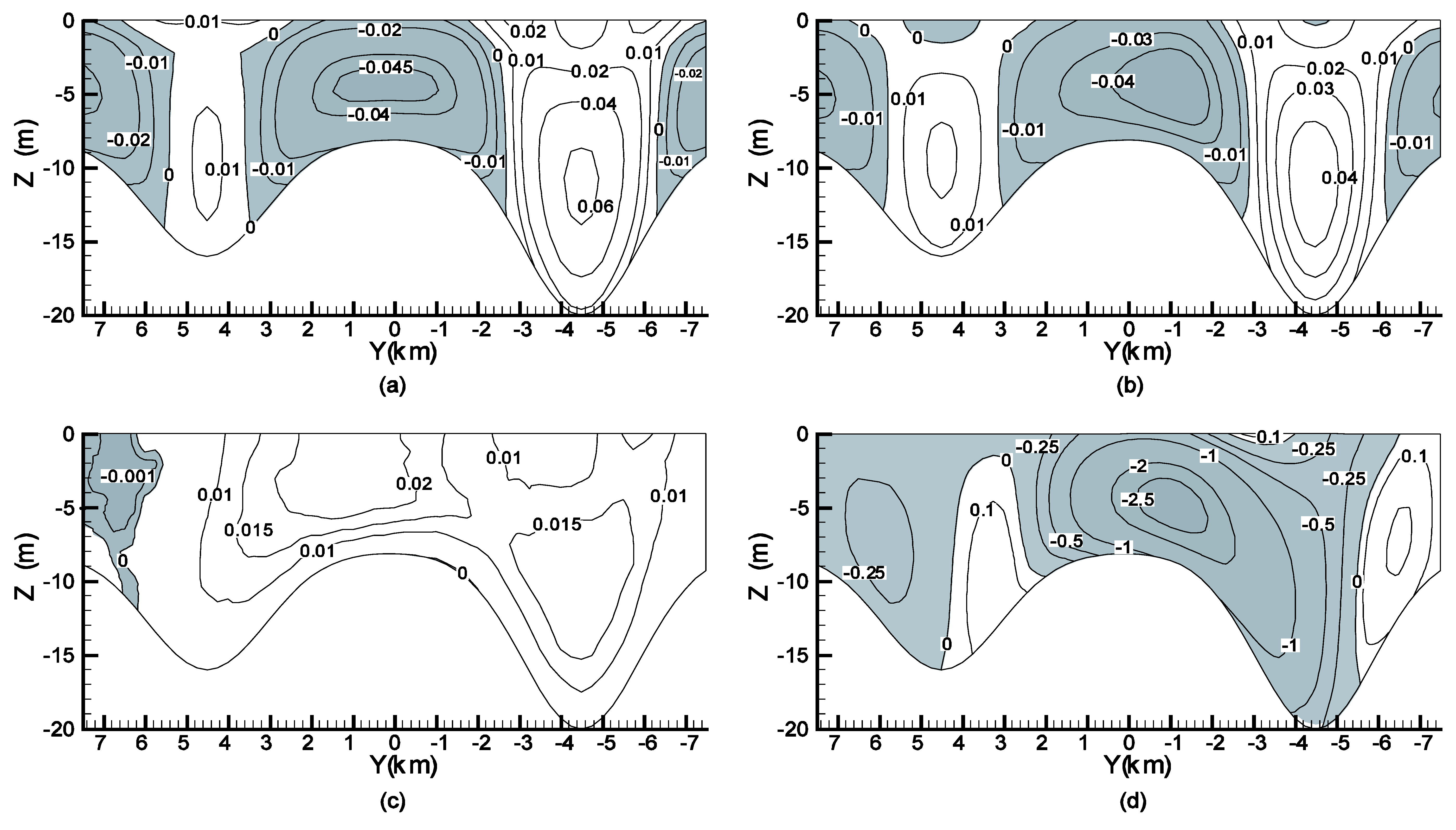
6. Numerical Experiments
6.1. GPU Performance
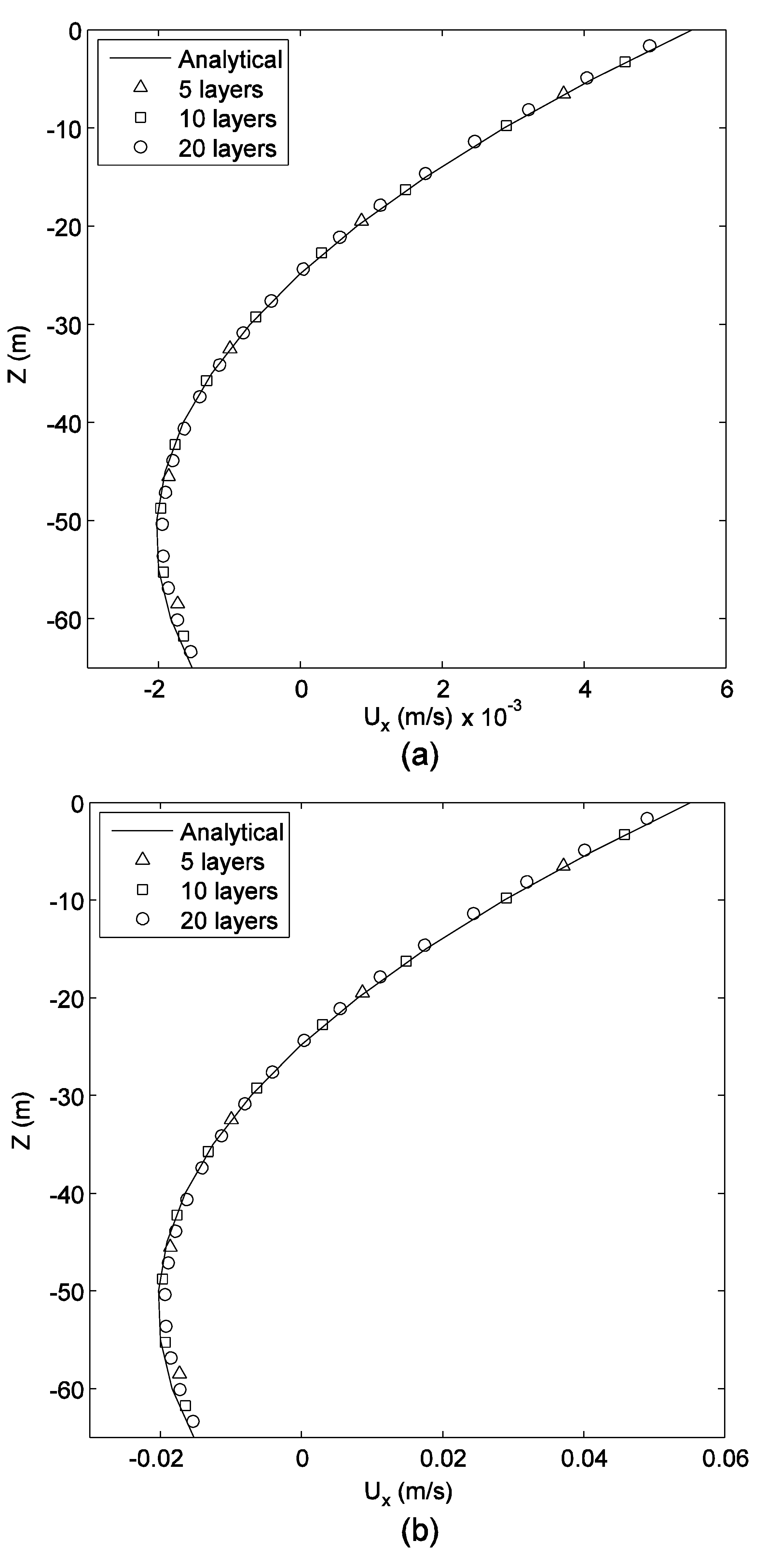
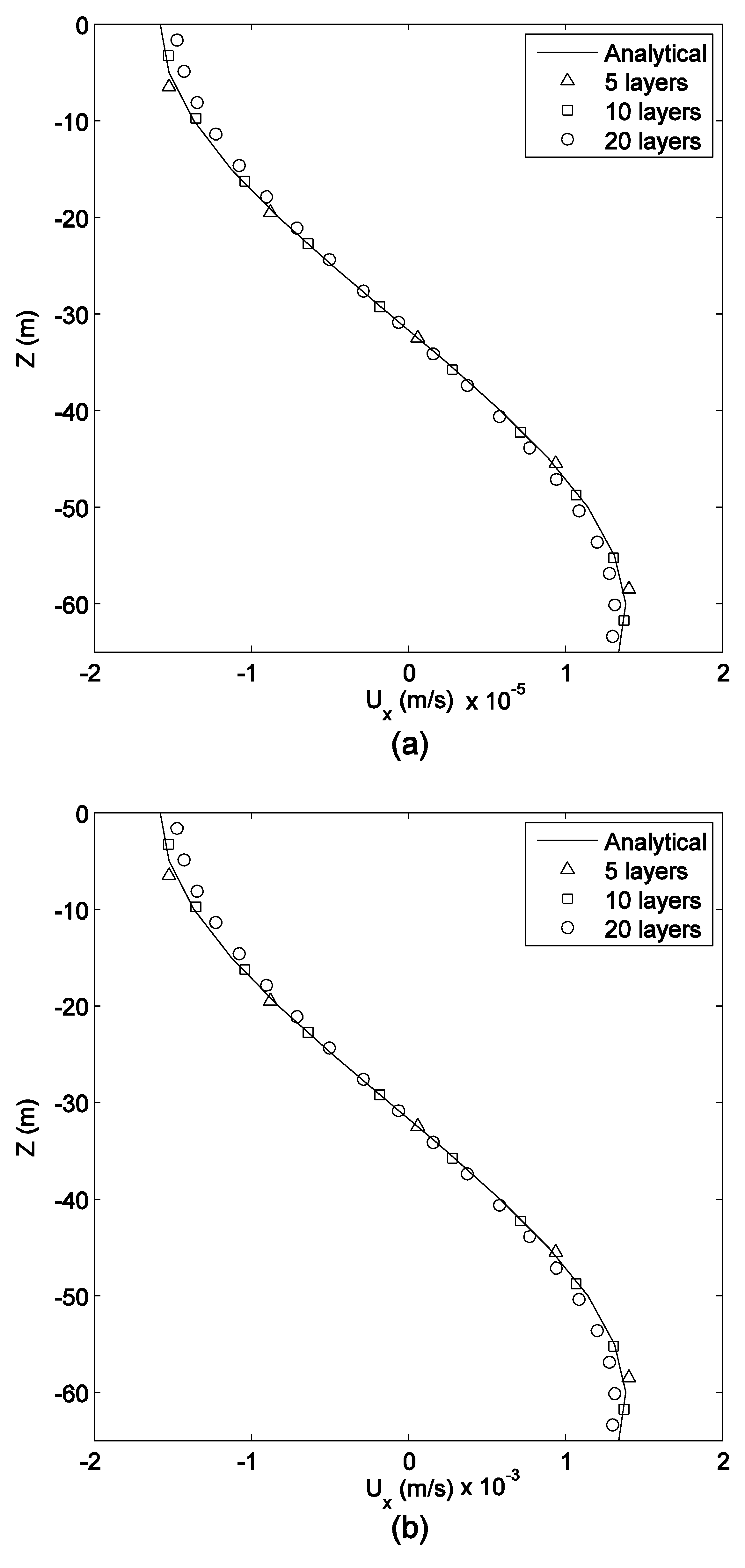
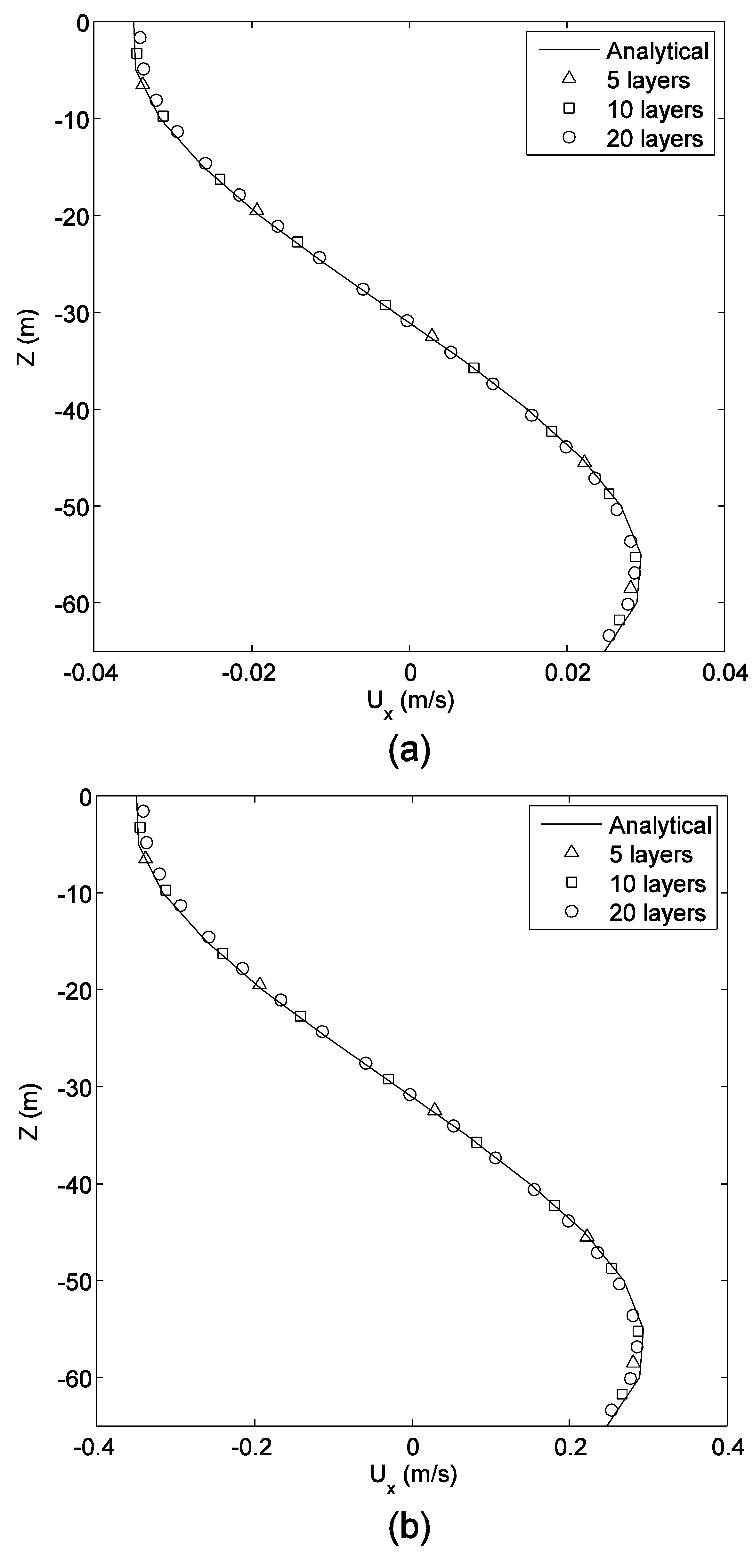
6.2. Verification
6.3. Wind-Driven and Density-Driven Circulation in Rotating Basins
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Meselhe, E.A.; Sotiropoulos, F.; Holly, F.M. Numerical simulation of transcritical flow in open channels. J. Hydraul. Eng. 1997, 123, 774–783. [Google Scholar] [CrossRef]
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational dam-break hydraulics over erodible sediment bed. J. Hydraul. Eng. 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Zhou, J.G. Lattice Boltzmann Methods for Shallow Water Flows; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Teeter, A.M.; Johnson, B.H.; Berger, C.; Stelling, G.; Scheffner, N.W.; Garcia, M.H.; Parchure, T.M. Hydrodynamic and sediment transport modeling with emphasis on shallow-water, vegetated areas (lakes, reservoirs, estuaries and lagoons). Hydrobiologia 2001, 444, 1–23. [Google Scholar] [CrossRef]
- García-Navarro, P.; Alcrudo, F.; Savirón, J.M. 1-D open-channel flow simulation using TVD-McCormack scheme. J. Hydraul. Eng. 1992, 118, 1359–1372. [Google Scholar] [CrossRef]
- Simpson, G.; Castelltort, S. Coupled model of surface water flow, sediment transport and morphological evolution. Comput. Geosci. 2006, 32, 1600–1614. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Deng, J.Q.; Gray, W.G.; Xu, K. A Boltzmann based model for open channel flows. Int. J. Numer. Methods Fluids 2001, 35, 449–494. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Elmahi, I.; Seaı¨d, M. Well-balanced finite volume schemes for pollutant transport by shallow water equations on unstructured meshes. J. Comput. Phys. 2007, 226, 180–203. [Google Scholar] [CrossRef][Green Version]
- Navarrina, F.; Colominas, I.; Casteleiro, M.; Gómez, H.; Fe, J.; Soage, A.; Cueto-Felgueroso, L.; Cueto-Felgueroso, L. A numerical model for the transport of salinity in estuaries. Int. J. Numer. Methods Fluids 2008, 56, 507–523. [Google Scholar] [CrossRef]
- Wu, W. Depth-averaged two-dimensional numerical modeling of unsteady flow and nonuniform sediment transport in open channels. J. Hydraul. Eng. 2004, 130, 1013–1024. [Google Scholar] [CrossRef]
- Teshukov, V.M. Gas-dynamic analogy for vortex free-boundary flows. J. Appl. Mech. Tech. Phys. 2007, 48, 303–309. [Google Scholar] [CrossRef]
- Gavrilyuk, S.; Ivanova, K.; Favrie, N. Multi-dimensional shear shallow water flows: Problems and solutions. J. Comput. Phys. 2018, 366, 252–280. [Google Scholar] [CrossRef]
- Gavrilyuk, S.L.; Liapidevskii, V.Y.; Chesnokov, A.A. Spilling breakers in shallow water: Applications to Favre waves and to the shoaling and breaking of solitary waves. J. Fluid Mech. 2016, 808, 441–468. [Google Scholar] [CrossRef]
- Kazakova, M.; Richard, G.L. A new model of shoaling and breaking waves: One-dimensional solitary wave on a mild sloping beach. J. Fluid Mech. 2019, 862, 552–591. [Google Scholar] [CrossRef]
- Tan, W.Y. Shallow Water Hydrodynamics Mathematical Theory and Numerical Solution for a Two-Dimensional System of Shallow Water Equations; Water & Power Press: Beijing, China, 1992. [Google Scholar]
- Casulli, V.; Walters, R.A. An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Vreugdenhil, C.B. Numerical Methods for Shallow-Water Flow; Springer Science & Business Media: Berlin, Germany, 2013; p. 273. [Google Scholar]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equation. Phys. Rev. Lett. 1986, 56, 1505–1508. [Google Scholar] [CrossRef] [PubMed]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef]
- Chen, H.; Chen, S.; Matthaeus, W.H. Recovery of the Navier-Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 1992, 45, R5339–R5342. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.-S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models: An Introduction; Springer Science & Business Media: Berlin, Germany, 2000; p. 324. [Google Scholar]
- He, X.; Chen, S.; Doolen, G.D. A novel thermal model for the lattice Boltzmann method in incompressible limit. J. Comput. Phys. 1998, 146, 282–300. [Google Scholar] [CrossRef]
- Pullin, D. Direct simulation methods for compressible inviscid ideal-gas flow. J. Comput. Phys. 1980, 34, 231–244. [Google Scholar] [CrossRef]
- La Rocca, M.; Montessori, A.; Prestininzi, P.; Succi, S. A multispeed discrete Boltzmann model for transcritical 2D shallow water flows. J. Comput. Phys. 2015, 284, 117–132. [Google Scholar] [CrossRef]
- Martínez, D.O.; Matthaeus, W.H.; Chen, S.; Montgomery, D.C. Comparison of spectral method and lattice Boltzmann simulations of two-dimensional hydrodynamics. Phys. Fluids 1994, 6, 1285–1298. [Google Scholar] [CrossRef]
- Deeks, L.K.; Young, I.M.; Zhang, X.; Bengough, A.G.; Crawford, J.W. A novel three-dimensional lattice Boltzmann model for solute transport in variably saturated porous media. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Ginzburg, I. Variably saturated flow described with the anisotropic lattice Boltzmann methods. Comput. Fluids 2006, 35, 831–848. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Tsai, F.T.-C. Lattice Boltzmann method with two relaxation times for advection–diffusion equation: Third order analysis and stability analysis. Adv. Water Resour. 2008, 31, 1113–1126. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Tsai, F.T.-C.; Servan-Camas, B. Two-relaxation-time lattice Boltzmann method for the anisotropic dispersive Henry problem. Water Resour. Res. 2010, 46, 02515. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Tsai, F.T.-C. Non-negativity and stability analyses of lattice Boltzmann method for advection–diffusion equation. J. Comput. Phys. 2009, 228, 236–256. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Tsai, F.T.-C. Saltwater intrusion modeling in heterogeneous confined aquifers using two-relaxation-time lattice Boltzmann method. Adv. Water Resour. 2009, 32, 620–631. [Google Scholar] [CrossRef]
- Salmon, R. The lattice Boltzmann method as a basis for ocean circulation modeling. J. Mar. Res. 1999, 57, 503–535. [Google Scholar] [CrossRef]
- Prestininzi, P.; Montessori, A.; La Rocca, M.; Sciortino, G. Simulation of arrested salt wedges with a multi-layer Shallow Water Lattice Boltzmann model. Adv. Water Resour. 2016, 96, 282–289. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Zhang, J.M.; Liu, H. Lattice Boltzmann modeling of shallow water flows over discontinuous beds. Int. J. Numer. Methods Fluids 2014, 75, 608–619. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.G. Lattice Boltzmann approach to simulating a wetting–drying front in shallow flows. J. Fluid Mech. 2014, 743, 32–59. [Google Scholar] [CrossRef]
- La Rocca, M.; Adduce, C.; Lombardi, V.; Sciortino, G.; Hinkelmann, R. Development of a lattice Boltzmann method for two-layered shallow-water flow. Int. J. Numer. Methods Fluids 2012, 70, 1048–1072. [Google Scholar] [CrossRef]
- Tubbs, K.R.; Tsai, F.T.-C. Multilayer shallow water flow using lattice Boltzmann method with high performance computing. Adv. Water Resour. 2009, 32, 1767–1776. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001; p. 308. [Google Scholar]
- Pohl, T.; Deserno, F.; Thurey, N.; Rude, U.; Lammers, P.; Wellein, G.; Zeiser, T. Performance evaluation of parallel large-scale lattice Boltzmann applications on three supercomputing architectures. In Proceedings of the SC ’04: 2004 ACM/IEEE Conference on Supercomputing, Pittsburgh, PA, USA, 6–12 November 2004; IEEE Computer Society: Washington, DC, USA, 2004; p. 21. [Google Scholar] [CrossRef]
- Desplat, J.-C.; Pagonabarraga, I.; Bladon, P. LUDWIG: A parallel lattice-Boltzmann code for complex fluids. Comput. Phys. Commun. 2001, 134, 273–290. [Google Scholar] [CrossRef]
- OpenMP Architecture Review Board. OpenMp Application Programming Interface; OpenMP Architecture Review Board: 2008. Available online: https://www.openmp.org/wp-content/uploads/spec30.pdf (accessed on 5 August 2019).
- Bella, G.; Rossi, N.; Filippone, S.; Ubertini, S. Using OpenMP on a hydrodynamic lattice-Boltzmann code. In Proceedings of the Fourth European Workshop on OpenMP, Roma, Italy, 18–20 September 2002. [Google Scholar]
- Kuznik, F.; Obrecht, C.; Rusaouën, G.; Roux, J.-J. LBM based flow simulation using GPU computing processor. Comput. Math. Appl. 2010, 59, 2380–2392. [Google Scholar] [CrossRef]
- Tubbs, K.R.; Tsai, F.T.-C. GPU accelerated lattice Boltzmann model for shallow water flow and mass transport. Int. J. Numer. Methods Eng. 2011, 86, 316–334. [Google Scholar] [CrossRef]
- Fan, Z.; Qiu, F.; Kaufman, A.; Yoakum-Stover, S. GPU cluster for high performance computing. In Proceedings of the SC’04 2004 ACM/IEEE Conference on Supercomputing, Pittsburgh, PA, USA, 6–12 November 2004; IEEE Computer Society: Washington, DC, USA, 2004; p. 47. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Wang, X.; Ge, W. GPU-based numerical simulation of multi-phase flow in porous media using multiple-relaxation-time lattice Boltzmann method. Chem. Eng. Sci. 2013, 102, 209–219. [Google Scholar] [CrossRef]
- Audusse, E. A multilayer Saint-Venant model: Derivation and numerical validation. Discret. Contin. Dyn. Syst. Ser. B 2005, 5, 189–214. [Google Scholar] [CrossRef]
- Audusse, E.; Bristeau, M.O.; Decoene, A. 3D free surface flows simulations using a multilayer Saint-Venant model. Comparisons with Navier-Stokes Solutions. In Numerical Mathematics and Advanced Applications; de Castro, A.B., Gómez, D., Quintela, P., Salgado, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 181–189. [Google Scholar]
- Audusse, E.; Bristeau, M.O.; Decoene, A. Numerical simulations of 3D free surface flows by a multilayer Saint-Venant model. Int. J. Numer. Methods Fluids 2008, 56, 331–350. [Google Scholar] [CrossRef]
- Shankar, N.; Cheong, H.; Sankaranarayanan, S. Multilevel finite-difference model for three-dimensional hydrodynamic circulation. Ocean Eng. 1997, 24, 785–816. [Google Scholar] [CrossRef]
- D’Humières, D. Multiple–relaxation–time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Liu, H.; Luo, L.-S.; Xu, K. A comparative study of the LBE and GKS methods for 2D near incompressible laminar flows. J. Comput. Phys. 2008, 227, 4955–4976. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.-S. Theory of the lattice Boltzmann method: Acoustic and thermal properties in two and three dimensions. Phys. Rev. E 2003, 68, 036706. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.G. A lattice Boltzmann model for the shallow water equations. Comput. Methods Appl. Mech. Eng. 2002, 191, 3527–3539. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- NVIDIA. NVIDIA CUDA Programming Guide 3.2; NVIDIA: Santa Clara, CA, USA, 2010. [Google Scholar]
- MATLAB GPU Computing; Accelereyes: Atlanta, GA, USA, 2008.
| Grid Size | CPU | Speedup | |
|---|---|---|---|
| Execution Time per Time Step (sec) | |||
| 171 × 61 × 10 | 0.44 | 0.19 | 2.2 |
| 341 × 121 × 10 | 3.04 | 0.30 | 10.1 |
| 681 × 241 × 10 | 14.19 | 0.95 | 14.9 |
| 1361 × 481× 10 | 56.60 | 2.57 | 22.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tubbs, K.R.; Tsai, F.T.-C. MRT-Lattice Boltzmann Model for Multilayer Shallow Water Flow. Water 2019, 11, 1623. https://doi.org/10.3390/w11081623
Tubbs KR, Tsai FT-C. MRT-Lattice Boltzmann Model for Multilayer Shallow Water Flow. Water. 2019; 11(8):1623. https://doi.org/10.3390/w11081623
Chicago/Turabian StyleTubbs, Kevin R., and Frank T.-C. Tsai. 2019. "MRT-Lattice Boltzmann Model for Multilayer Shallow Water Flow" Water 11, no. 8: 1623. https://doi.org/10.3390/w11081623
APA StyleTubbs, K. R., & Tsai, F. T.-C. (2019). MRT-Lattice Boltzmann Model for Multilayer Shallow Water Flow. Water, 11(8), 1623. https://doi.org/10.3390/w11081623






