Forcing the Penman-Montheith Formulation with Humidity, Radiation, and Wind Speed Taken from Reanalyses, for Hydrologic Modeling
Abstract
1. Introduction
2. Domain, Data, and Methodology
2.1. Domain
2.2. Data
2.3. Hydrologic Modeling Setup
2.4. Correction of Simulated HRW Fields
3. Results
3.1. Meteorological Performance Values
3.2. Hydrologic Performance Values
3.3. Simulated Evapotranspiration
4. Discussion
4.1. Forcing PM Formulation with Simulated HRW Fields Provides an Appropriate Hydrologic Response
4.2. Correcting HRW Fields Moderately Improves the Simulated Hydrologic Response
4.3. PM Formulation Improves the Representation of Evapotranspiration
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F. How do potential evapotranspiration formulas influence hydrological projections? Hydrolog. Sci. J. 2016, 61, 2249–2266. [Google Scholar] [CrossRef]
- Kay, A.L.; Bell, V.A.; Blyth, E.M.; Crooks, S.M.; Davies, H.N.; Reynard, N.S. A hydrological perspective on evapotranspiration: historical trends and future projections in Britains. J. Water Clim. Chang. 2013, 4, 193–208. [Google Scholar] [CrossRef]
- Sherwood, S.; Fu, Q. A drier future? Science 2014, 343, 737–739. [Google Scholar] [CrossRef] [PubMed]
- Lofgren, B.M.; Gronewold, A.D.; Acciaioli, A.; Cherry, J.; Steiner, A.; Watkins, D. Methodological approaches to projecting the hydrologic impacts of climate change. Earth Interact. 2013, 17, 2–19. [Google Scholar] [CrossRef]
- Oudin, L.; Michel, C.; Anctil, F. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 1—Can rainfall-runoff models effectively handle detailed potential evapotranspiration inputs? J. Hydrol. 2005, 303, 275–289. [Google Scholar] [CrossRef]
- Auerbach, D.A.; Easton, Z.M.; Walter, M.T.; Flecker, A.S.; Fuka, D.R. Evaluating weather observations and the climate forecast system reanalysis as inputs for hydrologic modelling in the tropics. Hydrol. Process. 2016, 30, 3466–3477. [Google Scholar] [CrossRef]
- Essou, G.R.C.; Sabarly, F.; Lucas-Picher, P.; Brissette, F.; Poulin, A. Can precipitation and temperature from meteorological reanalyses be used for hydrological modeling? J. Hydrometeorol. 2016, 17, 1929–1950. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the climate forecast system reanalysis as weather input data for watershed Models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Hwang, S.; Graham, W.D.; Geurink, J.S.; Adams, A. Hydrologic implications of errors in bias-corrected regional reanalysis data for west central Florida. J. Hydrol. 2014, 510, 513–529. [Google Scholar] [CrossRef]
- Lauri, H.; Räsänen, T.A.; Kummu, M. Using reanalysis and remotely sensed temperature and precipitation data for hydrological modeling in monsoon climate: Mekong river case study. J. Hydrometeorol. 2014, 15, 1532–1545. [Google Scholar] [CrossRef]
- Praskievicz, S.; Bartlein, P. Hydrologic Modeling Using Elevationally Adjusted NARR and NARCCAP regional climate-model simulations: Tucannon River, Washington. J. Hydrol. 2014, 517, 803–814. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic evaluation of satellite and reanalysis precipitation datasets over a mid-latitude basin. Atmos. Res. 2015, 164–165, 37–48. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.Y.; Chen, S.; Chen, H. Similarity and difference of global reanalysis datasets (WFD and APHRODITE) in driving lumped and distributed hydrological models in a humid region of China. J. Hydrol. 2016, 542, 343–356. [Google Scholar] [CrossRef]
- Boulard, D.; Castel, T.; Camberlin, P.; Sergent, A.S.; Bréda, N.; Badeau, V.; Rossi, A.; Pohl, B. Capability of a regional climate model to simulate climate variables requested for water balance computation: A case study over northeastern France. Clim. Dyn. 2016, 46, 2689–2716. [Google Scholar] [CrossRef]
- Canon, D.J.; Brayshaw, D.J.; Methven, J.; Coker, P.J.; Lenaghan, D. Using reanalysis data to quantify extreme wind power generation statistics: A 33 year case study in Great Britain. Ren. Energy 2015, 75, 767–778. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF reanalysis interim and the NCEP climate forecast system reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, K. Comparison of evapotranspiration estimates based on the surface water balance, modified penman-monteith model, and reanalysis data sets for continental China. J. Geophys. Res. Atmos. 2017, 122, 3228–3244. [Google Scholar] [CrossRef]
- Martins, D.S.; Paredes, P.; Raziei, T.; Pires, C.; Cadima, J.; Pereira, L.S. Assessing reference evapotranspiration estimation from reanalysis weather products. An application to the Iberian Peninsula. Int. J. Climatol. 2017, 37, 2378–2397. [Google Scholar] [CrossRef]
- Huang, S.Y.; Deng, Y.; Wang, J. Revisiting the global surface energy budgets with maximum-entropy-production model of surface heat fluxes. Clim. Dyn. 2017, 49, 1531–1545. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, S.; Zhang, Y.; Jia, K.; Liu, M. Spatial and decadal variations in potential evapotranspiration of china based on reanalysis datasets during 1982–2010. Atmosphere 2014, 5, 737–754. [Google Scholar] [CrossRef]
- Sperna Weiland, F.C.; Tisseuil, C.; Dürr, H.H.; Vrac, M.; Van Beek, L.P.H. Selecting the optimal method to calculate daily global reference potential evaporation from CFSR reanalysis data for application in a hydrological model study. Hydrol. Earth Syst. Sci. 2012, 16, 983–1000. [Google Scholar] [CrossRef]
- Jones, P.D.; Harpham, C.; Troccoli, A.; Gschwind, B.; Ranchin, T.; Wald, L.; Goodess, C.M.; Dorling, S. Using ERA-interim reanalysis for creating datasets of energy-relevant climate variables. Earth Syst. Sci. Data 2017, 9, 471–495. [Google Scholar] [CrossRef]
- Sen Gupta, A.; Tarboton, D.G. A Tool for Downscaling weather data from large-grid reanalysis products to finer spatial scales for distributed hydrological applications. Environ. Modell. Softw. 2016, 84, 50–69. [Google Scholar] [CrossRef]
- Essou, G.R.C.; Brissette, F.; Lucas-Picher, P. Impacts of combining reanalyses and weather station data on the accuracy of discharge modelling. J. Hydrol. 2017, 545, 120–131. [Google Scholar] [CrossRef]
- Mailhot, A.; Talbot, G.; Ricard, S.; Turcotte, R.; Guinard, K. Assessing the potential impacts of dam operation on daily flow at ungauged river reaches. J. Hydrol. Regional Stud. 2018, 18, 156–167. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Tolding, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Climate 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-interim reanalysis: Configuration and performance of the data assimilation system. QJR Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Chen, G.; Iwasaki, T.; Qin, H.; Sha, W. Evaluation of the warm-season diurnal variability over east asia in recent reanalyses JRA-55, ERA-interim, NCEP CFSR, and NASA MERRA. J. Clim. 2014, 27, 5517–5537. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Cornelissen, T.; Diekkrüger, B.; Giertz, S. A comparison of hydrological models for assessing the impact of land use and climate change on discharge in a tropical catchment. J. Hydrol. 2013, 498, 221–236. [Google Scholar] [CrossRef]
- Ott, I.; Duethmann, D.; Liebert, J.; Berg, P.; Feldmann, H.; Ihringer, J.; Kunstmann, H.; Merz, B.; Schaedler, G.; Wagner, S. High-resolution climate change impact analysis on medium-sized river catchments in germany: an ensemble assessment. J. Hydrometeorol. 2013, 14, 1175–1193. [Google Scholar] [CrossRef]
- Smiatek, G.; Kunstmann, H.; Werhahn, J. Implementation and performance analysis of a high resolution coupled numerical weather and river runoff prediction model system for an alpine catchment. Environ. Modell. Softw. 2012, 38, 231–243. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, S. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; pp. 1–15. [Google Scholar]
- Shangguan, W.; Dai, Y.; Duan, Q.; Liu, B.; Yuan, H. A global soil data set for earth system modeling. J. Adv. Model. Earth Syst. 2014, 6, 249–263. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Tolson, B.A. Hybrid pareto archived dynamically dimensioned search for multi-objective combinatorial optimization: application to water distribution network design. J. Hydroinform. 2012, 14, 192–205. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and nse performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Muerth, M.J.; Gauvin St-Denis, B.; Ricard, S.; Velázquez, J.A.; Schmid, J.; Minville, M.; Caya, D.; Chaumont, D.; Ludwig, R.; Turcotte, R. On the need for bias correction in regional climate scenarios to assess climate change impacts on river runoff. Hydrol. Earth Syst. Sci. 2013, 17, 1189–1204. [Google Scholar] [CrossRef]
- Velázquez, J.A.; Schmid, J.; Ricard, S.; Muerth, M.J.; Gauvin St-Denis, B.; Minville, M.; Caya, D.; Chaumont, D.; Ludwig, R.; Turcotte, R. An ensemble approach to assess hydrological models’ contribution to uncertainties in the analysis of climate change impact on water resources. Hydrol. Earth Syst. Sci. 2013, 17, 565–578. [Google Scholar] [CrossRef]
- Hajji, I.; Nadeau, D.F.; Music, B.; Anctil, F.; Wang, J. Application of the maximum entropy production model of evapotranspiration over partially vegetated water-limited land surfaces. J. Hydrometeorol. 2019, 19, 989–1005. [Google Scholar] [CrossRef]
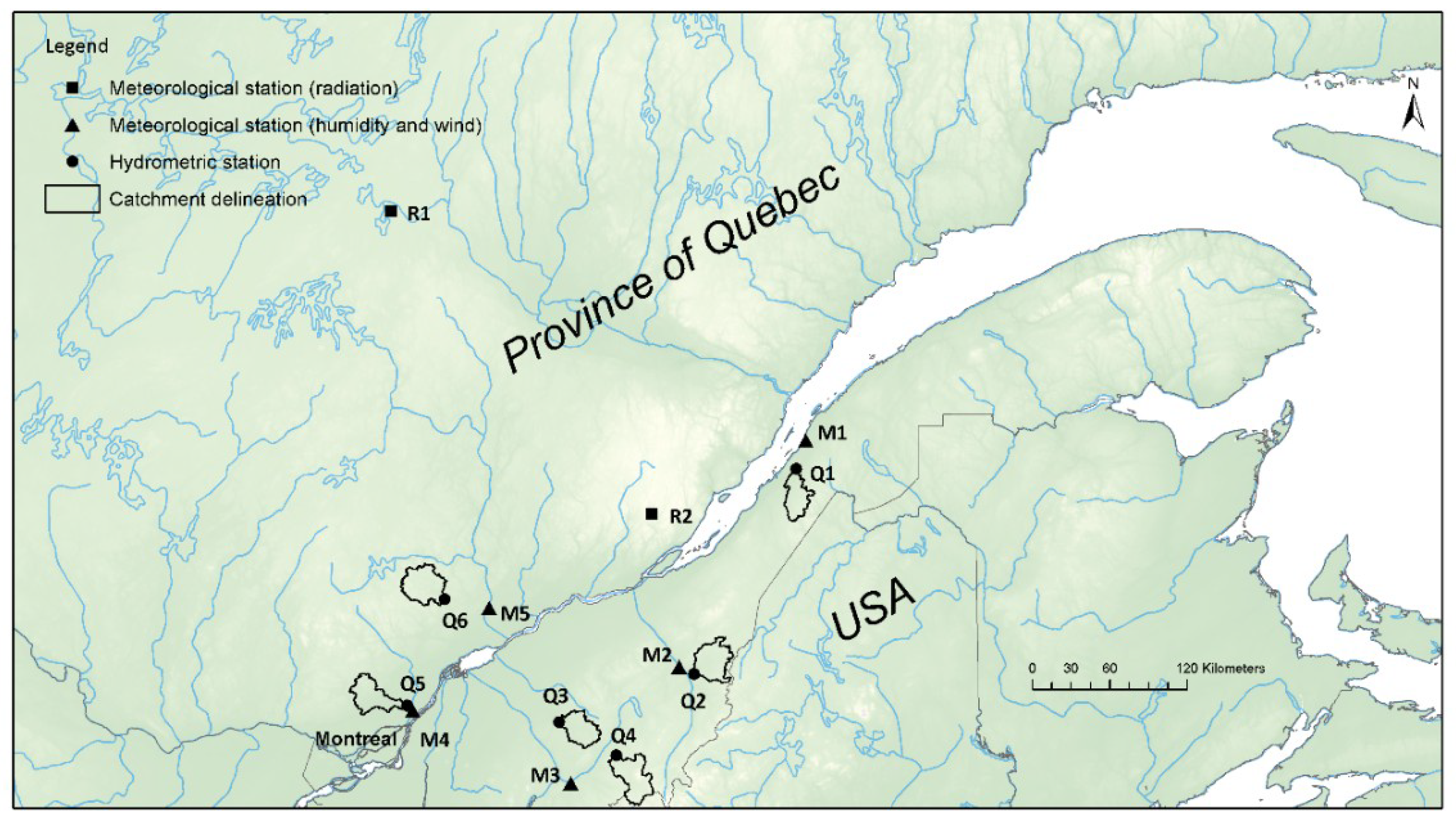

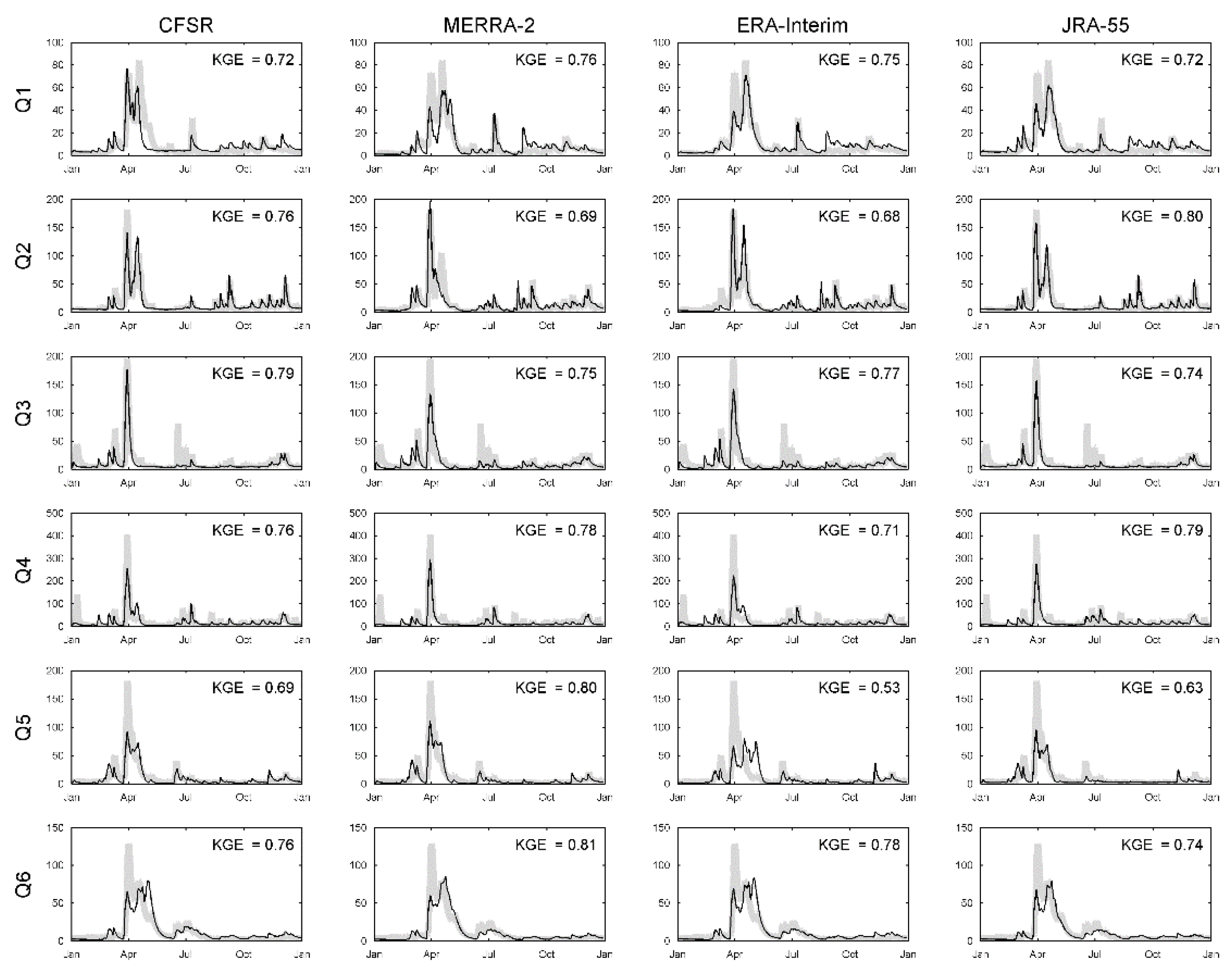
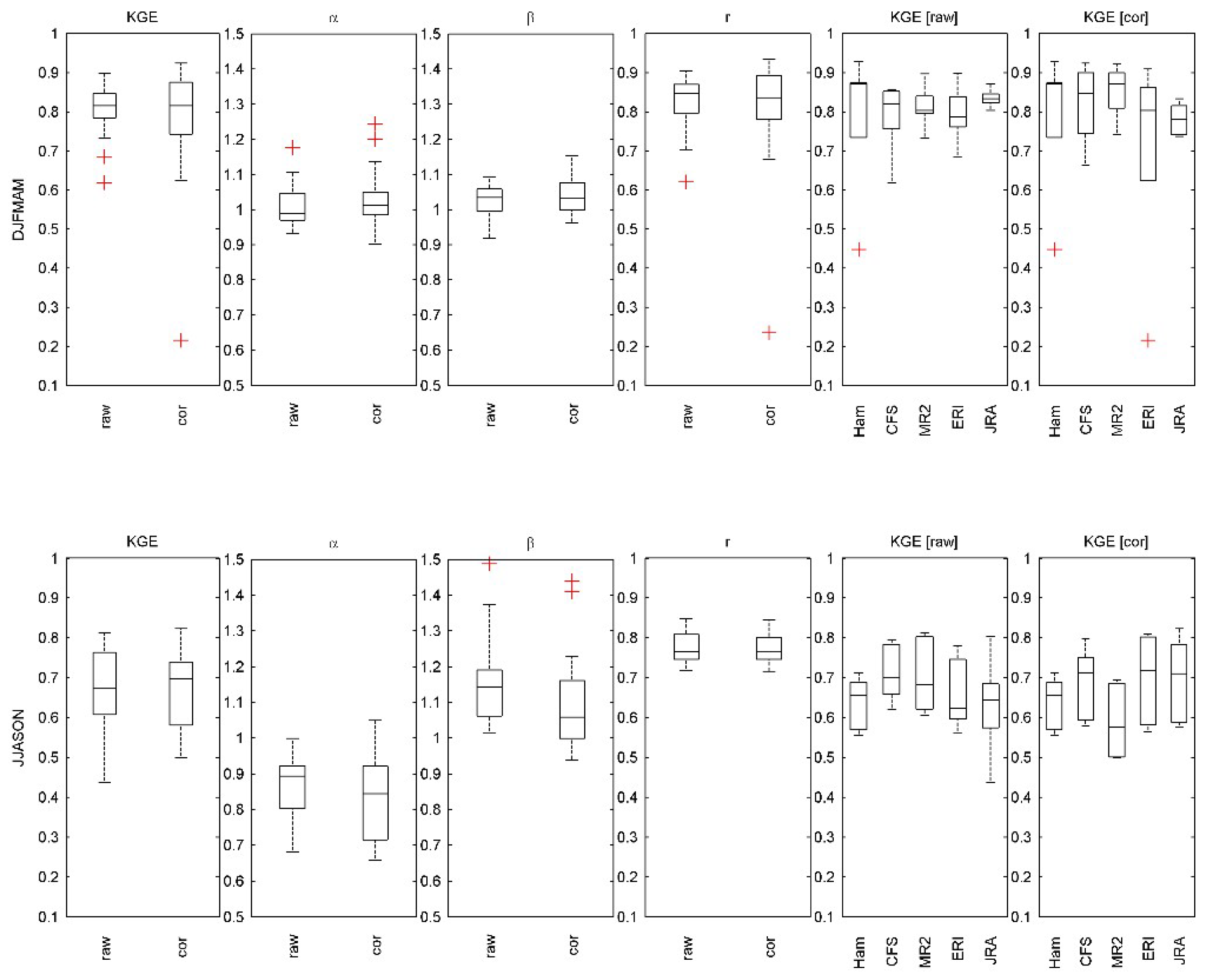
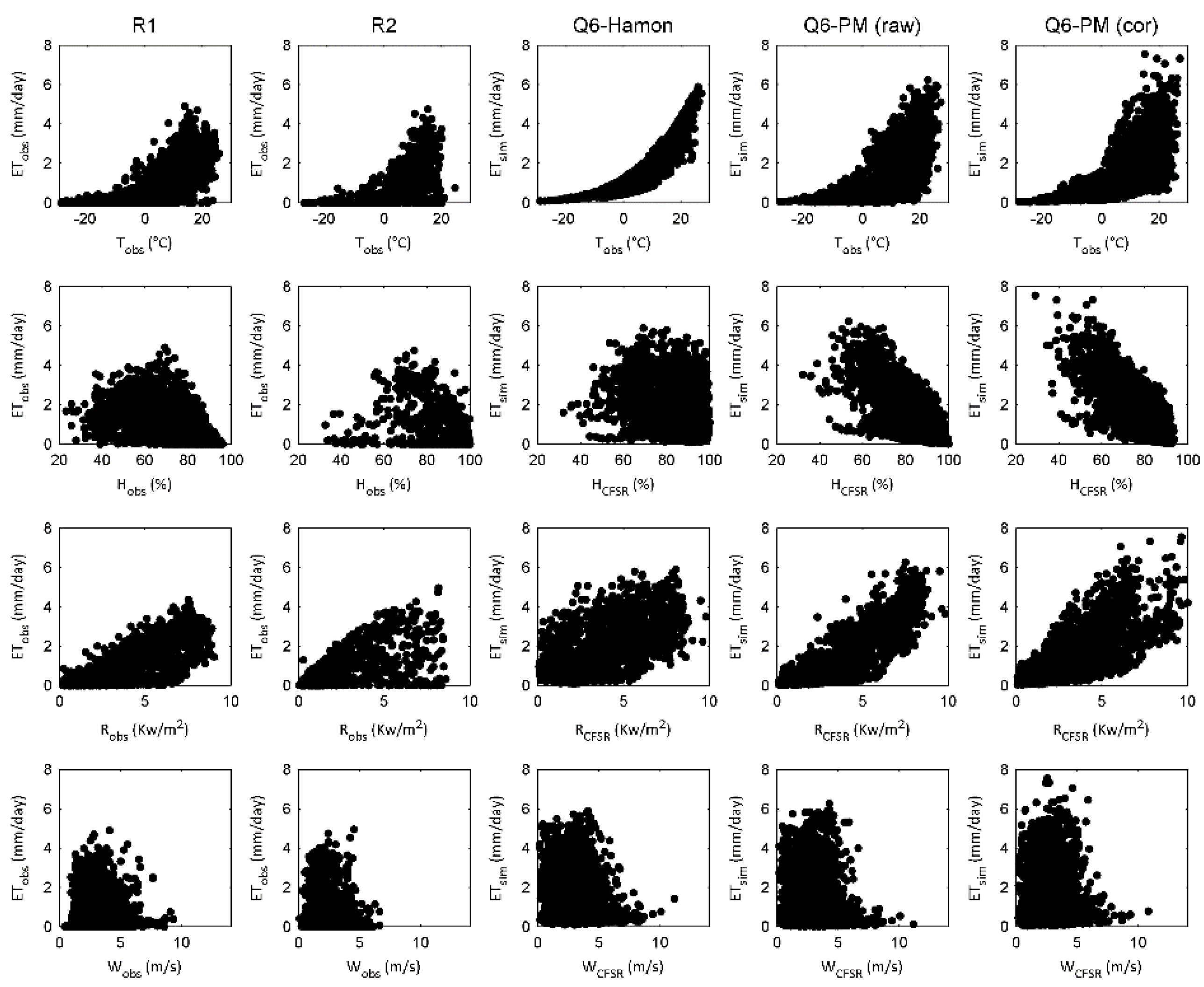
| Site | Latitude (°N) | Longitude (°E) | Area (km2) | Forest Land Use (%) | Slope (%) | Corresponding Meteorological Station |
|---|---|---|---|---|---|---|
| Q1 | 47.6 | −69.7 | 512 | 77 | 5.9 | M1 |
| Q2 | 46.2 | −70.6 | 695 | 75 | 4.1 | M2 |
| Q3 | 45.8 | −72.0 | 549 | 60 | 5.8 | M3 |
| Q4 | 45.6 | −71.4 | 736 | 79 | 7.9 | M3 |
| Q5 | 45.9 | −73.5 | 633 | 59 | 6.4 | M4 |
| Q6 | 46.6 | −73.2 | 761 | 83 | 13.4 | M5 |
| Hydrologic Process | Description | Climate Input Data | Free Parameters |
|---|---|---|---|
| ET0 | Penman-Monteith | Temperature Humidity Radiation Wind speed | none |
| Hamon | Temperature | fi [0.5;2] | |
| Precipitation correction | Separation liquid/solid precipitation | Temperature Precipitation | Ttr [−0.5;0.5] as [1;1.5] |
| Snow melt | T-Index degree day method | Temperature | c0 [0;5] Tm [−2;2] |
| Unsaturated zone fluxes | Surface runoff generation | None | QDsnw [0;1] |
| Interflow generation | None | dr [1;100] | |
| Discharge routing | Surface and interflow flow recession | None | ks [1;100] kh [1;150] |
| CFSR | MERRA-2 | ERA-Interim | JRA-55 | M | R | |
|---|---|---|---|---|---|---|
| Humidity | ||||||
| KGE | 0.66 | 0.64 | 0.62 | 0.70 | 0.65 | 0.07 |
| α | 1.19 | 0.82 | 1.25 | 1.04 | 1.07 | 0.43 |
| β | 1.01 | 1.05 | 0.94 | 0.98 | 0.99 | 0.11 |
| r | 0.72 | 0.70 | 0.73 | 0.71 | 0.71 | 0.02 |
| Radiation | ||||||
| KGE | 0.84 | 0.90 | 0.89 | 0.88 | 0.88 | 0.06 |
| α | 1.03 | 0.98 | 0.96 | 0.96 | 0.98 | 0.07 |
| β | 0.92 | 1.07 | 1.07 | 1.09 | 1.04 | 0.17 |
| r | 0.87 | 0.93 | 0.93 | 0.93 | 0.91 | 0.06 |
| Wind speed | ||||||
| KGE | 0.40 | 0.63 | 0.43 | 0.44 | 0.48 | 0.23 |
| α | 1.47 | 0.74 | 1.35 | 0.62 | 1.05 | 0.84 |
| β | 1.26 | 0.87 | 1.36 | 0.67 | 1.04 | 0.69 |
| r | 0.77 | 0.82 | 0.77 | 0.79 | 0.79 | 0.05 |
| Parameters | Hamon (n = 6) | PM Raw (n = 24) | PM Cor (n = 24) | |||||
|---|---|---|---|---|---|---|---|---|
| Equation | Mean | [Min;Max] | Mean | [Min;Max] | Mean | [Min;Max] | ||
| fi,DJFMAM | Correction of Hamon ET0 | (3) | 0.96 | [0.50;1.42] | - | - | - | - |
| fi,JJASON | 1.26 | [1.14;1.40] | - | - | - | - | ||
| Ttr | Temperature snow/rain transition | (4) | 0.42 | [0.23;0.5] | 0.0063 | [−0.5;0.5] | 0.22 | [−0.44;0.5] |
| as | Correction of solid precipitation | (4) | 1.28 | [1.18;1.5] | 1.17 | [1;1.49] | 1.26 | [1;1.49] |
| c0 | Melt factor | (5) | 2.61 | [1.41;3.99] | 2.42 | [0.6;5] | 2.53 | [1.11;5] |
| Tm | Temperature limit for snow melt | (5) | −1.56 | [−2;0.18] | −0.47 | [−2;2] | −0.95 | [−2;1.71] |
| QDsnw | Fraction of surface runoff on snow melt | (6) | 0.51 | [0;1] | 0.67 | [0;1] | 0.40 | [0;1] |
| dr | Drainage density | (7) | 81.50 | [40.29;100] | 33.55 | [1;100] | 73.12 | [1;100] |
| ks | Surface runoff recession constant | (8) | 78.94 | [51.33;100] | 73.49 | [28.80;100] | 66.24 | [30.36;100] |
| kh | Inteflow recession constant | (9) | 45.87 | [16.65;139.82] | 50.68 | [11.81;150] | 50.08 | [10.36;150] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricard, S.; Anctil, F. Forcing the Penman-Montheith Formulation with Humidity, Radiation, and Wind Speed Taken from Reanalyses, for Hydrologic Modeling. Water 2019, 11, 1214. https://doi.org/10.3390/w11061214
Ricard S, Anctil F. Forcing the Penman-Montheith Formulation with Humidity, Radiation, and Wind Speed Taken from Reanalyses, for Hydrologic Modeling. Water. 2019; 11(6):1214. https://doi.org/10.3390/w11061214
Chicago/Turabian StyleRicard, Simon, and François Anctil. 2019. "Forcing the Penman-Montheith Formulation with Humidity, Radiation, and Wind Speed Taken from Reanalyses, for Hydrologic Modeling" Water 11, no. 6: 1214. https://doi.org/10.3390/w11061214
APA StyleRicard, S., & Anctil, F. (2019). Forcing the Penman-Montheith Formulation with Humidity, Radiation, and Wind Speed Taken from Reanalyses, for Hydrologic Modeling. Water, 11(6), 1214. https://doi.org/10.3390/w11061214





