Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Sources
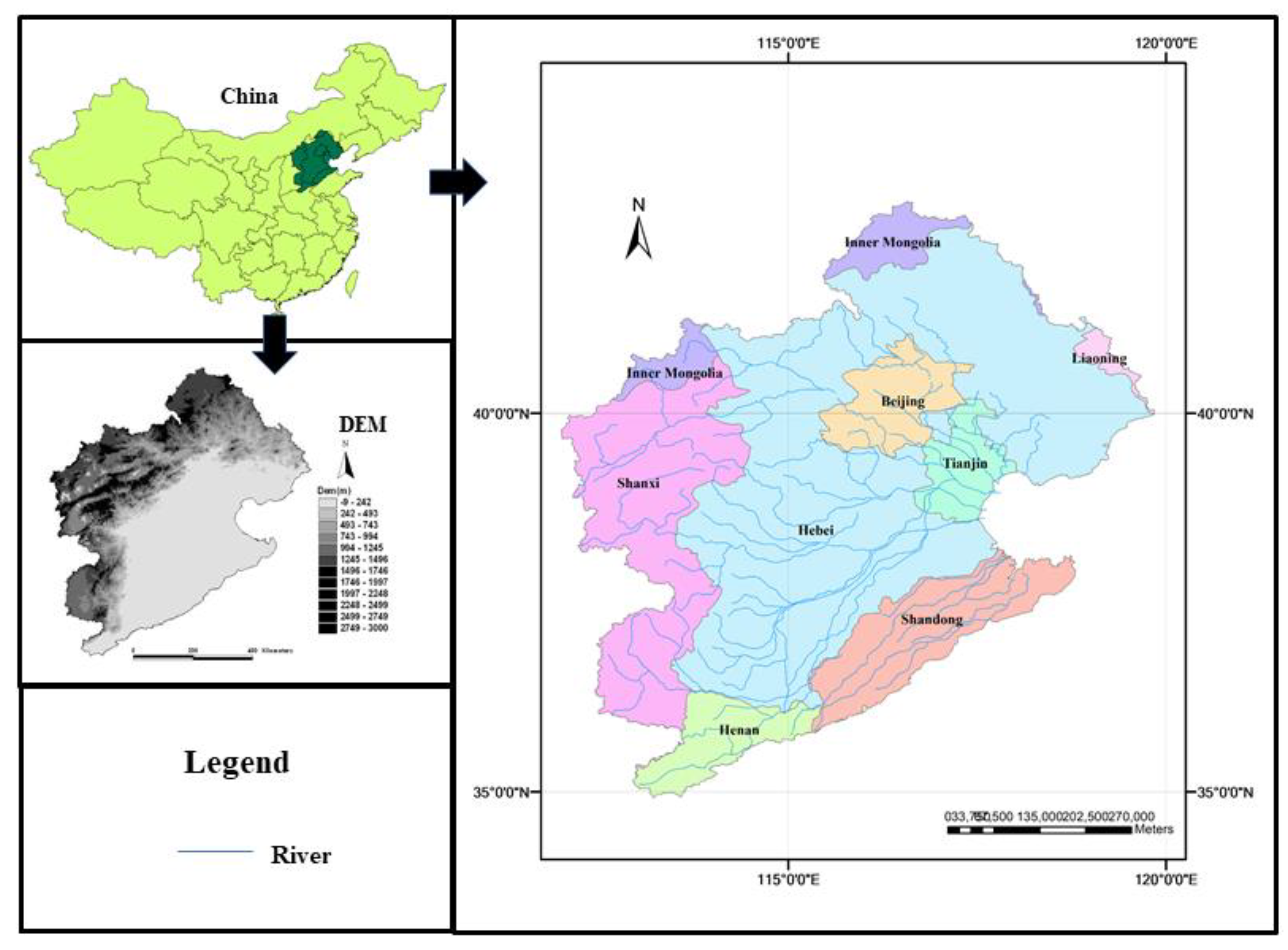
2.1.1. Study Area
2.1.2. Data Sources
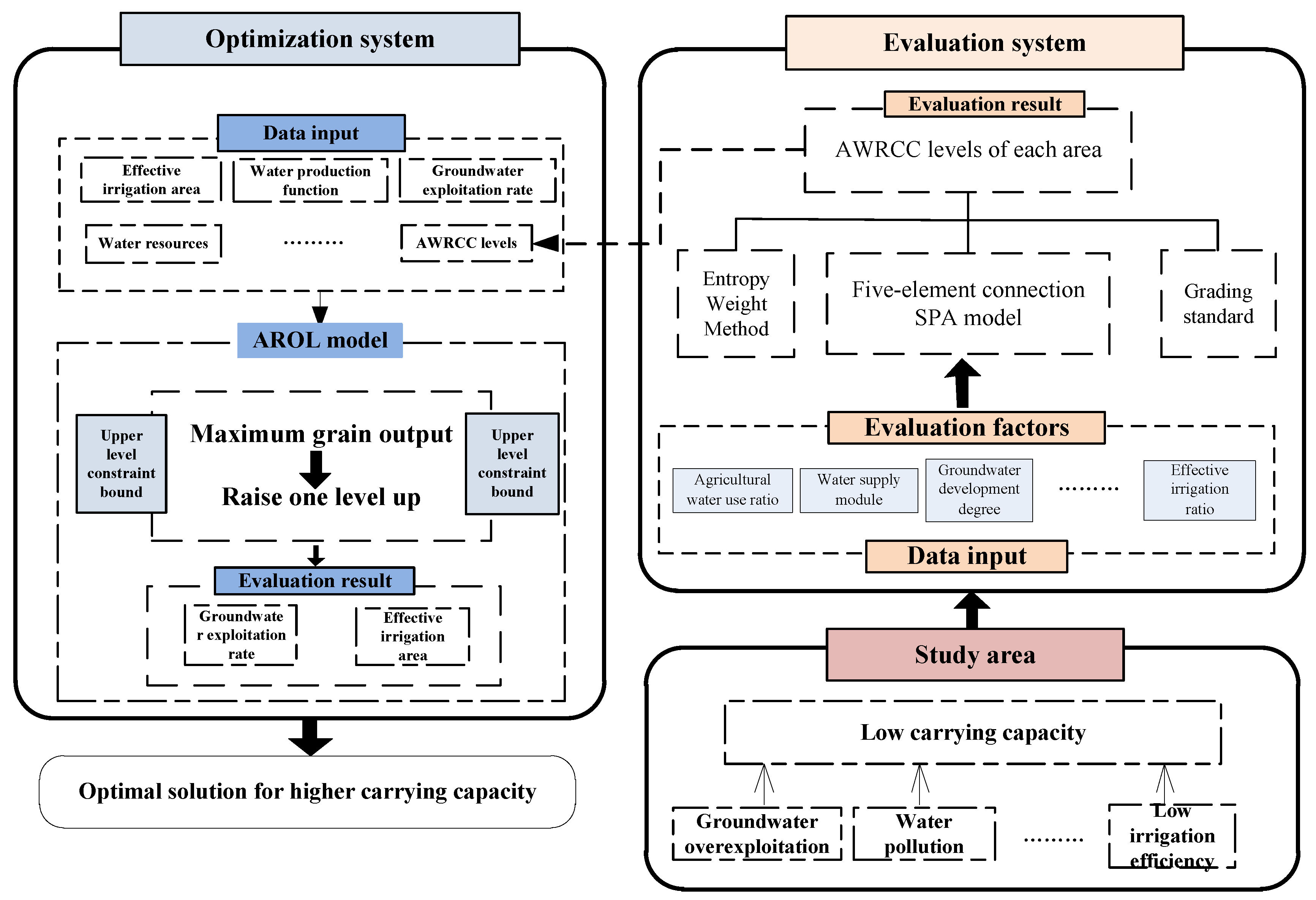
2.1.3. Framework
2.2. Construction of AWRCC Evaluation System and Gradation of Evaluation Factors
2.3. Evaluation of AWRCC by Five-Element Connection Number Set Pair Analysis Model Based on the Entropy Weight Method
2.3.1. Determination of the Weight Coefficient by the Entropy Weight Method
2.3.2. Five-Element Connection Number Set Pair Analysis Model
2.4. AROL Optimization Model
2.4.1. Construction of the AROL Model
2.4.2. AROL Model of Groundwater Exploitation Rate and Effective Irrigation Area
3. Results
3.1. Evaluation Factor Weights
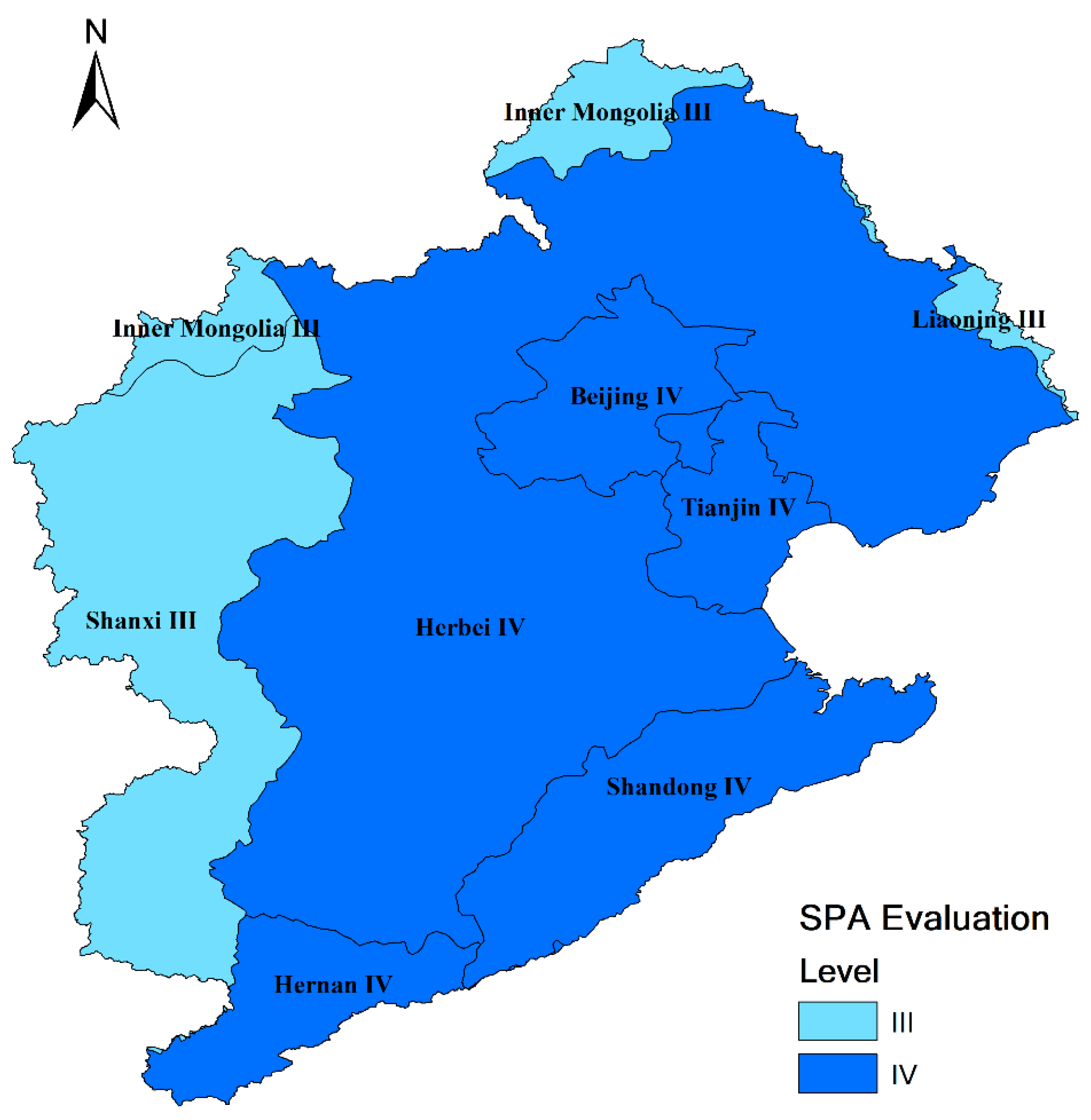
3.2. Evaluation Results
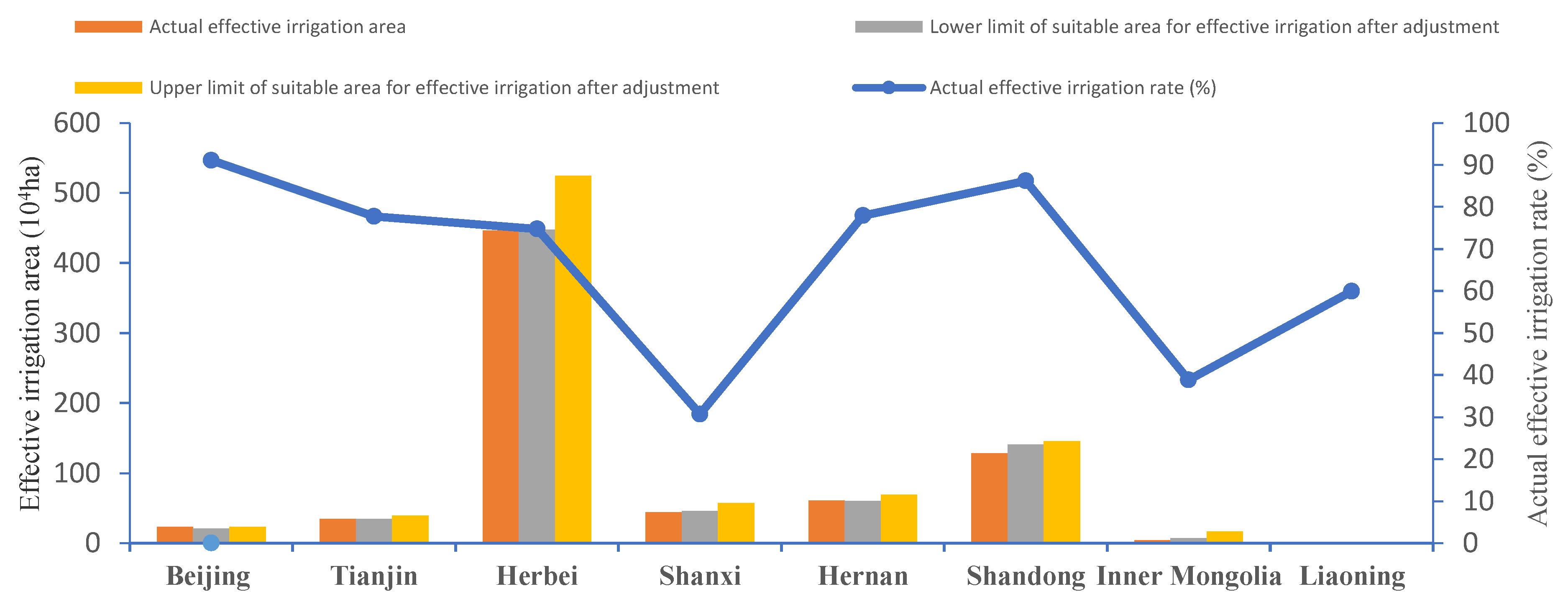
3.3. Optimization Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Deng, X.P.; Shan, L.; Zhang, H. Improving agricultural water use efficiency in arid and semiarid areas of China. Agric. Water Manag. 2006, 80, 23–40. [Google Scholar] [CrossRef]
- Sun, C.Z.; Liu, Y.Y. Analysis of the spatial-temporal pattern of water resources utilization relative efficiency based on DEA-ESDA in China. Resour. Sci. 2009, 31, 1696–1703. [Google Scholar]
- Zhu, Y.; Drake, S.; Lü, H. Analysis of Temporal and Spatial Differences in Eco-environmental Carrying Capacity Related to Water in the Haihe River Basins, China. Water Resour. Manag. 2010, 24, 1089. [Google Scholar] [CrossRef]
- Joardar, S.D. Carrying capacities and standards as bases towards urban infrastructure planning in India: A case of urban water supply and sanitation. Habitat Int. 1998, 3, 327–337. [Google Scholar] [CrossRef]
- Hunter, C. Perception of sustainable city and implications for fresh water resources management. Int. J. Environ. Pollut 1998, 1, 84–103. [Google Scholar] [CrossRef]
- Ofoezie, I.E. Human health and sustainable water resources development in Nigeria: Schistosmiasis inartificial lakes. Nat. Resour. Forum 2002, 2, 150–160. [Google Scholar] [CrossRef]
- Harris, J.M.; Kennedy, S. Carrying capacity in agriculture: Globe and regional issue. Ecol. Econ. 1999, 3, 443–461. [Google Scholar] [CrossRef]
- Xia, J.; Zhu, Y. The measurement of water resources security: A study and challenge on water resources carrying capacity. J. Nat. Resour. 2002, 3, 262–269. [Google Scholar]
- Meng, C.; Wang, X.; Li, Y. An optimization model for water management based on water resources and environmental carrying capacities: A case study of the Yinma River Basin, Northeast China. Water 2018, 10, 565. [Google Scholar] [CrossRef]
- Ait-Aoudia, M.N.; Berezowska-Azzag, E. Water resources carrying capacity assessment: The case of Algeria’s capital city. Habitat Int. 2016, 58, 51–58. [Google Scholar] [CrossRef]
- Wang, W.; Jin, J.; Ding, J.; Li, Y. A new approach to water resources system assessment—Set pair analysis method. Sci. China Ser. E-Technol. Sci. 2019, 52, 3017–3023. [Google Scholar] [CrossRef]
- Gong, L.; Jin, C. Fuzzy comprehensive evaluation for carrying capacity of regional water resources. Water Resour. Manag. 2009, 23, 2505–2513. [Google Scholar] [CrossRef]
- Falkenmark, M.; Lundqvist, J. Towards water security: Political determination and human adaptation crucial. Nat. Resour. Forum 1998, 1, 37–51. [Google Scholar] [CrossRef]
- Yuan, X.G. Bearing Capacity of Water Resources in Ganjiang Basin Based on Principal Component Analysis. Geomat. Spat. Inf. Technol. 2014, 3, 62–64, 80. [Google Scholar]
- Zhang, G.F.; Liu, T.X.; Jiang, Y.Q. Fuzzy Comprehensive Evaluation of Carrying Capacity of Water Resources of Hailaer River Basin. Yellow River 2011, 10, 48–50. [Google Scholar]
- Yu, P. Study on the Assessment of Water Resources Carrying Capacity Based on SD. Ind. Saf. Environ. Prot. 2013, 2, 38–41. [Google Scholar]
- Rijsberman, M.A.; Van De Ven F, H. Different approaches to assessment of design and management of sustainable urban water systems. Environ. Impact Assess. Rev. 2000, 3, 333–345. [Google Scholar] [CrossRef]
- Duan, Q.C.; Qiu, L.; Huang, Q. Research on quantitative model of water resources carrying capacity in irrigation area. J. Northwest A&F Univ. (Nat. Sci. Ed.) 2005, 4, 135–138. [Google Scholar]
- Mitchell, G. Demand forecasting as a tool for sustainable water resource management. Int. J. Sustain. Dev. World Ecol. 1999, 6, 231–241. [Google Scholar] [CrossRef]
- Liu, Z.B. Study on Carrying Capacity of Agricultural Water Resources in Large Irrigation Districts in North China. Master’s Thesis, Northwest A&F University, Shanxi, China, 2010. [Google Scholar]
- Xiong, H.G.; Chang, C.H.; Mao, J. Analysis of Agricultural Water Resources Carrying Capacity in Qitai County of Xinjiang Based on Fuzzy Comprehensive Evaluation. J. Water Resour. Water Eng. 2010, 4, 38–42. [Google Scholar]
- He, J.; Zhang, S.F.; Li, J.Y. The Optimal Allocation of Agricultural Water Resources Carrying Capacity under Grain Production Increases in Songhuajiang. Resour. Sci. 2014, 36, 1780–1788. [Google Scholar]
- Liu, D.; Fu, Q.; Meng, J. Application of Set Pair Analysis Method on Groundwater Resources Carrying Capacity Evaluation in Well-Irrigation Area in Sanjiang Plain. China Rural Water Hydropower 2009, 2, 1–4, 8. [Google Scholar]
- Cui, Y.; Feng, P.; Jin, J. Water resources carrying capacity evaluation and diagnosis based on set pair analysis and improved the entropy weight method. Entropy 2018, 20, 359. [Google Scholar] [CrossRef]
- Zhao, X.U.; Yang, H.; Yang, Z. Applying the input-output method to account for water footprint and virtual water trade in the Haihe River basin in China. Environ. Sci. Technol. 2010, 44, 9150–9156. [Google Scholar] [CrossRef]
- Li, C.; Xu, M.; Wang, X. Spatial analysis of dual-scale water stresses based on water footprint accounting in the Haihe River Basin, China. Ecol. Indic. 2018, 92, 254–267. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, L.; Wan, L. Assessing the trade-off between shallow groundwater conservation and crop production under limited exploitation in a well-irrigated plain of the Haihe River basin using the SWAT model. J. Hydrol. 2018, 567, 253–266. [Google Scholar] [CrossRef]
- Gong, H.; Pan, Y.; Zheng, L. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef]
- Haihe River Water Conservancy Commission, MWR. Haihe Yearbook; Local Chronicle Publishing House: Beijing, China, 2013. [Google Scholar]
- Wang, X.J.; Zhang, J.Y.; Shahid, S. Forecasting domestic water demand in the Haihe river basin under changing environment. Proc. Int. Assoc. Hydrol. Sci. 2018, 376, 51–55. [Google Scholar] [CrossRef]
- Moore, R.E. Methods and Applications of Interval Analysis; Prentice-HallInc: London, UK, 1979. [Google Scholar]
- Chanas, S.; Kuchta, D. Multiobjective programming in optimsization of interval objective functions—A generalized approach. Eur. J. Oper. Res. 1996, 94, 594–598. [Google Scholar] [CrossRef]
- Muzhikov, V.; Vershinina, E.; Muzhikov, R. Structure of Interchannel and Five Primary Elements Connections According to the Test of Akabane. Int. J. Chin. Med. 2018, 2, 18–29. [Google Scholar]
- Fang, H.; Gong, C.; Li, C. A surrogate model based nested optimization framework for inverse problem considering interval uncertainty. Struct. Multidiscip. Optim. 2018, 58, 869–883. [Google Scholar] [CrossRef]
- Hussein, H. Whose ‘reality’? Discourses and hydropolitics along the Yarmouk River. Contemp. Levant 2017, 2, 103–115. [Google Scholar] [CrossRef]
- Da Silva, L.P.B.; Hussein, H. Production of scale in regional hydropolitics: An analysis of La Plata River Basin and the Guarani Aquifer System in South America. Geoforum 2019, 99, 42–53. [Google Scholar] [CrossRef]
- Hussein, H. Tomatoes, tribes, bananas, and businessmen: An analysis of the shadow state and of the politics of water in Jordan. Environ. Sci. Policy 2018, 84, 170–176. [Google Scholar] [CrossRef]
- Ferragina, E.; Greco, F. The Disi project: An internal/external analysis. Water Int. 2008, 33, 451–463. [Google Scholar] [CrossRef]
- Hussein, H. The Guarani Aquifer System, highly present but not high profile: A hydropolitical analysis of transboundary groundwater governance. Environ. Sci. Policy 2018, 83, 54–62. [Google Scholar] [CrossRef]
- Stephan, R.M. Transboundary aquifers in international law: Towards an evolution. In Overexploitation and Contamination of Shared Groundwater Resources; Springer: Dordrecht, The Netherlands, 2008; pp. 33–45. [Google Scholar]
- Hussein, H.; Menga, F.; Greco, F. Monitoring transboundary water cooperation in SDG 6.5. 2: How a critical hydropolitics approach can spot inequitable outcomes. Sustainability 2018, 10, 3640. [Google Scholar] [CrossRef]
- Ortigara, A.; Kay, M.; Uhlenbrook, S. A review of the SDG 6 synthesis report 2018 from an education, training, and research perspective. Water 2018, 10, 1353. [Google Scholar] [CrossRef]
| Date | Data Sources and Links | Date | Date Sources and Links |
|---|---|---|---|
| Effective irrigation area | Hiahe Yearbook 2013 (http://cyfd.cnki.com.cn/N2017110269.htm) | Water supply quantity | China Statistical Yearbook 2013 (http://www.stats.gov.cn/tjsj/ndsj/2013/indexch.htm) |
| Irrigated area | |||
| Agricultural water consumption | Total water consumption | ||
| Annual groundwater supply quantity | Irrigation water | ||
| Exploitable amount of groundwater resources | Irrigated land area | China National Digital Library (http://www.nlc.cn/) | |
| Calculated land area | |||
| Surface water supply quantity | Population | Haihe River Water Conservancy Commission, MWR (http://www.hwcc.gov.cn/hwcc/static/szygb/gongbao2013/index.htm) | |
| Available amount of surface water resources | Water saving irrigation data |
| Index | Unit | Grading Standards | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| Re | % | 90 | 70 | 50 | 30 | 10 |
| Mw | 104 m3/km2 | 4.3 | 5.7 | 7.1 | 8.6 | 10 |
| Ra | % | 32 | 43 | 54 | 64 | 75 |
| Qw | m3/ha | 180 | 215 | 250 | 285 | 320 |
| Dgw | % | 13.7 | 18.3 | 22.8 | 27.4 | 31.9 |
| Dsw | % | 40.9 | 54.5 | 68.2 | 81.8 | 95.4 |
| Five-Element Connection Numbers usk | Cost Index | Benefit Index |
|---|---|---|
| x ≤ k1 | x ≥ k1 | |
| k1 ≤ x ≤ k2 | k2 ≤ x ≤ k1 | |
| k2 ≤ x ≤ k3 | k3 ≤ x ≤ k2 | |
| k3 ≤ x ≤ k4 | k4 ≤ x ≤ k3 | |
| k4 ≤ x ≤ k5 | k5 ≤ x ≤ k4 | |
| x ≥ k5 | x ≤ k5 |
| Index | Weight | Index | Weight |
|---|---|---|---|
| Re | 0.164 | Qw | 0.139 |
| Mw | 0.199 | Dgw | 0.217 |
| Ra | 0.156 | Dsw | 0.126 |
| Districts | Set Pair Analysis Method for Comprehensive Evaluation | Corresponding Level |
|---|---|---|
| Beijing | −0.2145 | Ⅳ |
| Tianjin | −0.3890 | Ⅳ |
| Hebei | −0.3771 | Ⅳ |
| Shanxi | 0.1351 | Ⅲ |
| Henan | −0.4944 | Ⅳ |
| Shandong | −0.5140 | Ⅳ |
| Inner Mongolia | −0.0850 | Ⅲ |
| Liaoning | 0.1311 | Ⅲ |
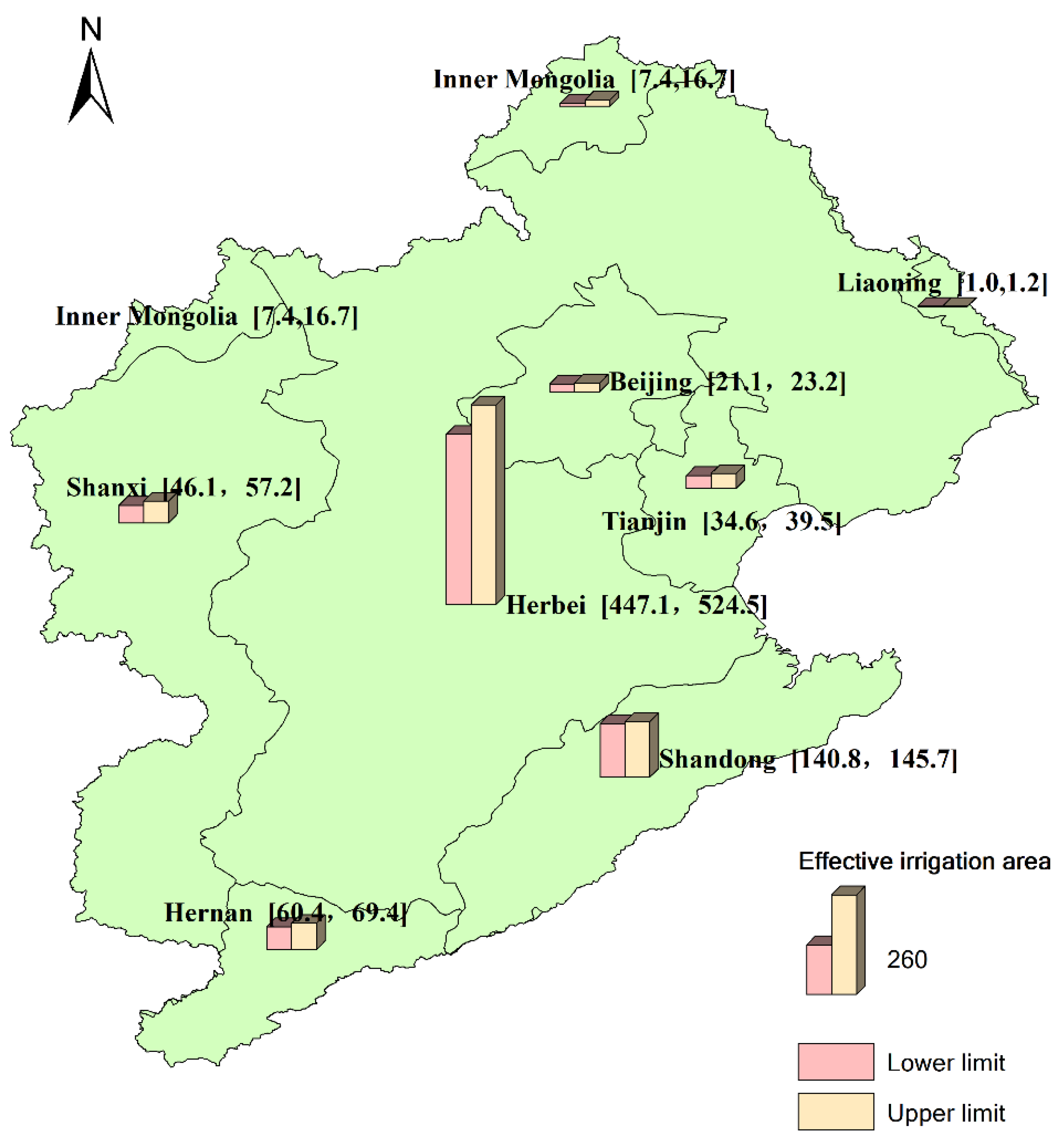
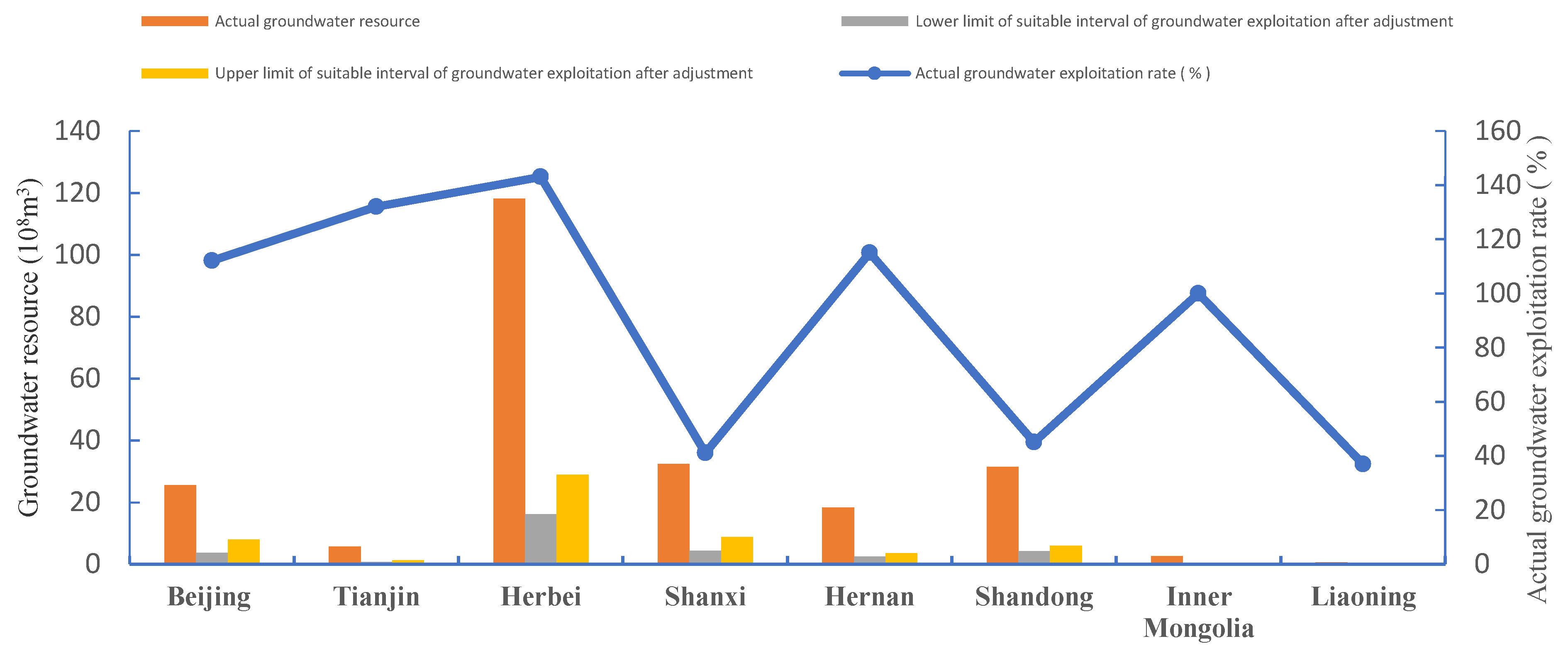
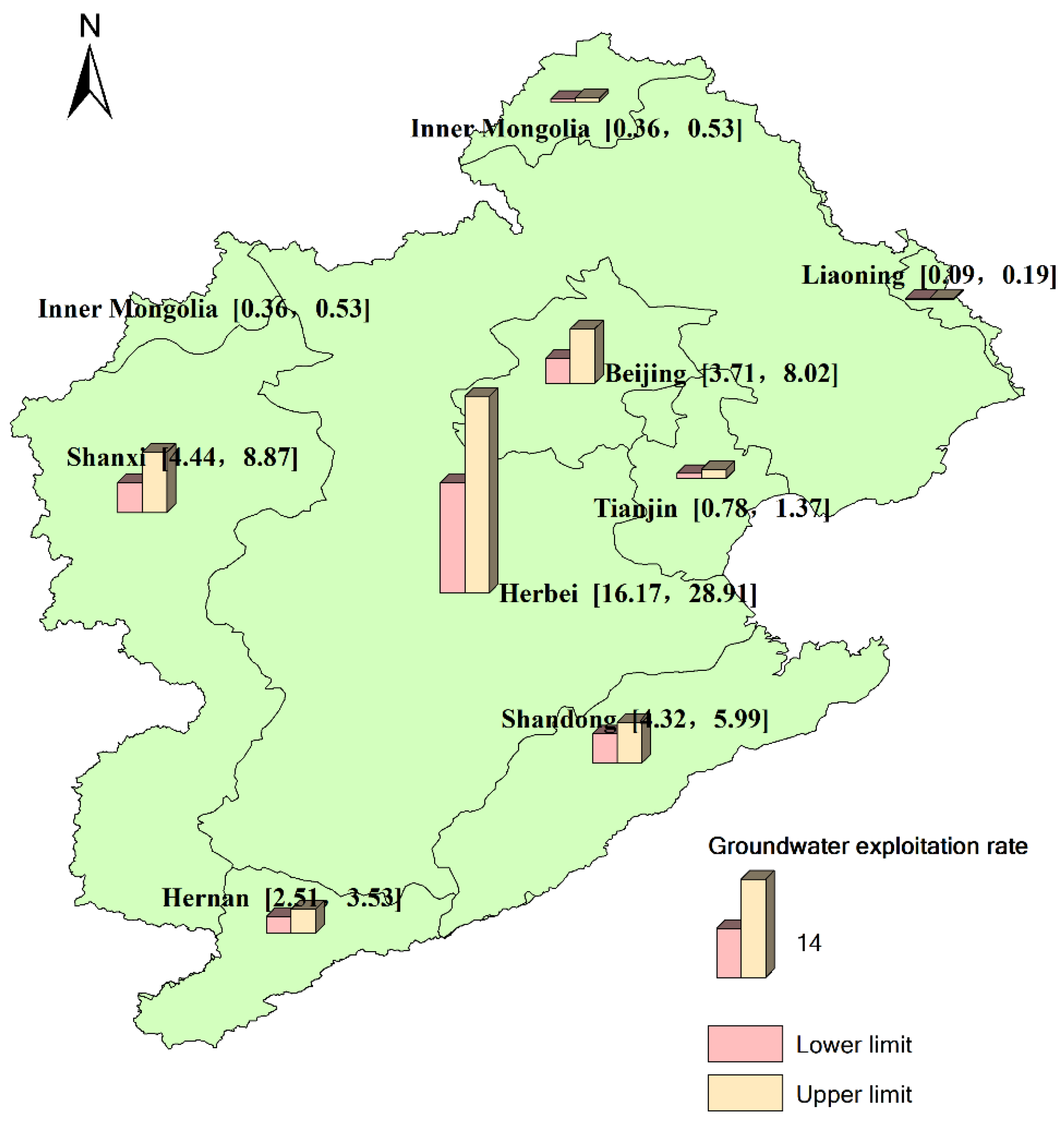
| Districts | Actual Effective Irrigation Rate % | Actual Effective Irrigation Area 104 ha | Appropriate Range of Effective Irrigation Area after Adjustment 104 ha | Actual Groundwater Exploitation Rate % | Actual Groundwater Exploitation Rate 108 m3 | Appropriate Interval of Groundwater Exploitation after Adjustment 108 m3 |
|---|---|---|---|---|---|---|
| Beijing | 91.13 | 23.1 | [23.1,23.2] | 112 | 25.6 | [3.71,8.02] |
| Tianjin | 77.70 | 34.9 | [34.6,39.5] | 132 | 5.71 | [0.78,1.37] |
| Hebei | 74.81 | 446.4 | [447.1,524.5] | 143 | 118.06 | [16.17,28.91] |
| Shanxi | 30.70 | 44.3 | [46.1,57.2] | 41 | 32.4 | [4.44,8.87] |
| Henan | 77.98 | 61.0 | [60.4,69.4] | 115 | 18.32 | [2.51,3.53] |
| Shandong | 86.22 | 128.6 | [140.8,145.7] | 45 | 31.54 | [4.32,5.99] |
| Inner Mongolia | 38.80 | 4.5 | [7.4, 16.7] | 100 | 2.64 | [0.36, 0.53] |
| Liaoning | 59.92 | 1.1 | [1.0,1.2] | 37 | 0.66 | [0.09,0.19] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.; Zi, X.; Wang, S.; He, L. Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China. Water 2019, 11, 999. https://doi.org/10.3390/w11050999
Kang J, Zi X, Wang S, He L. Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China. Water. 2019; 11(5):999. https://doi.org/10.3390/w11050999
Chicago/Turabian StyleKang, Jian, Xin Zi, Sufen Wang, and Liuyue He. 2019. "Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China" Water 11, no. 5: 999. https://doi.org/10.3390/w11050999
APA StyleKang, J., Zi, X., Wang, S., & He, L. (2019). Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China. Water, 11(5), 999. https://doi.org/10.3390/w11050999




