Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network
Abstract
1. Introduction
2. Study Area and Datasets
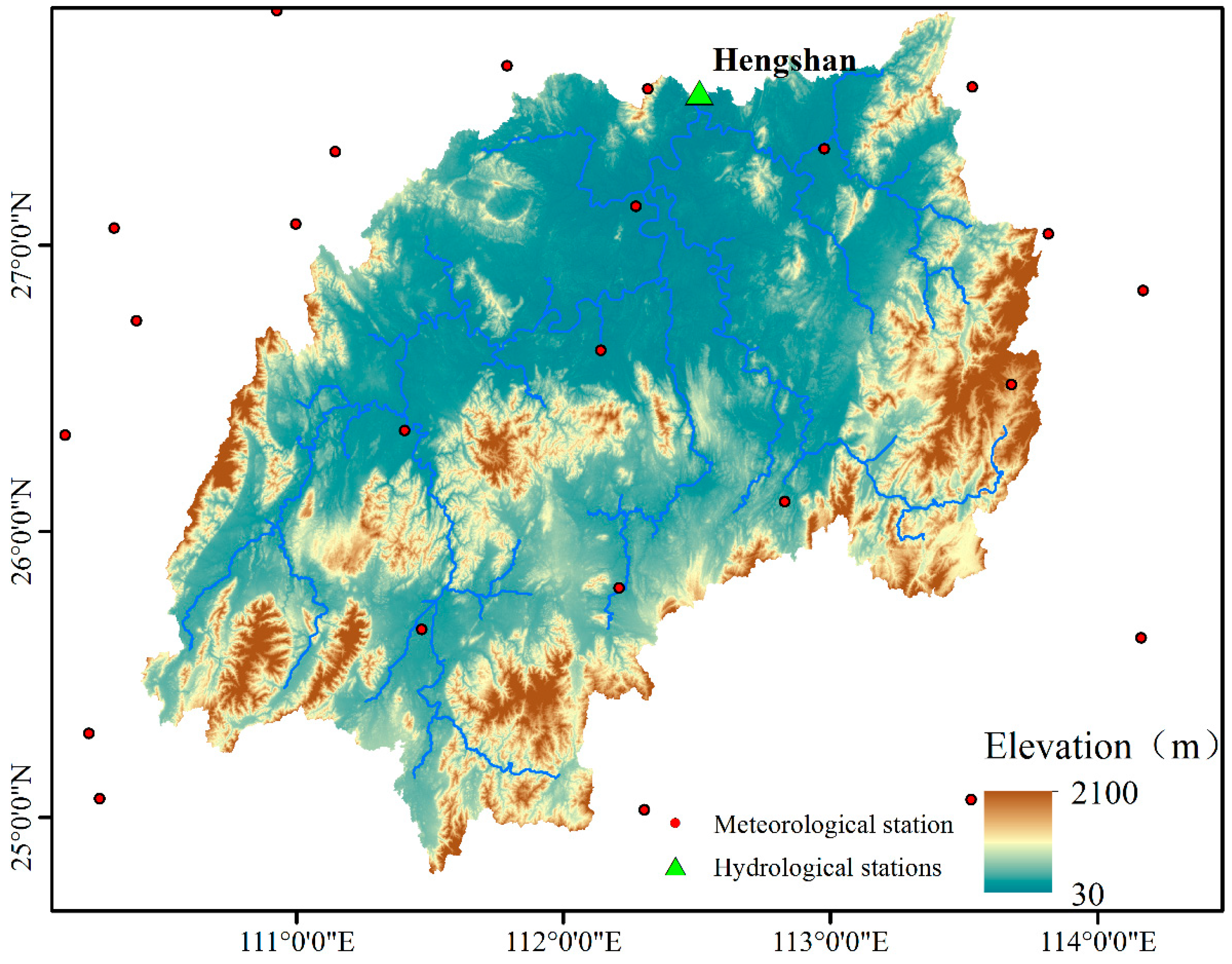
2.1. Study Area
2.2. Datasets
3. Methods
3.1. Downscaling Methods
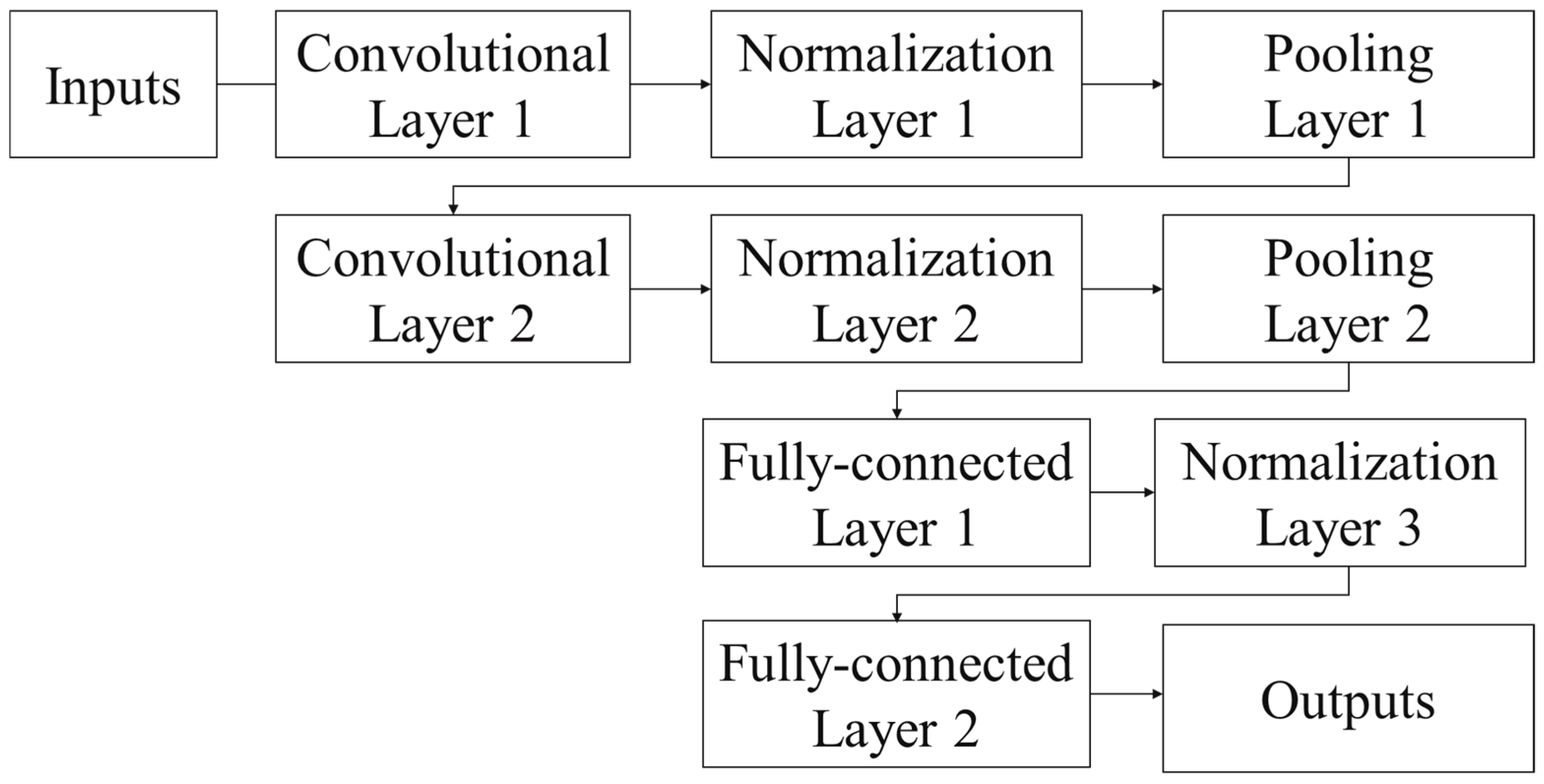
3.1.1. Convolutional Neural Networks
3.1.2. Combination of CNN and Long Short Term Memory Networks
3.1.3. Support Vector Machine
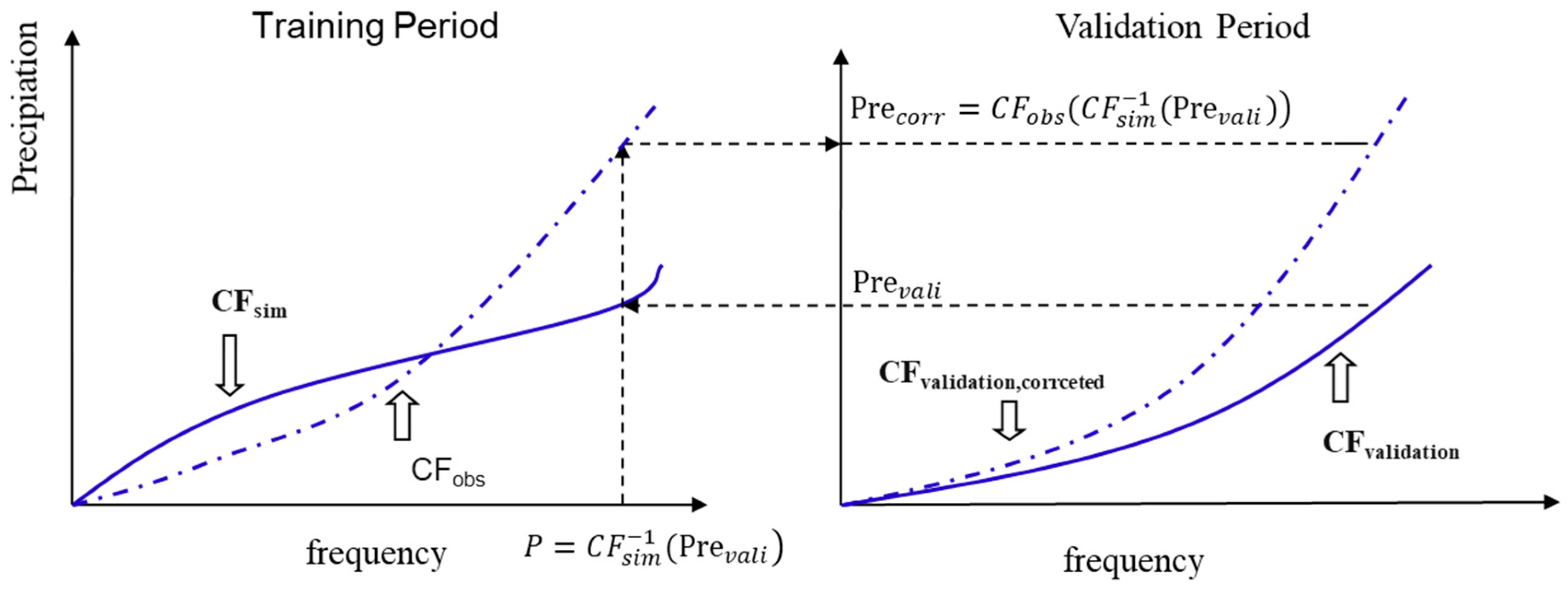
3.1.4. Quantile Mapping Method
3.2. Statistical Evaluation Based on Gauge Rainfall Data
3.3. Evaluation through Hydrological Modeling
Description of the Distributed Hydrological Model and Model Validation
4. Results and Discussion
4.1. Precipitation Estimation Performance with Different Predictors
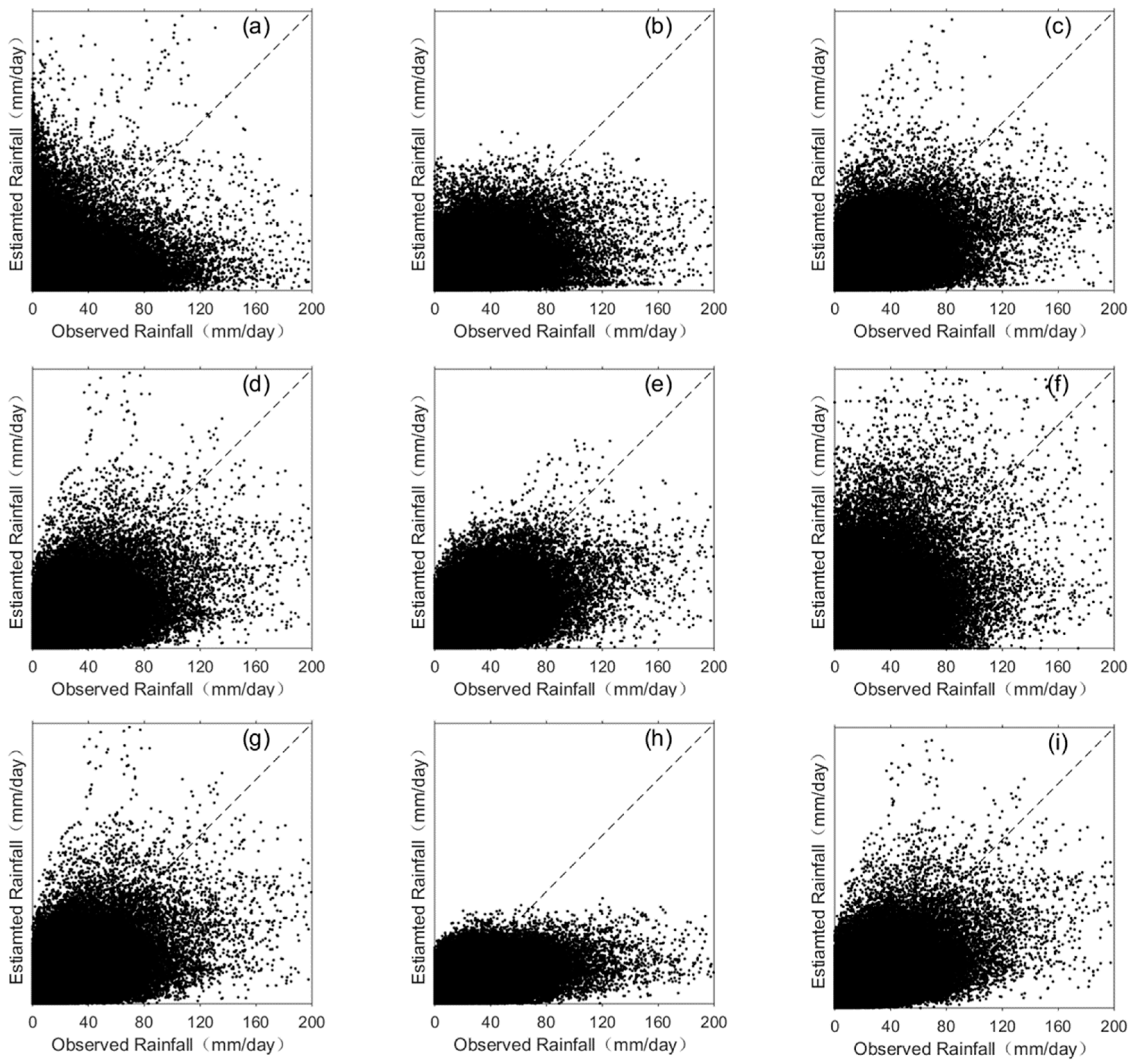
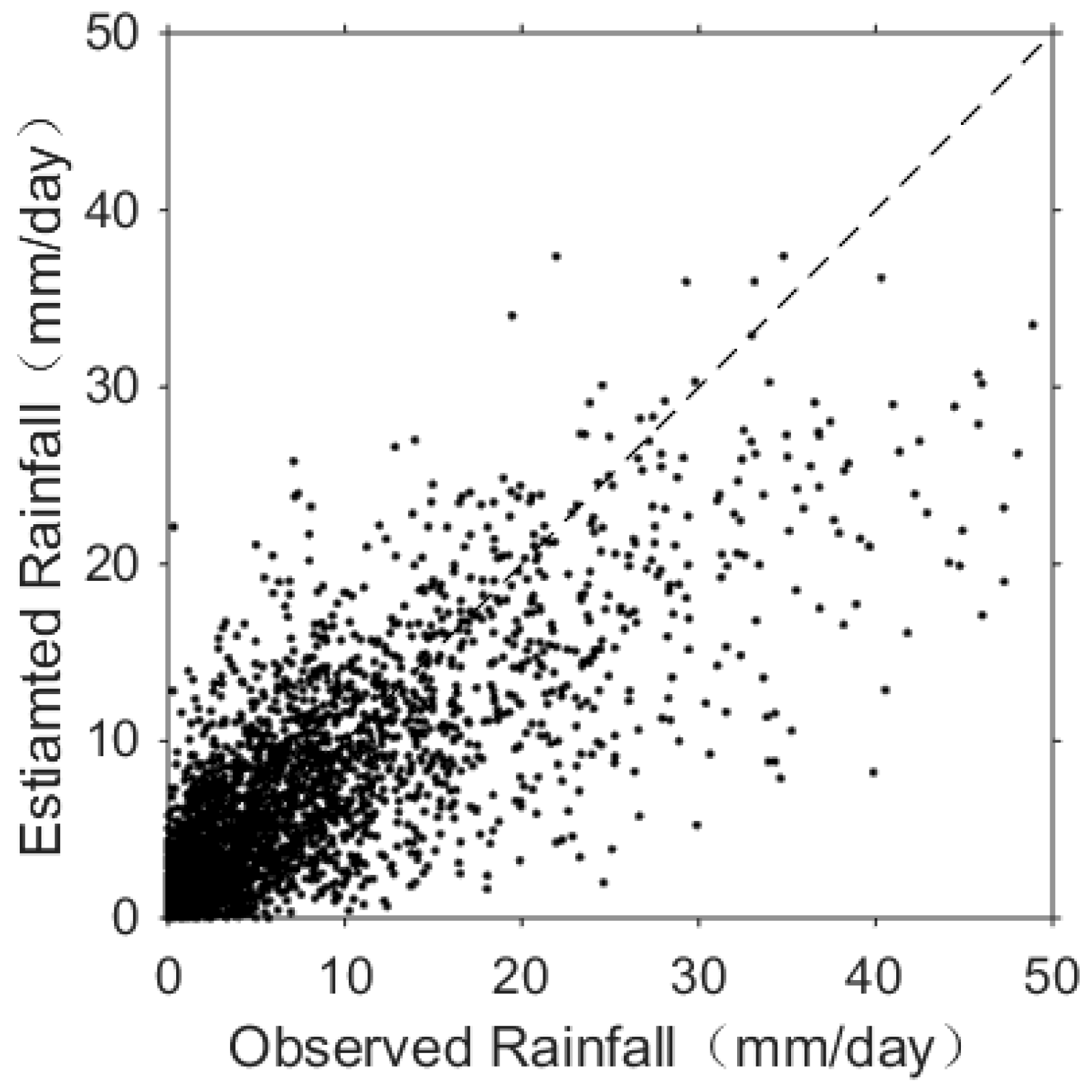
4.2. Precipitation Estimation Performance of Different Methods
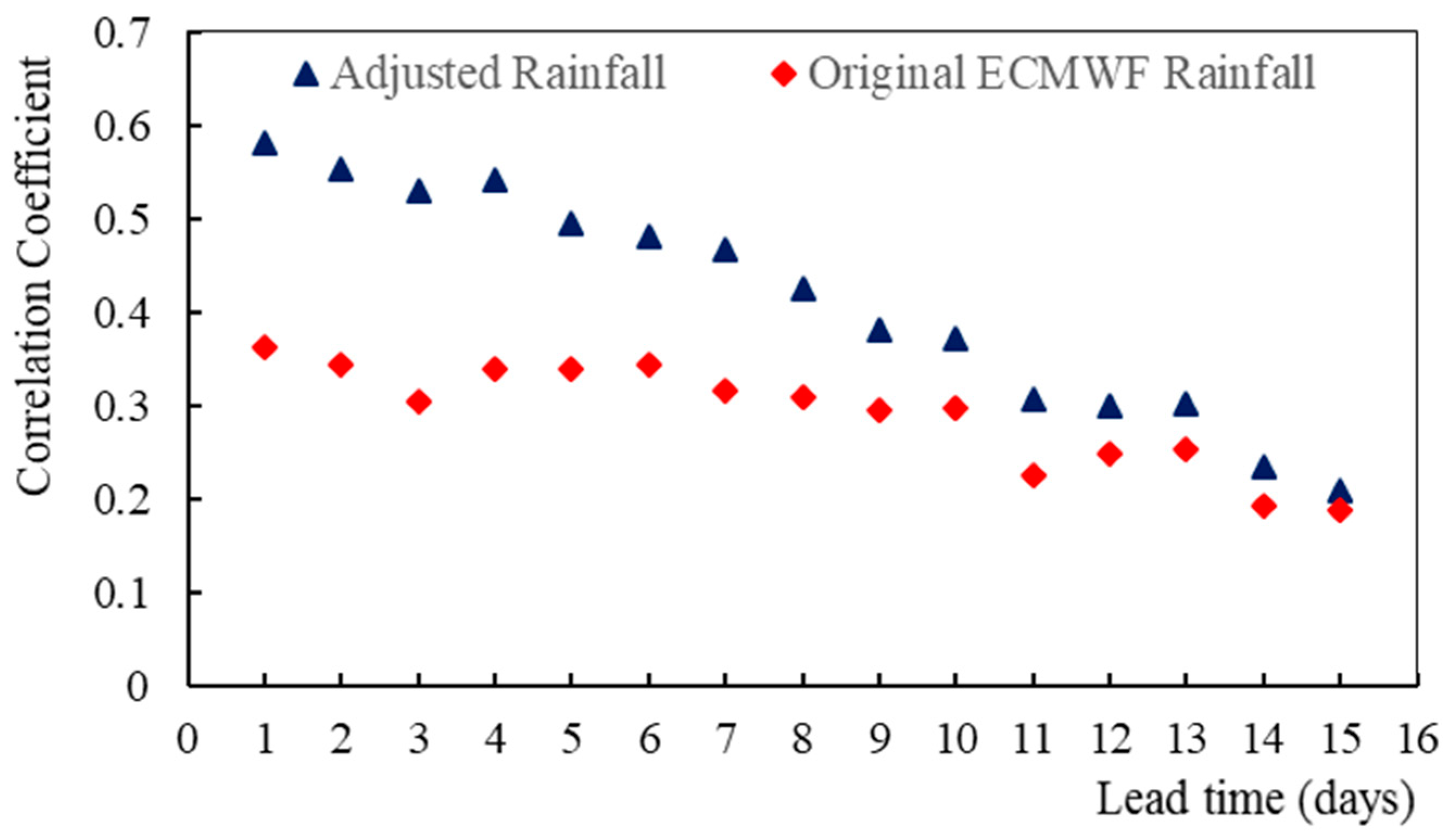
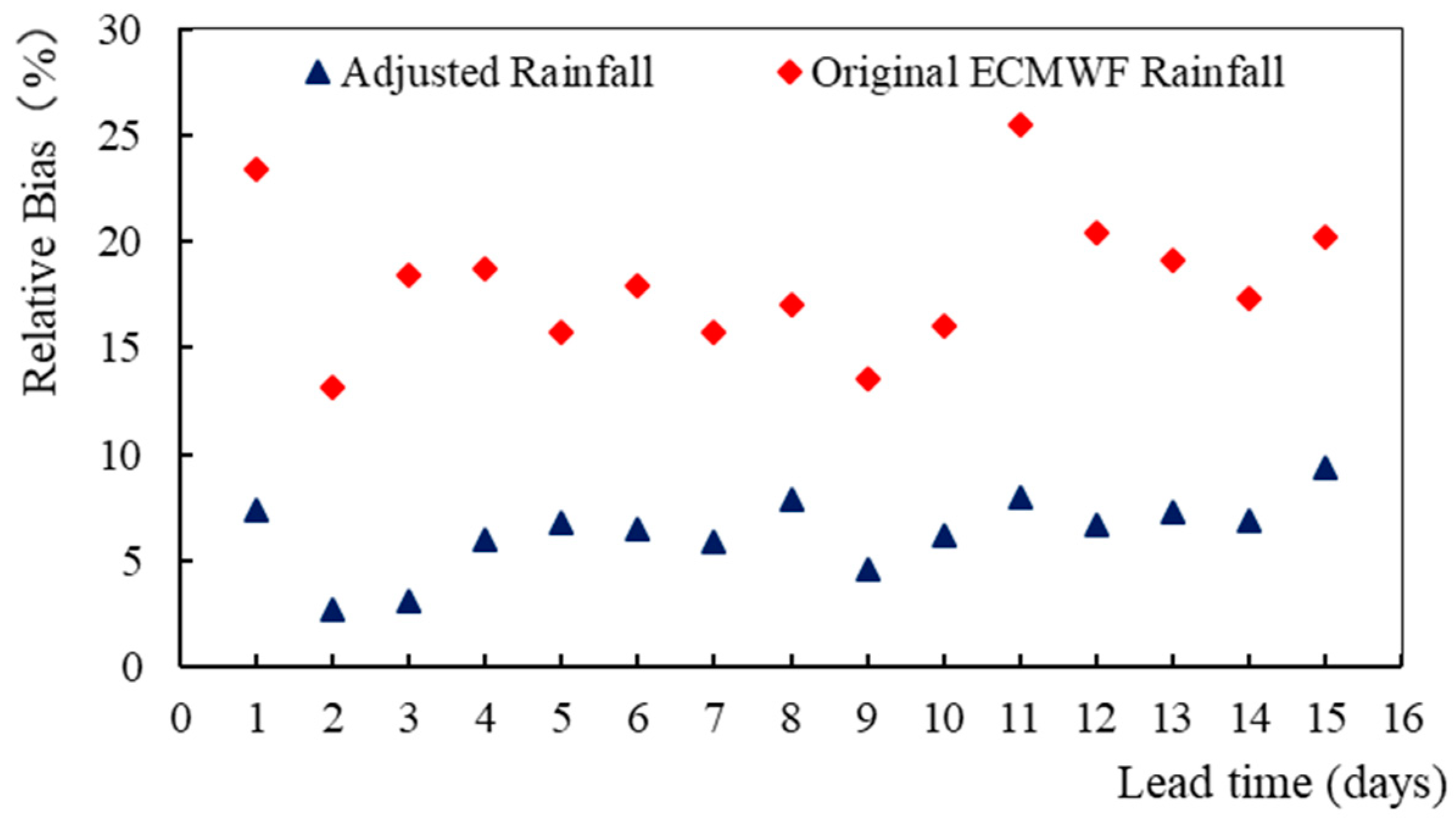
4.3. Application of Methods in Precipitation Forecast
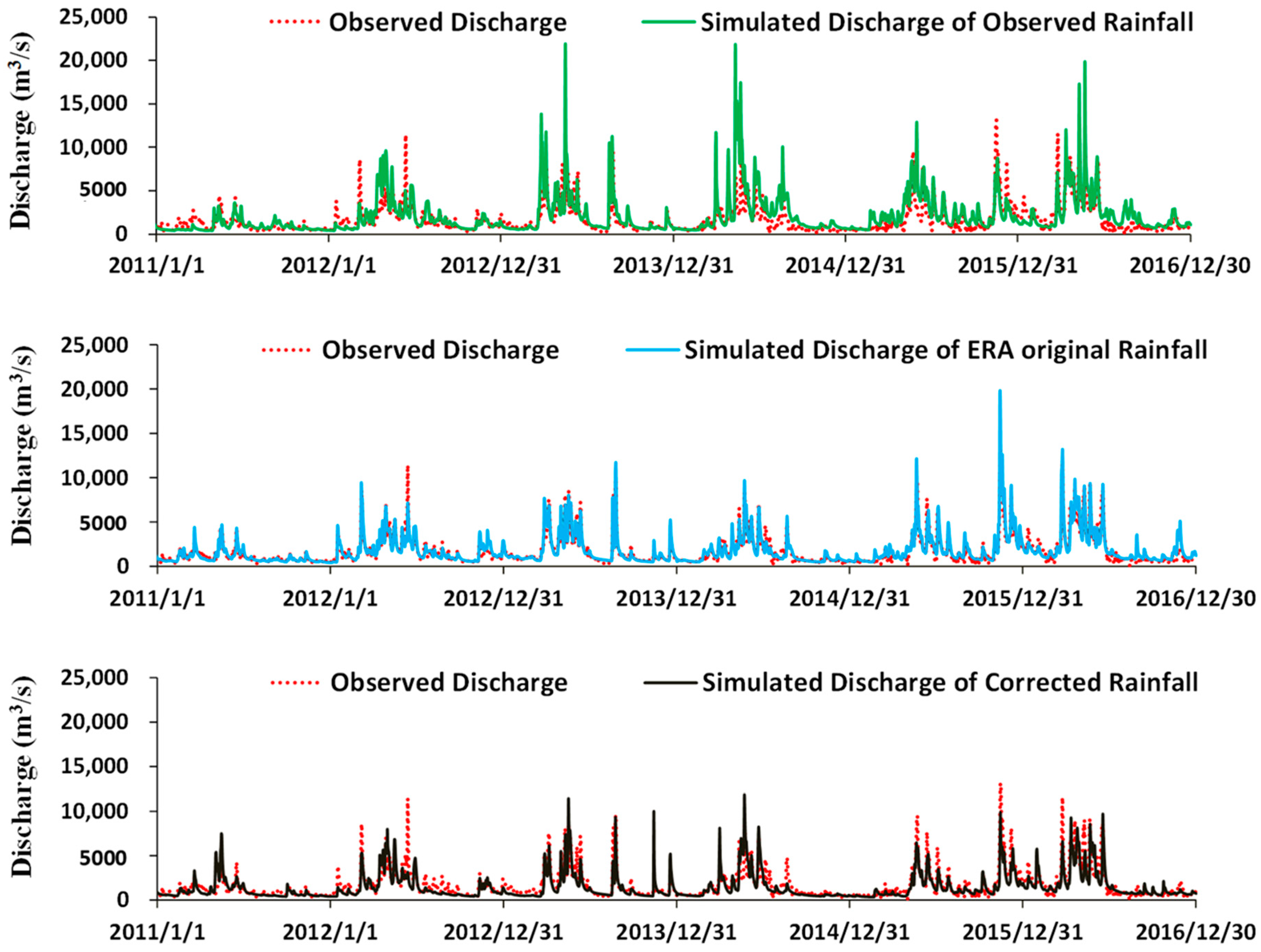
4.4. Application in Hydrological Simulation
5. Summary and Conclusions
- Four experiments using different circulation predictors were designed to test the effectiveness of those predictors. Results show that using as many meteorological variables as possible is conducive to improving the rainfall estimation while using mean sea level alone can only provide limited improvement. Among all the meteorological variables, the geopotential height might be the most important one. Considering both the accuracy and complexity of the model, we suggest that the combination of geopotential height and total water vapor might be reasonable.
- Another four experiments were designed to compare the different performance of the Quantile Mapping method, SVM, CNN networks, and ConvLSTM networks. Precipitation estimated by ConvLSTM networks gave the best performance (with highest correlation coefficient of 0.73), along with CNN, SVM, and the Quantile Mapping method, with correlation coefficient of 0.69, 0.65, 0.54 respectively. We also found that the method based on SVM could not predict very high intensity rainfall.
- The trained ConvLSTM networks were applied to S2S-ECMWF hindcast datasets to further test their robustness. We found the corrected precipitation was superior to the original S2S-ECMWF precipitation all the time, but the superiority (in terms of correlation coefficient) gradually decreased with the increase of the lead time. We think the improvement mainly comes from the use of observed data and the effective networks, which can reduce the parameterization error. However, when the lead time extends, the parameterization error becomes subordinate. Thus the superiority of the proposed method gradually fades away. However, the improvement for systematic deviation always holds for all lead times.
- Different rainfall inputs are fed into the distributed hydrological model. The original EAR-Interim rainfall shows little usage in hydrological simulation with an NSE of 0.06 and RB of 24%, while the corrected rainfall forced simulation improves the NSE to 0.64 and reduces RB to −10%, which is comparable to the simulation forced by the observed rainfall. This further proves the value of the proposed method.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. Biogeosci. 2004, 109, 02103. [Google Scholar] [CrossRef]
- Panagoulia, D.; Dimou, G. Sensitivity of flood events to global climate change. J. Hydrol. 1997, 191, 208–222. [Google Scholar] [CrossRef]
- Panagoulia, D.; Dimou, G. Definitions and effects of droughts. In Proceedings of the Conference on Mediterranean Water Policy: Building on Existing Experience, Mediterranean Water Network, Valencia, Spain, 16 April 1998; General Lecture, Invited Presentation, ResearchGate: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Roca, R.; Del Genio, A.; Dewitte, B.; Petersen, W.; Zhang, F. Is precipitation a good metric for model performance? Bull. Am. Meteorol. Soc. 2019, 100, 223–233. [Google Scholar] [CrossRef]
- Stephens, G.L.; L’Ecuyer, T.; Forbes, R.; Gettelmen, A.; Golaz, J.-C.; Bodas-Salcedo, A.; Suzuki, K.; Gabriel, P.; Haynes, J. Dreary state of precipitation in global models. J. Geophys. Res. Atmos. 2010, 115, D24211. [Google Scholar] [CrossRef]
- Kang, I.-S.; Jin, K.; Wang, B.; Lau, K.-M.; Shukla, J.; Krishnamurthy, V.; Schubert, S.; Wailser, D.; Stern, W.; Kitoh, A.; et al. Intercomparison of the climatological variations of Asian summer monsoon precipitation simulated by 10 GCMs. Clim. Dyn. 2002, 19, 383–395. [Google Scholar]
- Wang, B.; Kang, I.-S.; Lee, J.-Y. Ensemble Simulations of Asian—Australian Monsoon Variability by 11 AGCMs*. J. Clim. 2004, 17, 803–818. [Google Scholar] [CrossRef]
- Xu, C.-Y. From GCMs to river flow: A review of downscaling methods and hydrologic modelling approaches. Prog. Phys. Geogr. Earth 1999, 23, 229–249. [Google Scholar] [CrossRef]
- Ghosh, S. SVM-PGSL coupled approach for statistical downscaling to predict rainfall from GCM output. J. Geophys. Res. Biogeosci. 2010, 115, D22102. [Google Scholar] [CrossRef]
- Meehl, G.A.; Stocker, T.F.; Collins, W.D.; Friedlingstein, P.; Gaye, T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Chap. Global Climate Projections; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Benestad, R. Novel methods for inferring future changes in extreme rainfall over Northern Europe. Clim. Res. 2007, 34, 195–210. [Google Scholar] [CrossRef]
- Benestad, R.E.; Haugen, J.E. On complex extremes: Flood hazards and combined high spring-time precipitation and temperature in Norway. Clim. Chang. 2007, 85, 381–406. [Google Scholar] [CrossRef]
- Christensen, J.H.; Machenhauer, B.; Jones, R.G.; Schär, C.; Ruti, P.M.; Castro, M.; Visconti, G. Validation of present-day regional climate simulations over Europe: LAM simulations with observed boundary conditions. Clim. Dyn. 1997, 13, 489–506. [Google Scholar] [CrossRef]
- Hanssen-Bauer, I.; Achberger, C.; Benestad, R.E.; Chen, D.; Forland, E.J. Statistical downscaling of climate scenarios over Scandinavia. Clim. Res. 2005, 29, 255–268. [Google Scholar] [CrossRef]
- Prudhomme, C.; Reynard, N.; Crooks, S. Downscaling of global climate models for flood frequency analysis: Where are we now? Hydrol. Process. 2002, 16, 1137–1150. [Google Scholar] [CrossRef]
- Panagoulia, D.; Bárdossy, A.; Lourmas, G. Multivariate stochastic downscaling models generating precipitation and temperature scenarios of climate change based on atmospheric circulation. Glob. Nest J. 2008, 10, 263–272. [Google Scholar]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Murphy, J. Predictions of climate change over Europe using statistical and dynamical downscaling techniques. Int. J. Clim. 2000, 20, 489–501. [Google Scholar] [CrossRef]
- Schoof, J.T.; Pryor, S. Downscaling temperature and precipitation: A comparison of regression-based methods and artificial neural networks. Int. J. Clim. 2001, 21, 773–790. [Google Scholar] [CrossRef]
- Li, Y.; Smith, I. A Statistical Downscaling Model for Southern Australia Winter Rainfall. J. Clim. 2009, 22, 1142–1158. [Google Scholar] [CrossRef]
- Hope, P.K. Projected future changes in synoptic systems influencing southwest Western Australia. Clim. Dyn. 2006, 26, 765–780. [Google Scholar] [CrossRef]
- Kannan, S.; Ghosh, S. A nonparametric kernel regression model for downscaling multisite daily precipitation in the Mahanadi basin. Water Resour. Res. 2013, 49, 1360–1385. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Pan, B.; Cong, Z. Information Analysis of Catchment Hydrologic Patterns across Temporal Scales. Adv. Meteorol. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Anandhi, A.; Srinivas, V.V.; Nanjundiah, R.S.; Kumar, D.N. Downscaling precipitation to river basin in India for IPCC SRES scenarios using support vector machine. Int. J. Clim. 2008, 28, 401–420. [Google Scholar] [CrossRef]
- Guhathakurta, P. Long lead monsoon rainfall prediction for meteorological sub-divisions of India using deterministic artificial neural network model. Theor. Appl. Clim. 2008, 101, 93–108. [Google Scholar] [CrossRef]
- Taylor, J.W. A quantile regression neural network approach to estimating the conditional density of multi-period returns. J. Forecast. 2000, 19, 299–311. [Google Scholar] [CrossRef]
- Norton, C.W.; Chu, P.-S.; Schroeder, T.A. Projecting changes in future heavy rainfall events for Oahu, Hawaii: A statistical downscaling approach. J. Geophys. Res. Atmos. 2011, 116, D17110. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. DeepSD: Generating High Resolution Climate Change Projections through Single Image Super-Resolution. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar]
- Pan, B.; Hsu, K.; AghaKouchak, A.; Sorooshian, S. Improving Precipitation Estimation Using Convolutional Neural Network. Water Resour. Res. 2019, 55, 2301–2321. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting. Int. Conf. Neural Inf. Process. Syst. 2015. [Google Scholar] [CrossRef]
- Kidson, J.W.; Thompson, C.S. A Comparison of Statistical and Model-Based Downscaling Techniques for Estimating Local Climate Variations. J. Clim. 1998, 11, 735–753. [Google Scholar] [CrossRef]
- Cavazos, T. Large-Scale Circulation Anomalies Conducive to Extreme Precipitation Events and Derivation of Daily Rainfall in Northeastern Mexico and Southeastern Texas. J. Clim. 1999, 12, 1506–1523. [Google Scholar] [CrossRef]
- Wilby, R.; Wigley, T. Precipitation predictors for downscaling: Observed and general circulation model relationships. Int. J. Clim. 2000, 20, 641–661. [Google Scholar] [CrossRef]
- Murphy, J. An Evaluation of Statistical and Dynamical Techniques for Downscaling Local Climate. J. Clim. 1999, 12, 2256–2284. [Google Scholar] [CrossRef]
- Anandhi, A.; Srinivas, V.V.; Kumar, D.N.; Nanjundiah, R.S. Role of predictors in downscaling surface temperature to river basin in India for IPCC SRES scenarios using support vector machine. Int. J. Climatol. 2009, 29, 583–603. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total. Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef] [PubMed]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin climate for hydro-meteorological studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Vitart, F.; Ardilouze, C.; Bonet, A.; Brookshaw, A.; Chen, M.; Codorean, C.; Déqué, M.; Ferranti, L.; Fucile, E.; Fuentes, M.; et al. The Subseasonal to Seasonal (S2S) Prediction Project Database. Am. Meteorol. Soc. 2017, 98, 163–173. [Google Scholar] [CrossRef]
- Dai, Y.; Shangguan, W.; Duan, Q.; Liu, B.; Fu, S.; Niu, G. Development of a China Dataset of Soil Hydraulic Parameters Using Pedotransfer Functions for Land Surface Modeling. J. Hydrometeorol. 2013, 14, 869–887. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Int. Conf. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors. Available online: https://arxiv.org/pdf/1207.0580v1.pdf (accessed on 3 July 2012).
- Loffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Available online: https://arxiv.org/pdf/1502.03167.pdf (accessed on 2 March 2015).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. Available online: http://download.tensorflow.org/paper/whitepaper2015.pdf (accessed on 9 November 2015).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A. Generating Sequences with Recurrent Neural Networks. Available online: https://arxiv.org/pdf/1308.0850.pdf (accessed on 5 June 2014).
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer Nature: New York, NY, USA, 1995. [Google Scholar]
- Sehad, M.; Lazri, M.; Ameur, S. Novel SVM-based technique to improve rainfall estimation over the Mediterranean region (north of Algeria) using the multispectral MSG SEVIRI imagery. Adv. Space Res. 2016, 59, 1381–1394. [Google Scholar] [CrossRef]
- Cover, T.M. Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Trans. Electron. Comput. 1965, EC-14, 326–334. [Google Scholar] [CrossRef]
- Smola, A.J. Regression Estimation with Support Vector Learning Machines; Technische Universitat Munchen: Munich, Germany, 1996. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Fourth Indian Reprint; Pearson Education: Singapore, 2003; p. 842. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Baesens, B.; Viaene, S.; Gestel, T.V.; Suykens, J.A.K.; Dedene, G.; De Moor, B.; Vanthienen, J. An empirical assessment of kernel type performance for least squares support vector machine classifiers. In Proceedings of the Fourth International Conference on Knowledge-Based Intelligent Engineering Systems and Allied Technologies, Brighton, UK, 30 August–1 September 2000; pp. 313–316. [Google Scholar]
- Panofsky, H.A.; Brier, G.W. Some Application of Statistics to Meteorology; University Park, Penn. State University, College of Earth and Mineral Sciences: State College, PA, USA, 1968; p. 224. [Google Scholar]
- Yang, D.; Herath, S.; Musiake, K. Development of a geomorphology-based hydrological model for large catchments. Proc. Hydraul. Eng. 1998, 42, 169–174. [Google Scholar] [CrossRef]
- Yang, D.; Herath, S.; Musiake, K. A hillslope-based hydrological model using catchment area and width functions. Hydrol. Sci. J. 2002, 47, 49–65. [Google Scholar] [CrossRef]
- Yang, D.; Koike, T.; Tanizawa, H. Application of a distributed hydrological model and weather radar observations for flood management in the upper Tone River of Japan. Hydrol. Process. 2004, 18, 3119–3132. [Google Scholar] [CrossRef]
- Yang, D.W.; Gao, B.; Jiao, Y.; Lei, H.M.; Zhang, Y.L.; Yang, H.B.; Cong, Z.T. A distributed scheme developed for eco-hydrological modeling in the upper Heihe River. Sci. China Earth Sci. 2015, 58, 36–45. [Google Scholar] [CrossRef]
- Miao, Q.; Yang, D.; Yang, H.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef]
- Yang, D.; Herath, S.; Musiake, K. Spatial resolution sensitivity of catchment geomorphologic properties and the effect on hydrological simulation. Hydrol. Process. 2001, 15, 2085–2099. [Google Scholar] [CrossRef]
| Period | NSE | RB |
|---|---|---|
| Calibration period | 0.89 | 0.04 |
| Validation period | 0.88 | 0.02 |
| Exp | Predictors | Training Period (1979–2002) | Validation Period (2003–2016) | ||||
|---|---|---|---|---|---|---|---|
| CC | RB (%) | RMSE (mm/day) | CC | RB (%) | RMSE (mm/day) | ||
| a | p | 0.31 | 16.53 | 11.16 | 0.29 | 12.75 | 11.48 |
| b | msl* | 0.69 | 4.73 | 7.42 | 0.54 | 5.53 | 8.86 |
| c | gp* | 0.79 | 4.46 | 6.2 | 0.66 | 4.08 | 7.93 |
| d | gp, tcw* | 0.85 | 2.27 | 5.36 | 0.69 | 1.87 | 7.54 |
| e | gp, tcw, tem, uw, vw, cape, vv, pv* | 0.94 | 3.08 | 3.4 | 0.72 | 6.92 | 7.28 |
| Exp | Method | Training Period (1979–2002) | Validation Period (2003–2016) | ||||
|---|---|---|---|---|---|---|---|
| CC | RB (%) | RMSE (mm/day) | CC | RB (%) | RMSE (mm/day) | ||
| a | ERA-interim | 0.31 | 16.53 | 11.16 | 0.29 | 12.75 | 11.48 |
| f | QM | 0.54 | 0.21 | 9.77 | 0.54 | −2.82 | 10.01 |
| g | CNN | 0.85 | 2.27 | 5.36 | 0.69 | 1.87 | 7.54 |
| h | SVM | 0.70 | 2.31 | 7.33 | 0.65 | −5.05 | 7.91 |
| i | ConvLSTM | 0.85 | 2.27 | 5.36 | 0.73 | 1.73 | 7.17 |
| Precipitation Inputs | NSE | RB (%) |
|---|---|---|
| Observed Precipitation | 0.82 | 7 |
| Original ERA-interim Precipitation | 0.06 | 24 |
| Corrected Precipitation | 0.64 | −10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water 2019, 11, 977. https://doi.org/10.3390/w11050977
Miao Q, Pan B, Wang H, Hsu K, Sorooshian S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water. 2019; 11(5):977. https://doi.org/10.3390/w11050977
Chicago/Turabian StyleMiao, Qinghua, Baoxiang Pan, Hao Wang, Kuolin Hsu, and Soroosh Sorooshian. 2019. "Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network" Water 11, no. 5: 977. https://doi.org/10.3390/w11050977
APA StyleMiao, Q., Pan, B., Wang, H., Hsu, K., & Sorooshian, S. (2019). Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water, 11(5), 977. https://doi.org/10.3390/w11050977







