1. Introduction
A typical rainwater harvesting and reuse (RWHR) system consists of: (1) A catchment area, collecting rainfall; (2) a drainage system, diverting collected runoff to a storage capacity; and (3) a distribution system for reuse. Sustainable water management, by the use of RWHR systems, is limited by the possibility to collect enough rainfall over a sufficiently large catchment area and store it in a tank whose capacity allows to fulfill a prescribed reuse schedule. Rainfall intermittency, long dry spells in climate change scenarios, and unsteady water demand, threaten the reliability of RWHR systems and increase the probability of experiencing a system failure within its life. Despite uncertainty, the long-term observation of many RWHR systems around the world demonstrates that efficiency of RWHR in the high demand ratio may be up to 98% [
1]. Efficiency analysis of RWHR may be performed on the base of probability analysis (PA), assuming that daily rainfall depth and dry spell in between two rain events are random variables and considering two consecutive rain events [
2]. According to Reference [
3], results obtained on the base of PA are in good agreement with experimental evidence [
1].
RWHR practice matches multiple UN sustainable development goals [
4]. RWHR systems bridge and improve infrastructures for
Clean Water and Sanitation, they contribute to a more sustainable use of water resources and preserve clean water for domestic use. The realization of RWHR systems provides opportunities for
Good Jobs and Economic Growth, because they may create job opportunities where implemented. RWHR systems mitigate the effect of the flash flood and complement grey-infrastructure, thus promoting more
Sustainable Cities and Community. They not only preserve environmental resources, but also contribute to creating a conscious attitude toward limited resources and, in the case study discussed here, they preserve and add value to historical cultural heritage. They represent an example of
Responsible Consumption.
The city centers of old town, as historical heritage, are protected against the introduction of new architectural elements that may alter their original structure. The construction of storage capacities above ground does not allow to preserve the original architecture. The structural vulnerability of old buildings often restricts the possibility to realize new infrastructures below ground. Reconditioned heritage water-harvesting systems, which just lay unused since ancient times of realization, may represent a valid alternative to new built infrastructures.
Venice ancient buildings are founded on wooden poles on islands within a man-made water basin carefully maintained against the natural processes of flooding, costal erosion, and sediment transport. In the man-made lagoon of Venice as well as on the islands, fresh groundwater was not easily accessible and rain water was collected within thousands of small squares (named “campi” and “campielli”) and drained toward subterranean cisterns realized below the squares itself, via two or four stone manholes. The cisterns (named “veras”) were filled with sand, in order to store and filter water. The center of each square (acting as catchment) hosted a well, capturing filtered water from the cistern for all uses. In addition, the squares had and still have social and viability value.
Venice is an extraordinary ensemble of anthropogenic landforms where the nature signature was cancelled by centuries of control over hydrological and geomorphological processes. The lagoon provided protection against enemies for the economic and social development of the Venetian Republic approximately between the 9th and 15th centuries. Artificial fluvial diversion and the construction of defenses against the sea, preserved the lagoon.
If we identify as “natural” the state which characterizes the lagoon environment before the development of the Venetian Republic, a solution aiming at restoring predevelopment natural conditions would probably lead to the disappearance of the unstable lagoon system. The artificial disconnection of the lagoon from the rivers and from the sea limited solid transport and erosion. The lagoon “naturally” would evolve toward a coastal area in the absence of defenses against the sea, if the sea would erode the costal strips lying between lagoon and Adriatic Sea (
Lido, Pellestrina and
Treporti), or the lagoon would evolve to reclaimed land, filled by transported sediments if the original flow direction of diverted rivers would be restored [
5]. Paradoxically, solutions based on nature could cancel centuries of historical heritage restoring natural processes.
Today, Venice is at risk of depopulation because of the high cost of maintenance of its buildings and infrastructures. Cultural heritage has its economic value in driving tourism, ensuring a percentage of gross domestic product and should be preserved, whenever possible. “
Preserving the environmental, urban and cultural heritage means preserving the existing assets, but also and above all upgrading, reviving and revitalizing natural elements and historic and rural settlements from a perspective of modernity and intelligent, sustainable progress.” [
6]. Heritage-based solutions (HBSs) for RWHR could match sustainable development goals restoring lost man-managed hydrological processes.
Venice historical center emerges only 90 cm above the mean sea level. Anthropogenic subsidence due to groundwater pumping, ended with the industrial activity a few decades ago [
7], “
with a sea-level rise of 50 centimeters, as predicted by the IPCC report, the frequency of exceptionally high tides (higher than 110 cm), will become more frequent. Consequently, the lagoon would need to be closed by flap gates for up to 187 days each year, occasionally for weeks at a time, or be flooded” [
8]. This delicate equilibrium would certainly treat the quality of water harvested above ground surfaces. We will not address the water quality problem, but rather highlight the potential of ancient cisterns as storage systems for rain water, provided that citizens still residing in the historical city center will reuse rain water collected in the cisterns for sanitary purposes.
Ancient rain water harvesting systems (
veras) in Venice have been counted by Reference [
9] (
Figure 1, shows two pages of an old census), and a number of photographic data collection is available online (e.g., Reference [
10]). Now that the veras are not in use anymore, they are hidden, disregarded, and often overlooked by tourists. Rehabilitation of ancient veras would match the need for conservation of precious water resources and cultural heritage, celebrating and adding value to historic environments.
According to land forms and characteristics, a variety of solutions for water harvesting were developed in the past [
11,
12,
13,
14], and the population may still have an interest in such ancient solutions.
Would heritage cisterns fulfill the population expectancies and be still a technically valuable solution, despite the deep changes undergone by society’s habits, composition, and distribution? This study analyzes on the base of PA [
2] and hydrological modelling, the hydraulic efficiency [
3] of a typical vera, suitably converted into a modern RWHR system and suggests that other HBS could be considered for rehabilitation and conversion into modern infrastructures for sustainable water management.
2. Materials and Methods
Rainwater harvesting and reuse (RWHR) systems include a contributing area S characterized by runoff coefficient f a cistern with storage capacity V and a reuse distribution system, allowing use of the collected rainwater volume fhS (where h is rainfall depth) during the inter-event time τ at rate Q.
The RWHR solution proposed here replicates a typical ancient vera: A waterproof pit filled with gravel and sand, which gathers the water and filters it. The top of the pit, the contributing area, and a small square (campo or campiello) hosting a well in the middle, for manual water collection in the ancient times, coincide in the first of three examples proposed here. In the renewed RWHR system, water is drained from campiellos and roof tops and pumped through a small pipe from storage capacity to the utilities.
Typical catchment
S and cistern size (depth
H and volume
SH), according to Reference [
9], are reported in
Table 1. The effective storage capacity is the volume of voids of the granular medium which fills the cistern, thus the storage capacity is
V = SHn, where
n is medium porosity. Runoff coefficient on paved surfaces was set at
f = 1, and rainwater reuse rate was estimated on the base of buildings size and typology surrounding the cistern as
Q = Nd, where
N is the number of habitants relying on the cistern and
d is the daily reuse rate.
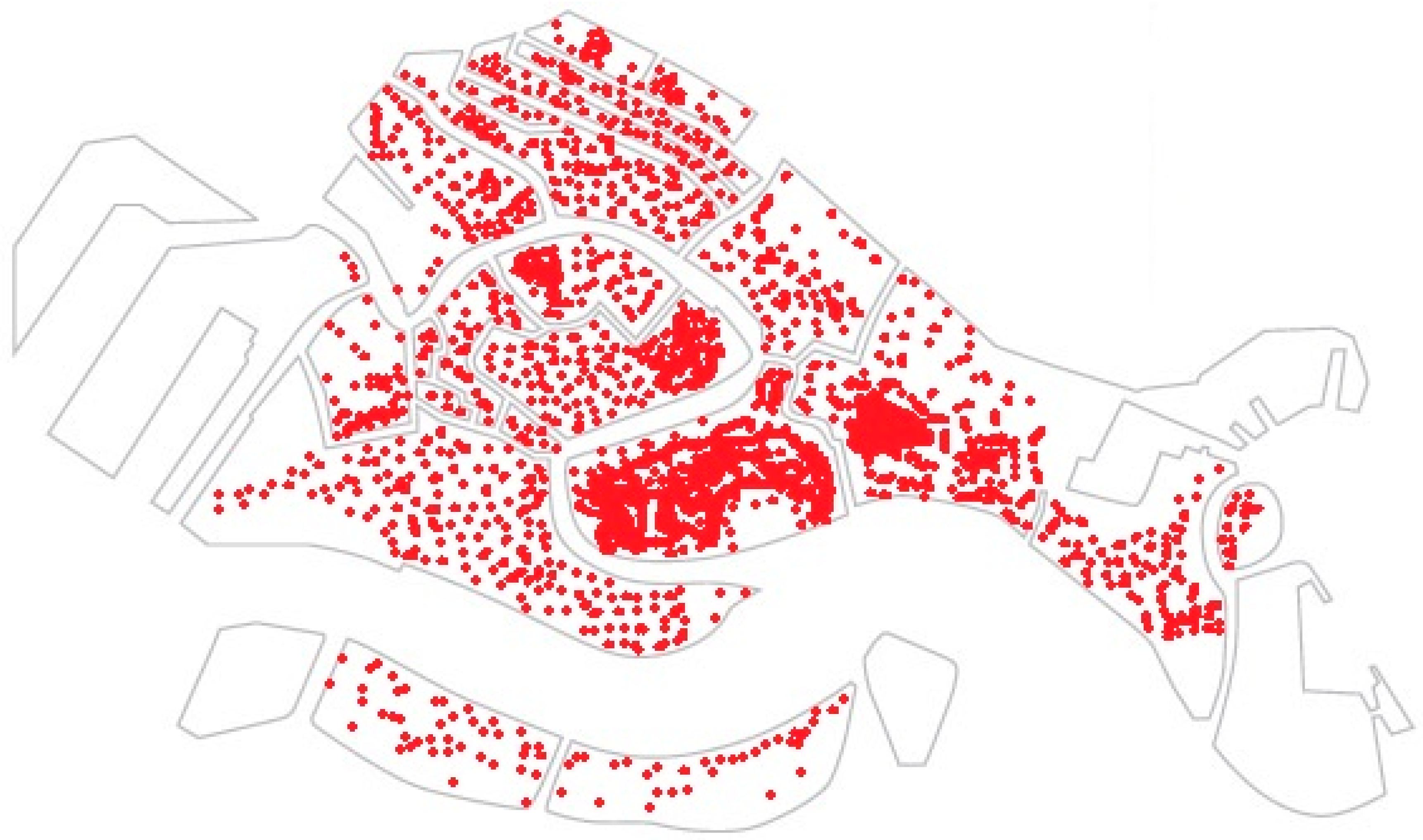
In the city center, there are less than 60,000 habitants, and cisterns that could be rehabilitated are about 600, with a ratio of 100 habitants per cistern (
Figure 2). In the 19th century, the ratio was 20 habitants per cistern with 6000 active cisterns. If the original number of cisterns would be recovered, the number of habitants per cisterns would drop to 10. Water demand was restricted to potable water use in the past (reasonably
Q = 5 × 20 = 100 L/day/cistern). RWHR systems today may be realized e.g., to fulfill demand for sanitary use (approximately
Q = 50 × 10 = 500 L/day/cistern), resulting in a much higher water demand, if compared to past potable water demand, despite the demographic decline. Campiellos’ drainage surface
S typically ranges between 15 and 25 m
2, veras’ depth between 2 and 3 m.
In the following, we verify the efficiency of a typical ancient vera draining water from campiello, and discuss two slightly different solutions that do not alter the urbanistic setup (
Table 1): the first considers an enhanced surface drainage, including the surrounding buildings’ rooftops in addition to paved cistern ceiling. The second, in addition, also has enhanced storage capacity, obtained by removing the granular filling within the cistern (thus, with
V = SH).
Rainfall characteristics in Venice are provided by the local environmental protection agency: (
ARPAV—
http://www.arpa.veneto.it). Namely, 24 years of daily rainfall data measured by the rain gauge at the meteorological station located in Venice-Chioggia (45°13′08.08″ N 12°16′42.74″ E) in the time period 1992–2016, were used to estimate:
Average daily rainfall depth ζ−1 = 5.2 mm, and
Average duration of dry spell in between two rain events λ−1 = 3.31 days
Based on probability analysis (PA) [
2], upper and lower limits of efficiency could be estimated as a function of two dimensionless parameters [
3]:
and
where
n = 0.3 is the porosity of the granular medium within the cistern according to the ancient design criteria. By PA, efficiency is evaluated as the probability that shortly before a rain event water, the cistern is still able to fulfill demand
Q. Random variables involved in PA are: Daily rainfall depth
h, collected volume
hS, the duration of the dry spell in between two rain events
τ and demand volume during the dry spell
Qτ; daily rainfall depth
h and the duration of the dry spell in between two rain events
τ are supposed to join an exponential distribution according to References [
2,
3].
According to Reference [
3], efficiency E is expected to be comprised between the limits resulting from two different simplifying hypothesis that concern the volume initially stored in the cistern before the random rain event
h, namely: (1) That the cistern is empty at the end of any dry spell (least conservative assumption) or (2) that the cistern is empty at the beginning of the first of two consecutive rain events (in which case efficiency is the probability that it is not empty at the end of the following rain event (most conservative assumption).
Corresponding demand ratio (the ratio between the expected water demand and the expected drainage volume collected within the cistern), is
Numerical simulation overcomes the limits of PA, which relies on simplified initial conditions, by numerical integration of the water balance,
where
Vw is the water volume stored in the cistern at day
t,
h is the measured daily rainfall depth,
Q the daily reuse rate. Provided that the series of rainfall measurements is sufficiently long, numerical simulation returns an estimate of
E and
DR unaffected by simplifying hypothesis on the condition of the cistern before any rain event, which may be evaluated according to the following Equations (6) and (7):
3. Results
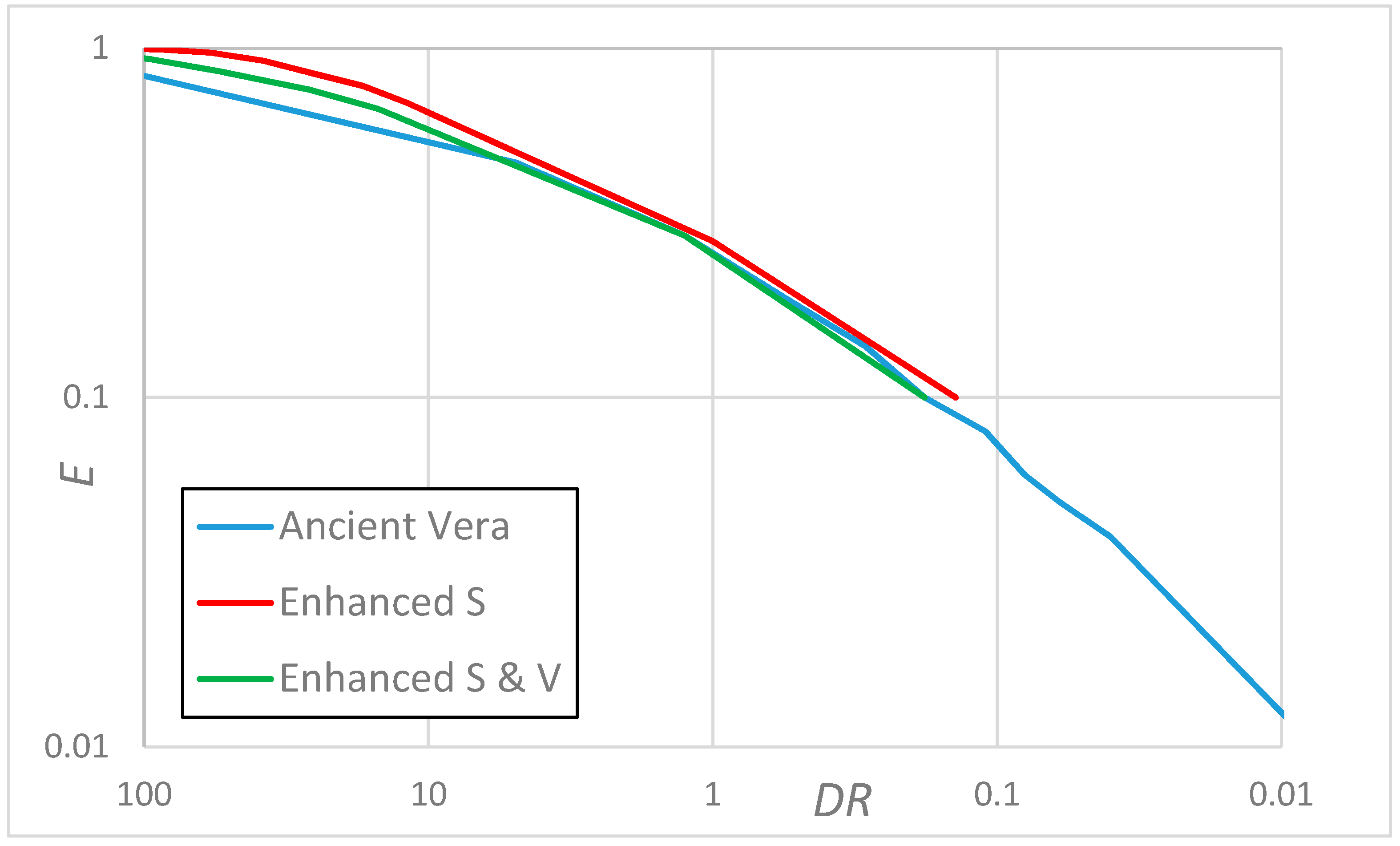
According to probability analysis, efficiency
E was estimated (for the typical applications described in
Table 1) as a function of demand ratio DR and
, under the most conservative assumptions, as
where
. Results obtained for the ancient vera draining water from campiello only and the two enhanced solutions are shown with red dots. The two enhanced solutions are in the range of low
DR achieving efficiency values close to
E = 0.99.
In
Figure 3, water reuse rate was set at
Q = 50 − 1000 L/day/cistern and cisterns’ efficiency were calculated repeatedly for different values of
b(Q). At the cost of lower efficiency values, water reuse may be increased significantly, up to a factor 20, to reach efficiency of ancient veras with enhanced solutions.
To refine the estimate of efficiency, Equation (5) was integrated over time for the rainfall observation time period 1992–2016. Efficiency E and demand ratio DR were estimated by Equations (6) and (7). Results for the three-case study described in
Table 1 are plotted in
Figure 4.
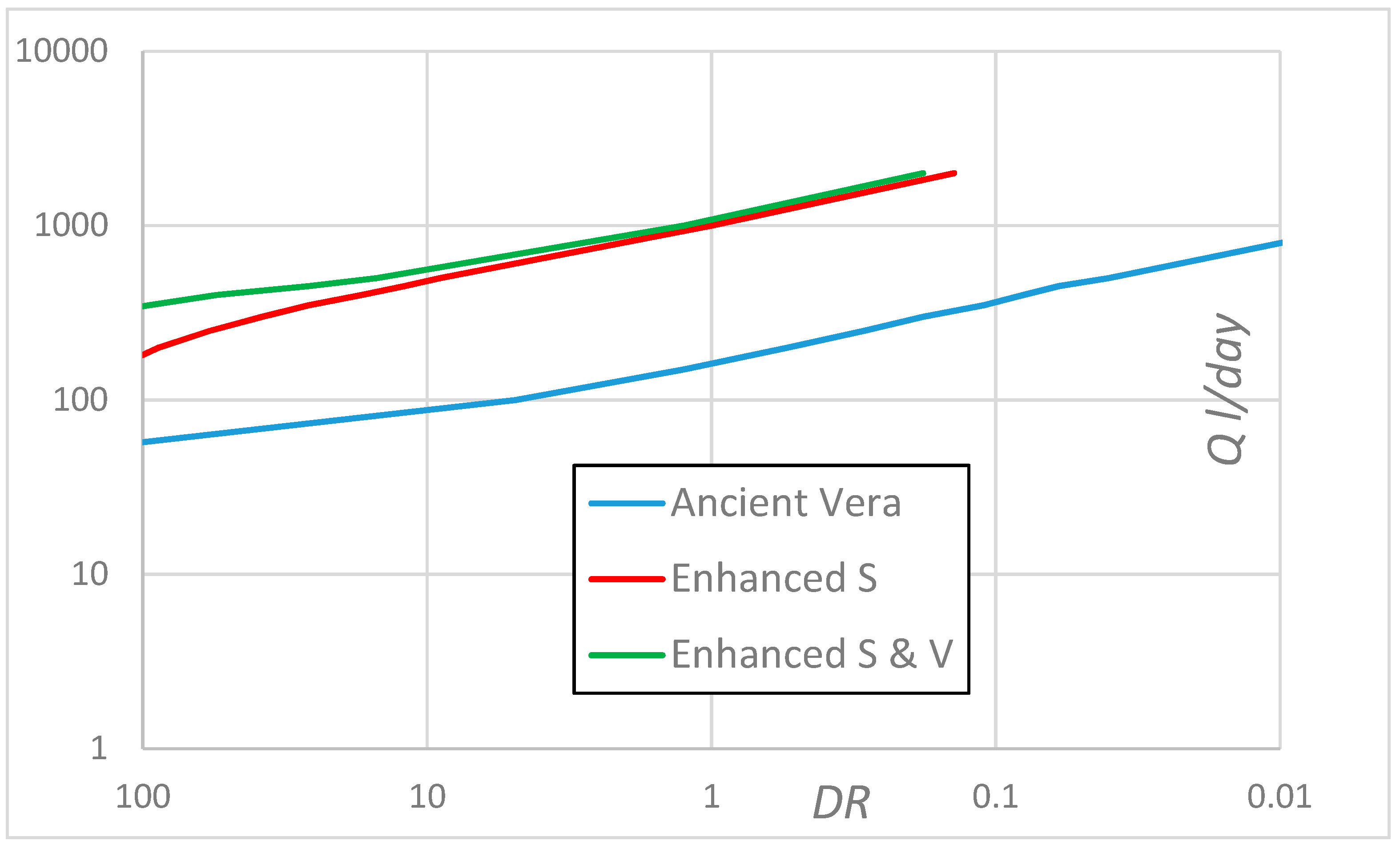
In
Figure 5, the relation between demand ratio
DR and water demand is indicated for the three technical solution analyzed here: The typical ancient veras draining water from campiello only and the two enhanced solutions.
The two enhanced solutions allow higher drainage volumes and (the second of the two) also higher storage capacity but are expected to fulfill a higher demand compared to the ancient vera, provided the same
DR (
Figure 5).
For
DR between 10 and 100,
E grows from 70% to more than 95%, and the solution with enhanced
S and
V may provide
Q up to 350 L/day/cistern, whereas the solution with enhanced
S potentially provides only
Q = 170 L/day/cistern (
Figure 4 and
Figure 5).
Actual demand for reuse may be expected in the range of 1 ≤ DR ≤ 10, corresponding to efficiency 50% ≤ E ≤ 70% of enhanced solutions. Enhanced drainage surface may definitely improve the performance of the RWHR system, allowing the fulfillment of the expectancies of population with higher water demand, if reuse is restricted to sanitary use. Up to DR = 10, the RWHR system performance is not limited by the storage capacity, efficiency at DR = 10 is E = 70% for both enhanced solutions, with slightly higher values for the solution with enhanced S and V. In the high DR range, removing the granular filling and increasing the storage volume may represent an advantage, to be evaluated on the base of a contextual water quality analysis (not considered here).
4. Discussion
Heritage water distribution systems are precious historical and social elements of the urban environment. Revitalizing selected elements of heritage water distribution systems provides social, cultural, economic. and environmental benefits for sustainable water management practices, despite the enormous increase in water consumption since their first realization. PA models and numerical simulation were used to evaluate efficiency of typical ancient veras in Venice, and to demonstrate that veras may still be transformed in efficient storage capacities for RWHR.
Minor changes, operated in the respect of architectural constraint, may improve the performance of ancient water harvesting systems and transform heritage solutions into instruments of sustainable water management. Three hypotheses have been tested: Veras draining water from campiello only, veras with enhanced drainage surface (including rooftops in addition to paved cistern ceiling) and veras with enhanced drainage surface and storage capacity (obtained by removing the granular filling within the cistern). Due to the demographic decline in the historical city center and the restriction of reuse to sanitary use only, veras may still efficiently fulfill the population demand. Granular filling moderately reduces the efficiency of the enhanced solution 1 (enhanced S), while providing a primary mechanical treatment. Based on this preliminary result, enhanced solution 1 could be preferable to enhanced solution 2 (enhanced S and V).
A variety of solutions for water harvesting have been developed in the past [
11,
12,
13]. Despite land use change, economic development, and society evolution, there is still interest in such ancient solutions. We presented here a preliminary study to be further elaborated. Aspects concerning water supply and health [
15] have been neglected here, since the focus was set on water availability, although they cannot be neglected in further research on HBS.
5. Conclusions
Heritage-based solutions (HBSs) are sustainable water management systems based on imported ancient technology and designed modern versions of ancient infrastructures. They may be efficient solutions for sustainable water management and implement social cultural and economic co-values. Returning traditional infrastructures to life preserves culture and environmental resources at the same time. HBSs aim at recovering lost processes of ancient urban water cycle instead of recovering the natural water cycle (as nature-based solutions do) and by so doing, recognize the value of development which is worth to be preserved.
Recovering elements of old RWHR systems preserves heritage value and water resources, increases the modularity of the water distribution system and the circularity of urban water fluxes. Recovering tradition of local water management makes multiple options and benefits possible, adds value to heritage, and preserves ancient traditions. Sharing ideas, methods, results, and being open to other sectors approaches and methods is expected to lead to new valuable solutions in terms of art, architecture, and cultural conservation, as well as environment and water resources sustainable management.