On the Predictability of Daily Rainfall during Rainy Season over the Huaihe River Basin
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Description
3. Methods
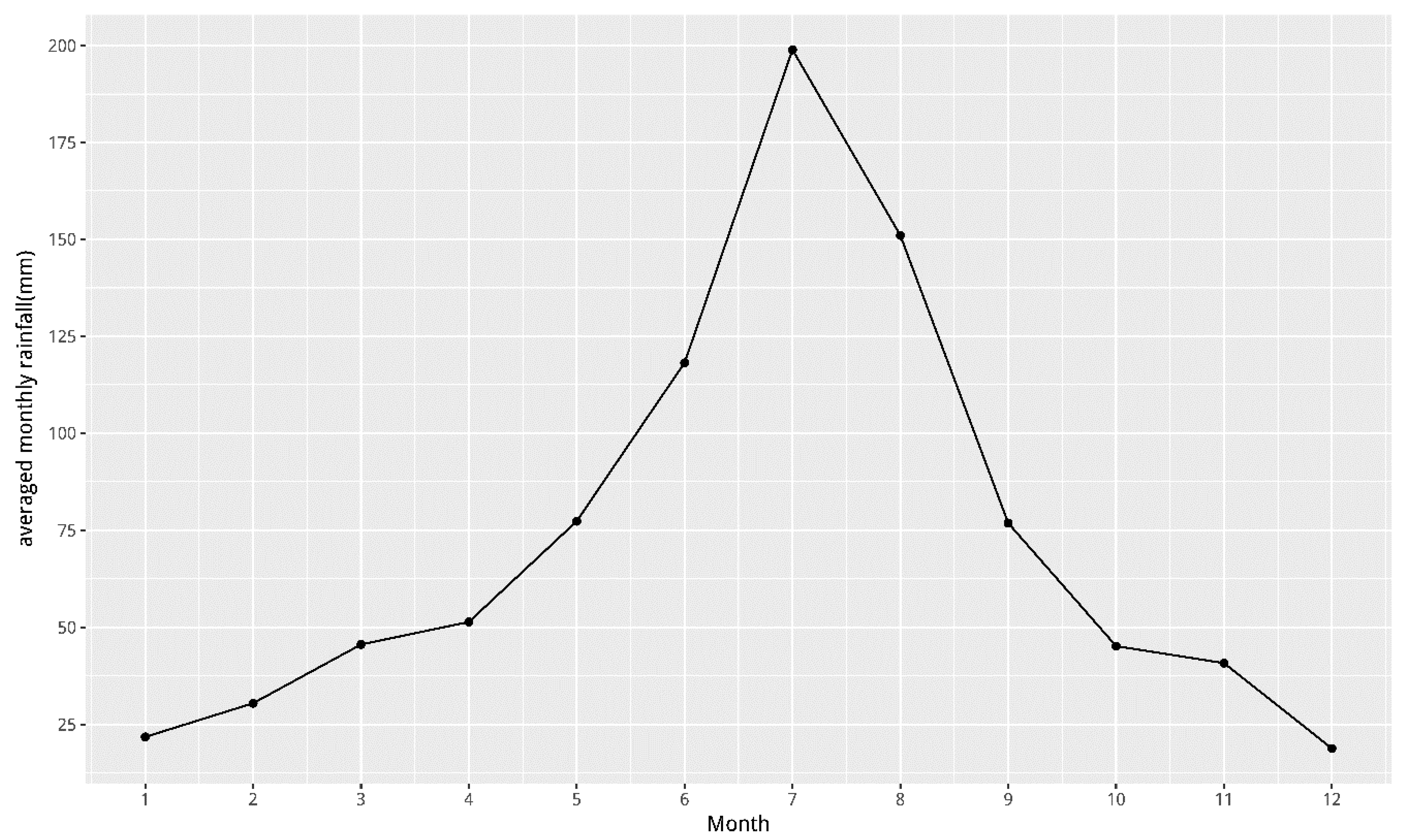
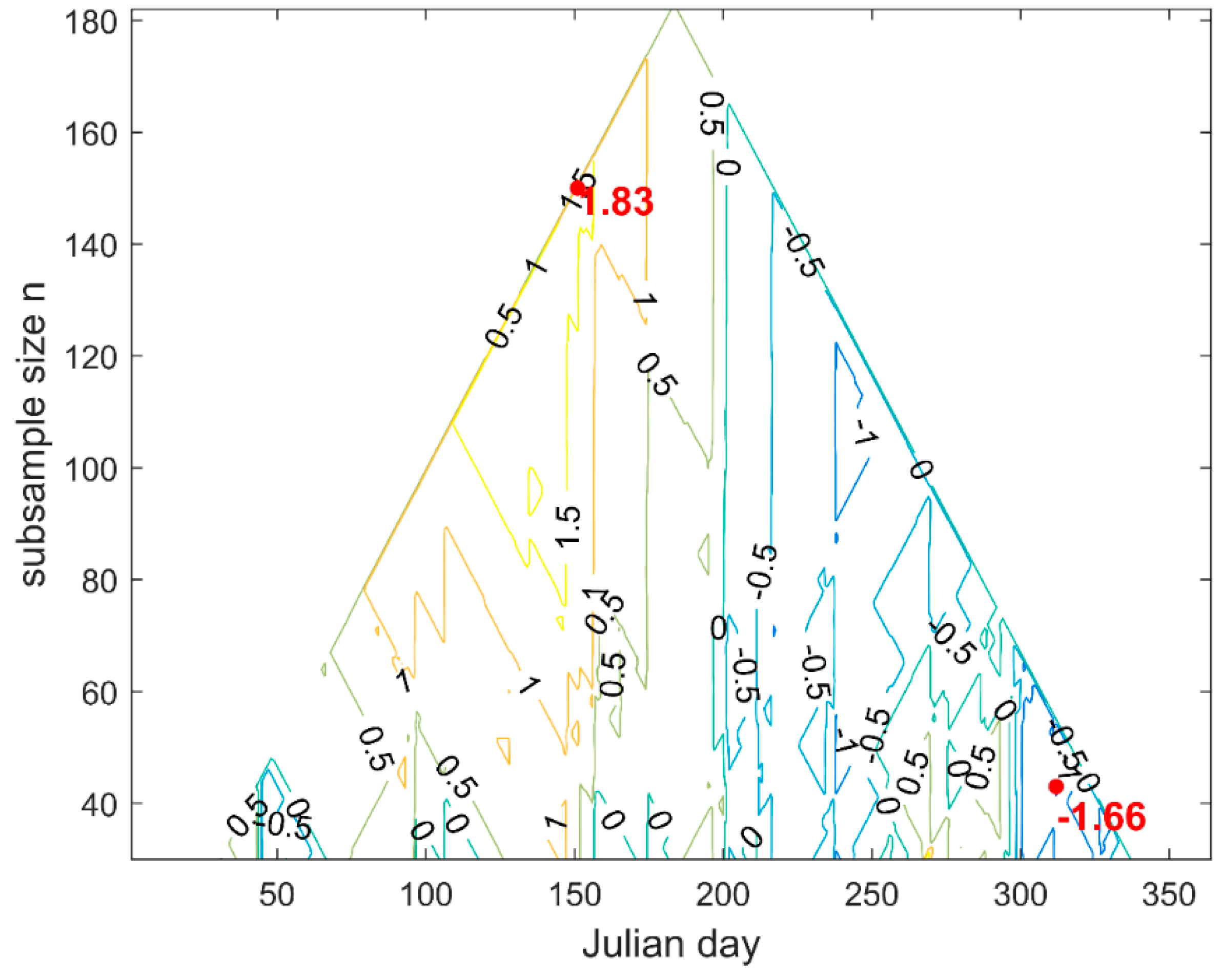
3.1. Determination of Rainy Season
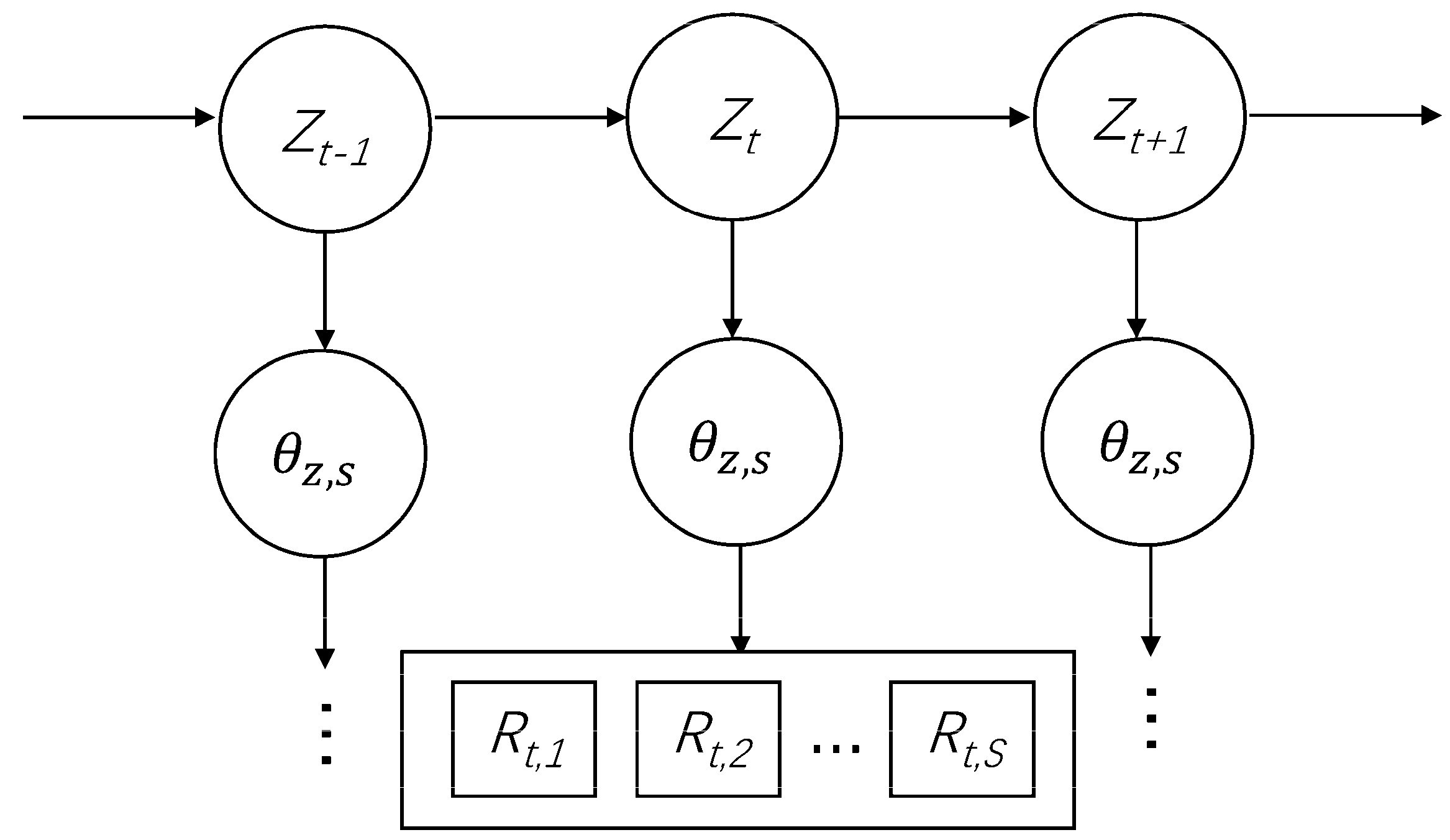
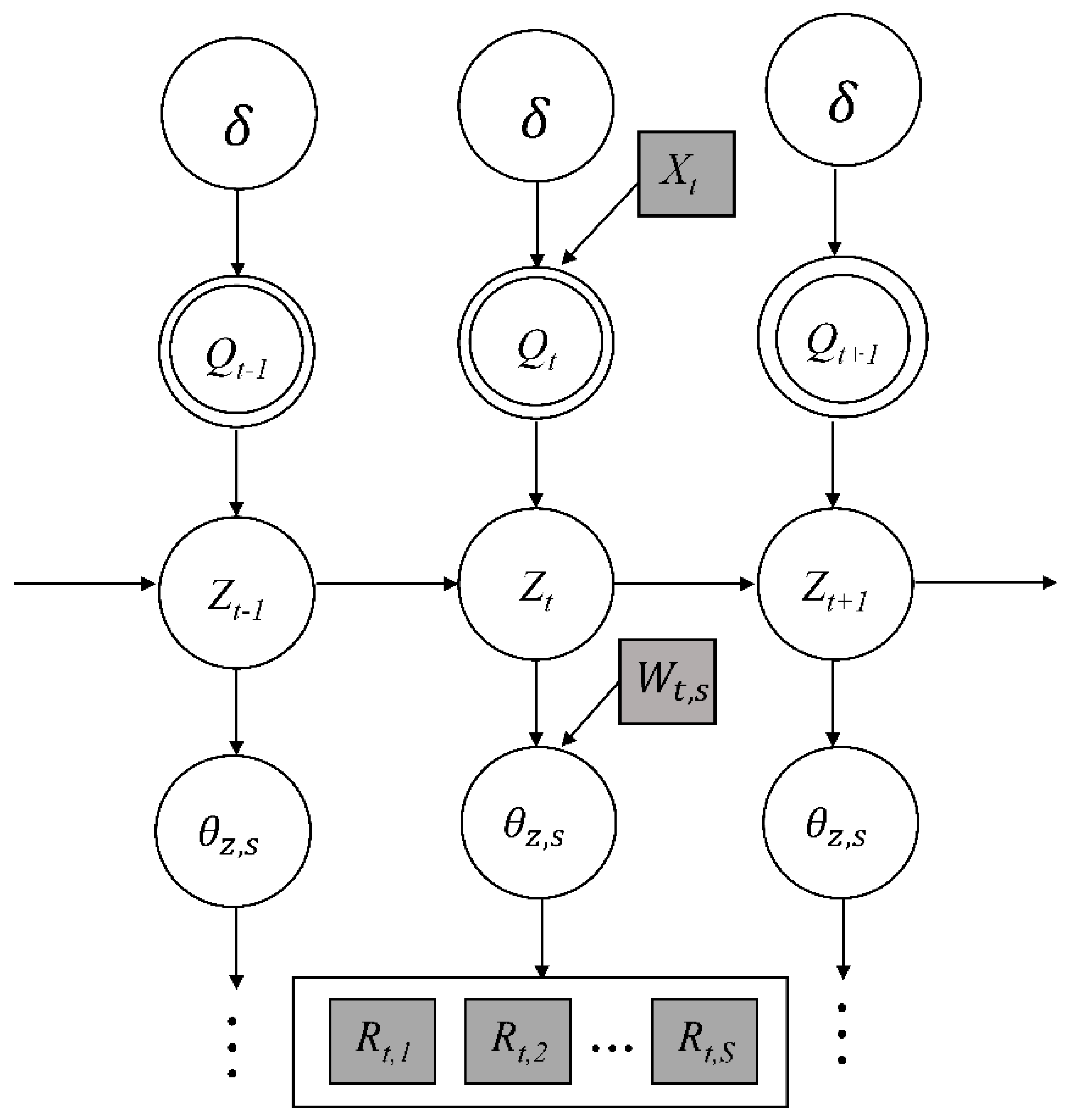
3.2. The Bayesian Homogeneous Markov Model
3.3. Bayesian Nonhomogeneous Markov Model
4. Results and Discussion
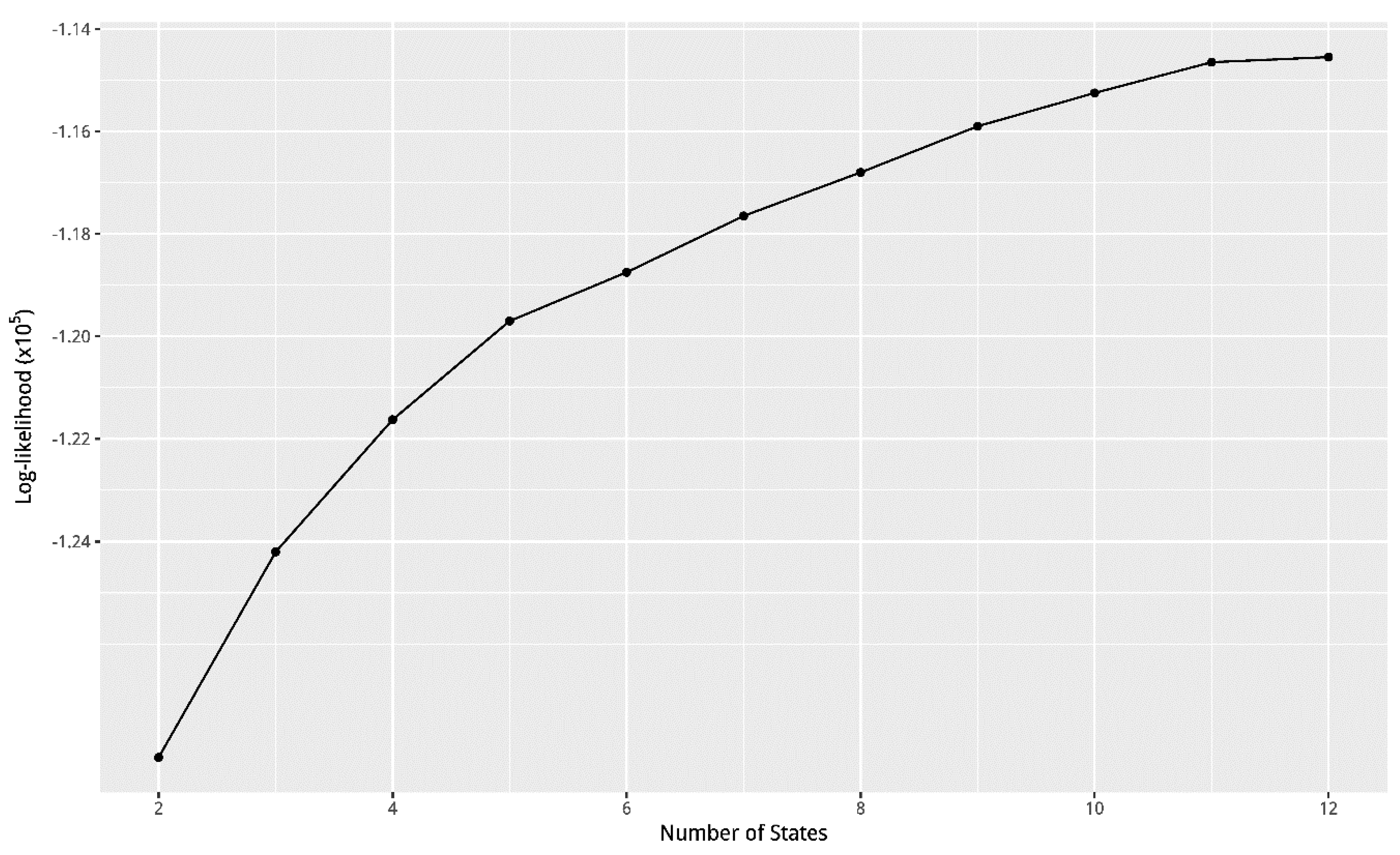
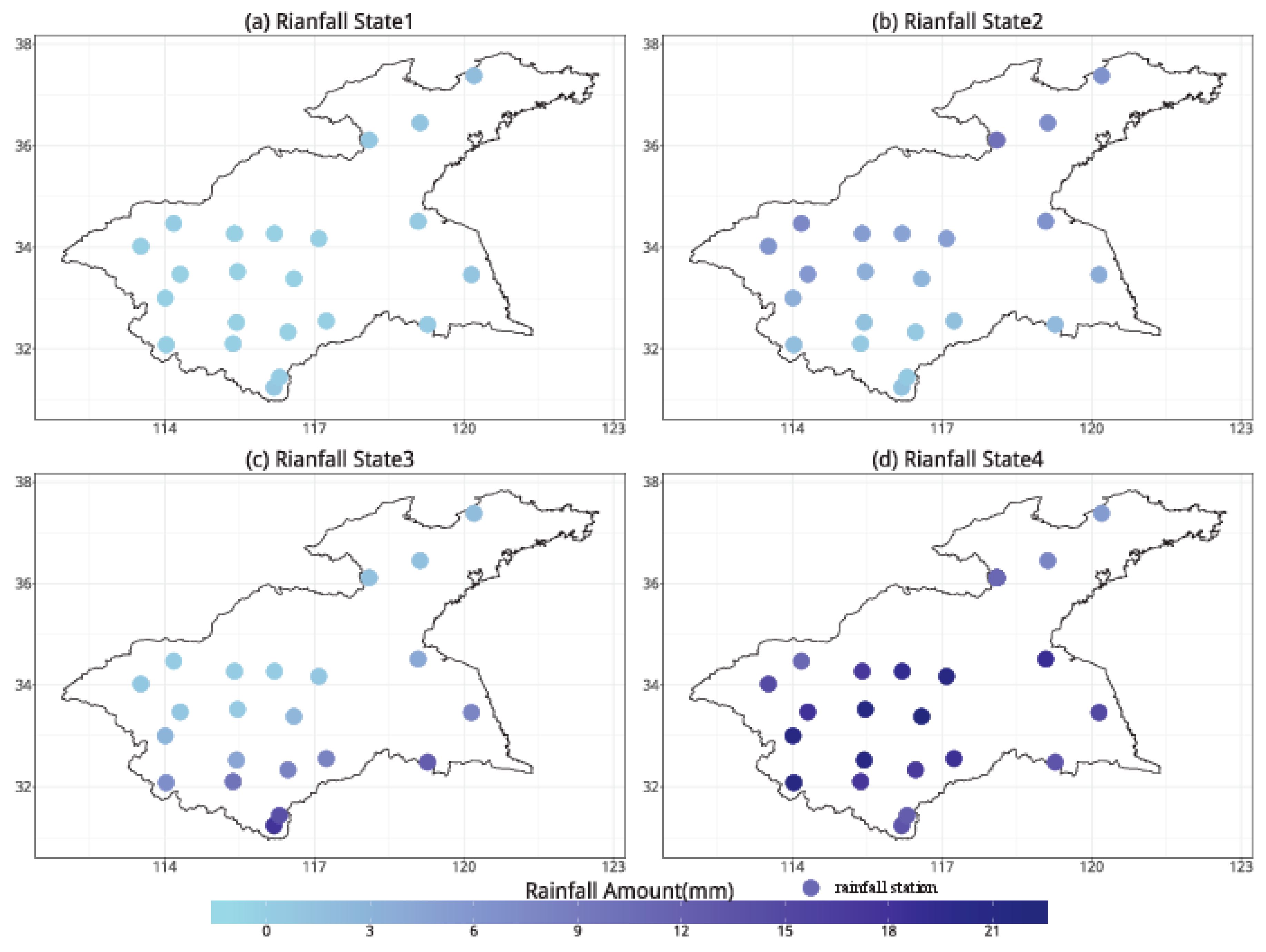
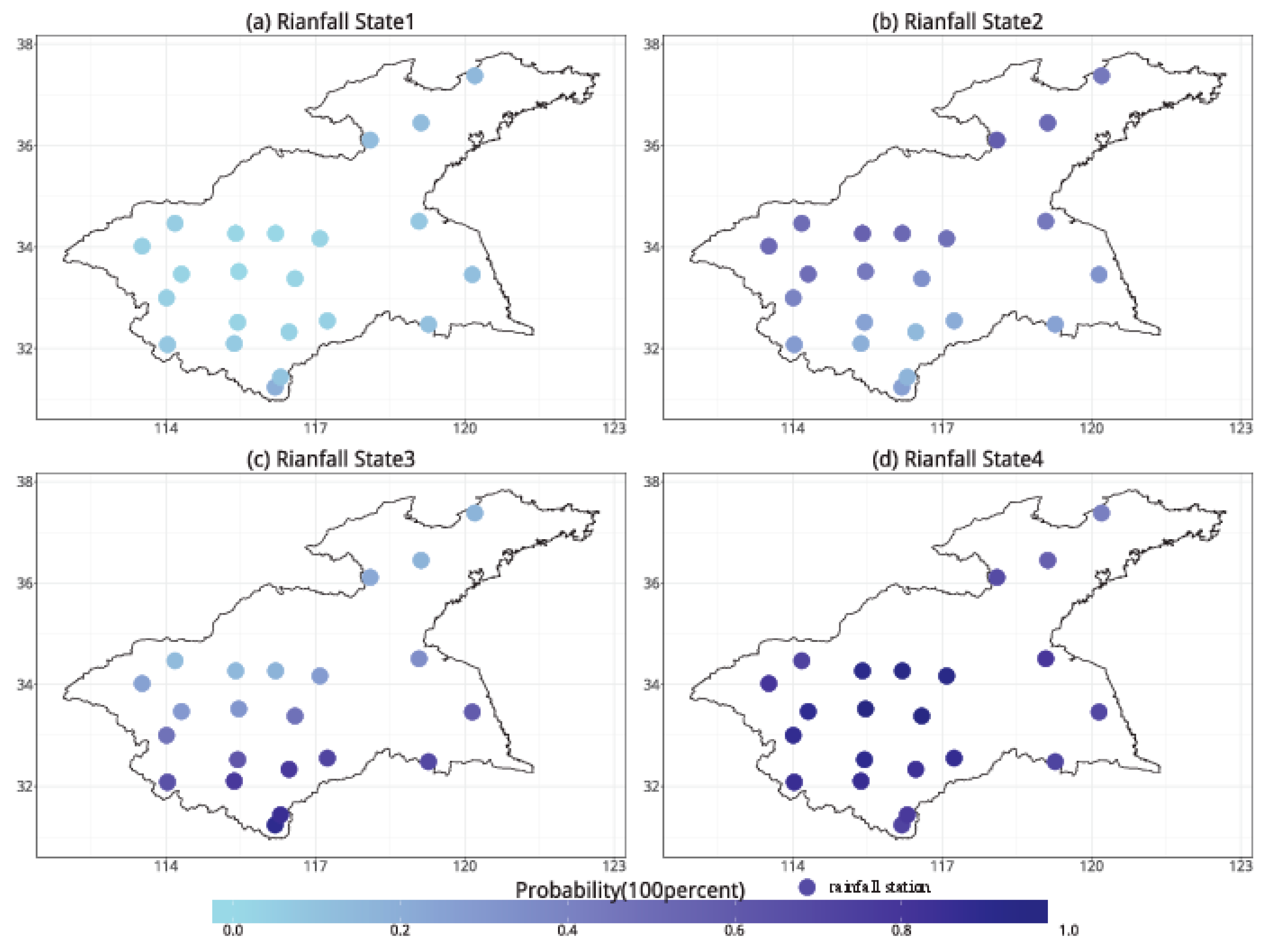
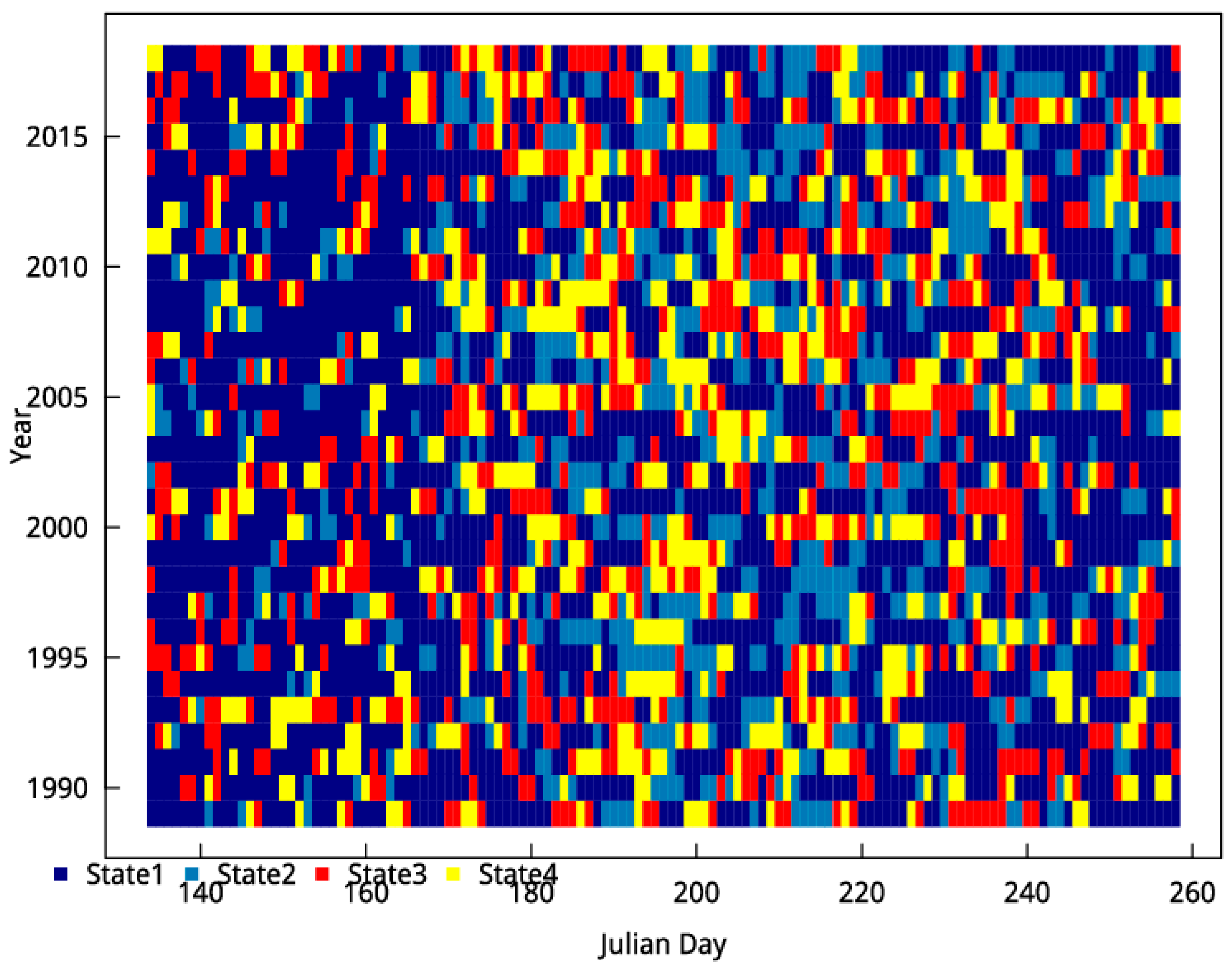
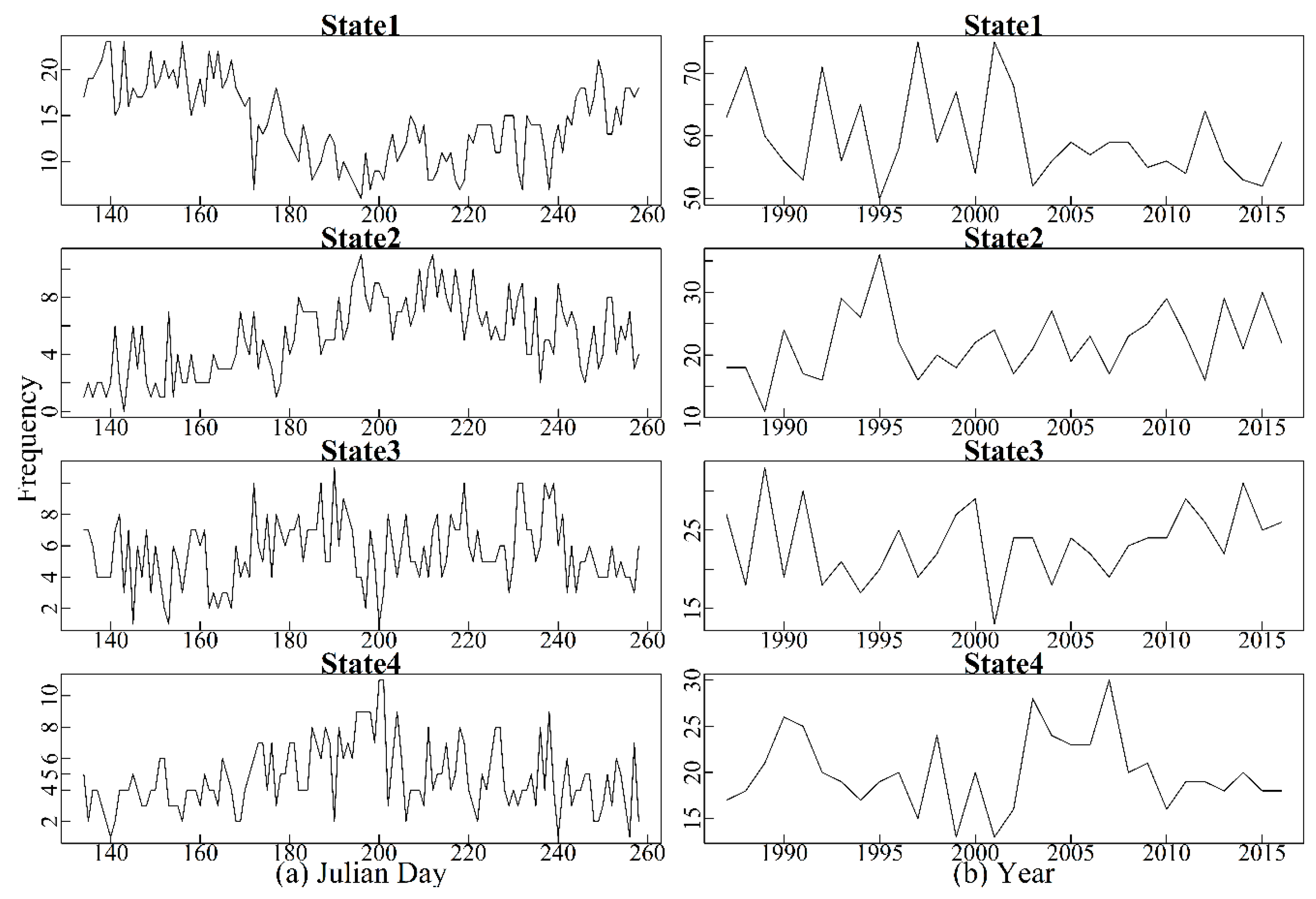
4.1. Identification of Hidden States and Spatial Precipitation Dependence
4.2. Meteorological Patterns Associated with the Hidden States
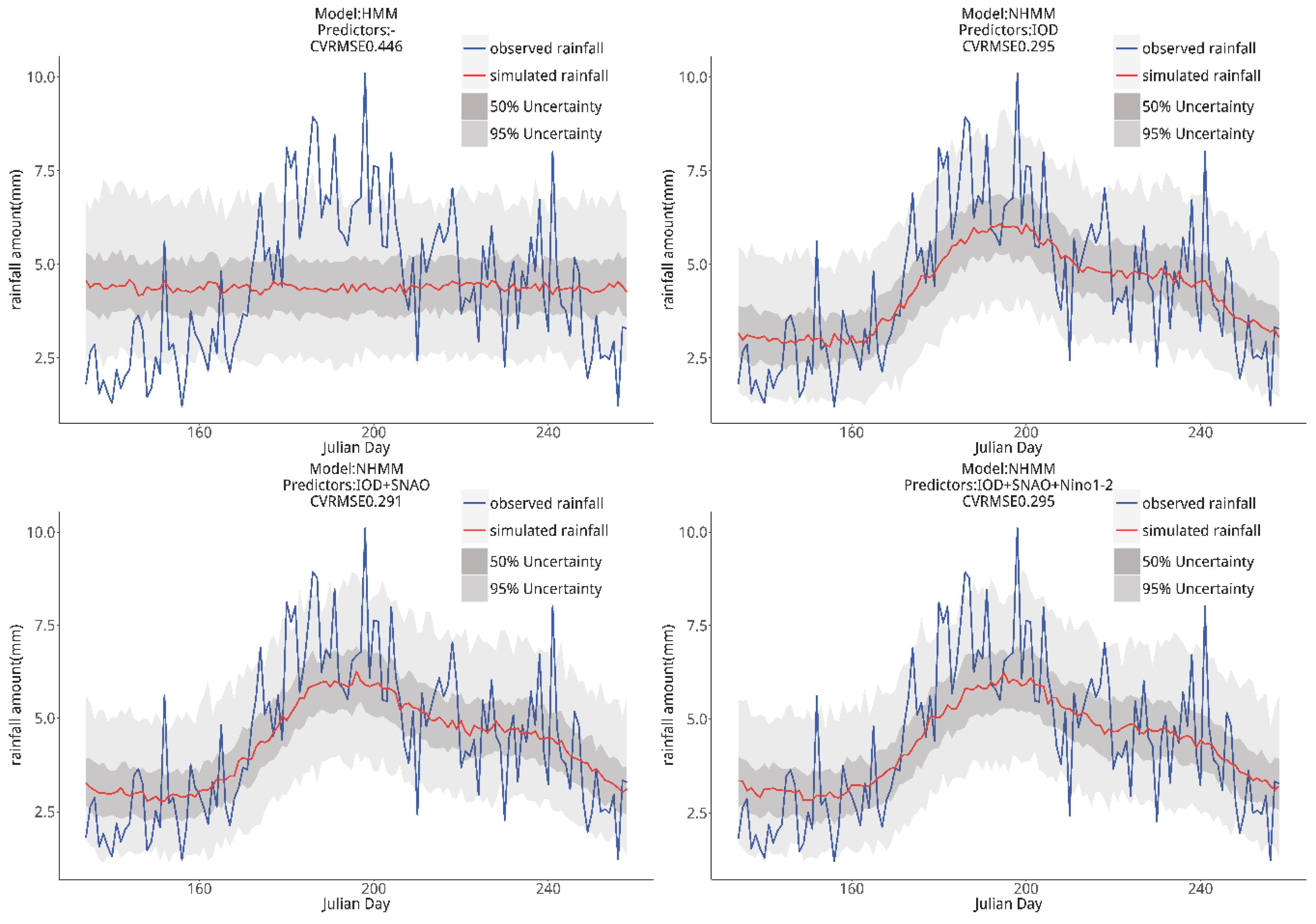
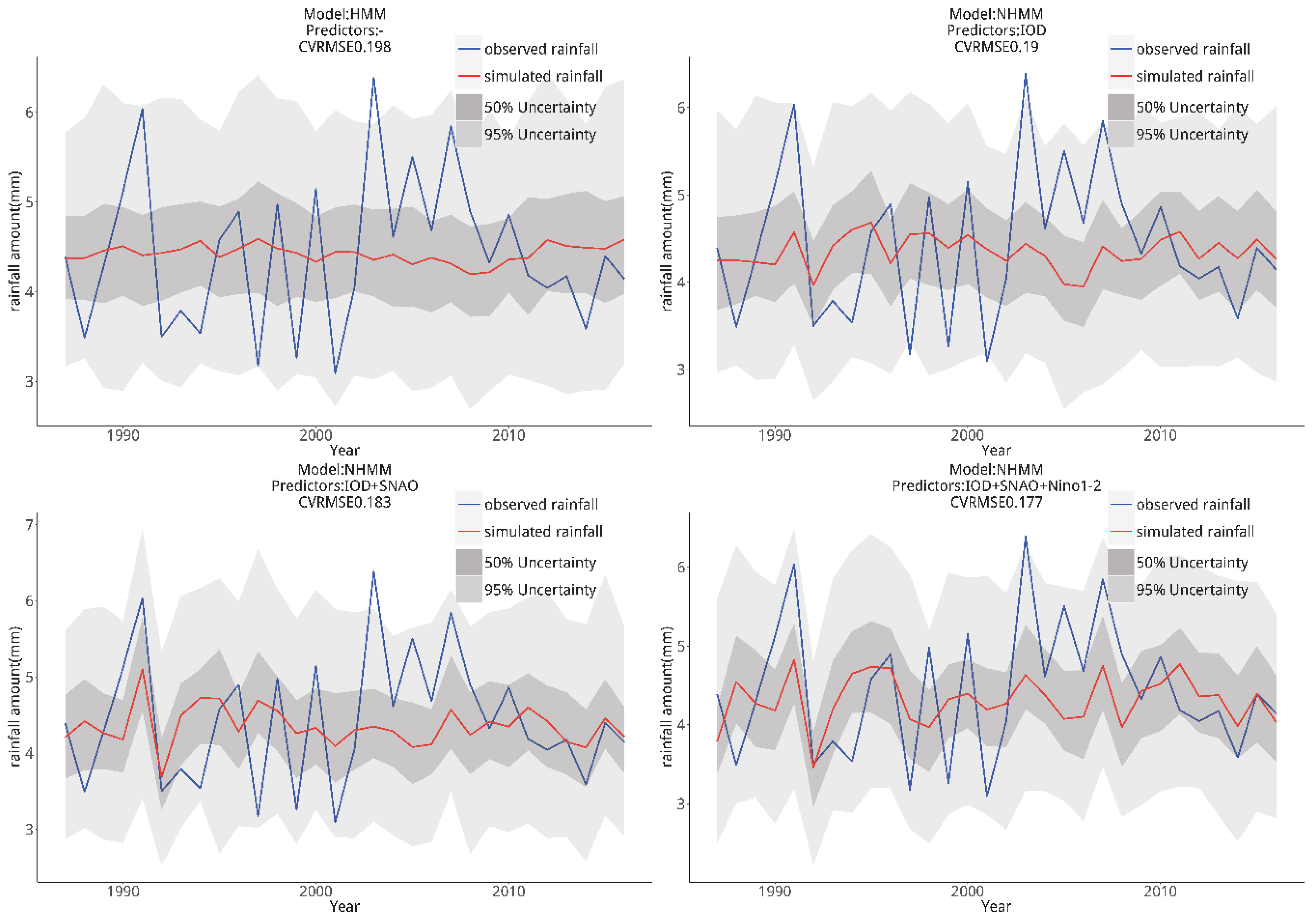
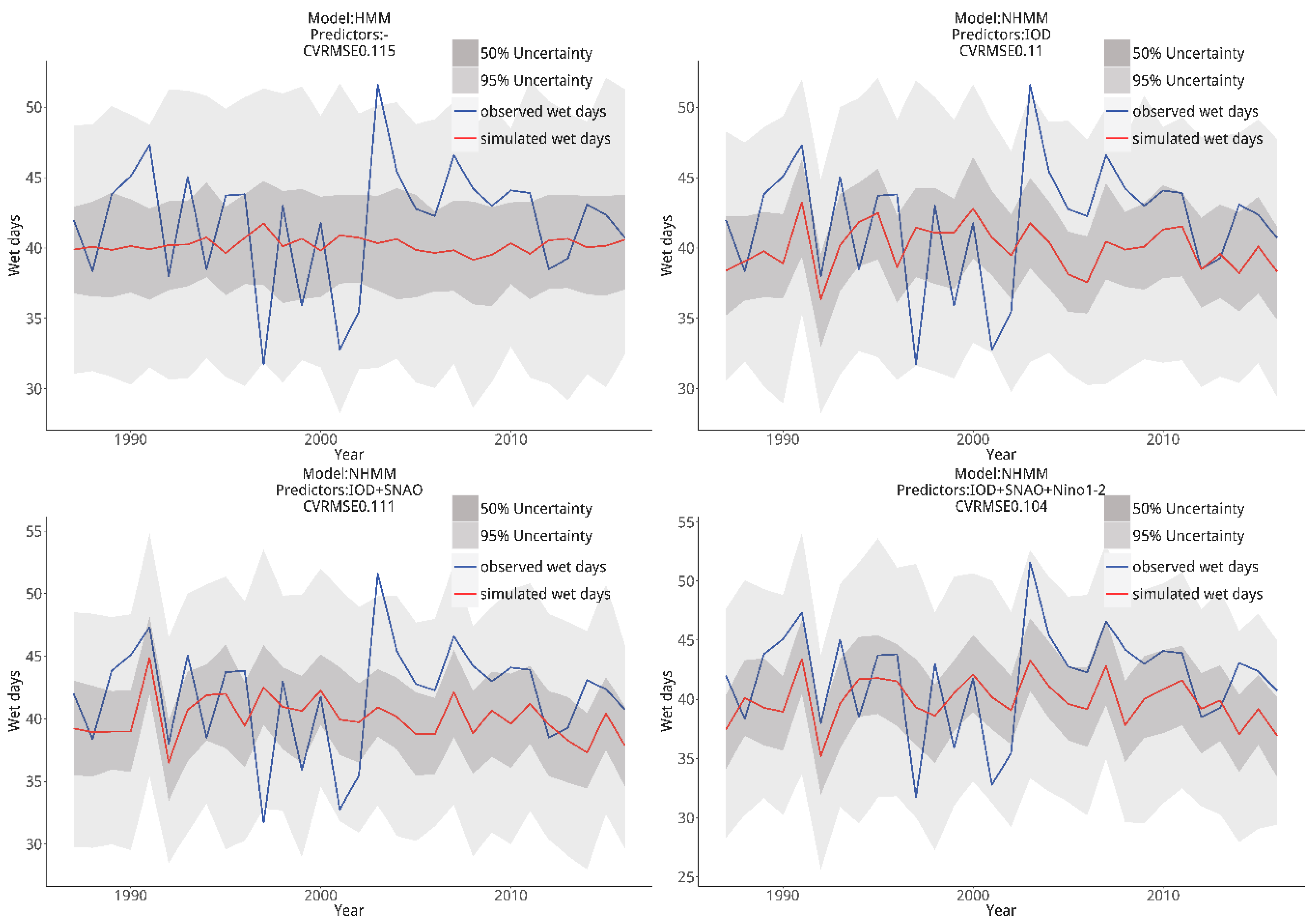
4.3. Bayesian-NHMM Calibration and Validation
4.3.1. Selection of Potential Predictors for Bayesian-NHMM
4.3.2. Seasonality
4.3.3. Interannual Variability
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khalil, A.F.; Kwon, H.-H.; Lall, U.; Kaheil, Y.H. Predictive downscaling based on non-homogeneous hidden markov models. Hydrolog. Sci. J. 2010, 55, 333–350. [Google Scholar] [CrossRef]
- Hewitson, B.; Crane, R. Climate downscaling: Techniques and application. Clim. Res. 1996, 7, 85–95. [Google Scholar] [CrossRef]
- Zorita, E.; Von Storch, H. The analog method as a simple statistical downscaling technique: Comparison with more complicated methods. J. Clim. 1999, 12, 2474–2489. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.; Sauter, T.; Themeßl, M. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of average, uncertainty range, and reliability of regional climate changes from aogcm simulations via the “reliability ensemble averaging”(rea) method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Von Storch, H. Regional climate development under global warming. General technical report no. 4. In Review of Empirical Downscaling Techniques; GKSS Research Center: Hamburg, Germany, 2000. [Google Scholar]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Hashmi, M.; Shamseldin, A.; Melville, B. Statistical downscaling of precipitation: State-of-the-art and application of bayesian multi-model approach for uncertainty assessment. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 6535–6579. [Google Scholar] [CrossRef]
- Wilby, R.L.; Charles, S.; Zorita, E.; Timbal, B.; Whetton, P.; Mearns, L. Guidelines for use of climate scenarios developed from statistical downscaling methods. Available online: http://www.ipcc-data.org/guidelines/dgm_no2_v1_09_2004.pdf (accessed on 30 April 2019).
- Robertson, A.W.; Kirshner, S.; Smyth, P.; Charles, S.P.; Bates, B.C. Subseasonal-to-interdecadal variability of the Australian monsoon over north queensland. Q. J. R. Meteor. Soc. 2006, 132, 519–542. [Google Scholar] [CrossRef]
- Robertson, A.W.; Kirshner, S.; Smyth, P. Downscaling of daily rainfall occurrence over northeast Brazil using a hidden markov model. J. Clim. 2004, 17, 4407–4424. [Google Scholar] [CrossRef]
- Robertson, A.W.; Kirshner, S.; Smyth, P. Hidden Markov Models for Modeling Daily Rainfall Occurrence over Brazil; University of California: San Francisco, CA, USA, 2003. [Google Scholar]
- Lianyi, G.; JIANG, Z.; Weilin, C. Using a hidden markov model to analyze the flood-season rainfall pattern and its temporal variation over east China. J. Meteor. Res. 2018, 32, 410–420. [Google Scholar]
- Cioffi, F.; Conticello, F.; Lall, U.; Marotta, L.; Telesca, V. Large scale climate and rainfall seasonality in a mediterranean area: Insights from a non-homogeneous markov model applied to the agro-pontino plain. Hydrol. Process. 2017, 31, 668–686. [Google Scholar] [CrossRef]
- Pal, I.; Robertson, A.W.; Lall, U.; Cane, M.A. Modeling winter rainfall in northwest india using a hidden markov model: Understanding occurrence of different states and their dynamical connections. Clim. Dyn. 2015, 44, 1003–1015. [Google Scholar] [CrossRef]
- Städler, N.; Mukherjee, S. Penalized estimation in high-dimensional hidden markov models with state–specific graphical models. Ann. Appl. Stat. 2013, 2157–2179. [Google Scholar] [CrossRef]
- Greene, A.M.; Holsclaw, T.; Robertson, A.W.; Smyth, P. A bayesian multivariate nonhomogeneous markov model. In Machine Learning and Data Mining Approaches to Climate Science; Springer: New York, NY, USA, 2015; pp. 61–69. [Google Scholar]
- Holsclaw, T.; Greene, A.M.; Robertson, A.W.; Smyth, P. A bayesian hidden markov model of daily precipitation over South and East Asia. J. Hydrometeorol. 2016, 17, 3–25. [Google Scholar] [CrossRef]
- Holsclaw, T.; Greene, A.M.; Robertson, A.W.; Smyth, P. Bayesian nonhomogeneous markov models via pólya-gamma data augmentation with applications to rainfall modeling. Ann. Appl. Stat. 2017, 11, 393–426. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Singh, V.P. Spatiotemporal patterns of precipitation regimes in the Huai River Basin, China, and possible relations with Enso events. Nat. Hazards 2016, 82, 2167–2185. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Tang, Q.; Zhang, P.; Liu, Y. Warm season heavy rainfall events over the Huaihe River valley and their linkage with wintertime thermal condition of the tropical oceans. Clim. Dyn. 2016, 46, 71–82. [Google Scholar]
- Xiao, M.; Zhang, Q.; Singh, V.P.; Chen, X. Probabilistic forecasting of seasonal drought behaviors in the Huai River Basin, China. Theor. Appl. Climatol. 2017, 128, 667–677. [Google Scholar] [CrossRef]
- Yan, D.; Wu, D.; Huang, R.; Wang, L.; Yang, G. Drought evolution characteristics and precipitation intensity changes during alternating dry–wet changes in the Huang–Huai–Hai River Basin. Hydrol. Earth Syst. Sci. 2013, 17, 2859–2871. [Google Scholar] [CrossRef]
- Chen, X.; Hao, Z.; Devineni, N.; Lall, U. Climate information based streamflow and rainfall forecasts for Huai River Basin using hierarchical bayesian modeling. Hydrol. Earth Syst. Sci. 2014, 18, 1539–1548. [Google Scholar] [CrossRef]
- Yang, M.; Chen, X.; Cheng, C.S. Hydrological impacts of precipitation extremes in the Huaihe River Basin, China. SpringerPlus 2016, 5, 1731. [Google Scholar]
- The China meteorological data sharing service system. Available online: http://data.cma.cn/data/detail/dataCode/SURF_CLI_CHN_MUL_DAY_V3.0.html (accessed on 30 April 2019).
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The ncep/ncar 40-year reanalysis project. Bull. Am. Meteor. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- The koningklijk nederlands meterologisch instituut (knmi) climate explorer database. Available online: http://climexp.knmi.nl/ (accessed on 30 April 2019).
- Goswami, B.; Xavier, P.K. Enso control on the south asian monsoon through the length of the rainy season. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Reason, C.J.C.; Hachigonta, S.; Phaladi, R.F. Interannual variability in rainy season characteristics over the Limpopo region of Southern Africa. Int. J. Climatol. 2005, 25, 1835–1853. [Google Scholar] [CrossRef]
- Cao, Q.; Hao, Z.; Yuan, F.; Su, Z.; Berndtsson, R.; Hao, J.; Tsring, N. Impact of Enso regimes on developing- and decaying-phase precipitation during rainy season in China. Hydrol. Earth Syst. Sci. 2017, 21, 1–12. [Google Scholar] [CrossRef]
- Fraedrich, K.; Jiang, J.; Gerstengarbe, F.W.; Werner, P.C. Multiscale detection of abrupt climate changes: Application to river nile flood levels. Int. J. Climatol. 1997, 17, 1301–1315. [Google Scholar] [CrossRef]
- Olaguera, L.M.; Matsumoto, J.; Kubota, H.; Inoue, T.; Cayanan, E.O.; Hilario, F.D. Interdecadal shifts in the winter monsoon rainfall of the Philippines. Atmos. 2018, 9, 464. [Google Scholar] [CrossRef]
- Kwon, H.-H.; Lall, U.; Obeysekera, J. Simulation of daily rainfall scenarios with interannual and multidecadal climate cycles for south florida. Stoch. Environ. Res. Risk A 2009, 23, 879–896. [Google Scholar] [CrossRef]
- Robertson, A.W.; Moron, V.; Swarinoto, Y. Seasonal predictability of daily rainfall statistics over indramayu district, Indonesia. Int. J. Climatol. 2009, 29, 1449–1462. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Juang, B.-H. An introduction to hidden markov models. Ieee Assp Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Forney, G.D. The viterbi algorithm. Proc. IEEE 1973, 61, 268–278. [Google Scholar] [CrossRef]
- Kirshner, S. Modeling of Multivariate Time Series Using Hidden Markov Models; University of California Press: Berkeley, CA, USA, 2005. [Google Scholar]
- Zhang, Q.; Wang, Y.; Singh, V.P.; Gu, X.; Kong, D.; Xiao, M. Impacts of Enso and Enso modoki+a regimes on seasonal precipitation variations and possible underlying causes in the Huai River Basin, China. J. Hydrol. 2016, 533, 308–319. [Google Scholar] [CrossRef]
- Lu, G.; Wu, Z.; Wen, L.; Lin, C.A.; Zhang, J.; Yang, Y. Real-time flood forecast and flood alert map over the Huaihe River Basin in China using a coupled hydro-meteorological modeling system. Sci. China Ser. E 2008, 51, 1049–1063. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X.; Jiang, X. Evaluation of the latest satellite–gauge precipitation products and their hydrologic applications over the Huaihe River Basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; You, W.-J. Social vulnerability to floods: A case study of Huaihe River Basin. Nat. Hazards 2014, 71, 2113–2125. [Google Scholar] [CrossRef]
- Lin, C.A.; Wen, L.; Lu, G.; Wu, Z.; Zhang, J.; Yang, Y.; Zhu, Y.; Tong, L. Real-time forecast of the 2005 and 2007 summer severe floods in the Huaihe River Basin of China. J. Hydrol. 2010, 381, 33–41. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Sun, J. Study of heavy rainfall and related mesoscale systems causing severe flood in Huaihe River Basin during the summer of 2007. Clim. Environ. Res. 2007, 12, 713–727. [Google Scholar]
- Cao, Q.; Hao, Z.; Zhou, J.; Wang, W.; Yuan, F.; Zhu, W.; Yu, C. Impacts of various types of el niño–southern oscillation (Enso) and Enso modoki on the rainy season over the Huaihe River Basin. Int. J. Climatol. 2019, 39, 2811–2824. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, Q.; Du, L.; Sun, S. Analysis of spatial-temporal variation of agricultural drought and its response to Enso over the past 30 years in the Huang-Huai-Hai region, China. Terr. Atmos. Ocean. Sci. 2013, 24, 745. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, H.; Guan, Z. Effects of Enso on the relationship between iod and summer rainfall in China. J. Trop. Meteorol. 2009, 15, 59–62. [Google Scholar]
- Ping, F.; Tang, X.; Gao, S.; Luo, Z. A comparative study of the atmospheric circulations associated with rainy-season floods between the Yangtze and Huaihe River Basins. Sci. China Earth Sci. 2014, 57, 1464–1479. [Google Scholar]
- Yang, L.; Zhao, J.; Feng, G. Classification of typical summer rainfall patterns in the east China monsoon region and their association with the east Asian summer monsoon. Theor. Appl. Climatol. 2017, 129, 1201–1209. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, T. Oscillation characteristics of summer precipitation in the Huaihe River valley and relevant climate background. Sci. China Earth Sci. 2010, 53, 301–316. [Google Scholar]
- Zhang, J.; Zhu, W.; Li, Z. Relationship between winter north pacific oscillations and summer precipitation anomalies in the Huaihe River Basin. J. Nanjing Inst. Meteor. 2007, 30, 546–550. [Google Scholar]
- Linderholm, H.W.; Ou, T.; Jeong, J.H.; Folland, C.K.; Gong, D.; Liu, H.; Liu, Y.; Chen, D. Interannual teleconnections between the summer north atlantic oscillation and the East Asian summer monsoon. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Xin, X.; Li, Z.; Yu, R.; Zhou, T. Impacts of upper tropospheric cooling upon the late spring drought in East Asia simulated by a regional climate model. Adv. Atmos. Sci. 2008, 25, 555–562. [Google Scholar] [CrossRef][Green Version]
- Ying, K.; Zheng, X.; Quan, X.W.; Frederiksen, C.S. Predictable signals of seasonal precipitation in the Yangtze–Huaihe River valley. Int. J. Climatol. 2013, 33, 3002–3015. [Google Scholar] [CrossRef]
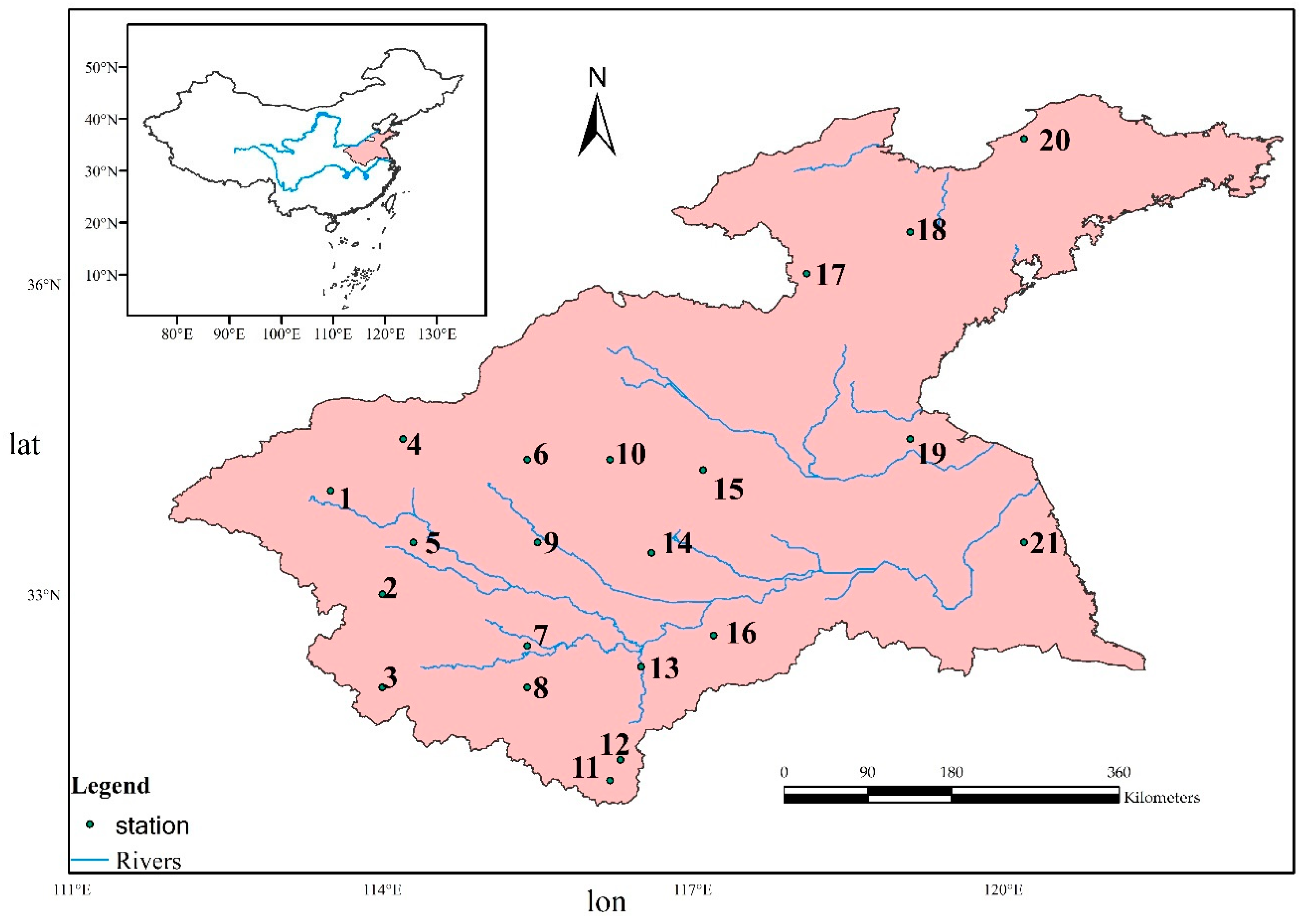
| No. | Name | Longitude (E) | Latitude (N) | Elevation (m) | Onset (Julian Day) | Retreat (Julian Day) | Rainy-Season Precipitation (mm) | Annual Precipitation (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | XuChang | 113.5 | 34.0 | 66.8 | 131 | 271 | 534.0 | 712.2 |
| 2 | ZhuMaDian | 114.0 | 33.0 | 82.7 | 123 | 273 | 791.6 | 925.3 |
| 3 | XinYang | 114.0 | 32.1 | 114.5 | 114 | 262 | 853.8 | 1081.9 |
| 4 | KaiFeng | 114.2 | 34.5 | 73.7 | 126 | 277 | 656.4 | 620.7 |
| 5 | XiHua | 114.3 | 33.5 | 52.6 | 128 | 273 | 816.6 | 786.1 |
| 6 | ShangQiu | 115.4 | 34.3 | 50.1 | 130 | 264 | 579.7 | 721.4 |
| 7 | BuYang | 115.4 | 32.5 | 32.7 | 126 | 259 | 721.7 | 906.2 |
| 8 | GuShi | 115.4 | 32.1 | 42.9 | 122 | 250 | 696.5 | 1055.3 |
| 9 | HaoZhou | 115.5 | 33.5 | 37.7 | 131 | 258 | 617.1 | 794.5 |
| 10 | DangShan | 116.2 | 34.3 | 44.2 | 132 | 261 | 590.9 | 738.9 |
| 11 | HuoShan | 116.2 | 31.2 | 86.4 | 104 | 255 | 882.8 | 1382.3 |
| 12 | LiuAn | 116.3 | 31.4 | 74.1 | 107 | 259 | 888.1 | 1117.8 |
| 13 | ShouXian | 116.5 | 32.3 | 22.7 | 124 | 256 | 660.5 | 915.4 |
| 14 | SuZhou | 116.6 | 33.4 | 25.9 | 133 | 258 | 679.1 | 868.3 |
| 15 | XuZhou | 117.1 | 34.2 | 41.2 | 141 | 261 | 639.2 | 822.6 |
| 16 | BengBu | 117.2 | 32.6 | 21.9 | 116 | 249 | 732.7 | 967.8 |
| 17 | XinYuan | 118.1 | 36.1 | 305.1 | 132 | 261 | 585.0 | 709.0 |
| 18 | WeiFang | 119.1 | 36.5 | 22.2 | 139 | 257 | 517.1 | 1071.1 |
| 19 | GanYu | 119.1 | 34.5 | 5.3 | 134 | 263 | 740.5 | 925.8 |
| 20 | LongKou | 120.2 | 37.4 | 4.8 | 135 | 259 | 496.5 | 591.5 |
| 21 | SheYang | 120.2 | 33.5 | 2 | 131 | 261 | 695.1 | 985.8 |
| Predictors | Lag | rs | p-Value |
|---|---|---|---|
| IOD | 4 | 0.342 | 0.064 |
| SNAO | 5 | 0.332 | 0.079 |
| Niño 1–2 | 2 | −0.314 | 0.091 |
| Niño 4 | 12 | 0.297 | 0.117 |
| Niño 3.4 | 9 | 0.206 | 0.283 |
| NAO | 10 | −0.191 | 0.322 |
| Niño 3 | 8 | 0.149 | 0.440 |
| PDO | 7 | −0.054 | 0.780 |
| ID | Model | Predictors |
|---|---|---|
| 1 | Bayesian-HMM | - |
| 2 | Bayesian-NHMM | IOD |
| 3 | Bayesian-NHMM | IOD + SNAO |
| 4 | Bayesian-NHMM | IOD + SNAO + Niño 1–2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Hao, Z.; Yuan, F.; Berndtsson, R.; Xu, S.; Gao, H.; Hao, J. On the Predictability of Daily Rainfall during Rainy Season over the Huaihe River Basin. Water 2019, 11, 916. https://doi.org/10.3390/w11050916
Cao Q, Hao Z, Yuan F, Berndtsson R, Xu S, Gao H, Hao J. On the Predictability of Daily Rainfall during Rainy Season over the Huaihe River Basin. Water. 2019; 11(5):916. https://doi.org/10.3390/w11050916
Chicago/Turabian StyleCao, Qing, Zhenchun Hao, Feifei Yuan, Ronny Berndtsson, Shijie Xu, Huibin Gao, and Jie Hao. 2019. "On the Predictability of Daily Rainfall during Rainy Season over the Huaihe River Basin" Water 11, no. 5: 916. https://doi.org/10.3390/w11050916
APA StyleCao, Q., Hao, Z., Yuan, F., Berndtsson, R., Xu, S., Gao, H., & Hao, J. (2019). On the Predictability of Daily Rainfall during Rainy Season over the Huaihe River Basin. Water, 11(5), 916. https://doi.org/10.3390/w11050916






