Comparative Study of Two State-of-the-Art Semi-Distributed Hydrological Models
Abstract
1. Introduction
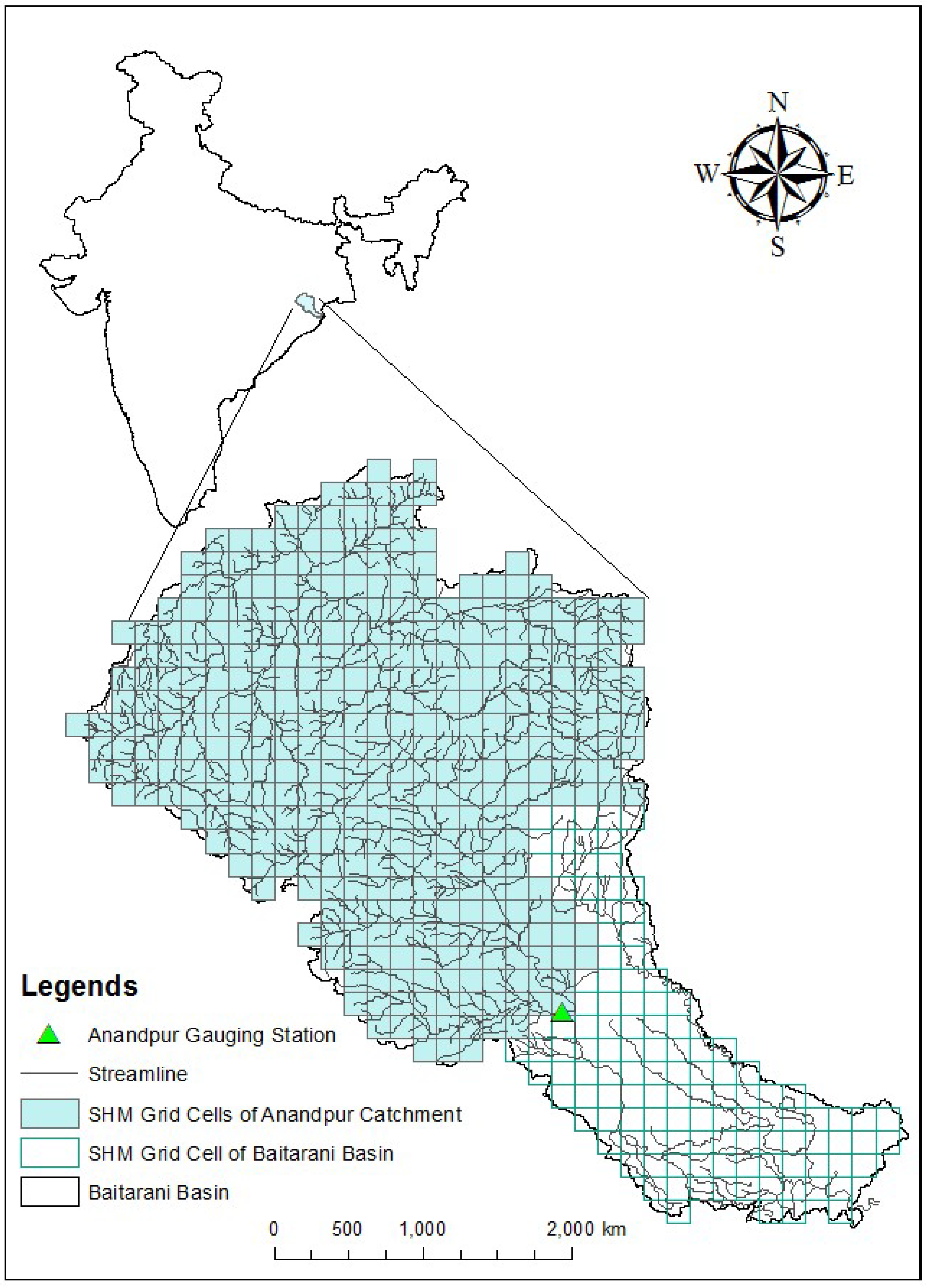
2. Study Area and Data
3. Comparative Discussion on SHM and SWAT
3.1. Description of the SHM
3.2. Description of SWAT
3.3. Sensitive Parameters of Both the Models Used for Calibration
4. Methodology
4.1. Model Setup, Calibration, Validation
4.1.1. Nash Sutcliffe Efficiency (NSE)
4.1.2. Coefficient of Determination (R2)
4.1.3. Percent Bias (PBIAS)
4.2. Analysis of Results
Uncertainty Analysis
5. Results and Discussion
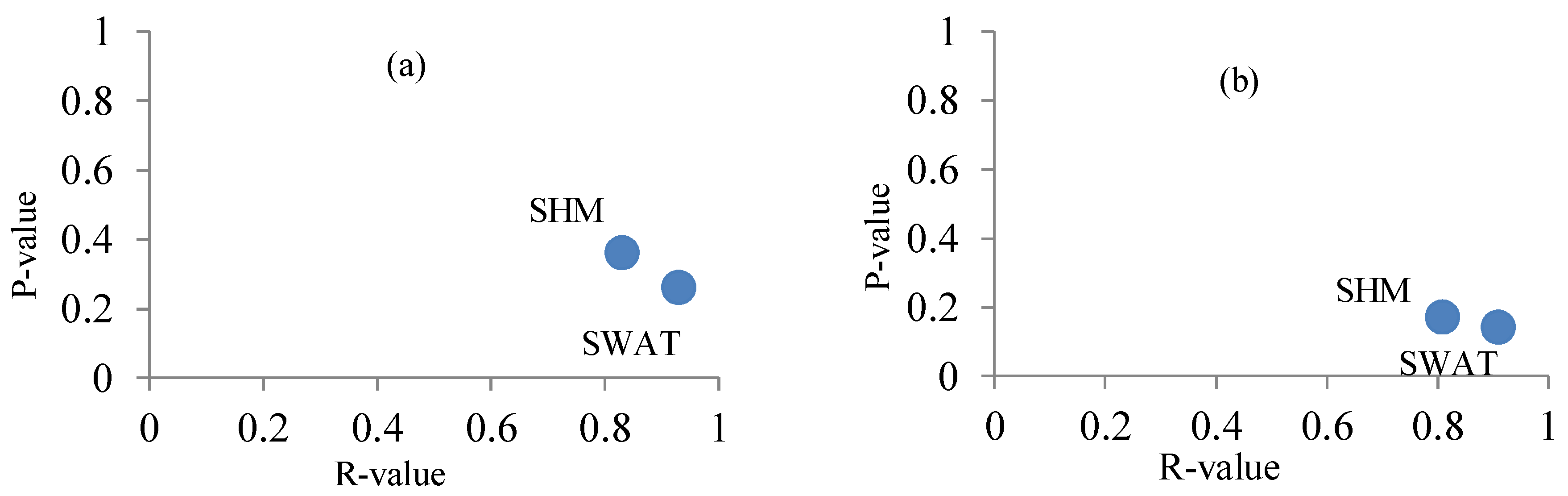
5.1. Calibration and Validation of the Models
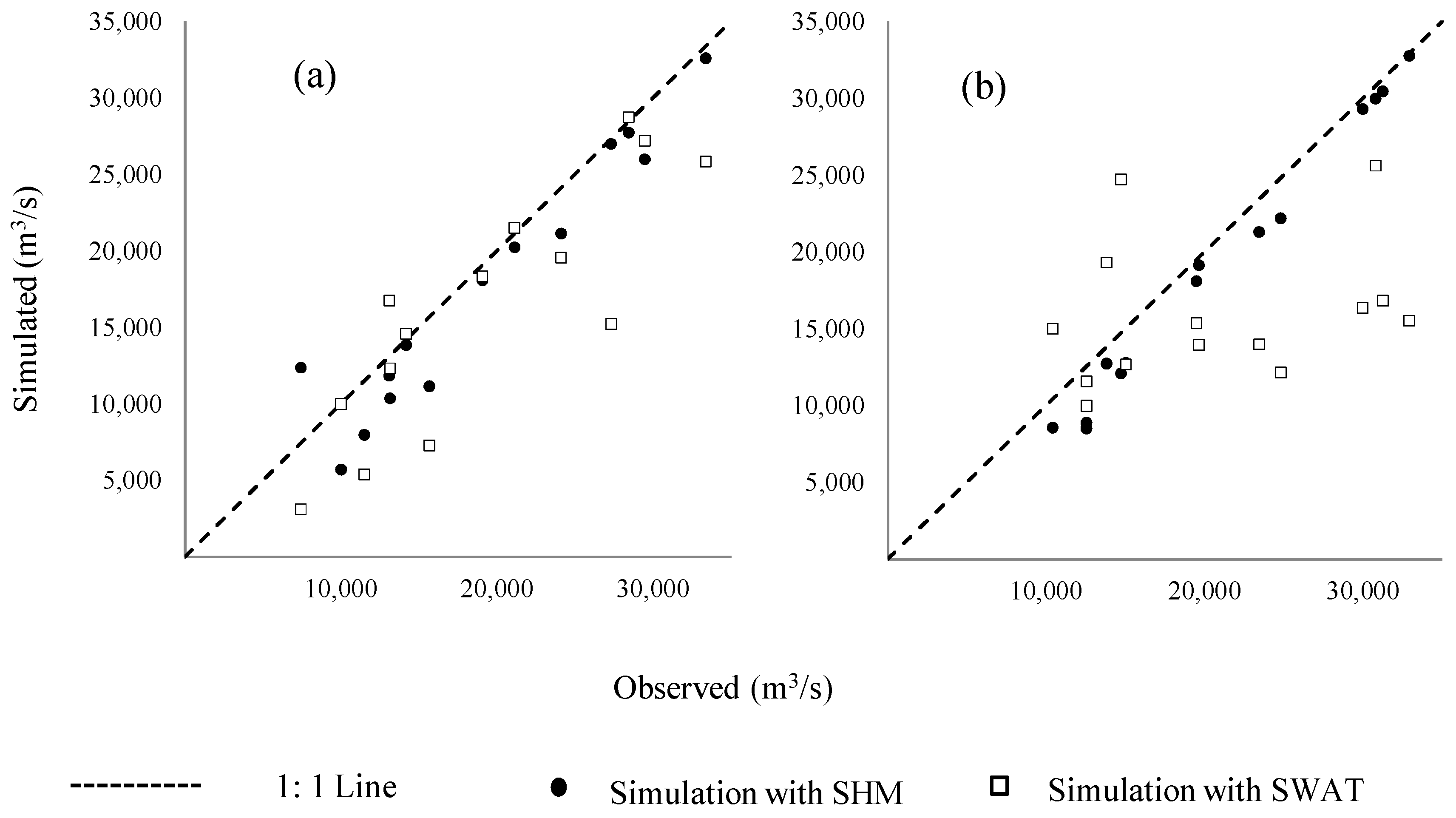
5.2. Analysis to Compare Annual Peaks
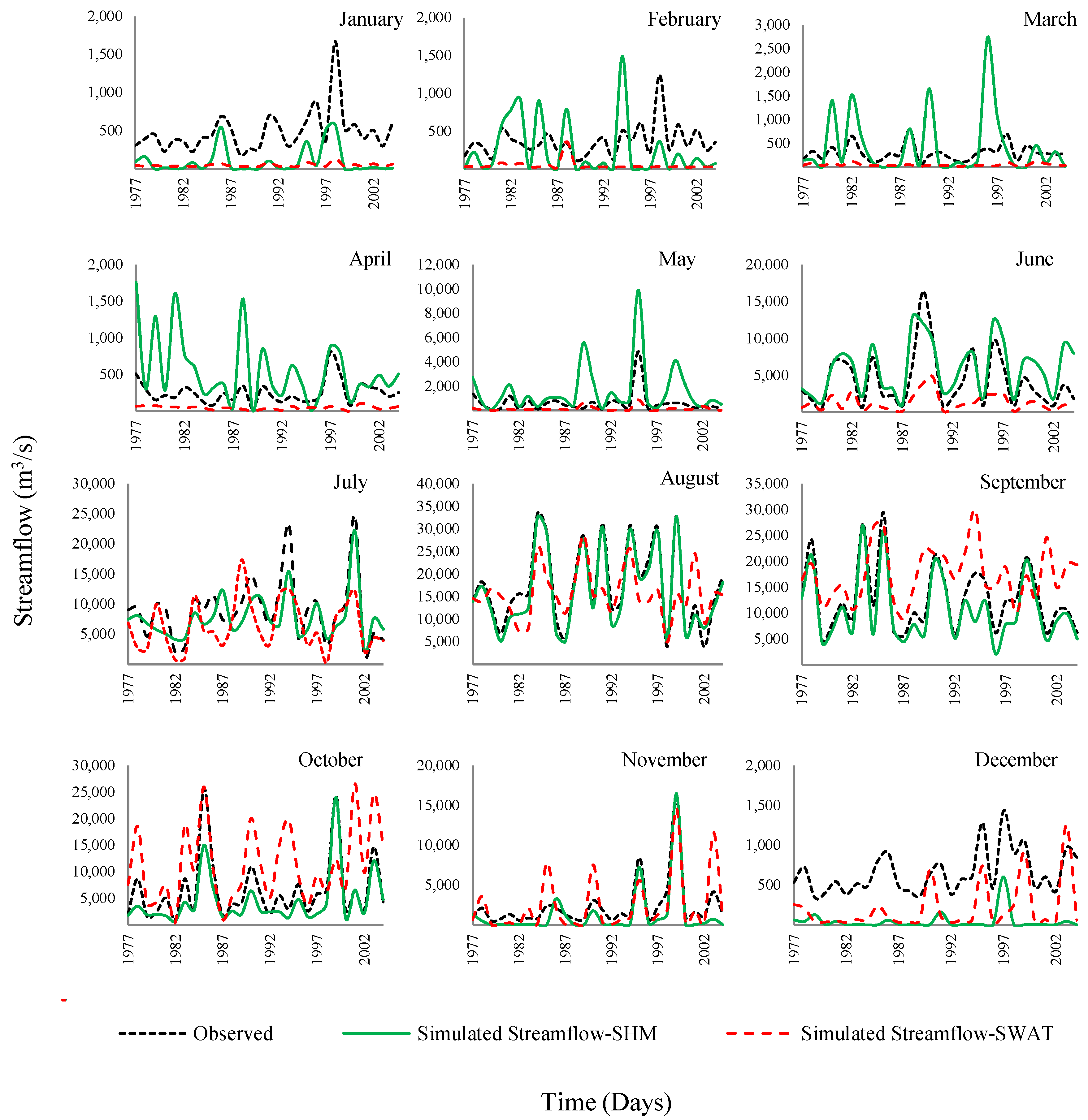
5.3. Inter-Annual Variability of Model Simulations
5.4. Comparison of Model Simulations for Percentile Flows
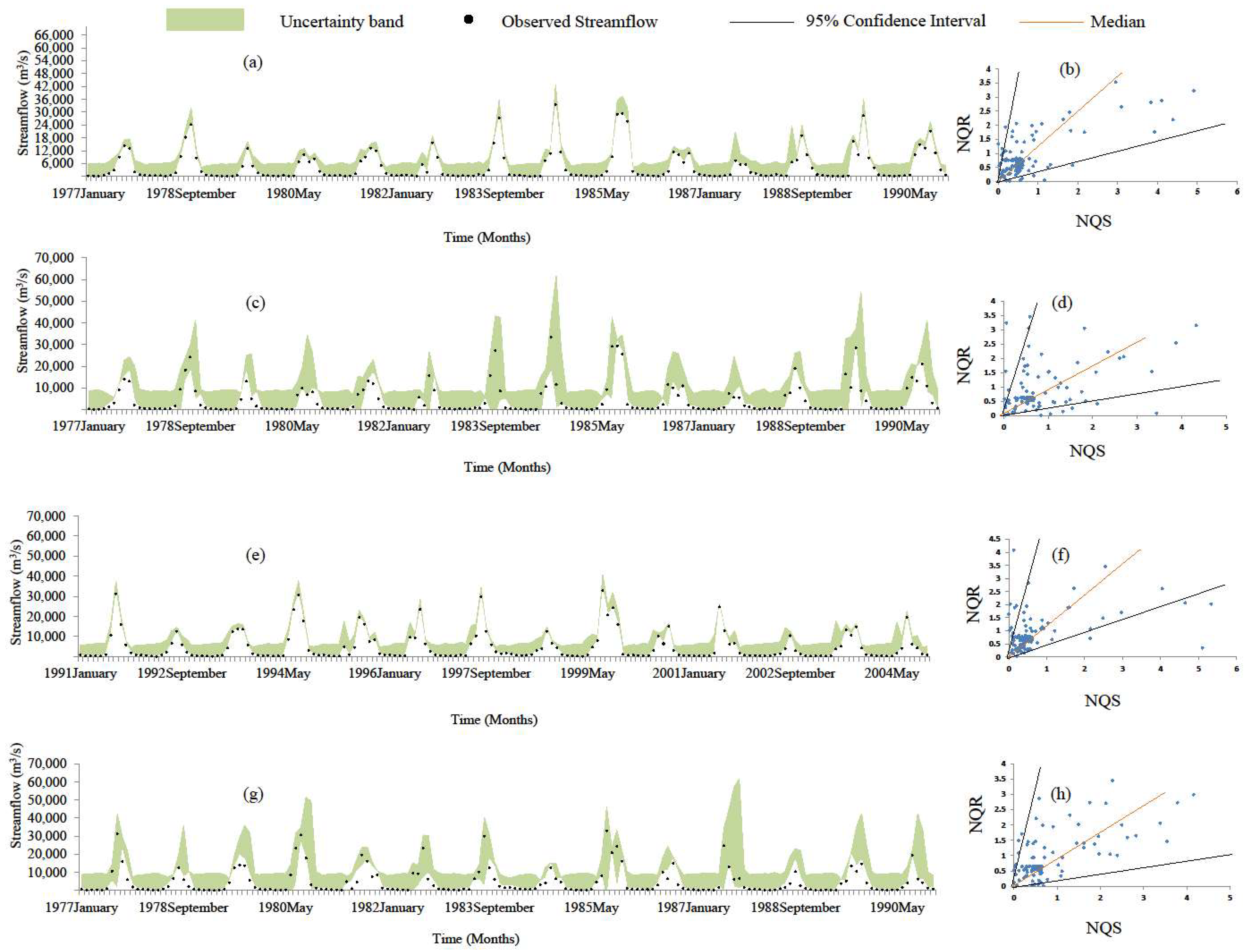
5.5. Uncertainty Analysis of Monthly Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, X.; Guo, J.; Leung, L.R. Assessment of the effects of spatial resolutions on daily water flux simulations. J. Hydrol. 2004, 298, 287–310. [Google Scholar] [CrossRef]
- Kampf, S.K.; Burges, S.J. A framework for classifying and comparing distributed hillslope and catchment hydrologic models. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Khakbaz, B.; Imam, B.; Hsu, K.; Sorooshian, S. From lumped to distributed via semi-distributed: Calibration strategies for semi-distributed hydrologic models. J. Hydrol. 2012, 418–419, 61–77. [Google Scholar] [CrossRef]
- Smith, M.B.; Gupta, H.V. The Distributed Model Intercomparison Project (DMIP)—Phase 2 experiments in the Oklahoma region, USA. J. Hydrol. 2012, 418–419, 1–2. [Google Scholar] [CrossRef]
- Wood, E.F.; Sivapalan, M.; Beven, K.; Band, L. Effects of spatial variability and scale with implications to hydrologic modeling. J. Hydrol. 1988, 102, 29–47. [Google Scholar] [CrossRef]
- Kouwen, N.; Soulis, E.D.; Pietroniro, A.; Donald, J.; Harrington, R.A. Grouped response units for distributed hydrologic modelling. J. Water Resour. Plan. Manag. 1993, 119, 289–305. [Google Scholar] [CrossRef]
- Reggiani, P.; Sivapalan, M.; Majid Hassanizadeh, S. A unifying framework for watershed thermodynamics: Balance equations for mass, momentum, energy and entropy, and the second law of thermodynamics. Adv. Water Resour. 1998, 22, 367–398. [Google Scholar] [CrossRef]
- Winter, T.C. The concept of hydrologic landscapes. J. Am. Water Resour. Assoc. 2001, 37, 335–349. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Ivanov, V.Y.; Bras, R.L.; Entekhabi, D. Generation of triangulated irregular networks based on hydrological similarity. J. Hydrol. Eng. 2004, 9, 288–302. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute Technical Report 406; Texas A & M University System, College Station: College Station, TX, USA, 2011. [Google Scholar]
- Rathjens, H.; Oppelt, N. SWAT model calibration of a grid-based setup. Adv. Geosci. 2012, 32, 55–61. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical development, applications, and future research directions. Trans. ASAE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Volk, M.; Williams, J.R.; Bosch, D.D. Assessment of different representations of spatial variability on SWAT model performance. Trans. ASABE 2010, 53, 1433–1443. [Google Scholar] [CrossRef]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Finnerty, B.D.; Smith, M.B.; Seo, D.J.; Koren, V.; Moglen, G.E. Space-time scale sensitivity of the Sacramento model to radar-gage precipitation inputs. J. Hydrol. 1997, 203, 21–38. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.; Liang, X.; Nijssen, B.; Wetzel, S.W. Hydrological modeling of continental-scale basins. Annu. Rev. Earth Planet. Sci. 1997, 25, 279–300. [Google Scholar] [CrossRef]
- Kuo, W.-L.; Steenhuis, T.S.; McCulloch, C.E.; Mohler, C.L.; Weinstein, D.A.; DeGloria, S.D.; Swaney, D.P. Effect of grid size on runoff and soil moisture for a variable-source-area hydrology model. Water Resour. Res. 1999, 35, 3419–3428. [Google Scholar] [CrossRef]
- Andersen, J.; Refsgaard, J.C.; Jensen, K.H. Distributed hydrological modelling of the Senegal River BasinModel construction and validation. J. Hydrol. 2001, 247, 200–214. [Google Scholar] [CrossRef]
- Booij, M.J. Impact of climate change on river flooding assessed with different spatial model resolutions. J. Hydrol. 2005, 303, 176–198. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- Haghnegahdar, A.; Tolson, B.A.; Craig, J.R.; Paya, K.T. Assessing the performance of a semi-distributed hydrological model under various watershed discretization schemes. Hydrol. Process. 2015, 29, 4018–4031. [Google Scholar] [CrossRef]
- Abu El-Nasr, A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modelling the hydrology of a catchment using a distributed and a semi-distributed model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Im, S.; Brannan, K.M.; Mostaghimi, S.; Kim, S.M. Comparison of HSPF and SWAT models performance for runoff and sediment yield prediction. J. Environ. Sci. Health Part A Toxic/Hazard. Subst. Environ. Eng. 2007, 42, 1561–1570. [Google Scholar] [CrossRef]
- Nasr, A.; Bruen, M.; Jordan, P.; Moles, R.; Kiely, G.; Byrne, P. A comparison of SWAT, HSPF and SHETRAN/GOPC for modelling phosphorus export from three catchments in Ireland. Water Res. 2007, 41, 1065–1073. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Li, Z. Performance of WASMOD and SWAT on hydrological simulation in Yingluoxia watershed in northwest of China. Hydrol. Process. 2011, 25, 2001–2008. [Google Scholar] [CrossRef]
- Cornelissen, T.; Diekkrüger, B.; Giertz, S. A comparison of hydrological models for assessing the impact of land use and climate change on discharge in a tropical catchment. J. Hydrol. 2013, 498, 221–236. [Google Scholar] [CrossRef]
- Xie, H.; Lian, Y. Uncertainty-based evaluation and comparison of SWAT and HSPF applications to the Illinois River Basin. J. Hydrol. 2013, 481, 119–131. [Google Scholar] [CrossRef]
- Sommerlot, A.R.; Nejadhashemi, A.P.; Woznicki, S.A.; Giri, S.; Prohaska, M.D. Evaluating the capabilities of watershed-scale models in estimating sediment yield at field-scale. J. Environ. Manag. 2013, 127, 228–236. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, X.; He, C.; Zhang, B.; Zhang, X.; Li, J.; Zhao, C.; Tian, J.; DeMarchi, C. Comparison of SWAT and DLBRM for hydrological modeling of a mountainous watershed in arid northwest China. J. Hydrol. Eng. 2016, 21, 4016007. [Google Scholar] [CrossRef]
- Pignotti, G.; Rathjens, H.; Cibin, R.; Chaubey, I.; Crawford, M. Comparative analysis of HRU and grid-based SWAT models. Water 2017, 9, 272. [Google Scholar] [CrossRef]
- Surfleet, C.G.; Tullos, D.; Chang, H.; Jung, I.-W. Selection of hydrologic modeling approaches for climate change assessment: A comparison of model scale and structures. J. Hydrol. 2012, 464–465, 233–248. [Google Scholar] [CrossRef]
- Flügel, W.-A. Combining GIS with regional hydrological modelling using hydrological response units (HRUs): An application from Germany. Math. Comput. Simul. 1997, 43, 297–304. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, Y.D.; Xu, C.Y.; Chen, X.; Chen, X.; Singh, V.P. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. J. Hydrol. 2007, 336, 316–333. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Jung, I.W. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrol. Process. 2011, 25, 2814–2826. [Google Scholar] [CrossRef]
- Singh, V.P. Computer Models of Watershed Hydrology; Water Resources Publications, LLC: Littleton, CO, USA, 1995. [Google Scholar]
- Haverkamp, S.; Srinivasan, R.; Frede, H.G.; Santhi, C. Subwatershed spatial analysis tool: Discretization of a distributed hydrologic model by statistical criteria. J. Am. Water Resour. Assoc. 2002, 38, 1723–1733. [Google Scholar] [CrossRef]
- Dahm, R.J.; Singh, U.K.; Lal, M.; Marchand, M.; Sperna Weiland, F.C.; Singh, S.K.; Singh, M.P. Downscaling GCM data for climate change impact assessments on rainfall: A practical application for the Brahmani-Baitarani river basin. Hydrol. Earth Syst. Sci. Discuss. 2016, 499, 1–42. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.P.; Rangan, D.M.; Ramasastri, K.S. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Sharpley, A.N.; Williams, J.R. EPIC—Erosion/Productivity Impact Calculator: 1. Model Documentation; USDA Technical Bulletin No. 1768; USDA: Washington, DC, USA, 1990.
- Paul, P.K.; Kumari, N.; Panigrahi, N.; Mishra, A.; Singh, R. Implementation of cell-to-cell routing scheme in a large scale conceptual hydrological model. Environ. Model. Softw. 2018, 101, 23–33. [Google Scholar] [CrossRef]
- Paul, P.K.; Gaur, S.; Yadav, B.; Panigrahy, N.; Mishra, A.; Singh, R. Diagnosing credibility of a large-scale conceptual hydrological model in simulating streamflow. J. Hydrol. Eng. 2019, 24, 4019004. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 2005; pp. 147–155. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from ambient air temperature. Am. Soc. Agric. Eng. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Das, P.; Islam, A.; Dutta, S.; Dubey, A.K.; Sarkar, R. Estimation of runoff curve numbers using a physically-based approach of preferential flow modelling. In Hydrology in a Changing World: Environmental and Human Dimensions: Proceedings of the FRIEND-Water 2014; IAHS Publication: Wallingford, Germany, 2014; Volume 363, pp. 443–448. [Google Scholar]
- Smith, J.L.; Halverson, H.G. Estimating Snowpack Density from Albedo Measurement; Research Paper PSW-RP-136; U.S. Department of Agriculture, Forest Service, Pacific Southwest Forest and Range Experiment Station: Portland, OR, USA, 1979.
- Sekhar, M.; Rasmi, S. Groundwater flow modeling of Gundal sub-basin in Kabini river basin, India. Asian J. Water Environ. Pollut. 2004, 1, 65–77. [Google Scholar] [CrossRef]
- Du, J.; Xie, H.; Hu, Y.; Xu, Y.; Xu, C.Y. Development and testing of a new storm runoff routing approach based on time variant spatially distributed travel time method. J. Hydrol. 2009, 369, 44–54. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Indian Institute of Technology Kharagpur. Development of Conceptual Hydrological Model for Different Ecosystems of India; Annual Report; Indian Institute of Technology Kharagpur: West Bengal, India, 2017; pp. 1–19. [Google Scholar]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Mockus, V. Estimation of direct runoff from storm rainfall. In SCS National Engineering Handbook; U.S. Department of Agriculture: Washington, DC, USA, 1972; pp. 10.1–10.16. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Weerts, A.H.; Winsemius, H.C.; Verkade, J.S. Estimation of predictive hydrological uncertainty using quantile regression: Examples from the National Flood Forecasting System (England and Wales). Hydrol. Earth Syst. Sci. 2011, 15, 255–265. [Google Scholar] [CrossRef]
- Xue, C.; Chen, B.; Wu, H. Parameter uncertainty analysis of surface flow and sediment yield in the Huolin Basin, China. J. Hydrol. Eng. 2014, 19, 1224–1236. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Mujumdar, P.P.; Ghosh, S. Modeling GCM and scenario uncertainty using a possibilistic approach: Application to the Mahanadi River, India. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Gosain, A.K.; Rao, S.; Arora, A. Climate change impact assessment of water resources of India. Curr. Sci. 2011, 101, 356–371. [Google Scholar]
- Islam, A.; Sikka, A.K.; Saha, B.; Singh, A. Streamflow response to climate change in the Brahmani river basin, India. Water Resour. Manag. 2012, 26, 1409–1424. [Google Scholar] [CrossRef]
- Mitra, S.; Mishra, A. Hydrologic response to climatic change in the Baitarni river basin. J. Indian Water Resour. Soc. 2014, 34, 10. [Google Scholar]
- Paul, P.K.; Mishra, A. Streamflow assessment in changing monsoon climate in two neighbouring river basins of eastern India. J. Indian Water Resour. Soc. 2018, 38, 1–10. [Google Scholar]
- Sindhu, K.; Durga Rao, K.H.V. Hydrological and hydrodynamic modeling for flood damage mitigation in Brahmani–Baitarani river basin, India. Geocarto Int. 2016, 32, 1004–1016. [Google Scholar] [CrossRef]
- Baratti, E.; Montanari, A.; Castellarin, A.; Salinas, J.L.; Viglione, A.; Bezzi, A. Estimating the flood frequency distribution at seasonal and annual time scales. Hydrol. Earth Syst. Sci. 2012, 16, 4651–4660. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. SCS-CN Method. Soil Conservation Service Curve Number (SCS-CN) Methodology; Mishra, S.K., Singh, V.P., Eds.; Springer: Berlin, Germany, 2003; pp. 84–146. [Google Scholar]
- Dogulu, N.; López López, P.; Solomatine, D.P.; Weerts, A.H.; Shrestha, D.L. Estimation of predictive hydrologic uncertainty using the quantile regression and UNEEC methods and their comparison on contrasting catchments. Hydrol. Earth Syst. Sci. 2015, 19, 3181–3201. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, R.; Jena, P.P.; Chatterjee, C.; Mishra, A. Identification of the best multi-model combination for simulating river discharge. J. Hydrol. 2015, 525, 313–325. [Google Scholar] [CrossRef]


| SWAT | SHM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| List of Sensitive Parameters | Process | Method | Theoretical Range of Parameter Values | Calibrated Range of Parameter Values | Spatially Varied or Not | List of Sensitive Parameters | Process | Method | Theoretical Range of Parameter Values | Calibrated Range of Parameter Values | Spatially Varied or Not |
| Cn2 | Runoff | SCS-CN [52] | 0–100 | 50–100 | Yes | CN | Runoff (SW) | SCS-CN [52] | 0–100 | 30–100 | Yes |
| Gwqmn | Baseflow | Threshold value based contribution from shallow aquifer storage | 0–5000 (mm) | 0–300 | Yes | ||||||
| Gw_delay | 0–500 (day) | 8 | No | ||||||||
| Alpha_bf | 0–1 | 0.5 | Yes | ||||||||
| Ch_N2 | River flow Routing | Variable storage/Muskingum | −0.01–0.03 | 0.03 | No | no | Routing (ROU) | SDDH [48] | 0.01–0.05 | 0.01–0.03 | Yes |
| Ch_K2 | 0–500 (mm/h) | 0.45 | No | nc | 0.01–0.05 | 0.015 | No | ||||
| Esco | To compensate the soil evaporative demand with the depth of soil layers | Water balance | 0–1 | 0.01–0.95 | Yes | ||||||
| Total | 7 | 3 | |||||||||
| Period | Statistics | SHM | SWAT |
|---|---|---|---|
| Calibration | R2 | 0.93 | 0.75 |
| NSE | 0.92 | 0.72 | |
| PBIAS | 11.62 | 2.01 | |
| Validation | R2 | 0.93 | 0.58 |
| NSE | 0.92 | 0.50 | |
| PBIAS | 8.67 | −1.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paul, P.K.; Zhang, Y.; Mishra, A.; Panigrahy, N.; Singh, R. Comparative Study of Two State-of-the-Art Semi-Distributed Hydrological Models. Water 2019, 11, 871. https://doi.org/10.3390/w11050871
Paul PK, Zhang Y, Mishra A, Panigrahy N, Singh R. Comparative Study of Two State-of-the-Art Semi-Distributed Hydrological Models. Water. 2019; 11(5):871. https://doi.org/10.3390/w11050871
Chicago/Turabian StylePaul, Pranesh Kumar, Yongqiang Zhang, Ashok Mishra, Niranjan Panigrahy, and Rajendra Singh. 2019. "Comparative Study of Two State-of-the-Art Semi-Distributed Hydrological Models" Water 11, no. 5: 871. https://doi.org/10.3390/w11050871
APA StylePaul, P. K., Zhang, Y., Mishra, A., Panigrahy, N., & Singh, R. (2019). Comparative Study of Two State-of-the-Art Semi-Distributed Hydrological Models. Water, 11(5), 871. https://doi.org/10.3390/w11050871






