Robustness Spatiotemporal Clustering and Trend Detection of Rainfall Erosivity Density in Greece
Abstract
1. Introduction
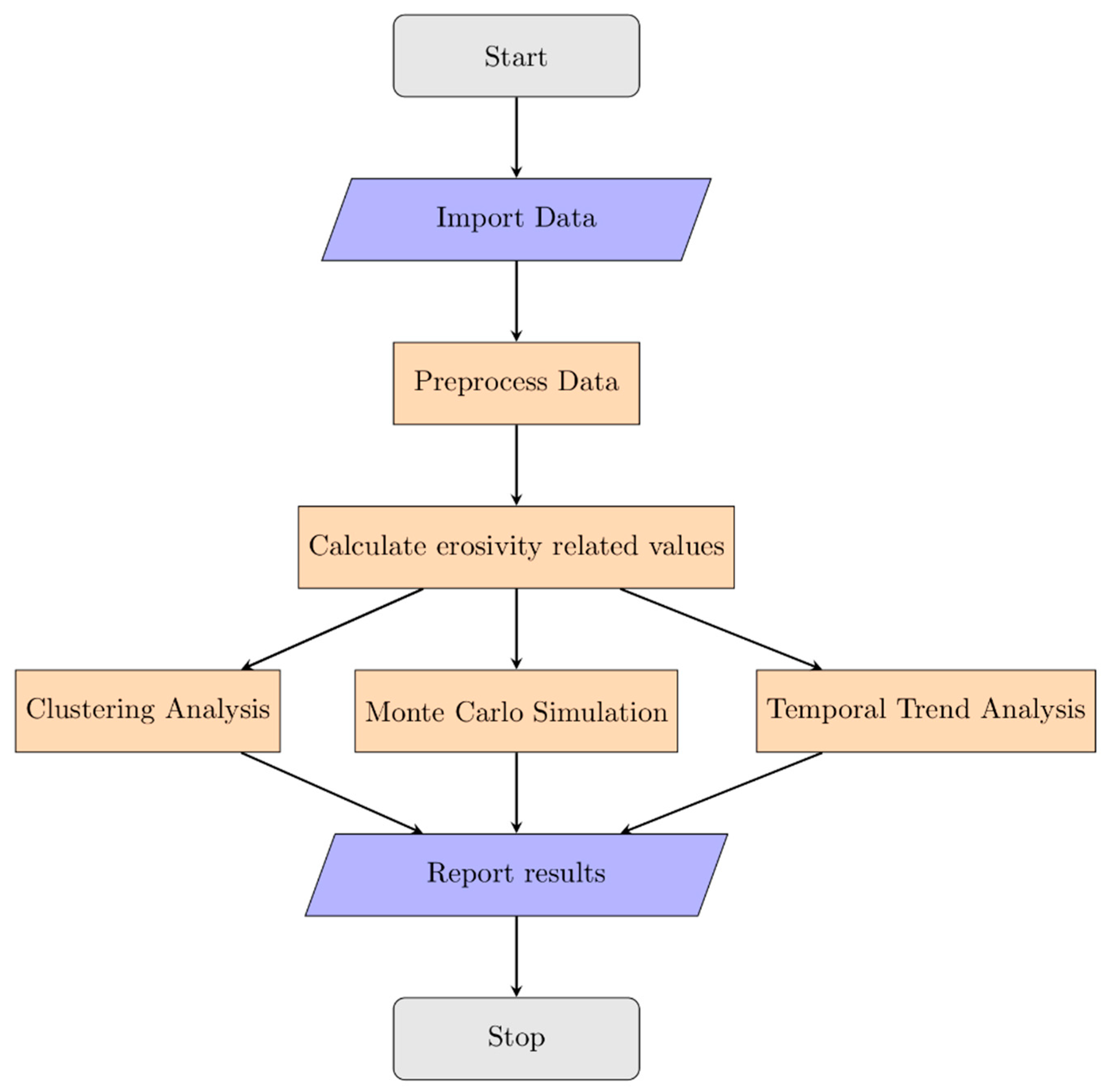
2. Materials and Methods
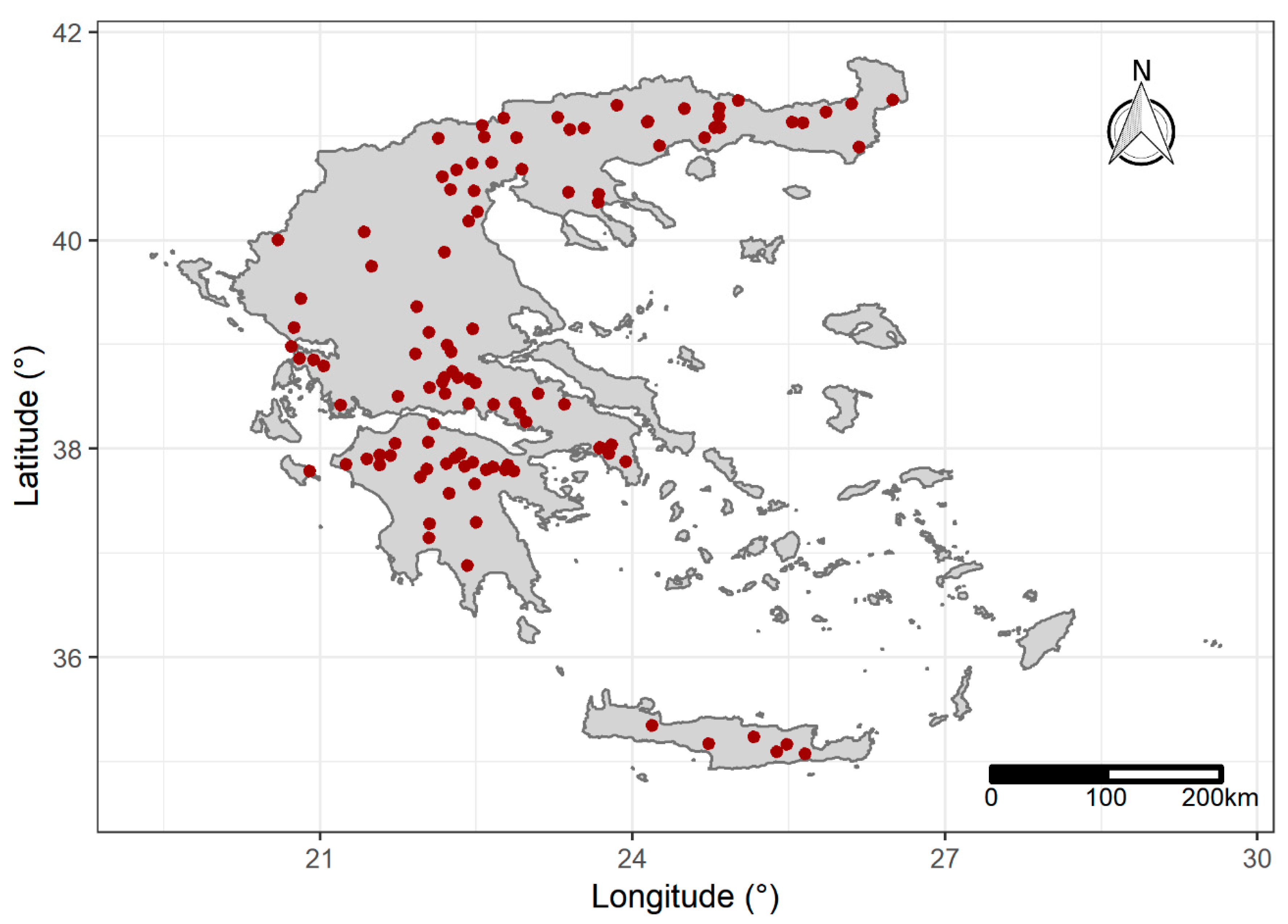
2.1. Data Acquisition and Processing
2.2. Comparative Assessment of the Impact of Missing Data
 |
2.3. Temporal Trend Detection
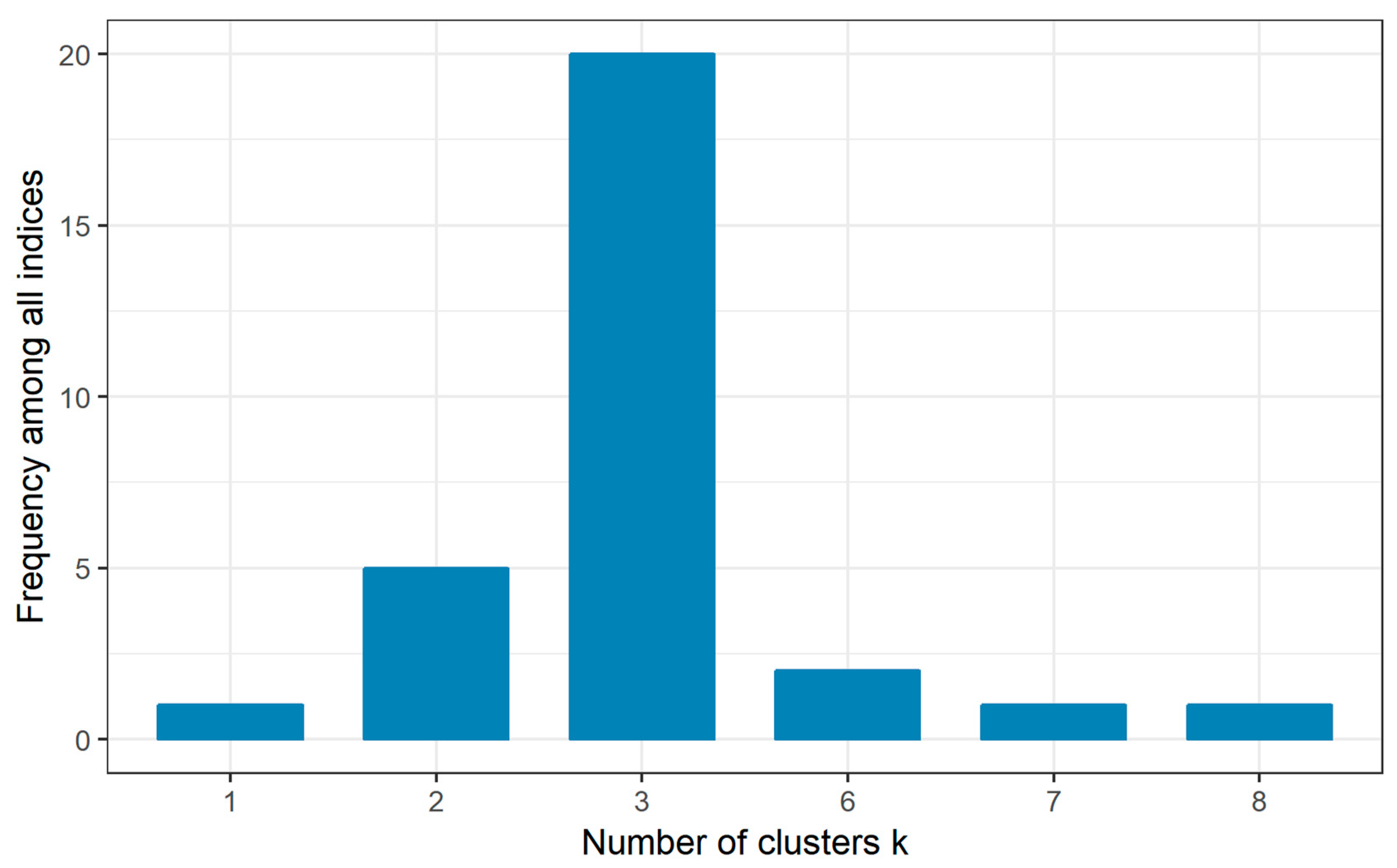
2.4. Clustering Analysis
3. Results and Discussion
3.1. Annual and Monthly Erosivity Density Calculations
3.2. Monte Carlo Procedure Results
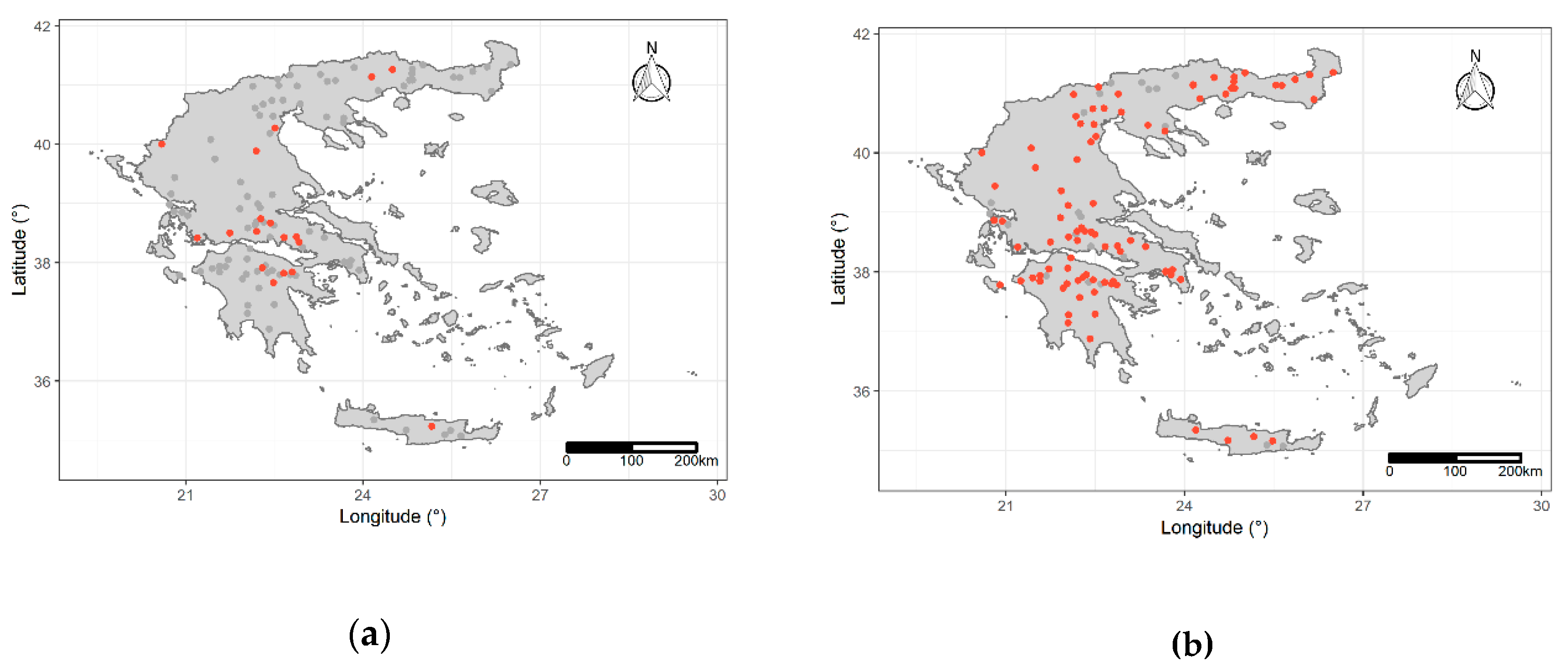
3.3. Erosivity Density Temporal Trends
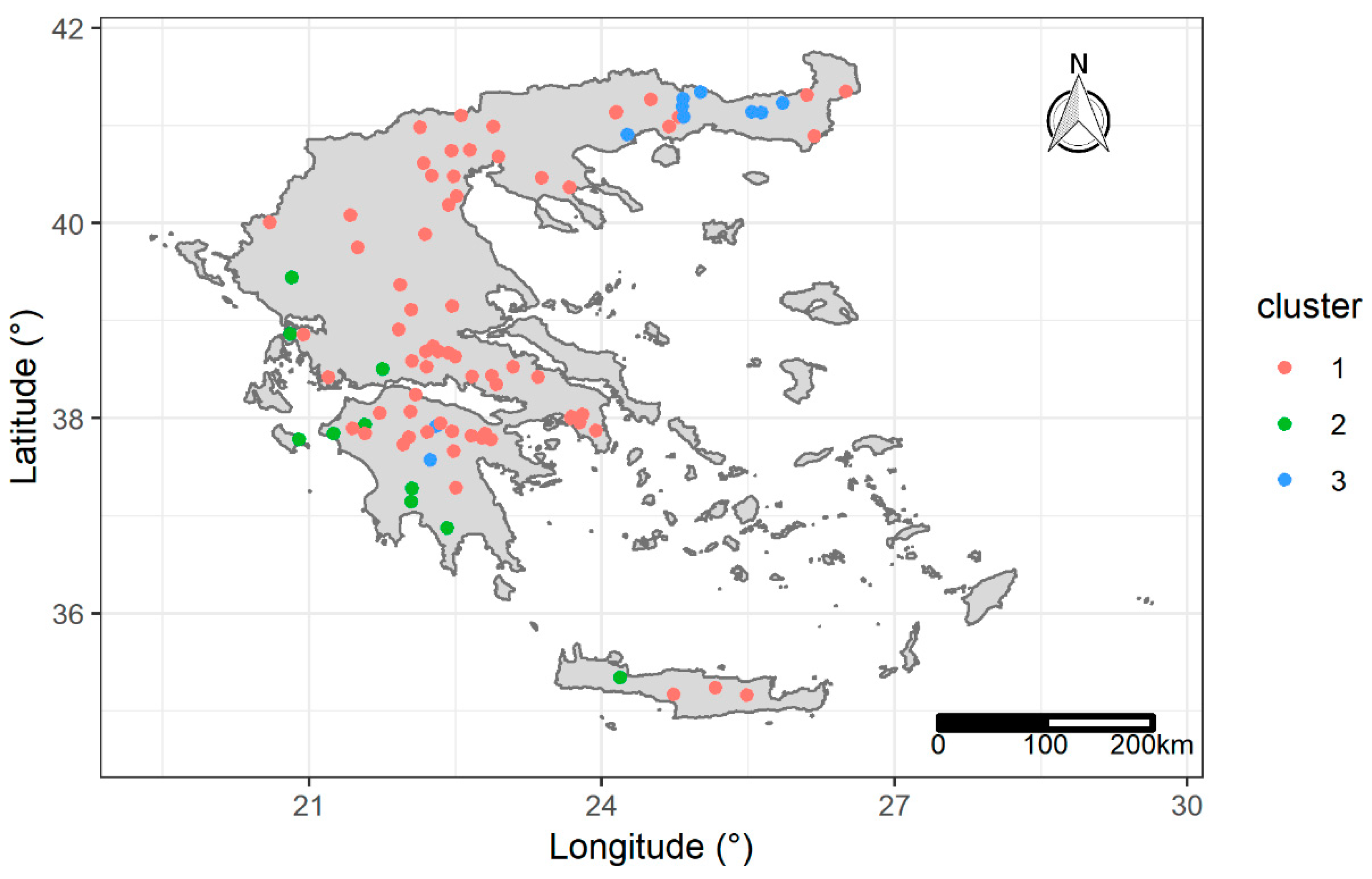
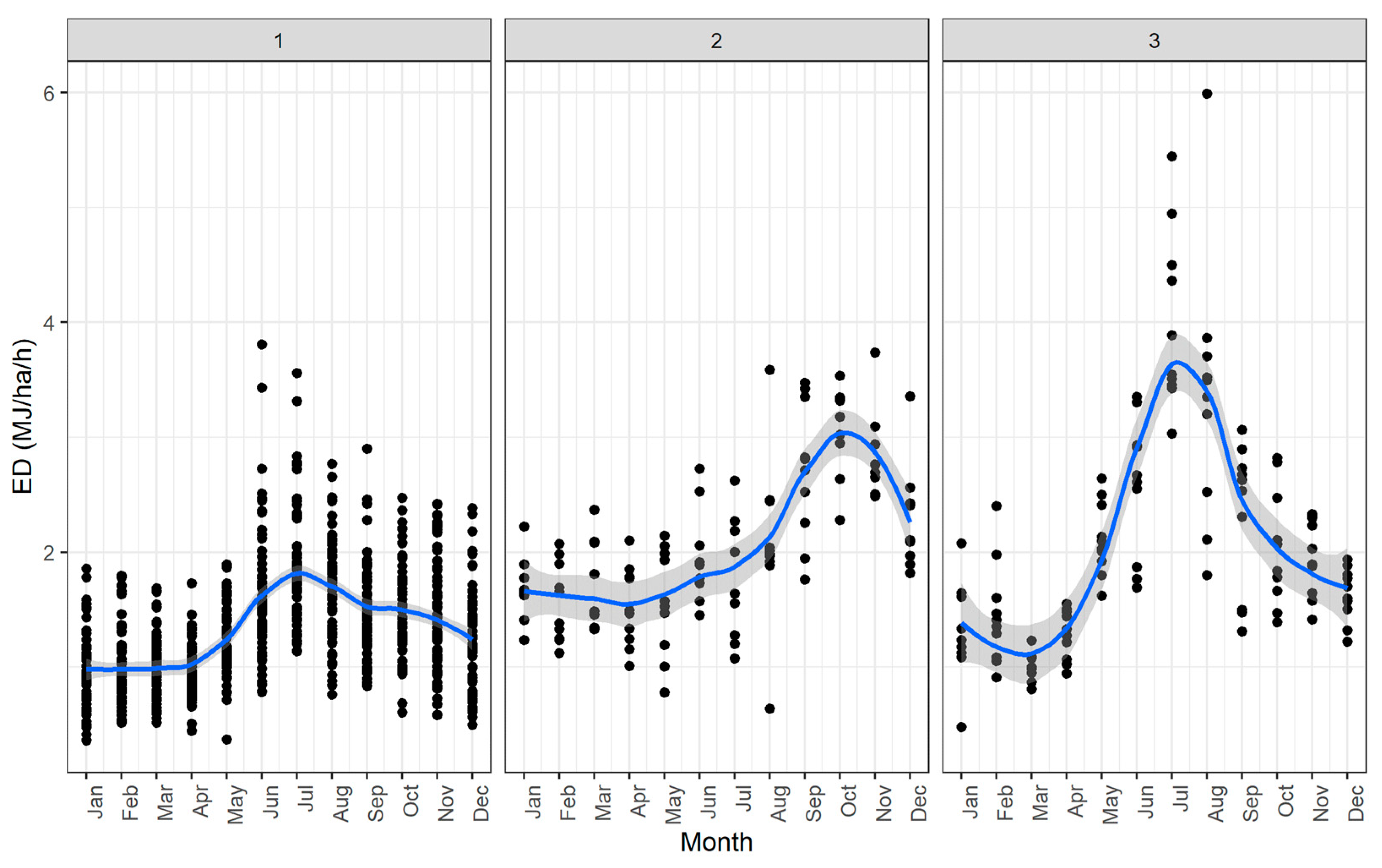
3.4. Erosivity Density Spatio-Temporal Clustering
4. Conclusions
- Incomplete pluviograph data can be used to compute and achieve acceptable accuracy on the estimation of .
- Stationarity of was found for the majority of the selected stations in Greece.
- Three clusters of stations define areas in Greece with different temporal patterns of .
- Only the stations that are located in the rainy part of western Greece have values that follow the seasonal cycle of precipitation that is common for the country.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Nearing, M.; Pruski, F.; O’neal, M. Expected climate change impacts on soil erosion rates: A review. J. Soil Water Conserv. 2004, 59, 43–50. [Google Scholar]
- Hellenic Republic. Acceptance of the Greek National Action Plan against Desertification; Joint Ministerial Decision: Athens, Greece, 2001. [Google Scholar]
- Kosmas, C.; Danalatos, N.; Kosma, D.; Kosmopoulou, P. Greece. In Soil Erosion in Europe; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 279–288. ISBN 978-0-470-85920-9. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; USDA, Agriculture Handbook No. 537; Government Printing Office: Washington, DC, USA, 1978.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Department of Agriculture: Washington, DC, USA, 1997; Volume 703.
- USDA-ARS. Science Documentation: Revised Universal Soil Loss Equation, Version 2 (RUSLE 2); USDA-Agricultural Research Service: Washington, DC, USA, 2013.
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K. Spatio-temporal analysis of rainfall erosivity and erosivity density in Greece. Catena 2016, 137, 161–172. [Google Scholar] [CrossRef]
- Vantas, K. Determination of Rainfall Erosivity in the Framework of Data Science Using Machine Learning and Geostatistics Methods. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2017. [Google Scholar]
- Vantas, K.; Sidiropoulos, E. Imputation of erosivity values under incomplete rainfall data by machine learning methods. Eur. Water 2017, 57, 193–199. [Google Scholar]
- Brown, L.C.; Foster, G.R. Storm erosivity using idealized intensity distributions. Trans. ASAE 1987, 30, 379–386. [Google Scholar] [CrossRef]
- Nearing, M.A.; Yin, S.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Hollinger, S.E.; Angel, J.R.; Palecki, M.A. Spatial Distribution, Variation, and Trends in Storm Precipitation Characteristics Associated with Soil Erosion in the United States; Illinois State Water Survey Atmospheric Environment Section: Champaign, IL, USA, 2002. [Google Scholar]
- Feidas, H.; Noulopoulou, C.; Makrogiannis, T.; Bora-Senta, E. Trend analysis of precipitation time series in Greece and their relationship with circulation using surface and satellite data: 1955–2001. Theor. Appl. Climatol. 2007, 87, 155–177. [Google Scholar] [CrossRef]
- Bartzokas, A.; Lolis, C.J.; Metaxas, D.A. A study on the intra-annual variation and the spatial distribution of precipitation amount and duration over Greece on a 10 day basis. Int. J. Climatol. J. R. Meteorol. Soc. 2003, 23, 207–222. [Google Scholar] [CrossRef]
- Xoplaki, E.; Luterbacher, J.; Burkard, R.; Patrikas, I.; Maheras, P. Connection between the large-scale 500 hPa geopotential height fields and precipitation over Greece during wintertime. Clim. Res. 2000, 14, 129–146. [Google Scholar] [CrossRef]
- Tolika, K.; Maheras, P. Spatial and temporal characteristics of wet spells in Greece. Theor. Appl. Climatol. 2005, 81, 71–85. [Google Scholar] [CrossRef]
- Maheras, P.; Tolika, K.; Anagnostopoulou, C.; Vafiadis, M.; Patrikas, I.; Flocas, H. On the relationships between circulation types and changes in rainfall variability in Greece. Int. J. Climatol. J. R. Meteorol. Soc. 2004, 24, 1695–1712. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Larissi, I.K.; Nastos, P.T.; Paliatsos, A.G. Spatial variability and trends of the rain intensity over Greece. Adv. Geosci. 2010, 26, 65–69. [Google Scholar] [CrossRef][Green Version]
- Markonis, Y.; Batelis, S.C.; Dimakos, Y.; Moschou, E.; Koutsoyiannis, D. Temporal and spatial variability of rainfall over Greece. Theor. Appl. Climatol. 2017, 130, 217–232. [Google Scholar] [CrossRef]
- Hatzianastassiou, N.; Katsoulis, B.; Pnevmatikos, J.; Antakis, V. Spatial and temporal variation of precipitation in Greece and surrounding regions based on global precipitation climatology project data. J. Clim. 2008, 21, 1349–1370. [Google Scholar] [CrossRef]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.-T. Learning from Data; AMLBook: New York, NY, USA, 2012. [Google Scholar]
- Sheikholeslami, G.; Chatterjee, S.; Zhang, A. Wavecluster: A multi-resolution clustering approach for very large spatial databases. In Proceedings of the VLDB Conference, New York, NY, USA, 24–27 August 1998; Volume 98, pp. 428–439. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkley, CA, USA; Los Angeles, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Academic Press: Burlington, MA, USA, 2008; ISBN 978-1-59749-272-0. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R package for determining the relevant number of clusters in a data set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Vantas, K.; Sidiropoulos, E.; Loukas, A. Temporal and elevation trend detection of rainfall erosivity density in Greece. Proceedings 2019, 7, 10. [Google Scholar] [CrossRef]
- Vantas, K. hydroscoper: R interface to the Greek national data bank for hydrological and meteorological information. J. Open Source Softw. 2018, 3, 625. [Google Scholar] [CrossRef]
- Weiss, L.L. Ratio of true to fixed-interval maximum rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar]
- Hershfield, D.M. Rainfall Frequency Atlas of the United States; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1961; Volume 40.
- Van Montfort, M.A.J. Concomitants of the Hershfield factor. J. Hydrol. 1997, 194, 357–365. [Google Scholar] [CrossRef]
- Yin, S.; Xie, Y.; Nearing, M.A.; Wang, C. Estimation of rainfall erosivity using 5-to 60-minute fixed-interval rainfall data from China. Catena 2007, 70, 306–312. [Google Scholar] [CrossRef]
- McGregor, K.C.; Bingner, R.L.; Bowie, A.J.; Foster, G.R. Erosivity index values for northern Mississippi. Trans. ASAE 1995, 38, 1039–1047. [Google Scholar] [CrossRef]
- Yin, S.; Nearing, M.A.; Borrelli, P.; Xue, X. Rainfall erosivity: An overview of methodologies and applications. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Hellenic Republic. Implementation of Directive 2007/60 EC—Development of Rainfall Curves in Greece; Special Water Secretariat: Athens, Greece, 2016. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Rank Correlation Methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econ. J. Econ. Soc. 1945, 1, 245–259. [Google Scholar] [CrossRef]
- Petek, M.; Mikoš, M.; Bezak, N. Rainfall erosivity in Slovenia: Sensitivity estimation and trend detection. Environ. Res. 2018, 167, 528–535. [Google Scholar] [CrossRef]
- Fiener, P.; Neuhaus, P.; Botschek, J. Long-term trends in rainfall erosivity–analysis of high resolution precipitation time series (1937–2007) from Western Germany. Agric. For. Meteorol. 2013, 171, 115–123. [Google Scholar] [CrossRef]
- Meusburger, K.; Steel, A.; Panagos, P.; Montanarella, L.; Alewell, C. Spatial and temporal variability of rainfall erosivity factor for Switzerland. Hydrol. Earth Syst. Sci. 2012, 16, 167–177. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Lawson, R.G.; Jurs, P.C. New index for clustering tendency and its application to chemical problems. J. Chem. Inf. Comput. Sci. 1990, 30, 36–41. [Google Scholar] [CrossRef]
- Hopkins, B.; Skellam, J.G. A new method for determining the type of distribution of plant individuals. Ann. Bot. 1954, 18, 213–227. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 4th ed.; Elsevier Academic Press: Amsterdam, The Netherlands, 2009; ISBN 978-1-59749-272-0. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Husson, F.; Lê, S.; Pagès, J. Exploratory Multivariate Analysis by Example Using R, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2017; ISBN 978-0-429-22543-7. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019.
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement Ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: Determining the Best Number of Clusters in a Data Set. 2015. Available online: https://cran.r-project.org/web/packages/NbClust/index.html (accessed on 17 May 2019).
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Shyu, W.M.; Grosse, E.; Cleveland, W.S. Local regression models. In Statistical Models in S; Routledge: London, UK, 2017; pp. 309–376. [Google Scholar]
- Krzanowski, W.J.; Lai, Y.T. A criterion for determining the number of groups in a data set using sum-of-squares clustering. Biometrics 1988, 44, 23–34. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat.-Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; Wiley Series in Probability and Mathematical Statistics; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Sarle, W.S. SAS technical report A-108, cubic clustering criterion. Cary NC SAS Inst. Inc. 1983, 56. [Google Scholar]
- Scott, A.J.; Symons, M.J. Clustering methods based on likelihood ratio criteria. Biometrics 1971, 27, 387–397. [Google Scholar] [CrossRef]
- Marriott, F.H.C. Practical problems in a method of cluster analysis. Biometrics 1971, 27, 501–514. [Google Scholar] [CrossRef]
- Friedman, H.P.; Rubin, J. On some invariant criteria for grouping data. J. Am. Stat. Assoc. 1967, 62, 1159–1178. [Google Scholar] [CrossRef]
- Hubert, L.J.; Levin, J.R. A general statistical framework for assessing categorical clustering in free recall. Psychol. Bull. 1976, 83, 1072–1080. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification and Scene Analysis; Wiley: New York, NY, USA, 1973; Volume 3. [Google Scholar]
- Beale, E.M.L. Cluster Analysis; Scientific Control Systems Limited: London, UK, 1969. [Google Scholar]
- Ratkowsky, D.A.; Lance, G.N. Criterion for determining the number of groups in a classification. Aust. Comput. J. 1978, 10, 115–117. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA, a Novel Method of Data Analysis and Pattern Classification; Stanford Research Inst.: Menlo Park, CA, USA, 1965. [Google Scholar]
- Milligan, G.W. A monte carlo study of thirty internal criterion measures for cluster analysis. Psychometrika 1981, 46, 187–199. [Google Scholar] [CrossRef]
- Frey, T.; van Groenewoud, H. A cluster analysis of the D2 matrix of white spruce stands in Saskatchewan based on the maximum-minimum principle. J. Ecol. 1972, 60, 873–886. [Google Scholar] [CrossRef]
- McClain, J.O.; Rao, V.R. Clustisz: A program to test for the quality of clustering of a set of objects. JMR J. Mark. Res. (pre-1986) 1975, 12, 456. [Google Scholar]
- Baker, F.B.; Hubert, L.J. Measuring the power of hierarchical cluster analysis. J. Am. Stat. Assoc. 1975, 70, 31–38. [Google Scholar] [CrossRef]
- Dunn, J.C. Well-separated clusters and optimal fuzzy partitions. J. Cybern. 1974, 4, 95–104. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Halkidi, M.; Vazirgiannis, M.; Batistakis, Y. Quality scheme assessment in the clustering process. In Proceedings of the Principles of Data Mining and Knowledge Discovery; Zighed, D.A., Komorowski, J., Żytkow, J., Eds.; Springer: Berlin, Germany, 2000; pp. 265–276. [Google Scholar]
- Lebart, L.; Morineau, A.; Piron, M. Statistique Exploratoire Multidimensionnelle; Dunod: Paris, France, 2000. [Google Scholar]
- Halkidi, M.; Vazirgiannis, M. Clustering validity assessment: Finding the optimal partitioning of a data set. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001; pp. 187–194. [Google Scholar]
- Cleveland, W.S.; Grosse, E.; Shyu, W.M. Local regression models. In Statistical Models in S; Chapman & Hall: New York, NY, USA, 1992; pp. 309–376. [Google Scholar]
- Vantas, K. Hyetor: R Package to Analyze Fixed Interval Precipitation Time Series. 2019. Available online: https://github.com/kvantas/hyetor (accessed on 17 May 2019).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009; ISBN 978-0-387-98140-6. [Google Scholar]
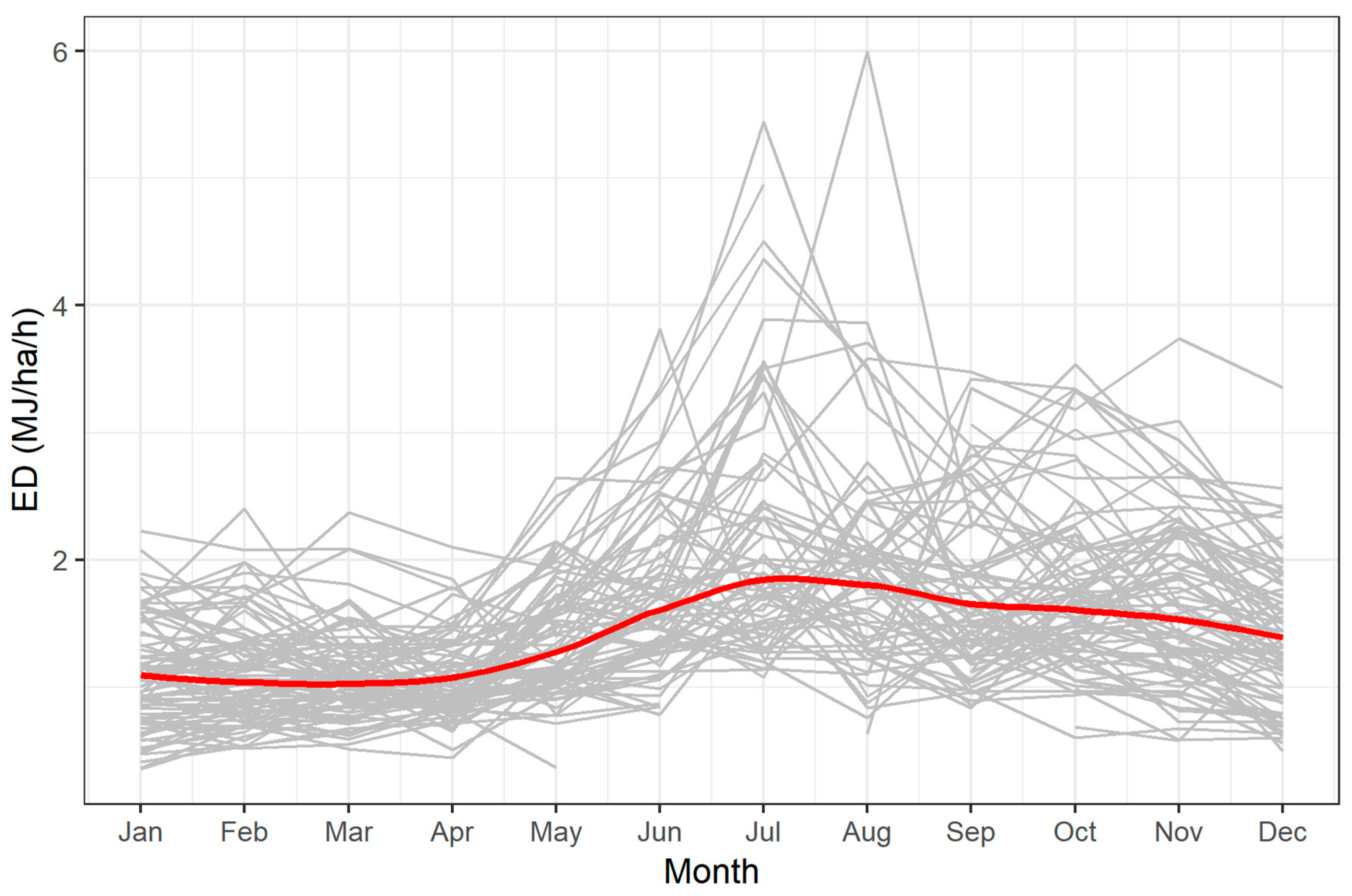
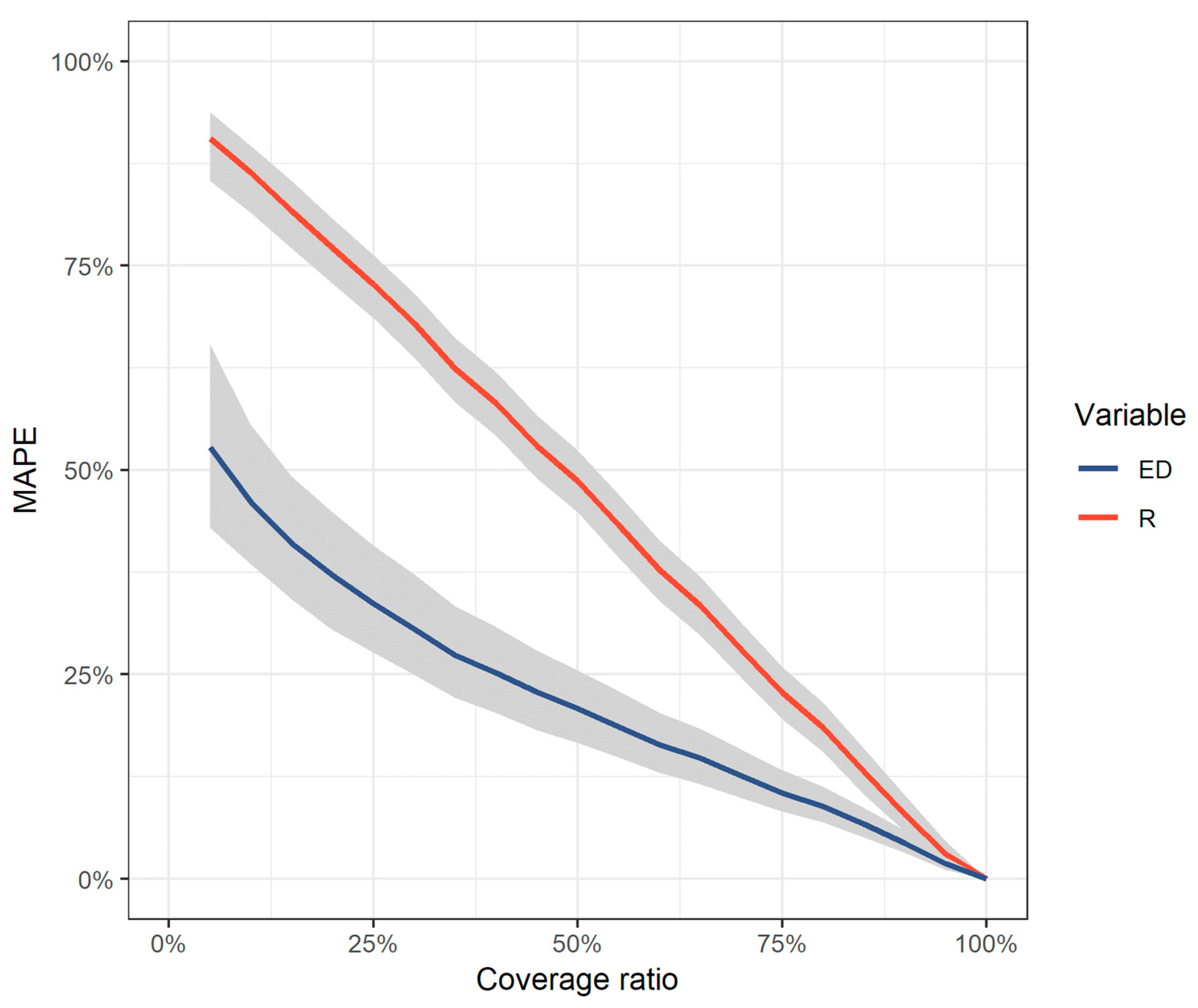
| ED (MJ/ha/h) | Min | Mean | Median | Max | SD | Skew | Kurtosis | CV |
|---|---|---|---|---|---|---|---|---|
| January | 0.36 | 1.10 | 1.08 | 2.23 | 0.43 | 0.38 | −0.58 | 0.39 |
| February | 0.52 | 1.13 | 1.07 | 2.40 | 0.41 | 0.77 | 0.10 | 0.36 |
| March | 0.52 | 1.10 | 1.05 | 2.37 | 0.36 | 1.06 | 1.47 | 0.32 |
| April | 0.45 | 1.07 | 1.03 | 2.10 | 0.32 | 0.80 | 0.50 | 0.30 |
| May | 0.37 | 1.39 | 1.30 | 2.64 | 0.44 | 0.53 | −0.13 | 0.32 |
| June | 0.78 | 1.76 | 1.57 | 3.81 | 0.68 | 0.93 | 0.31 | 0.38 |
| July | 1.08 | 2.19 | 1.89 | 5.45 | 0.99 | 1.30 | 1.23 | 0.45 |
| August | 0.64 | 1.92 | 1.84 | 5.99 | 0.87 | 1.80 | 5.35 | 0.45 |
| September | 0.84 | 1.75 | 1.57 | 3.48 | 0.67 | 0.82 | −0.25 | 0.38 |
| October | 0.61 | 1.78 | 1.66 | 3.54 | 0.67 | 0.90 | 0.18 | 0.38 |
| November | 0.58 | 1.68 | 1.56 | 3.74 | 0.65 | 0.53 | −0.21 | 0.39 |
| December | 0.50 | 1.40 | 1.38 | 3.36 | 0.56 | 0.62 | 0.45 | 0.40 |
| Annual | 1.28 | 2.89 | 2.75 | 5.51 | 1.13 | 0.60 | 0.14 | 0.39 |
| ID | Name | WD | Lon (°) | Lat (°) | El (m) | MCV (%) | Tau | padj | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 200003 | GRABIA | GR07 | 22.43 | 38.67 | 381 | 73.4 | 0.12 | 0.612 |
| 2 | 200011 | LIDORIKI | GR04 | 22.20 | 38.53 | 548 | 69.2 | −0.09 | 0.612 |
| 3 | 200015 | PYRA | GR04 | 22.27 | 38.74 | 1137 | 74.8 | −0.11 | 0.612 |
| 4 | 200018 | AG. TRIADA | GR07 | 22.92 | 38.35 | 400 | 65.4 | 0.31 | 0.081 |
| 5 | 200021 | DISTOMO | GR07 | 22.67 | 38.43 | 458 | 60.3 | −0.02 | 0.919 |
| 6 | 200024 | LEIBADIA | GR07 | 22.87 | 38.44 | 176 | 56 | −0.27 | 0.132 |
| 7 | 200059 | BASILIKO | GR05 | 20.59 | 40.01 | 747 | 75.8 | −0.11 | 0.612 |
| 8 | 200092 | ELASSONA | GR08 | 22.19 | 39.89 | 276 | 71.7 | 0.02 | 0.919 |
| 9 | 200135 | KALYBIA | GR02 | 22.30 | 37.92 | 822 | 65.3 | 0.29 | 0.123 |
| 10 | 200142 | NEMEA | GR02 | 22.66 | 37.83 | 306 | 63.8 | −0.26 | 0.132 |
| 11 | 200144 | SPATHOBOUNI | GR02 | 22.80 | 37.85 | 150 | 48.1 | −0.08 | 0.612 |
| 12 | 200181 | LESINIO | GR04 | 21.19 | 38.42 | 2 | 59.9 | 0.45 | 0.055 |
| 13 | 200190 | POROS REG. | GR04 | 21.75 | 38.51 | 182 | 67.8 | −0.11 | 0.612 |
| 14 | 200243 | NEOCHORIO | GR03 | 22.48 | 37.67 | 704 | 63.2 | 0.14 | 0.595 |
| 15 | 200291 | A. ARCHANES | GR13 | 25.16 | 35.24 | 392 | 51.6 | 0.09 | 0.612 |
| 16 | 200309 | DRAMA | GR11 | 24.15 | 41.14 | 100 | 69.6 | 0.10 | 0.612 |
| 17 | 200311 | PARANESTE | GR12 | 24.50 | 41.27 | 122 | 66.1 | −0.46 | 0.005 * |
| 18 | 200346 | KATERINE | GR09 | 22.51 | 40.28 | 30 | 64.2 | −0.15 | 0.595 |
| Method | KL [60] | CH [61] | Hartigan [62] | CCC [63] | Scott [64] | Marriot [65] | TrCovW [28] | TraceW [28] | Friedman [66] |
|---|---|---|---|---|---|---|---|---|---|
| NOC | 3 | 2 | 3 | 2 | 3 | 3 | 3 | 3 | 3 |
| Value | 2.27 | 39.70 | 11.13 | 12.61 | 109.02 | 1.40E+12 | 568.30 | 27.72 | 26.67 |
| Method | Cindex [67] | DB [68] | Silhouette [30] | Duda [69] | PseudoT2 [69] | Beale [70] | Ratkowsky [71] | Ball [72] | PtBiserial [73] |
| NOC | 6 | 3 | 3 | 3 | 3 | 7 | 2 | 3 | 3 |
| Value | 0.26 | 1.02 | 0.39 | 0.82 | 14.45 | 0.54 | 0.39 | 57.07 | 0.75 |
| Method | Frey [74] | McClain [75] | Gamma [76] | Gplus [73] | Tau [73] | Dunn [77] | Hubert [78] | SDindex [79] | Dindex [80] |
| NOC | 1 | 2 | 3 | 3 | 3 | 3 | 6 | 3 | 3 |
| Value | NA | 0.30 | 0.89 | 49.04 | 787.63 | 0.30 | Graphical | 1.97 | Graphical |
| Method | Rubin [66] | Gap [31] | SDbw [81] | ||||||
| NOC | 3 | 2 | 8 | ||||||
| Value | −1.06 | −0.36 | 0.34 |
| ED (MJ/ha/h) | Min | Mean | Median | Max | SD | Skew | Kurtosis | CV |
|---|---|---|---|---|---|---|---|---|
| Cluster 1 | 0.97 | 1.34 | 1.35 | 1.89 | 0.31 | 0.18 | −1.44 | 0.23 |
| Cluster 2 | 1.52 | 2.06 | 1.86 | 3.09 | 0.55 | 0.67 | −1.21 | 0.27 |
| Cluster 3 | 1.00 | 2.09 | 2.00 | 4.01 | 0.89 | 0.79 | −0.48 | 0.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vantas, K.; Sidiropoulos, E.; Loukas, A. Robustness Spatiotemporal Clustering and Trend Detection of Rainfall Erosivity Density in Greece. Water 2019, 11, 1050. https://doi.org/10.3390/w11051050
Vantas K, Sidiropoulos E, Loukas A. Robustness Spatiotemporal Clustering and Trend Detection of Rainfall Erosivity Density in Greece. Water. 2019; 11(5):1050. https://doi.org/10.3390/w11051050
Chicago/Turabian StyleVantas, Konstantinos, Epaminondas Sidiropoulos, and Athanasios Loukas. 2019. "Robustness Spatiotemporal Clustering and Trend Detection of Rainfall Erosivity Density in Greece" Water 11, no. 5: 1050. https://doi.org/10.3390/w11051050
APA StyleVantas, K., Sidiropoulos, E., & Loukas, A. (2019). Robustness Spatiotemporal Clustering and Trend Detection of Rainfall Erosivity Density in Greece. Water, 11(5), 1050. https://doi.org/10.3390/w11051050






