Fluid Structure Interaction of Buoyant Bodies with Free Surface Flows: Computational Modelling and Experimental Validation
Abstract
1. Introduction
2. Methodology
2.1. Fluid Flow
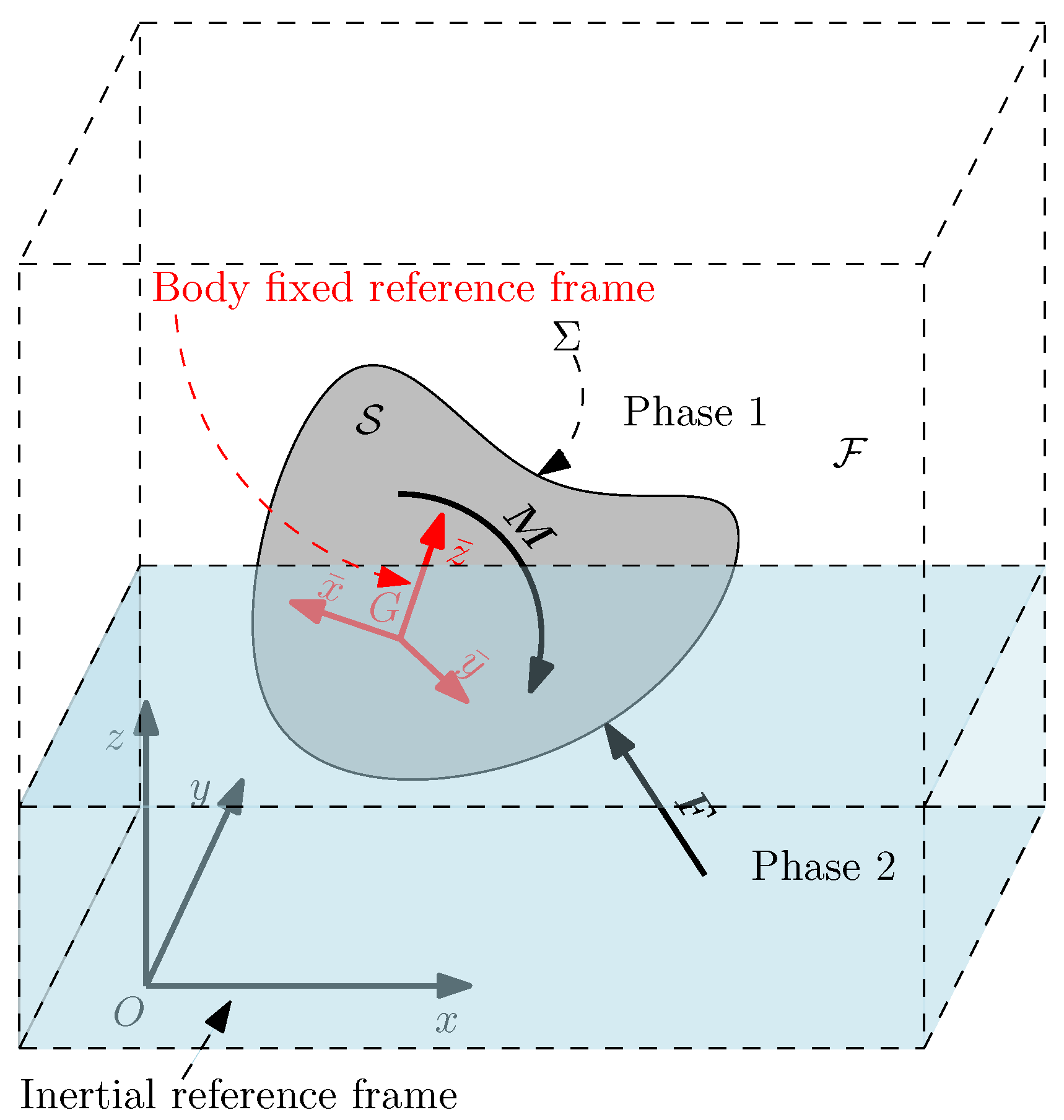
2.2. Rigid Body Dynamics in Space
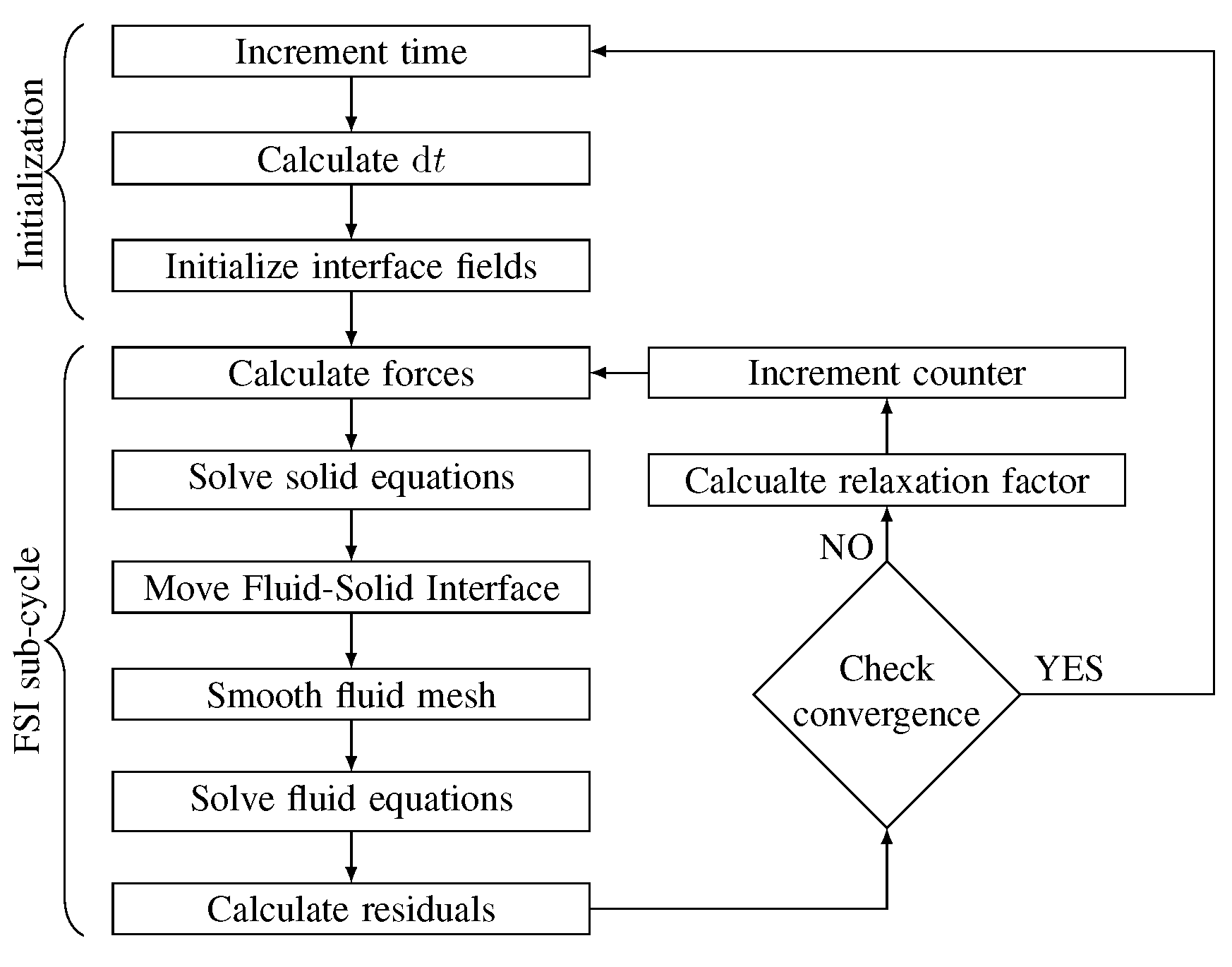
2.3. Coupling Algorithm
3. Validation
3.1. Water Entry of a Non-Buoyant Wedge
3.2. Water Entry of a Buoyant Wedge
3.3. Water Entry and Exit of a Buoyant Cylinder
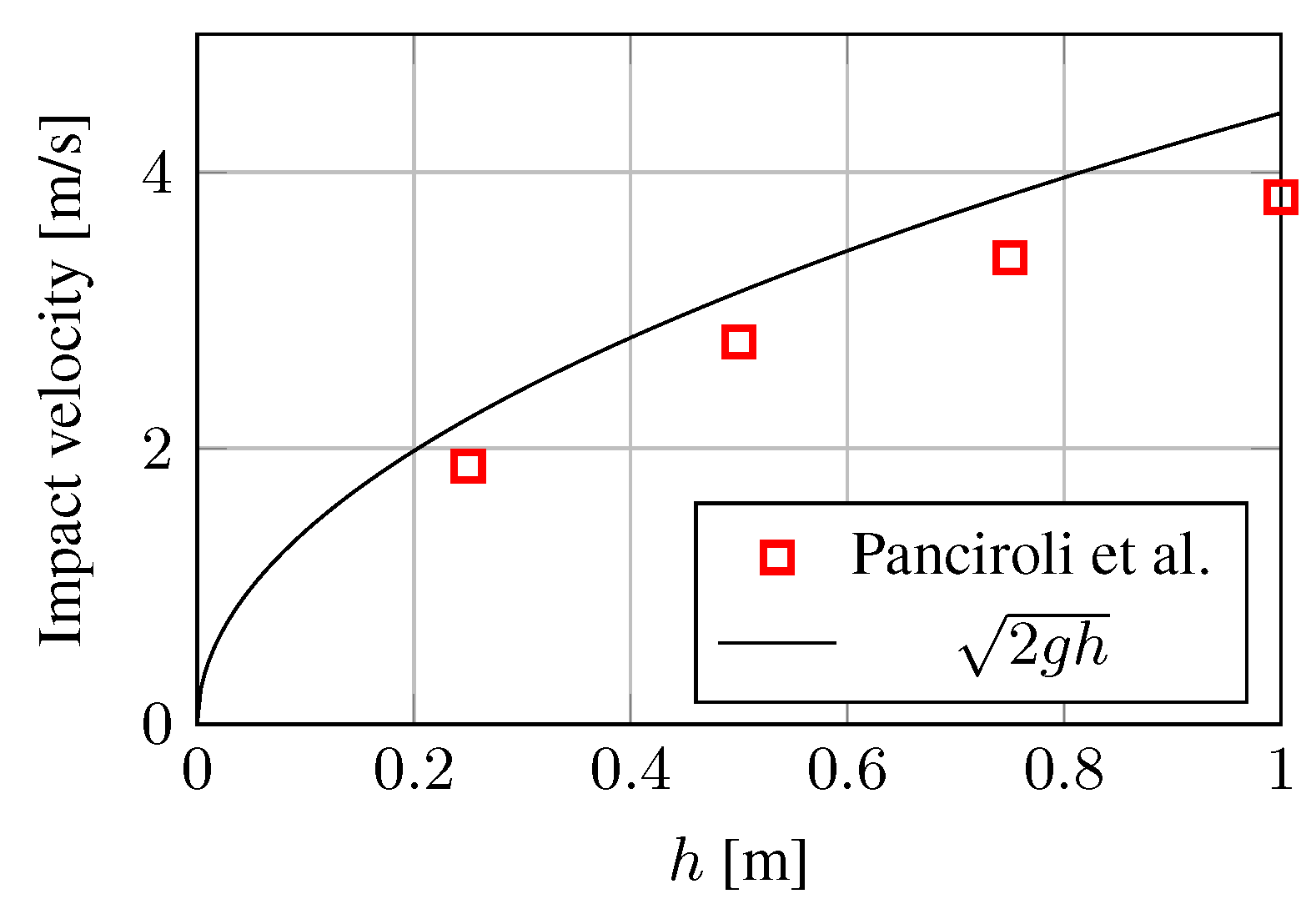
3.3.1. Experimental Setup
- (i)
- Numerical differentiation of the displacement measurement through central difference approximation;
- (ii)
- Numerical integration of the measured acceleration through the trapezoid rule;
- (iii)
- Least square fitting of the specimen displacement to a second order function and algebraic differentiation.
3.3.2. Numerical Setup
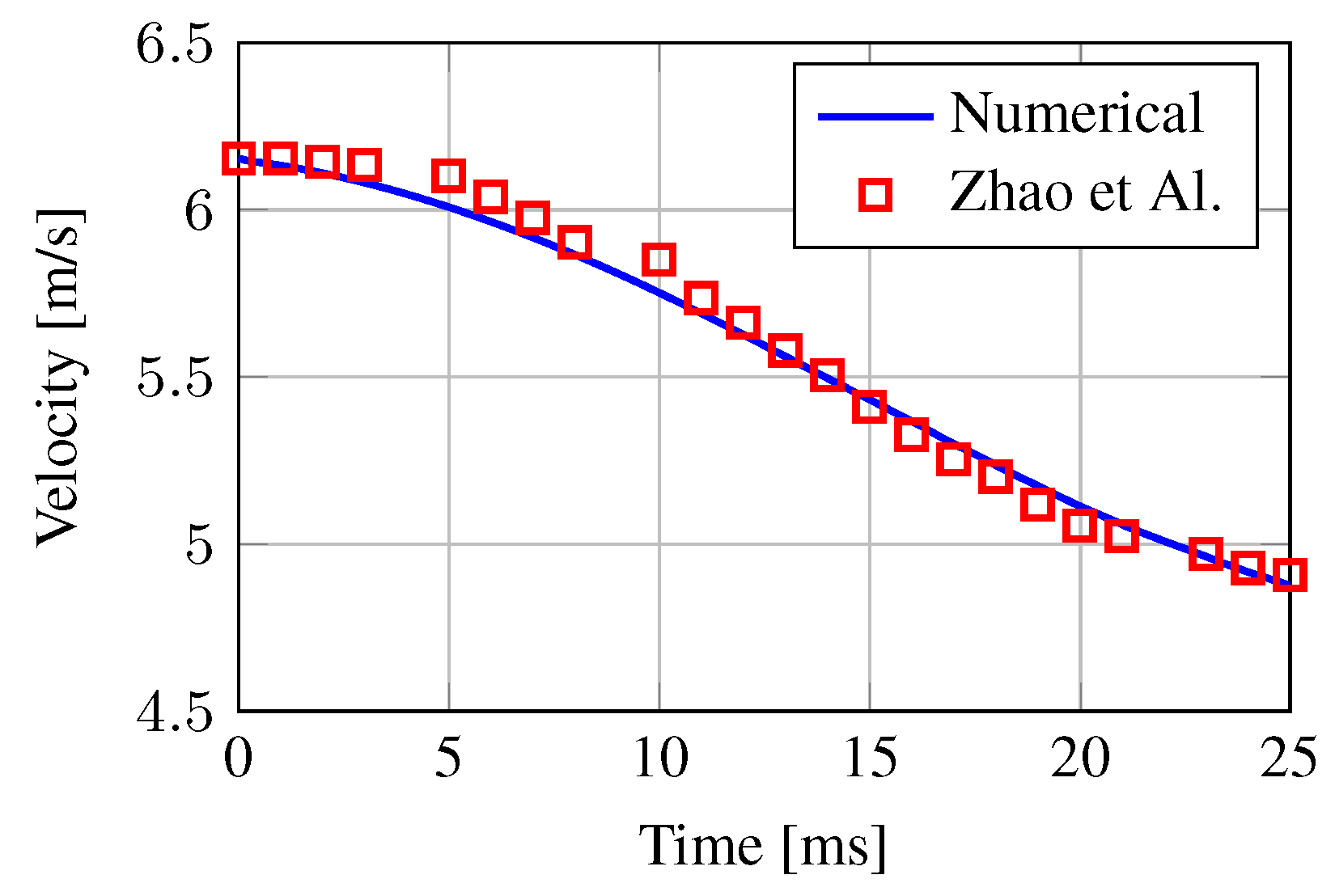
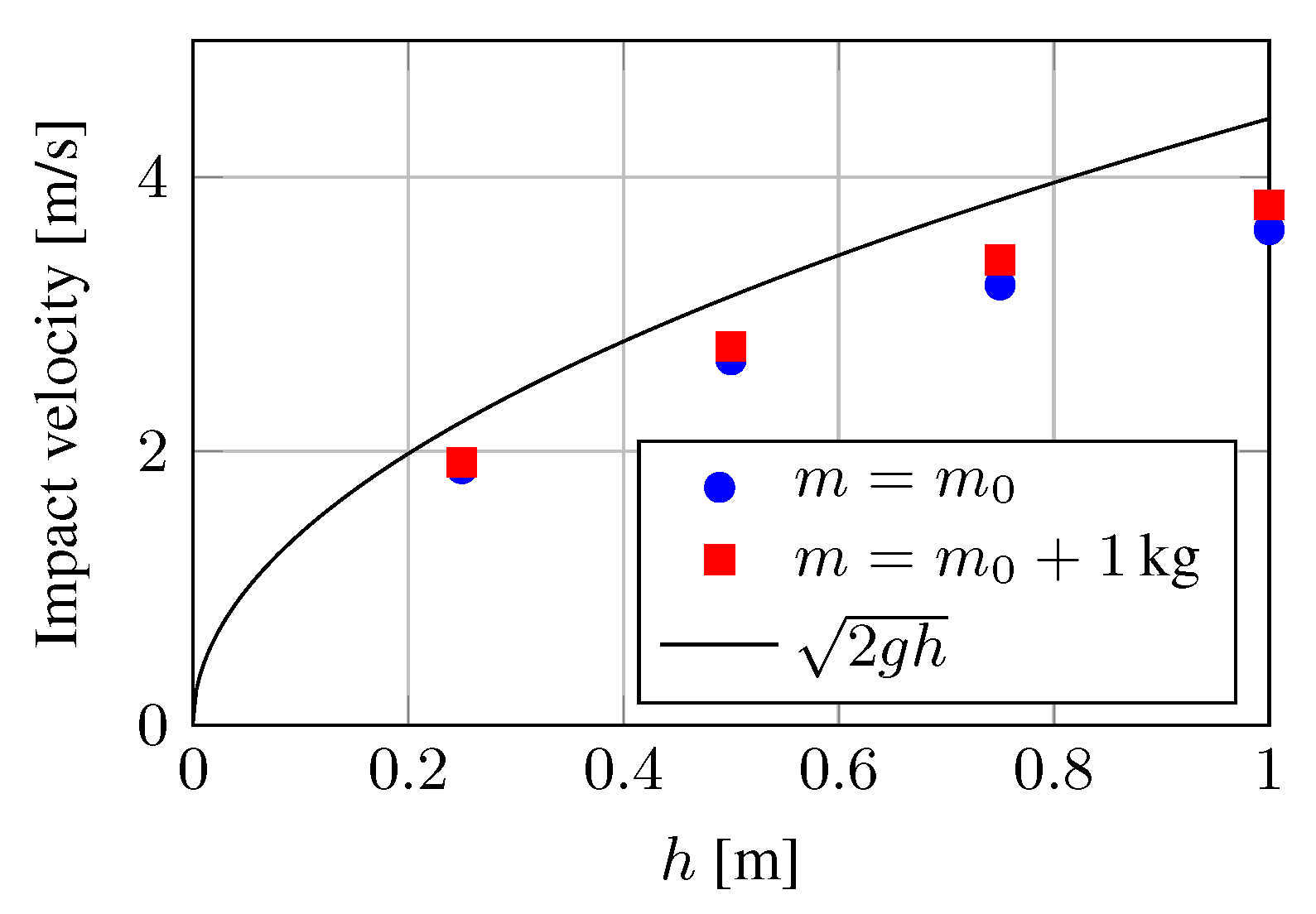
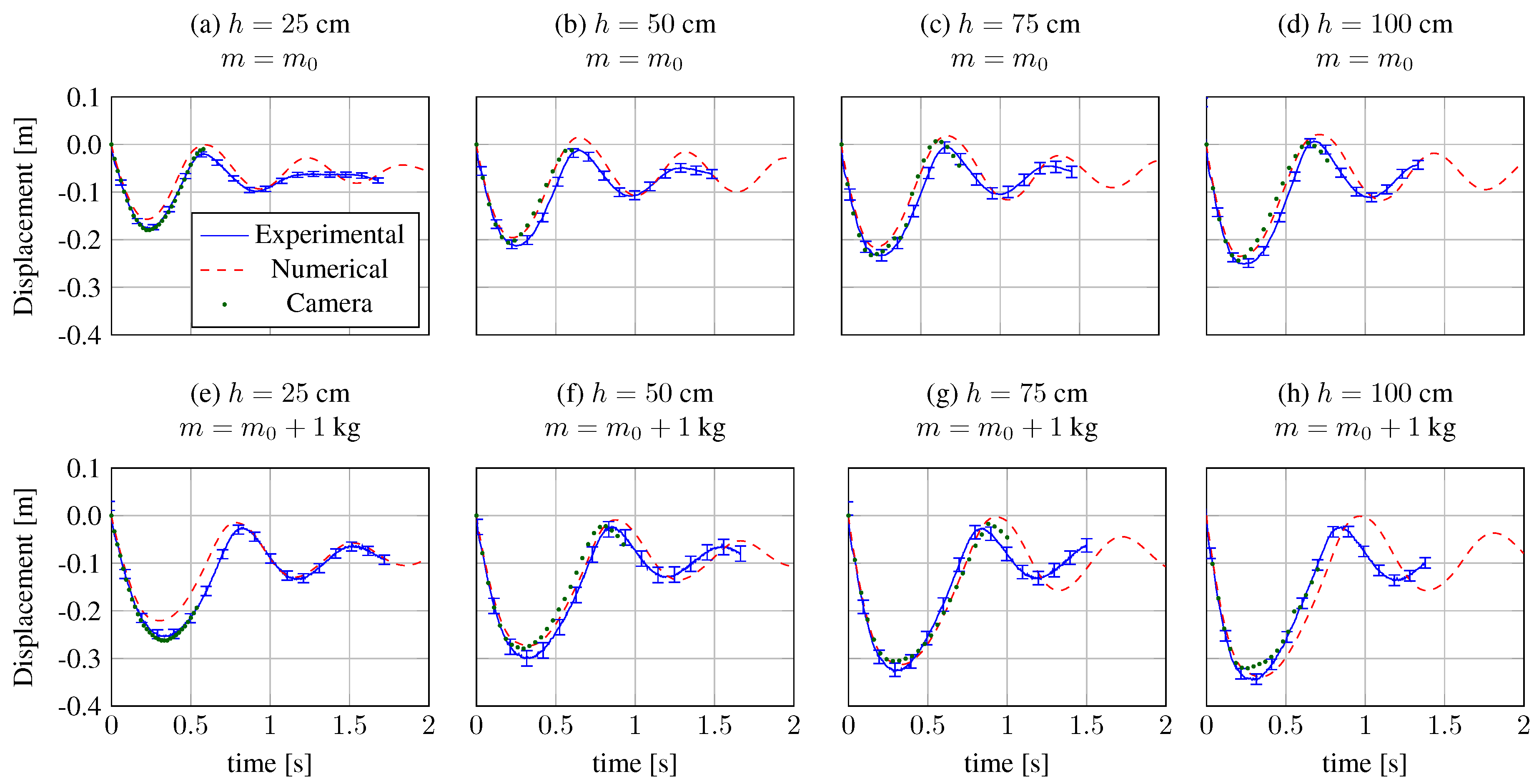
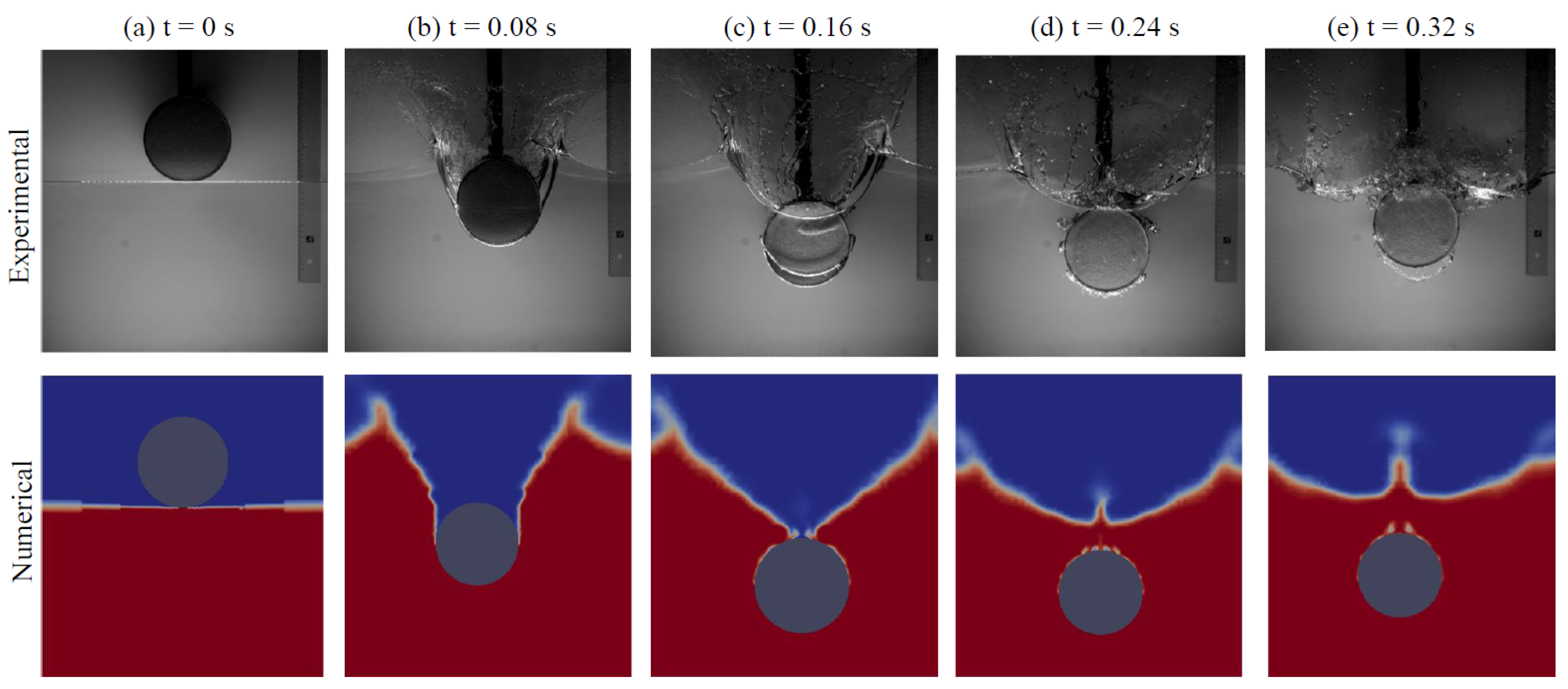
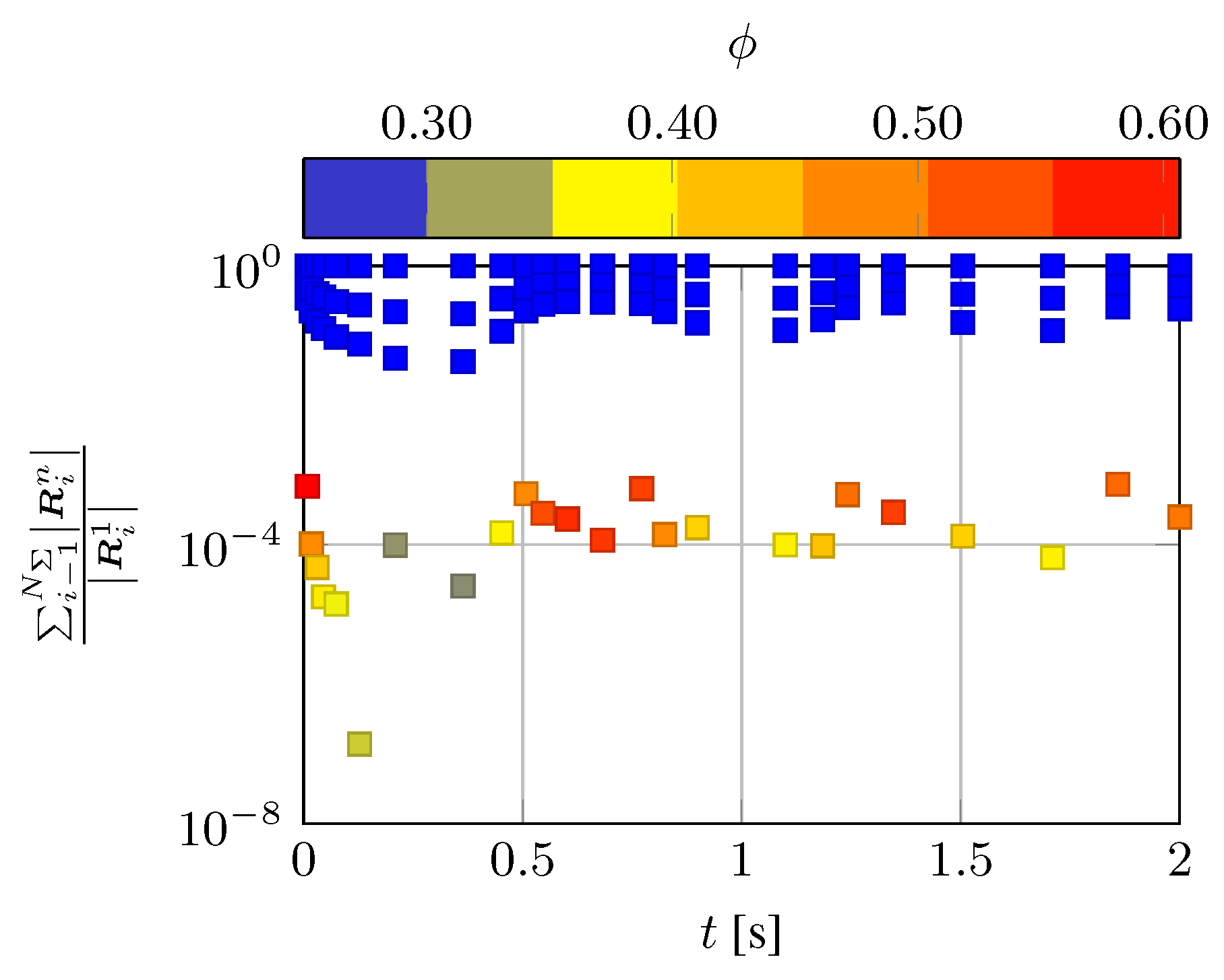
3.3.3. Results and Dicussion
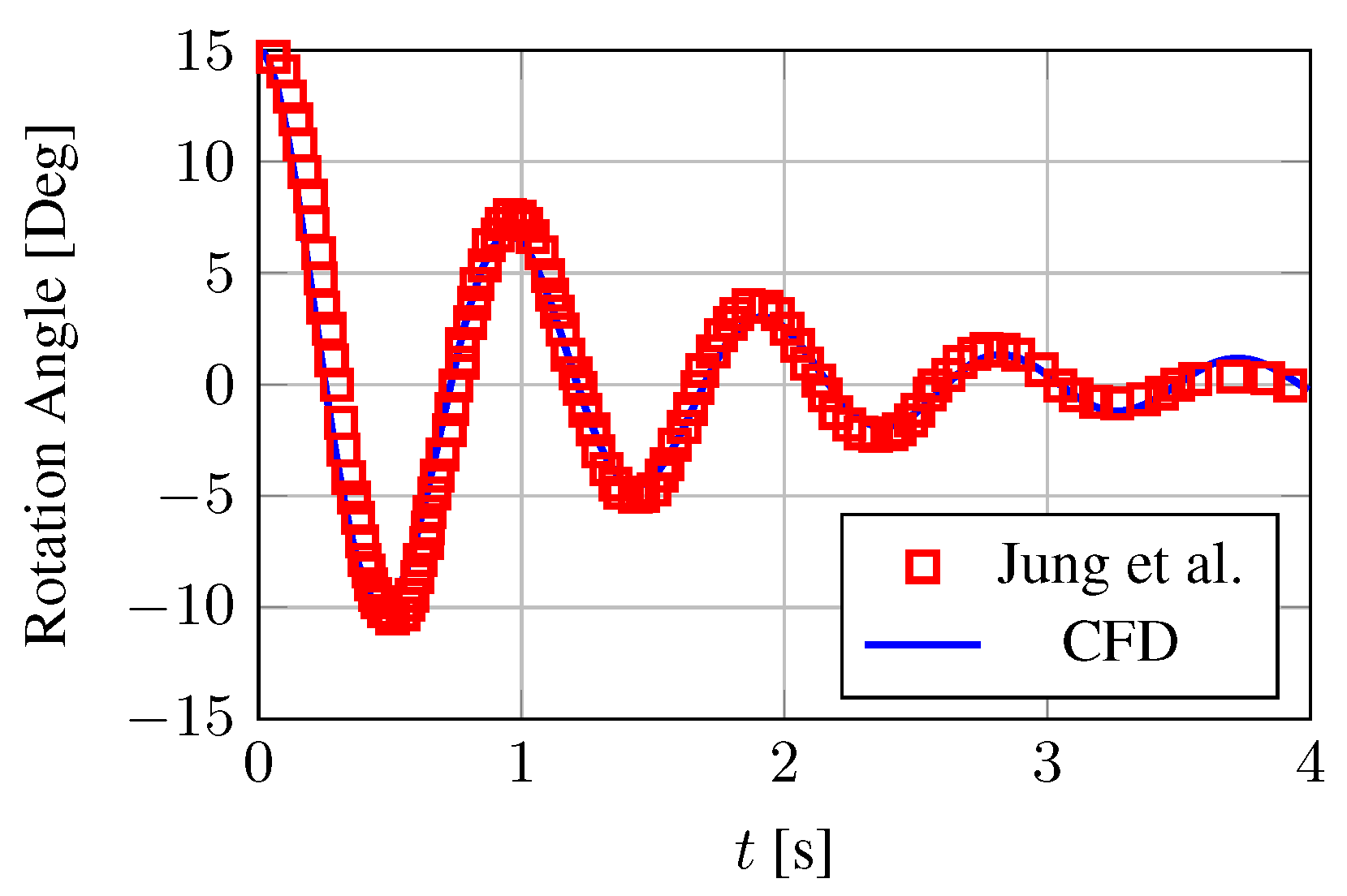
3.4. Roll Motion of a Rectangular Structure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Campbell, R.; Paterson, E. Fluid–structure interaction analysis of flexible turbomachinery. J. Fluids Struct. 2011, 27, 1376–1391. [Google Scholar] [CrossRef]
- Küttler, U.; Wall, W.A. Fixed-point fluid–structure interaction solvers with dynamic relaxation. Comput. Mech. 2008, 43, 61–72. [Google Scholar] [CrossRef]
- Montessori, A.; Falcucci, G. Lattice Boltzmann Modeling of Complex Flows for Engineering Applications; Morgan & Claypool Publishers: London, UK, 2018. [Google Scholar]
- Faltinsen, O.M. Hydroelastic slamming. J. Mar. Sci. Technol. 2000, 5, 49–65. [Google Scholar] [CrossRef]
- Wu, M.; Moan, T. Numerical prediction of wave-induced long-term extreme load effects in a flexible high-speed pentamaran. J. Mar. Sci. Technol. 2006, 11, 39–51. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G.; Zucchelli, A. Hydroelasticity in water-entry problems: Comparison between experimental and SPH results. Compos. Struct. 2012, 94, 532–539. [Google Scholar] [CrossRef]
- Abrate, S. Hull Slamming. Appl. Mech. Rev. 2013, 64, 060803. [Google Scholar] [CrossRef]
- De Rosis, A.; Falcucci, G.; Porfiri, M.; Ubertini, F.; Ubertini, S. Hydroelastic analysis of hull slamming coupling lattice Boltzmann and finite element methods. Comput. Struct. 2014, 138, 24–35. [Google Scholar] [CrossRef]
- Zarghami, A.; Falcucci, G.; Jannelli, E.; Succi, S.; Porfiri, M.; Ubertini, S. Lattice Boltzmann modeling of water entry problems. Int. J. Mod. Phys. C 2014, 25, 1441012. [Google Scholar] [CrossRef]
- Facci, A.L.; Panciroli, R.; Ubertini, S.; Porfiri, M. Assessment of PIV-based analysis of water entry problems through synthetic numerical datasets. J. Fluids Struct. 2015, 55, 484–500. [Google Scholar] [CrossRef]
- Panciroli, R.; Falcucci, G.; Erme, G.; De Santis, E.; Jannelli, E. Fluid-structure interaction during the water entry of flexible cylinders. AIP Conf. Proc. 2015, 1648, 570011. [Google Scholar]
- Zhao, X.; Gao, Y.; Cao, F.; Wang, X. Numerical modeling of wave interactions with coastal structures by a constrained interpolation profile/immersed boundary method. Int. J. Numer. Methods Fluids 2016, 81, 265–283. [Google Scholar] [CrossRef]
- De Tullio, M.; Cristallo, A.; Balaras, E.; Verzicco, R. Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 2009, 622, 259–290. [Google Scholar] [CrossRef]
- Chen, Z.; Shatara, S.; Tan, X. Modeling of biomimetic robotic fish propelled by an ionic polymer-metal composite caudal fin. IEEE/ASME Trans. Mechatron. 2010, 13, 519–529. [Google Scholar]
- Aureli, M.; Kopman, V.; Porfiri, M. Free-locomotion of underwater vehicles actuated by ionic polymer metal composites. IEEE/ASME Trans. Mechatron. 2010, 15, 603–614. [Google Scholar] [CrossRef]
- Erturk, A.; Delporte, G. Underwater thrust and power generation using flexible piezoelectric composites: An experimental investigation toward self-powered swimmer-sensor platforms. Smart Mater. Struct. 2011, 20, 125013. [Google Scholar] [CrossRef]
- Rosis, A.D.; Falcucci, G.; Ubertini, S.; Ubertini, F. Aeroelastic study of flexible flapping wings by a coupled lattice Boltzmann-finite element approach with immersed boundary method. J. Fluids Struct. 2014, 49, 516–533. [Google Scholar] [CrossRef]
- Amirante, D.; Hills, N.; Barnes, C. A moving mesh algorithm for aero-thermo-mechanical modelling in turbomachinery. Int. J. Numer. Methods Fluids 2012, 70, 1118–1138. [Google Scholar] [CrossRef]
- Falcucci, G.; Aureli, M.; Ubertini, S.; Porfiri, M. Transverse harmonic oscillations of laminae in viscous fluids: A lattice Boltzmann study. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2011, 369, 2456–2466. [Google Scholar] [CrossRef] [PubMed]
- Facci, A.L.; Porfiri, M. Nonlinear hydrodynamic damping of sharp-edged cantilevers in viscous fluids undergoing multi-harmonic base excitation. J. Appl. Phys. 2012, 112, 124908. [Google Scholar] [CrossRef]
- Facci, A.L.; Porfiri, M. Analysis of three-dimensional effects in oscillating cantilevers immersed in viscous fluids. J. Fluids Struct. 2013, 38, 205–222. [Google Scholar] [CrossRef]
- Brufau-Penella, J.; Puig-Vidal, M.; Giannone, P.; Graziani, S.; Strazzeri, S. Characterization of the harvesting capabilities of an ionic polymer metal composite device. Smart Mater. Struct. 2008, 17, 015009. [Google Scholar] [CrossRef]
- Aureli, M.; Prince, C.; Porfiri, M.; Peterson, S.D. Energy harvesting from base excitation of ionic polymer metal composites in fluid environments. Smart Mater. Struct. 2010, 19, 015003. [Google Scholar] [CrossRef]
- Biscarini, C. Computational fluid dynamics modelling of landslide generated water waves. Landslides 2010, 7, 117–124. [Google Scholar] [CrossRef]
- Fritz, H.; Hager, W.; Minor, H.E. Near field characteristics of landslide generated impulse waves. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 287–302. [Google Scholar] [CrossRef]
- Batra, R.C.; Porfiri, M.; Spinello, D. Review of modeling electrostatically actuated microelectromechanical systems. Smart Mater. Struct. 2007, 16, R23–R31. [Google Scholar] [CrossRef]
- Ihara, A.; Watanabe, H. On the flow around flexible plates, oscillating with large amplitude. J. Fluids Struct. 1994, 8, 601–619. [Google Scholar] [CrossRef]
- Kimber, M.; Garimella, S.V.; Raman, A. Local heat transfer coefficients induced by piezoelectrically actuated vibrating cantilevers. Trans. ASME J. Heat Transf. 2007, 129, 1168–1176. [Google Scholar] [CrossRef]
- Bidkar, R.A.; Kimber, M.; Raman, A.; Bajaj, A.K.; Garimella, S.V. Nonlinear aerodynamic damping of sharp-edged flexible beams oscillating at low Keulegan-Carpenter numbers. J. Fluid Mech. 2009, 634, 269–289. [Google Scholar] [CrossRef]
- Hay, A.; Leroyer, A.; Visonneau, M. H-adaptive Navier–Stokes simulations of free-surface flows around moving bodies. J. Mar. Sci. Technol. 2006, 11, 1–18. [Google Scholar] [CrossRef]
- Carcaterra, A.; Ciappi, E. Prediction of the compressible stage slamming force on rigid and elastic systems impacting on the water surface. Nonlinear Dyn. 2000, 21, 193–220. [Google Scholar] [CrossRef]
- Seng, S.; Jensen, J.J.; Pedersen, P.T. Numerical prediction of slamming loads. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2012, 226, 120–134. [Google Scholar] [CrossRef]
- Facci, A.L.; Porfiri, M.; Ubertini, S. Three-dimensional water entry of a solid body: A computational study. J. Fluids Struct. 2016, 66, 36–53. [Google Scholar] [CrossRef]
- Hermundstad, O.A.; Moan, T. Numerical and experimental analysis of bow flare slamming on a Ro–Ro vessel in regular oblique waves. J. Mar. Sci. Technol. 2005, 10, 105–122. [Google Scholar] [CrossRef]
- Panahi, R. Simulation of water-entry and water-exit problems using a moving mesh algorithm. J. Theor. Appl. Mech. 2012, 42, 79–92. [Google Scholar] [CrossRef]
- Uddin, E.; Sung, H.J. Simulation of flow-flexible body interactions with large deformation. Int. J. Numer. Methods Fluids 2012, 70, 1089–1102. [Google Scholar] [CrossRef]
- Zhang, Y.; Pin, F.; Yim, S. A heterogeneous flow model based on DD method for free surface fluid-structure interaction problems. Int. J. Numer. Methods Fluids 2014, 74, 292–312. [Google Scholar] [CrossRef]
- Eken, A.; Sahin, M. A parallel monolithic algorithm for the numerical simulation of large-scale fluid structure interaction problems. Int. J. Numer. Methods Fluids 2016, 80, 687–714. [Google Scholar] [CrossRef]
- Farhat, C.; Lesoinne, M.; Tallec, P.L. Load and motion transfer algorithms for fluid/structure interaction problems with non-matching discrete interfaces: Momentum and energy conservation, optimal discretization and application to aeroelasticity. Comput. Methods Appl. Mech. Eng. 1998, 157, 95–114. [Google Scholar] [CrossRef]
- Jung, K.H.; Chang, K.A.; Jo, H.J. Viscous effect on the roll motion of a rectangular structure. J. Eng. Mech. 2006, 132, 190–200. [Google Scholar] [CrossRef]
- Chen, Q.; Zang, J.; Dimakopoulos, A.S.; Kelly, D.M.; Williams, C.J. A Cartesian cut cell based two-way strong fluid–solid coupling algorithm for 2D floating bodies. J. Fluids Struct. 2016, 62, 252–271. [Google Scholar] [CrossRef]
- Cheon, J.S.; Jang, B.S.; Yim, K.H.; Lee, H.D.; Koo, B.Y.; Ju, H. A study on slamming pressure on a flat stiffened plate considering fluid-structure interaction. J. Mar. Sci. Technol. 2016, 21, 309–324. [Google Scholar] [CrossRef]
- Kassiotis, C. Nonlinear Fluid-Structure Interaction: A Partitioned Approach and Its Application through Component Technology. Ph.D. Thesis, Université Paris-Est, Champs-sur-Marne, France, 2009. [Google Scholar]
- Piperno, S.; Farhat, C. Partitioned procedures for the transient solution of coupled aeroelastic problems—Part II: Energy transfer analysis and three-dimensional applications. Comput. Methods Appl. Mech. Eng. 2001, 190, 3147–3170. [Google Scholar] [CrossRef]
- Habchi, C.; Russeil, S.; Bougeard, D.; Harion, J.L.; Lemenand, T.; Ghanem, A.; Della Valle, D.; Peerhossaini, H. Partitioned solver for strongly coupled fluid–structure interaction. Comput. Fluids 2013, 71, 306–319. [Google Scholar] [CrossRef]
- Causin, P.; Gerbeau, J.F.; Nobile, F. Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput. Methods Appl. Mech. Eng. 2005, 194, 4506–4527. [Google Scholar] [CrossRef]
- Förster, C.; Wall, W.A.; Ramm, E. Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 1278–1293. [Google Scholar] [CrossRef]
- Wood, C.; Gil, A.; Hassan, O.; Bonet, J. Partitioned block-Gauss–Seidel coupling for dynamic fluid–structure interaction. Comput. Struct. 2010, 88, 1367–1382. [Google Scholar] [CrossRef]
- Ángel Fernández, M.; Moubachir, M. A Newton method using exact jacobians for solving fluid-structure coupling. Comput. Struct. 2005, 83, 127–142. [Google Scholar] [CrossRef]
- Walhorn, E.; Kölke, A.; Hübner, B.; Dinkler, D. Fluid-structure coupling within a monolithic model involving free surface flows. Comput. Struct. 2005, 83, 2100–2111. [Google Scholar] [CrossRef]
- Degroote, J.; Bathe, K.J.; Vierendeels, J. Performance of a new partitioned procedure versus a monolithic procedure in fluid–structure interaction. Comput. Struct. 2009, 87, 793–801. [Google Scholar] [CrossRef]
- Scruggs, J.; Jacob, P. Harvesting ocean wave energy. Science 2009, 323, 1176–1178. [Google Scholar] [CrossRef]
- Wall, W.A.; Genkinger, S.; Ramm, E. A strong coupling partitioned approach for fluid–structure interaction with free surfaces. Comput. Fluids 2007, 36, 169–183. [Google Scholar] [CrossRef]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical simulation of fluid–structure interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- Potapov, S.; Maurel, B.; Combescure, A.; Fabis, J. Modeling accidental-type fluid–structure interaction problems with the SPH method. Comput. Struct. 2009, 87, 721–734. [Google Scholar] [CrossRef]
- Di Francesco, S.; Biscarini, C.; Manciola, P. Numerical simulation of water free-surface flows through a front-tracking lattice Boltzmann approach. J. Hydroinform. 2015, 17, 1–6. [Google Scholar] [CrossRef]
- Hu, C.; Kashiwagi, M. A CIP-based method for numerical simulations of violent free-surface flows. J. Mar. Sci. Technol. 2004, 9, 143–157. [Google Scholar] [CrossRef]
- Takizawa, K.; Yabe, T.; Tsugawa, Y.; Tezduyar, T.E.; Mizoe, H. Computation of free-surface flows and fluid–object interactions with the CIP method based on adaptive meshless soroban grids. Comput. Mech. 2007, 40, 167–183. [Google Scholar] [CrossRef]
- Aly, A.M.; Asai, M.; Sonoda, Y. Simulation of free falling rigid body into water by a stabilized incompressible SPH method. Ocean Syst. Eng. 2011, 1, 207–222. [Google Scholar] [CrossRef]
- Vandamme, J.; Zou, Q.; Reeve, D.E. Modeling floating object entry and exit using smoothed particle hydrodynamics. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 213–224. [Google Scholar] [CrossRef]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993; Volume 1. [Google Scholar]
- Korobkin, A. Water impact problems in ship hydrodynamics. In Advances in Marine Hydrodynamics; Computational Mechanics Publications: Norwich, UK, 1996; pp. 323–371. [Google Scholar]
- Carrica, P.; Huang, J.; Noack, R.; Kaushik, D.; Smith, B.; Stern, F. Large-scale DES computations of the forward speed diffraction and pitch and heave problems for a surface combatant. Comput. Fluids 2010, 39, 1095–1111. [Google Scholar] [CrossRef]
- Seddon, C.; Moatamedi, M. Review of water entry with applications to aerospace structures. Int. J. Impact Eng. 2006, 32, 1045–1067. [Google Scholar] [CrossRef]
- Extend Project. 2016. Available online: http://www.extend-project.de/ (accessed on 19 May 2017).
- Greenshields, C.J. OpenFOAM User’s Guide, 2.4.0 ed.; OpenFOAM Foundation Ltd.: London, UK, 2015. [Google Scholar]
- Rider, W.J.; Kothe, D.B. Reconstructing Volume Tracking. J. Comput. Phys. 1998, 141, 112–152. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamiccs of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, University of London, London, UK, 2002. [Google Scholar]
- Cavalagli, N.; Biscarini, C.; Facci, A.; Ubertini, F.; Ubertini, S. Experimental and numerical analysis of energy dissipation in a sloshing absorber. J. Fluids Struct. 2017, 68, 466–481. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Periç, M. Computational Methods for Fluid Dynamics, 3rd rev. ed.; Springer: Berlin, Germany; Tokyo, Japan, 2002. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for Finite Volume Method with Applications to Fluid Flow. Ph.D. Thesis, University of London, London, UK, 1996. [Google Scholar]
- Jasak, H. Dynamic Mesh Handling in OpenFOAM. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2008. [Google Scholar]
- Jasak, H.; Tukovic, Z. Automatic Mesh Motion for the Unstructured Finite Volume Method. Trans. FAMENA 2007, 30, 1–18. [Google Scholar]
- Kassiotis, C. Which Strategy to Move the Mesh in the Computational Fluid Dynamic Code OpenFOAM; Technical Report; WiRe, LMT-Cachan: Braunschweig, Germany, 2008; Available online: http://perso.crans.org/kassiotis/openfoam/movingmesh.pdf (accessed on 19 May 2017).
- Haug, E.J. Computer Aided Kinematics and Dynamics of Mechanical Systems; Allyn and Bacon: Boston, MA, USA, 1989; Volume 1. [Google Scholar]
- Sherif, K.; Nachbagauer, K.; Steiner, W. On the rotational equations of motion in rigid body dynamics when using Euler parameters. Nonlinear Dyn. 2015, 81, 343–352. [Google Scholar] [CrossRef]
- Zhao, R.; Faltinsen, O.; Aarsnes, J. Water entry of arbitrary two-dimensional sections with and without flow separation. In Proceedings of the 21st Symposium on Naval Hydrodynamics, Trondheim, Norway, 24–28 June 1996; The National Academies Press: Washington, DC, USA, 1996; pp. 408–423. [Google Scholar]
- Panciroli, R.; Shams, A.; Porfiri, M. Experiments on the water entry of curved wedges: High speed imaging and particle image velocimetry. Ocean Eng. 2015, 94, 213–222. [Google Scholar] [CrossRef]
- Jalalisendi, M.; Osma, S.J.; Porfiri, M. Three-dimensional water entry of a solid body: A particle image velocimetry study. J. Fluids Struct. 2015, 59, 85–102. [Google Scholar] [CrossRef]
- Russo, S.; Biscarini, C.; Facci, A.L.; Falcucci, G.; Jannelli, E.; Ubertini, S. Experimental assessment of buoyant cylinder impacts through high-speed image acquisition. J. Mar. Sci. Technol. 2017, 23, 67–80. [Google Scholar] [CrossRef]
- NationalInstruments. Version 2014. Available online: www.ni.com/labview (accessed on 19 May 2017).
- Facci, A.L.; Ubertini, S. Numerical assessment of similitude parameters and dimensional analysis for water entry problems. Math. Probl. Eng. 2015, 2015, 324961. [Google Scholar] [CrossRef]
- Panciroli, R.; Biscarini, C.; Falcucci, G.; Jannelli, E.; Ubertini, S. Live monitoring of the distributed strain field in impulsive events through fiber Bragg gratings. J. Fluids Struct. 2016, 61, 60–75. [Google Scholar] [CrossRef]
- Russo, S.; Krastev, V.; Jannelli, E.; Falcucci, G. Design and optimization of an experimental test bench for the study of impulsive fluid-structure interactions. AIP Conf. Proc. 2016, 1738, 270020. [Google Scholar]
- Goggins, J.; Finnegan, W. Numerical simulation of linear water waves and wave-structure interaction. Ocean Eng. 2012, 43, 23–31. [Google Scholar]
- Xing-Kaeding, Y.; Jensen, G.; Technical University of Hamburg-Harburg; Hadžić, I.; Perić, M.; CD Adapco Group. Simulation of flow-induced ship motions in waves using a RANSE method. Ship Technol. Res. 2004, 51, 56–68. [Google Scholar] [CrossRef]
- Hadžić, I.; Hennig, J.; Perić, M.; Xing-Kaeding, Y. Computation of flow-induced motion of floating bodies. Appl. Math. Model. 2005, 29, 1196–1210. [Google Scholar] [CrossRef]
- Yan, S.; Ma, Q. Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using the QALE-FEM method. J. Comput. Phys. 2007, 221, 666–692. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]



| h [m] | ||||
| [%] |
| + 1 kg | ||
|---|---|---|
| m | ||
| m | ||
| m | ||
| m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Facci, A.L.; Falcucci, G.; Agresta, A.; Biscarini, C.; Jannelli, E.; Ubertini, S. Fluid Structure Interaction of Buoyant Bodies with Free Surface Flows: Computational Modelling and Experimental Validation. Water 2019, 11, 1048. https://doi.org/10.3390/w11051048
Facci AL, Falcucci G, Agresta A, Biscarini C, Jannelli E, Ubertini S. Fluid Structure Interaction of Buoyant Bodies with Free Surface Flows: Computational Modelling and Experimental Validation. Water. 2019; 11(5):1048. https://doi.org/10.3390/w11051048
Chicago/Turabian StyleFacci, Andrea Luigi, Giacomo Falcucci, Antonio Agresta, Chiara Biscarini, Elio Jannelli, and Stefano Ubertini. 2019. "Fluid Structure Interaction of Buoyant Bodies with Free Surface Flows: Computational Modelling and Experimental Validation" Water 11, no. 5: 1048. https://doi.org/10.3390/w11051048
APA StyleFacci, A. L., Falcucci, G., Agresta, A., Biscarini, C., Jannelli, E., & Ubertini, S. (2019). Fluid Structure Interaction of Buoyant Bodies with Free Surface Flows: Computational Modelling and Experimental Validation. Water, 11(5), 1048. https://doi.org/10.3390/w11051048








