Abstract
Most hydrological models have fixed structures and their calibrations are typified by a conventional approach in which the overall water balance closure is considered (without a step-wise focus on sub-flows’ variation). Eventually, hydrological modelers are confronted with the difficulty of ensuring both the observed high flows and low flows are accurately reproduced in a single calibration. This study introduced Hydrological Model focusing on Sub-flows’ Variation (HMSV). Calibration of HMSV follows a carefully designed framework comprising sub-flow’s separation, modeling of sub-flows, and checking validity of hydrological extremes. The introduced model and calibration framework were tested using hydro-meteorological data from the Blue Nile Basin of Ethiopia in Africa. When the conventional calibration approach was adopted through automatic optimization strategy, results from the HMSV were found highly comparable with those of five internationally well recognized hydrological models (AWBM, IHACRES, SACRAMENTO, SIMHYD, and TANK). The new framework enhanced the HMSV performance for reproducing quantiles of both high flows and low flows. The combination of flow separation and step-wise calibration of hydrological model against sub-flows enhances the modeler’s physical insight in identifying which areas need focus in modeling to obtain meaningful simulation results, especially of extreme events. The link for downloading the HMSV is provided.
1. Introduction
Several hydrological models exist including those which are fully distributed process-based or conceptual in nature. Fully distributed models have detailed representation of hydrological processes; however, they require large amount of input data and are difficult to optimally calibrate due to their structural complexity and over-parameterization. On the other hand, conceptual models are simpler in their structures and have fewer parameters than the physically-based models. Examples of hydrological models include the Australian Water Balance Model (AWBM) [1], Identification of unit Hydrographs and Component Flows from Rainfall, Evaporation and Stream flow data (IHACRES) model [2], Sacramento (SAC) model [3], SIMHYD which is the simplified version of HYDROLOG [4], TANK model [5], Nedbør-Afstrømnings Model (NAM) [6,7], Precipitation Runoff Modeling System (PRMS) [8], and the Probability Distribution Model [9]. Even using conceptual models, a hydrological modeler is always confronted with the difficulty of ensuring the model accurately reproduces observed high and low flows simultaneously in a single calibration. This is because most of the hydrological models are structurally designed to perform better in capturing flooding events than drought conditions [10,11]. Furthermore, in a conventional modeling approach, objective function used for calibration is constrained to an overall water balance, and this gives more weights to high flows than low flows [11].
The difficulty in reproducing both high flows and low flows in a single calibration stems from the fact that available hydrological models have their structures fixed and they tend to be calibrated against the overall observed flow (not sub-flows). For a model to simultaneously capture both high flows and low flows in a single calibration, the model should be tailored towards the variation of each of the sub-flows. In this way, the quick flow can be modeled with respect to high flows while baseflow is taken to control the variation of low flows. Step-wise calibrations of the model against various streamflow components enables the modeler to make use of his or her physical insight to identify the major possible sources of bias (which can be with respect to baseflow, interflow, or overland flow) in reproducing the observed flow. This gives the modeler a reasonable area where to focus in the model calibration for more reasonable (and meaningful) modeling results than in the case when the total flow is considered in a lumped way (without separation of the various components of the flow).
Therefore this study aimed at introducing and testing the suitability of a Hydrological Model focused on Sub-flows’ Variation (HMSV). The calibration of the HMSV follows a carefully designed framework which depends on separation of sub-flows, modeling of sub-flows and checking the validity of hydrological extremes.
2. Materials and Methods
2.1. Separation of Sub-Flows
From the observed discharge Xo of size n, the baseflow Xbf can be separated using the following steps:
- (a)
- select a time scale t1 which denotes the baseflow filtering constant such that w = 0.5 × (1 + t1) and w = 0.5 × t1 in the cases when t1 is odd and even, respectively,
- (b)
- if Xo comprises a subset xo from the pth to the uth value of Xo, obtain the filter term b using:where hj is the size of the sub-sample in the jth time slice (i.e., xo from the pth to the uth data value), α1 denotes the baseflow coefficient, and the terms p and u can be varied for j = 1, 2, ..., n as follows:It is vital to note that the application of Equations (1) and (2) is done in a step-wise way. For instance, if t1 = 10, it means w = 5. Now, we have to vary j from 1 to n, and let us assume that n = 100. Each time a new j is being considered, the terms p and u of Equation (1) are determined based on the three conditions given in Equation (2). Using t1 = 10, w = 5, and n = 100, below is an illustration of how the terms p and u can be determined for every new value of j which is varied by setting j = 1, 2, ..., 100.
- (i)
- If j = 1, it means j < w and thus, using the first conditional part of Equation (2), p = 1, and u = 10 + 1 – 5 – 1 = 5. This means that for j = 1, the summation of the flow xo according to Equation (1) is done from the 1st to the 5th value.
- (ii)
- If j = 15, it means j > w and thus, using the second conditional component of Equation (2), p = 15 – 5 + 1 = 11, and u = 15 + 5 = 20. This means that for j = 15, the summation of the flow xo based on Equation (1) is done from the 11th to the 20th value.
- (iii)
- If j = 96, it means j > (n − w) and j ≤ n; therefore, using the third conditional part of Equation (2), p = 96 – 5 + 1 = 92, and u = 100. This means that for j = 96, the summation of the flow xo according to Equation (1) is done from the 92nd to the 100th value.
- (c)
- for j = 1, 2, ..., n, at the time step j, if b(j) < xo(j), xbf (j) = b(j), otherwise, xbf (j) = xo(j), and the quick flow component (Xqf) of Xo can be given by xqf (j) = xo(j) − xbf (j).
To separate the Xqf into interflow (Xif) and overland flow (Xof), the following steps can be taken:
- (a)
- select the time scale t2 which denotes the interflow filtering constant and let w = 0.5 × (1 + t2) and w = 0.5 × t2 in the cases when t2 is odd and even, respectively,
- (b)
- compute the interflow component c using:where α2 denotes the interflow coefficient, h(j) is the sub-sample size in the jth time slice (i.e., Xqf from the pth to the uth data point), and for j = 1, 2, ..., n, the terms p and u can be varied as in Equation (2). The application of Equation (3) is in a similar way as described for Equation (1).
- (c)
- for j = 1, 2, ..., n, if c(j) < xqf (j), xif (j) = c(j), otherwise, xif (j) = xqf (j), and the overland flow component (Xof) of Xo at the time step j can be given by xof (j) = xqf (j) − xif (j).
Though optional to compute for the Xof, we have t3 and α3 denoting the overland flow filtering constant, and overland flow coefficient, respectively. The unit of the t1 (which should be similar to that of t2 or t3) follows the resolution of the river flow the components of which are being separated. For instance, if the flow series is of daily time scale, the t1 (or t2 or t3) would be in days. From a typical hydrograph, the filtering constant may be expected to vary in magnitude from the highest to the lowest for Xbf, Xif and Xof, respectively. It can be assumed that the river flow during the dry weather period comes from baseflow. The implication of this assumption is that, lateral flows (for instance from households) are significantly small and negligible.
Figure 1 shows the diagrammatic illustration of the flow separation procedure. When baseflow (Xbf) is filtered from the total flow, what remains is the quick flow (Xqf). Similarly, when interflow (Xif) is extracted from the Xqf, only the overland flow (Xof) remains. It means that the most important parameters are t1, t2, α1, and α2. Therefore, just like the parameters t3 and α3 of the Xof, the quick flow filtering constant (tq) and the quick flow coefficient (αq) are optional.
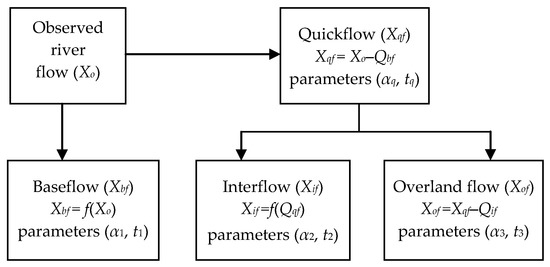
Figure 1.
Flow separation procedure.
2.2. Rainfall-Runoff Modeling
2.2.1. HMSV Structure Identification
A general structure of the HMSV is shown in Figure 2. The model requires precipitation (P), and potential evapotranspiration (Epot) as the input data. The requirements expected to be met by the precipitation include: (i) satisfying evapotranspiration demand, (ii) replenishing soil moisture, and generation of runoff from the excess amount. The HMSV splits runoff into simulated baseflow (Qbf), interflow (Qif) and overland flow (Qof). After the evaporation demand is met from the time-variable meteorological model inputs, the various sub-flows are derived as linear functions of the soil moisture storage. Exponential function could also be used in the generation of sub-flows. The simulated total runoff (Qsim), as the HMSV output, is the sum of the various flow components. The mathematical equations describing how the HMSV considers actual evapotranspiration (Eact), and soil moisture (S) to derive model outputs are presented next.
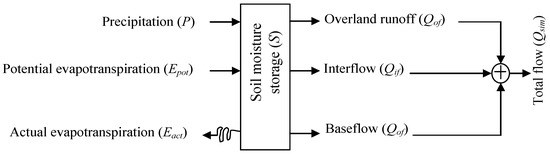
Figure 2.
Schematic representation of Hydrological Model focusing on Sub-flows’ Variation (HMSV).
Soil Moisture Storage
Let the current and previous soil moisture storage deficits be denoted by S(t), and S(t–1), respectively. The model adds or subtracts moisture from the soil water storage based on the magnitude of P(t) and Epot(t) such that:
where Smax denotes the maximum limit of soil moisture storage deficit (mm/day).
Evapotranspiration
In the HMSV, Eact is computed as a function of Epot based on the assumption that: (i) Eact occurs at a potential rate when water storage is zero, and (ii) Eact is zero when the storage deficit is at the maximum limit. Apart from the assumed cases,
and when the evaporation demand is met, the current runoff is generated as a function of the soil moisture at the previous time step.
Runoff
In the HMSV, it is assumed that Qbf (t) and Qif (t) linearly depend on the S(t–1). It is also possible that the dependence of Qbf (t) and Qif (t) on the S(t–1) may be in an exponential way. For the generation of the Qof (t), it is vital to note that when the moisture content is high (say, close to field capacity), the infiltration reduces, and the fraction of the precipitation that contributes to runoff is greater than that required to replenish the soil moisture storage. Therefore, Qof (t) depends on both the antecedent soil moisture state S(t–1) as well as P(t) and Epot (t) which are compounded into another term N(t) using
The following steps can be adopted to derive runoff:
- (1)
- To compute Qbf, select baseflow recession constant ta. Apply Equation (1) to soil moisture (S) instead of xo while replacing t1 with ta in Equations (1) and (2) to obtain instead of b.
- (2)
- To compute Qif, chose interflow recession constant tb. Apply Equation (1) to S instead of xo while replacing t1 with tb in Equations (1) and (2) to obtain in the place of b.
- (3)
- For Qof, chose constants tu and tv. By applying Equation (1) to S, replace t1 with tu in Equations (1) and (2) to obtain instead of b. Finally to the series N of Equation (7), apply Equation (1) while replacing t1 with tv in Equations (1) and (2) to obtain in the place of b.
The various modeled sub-flows can be computed using:
where a1 is baseflow parameter, a2 denotes interflow parameter, and overland flow has parameters a3 and c3. A cursory look at the equations can reveal that the term characterizes the baseflow coefficient. Similarly, the term comprises the interflow coefficient. However, overland coefficient is in terms of and .
To convert the various flow components from mm/day to m3/s, each of the sub-flows Qbf, Qif, and Qof, from Equations (8)–(10), respectively, is multiplied by (CA/86.4) where CA is the catchment area in km2. Finally, the model-based total flow (Qsim, m3/s) is computed using . Additional to the total runoff, there may (in some cases) be a constant or minimum river flow (Qmin) to account for any returns, abstractions, etc.
Initial Conditions
To obtain reasonable results, many rainfall-runoff models tend to require long “warm-up” periods. To avoid this, the HMSV considers initial model states. The antecedent soil moisture storage (S0), and initial simulated discharge (Qs0) are assumed to characterize catchment preconditions. To initialize the model simulation, Qs0 is assumed to be equal to the initial observed value. However, the value of S0 is required to be given by the user.
2.2.2. HMSV Calibration Framework
Figure 3 shows a framework through which the HMSV can be calibrated in a step-wise way. This calibration strategy is two-fold. Firstly, the preliminary calibration is done against sub-flows to yield satisfactory performance at least with respect to the mean flow conditions. To do so,
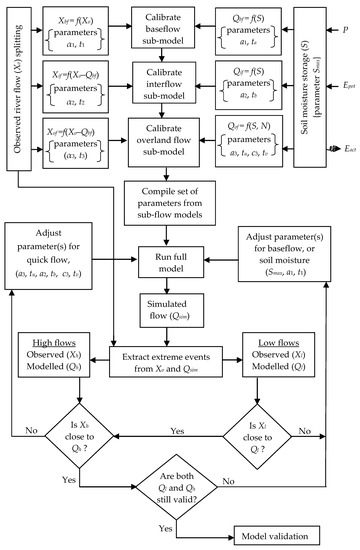
Figure 3.
Framework for model calibration.
- (1)
- the observed flow (Xo) is separated into various sub-flows including baseflow (Xbf), interflow (Xif), and overland flow (Xof),
- (2)
- using the baseflow sub-model, the modeled baseflow (Qbf) is calibrated against Xbf,
- (3)
- using the interflow sub-model, the modeled interflow (Qif) is calibrated against Xif,
- (4)
- using the overland sub-model, the modeled overland flow (Qof) is calibrated against Xof,
- (5)
- the parameters from the various sub-flow models are combined and used to run the full model from which total simulated flow (Qsim) is obtained.
The second part of the calibration strategy deals with fine-tuning the model to capture hydrological extremes, and the steps that can be taken include the following:
- (i)
- Hydrological extremes are extracted from both observed river flow (Xo) and simulated flow (Xsim). Here, the Peak Over Threshold (POT) approach can be adopted for extraction of the hydrological extremes (see Appendix A for details). It is important to note that the POT events from both Xo and Xsim should also be extracted using the same set of parameters stipulated to define the independency criteria. If the data for calibration is long enough (say 30 years or more), annual maxima and minima series could also be used for the checking the validity of the hydrological extremes.
- (ii)
- If the observed (Xl) and modeled (Ql) low flow quantiles are not comparable, parameter(s) which control baseflow generation can be adjusted to obtain new simulated flow. If Xl and Ql are comparable, focus is thereafter turned to high flows according to step (iii).
- (iii)
- To minimize the mismatch between the observed (Xh) and modeled (Qh) high flow quantiles, parameter(s) which control soil moisture and quick flow (interflow and overland flow) runoff generation can be adjusted, and when the full model is run, new simulated flow series is obtained.
- (iv)
- It is possible that Step (iii) can lead to some increase in the mismatch between the observed (Xl) and modeled (Ql) low flow quantiles based on Step (ii). Therefore, at this point, again, it is important to check on the validity of both high flows and low flows and some parameters may also be changed if need be.
- (v)
- The final simulated series is the model-based flow which reasonably reproduces both high and low flow quantiles.
2.3. Case Study
2.3.1. Data and Study Area
For illustrative purpose, the introduced framework was tested using data from the upper Blue Nile basin (Figure 4) in Ethiopia. Quality controlled hydro-meteorological data (including river flow observed at El Diem, as well as potential evapotranspiration and rainfall over and around the basin) were obtained from a previous study [11]. Each variable (or model input series) was from 1980 to 2000 and of daily temporal resolution. The catchment area upstream of El Diem is 176,000 km2. The rainfall stations labeled 1 to 7 are located at Bahr Dar, Debre Markos, Gonder, Addis Ababa Bole, Kombolcha, Jimma, and Gore, respectively. The corresponding coefficients of variation of the daily rainfall at these stations were 1.30, 1.00, 1.21, 1.02, 1.11, 1.92, 1.95, and 1.29. Thiessen polygon [12] was used to obtain basin-wide rainfall.
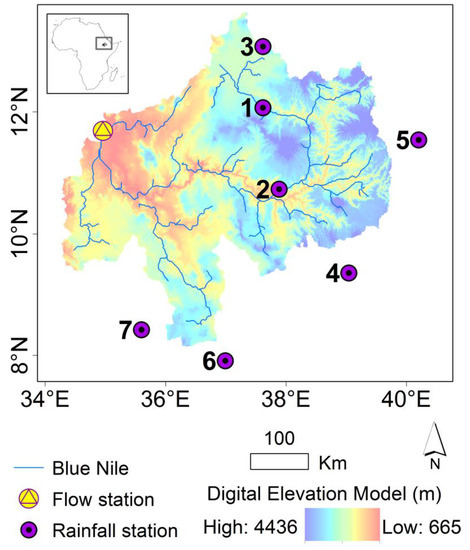
Figure 4.
The upper Blue Nile basin.
2.3.2. Rainfall-Runoff Modeling
Rainfall-runoff modeling was done using the hydro-meteorological data described in Section 2.3.1. For the purpose of comparison of HMSV results, outputs from five internationally well-known hydrological models were considered. These models include TANK model [5], SAC model [3], the AWBM [1], IHACRES [2], and SIMHYD [4]. The outputs from these models were obtained from a previous study by [11] in which the AWBM, TANK, SAC, and SIMHYD were optimized using the shuffled complex evolution [13]. The shuffled complex evolution evolves a number of potential solutions towards the region of the global optimum of the objective function by combining simplex method, competitive evolution, controlled random search, and complex shuffling strategies. For IHACRES, an automation of the calibration following Croke et al. [14] was two-fold. Firstly, linear module calibration was done based on the cross-correlation to calculate the delay between rainfall and stream flow. In the second step, the best parameter set was obtained using the non-linear module calibration. Like for other models, to eliminate the influence of subjectivity in changing of parameters for the introduced model, the HMSV was calibration strategy used was based on the Generalized Likelihood Uncertainty Estimation (GLUE) of Beven and Binley [15]. In the GLUE procedure (which is actually a Bayesian approach), the output (posterior) distribution is inferred from simulations based on parameters’ sets randomized from the prior distribution. Here, the upper and lower limits of parameters were first stipulated. Secondly, several (say, 2000) sets of parameters were randomized. Thirdly, the HMSV was run using each set of parameters. Finally, the optimal parameters were taken as those in the set which yielded the best value of the objective function.
For each of the six models, the calibration using automatic optimization was done based on daily series from 1 January 1980 to 31 December 1990. However, model validation was performed using daily data from 1 January 1991 to 31 December 2000. Nash-Sutcliffe Efficiency (NSE) [16] was used as the optimization objective function in the calibration of each model. NSE was also used to assess the statistical “goodness-of-fit” for both calibration and validation periods. Other statistical “goodness-of-fit” metrics were the correlation between the modeled (Qsim) and observed (X0) flow, Model Average Bias (MAB), and RRM which denotes the Ratio of the Root mean squared error to the Maximum event (Xmax) of the X0. Because the root mean squared error can be so large compared with the MAB, the RRM is small and has no unit. Considering X0 and Qsim,
where is the mean of the X0’s and n is as defined for Equation (1).
2.3.3. Comparison of Conventional Approach and New Framework for Calibration
The calibration in which the entire set of parameters are used to run the full model (not sub-flow models) is herein taken to denote the conventional approach. In the new framework as already highlighted in Figure 3, sub-models of baseflow, interflow, and overland flow are first calibrated in a step-wise way (against filtered sub-flows) to populate the full set of parameters required to run the full model.
The HMSV was calibrated using both the conventional approach and introduced framework. In each case, the GLUE technique was used to optimize the HMSV parameters. The calibration for the new framework was two-fold (see Section 2.2.2). The first case of the calibration which is analogous to the conventional approach comprised the use of NSE (Equation (11)) as the objective function. In the second step, the MAB (Equation (12)) was used as the objective function to reduce the mismatch between observed and modeled quantiles. The best set of parameters for the conventional approach and new framework was that which yielded the highest NSE and lowest MAB, respectively. Comparison of results from the introduced and conventional frameworks of calibration was statistically made in terms of NSE, MAB, RRM, and correlation. Graphically, comparison was made using observed and simulated maximum flow in each year, and minimum flow in each year. Frequency analyses based on the observed and simulated flows were compared based on the POT approach of extracting hydrological extremes (see Appendix A for details).
2.3.4. Comparison of HMSV and Conventional Models
Results from HMSV, AWBM, SAC, IHACRES, TANK, and SIMHYD obtained based on calibration using conventional framework were compared in terms of correlation, NSE, MAB, and RRM.
To determine which of the six models exhibited the best performance,
- (i)
- models were ranked from 1 to 6 based on the NSE values. The ranking was done such that ranks 1 and 6 were for the best and worst models, respectively. This procedure was done separately for calibration and validation periods as well as considering the full data period.
- (ii)
- just like in (i), the models were ranked based on MAB. The model with the lowest (highest) MAB was given rank 1 (6) denoting the best (worst) model. Again, this procedure was separately done for calibration and validation periods as well as the full data period.
- (iii)
- step (ii) was repeated using the RRM instead of MAB, and
- (iv)
- step (i) was repeated using the correlation instead of NSE,
- (v)
- the sum of ranks from calibration and validation periods as well as the full data period was obtained for NSE, MAB, RRM, and correlation, of steps (i) to (iv), respectively, and
- (vi)
- Finally, the best (worst) model was taken as that with the smallest (largest) sum of ranks.
3. Results and Discussion
3.1. Discharge Splitting and Modeling of Sub-Flows
Figure 5 shows results of the separation of discharge (into the various components) and graphical comparison of modeled and observed sub-flows. Figure 5d,e were obtained before some parameters were adjusted for capturing extreme hydrological conditions. To obtain Figure 5a, the baseflow and interflow filtering constants (or t1 and t2 of Equations (1)–(3)) were 60 and 40 days, respectively. The baseflow and interflow coefficients (α1 and α2 of Equations (1)–(3)) were set to 0.25 and 0.40, respectively. Furthermore, Figure 5a was only shown for a short data period for illustrative purpose to make the various sub-flows clearly visible. The parameters of the various sub-models are shown in Table 1. It may be realized that both the extraction of sub-flows from observed flow and the generation of model-based sub-flows depend on the same forms of equations (Equations (1)–(3)). However, note can also be taken that the extraction of sub-flows from observed flow depends on filtering constants (e.g. t1 and t2) while model-based sub-flows are generated using recession constants (e.g. ta and tb). If this analogy is to be considered in a strict sense especially for baseflow and interflow, the modeler may take the filtering and recession constants of the given sub-flow approximately equal. However, due to the issue of equifinality, the model-based recession constants may also be different from the filtering constants, as it was the case in this study.
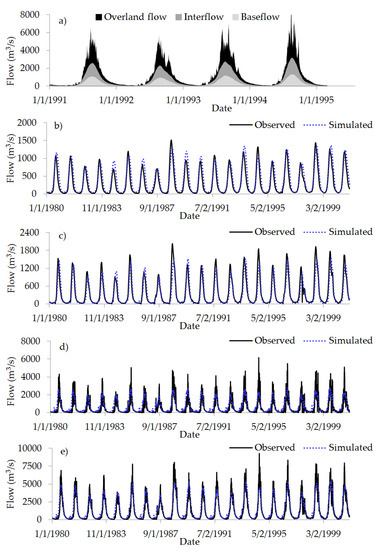
Figure 5.
(a) Separated sub-flows, and the comparison of modeled sub-flows including, (b) baseflow, (c) interflow, (d) overland flow and those extracted from observed flow, (e) comprises the total observed versus modeled flow.

Table 1.
Optimal parameters of Hydrological Model focusing on Sub-flows’ Variation (HMSV) sub-flow models.
The values of the NSE for the various sub-models as well as that of the full model considering both calibration and validation periods can be seen from Table 2. It is noticeable that the performance of the overland sub-model was worse than those for baseflow and interflow. This was due to the temporal variability which is usually higher for the overland flow than either interflow or baseflow. Furthermore, the peak high flows of the total modeled flow (Figure 5e) was under-estimated. This was because the overland flow sub-model was not calibrated with the objective function constrained to extreme flow conditions.

Table 2.
Statistical “goodness-of-fit” measure for the various models.
3.2. Comparison of HMSV and Conventional Models
Figure 6 shows the time series of the observed and simulated flow considering the various models applied to both calibration and validation periods. It should be noted that Figure 6f was obtained by running the full model (i.e., HMSV) using the set of parameters compiled from the various sub-flows’ models (see Table 1). The list of optimal parameters for other models (Figure 6a–e) can be found in Appendix B. It is evident that some peaks were under-estimated while others were over-estimated (Figure 6a–f). However, the variation in observed flow was generally well reproduced by the models. The closeness between the observed and modeled flow based on the various models were statistically summarized in Table 3.
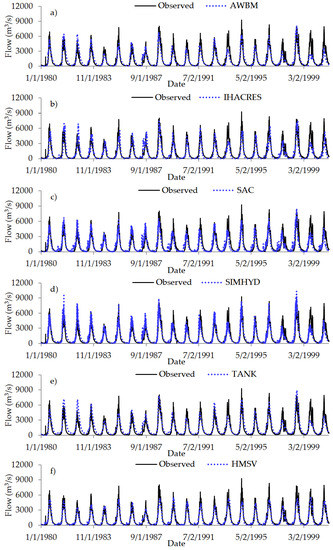
Figure 6.
Comparison of observed and simulated flow based on (a) Australian Water Balance Model (AWBM), (b) Identification of unit Hydrographs and Component Flows from Rainfall, Evaporation and Stream flow data (IHACRES), (c) Sacramento (SAC), (d) SIMHYD, (e) TANK, and (f) HMSV.

Table 3.
Statistical “goodness-of-fit” measures for conventional calibration framework.
Table 3 shows the statistical measure of mismatch between observed and modeled flow. It is noticeable that the difference between the NSE from calibration and validation period was small for each model. Similarly, the coefficients of correlation between observed and modeled flow from each model were comparable for both the calibration and validation periods. This indicates that all the models exhibited less loss of model performance for the hydro-meteorological conditions over the different periods, hence, high transferability. The MAB values tended to differ among the models. MAB was negative for some models and positive for others. This indicates the differences in the model structures or conceptual equations for generation of rainfall-runoff. The RRM values were within the intervals 128–149, and 130–261 for the calibration and validation periods, respectively. The closeness of the results from the HMSV with those of the well-known models indicate the acceptability of the HMSV for modeling hydrological processes.
The results of ranking the performance of the models can be seen in Figure 7. Considering all the statistical “goodness-of-fit” measures (see Figure 7a–d) in a combined way, the worst and best performance was exhibited by IHACRES and HMSV, respectively (Figure 7e). The best performance by the HMSV means that the HMSV captured the variation in the observed flow well. The HMSV models the sub-flows separately and this increases its capacity to explain the overall variation in observed flow. In other words, the best performance by the HMSV indicates the advantage of modeling sub-flows separately compared to the conventional approach of considering the flow as a whole (without separating the sub-flows).
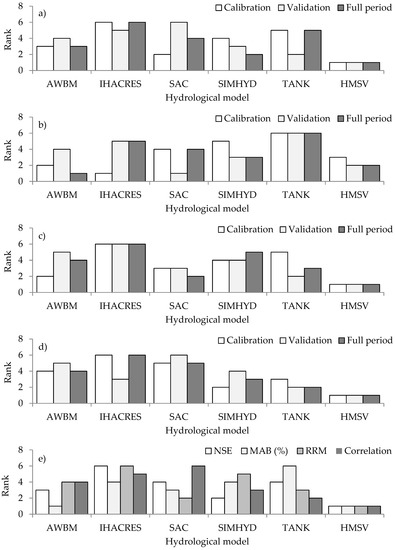
Figure 7.
Model performance in terms of ranks considering (a) Nash-Sutcliffe Efficiency (NSE), (b) Model Average Bias (MAB) (%), (c) Ratio of the Root mean squared error to the Maximum event (RRM), and (d) Correlation, and (e) overall performance indicator obtained through combination of ranks from NSE, MAB, RRM, and correlation. Ranks 1 and 6 is indicate the best and worst performance of a model, respectively.
By focusing on extreme conditions in terms of the maximum and minimum events in each year, it can be realized that the models performed better for high flows (Figure 8a–f) than low flows (Figure 9a–f). It is noticeable that the maximum event in each year was mostly under-estimated especially by the HMSV (Figure 8f) and the AWBM to some extent (Figure 8a). For HMSV, it is noticeable that the maximum events in each year were under-estimated (Figure 8f). This was also visually evident from Figure 6f. Considering other models (IHACRES, SIMHYD, SAC, and TANK), the scatter points fell on both sides of the bisector (1:1 line) indicating somewhat balanced under- and over-estimations (Figure 8b–e). The MAB (Equation (12)) for the maximum flow in each year based on AWBM, IHACRES, SAC, SIMHYD, TANK, and HMSV was −23.7%, −14.6%, −14.4%, −1.5%, −16.5%, and −26.7%, respectively.
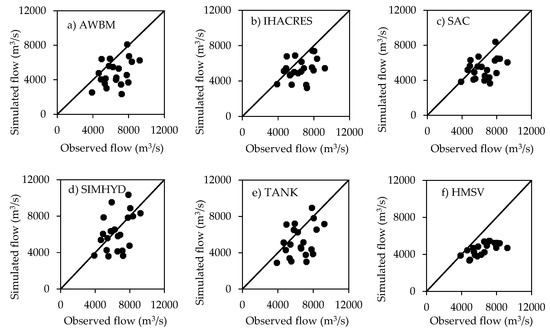
Figure 8.
Model performance evaluation in terms of observed versus simulated maximum flow in each year based on (a) AWBM, (b) IHACRES, (c) SAC, (d) SIMHYD, (e) TANK, and (f) HMSV.
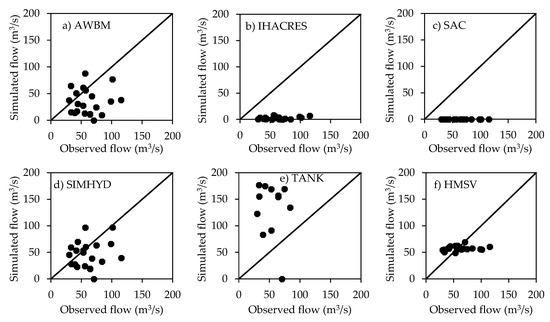
Figure 9.
Model performance evaluation in terms of observed versus simulated minimum flow in each year based on (a) AWBM, (b) IHACRES, (c) SAC, (d) SIMHYD, (e) TANK, and (f) HMSV.
For the minimum event in each year, it can be seen that there were strong under-estimations by IHACRES and SAC (Figure 9b,c) while TANK (Figure 9e) over-estimated the low flows. For each year, the simulated flows from the IHACRES and SAC comprised zeros (or nearly so) and this was why the scatter points appeared as a horizontal line. The low flows were better reproduced by the AWBM and SIMHYD (Figure 9a,d) than other models (IHACRES, SAC, and TANK). Although the scatter points for the HMSV fell close to the bisector, the model appears to exhibit some constant flow of about 50 m3/s. When Equation (12) was applied to the minimum event in each year for the AWBM, IHACRES, SAC, SIMHYD, TANK, and HMSV, the MAB values obtained were −34.2%, −95.4%, −100%, −14.7%, 232.3%, and 7.5%, respectively.
Figure 10 shows the comparison of models in reproducing observed high and low flow quantiles. For comparative analyses of the hydrological extremes, the nearly independent extreme high and low flows were extracted based on the POT approach (see Appendix A for the details). Furthermore, it can be noticed that the frequency of low flow quantiles was based on transformed (or 1/Flow) series (Figure 10b). This transformation enables the analyses of low flow frequency to be conducted in an analogous way to that of high flows [17]. From Figure 10b, scatter points for SAC and IHACRES are noticeably missing. This is because the simulated low flows from these models comprised several zeros despite the non-ephemeral condition of the watershed (or the study area). In other words, when there are zeros, the transformation by 1/Flow cannot be applied, and upon this basis, the simulated flows from SAC and IHACRES were not considered in Figure 10b. For high flows, the models generally under-estimated the quantiles. However, the quantiles with return periods above 3 years were only over-estimated by the SIMHYD (Figure 10a). Whereas TANK under-estimated the low flow quantiles (Figure 10b), over-estimations were realized from SIMHYD and AWBM. The under-estimation by the HMSV was mainly for high return periods (or 5 years and above).
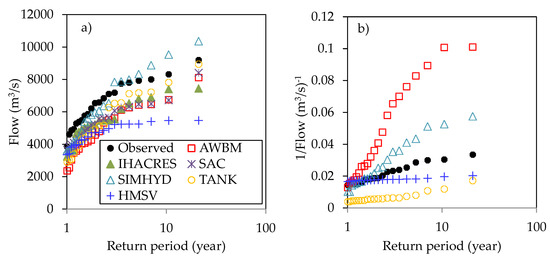
Figure 10.
Comparison of the frequency of observed and simulated (a) maximum flow in each year, and (b) minimum flow in each year. Except for IHACRES and SAC, (a) has the same legend entries as in (b).
3.3. New Framework versus the Conventional Approach
The implementation of the new framework for calibration relied on the list of parameters from Table 1 as the starting point. At the end of the calibration, all the values of the optimal parameters remained the same as in Table 1 except Smax, a1, ta, a2, and tv which were changed (from 101.79 mm, 6.25, 104 days, 6.3, 5 days) to 141.79 mm, 10, 84 days, 5.93, and 12 days, respectively. Compared with the conventional method in which the HMSV did not perform extremely well for the annual maxima (see Figure 8f and Figure 10a) or minima (see Figure 9f and Figure 10b), it is noticeable that the adoption of the new calibration framework which focuses on hydrological extremes greatly improved the model performance with respect to high flows (Figure 11a,c) and low flows (Figure 11b,d). This showed the advantage of the new framework over the conventional approach of calibrating rainfall-runoff model required to simulate extreme hydrological conditions.
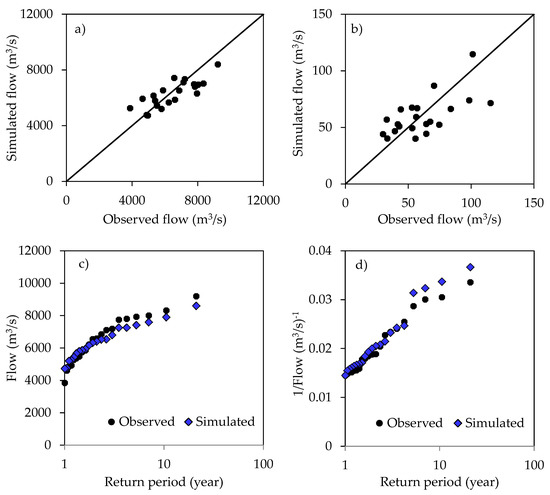
Figure 11.
Observed versus simulated (a) maximum flow in each year, (b) minimum flow in each year, as well as comparison of the frequency of (c) high flows, and (d) lows flows. Except for IHACRES and SAC, (d) has the same legend in (c).
The results of statistical “goodness-of-fit” measures considering the full time series of observed and simulated flow are summarized in Figure 12. Considering data over the full period, it is noticeable that the new framework may lead to a slight reduction in NSE and correlation (Figure 12a,d) and an increase in MAB and RMM (Figure 12b,c) compared with the conventional approach. By considering only the hydrological extremes, the MAB of the quantiles for return periods from 1 to 21 years based on the conventional approach was −9.17% and 2.64% for the high and low flows, respectively. However, when the new framework was adopted, the MAB reduced to 4.71% and −0.27% for the quantiles of high and low flows, respectively. These results indicate that for a case by case basis, the conventional approach can be used when the focus of modeling is on the mean hydrological conditions. However, when the focus of modeling is on high and low flow quantiles (for instance, in studies such as climate change impact investigation where hydrological extremes are highly relevant), the new framework is better than the conventional approach of calibration.
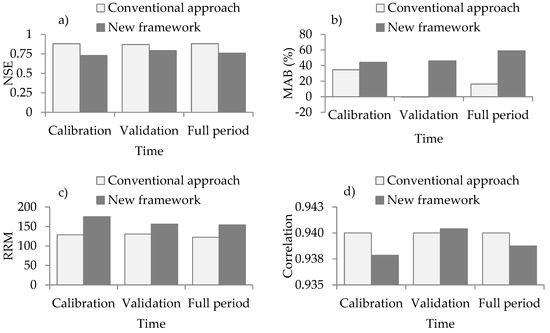
Figure 12.
Statistical “goodness-of-fit” measures for conventional approach and the new framework for calibration in terms of (a) NSE, (b) MAB (%), (c) RRM, and (d) correlation.
4. Conclusions
This study introduced Hydrological Model focusing on Sub-flows’ Variation (HMSV) the calibration of which follows a carefully designed framework which depends on the separation of sub-flows, and checking the validity of hydrological extremes. Hydro-meteorological data from the upper Blue Nile Basin were used test the suitability and applicability of the HMSV and the new framework for calibration. Results from the HMSV calibrated using the conventional approach were compared with the those obtained when the HMSV calibration was based on the new framework. Furthermore, results from the HMSV calibrated using the conventional approach were compared with those from five internationally recognized hydrological models (AWBM, IHACRES, SACRAMENTO, SIMHYD, and TANK) applied to the same study area.
Using the conventional calibration approach, results of the HMSV were highly comparable to those of the AWBM, IHACRES, SACRAMENTO, SIMHYD, and TANK. The new calibration framework leads to better results of hydrological extremes than the conventional approach. Therefore, when high flows and low flows are relevant for the purpose of the hydrological modeling, the new framework for calibration is better than the conventional technique. The technique for extracting extreme hydro-meteorological events which are independent (or nearly so) is not only relevant for hydrological modeling but may also be applicable for extreme value analyses. The HMSV-based approach for separation of sub-flows is important to a modeler (during a step-wise model calibration) for identifying the areas (such as baseflow, interflow, or overland flow) on which focus is required to obtain reasonable simulation results.
The introduced model (i.e., HMSV), HMSV-based baseflow separator and HMSV-based POT extractor can be freely downloaded online via the link https://sites.google.com/site/conyutha/tools-to-download (accessed on 27 January 2019).
Funding
This research received no external funding.
Acknowledgments
Apart from the introduced HMSV, the other hydrological models were obtained from the “eWater Toolkit” of the Cooperative Research Centre for Catchment Hydrology in Australia via the link http://www.toolkit.net.au/ (accessed on 25 August 2015). The hydro-meteorological data were obtained from a previous study [11].
Conflicts of Interest
The author declares no conflict of interest and no competing financial interests.
Appendix A Further Information on the Extraction of Hydrological Extremes
To extract extreme events, the Peak-Over-Threshold (POT) approach can be used. As stated in [18], the independence criteria for the POT extraction are with respect to the inter-event time, threshold, and independency ratio. Figure A1 summarizes how the parameters for extraction of POT events can be understood. The criteria to define the inter-event time, threshold, and independency ratio, can be considered in terms of z1, z2, and z3, respectively. Let qn be a drop-down event between the extreme peaks qm and qp. Furthermore, consider tm and tn as the time at which the peaks qm and qp were respectively observed, while qt denotes the threshold. The event qm is independent from qp if:
- (i)
- z1 or (tn – tm) is not less than the stipulated inter-event time τ,
- (ii)
- z3 or (qm – qn) divided by qm and multiplied by 100 is greater than the independency ratio γ stipulated in percentage,
- (iii)
- the event qm is greater than the threshold qt or z2. For a more stringent threshold than using qm > qt, we can consider qn < qt < qm.
For criterion (i), the stipulated time τ is in the time unit of the series. For instance, if the POT extraction is being done from daily series, the unit of τ is day. The τ expresses how fast the system responds to the input. If we are dealing with river flow, the system is a catchment with rainfall as the input. For a fast response, τ can be small. However, if the system is characterized by a slow response, τ becomes large. Some of the factors which determine the pace of catchment response include the rate of infiltration, amount of water losses through evaporation and/or storage in surface depressions, and the rate of percolation or the exchange of water between micro and macro fissure systems [19].
Regarding criterion (ii), the γ can be thought of in terms of the amount by which the input peak value is reduced through the response of the system. A large value of z3 (see Figure A1) indicates that the influence of the peak of the input into the system has subsided to a level at which the response of the system to another input can minimally be controlled by the effect of the previous one.
The purpose of the criterion (iii) is to ensure that only severe events are extracted. The qt should be expressed as a percentage of the maximum event in the series. For instance, if the given daily flow series has a maximum value of 1500 m3/s and we want the threshold to be 450 m3/s, it means the qt should be set to 30%. Because the qt is expressed as a percentage of the maximum event in the series, it is important that prior to POT extraction the data must be checked to ensure it does not have outliers (for instance stemming from observation errors, wrong placement of decimal points, etc.). If the use of qm > qt is deemed to be less stringent (or leading to events which are not that independent), additional condition qt > qn can be considered. This additional condition reinforces criterion (ii) to ensure that the response of the system to the given input can be considered nearly independent only when (qt – qn) > 0.
To implement the above independency criteria, there are three parameters required including the inter-event time τ, independency ratio γ, and threshold qt. The number of extracted POT events depends on how stringent or relaxed these parameters are set. Small (large) qt value leads to a large (small) number of POT events. A large (small) inter-event time likely leads to strong (weak) independence of the POT events. If the independency ratio is large (small), few (many) POTs events will be extracted.
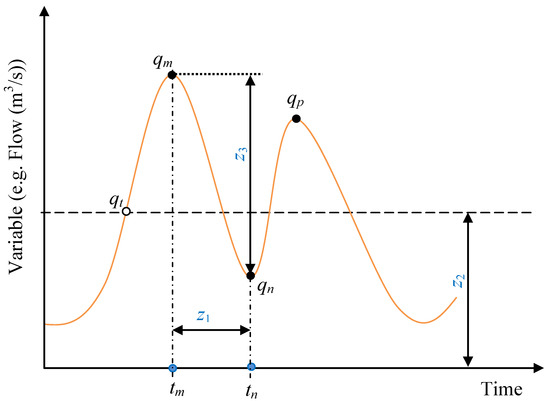
Figure A1.
Parameters used in extracting nearly independent extreme events.
Figure A2 shows, for illustration, POT events extracted to characterize both high and low flows. The threshold ratio (%), inter-event time (day), and independency ratio (%) used to obtain high flows shown in Figure A2a were 30%, 25 days, and 12%, respectively. The corresponding independency parameters for low flows shown in Figure A2b were 22%, 12 days, and 8%. It is vital to note that for the analyses of low flows, the given series is transformed by inversion prior to the POT extraction. As shown by Onyutha [17], the POTs based on inverted flow follow the Generalized Pareto Distribution [20] like those from untransformed discharge. In other words (as already highlighted in Section 3.2), the transformation of flow by inversion makes the extracted extreme events to be analyzed in a similar way to that of high flows.
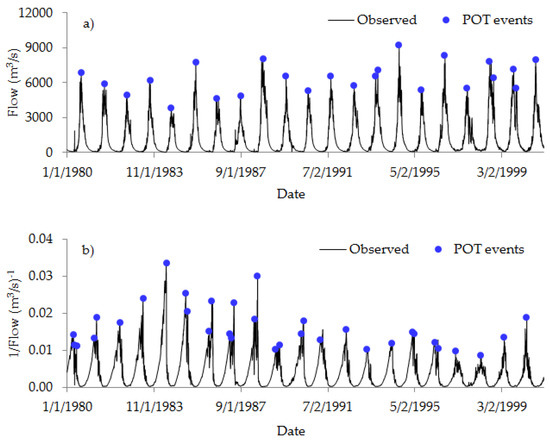
Figure A2.
Peak events from daily river flow for (a) untransformed and (b) inverted series.
Appendix B List of Optimal Model Parameters after Calibration

Table A1.
Parameters of SACRAMENTO, IHACRES, and AWBM.
Table A1.
Parameters of SACRAMENTO, IHACRES, and AWBM.
| SNo. | Parameter | Unit | Value |
|---|---|---|---|
| SACRAMENTO | |||
| 1 | Additional fraction of pervious area (Adimp) | (-) | 0.0025 |
| 2 | Lower Zone Free Water Primary Maximum (Lzfpm) | (mm) | 49.1030 |
| 3 | Lower Zone Free Water Supplemental Maximum (Lzfsm) | (m) | 49.5920 |
| 4 | Ratio of water in LZFPM (Lzpk) | (mm) | 0.0079 |
| 5 | Ratio of water in LZFSM (Lzsk) | (mm) | 0.0503 |
| 6 | Lower Zone Tension Water Maximum (Lztwm) | (mm) | 224.410 |
| 7 | Impervious fraction of the basin (Pctim) | (-) | 0.0201 |
| 8 | Minimum proportion of percolation (Pfree) | (-) | 0.9965 |
| 9 | Exponential percolation rate (Rexp) | (-) | 0.0329 |
| 10 | Fraction of water unavailable for transpiration (Rserv) | (-) | 0.3000 |
| 11 | Catchment portion that lose water by evaporation (Sarva) | (-) | 0.0099 |
| 12 | Fraction of base flow which is groundwater flow (Side) | (-) | 0.0000 |
| 13 | Flow volume through porous material (Ssout) | m3/s/km2 | 0.0010 |
| 14 | Upper Zone Free Water Maximum (Uzfwm) | 1/day | 61.736 |
| 15 | Ratio of water in UZFWM (Uzk) | 1/day | 0.0178 |
| 16 | Upper Zone Tension Water Maximum (Uztwm) | 1/day | 0.8152 |
| 17 | Factor applied to PBASE (Zperc) | (-) | 79.6920 |
| IHACRES | |||
| 1 | Delay | (day) | 29.0000 |
| 2 | Recession rate 1 (α(s)) | (1/day) | −0.9350 |
| 3 | Peak response 1 (β(s)) | (-) | 0.0650 |
| 4 | Time constant 1 (τ(s)) | (day) | 14.8720 |
| 5 | Volume proportion 1 (v(s)) | (°C) | 1.0000 |
| 6 | Mass balance term (c) | (-) | 0.0139 |
| 7 | Drying rate at reference temperature (tw) | (°C/day) | 2.0000 |
| 8 | Temperature dependence of drying rate (f) | (-) | 0.0000 |
| 9 | Reference temperature (tref) | (°C) | 20.0000 |
| 10 | Moisture threshold for producing flow (l) | (mm) | 0.0000 |
| 11 | Power on soil moisture (p) | (-) | 1.0000 |
| AWBM | |||
| 1 | Fraction of catchment area for the first store (A1) | (-) | 0.1340 |
| 2 | Fraction of catchment area for the second store (A2) | (-) | 0.4330 |
| 3 | Base flow index (BFI) | (-) | 0.8334 |
| 4 | Storage capacity of first store (C1) | (mm) | 1.8645 |
| 5 | Storage capacity of first store (C2) | (mm) | 0.6314 |
| 6 | Storage capacity of first store (C3) | (mm) | 2.4215 |
| 7 | Base flow recession constant (Kbase) | (day) | 0.9822 |
| 8 | Surface flow recession constant (Ksurf) | (day) | 0.9978 |

Table A2.
Parameters of TANK and SIMHYD.
Table A2.
Parameters of TANK and SIMHYD.
| SNo. | Parameter | Unit | Value |
|---|---|---|---|
| TANK | |||
| 1 | Depth below the top outlet of the first tank (H11) | (mm) | 34.035 |
| 2 | Overland runoff from the top outlet of first tank (a11) | (m3/s) | 0.0098 |
| 3 | Overland runoff from the lower outlet of first tank (a12) | (m3/s) | 0.14331 |
| 4 | Intermediate runoff (a21) | (m3/s) | 0.0110 |
| 5 | Sub-base runoff (a31) | (m3/s) | 0.0458 |
| 6 | Base flow (a41) | (m3/s) | 0.0200 |
| 7 | Alpha | (-) | 0.9999 |
| 8 | Outflow from the bottom of the first tank (b1) | (m3/s) | 0.1335 |
| 9 | Outflow from the bottom of the second tank (b2) | (m3/s) | 0.9980 |
| 10 | Outflow from the bottom of the third tank (b3) | (m3/s) | 0.9921 |
| 11 | Water depth in the first tank (C1) | (mm) | 21.6395 |
| 12 | Water depth in the first tank (C2) | (mm) | 11.2244 |
| 13 | Water depth in the first tank (C3) | (mm) | 41.7943 |
| 14 | Water depth in the first tank (C4) | (mm) | 5.4077 |
| 15 | Depth below the lower outlet of the first tank (H12) | (mm) | 75.9990 |
| 16 | Depth below the outlet of the second tank (H21) | (mm) | 6.0428 |
| 17 | Depth below the outlet of the third tank (H31) | (mm) | 63.6577 |
| 18 | Depth below the outlet of the fourth tank (H41) | (mm) | 94.7014 |
| SIMHYD | |||
| 1 | Baseflow coefficient | (-) | 0.02 |
| 2 | Impervious threshold | (-) | 0.0412 |
| 3 | Infiltration Coefficient | (-) | 148.156 |
| 4 | Infiltration shape | (-) | 0.7072 |
| 5 | Interflow coefficient | (-) | 0.1531 |
| 6 | Pervious Fraction | (-) | 0.9921 |
| 7 | Rainfall interception store capacity | (mm) | 1.9000 |
| 8 | Recharge coefficient | (-) | 1.0000 |
| 9 | Soil moisture store capacity | (mm) | 181.0200 |
References
- Boughton, W. The Australian water balance model. Environ. Model. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Littlewood, I.G.; Whitehead, P.G. Computation of the instantaneous unit hydrograph and identifiable component flows with application to two small upland catchments. J. Hydrol. 1990, 117, 275–300. [Google Scholar] [CrossRef]
- Burnash, R.J.C. The NWS River forecast system-catchment modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 311–366. [Google Scholar]
- Porter, J.W.; McMahon, T.A. A model for the simulation of streamflow data from climatic records. J. Hydrol. 1971, 13, 297–324. [Google Scholar] [CrossRef]
- Sugawara, M. Tank model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 165–214. [Google Scholar]
- Danish Hydraulic Institute (DHI). Reference manual. In MIKE11—A Modeling System for Rivers and Channels; DHI—Water & Environment: Hørsholm, Denmark, 2007; pp. 278–325. [Google Scholar]
- Nielsen, S.A.; Hansen, E. Numerical simulation of the rainfall-runoff process on a daily basis. Hydrol. Res. 1973, 4, 171–190. [Google Scholar] [CrossRef]
- Markstrom, S.L.; Regan, R.S.; Hay, L.E.; Viger, R.J.; Webb, R.M.; Payn, R.A.; LaFontaine, J.H. PRMS-IV, the Precipitation-Runoff Modeling System, Version 4. In U.S. Geological Survey Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2015; Volume 6, p. 158. [Google Scholar]
- Moore, R.J. The PDM rainfall–runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 483–499. [Google Scholar] [CrossRef]
- Staudinger, M.; Stahl, K.; Seibert, J.; Clark, M.P.; Tallaksen, L.M. Comparison of hydrological model structures based on recession and low flow simulations. Hydrol. Earth Syst. Sci. 2011, 15, 3447–3459. [Google Scholar] [CrossRef]
- Onyutha, C. Influence of hydrological model selection on simulation of moderate and extreme flow events: A case study of the Blue Nile basin. Adv. Meteorol. 2016, 2016, 7148326. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Croke, B.F.W.; Andrews, F.; Spate, J.; Cuddy, S.M. IHACRES User Guide, 2nd ed.; Technical Report 2005/19; iCAM, School of Resources, Environment and Society, The Australian National University: Canberra, Australia, 2005. [Google Scholar]
- Beven, K.J.; Binley, A.M. The future role of distributed models: Model calibration and predictive uncertainty. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Onyutha, C. Statistical modelling of FDC and return periods to characterise QDF and design threshold of hydrological extremes. J. Urban Environ. Eng. 2012, 6, 132–148. [Google Scholar] [CrossRef]
- Onyutha, C. On rigorous drought assessment using daily time scale: Non-stationary frequency analyses, revisited concepts, and a new method to yield non-parametric indices. Hydrology 2017, 4, 48. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall–runoff relations for karstic springs. Part I: Convolution and spectral analyses. J. Hydrol. 2000, 238, 123–148. [Google Scholar] [CrossRef]
- Pickands, J. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).