Changes in Physical Properties of Inland Streamwaters Induced by Earth and Atmospheric Tides
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoitink, A.J.F.; Jay, D.A. Tidal river dynamics: Implications for deltas. Rev. Geophys. 2016, 54, 240–272. [Google Scholar] [CrossRef]
- Dai, Z.; Du, J.; Tang, Z.; Ou, S.; Brody, S.; Mei, X.; Jing, J.; Yu, S. Detection of linkage between solar and lunar cycles and runoff of the world’s large rivers. Earth Space Sci. 2019, 6, 914–930. [Google Scholar] [CrossRef]
- Troxell, H.C. The diurnal fluctuation in the ground-water and flow of the Santa Anna River and its meaning. Trans. AGU 1936, 17, 496–504. [Google Scholar] [CrossRef]
- Briciu, A.-E.; Oprea-Gancevici, D.I. Diurnal thermal profiles of selected rivers in Romania. SGEM2015 Conf. Proc. 2015, 1, 221–228. [Google Scholar]
- Nimick, D.A.; Gammons, C.H.; Parker, S.R. Diel biogeochemical processes and their effect on the aqueous chemistry of streams: A review. Chem. Geol. 2011, 283, 3–17. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Szilagyi, J.; Kalicz, P. Diurnal fluctuations in shallow groundwater levels and streamflow rates and their inter-pretation—A review. J. Hydrol. 2010, 385, 371–383. [Google Scholar] [CrossRef]
- Robinson, T.W. Earth tides shown by fluctuations of water levels in wells in New Mexico and Iowa. Trans. AGU 1939, 20, 656–666. [Google Scholar] [CrossRef]
- Lambert, W.D. Report on earth tides. U.S. Coast Geodet. Surv. 1940, 223, 1–24. [Google Scholar]
- Bredehoeft, J.D. Response of well-aquifer systems to earth tides. J. Geophys. Res. 1967, 72, 3075–3087. [Google Scholar] [CrossRef]
- Merritt, M.L. Estimating hydraulic properties of the Floridan aquifer system by analysis of earth-tide, ocean-tide, and barometric effects, Collier and Hendry Counties, Florida. U.S. Geol. Surv. Water Resour. 2004, 2003–4267. [Google Scholar] [CrossRef]
- Luque-Espinar, J.A.; Pardo-Igúzquiza, E.; González-Ramón, A.; López-Chicano, M.; Durán-Valsero, J.J.; Pulido-Velázquez, D. Spectral Analysis of Time Series of Carbonate Aquifer of Sierra Gorda. In Advances in Karst Science; Renard, P., Bertrand, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Barberio, M.D.; Gori, F.; Barbieri, M.; Billi, A.; Devoti, R.; Doglioni, C.; Petitta, M.; Riguzzi, F.; Rusi, S. Diurnal and semidiurnal cyclicity of Radon (222Rn) in groundwater, Giardino Spring, Central Apennines, Italy. Water 2018, 10, 1276. [Google Scholar] [CrossRef]
- Briciu, A.-E. Wavelet analysis of lunar semidiurnal tidal influence on selected inland rivers across the globe. Sci. Rep. 2014, 4, 4193. [Google Scholar] [CrossRef] [PubMed]
- Jasonsmith, J.F.; Macdonald, B.C.T.; White, I. Earth-tide-induced fluctuations in the salinity of an inland river, New South Wales, Australia: A short-term study. Environ. Monit. Assess. 2017, 189, 188. [Google Scholar] [CrossRef] [PubMed]
- Kulessa, B.; Hubbard, B.; Brown, G.H.; Becker, J. Earth tide forcing of glacier drainage. Geophys. Res. Lett. 2003, 30, 1011. [Google Scholar] [CrossRef]
- Briciu, A.-E.; Mihăilă, D.; Oprea, D.I.; Bistricean, P.-I.; Lazurca, L.G. Orthotidal signal in the electrical conductivity of an inland river. Environ. Monit. Assess. 2018, 190, 282. [Google Scholar] [CrossRef]
- Briciu, A.-E. Diurnal, semidiurnal, and fortnightly tidal components in orthotidal proglacial rivers. Environ. Monit. Assess. 2018, 190, 160. [Google Scholar] [CrossRef]
- Cerveny, R.S.; Svoma, B.M.; Vose, R.S. Lunar tidal influence on inland river streamflow across the conterminous United States. Geophys. Res. Lett. 2010, 37, L22406. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteor. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Ng, E.K.W.; Chan, J.C.L. Geophysical applications of partial wavelet coherence and multiple wavelet coherence. J. Atmos. Oceanic Technol. 2012, 29, 1845–1853. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin. Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P. Interdecadal Changes in the ENSO-Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal har-monic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Tamura, Y. A harmonic development of the tide generating potential. Bull. Info. Marées Terr. 1987, 99, 6813–6855. [Google Scholar]
- Dehant, V.; Defraigne, P.; Wahr, J. Tides for a convective Earth. J. Geophys. Res. 1999, 104, 1035–1058. [Google Scholar] [CrossRef]
- Miller, J.A. Groundwater atlas of the United States: Segment 6, Alabama, Florida, Georgia, and South Carolina. U.S. Geol. Surv. Hydrol. Investig. Atlas 1993, 30, 116. [Google Scholar]
- Plummer, L.N.; Busenberg, E.; Drenkard, S.; Schlosser, P.; Ekwurzel, B.; Weppernig, R.; McConnell, J.B.; Michel, R.L. Flow of river water into a karstic limestone aquifer—2. Dating the young fraction in groundwater mixtures in the Upper Floridan aquifer near Valdosta, Georgia. Appl. Geochem. 1998, 13, 1017–1043. [Google Scholar] [CrossRef]
- Planert, M. Simulation of Regional Ground-Water Flow in the Suwannee River Basin, Northern Florida and Southern Georgia. U.S. Geol. Surv. Sci. Investig. Rep. 2007, 2007–5031. [Google Scholar] [CrossRef]
- Acworth, R.I.; Brain, T. Calculation of barometric efficiency in shallow piezometers using water levels, atmospheric and earth tide data. Hydrogeol. J. 2008, 16, 1469–1481. [Google Scholar] [CrossRef]
- Jasonsmith, J.F. Origins of Salinity and Salinisation Processes in the Wybong Creek Catchment, New South Wales, Australia. Ph.D. Thesis, Australian National University, Canberra, Australia, 2010. [Google Scholar]
- Hsieh, P.A.; Bredehoeft, J.D.; Farr, J.M. Determination of aquifer transmissivity from Earth tide analysis. Water Resour. Res. 1987, 23, 1824–1832. [Google Scholar] [CrossRef]
- Acworth, R.I.; Halloran, L.J.S.; Rau, G.C.; Cuthbert, M.O.; Bernardi, T.L. An objective frequency domain method for quantifying confined aquifer compressible storage using Earth and atmospheric tides. Geophys. Res. Let. 2016, 43, 11671–11678. [Google Scholar] [CrossRef]
- Hanson, J.M.; Owen, L.B. Fracture orientation analysis by the solid earth tidal strain method. In Proceedings of the 57th Annual Fall Technical Conference and Exhibition of the Society of Petroleum Engineers of AIME, American Institute of Mechanical Engineers, New Orleans, LA, USA, 26–29 September 1982. [Google Scholar]
- Bower, D.R. Bedrock fracture parameters from the interpretation of well tides. J. Geophys. Res. 1983, 88, 5025–5035. [Google Scholar] [CrossRef]
- Gieske, A.; De Vries, J.J. An analysis of earth-tide-induced groundwater flow in eastern Botswana. J. Hydrol. 1985, 82, 211–232. [Google Scholar] [CrossRef]
- McMillan, T.C.; Rau, G.C.; Timms, W.A.; Andersen, M.S. Utilizing the impact of earth and atmospheric tides on groundwater systems: A review reveals the future potential. Rev. Geophys. 2019, 57, 281–315. [Google Scholar] [CrossRef]
- Shuai, P.; Knappett, P.S.K.; Hossain, S.; Hosain, A.; Rhodes, K.; Ahmed, K.M.; Cardenas, M.B. The impact of the degree of aquifer confinement and anisotropy on tidal pulse propagation. Ground Water 2017, 55, 519–531. [Google Scholar] [CrossRef] [PubMed]
- Rojstaczer, S.; Agnew, D.C. The influence of formation material properties on the response of water levels in wells to Earth tides and atmospheric loading. J. Geophys. Resear. 1989, 94, 12403–12411. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, Z.; Wang, G.; Sun, X.; Yan, R.; Liu, C. Large earthquake reshapes the groundwater flow system: Insight from the water-level response to earth tides and atmospheric pressure in a deep well. Water Resour. Res. 2019, 55, 4207–4219. [Google Scholar] [CrossRef]
- Lee, M.; You, Y.; Kim, S.; Kim, K.T.; Kim, H.S. Decomposition of water level time series of a tidal river into tide, wave and rainfall-runoff components. Water 2018, 10, 1568. [Google Scholar] [CrossRef]
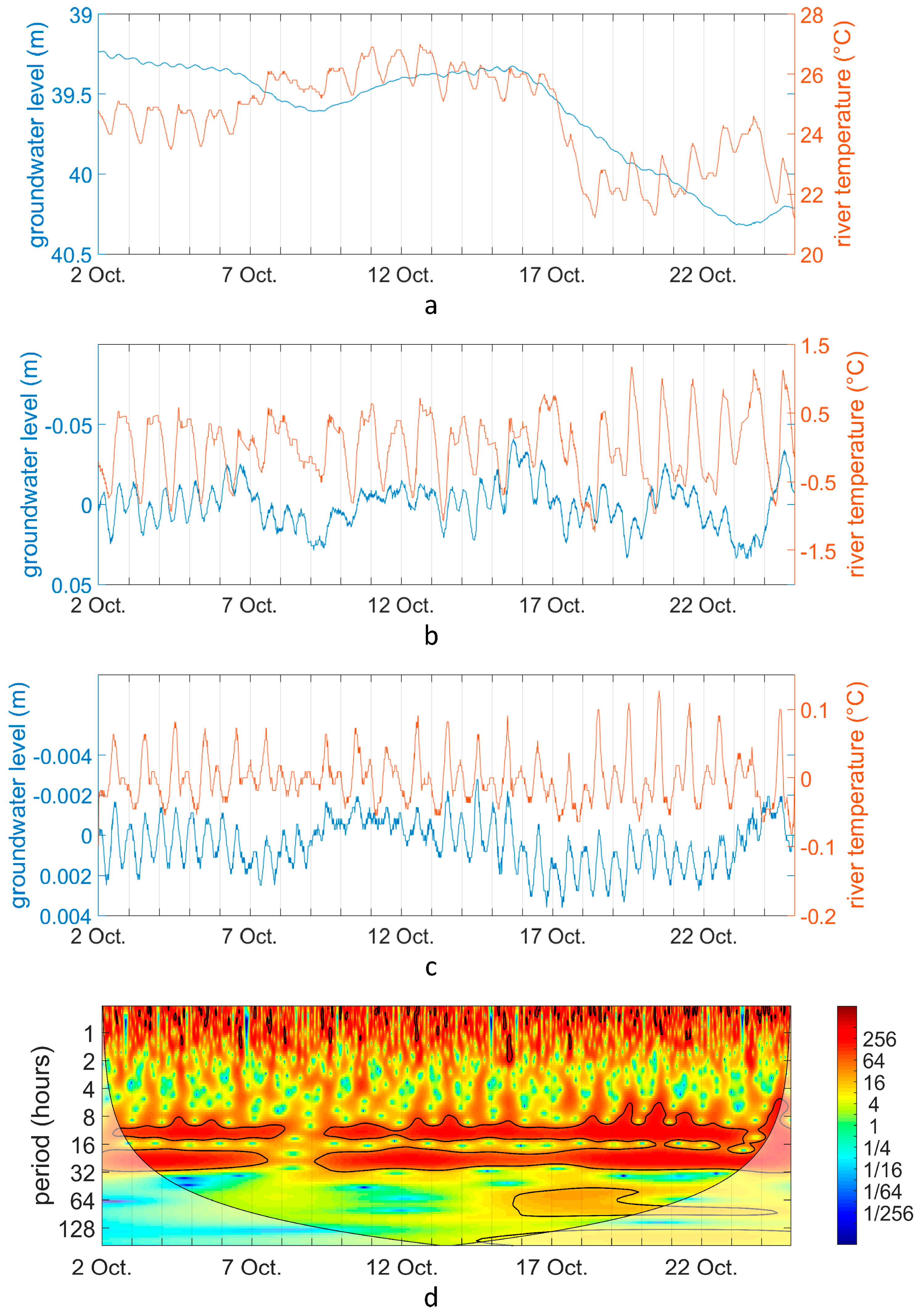
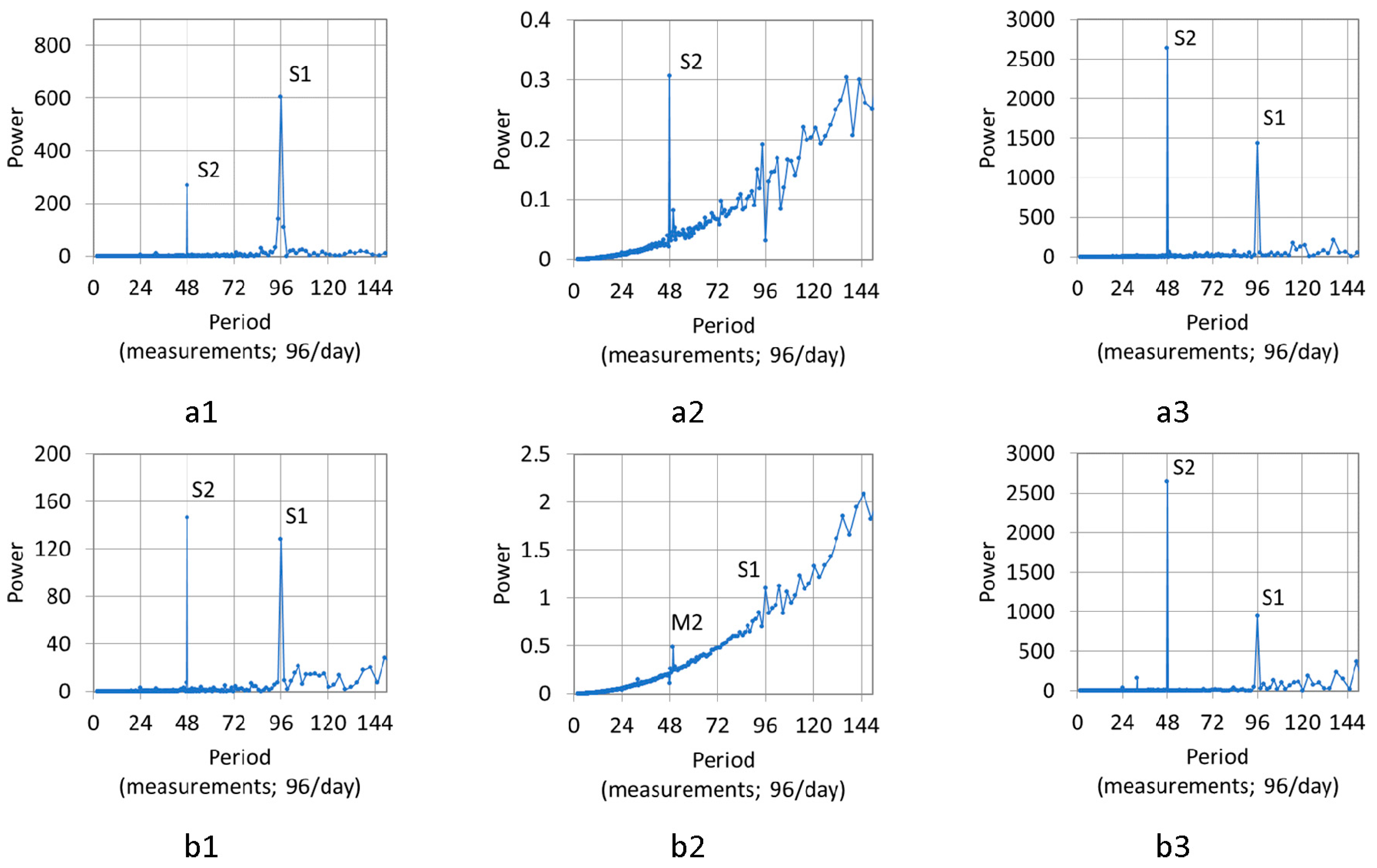
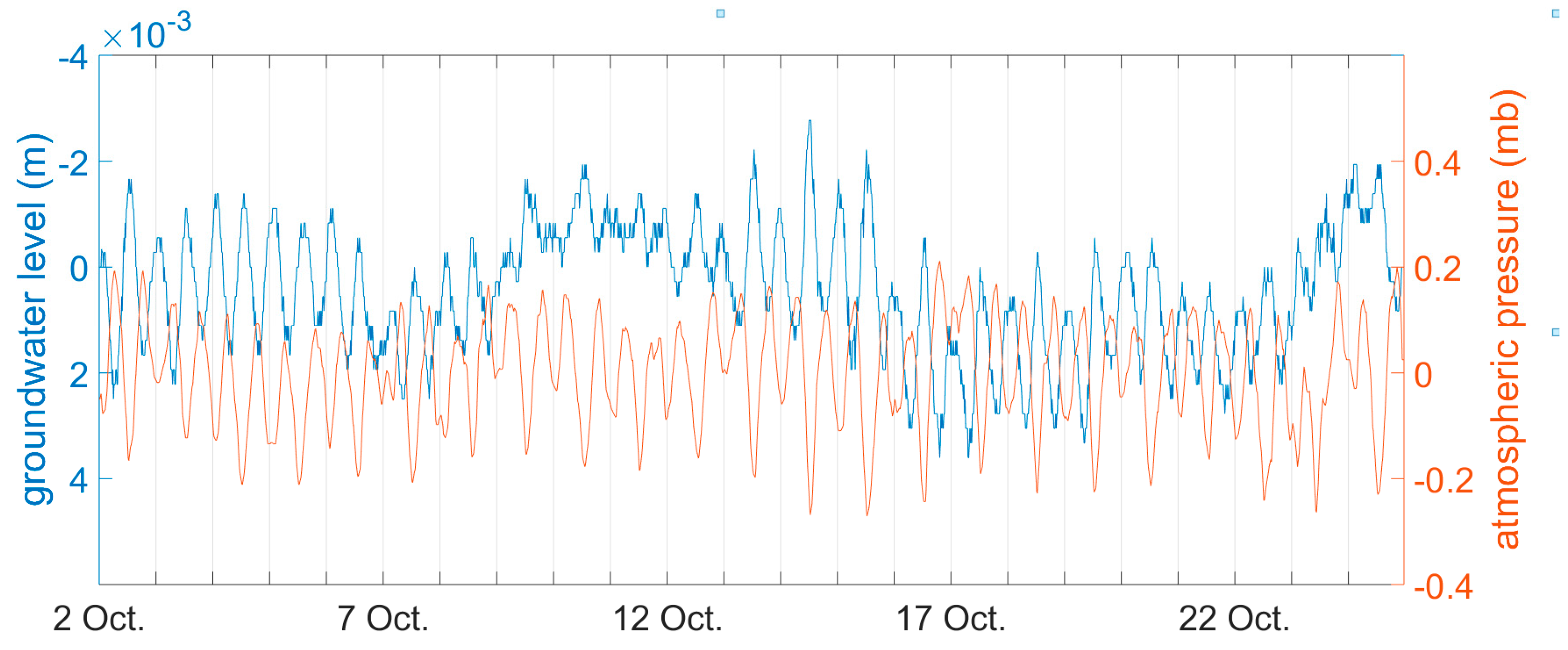
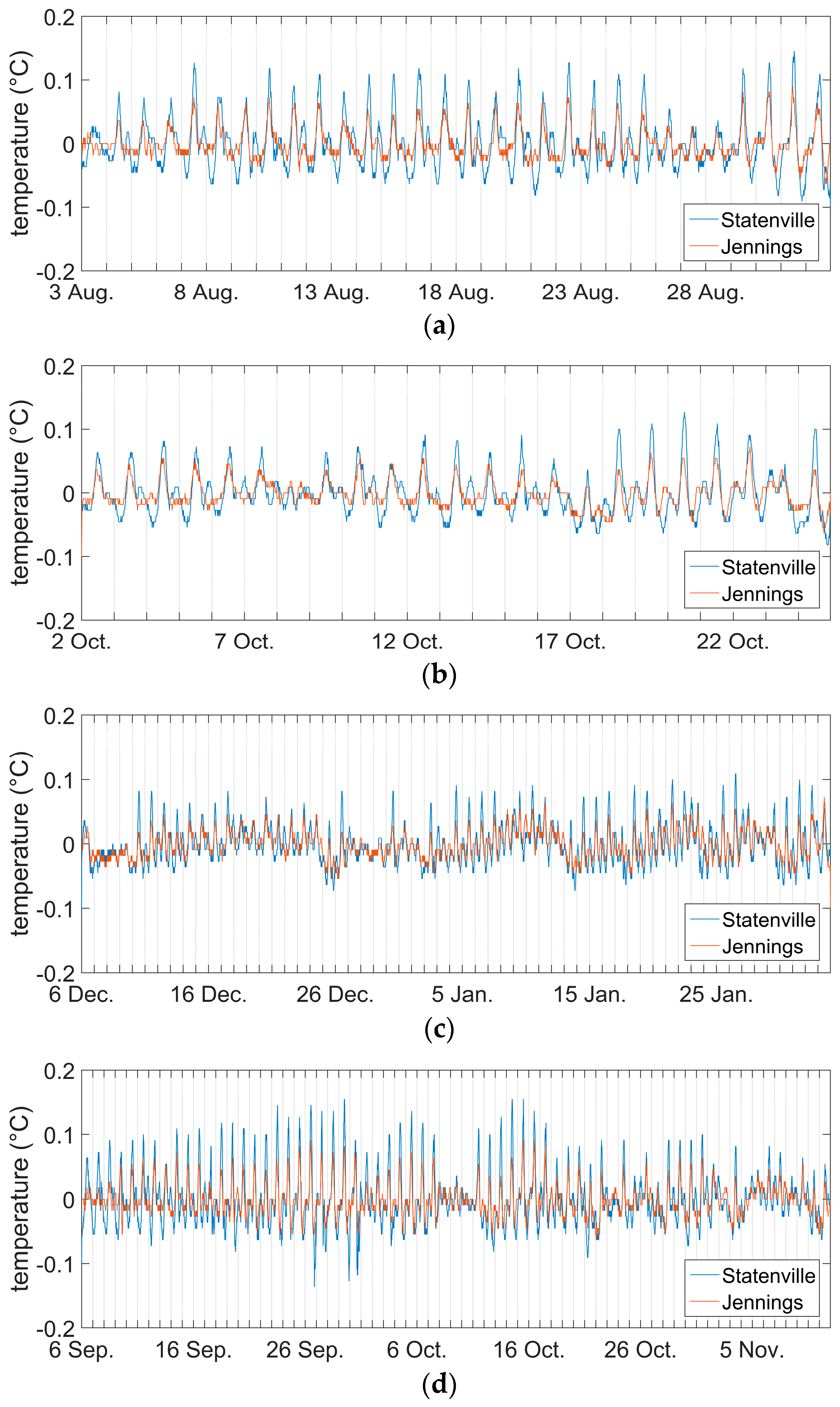
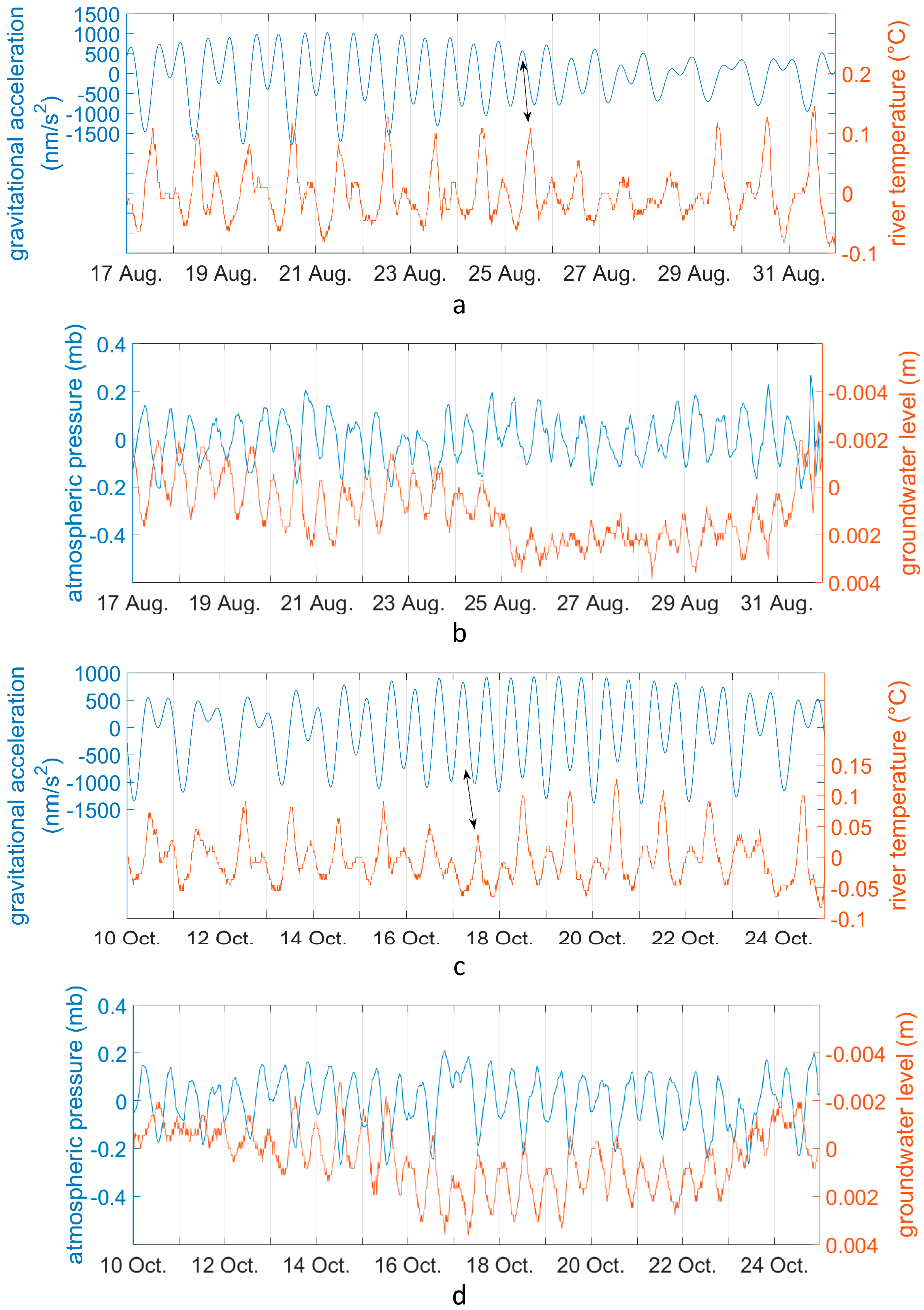
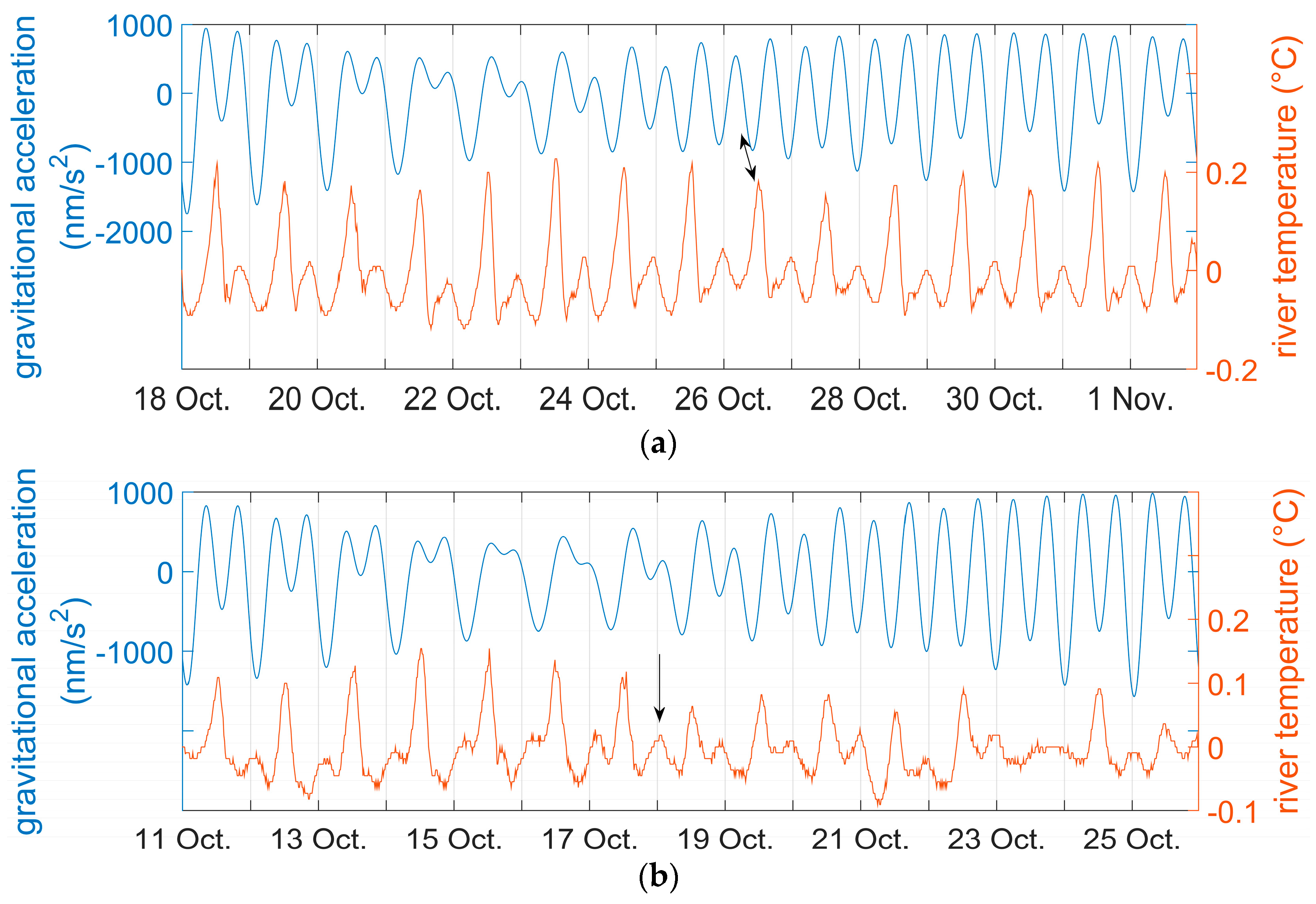
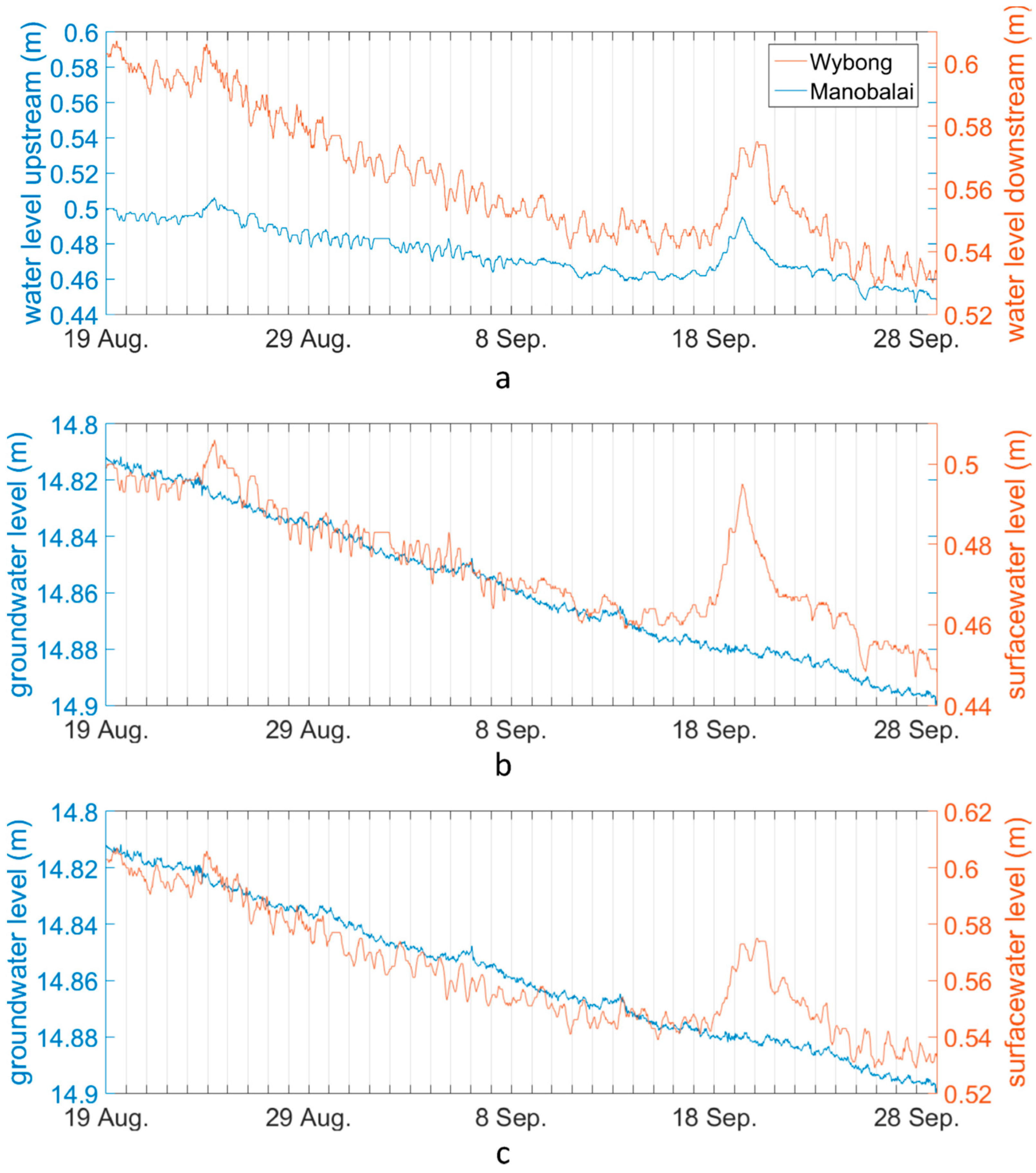
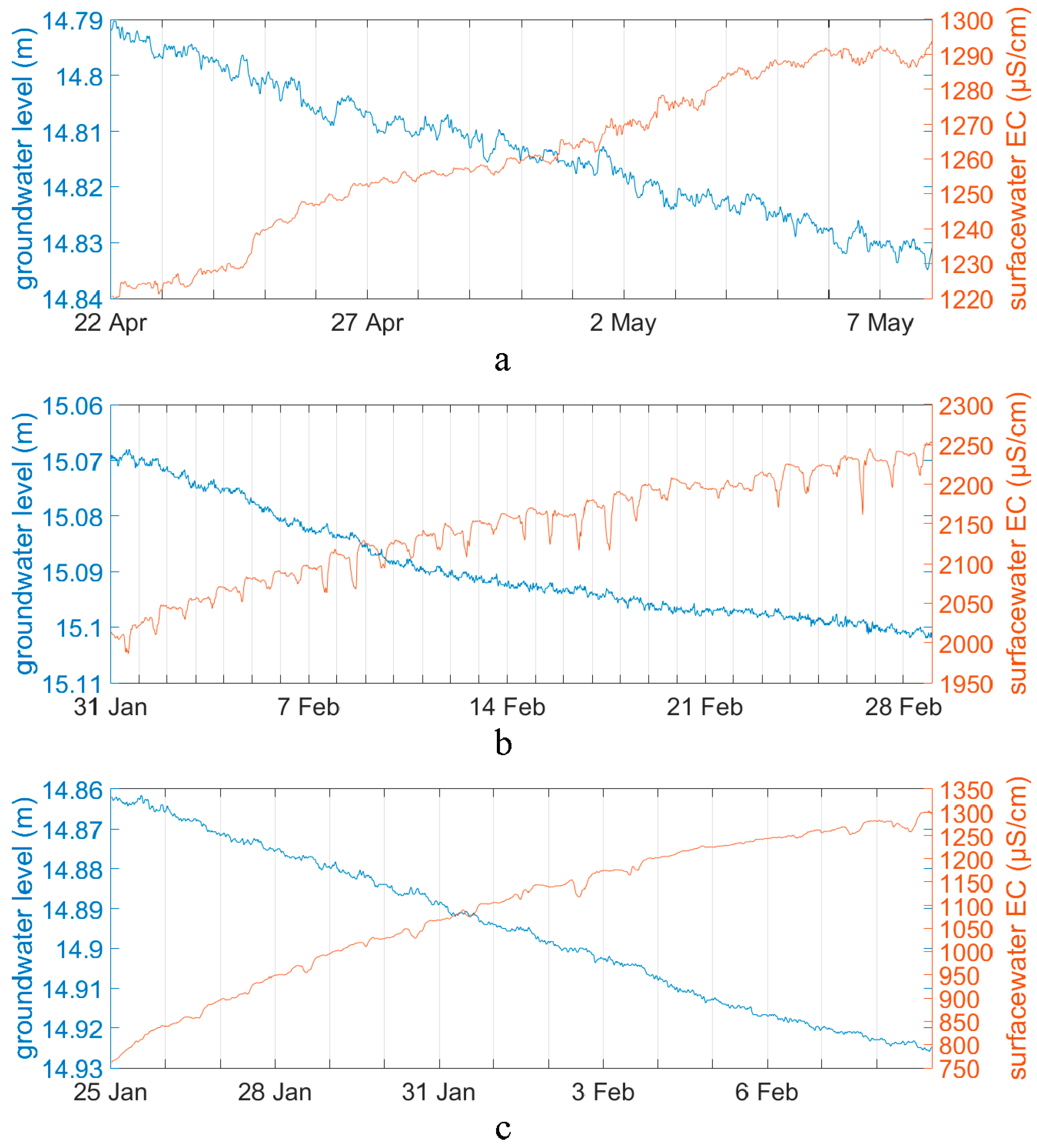
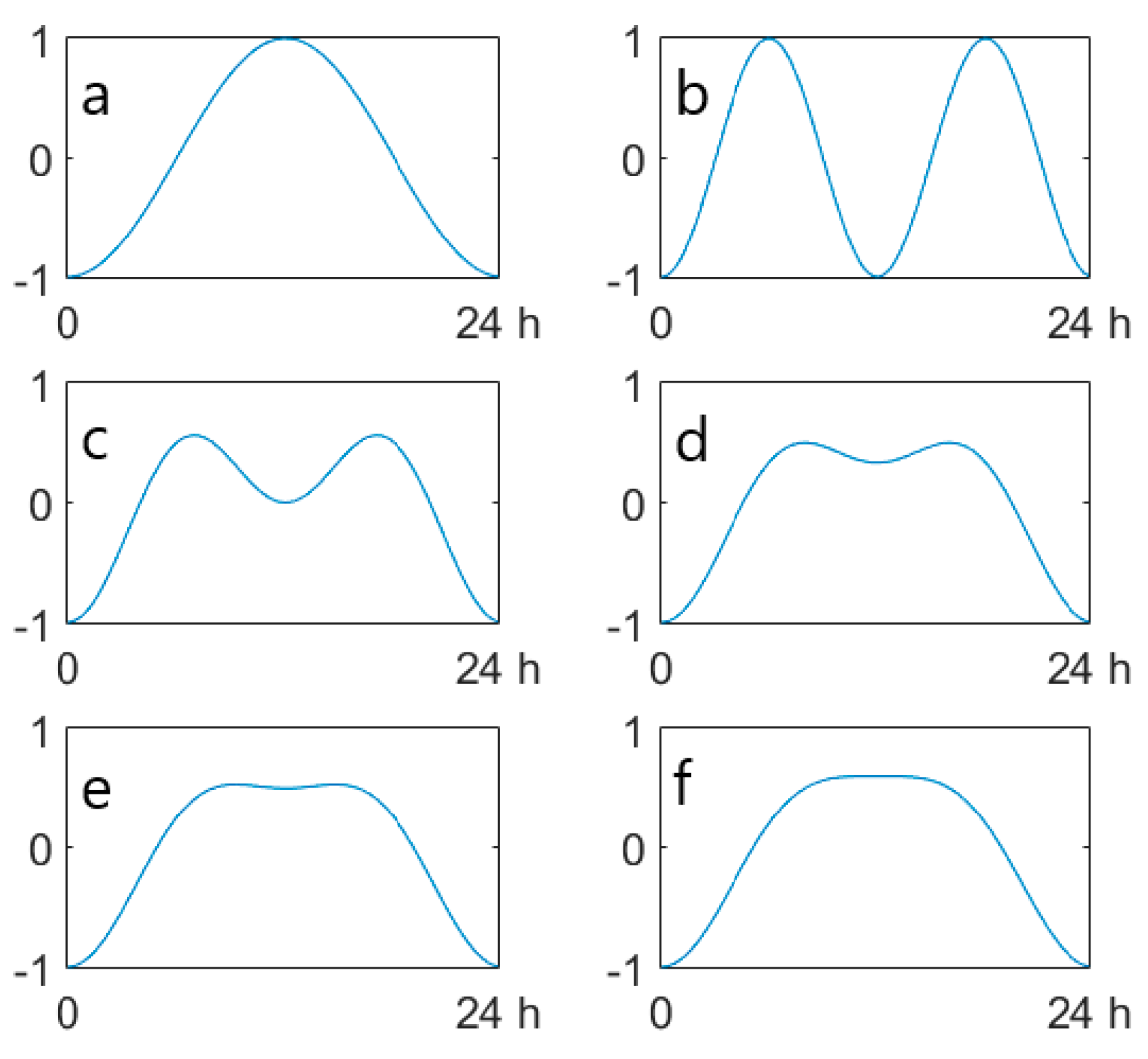
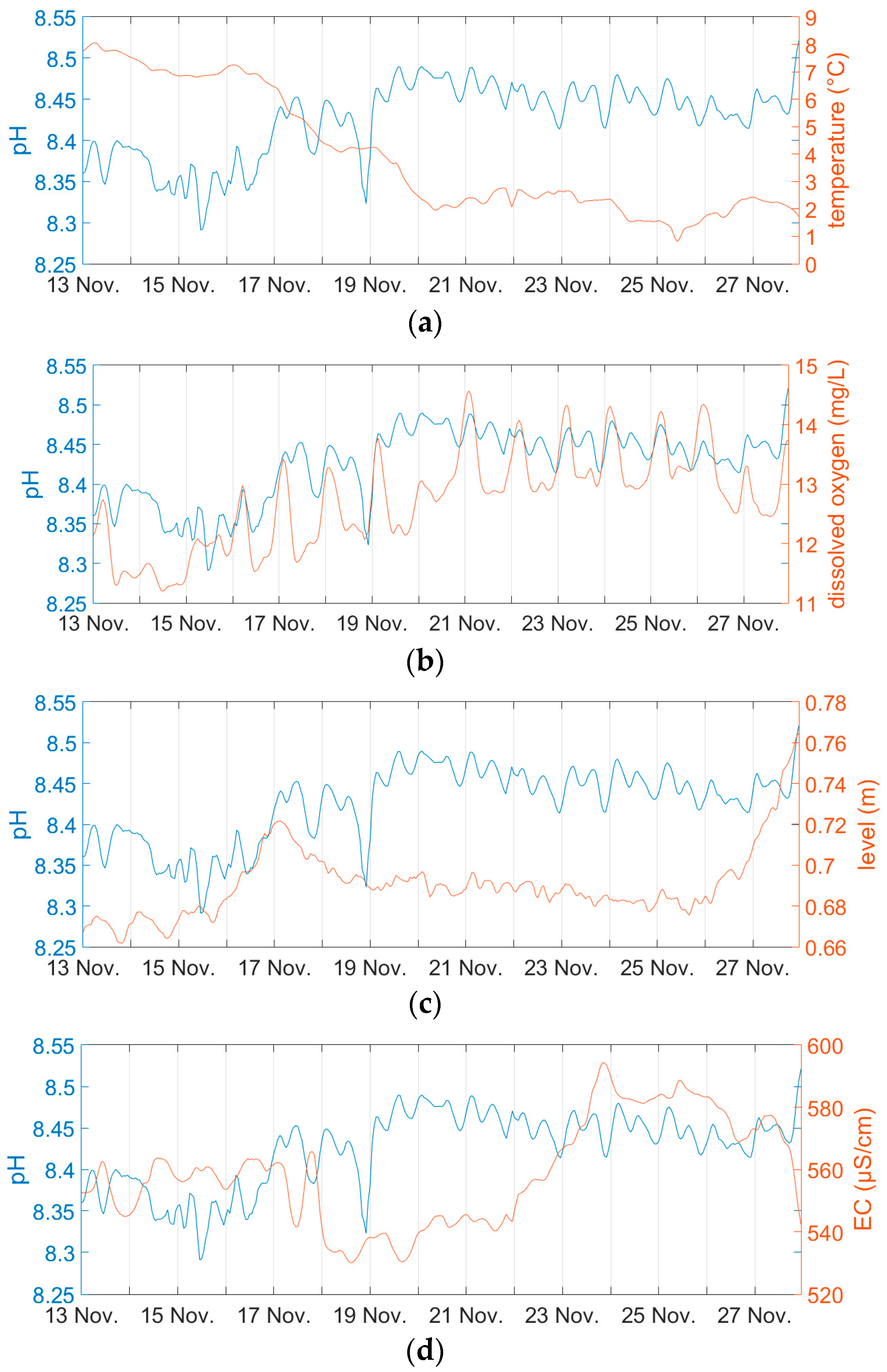
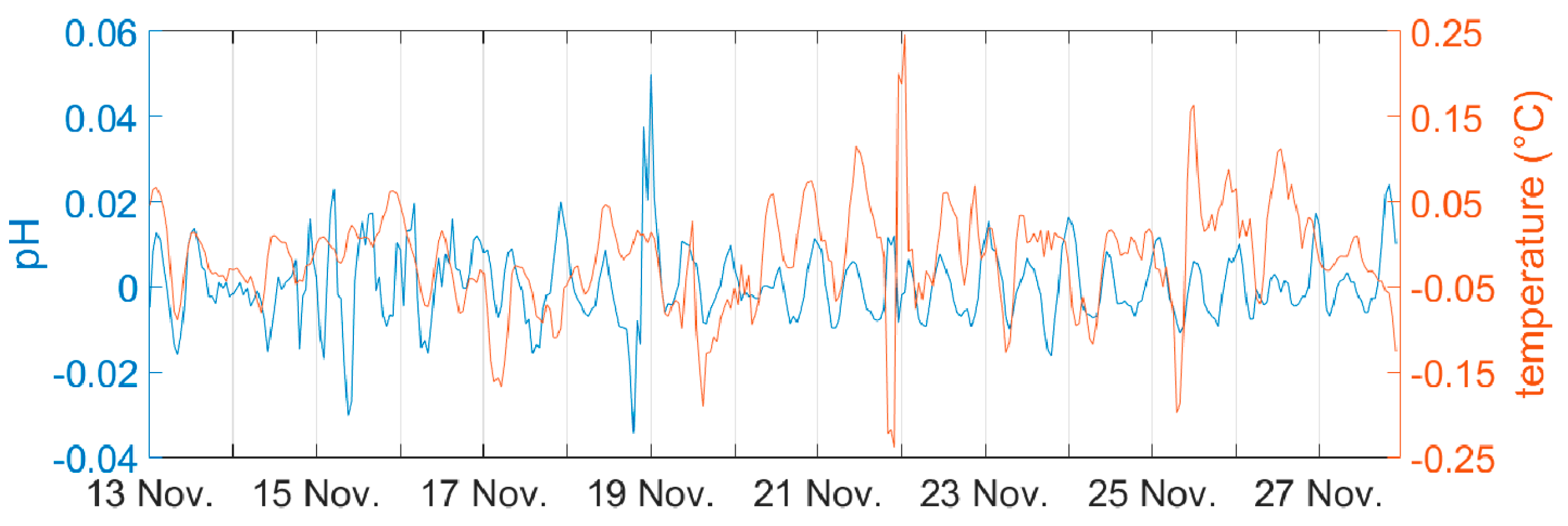
| No. | Monitoring Point | Latitude, Longitude | Elevation (m a.s.l.) * | Parameters | Time Interval |
|---|---|---|---|---|---|
| USA | |||||
| 1 | USGS 02317500 ALAPAHA RIVER AT STATENVILLE, Georgia | 30°42′14” N, 83°02′00” W | 23 | level/discharge | 2007–2018 |
| temperature | 2016–2018 | ||||
| 2 | USGS 02317620 ALAPAHA RIVER NEAR JENNINGS, Florida | 30°35′53” N, 83°04′24” W | 19 | level/discharge | 2007–2018 |
| temperature | 2017–2018 | ||||
| electrical conductivity | 2017–2018 | ||||
| 3 | USGS 304949083165301 19E009 (Valdosta, Upper Floridan Aquifer), Georgia | 30°49′51” N, 83°16′58” W | 65 | level | 2007–2018 |
| Australia | |||||
| 4 | WYBONG CREEK AT MANOBALAI—210147, New South Wales | 32°10′57” S, 150°39′39” E | 172 | level/discharge | 2010–2018 |
| 5 | WYBONG CREEK AT WYBONG—210040, New South Wales | 32°16′9” S, 150°38′10” E | 145 | level/discharge, electrical conductivity | 1993–2018 |
| temperature | 1999–2018 | ||||
| 6 | GW080434.1.1 (Wybong Bridge, Wybong alluvial aquifer), New South Wales | 32°12′4” S, 150°22′18” E | 148 | level | 2003–2018 |
| temperature | 2007–2018 | ||||
| Romania | |||||
| 7 | SUCEAVA RIVER AT MIHOVENI, Suceava | 47°40′53” N, 26°11′60” E | 280 | level, temperature, electrical conductivity, dissolved oxygen, pH, ORP | 2018 |
| Time Interval | Site-Parameter | Tidal Component | Period (h) | Amplitude * | Amplitude Error * | Phase (°) | Phase Error (°) | Signal to Noise Ratio |
|---|---|---|---|---|---|---|---|---|
| 17–31 August 2017 | Statenville—streamwater temperature | MSF | 354 | 1.0118 | 0.172 | 293.08 | 9.76 | 34 |
| O1 | 25.82 | 0.2013 | 0.142 | 253.11 | 42.61 | 2 | ||
| S1/K1 | 24/23.93 | 0.5116 | 0.145 | 111.72 | 18.71 | 12 | ||
| M2 | 12.42 | 0.0317 | 0.081 | 88.35 | 125.88 | 0.15 | ||
| S2 | 12 | 0.3059 | 0.097 | 107.56 | 17.67 | 9.9 | ||
| Jennings—streamwater temperature | MSF | 354 | 0.8527 | 0.066 | 298.19 | 4.39 | 170 | |
| O1 | 25.82 | 0.1224 | 0.059 | 194.87 | 29.7 | 4.3 | ||
| S1/K1 | 24/23.93 | 0.3421 | 0.063 | 94.01 | 10.65 | 30 | ||
| M2 | 12.42 | 0.0408 | 0.034 | 327.71 | 46.72 | 1.4 | ||
| S2 | 12 | 0.1493 | 0.033 | 90.18 | 15.28 | 20 | ||
| Valdosta—groundwater level | MSF | 354 | 0.6332 | 0.02 | 293.4 | 1.78 | 970 | |
| O1 | 25.82 | 0.0297 | 0.02 | 88.58 | 38.65 | 2.3 | ||
| S1/K1 | 24/23.93 | 0.0282 | 0.019 | 260.08 | 41.26 | 2.2 | ||
| M2 | 12.42 | 0.021 | 0.008 | 269.03 | 24.65 | 6.3 | ||
| S2 | 12 | 0.0196 | 0.01 | 104.12 | 28.25 | 4.1 | ||
| 10–24 October 2017 | Statenville—streamwater temperature | MSF | 354 | 2.1746 | 0.152 | 257.29 | 4.1 | 200 |
| O1 | 25.82 | 0.1302 | 0.129 | 330.74 | 70.7 | 1 | ||
| S1/K1 | 24/23.93 | 0.3621 | 0.15 | 102.9 | 24.61 | 5.8 | ||
| M2 | 12.42 | 0.0151 | 0.038 | 111.01 | 174.52 | 0.16 | ||
| S2 | 12 | 0.2973 | 0.062 | 108.66 | 10.7 | 23 | ||
| Jennings—streamwater temperature | MSF | 354 | 2.2924 | 0.1 | 258.79 | 2.21 | 530 | |
| O1 | 25.82 | 0.082 | 0.075 | 178.76 | 58.84 | 1.2 | ||
| S1/K1 | 24/23.93 | 0.1865 | 0.09 | 90.07 | 29.37 | 4.3 | ||
| M2 | 12.42 | 0.0724 | 0.038 | 315.25 | 35.46 | 3.6 | ||
| S2 | 12 | 0.1807 | 0.04 | 94.5 | 10.88 | 20 | ||
| Valdosta—groundwater level | MSF | 354 | 0.4659 | 0.01 | 289.05 | 1.2 | 2300 | |
| O1 | 25.82 | 0.0125 | 0.008 | 101.08 | 40.33 | 2.4 | ||
| S1/K1 | 24/23.93 | 0.0094 | 0.009 | 260.8 | 60.54 | 1.2 | ||
| M2 | 12.42 | 0.0058 | 0.004 | 237.32 | 41.01 | 2.6 | ||
| S2 | 12 | 0.0134 | 0.004 | 112.42 | 19.24 | 11 | ||
| 11–25 October 2018 | Statenville—streamwater temperature | MSF | 354 | 1.6057 | 0.256 | 332.98 | 8.98 | 39 |
| O1 | 25.82 | 0.336 | 0.256 | 129.78 | 40.3 | 1.7 | ||
| S1/K1 | 24/23.93 | 0.3991 | 0.254 | 99.56 | 34.11 | 2.5 | ||
| M2 | 12.42 | 0.0782 | 0.046 | 246.26 | 34.95 | 2.9 | ||
| S2 | 12 | 0.3375 | 0.043 | 109.23 | 8.31 | 62 | ||
| Jennings—streamwater temperature | MSF | 354 | 1.397 | 0.155 | 335.3 | 6.3 | 81 | |
| O1 | 25.82 | 0.2845 | 0.152 | 94.31 | 32.26 | 3.5 | ||
| S1/K1 | 24/23.93 | 0.2056 | 0.153 | 100.97 | 37.59 | 1.8 | ||
| M2 | 12.42 | 0.0753 | 0.049 | 228.89 | 39.15 | 2.4 | ||
| S2 | 12 | 0.1884 | 0.048 | 87.7 | 13.93 | 15 | ||
| Valdosta—groundwater level | MSF | 354 | 0.1404 | 0.003 | 354.86 | 1.32 | 1900 | |
| O1 | 25.82 | 0.0053 | 0.003 | 83.9 | 32.84 | 2.9 | ||
| S1/K1 | 24/23.93 | 0.0012 | 0.002 | 80.98 | 133.03 | 0.36 | ||
| M2 | 12.42 | 0.0022 | 0.001 | 50.33 | 25.12 | 7.8 | ||
| S2 | 12 | 0.0081 | 0.001 | 127.21 | 5.59 | 83 | ||
| 18 October–1 November 2016 | Statenville—streamwater temperature | MSF | 354 | 1.7623 | 0.172 | 189.37 | 5.55 | 100 |
| O1 | 25.82 | 0.0533 | 0.126 | 195.39 | 141.16 | 0.18 | ||
| S1/K1 | 24/23.93 | 0.8898 | 0.17 | 105.55 | 10.56 | 27 | ||
| M2 | 12.42 | 0.0508 | 0.055 | 104.83 | 74.27 | 0.84 | ||
| S2 | 12 | 0.6377 | 0.061 | 88.5 | 4.58 | 110 | ||
| Valdosta—groundwater level | MSF | 354 | 0.2263 | 0.01 | 263.02 | 2.57 | 470 | |
| O1 | 25.82 | 0.0151 | 0.009 | 93.1 | 34.84 | 2.6 | ||
| S1/K1 | 24/23.93 | 0.0086 | 0.009 | 246.6 | 65.7 | 0.84 | ||
| M2 | 12.42 | 0.0044 | 0.005 | 283.26 | 67.1 | 0.88 | ||
| S2 | 12 | 0.0137 | 0.005 | 109.94 | 19.57 | 8.3 |
| Time Interval | Site-Parameter | Tidal Component | Period (h) | Amplitude * | Amplitude Error * | Phase (°) | Phase Error (°) | Signal to Noise Ratio |
|---|---|---|---|---|---|---|---|---|
| 24 July–17 November 2013 | river specific conductivity | M2 | 12.42 | 1.5291 | 1.425 | 279.46 | 64.17 | 1.2 |
| S2 | 12 | 9.1281 | 1.346 | 239.58 | 8.78 | 46 | ||
| groundwater level | M2 | 12.42 | 0.0002 | 0 | 92.14 | 29.2 | 4.3 | |
| S2 | 12 | 0.0007 | 0 | 66.24 | 10.74 | 45 | ||
| 14 August–6 October 2014 | river specific conductivity | M2 | 12.42 | 1.0928 | 1.945 | 29.59 | 115.94 | 0.32 |
| S2 | 12 | 11.3425 | 2.61 | 233.4 | 10.78 | 19 | ||
| groundwater level | M2 | 12.42 | 0.0001 | 0 | 135.83 | 39.69 | 2.2 | |
| S2 | 12 | 0.0005 | 0 | 59.38 | 7.37 | 74 | ||
| 15 April 15–5 June 2017 | river specific conductivity | M2 | 12.42 | 0.6213 | 1.212 | 212.38 | 133.85 | 0.26 |
| S2 | 12 | 6.6299 | 1.673 | 241.32 | 12.59 | 16 | ||
| groundwater level | M2 | 12.42 | 0.0001 | 0 | 21.41 | 94.47 | 0.46 | |
| S2 | 12 | 0.0006 | 0 | 53.51 | 18.41 | 12 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Briciu, A.-E. Changes in Physical Properties of Inland Streamwaters Induced by Earth and Atmospheric Tides. Water 2019, 11, 2533. https://doi.org/10.3390/w11122533
Briciu A-E. Changes in Physical Properties of Inland Streamwaters Induced by Earth and Atmospheric Tides. Water. 2019; 11(12):2533. https://doi.org/10.3390/w11122533
Chicago/Turabian StyleBriciu, Andrei-Emil. 2019. "Changes in Physical Properties of Inland Streamwaters Induced by Earth and Atmospheric Tides" Water 11, no. 12: 2533. https://doi.org/10.3390/w11122533
APA StyleBriciu, A.-E. (2019). Changes in Physical Properties of Inland Streamwaters Induced by Earth and Atmospheric Tides. Water, 11(12), 2533. https://doi.org/10.3390/w11122533





