Conceptual Models and Calibration Performance—Investigating Catchment Bias
Abstract
:1. Introduction
2. Materials and Methods
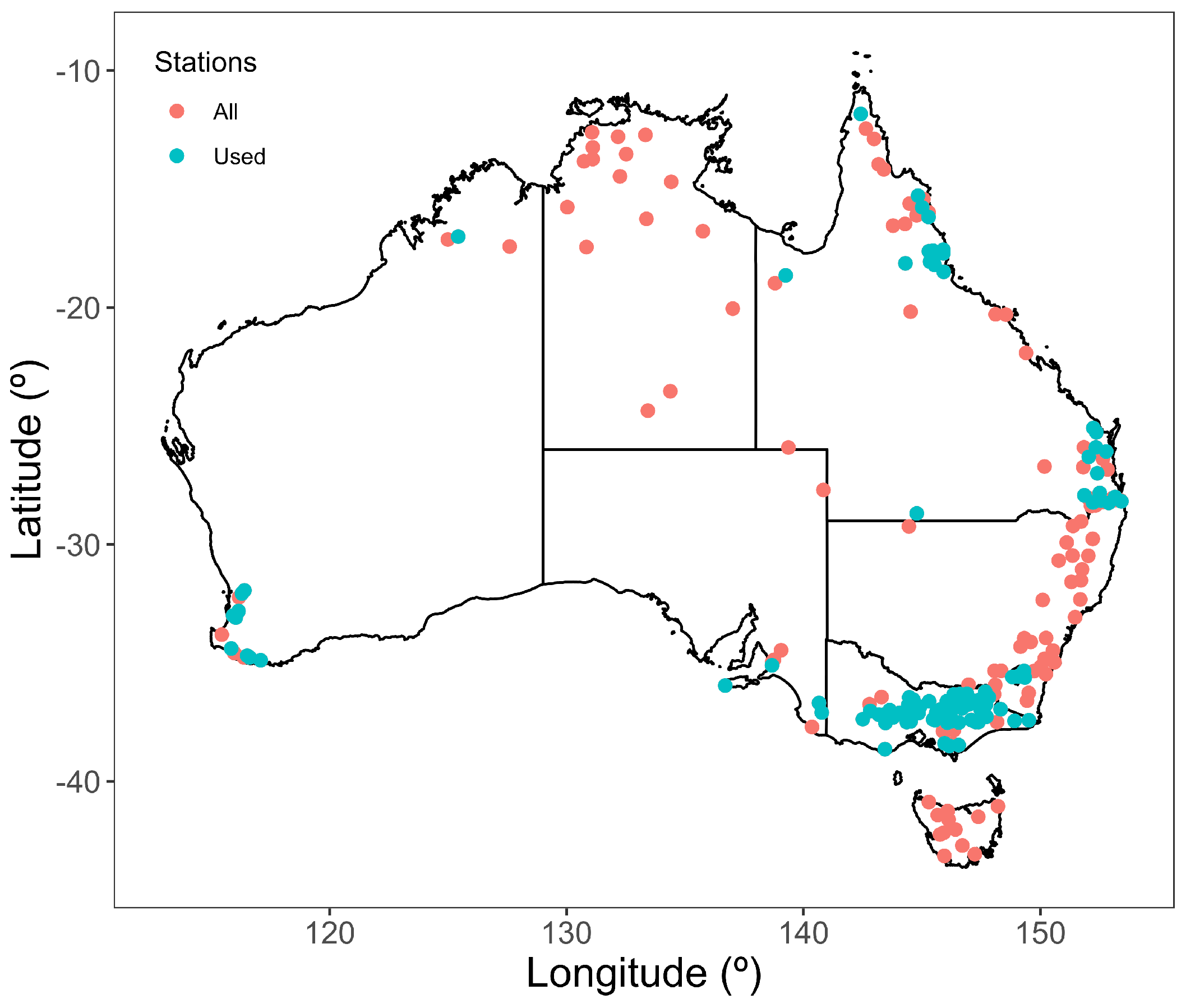
2.1. Study Area and Data Sources
2.2. Model Selection
2.3. Objective Functions
2.4. Analysis
3. Results
3.1. Overview of the Observed Signatures
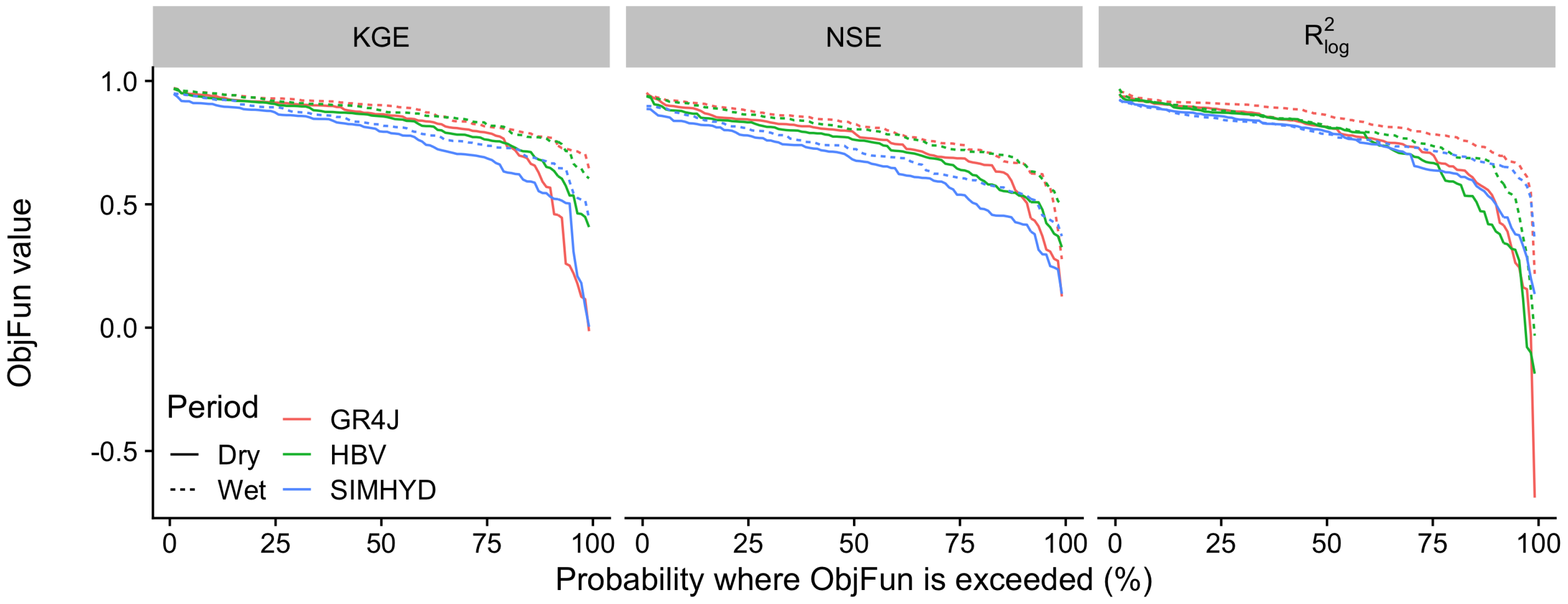
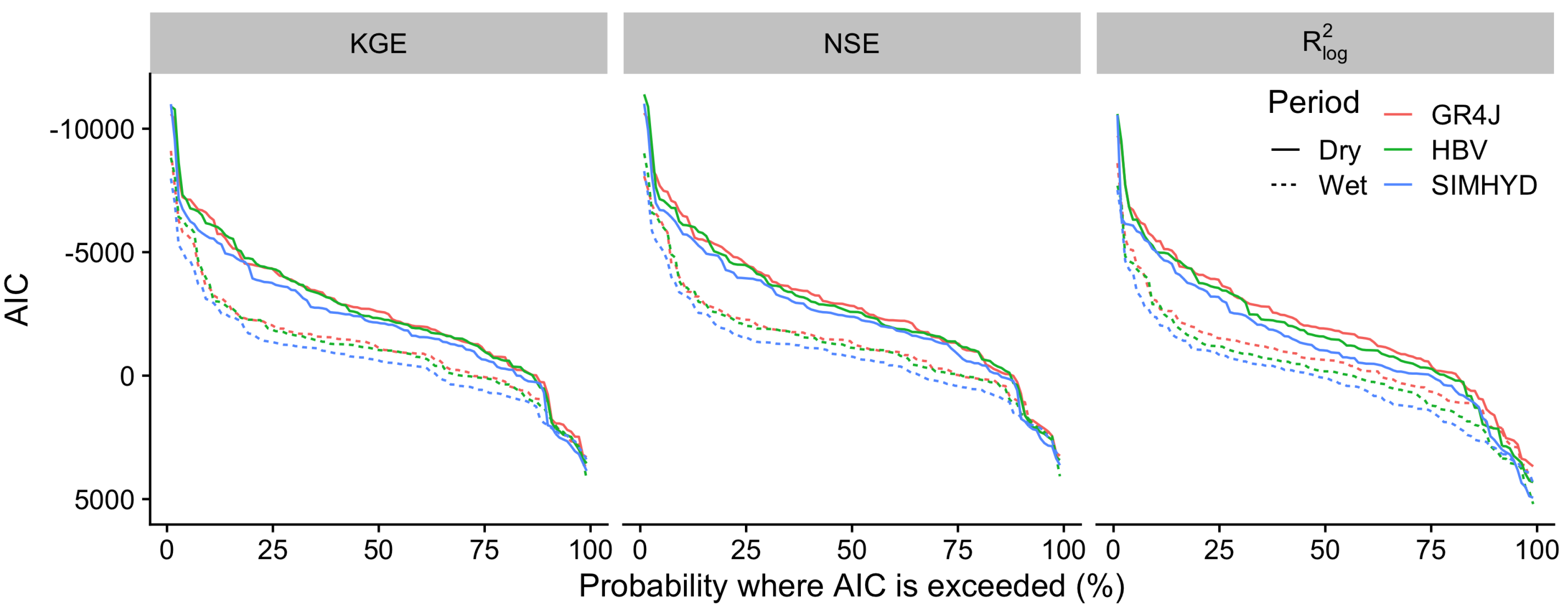
3.2. Model Performance
3.3. Principal Component Analysis
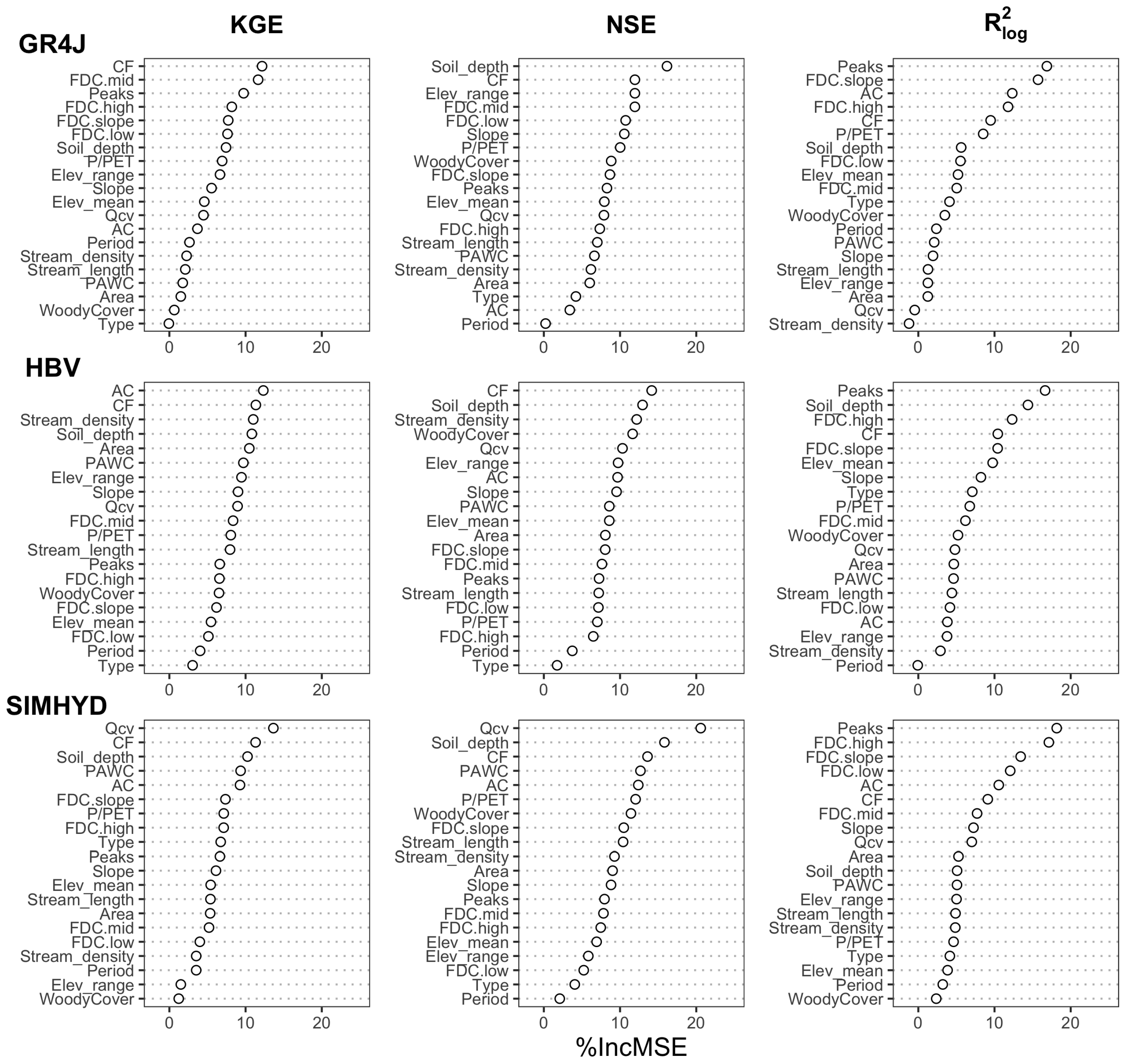
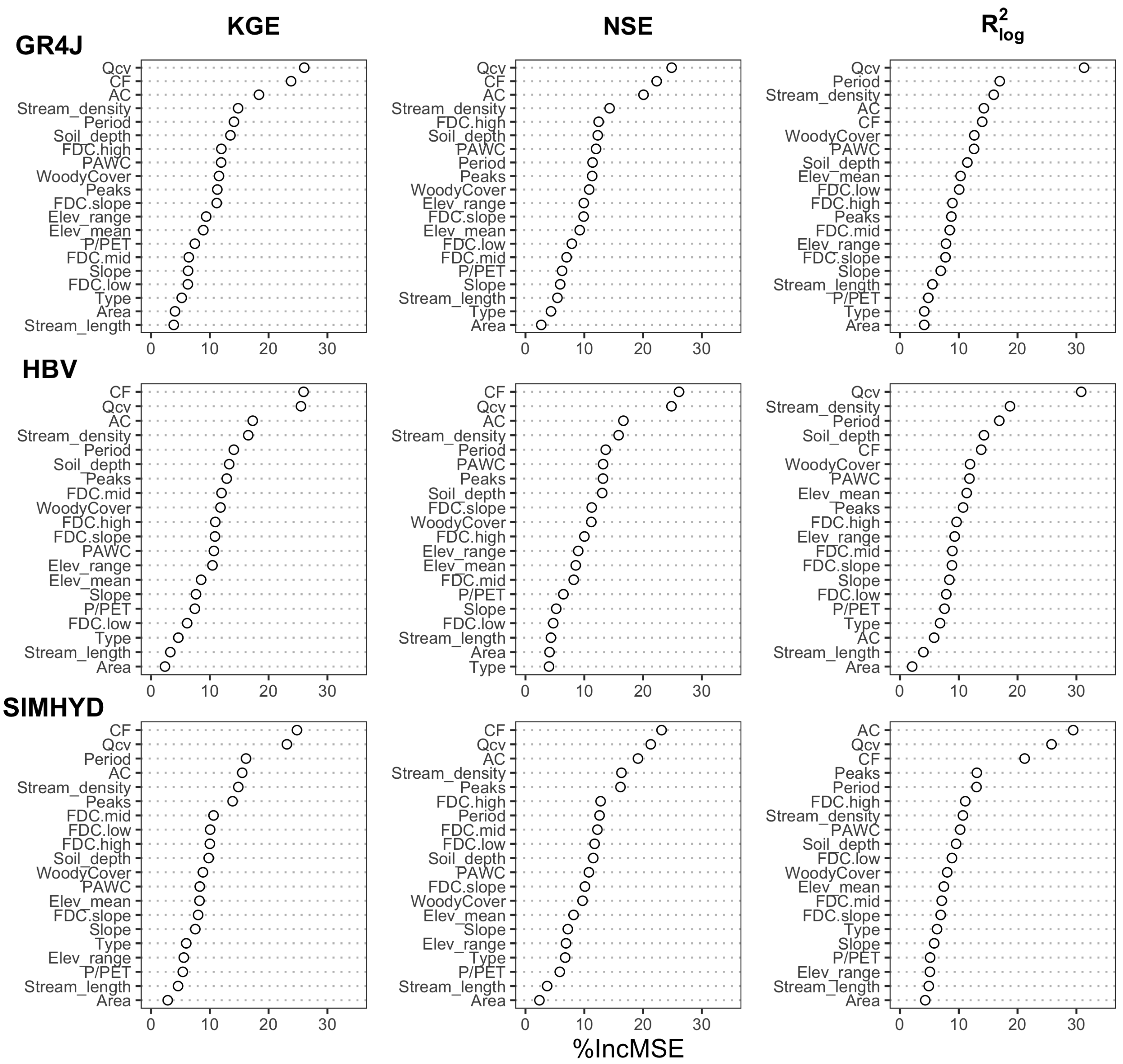
3.4. Random Forest
4. Discussion
4.1. General Performance
4.2. Interpretation of the PCA
4.3. Random Forest
4.4. Model Comparison
4.5. Sources of Uncertainty
4.5.1. Gap Filling
4.5.2. Observed Data
4.5.3. Climate Classification
4.6. Implications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Description | Range |
|---|---|---|
| GR4J | ||
| x1 | Capacity of the production soil (SMA) store (mm) | 50–2000 |
| x2 | Water exchange coefficient (mm) | −10–10 |
| x3 | Capacity of the routing store (mm) | 5–500 |
| x4 | Time parameter (days) for unit hydrographs | 0.5–10 |
| SIMHYD | ||
| INSC | Interception store capacity (mm) | 0.5–5 |
| COEFF | Maximum infiltration loss (mm) | 50–500 |
| SQ | Infiltration loss exponent | 0–6 |
| SMSC | Soil moisture store capcaity (mm) | 50–2000 |
| SUB | Constant of proportionality in interflow equation | 0–1 |
| CRAK | Constant of proportionality in groundwater recharge equation | 0–1 |
| K | Baseflow linear recession parameter | 0.003–0.3 |
| HBV | ||
| FC | Maximum value of soil moisture storage (mm) | 50–2000 |
| Fraction of FC above which AET equals PET | 0.3–1 | |
| Shape coefficient | 1–6 | |
| Recession coefficient | 0.05–0.5 | |
| Recession coefficient | 0.01–0.4 | |
| Recession coefficient | 0.001–0.15 | |
| MAXBAS | Length of triangular weighting function in routing routine (days) | 1–7 |
| PERC | Maximum rate of recharge between upper and lower groundwater boxes | 0–3 |
| Threshold for quick runoff | 10–100 | |
| CFMAX | Snow degree day factor (mm day°C) | 0–20 |
| Snowmelt threshold (°C) | 1 | |
| Snowfall threshold (°C) | −1.419 |
References
- Doherty, J.; Johnston, J.M. Methodologies for Calibration and Predictive Analysis of a Watershed Model1. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 251–265. [Google Scholar] [CrossRef]
- Jones, C.; Sultan, M.; Yan, E.; Milewski, A.; Hussein, M.; Al-Dousari, A.; Al-Kaisy, S.; Becker, R. Hydrologic Impacts of Engineering Projects on the Tigris–Euphrates System and Its Marshlands. J. Hydrol. 2008, 353, 59–75. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought Modeling—A Review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An Overview of Current Applications, Challenges, and Future Trends in Distributed Process-Based Models in Hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Seager, R.; Tzanova, A.; Nakamura, J. Drought in the Southeastern United States: Causes, Variability over the Last Millennium, and the Potential for Future Hydroclimate Change. J. Clim. 2009, 22, 5021–5045. [Google Scholar] [CrossRef]
- Bastola, S.; Murphy, C.; Sweeney, J. The Role of Hydrological Modelling Uncertainties in Climate Change Impact Assessments of Irish River Catchments. Adv. Water Resour. 2011, 34, 562–576. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F.; Perrin, C. Multimodel Evaluation of Twenty Lumped Hydrological Models under Contrasted Climate Conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1171–1189. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L.; Peterson, T. Simulating Runoff under Changing Climatic Conditions: Revisiting an Apparent Deficiency of Conceptual Rainfall-Runoff Models. Water Resour. Res. 2016, 52, 1820–1846. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Does a Large Number of Parameters Enhance Model Performance? Comparative Assessment of Common Catchment Model Structures on 429 Catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J.; DMIP Participants. Overall Distributed Model Intercomparison Project Results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Smith, M.B.; Koren, V.; Reed, S.; Zhang, Z.; Zhang, Y.; Moreda, F.; Cui, Z.; Mizukami, N.; Anderson, E.A.; Cosgrove, B.A. The Distributed Model Intercomparison Project—Phase 2: Motivation and Design of the Oklahoma Experiments. J. Hydrol. 2012, 418–419, 3–16. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Van Steenbergen, N.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of Five Lumped and Distributed Models for Catchment Runoff and Extreme Flow Simulation. J. Hydrol. 2014, 511, 335–349. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Henriksen, H.J.; Harrar, W.G.; Scholten, H.; Kassahun, A. Quality Assurance in Model Based Water Management—Review of Existing Practice and Outline of New Approaches. Environ. Model. Softw. 2005, 20, 1201–1215. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.; McMillan, H.; Gupta, H. Use of an Entropy-Based Metric in Multiobjective Calibration to Improve Model Performance. Water Resour. Res. 2014, 50, 8066–8083. [Google Scholar] [CrossRef]
- Gupta, H.V.; Beven, K.J.; Wagener, T. Model Calibration and Uncertainty Estimation. In Encyclopedia of Hydrological Sciences; American Cancer Society: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Pechlivanidis, I.; Jackson, B.; McIntyre, N.; Wheater, H. Catchment Scale Hydrological Modelling: A Review of Model Types, Calibration Approaches and Uncertainty Analysis Methods in the Context of Recent Developments in Technology and Applications. Glob. NEST J. 2011, 13, 193–214. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Teng, J.; Vaze, J.; Post, D.A.; Perraud, J.M.; Kirono, D.G.C.; Viney, N.R. Estimating Climate Change Impact on Runoff across Southeast Australia: Method, Results, and Implications of the Modeling Method. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Lerat, J.; Vaze, J.; Bourqui, M.; Hendrickx, F. Crash Testing Hydrological Models in Contrasted Climate Conditions: An Experiment on 216 Australian Catchments. Water Resour. Res. 2012, 48, W05552. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A Decade of Predictions in Ungauged Basins (PUB)—A Review. J. Des. Sci. Hydrol. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Trancoso, R.; Larsen, J.R.; McAlpine, C.; McVicar, T.R.; Phinn, S. Linking the Budyko Framework and the Dunne Diagram. J. Hydrol. 2016, 535, 581–597. [Google Scholar] [CrossRef]
- Andréassian, V.; Moine, N.L.; Perrin, C.; Ramos, M.H.; Oudin, L.; Mathevet, T.; Lerat, J.; Berthet, L. All That Glitters Is Not Gold: The Case of Calibrating Hydrological Models. Hydrol. Process. 2012, 26, 2206–2210. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gupta, V.K.; Fulton, J.L. Evaluation of Maximum Likelihood Parameter Estimation Techniques for Conceptual Rainfall-Runoff Models: Influence of Calibration Data Variability and Length on Model Credibility. Water Resour. Res. 1983, 19, 251–259. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. A Comparison of Alternative Multiobjective Calibration Strategies for Hydrological Modeling. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time Stability of Catchment Model Parameters: Implications for Climate Impact Analyses. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Singh, R.; Wagener, T.; van Werkhoven, K.; Mann, M.E.; Crane, R. A Trading-Space-for-Time Approach to Probabilistic Continuous Streamflow Predictions in a Changing Climate—Accounting for Changing Watershed Behavior. Hydrol. Earth Syst. Sci. 2011, 15, 3591–3603. [Google Scholar] [CrossRef]
- Vaze, J.; Chiew, F.H.S.; Perraud, J.M.; Viney, N.; Post, D.; Teng, J.; Wang, B.; Lerat, J.; Goswami, M. Rainfall-Runoff Modelling Across Southeast Australia: Datasets, Models and Results. Aust. J. Water Resour. 2011, 14, 101–116. [Google Scholar] [CrossRef]
- Saft, M.; Western, A.W.; Zhang, L.; Peel, M.C.; Potter, N.J. The Influence of Multiyear Drought on the Annual Rainfall-Runoff Relationship: An Australian Perspective. Water Resour. Res. 2015, 51, 2444–2463. [Google Scholar] [CrossRef]
- Saft, M.; Peel, M.C.; Western, A.W.; Zhang, L. Predicting Shifts in Rainfall-Runoff Partitioning during Multiyear Drought: Roles of Dry Period and Catchment Characteristics. Water Resour. Res. 2016, 52, 9290–9305. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L. Improved Rainfall-Runoff Calibration for Drying Climate: Choice of Objective Function. Water Resour. Res. 2018, 54, 3392–3408. [Google Scholar] [CrossRef] [Green Version]
- Klemeš, V. Operational Testing of Hydrological Simulation Models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Knudsen, J. Operational Validation and Intercomparison of Different Types of Hydrological Models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Fowler, K.; Coxon, G.; Freer, J.; Peel, M.; Wagener, T.; Western, A.; Woods, R.; Zhang, L. Simulating Runoff Under Changing Climatic Conditions: A Framework for Model Improvement. Water Resour. Res. 2018, 54, 9812–9832. [Google Scholar] [CrossRef] [Green Version]
- Van Esse, W.R.; Perrin, C.; Booij, M.J.; Augustijn, D.C.M.; Fenicia, F.; Kavetski, D.; Lobligeois, F. The Influence of Conceptual Model Structure on Model Performance: A Comparative Study for 237 French Catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4227–4239. [Google Scholar] [CrossRef] [Green Version]
- Broderick, C.; Matthews, T.; Wilby, R.L.; Bastola, S.; Murphy, C. Transferability of Hydrological Models and Ensemble Averaging Methods between Contrasting Climatic Periods. Water Resour. Res. 2016, 52, 8343–8373. [Google Scholar] [CrossRef] [Green Version]
- Bloomfield, J.P.; Allen, D.J.; Griffiths, K.J. Examining Geological Controls on Baseflow Index (BFI) Using Regression Analysis: An Illustration from the Thames Basin, UK. J. Hydrol. 2009, 373, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.S.; Amirthanathan, G.E.; Bari, M.A.; Laugesen, R.M.; Shin, D.; Kent, D.M.; MacDonald, A.M.; Turner, M.E.; Tuteja, N.K. How Streamflow Has Changed across Australia since the 1950s: Evidence from the Network of Hydrologic Reference Stations. Hydrol. Earth Syst. Sci. 2016, 20, 3947–3965. [Google Scholar] [CrossRef] [Green Version]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in Southeast Australia (2001–2009): Natural and Human Causes and Implications for Water Resources, Ecosystems, Economy, and Society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Morton, F.I. Operational Estimates of Areal Evapotranspiration and Their Significance to the Science and Practice of Hydrology. J. Hydrol. 1983, 66, 1–76. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using Spatial Interpolation to Construct a Comprehensive Archive of Australian Climate Data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W. Application and Testing of the Simple Rainfall Runoff Model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Singh, V., Frevert, D., Eds.; Water Resources Publications: Littleton, CO, USA, 2002; pp. 335–367. [Google Scholar]
- Bergström, S. The HBV Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 443–476. [Google Scholar]
- Andrews, F.T.; Croke, B.F.W.; Jakeman, A.J. An Open Software Environment for Hydrological Model Assessment and Development. Environ. Model. Softw. 2011, 26, 1171–1185. [Google Scholar] [CrossRef]
- Herman, J.D.; Reed, P.M.; Wagener, T. Time-Varying Sensitivity Analysis Clarifies the Effects of Watershed Model Formulation on Model Behavior. Water Resour. Res. 2013, 49, 1400–1414. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising Performance of Environmental Models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and Efficient Global Optimization for Conceptual Rainfall-Runoff Models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Chu, W.; Gao, X.; Sorooshian, S. Improving the Shuffled Complex Evolution Scheme for Optimization of Complex Nonlinear Hydrological Systems: Application to the Calibration of the Sacramento Soil-Moisture Accounting Model. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Arsenault, R.; Poulin, A.; Côté, P.; Brissette, F. Comparison of Stochastic Optimization Algorithms in Hydrological Model Calibration. J. Hydrol. Eng. 2014, 19, 1374–1384. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Sawicz, K.; Wagener, T.; Sivapalan, M.; Troch, P.A.; Carrillo, G. Catchment Classification: Empirical Analysis of Hydrologic Similarity Based on Catchment Function in the Eastern USA. Hydrol. Earth Syst. Sci. 2011, 15, 2895–2911. [Google Scholar] [CrossRef] [Green Version]
- Euser, T.; Winsemius, H.C.; Hrachowitz, M.; Fenicia, F.; Uhlenbrook, S.; Savenije, H.H.G. A Framework to Assess the Realism of Model Structures Using Hydrological Signatures. Hydrol. Earth Syst. Sci. 2013, 17, 1893–1912. [Google Scholar] [CrossRef] [Green Version]
- Stein, J.L.; Hutchinson, M.F.; Stein, J.A. A New Stream and Nested Catchment Framework for Australia. Hydrol. Earth Syst. Sci. 2014, 18, 1917–1933. [Google Scholar] [CrossRef] [Green Version]
- Gallant, J.; Read, A.; Dowling, T. Building the National One-Second Digital Elevation Model for Australia. In Science Symposium Proceedings; CSIRO: Melbourne, Australia, 2012; pp. 250–256. [Google Scholar]
- Grundy, M.J.; Rossel, R.A.V.; Searle, R.D.; Wilson, P.L.; Chen, C.; Gregory, L.J. Soil and Landscape Grid of Australia. Soil Res. 2015, 53, 835–844. [Google Scholar] [CrossRef]
- Johnston, R.M.; Barry, S.J.; Bleys, E.; Bui, E.N.; Moran, C.J.; Simon, D.A.P.; Carlile, P.; McKenzie, N.J.; Henderson, B.L.; Chapman, G.; et al. ASRIS: The Database. Soil Res. 2003, 41, 1021–1036. [Google Scholar] [CrossRef]
- Gill, T.; Johansen, K.; Phinn, S.; Trevithick, R.; Scarth, P.; Armston, J. A Method for Mapping Australian Woody Vegetation Cover by Linking Continental-Scale Field Data and Long-Term Landsat Time Series. Int. J. Remote Sens. 2017, 38, 679–705. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Grimm, R.; Behrens, T.; Märker, M.; Elsenbeer, H. Soil Organic Carbon Concentrations and Stocks on Barro Colorado Island—Digital Soil Mapping Using Random Forests Analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene Selection and Classification of Microarray Data Using Random Forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [Green Version]
- Van Dijk, A.I.J.M.; Keenan, R.J. Planted Forests and Water in Perspective. For. Ecol. Manag. 2007, 251, 1–9. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable Nonstationarity: An Assessment of the Fitness for Purpose of Trend Tests in Hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Yuan, N.; Fu, Z.; Liu, S. Long-Term Memory in Climate Variability: A New Look Based on Fractional Integral Techniques. J. Geophys. Res. Atmos. 2013, 118, 12962–12969. [Google Scholar] [CrossRef]
- Seibert, J. On the Need for Benchmarks in Hydrological Modelling. Hydrol. Process. 2001, 15, 1063–1064. [Google Scholar] [CrossRef]
- Schaefli, B.; Gupta, H.V. Do Nash Values Have Value? Hydrol. Process. 2007, 21, 2075–2080. [Google Scholar] [CrossRef] [Green Version]
- Breuer, L.; Huisman, J.; Willems, P.; Bormann, H.; Bronstert, A.; Croke, B.; Frede, H.G.; Graff, T.; Hubrechts, L.; Jakeman, A.; et al. Assessing the Impact of Land Use Change on Hydrology by Ensemble Modeling (LUCHEM). I: Model Intercomparison with Current Land Use. Adv. Water Resour. 2009, 32, 18. [Google Scholar] [CrossRef]
- Moine, N.L.; Andréassian, V.; Perrin, C.; Michel, C. How Can Rainfall-Runoff Models Handle Intercatchment Groundwater Flows? Theoretical Study Based on 1040 French Catchments. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zhang, Y.; Post, D. How Good Are Hydrological Models for Gap-Filling Streamflow Data? Hydrol. Earth Syst. Sci. 2018, 22, 4593–4604. [Google Scholar] [CrossRef] [Green Version]
- Renard, B.; Kavetski, D.; Leblois, E.; Thyer, M.; Kuczera, G.; Franks, S.W. Toward a Reliable Decomposition of Predictive Uncertainty in Hydrological Modeling: Characterizing Rainfall Errors Using Conditional Simulation. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Tozer, C.R.; Kiem, A.S.; Verdon-Kidd, D.C. On the Uncertainties Associated with Using Gridded Rainfall Data as a Proxy for Observed. Hydrol. Earth Syst. Sci. 2012, 16, 1481–1499. [Google Scholar] [CrossRef] [Green Version]
- Baldassarre, G.D.; Montanari, A. Uncertainty in River Discharge Observations: A Quantitative Analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913–921. [Google Scholar] [CrossRef] [Green Version]
- Tomkins, K.M. Uncertainty in Streamflow Rating Curves: Methods, Controls and Consequences. Hydrol. Process. 2014, 28, 464–481. [Google Scholar] [CrossRef]
- Beven, K.; Westerberg, I. On Red Herrings and Real Herrings: Disinformation and Information in Hydrological Inference. Hydrol. Process. 2011, 25, 1676–1680. [Google Scholar] [CrossRef]
- Silberstein, R.P.; Aryal, S.K.; Durrant, J.; Pearcey, M.; Braccia, M.; Charles, S.P.; Boniecka, L.; Hodgson, G.A.; Bari, M.A.; Viney, N.R.; et al. Climate Change and Runoff in South-Western Australia. J. Hydrol. 2012, 475, 441–455. [Google Scholar] [CrossRef]
- Bates, B.C.; Hope, P.; Ryan, B.; Smith, I.; Charles, S. Key Findings from the Indian Ocean Climate Initiative and Their Impact on Policy Development in Australia. Clim. Chang. 2008, 89, 339–354. [Google Scholar] [CrossRef]

| Unit | Description | |
|---|---|---|
| Signature | ||
| FDC.low | mm | 90th quantile of flow |
| FDC.mid | mm | 50th quantile of flow |
| FDC.high | mm | 1st quantile of flow |
| FDC.slope | - | Slope of the middle part of the flow duration curve |
| AC | - | Correlation coefficient between 2 points-1 day |
| Peaks | - | Calculates difference between the height of peak events |
| CF | mm | Cumulative flow over the time period |
| Characteristic | ||
| Qcv | - | Coefficient of variation of annual streamflow |
| P/PET | - | Aridity index: ratio of annual P to annual PET |
| Area | km | Catchment area |
| Elevation | m | Mean elevation within the catchment |
| Elevation range | m | Elevation range within the catchment |
| PAWC | mm | Mean plant available water capacity in the top 1 m of soil |
| Slope | ° | Mean slope within the catchment |
| Soil depth | m | Mean depth of soil within the catchment |
| Stream length | km | Sum of the length of streams |
| Stream density | km/km | Density of streams (stream length/catchment area) |
| Woody cover | % | Mean percent cover of woody vegetation |
| River type | - | Perennial: no flow ≤ 1% of the time |
| Ephemeral: no flow > 1% of the time |
| Characteristic | Ephemeral | Perennial | ||||
|---|---|---|---|---|---|---|
| Mean | Median | SD | Mean | Median | SD | |
| Qcv | 17,921 | 7532 | 35,273 | 59,007 | 23,584 | 122,439 |
| Aridity index (P/PET) | 0.57 | 0.54 | 0.20 | 0.90 | 0.90 | 0.32 |
| Catchment area (km) | 1028 | 304 | 2907 | 727 | 316 | 1987 |
| Mean elevation (m) | 427 | 398 | 252 | 656 | 678 | 303 |
| Elevation range (m) | 575 | 491 | 340 | 918 | 990 | 434 |
| Mean PAWC (mm) | 93 | 88 | 31 | 125 | 127 | 38 |
| Mean slope (°) | 5.4 | 4.5 | 3.7 | 11.5 | 12.2 | 5.3 |
| Mean soil depth (m) | 0.97 | 0.96 | 0.10 | 0.99 | 1.00 | 0.13 |
| Stream length (km) | 689 | 232 | 1631 | 555 | 234 | 1435 |
| Stream density (km/km) | 0.76 | 0.79 | 0.21 | 0.81 | 0.82 | 0.15 |
| Woody cover (%) | 33 | 31 | 19 | 50 | 51 | 19 |
| Period | Statistic | CF | FDC.low | FDC.mid | FDC.high | FDC.slope | AC | Peaks |
|---|---|---|---|---|---|---|---|---|
| Wet | Median | 1183 | 0.018 | 0.121 | 5.683 | 0.223 | 0.723 | 2.110 |
| Wet | Mean | 1719 | 0.091 | 0.330 | 7.094 | 0.505 | 0.724 | 3.313 |
| Dry | Median | 739 | 0.005 | 0.065 | 2.793 | 0.149 | 0.763 | 1.438 |
| Dry | Mean | 1375 | 0.064 | 0.236 | 4.832 | 0.419 | 0.741 | 2.504 |
| ObjFun Value | AIC | |||||
|---|---|---|---|---|---|---|
| Model | KGE | NSE | KGE | NSE | ||
| GR4J | 37.82 | 40.21 | 57.86 | 84.86 | 86.48 | 76.17 |
| HBV | 47.20 | 45.35 | 57.13 | 87.76 | 88.55 | 78.54 |
| SIMHYD | 60.71 | 61.80 | 73.13 | 85.10 | 87.71 | 79.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buzacott, A.J.V.; Tran, B.; van Ogtrop, F.F.; Vervoort, R.W. Conceptual Models and Calibration Performance—Investigating Catchment Bias. Water 2019, 11, 2424. https://doi.org/10.3390/w11112424
Buzacott AJV, Tran B, van Ogtrop FF, Vervoort RW. Conceptual Models and Calibration Performance—Investigating Catchment Bias. Water. 2019; 11(11):2424. https://doi.org/10.3390/w11112424
Chicago/Turabian StyleBuzacott, Alexander J. V., Bruce Tran, Floris F. van Ogtrop, and R. Willem Vervoort. 2019. "Conceptual Models and Calibration Performance—Investigating Catchment Bias" Water 11, no. 11: 2424. https://doi.org/10.3390/w11112424
APA StyleBuzacott, A. J. V., Tran, B., van Ogtrop, F. F., & Vervoort, R. W. (2019). Conceptual Models and Calibration Performance—Investigating Catchment Bias. Water, 11(11), 2424. https://doi.org/10.3390/w11112424





