Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads
Abstract
1. Introduction
- (1)
- Do varying constant hydraulic heads affect flow regime and hydraulic conductivity?
- (2)
- What are the flow characteristics in low-permeability porous media with very low Re values?
- (3)
- What is the upper boundary of Re for Darcy’s law in porous media with very low Re values?
2. Materials and Methods
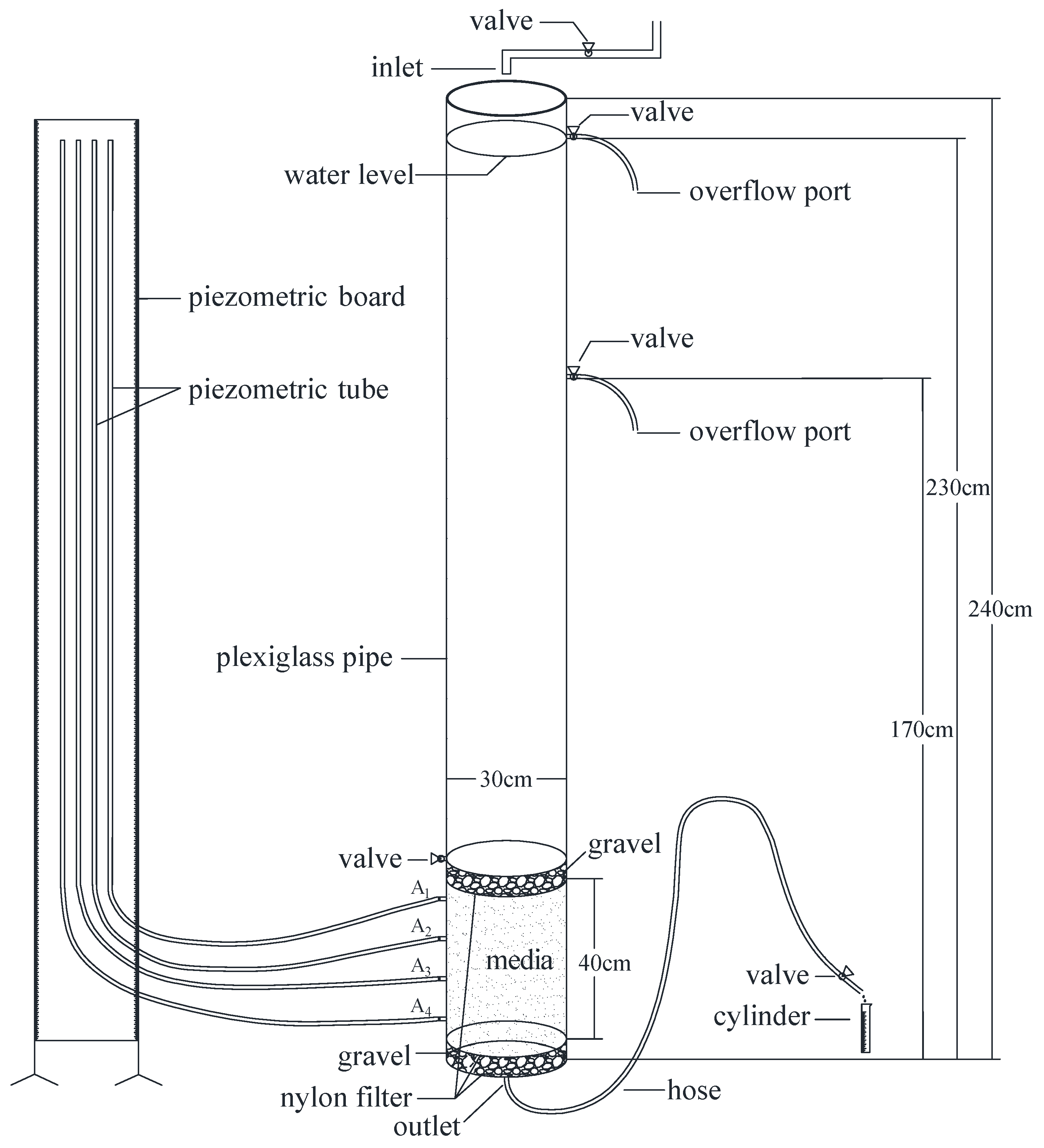
2.1. Experimental Setup
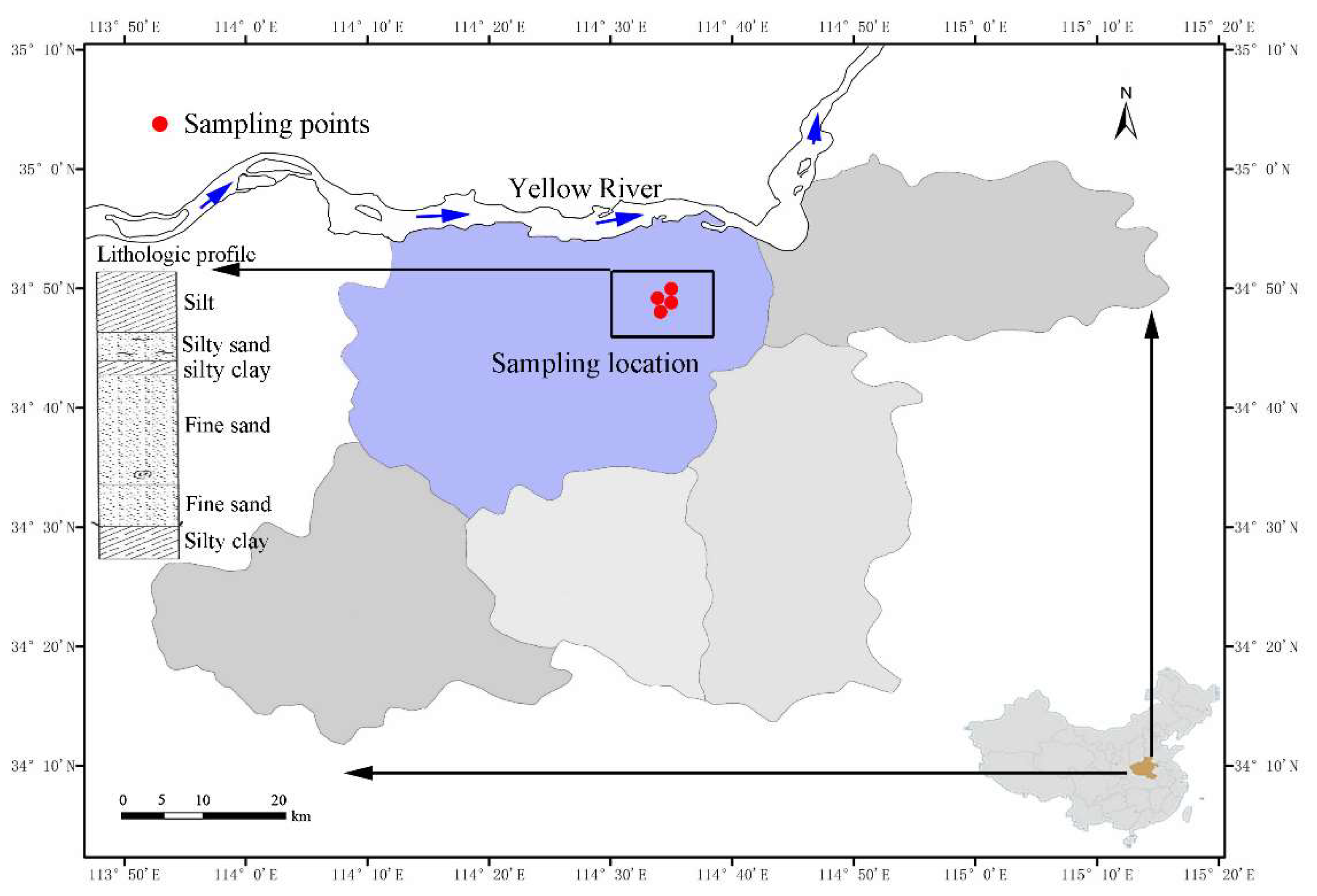
2.2. Experimental Media and Scheme
3. Results and Discussion
3.1. Reynolds Numbers of Experimental Media
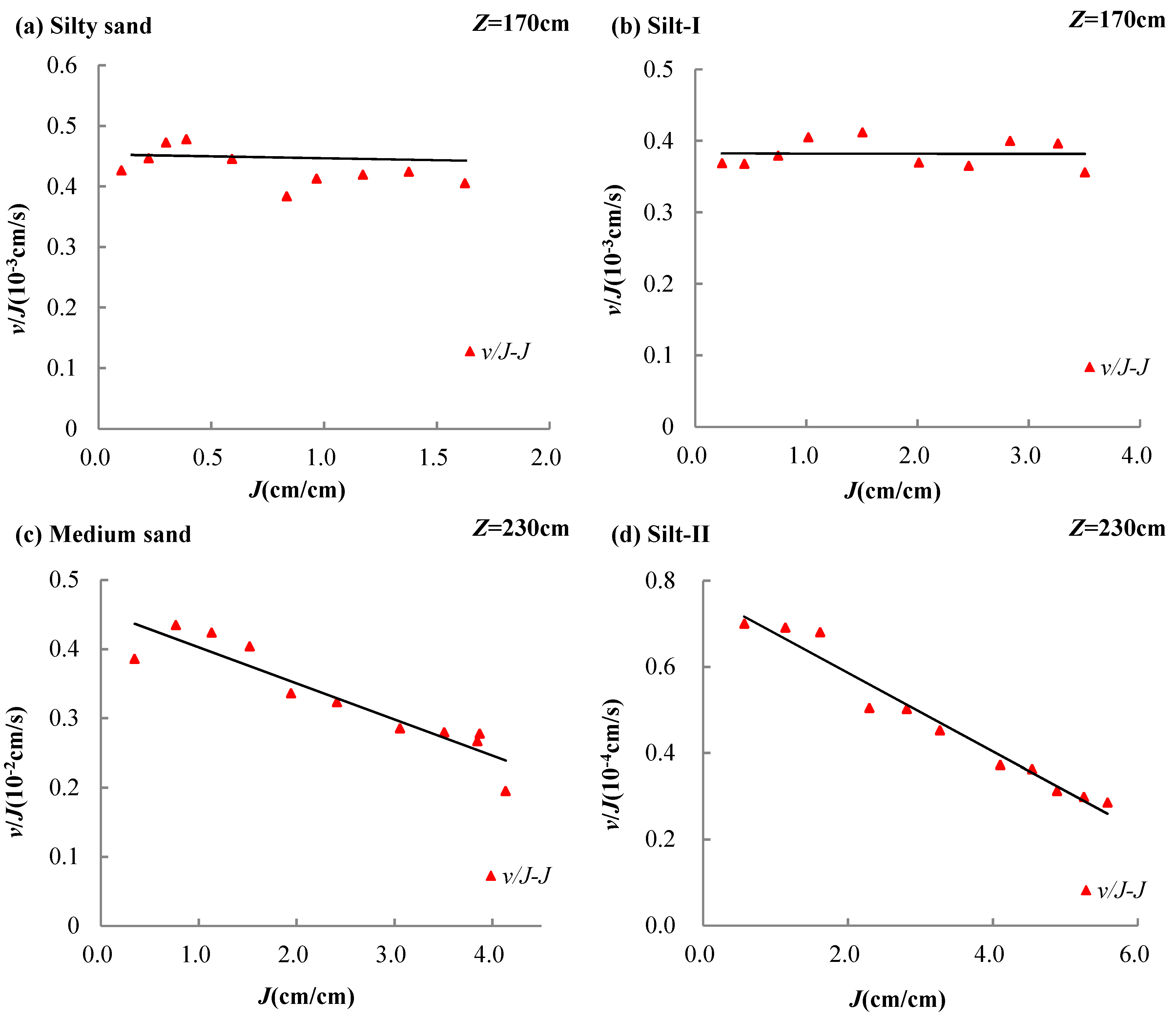
3.2. Effect of Constant Hydraulic Head on Flow Regime and Hydraulic Conductivity
3.3. Characteristics of the Flow in Porous Media with Weak Permeability at Low Reynolds Numbers (Re→0)
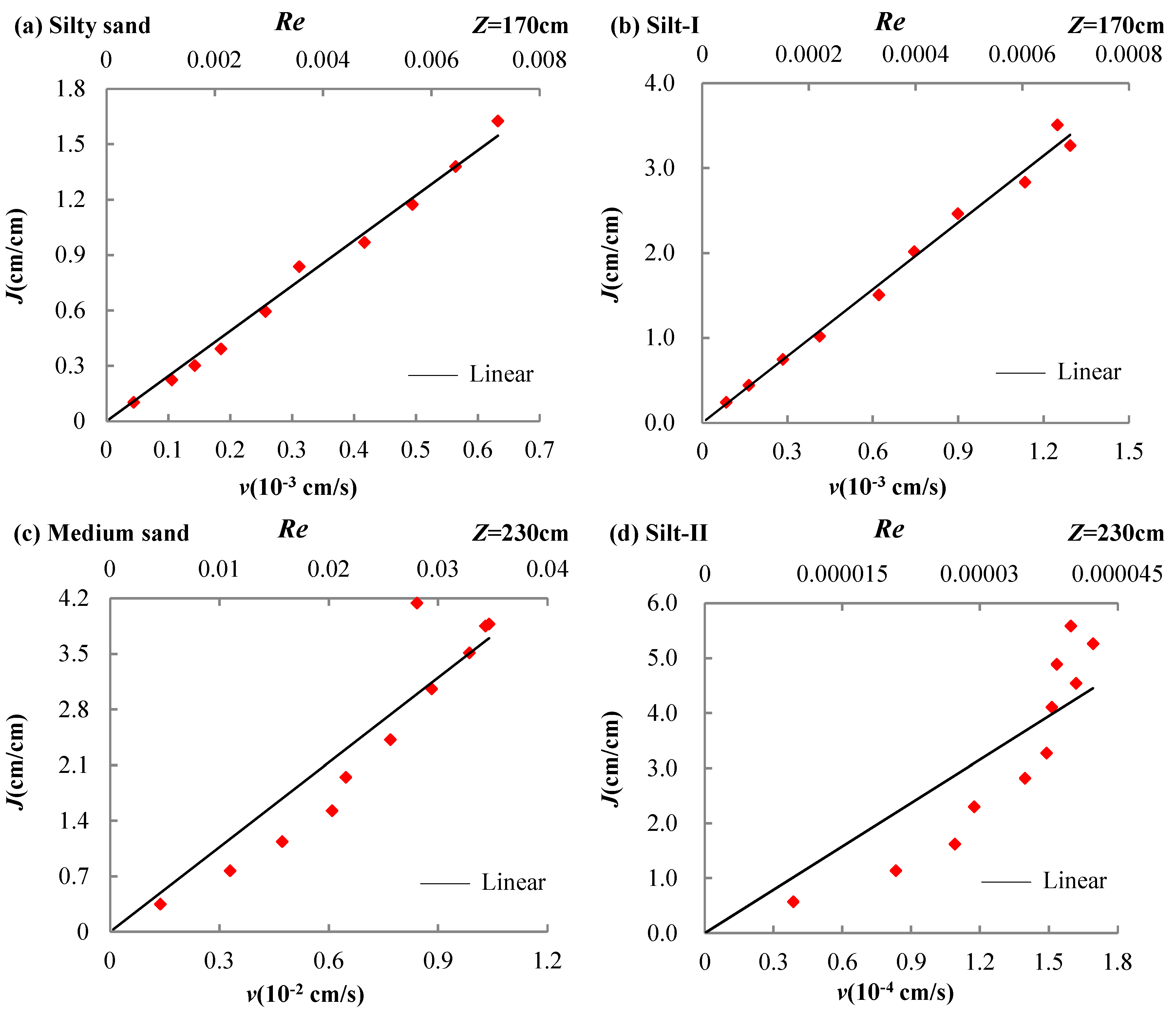
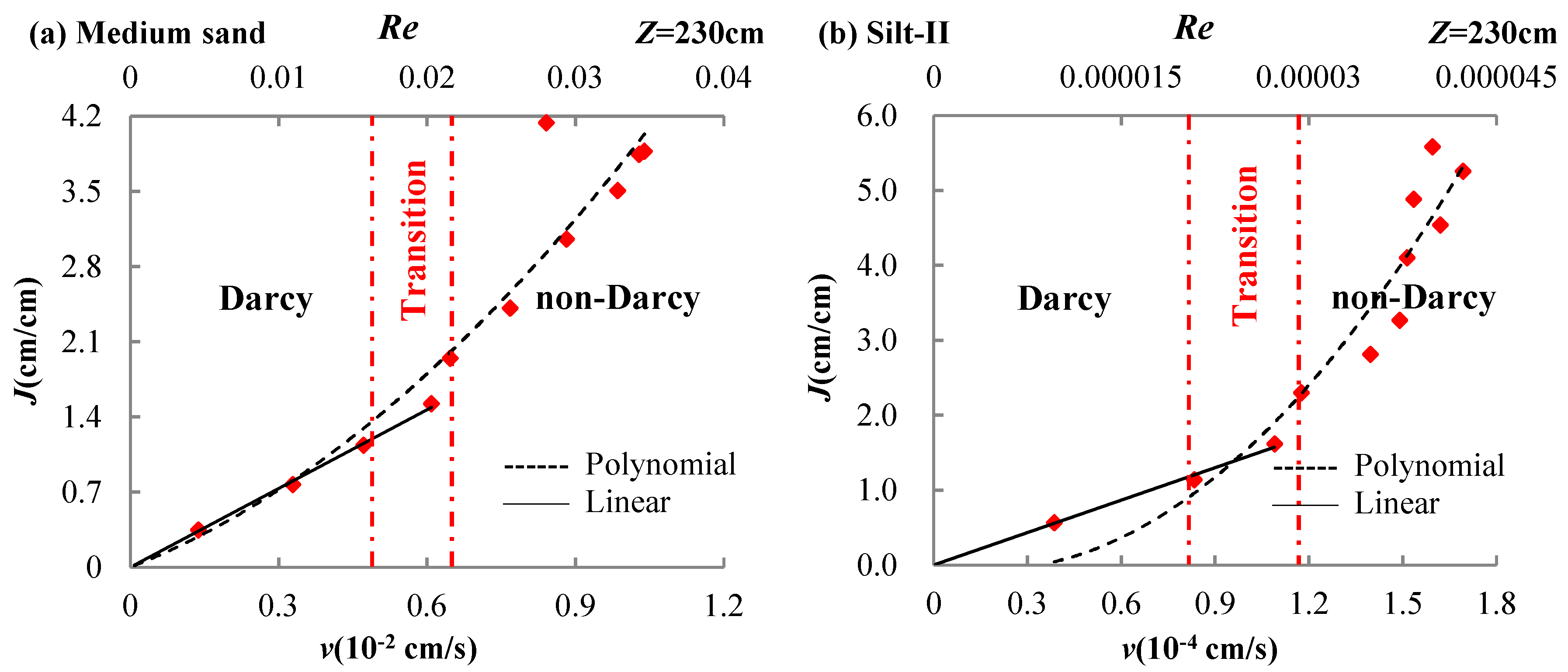
3.4. Upper Limit of the Validity of Darcy’s Law for Porous Media at Low Reynolds Numbers (Re→0)
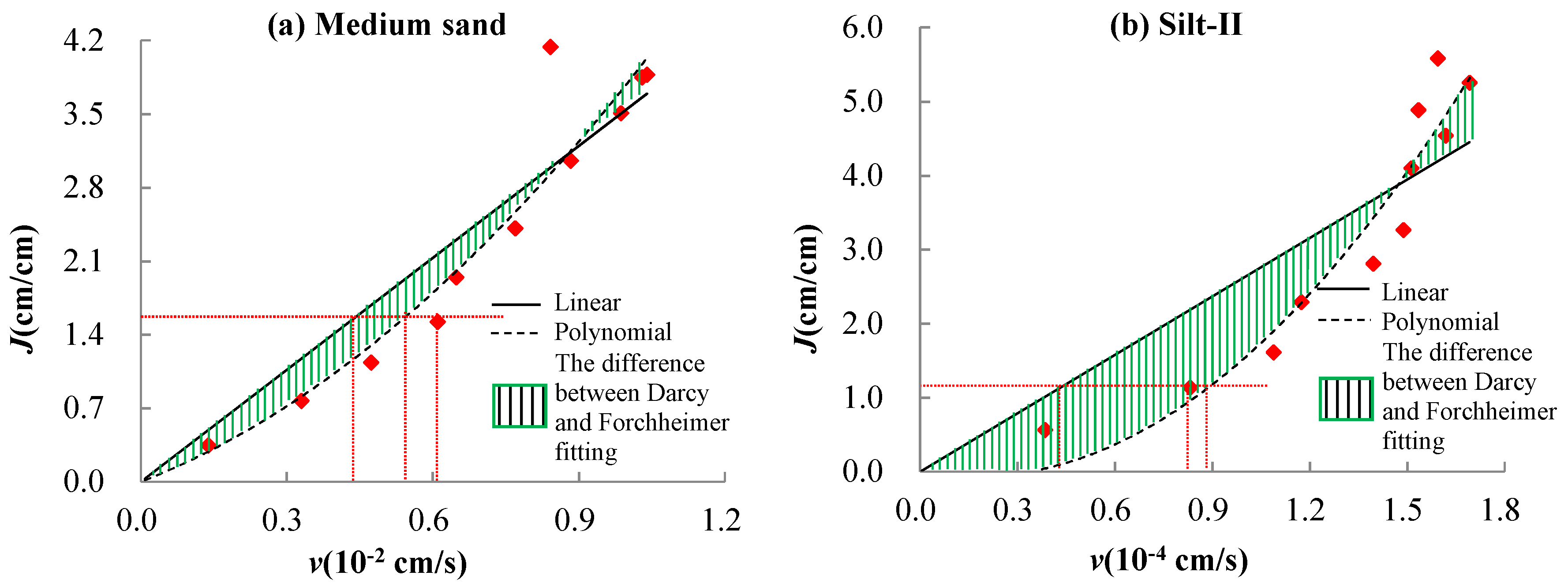
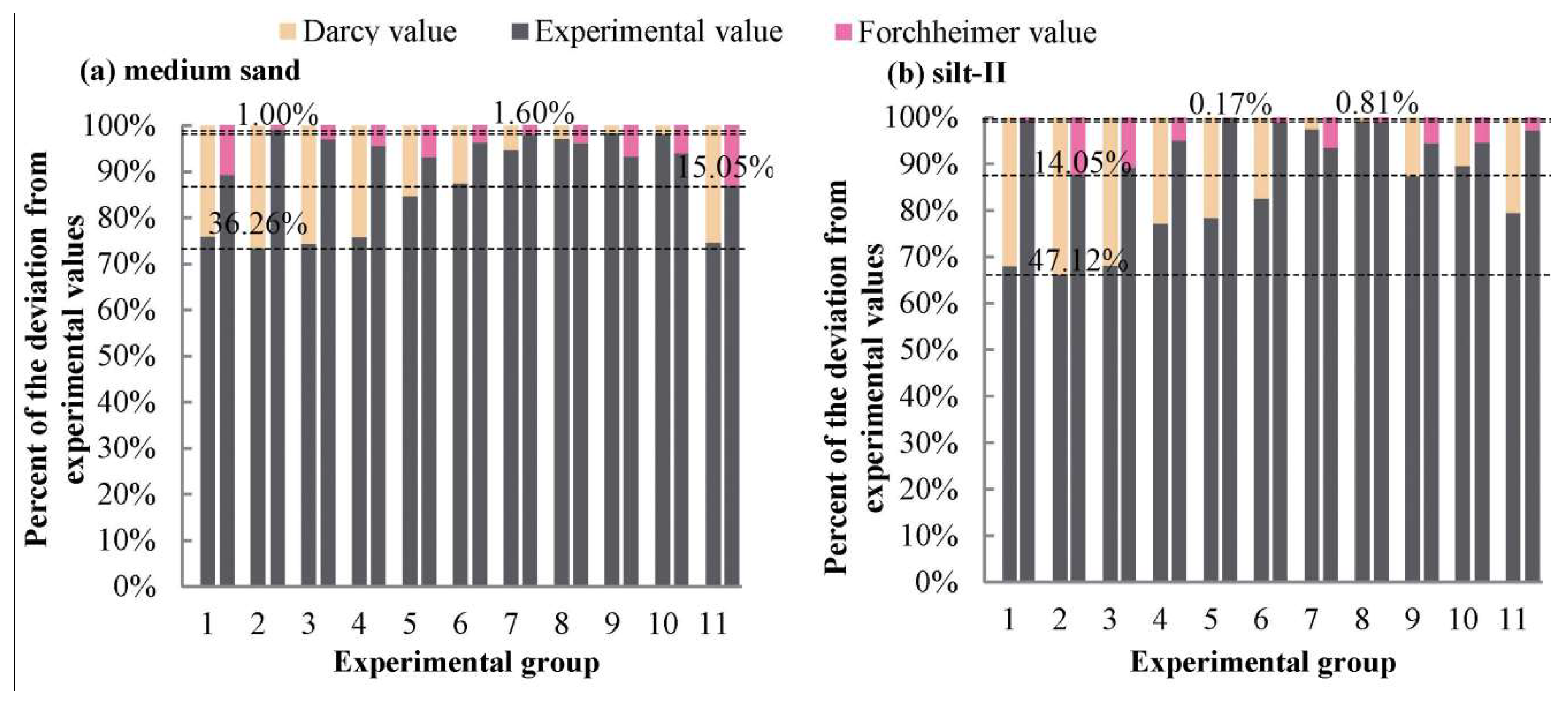
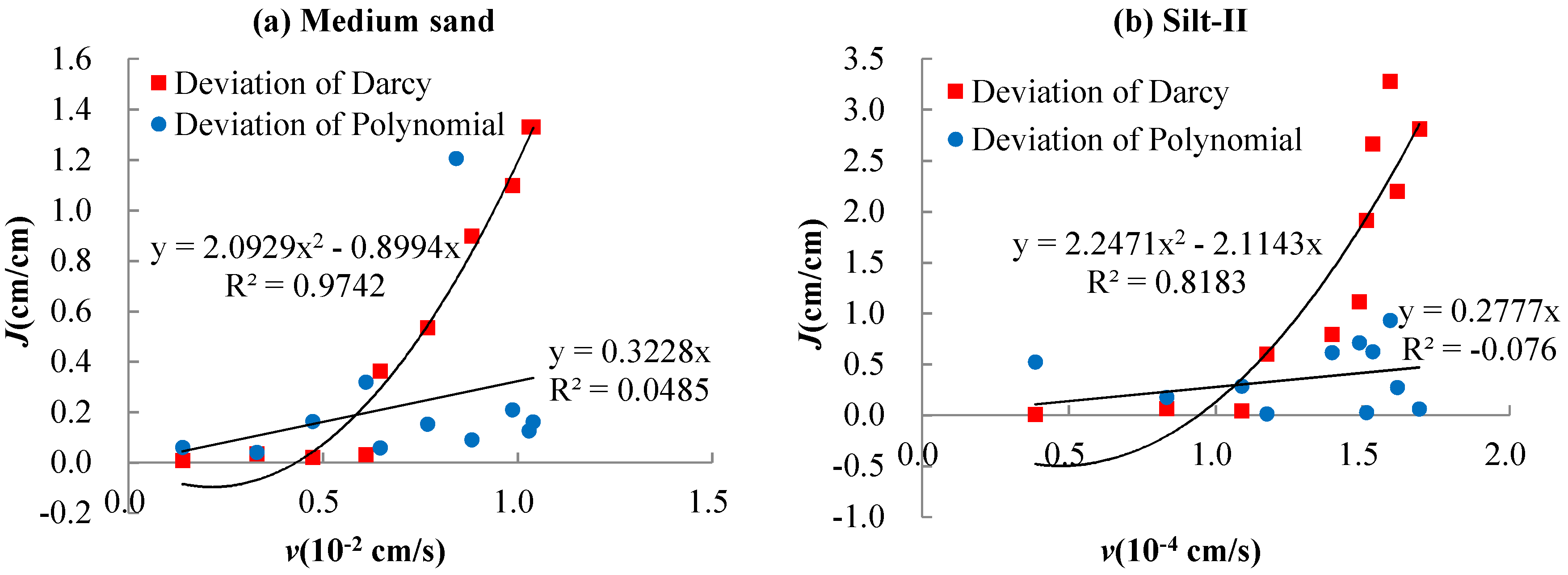
3.5. Error Analysis on Darcy’s Law and Forchheimer Equation in Non-Darcy Flow
3.6. Limitations, Uncertainties, and Future Work
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Childs, E.C.; Collis-George, N. The permeability of porous materials. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 201, 392–405. [Google Scholar]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Lin, H.Z.; Peng, J.B.; Yang, H.; Jia, S.L. A simple estimation approach for the saturated permeability of loess in field by a double-ring infiltrometer. Adv. Water Sci. 2017, 28, 523–533. [Google Scholar]
- Chen, C.X.; Lin, M. Groundwater Dynamics; China University of Geosciences Press: Wuhan, China, 1999; p. 3. [Google Scholar]
- Wan, J.W.; Huang, K.; Chen, C.X. Reassessing Darcy’s law on Water in Porous Media. Earth Sci. J. China Univ. Geosci. 2013, 38, 1327–1330. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon. Librairie des Corps Imperiaux des Ponts et Chaussees et des Mines, Paris. 1856. Available online: https://gallica.bnf.fr/ark:/12148/bpt6k624312.image (accessed on 5 November 2019).
- Brown, G.O. Henry Darcy and the making of a law. Water Resour. Res. 2002, 38, 11-1-11-12. [Google Scholar] [CrossRef]
- Chaudhary, K.; Cardenas, M.B.; Deng, W.; Bennett, P.C. The role of eddies inside pores in the transition from Darcy to Forchheimer flows. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Yamada, H.; Nakamura, F.; Watanabe, Y.; Murakami, M.; Nogami, T. Measuring hydraulic permeability in a streambed using the packer test. Hydrol. Process. 2005, 19, 2507–2524. [Google Scholar] [CrossRef]
- Dupuit, J. Études théoriques et pratiques sur le mouvement des eaux; Dunod: Paris, France, 1863. [Google Scholar]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; No. 532.5 M88; The Mapple Press Company: York, PA, USA, 1946. [Google Scholar]
- Izbash, S.V. O Filtracii V Kropnozernstom Materiale; USSR: Leningrad, Russia, 1931. (In Russian) [Google Scholar]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Flow Turbul. Combust. 1949, 1, 27. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Schneebeli, G. Expériences sur la limite de validité de la loi de Darcy et l’apparition de la turbulence dans un écoulement de filtration. La Houille Blanche 1955, 2, 141–149. [Google Scholar] [CrossRef]
- Irmay, S. On the theoretical derivation of Darcy and Forchheimer equations. Eos Trans. Am. Geophys. Union 1958, 39, 702–707. [Google Scholar] [CrossRef]
- Bachmat, Y. Basic transport coefficients as aquifer characteristics. In Proceedings of the IASH Symposium Hydrology of Fractured Rocks, Paris, France, 20 August 1965. [Google Scholar]
- Scheidegger, A. The Physics of Flow through Porous Media; University of Toronto Press: London, UK, 1958. [Google Scholar]
- Berkowitz, B. Boundary conditions along permeable fracture walls: Influence on flow and conductivity. Water Resour. Res. 1989, 25, 1919–1922. [Google Scholar] [CrossRef]
- Lee, S.L.; Yang, J.H. Modeling of Darcy—Forchheimer drag for fluid flow across a bank of circular cylinders. Int. J. Heat Mass Transf. 1997, 40, 3149–3155. [Google Scholar] [CrossRef]
- Comiti, J.; Renaud, M. A new model for determining mean structure parameters of fixed beds from pressure drop measurements: Application to packed beds with parallepipedal particles. Chem. Eng. Sci. 1989, 44, 1539–1545. [Google Scholar] [CrossRef]
- Fancher, G.H.; Lewis, J.A. Flow of simple fluids through porous materials. Ind. Eng. Chem. 1933, 25, 1139–1147. [Google Scholar] [CrossRef]
- Zeng, Z.; Grigg, R. A criterion for non-Darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Huang, K.; Wan, J.W.; Chen, C.X.; He, L.Q.; Mei, W.B.; Zhang, M.Y. Experimental investigation on water flow in cubic arrays of spheres. J. Hydrol. 2013, 492, 61–68. [Google Scholar] [CrossRef]
- Andrade, J.S.; Costa, U.M.S.; Almeida, M.P.; Makse, H.A.; Stanley, H.E. Inertial effects on fluid flow through disordered porous media. Phys. Rev. Lett. 1999, 82, 5249. [Google Scholar] [CrossRef]
- Li, J.; Huang, G.H.; Wen, Z.; Zhan, H.B. Experimental study on non-Darcian flow in two kinds of media with different diameters. Chin. J. Hydraul. Eng. 2008, 39, 726–732. [Google Scholar]
- Dybbs, A.; Edwards, R.V. A New Look at Porous Media Fluid Mechanics—Darcy to Turbulent. In Fundamentals of Transport Phenomena in Porous Media; Springer: Dordrecht, The Netherlands, 1984; pp. 199–256. [Google Scholar]
- Sedghi-Asl, M.; Rahimi, H.; Salehi, R. Non-Darcy flow of water through a packed column test. Transp. Porous Media 2014, 101, 215–227. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier: New York, NY, USA, 1972; pp. 125–129. [Google Scholar]
- Leonalds, G. Foundation Engineering; McGraw-Hill: New York, NY, USA, 1962; pp. 124–127. [Google Scholar]
- Schneebeli, G. Hydraulique Souterraine; No. BOOK; Eyrolles: Paris, France, 1966. [Google Scholar]
- Xu, K.; Lei, X.; Meng, Q.; Liang, P. Study of non-Darcy seepage fields of rockfill dams. Chin. Rock Soil Mech. 2011, 32, 562–567. [Google Scholar]
- Reynolds, A.M.; Reavell, S.V.; Harral, B.B. Flow and dispersion through a close-packed fixed bed of spheres. Phys. Rev. E 2000, 62, 3632. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.J.; Koch, D.L.; Ladd, A.J. The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 2001, 448, 213–241. [Google Scholar] [CrossRef]
- Hill, R.J.; Koch, D.L.; Ladd, A.J. Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 2001, 448, 243–278. [Google Scholar] [CrossRef]
- Chaudhary, K.; Cardenas, M.B.; Deng, W.; Bennett, P.C. Pore geometry effects on intrapore viscous to inertial flows and on effective hydraulic parameters. Water Resour. Res. 2013, 49, 1149–1162. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Cui, G.X. Fluid Dynamics, 3rd ed.; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
- Yang, F.J.; Hu, D.W.; Tian, Z.B.; Zhou, H. Evolution and Mechanism of Permeability of Unconsolidated Sandstone under the Compaction of a High Hydrostatic Pressure. Rock Soil Mech. 2020, 41, 1–12. [Google Scholar]
- Rojas, S.; Koplik, J. Nonlinear flow in porous media. Phys. Rev. E 1998, 58, 4776–4782. [Google Scholar] [CrossRef]
- Firdaouss, M.; Guermond, J.L.; Le Quéré, P. Nonlinear corrections to Darcy’s law at low Reynolds numbers. J. Fluid Mech. 1997, 343, 331–350. [Google Scholar] [CrossRef]
- Hazen, A. The Filtration of Public Water-Supplies; John Wiley & Sons: Hoboken, NJ, USA, 1895. [Google Scholar]
- Panfilov, M.; Fourar, M. Physical splitting of nonlinear effects in high-velocity stable flow through porous media. Adv. Water Resour. 2006, 29, 30–41. [Google Scholar] [CrossRef]
- Jolls, K.R.; Hanratty, T.J. Transition to turbulence for flow through a dumped bed of spheres. Chem. Eng. Sci. 1966, 21, 1185–1190. [Google Scholar] [CrossRef]
- Huang, H.; Ayoub, J. Applicability of the Forchheimer Equation for Non-Darcy Flow in Porous Media. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: Houston, TX, USA, 2006. [Google Scholar]
- Burcharth, H.F.; Andersen, O.K. On the one-dimensional steady and unsteady porous flow equations. Coast. Eng. 1995, 24, 233–257. [Google Scholar] [CrossRef]
- Fourar, M.; Radilla, G.; Lenormand, R.; Moyne, C. On the non-linear behavior of a laminar single-phase flow through two and three-dimensional porous media. Adv. Water Resour. 2004, 26, 669–677. [Google Scholar] [CrossRef]
- Green, L.; Duwez, P. Fluid flow through porous metals. J. Appl. Mech. 1951, 18, 39–45. [Google Scholar]
- Du Plessis, J.P.; Masliyah, J.H. Mathematical modeling of flow through consolidated isotropic porous media. Transp. Porous Media 1988, 3, 145–161. [Google Scholar] [CrossRef]
- Chen, S.Q.; Xu, L.X.; Zhang, D.C. Typical curve matching of well test data for non-Darcy flow velocity. Pet. Explor. Dev. 1996, 23, 50–53. [Google Scholar]
- Zhu, W.; Cheng, N.J.; Chen, X.D.; Chiu, C.F. Some fundamental problems of unsaturated seepage. Chin. J. Geotech. Eng. 2006, 28, 235–240. [Google Scholar]
- Liu, K.; Wen, Z.; Liang, X.; Pan, H.Y.; Liu, J.G. One-dimensional column test for non-Darcy flow in low permeability media. Chin. J. Hydrodyn. 2013, 1, 81–87. [Google Scholar]
| Field Sample Number | Particle Size Analysis (mm) | Coefficient of Uniformity Cu | Effective Grain Size d10 | Average Grain Size d50 | Classification of Soil Naming Standards (GB50021-2001) * | ||||
|---|---|---|---|---|---|---|---|---|---|
| Sand | Powder | Clay | |||||||
| 2–0.5 | 0.5–0.25 | 0.25–0.075 | 0.075–0.005 | <0.005 | |||||
| % | % | % | % | % | - | mm | mm | ||
| 1 | 3.3 | 30.7 | 23.6 | 38.2 | 0.5 | 3.10 | 0.062 | 0.124 | Silty sand |
| 2 | 16.0 | 80.4 | 3.6 | 3.50 | 0.018 | 0.059 | Silt | ||
| 3 | 18.3 | 49.0 | 16.7 | 15.6 | 0.4 | 5.33 | 0.069 | 0.319 | Medium sand |
| 4 | 4.3 | 80.8 | 14.9 | 11.67 | 0.003 | 0.025 | Silt | ||
| Group A (170 cm) | Group B (230 cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Silty Sand (d0 = 0.124 mm) | Silt-I (d0 = 0.059 mm) | Medium Sand (d0 = 0.319 mm) | Silt-II (d0 = 0.025 mm) | ||||||||
| v (cm/s) | J (cm/cm) | Re | v (cm/s) | J (cm/cm) | Re | v (cm/s) | J (cm/cm) | Re | v (cm/s) | J (cm/cm) | Re |
| 4.45 × 10−5 | 0.10 | 0.000055 | 8.30 × 10−5 | 0.23 | 0.000048 | 1.39 × 10−3 | 0.35 | 0.004378 | 3.86 × 10−5 | 0.57 | 0.0000095 |
| 1.06 × 10−4 | 0.22 | 0.000130 | 1.63 × 10−4 | 0.44 | 0.000095 | 3.30 × 10−3 | 0.77 | 0.010409 | 8.33 × 10−5 | 1.14 | 0.000021 |
| 1.43 × 10−4 | 0.30 | 0.000175 | 2.83 × 10−4 | 0.75 | 0.000165 | 4.73 × 10−3 | 1.14 | 0.014933 | 1.09 × 10−4 | 1.62 | 0.000027 |
| 1.85 × 10−4 | 0.39 | 0.000228 | 4.12 × 10−4 | 1.02 | 0.000241 | 6.10 × 10−3 | 1.52 | 0.019253 | 1.17 × 10−4 | 2.30 | 0.000029 |
| 2.57 × 10−4 | 0.59 | 0.000316 | 6.20 × 10−4 | 1.51 | 0.000362 | 6.47 × 10−3 | 1.95 | 0.020442 | 1.40 × 10−4 | 2.81 | 0.000035 |
| 3.12 × 10−4 | 0.84 | 0.000383 | 7.45 × 10−4 | 2.01 | 0.000435 | 7.69 × 10−3 | 2.42 | 0.024287 | 1.49 × 10−4 | 3.27 | 0.000037 |
| 4.17 × 10−4 | 0.97 | 0.000512 | 8.98 × 10−4 | 2.46 | 0.000525 | 8.83 × 10−3 | 3.06 | 0.027880 | 1.51 × 10−4 | 4.10 | 0.000037 |
| 4.94 × 10−4 | 1.17 | 0.000607 | 1.13 × 10−3 | 2.83 | 0.000662 | 9.86 × 10−3 | 3.51 | 0.031147 | 1.62 × 10−4 | 4.54 | 0.000040 |
| 5.64 × 10−4 | 1.38 | 0.000693 | 1.29 × 10−3 | 3.26 | 0.000755 | 1.04 × 10−2 | 3.87 | 0.032839 | 1.53 × 10−4 | 4.88 | 0.000038 |
| 6.33 × 10−4 | 1.63 | 0.000777 | 1.25 × 10−3 | 3.51 | 0.000729 | 1.03 × 10−2 | 3.85 | 0.032521 | 1.69 × 10−4 | 5.26 | 0.000042 |
| 8.42 × 10−3 | 4.14 | 0.026586 | 1.59 × 10−4 | 5.58 | 0.000039 | ||||||
| Experimental Media | Constant Hydraulic Head | Regression Equation | Correlation Coefficient |
|---|---|---|---|
| Silty sand | Z = 170 cm | v = 0.408 J | R2 = 0.9890 |
| Silt-I | v = 0.3802 J | R2 = 0.9901 | |
| Medium sand | Z = 230 cm | v = 0.5456 J | R2 = 0.7810 |
| Silt-II | v = 0.3594 J | R2 = 0.3130 |
| Experimental Media | Constant Hydraulic Head | Regression Equation | Correlation Coefficient |
|---|---|---|---|
| Medium sand | Z = 230 cm | J = 1.9973 v2 + 1.8024 v | R2 = 0.9072 |
| Silt-II | J = 2.3171 v2 − 0.7785 v | R2 = 0.9129 |
| Experimental Media | Constant Hydraulic Head | Regression Equation | Correlation Coefficient |
|---|---|---|---|
| Medium sand | Z = 230 cm | v = 0.409 J | R2 = 0.9961 |
| Silt-II | v = 0.6923 J | R2 = 0.9878 |
| ID | Method | Experimental Media | Re | Reference |
|---|---|---|---|---|
| 1 | field survey | gravel | 0.9–414 | [4] |
| 2 | laboratory experiment | loosely consolidated sandstones | 0.4–3 | [18] |
| unconsolidated sands and lead shot | 10–1000 | |||
| 3 | overview | packed particles | 1–100 | [19] |
| 4 | simulation experiment | cubic arrays of spheres in diameter from 3 mm–10 mm | 30 | [20] |
| 5 | numerical simulation | disordered porous media | 0.01–0.1 | [21] |
| 6 | sand columns experiment | quartz sands with different diameters | 22–2752–104 | [22] |
| 7 | physical model | plexiglass spheres | 0.16–700 | [23] |
| 8 | flow experiment | porous metal samples | 0.1–0.2 | [48] |
| 9 | mathematical modeling | unit cell | 3–17 | [49] |
| 10 | laboratory filtration experiment | silt, silty sand (0.025–0.319 mm) | <0.03 | this study |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, Y.; Zhao, G.; Chen, N.; Xu, Y. Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads. Water 2019, 11, 2317. https://doi.org/10.3390/w11112317
Wang L, Li Y, Zhao G, Chen N, Xu Y. Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads. Water. 2019; 11(11):2317. https://doi.org/10.3390/w11112317
Chicago/Turabian StyleWang, Lili, Yunliang Li, Guizhang Zhao, Nanxiang Chen, and Yuanzhi Xu. 2019. "Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads" Water 11, no. 11: 2317. https://doi.org/10.3390/w11112317
APA StyleWang, L., Li, Y., Zhao, G., Chen, N., & Xu, Y. (2019). Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads. Water, 11(11), 2317. https://doi.org/10.3390/w11112317





