Flood Hazard Mapping Using the Flood and Flash-Flood Potential Index in the Buzău River Catchment, Romania
Abstract
:1. Introduction
2. Study Area and Data
2.1. General Characteristics of the Study Area
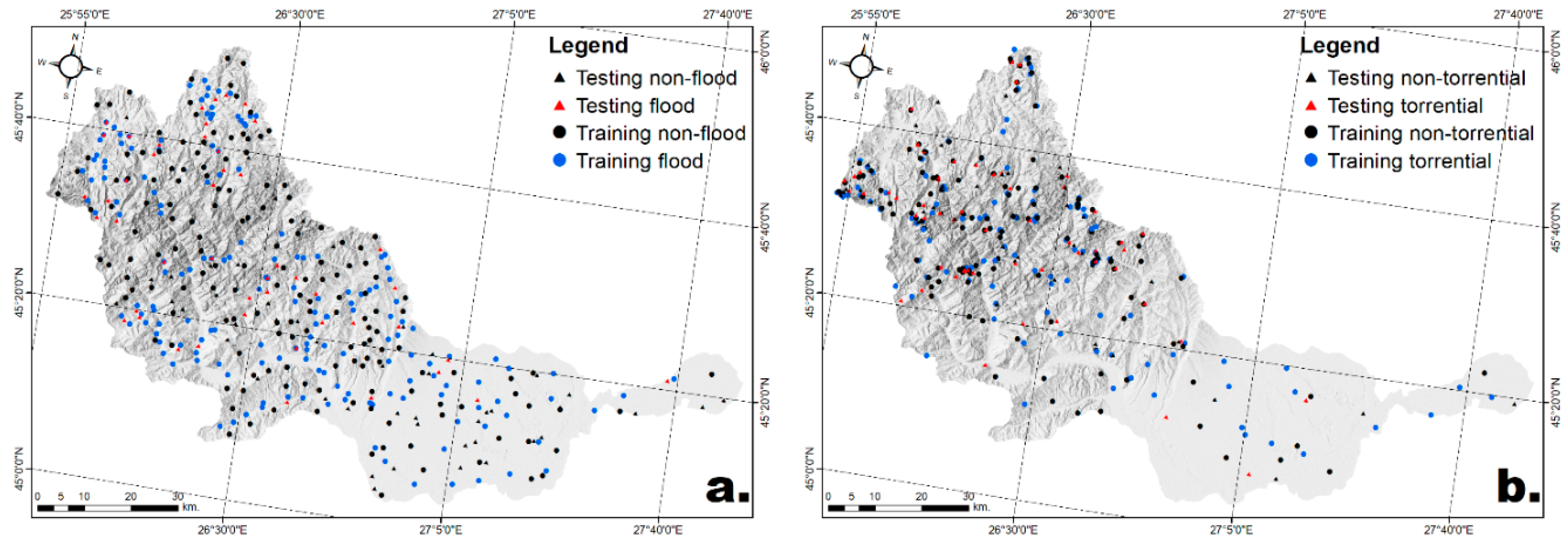
2.2. Inventory of the Historical Flood Locations and Areas Affected by Torrentiality
2.3. Flood and Flash-Flood Conditioning Variables
3. Flood and Flash-Flood Modelling Methods
3.1. Training and Testing the Models
3.2. Frequency Ratio Model (FR)
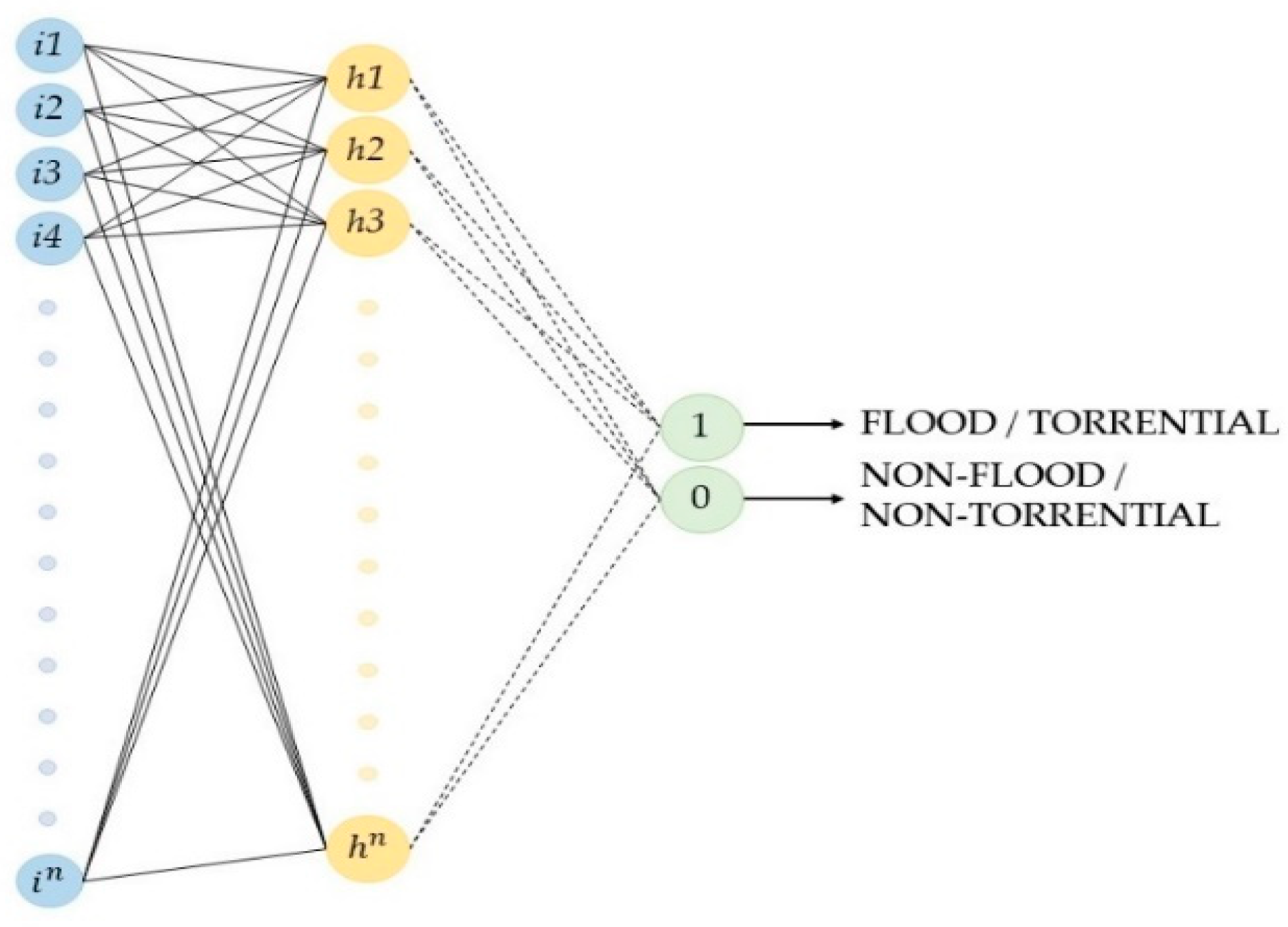
3.3. Multilayer Perceptron Neural Networks (MLP)
4. Results
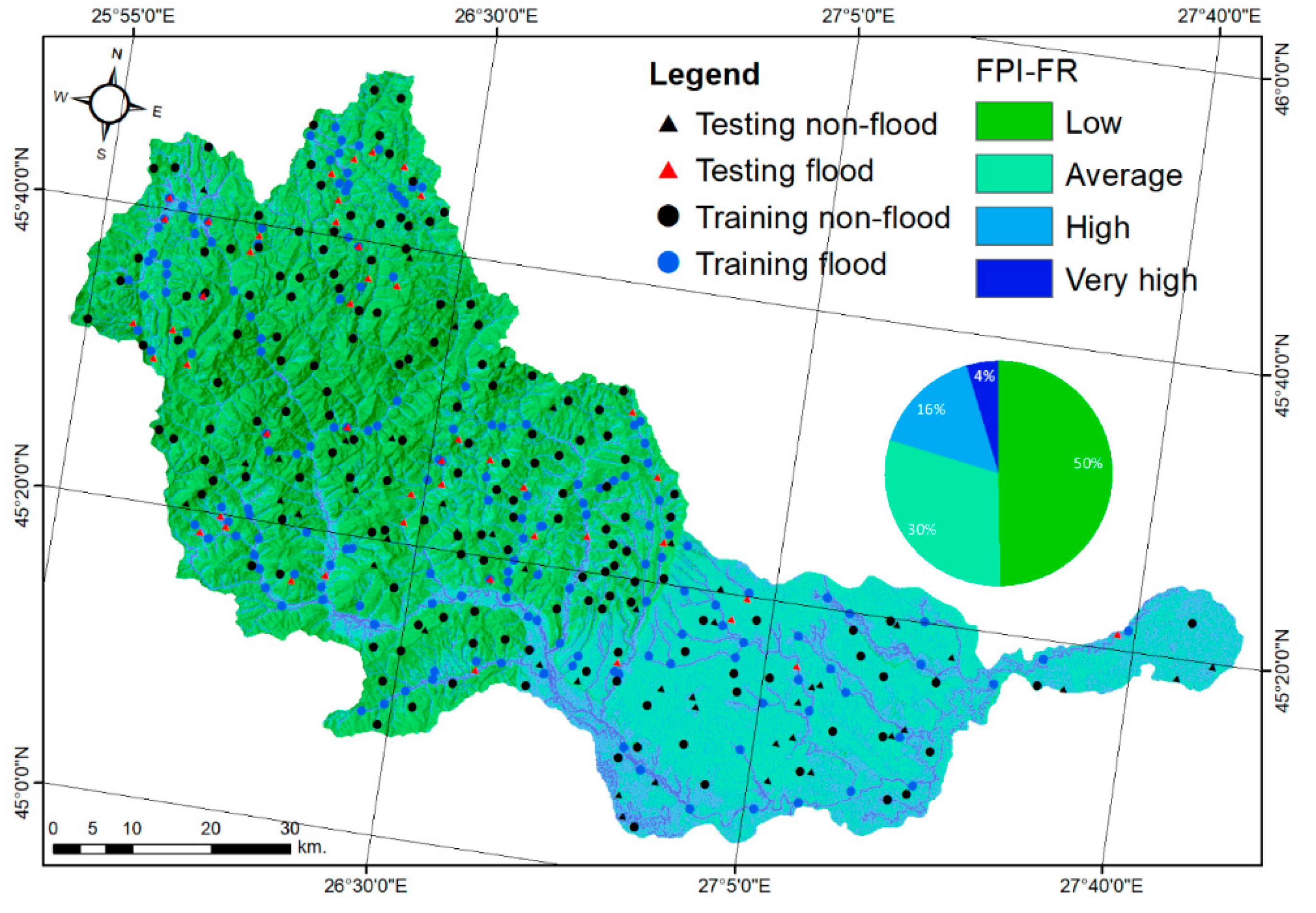
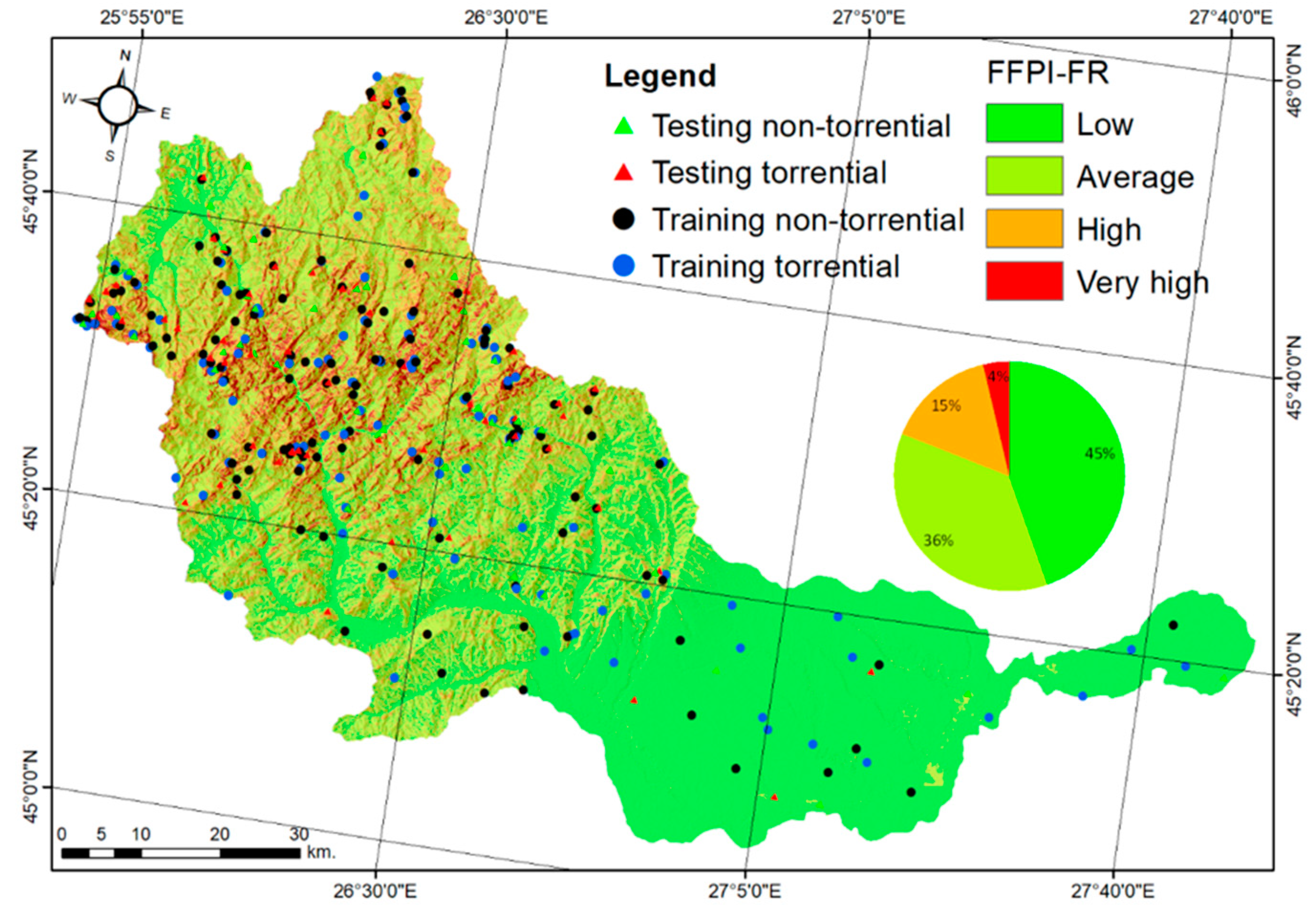
4.1. Flood and Flash-Flood Hazard Mapping Using the Frequency Ratio (FR) Model
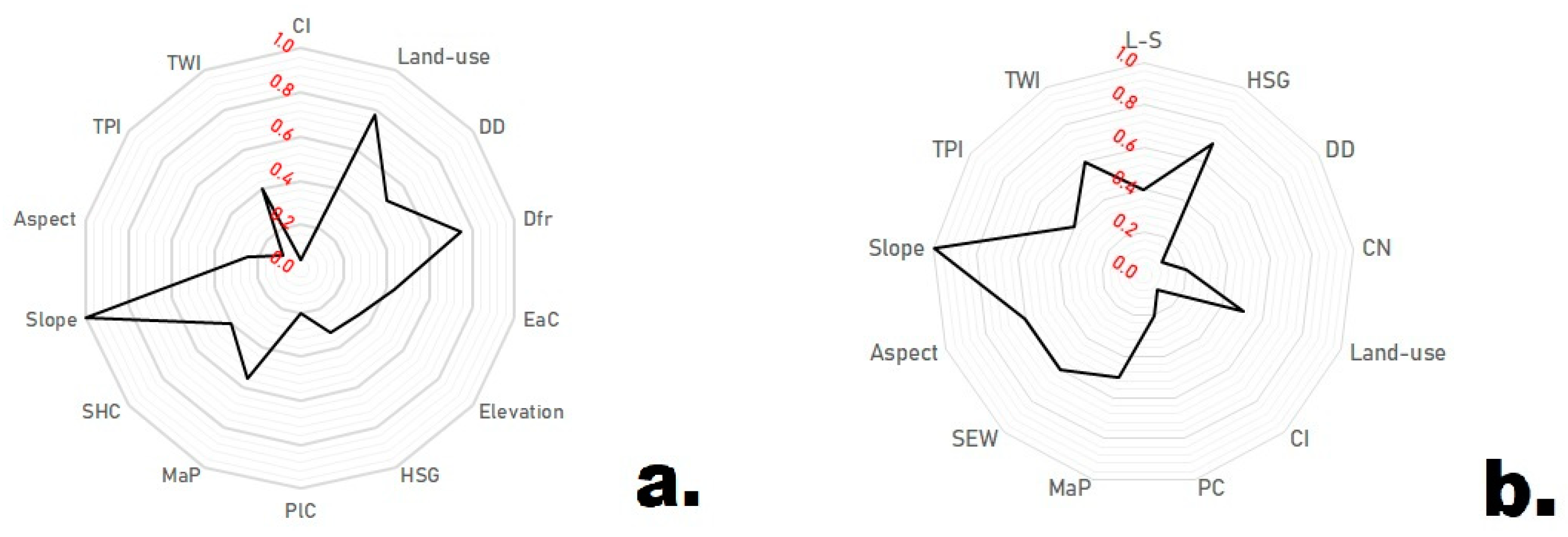
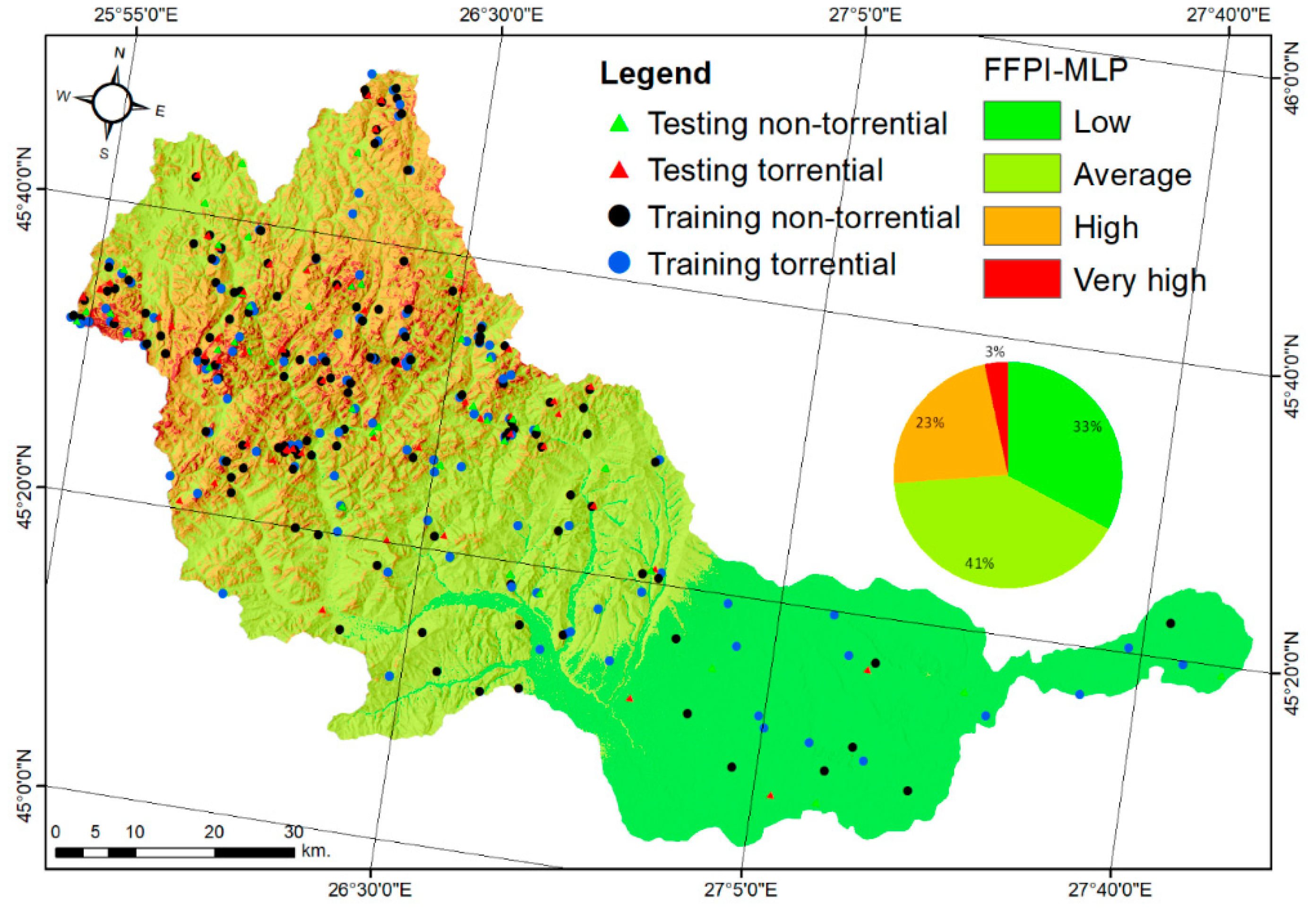
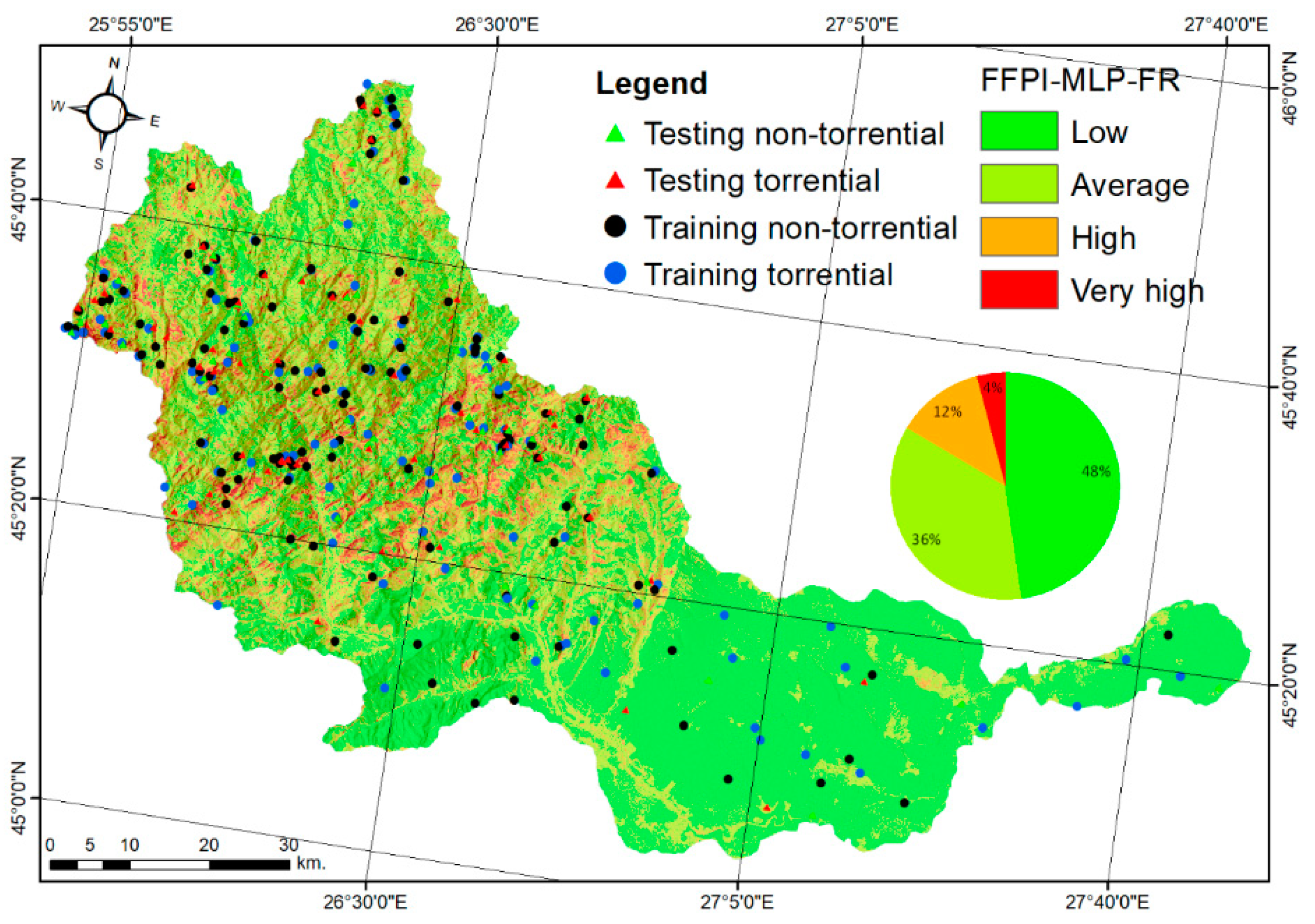
4.2. Flood and Flash-Flood Hazard Mapping Using the Multilayer Percepton Neural Networks Model
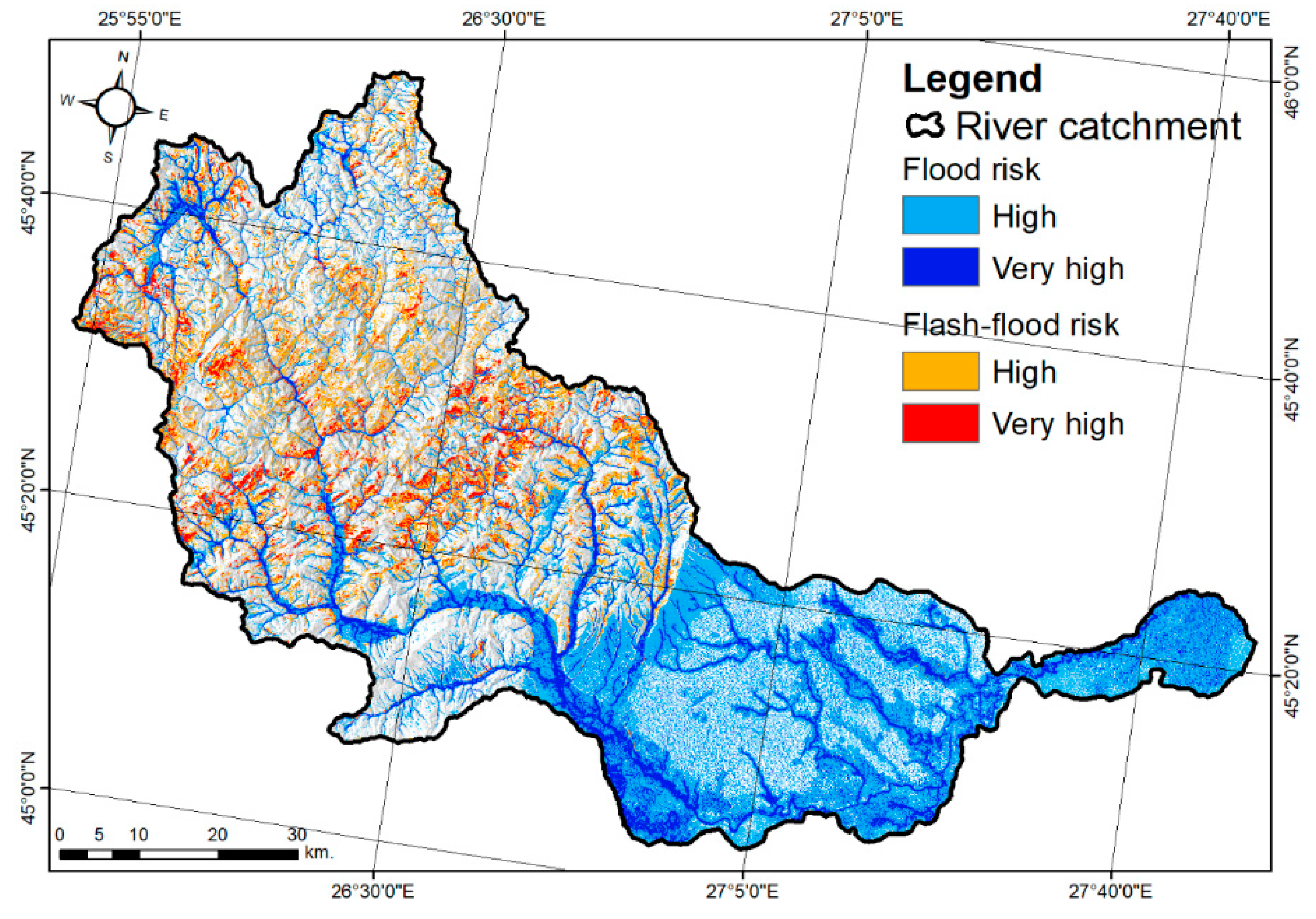
4.3. Flood and Flash-Flood Mapping Using the Hybrid Integration between the Frequency Ratio and the Multilayer Perceptron Neural Networks
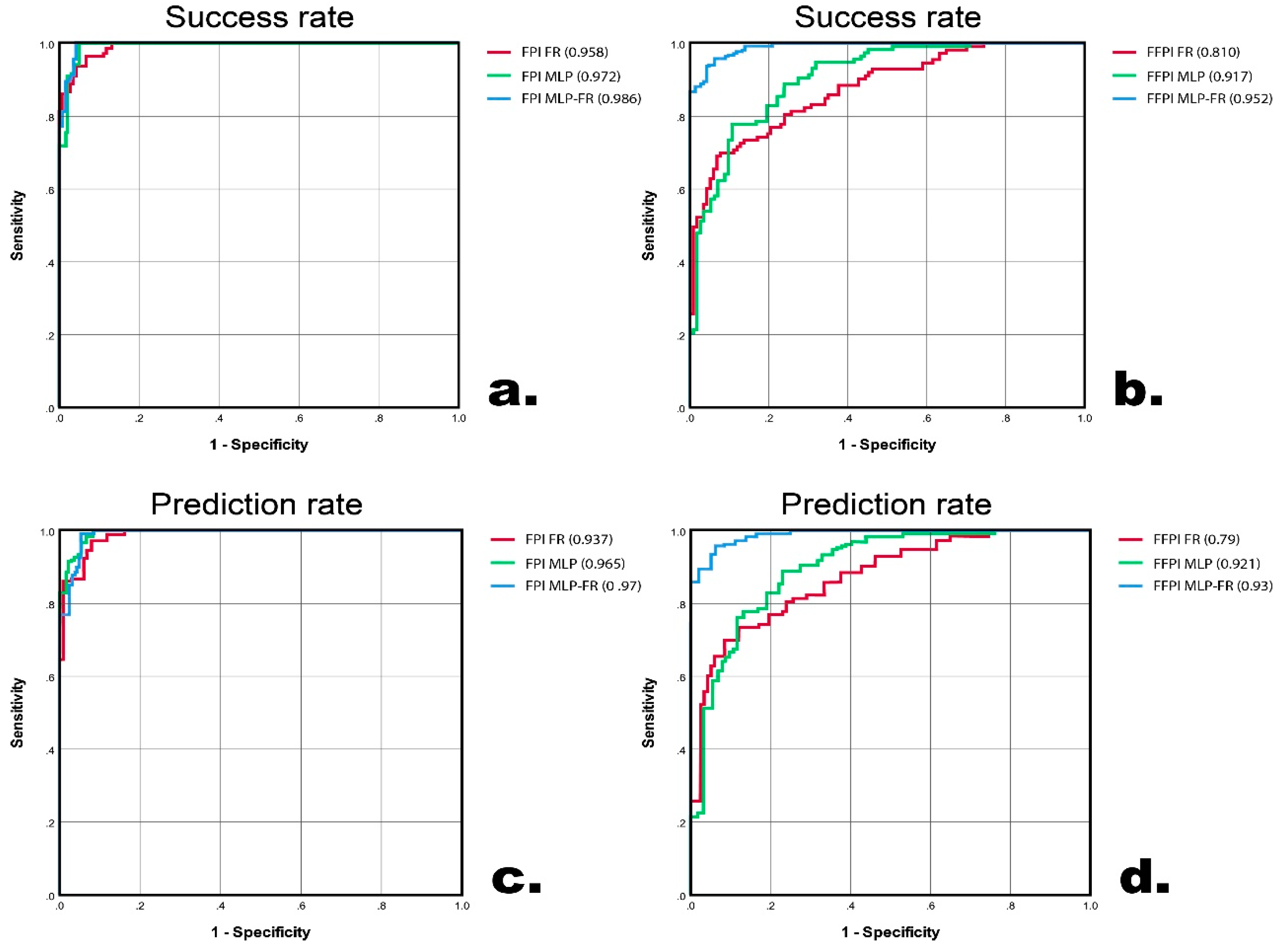
4.4. Flood and Flash-Flood Model Performance Evaluation with ROC Curves
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Assessment and Adaptation to Climate Change-Related Flood Risks: Oxford Research Encyclopedia of Natural Hazard Science—OI. Available online: https://oxfordindex.oup.com/view/10.1093/acrefore/9780199389407.013.278?lang=en,//oxfordindex.oup.com:443/view/10.1093/acrefore/9780199389407.013.278 (accessed on 19 August 2019).
- Didovets, I.; Krysanova, V.; Bürger, G.; Snizhko, S.; Balabukh, V.; Bronstert, A. Climate change impact on regional floods in the Carpathian region. J. Hydrol. Reg. Stud. 2019, 22, 100590. [Google Scholar] [CrossRef]
- Barriers and Guidelines for Public Policies on Climate Change Adaptation: A Missed Opportunity of Scientific Knowledge-Brokerage—Clar—2013—Natural Resources Forum—Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1111/1477-8947.12013 (accessed on 31 August 2019).
- Barredo, J.I.; de Roo, A.; Lavalle, C. Flood risk mapping at European scale. Water Sci. Technol. 2007, 56, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Paprotny, D.; Morales-Nápoles, O.; Jonkman, S.N. Efficient pan-European river flood hazard modelling through a combination of statistical and physical models. Nat. Hazards Earth Syst. Sci. 2017, 17, 1267–1283. [Google Scholar] [CrossRef] [Green Version]
- Massazza, G.; Tamagnone, P.; Wilcox, C.; Belcore, E.; Pezzoli, A.; Vischel, T.; Panthou, G.; Housseini Ibrahim, M.; Tiepolo, M.; Tarchiani, V.; et al. Flood Hazard Scenarios of the Sirba River (Niger): Evaluation of the Hazard Thresholds and Flooding Areas. Water 2019, 11, 1018. [Google Scholar] [CrossRef]
- Hennessey, R.; Pittman, J.; Morand, A.; Douglas, A. Co-benefits of integrating climate change adaptation and mitigation in the Canadian energy sector. Energy Policy 2017, 111, 214–221. [Google Scholar] [CrossRef]
- Dobler, C.; Bürger, G.; Stötter, J. Assessment of climate change impacts on flood hazard potential in the Alpine Lech watershed. J. Hydrol. 2012, 460, 29–39. [Google Scholar] [CrossRef]
- Zeleňáková, M.; Purcz, P.; Blišťan, P.; Vranayová, Z.; Hlavatá, H.; Diaconu, D.C.; Portela, M.M. Trends in Precipitation and Temperatures in Eastern Slovakia (1962–2014). Water 2018, 10, 727. [Google Scholar] [CrossRef]
- Yohe, G.W. Mitigative Capacity–the Mirror Image of Adaptive Capacity on the Emissions Side. Clim. Chang. 2001, 49, 247–262. [Google Scholar] [CrossRef]
- Filatova, T. Market-based instruments for flood risk management: A review of theory, practice and perspectives for climate adaptation policy. Environ. Sci. Policy 2013, 37, 227–242. [Google Scholar] [CrossRef]
- Balica, S.F.; Popescu, I.; Wright, N.G.; Beevers, L. Parametric and physically based modelling techniques for flood risk and vulnerability assessment: A comparison. Environ. Model. Softw. 2013, 41, 84–92. [Google Scholar] [CrossRef]
- Pradhan, B. Flood susceptible mapping and risk area delineation using logistic regression, GIS and remote sensing. J. Spat. Hydrol. 2009, 9, 1–18. [Google Scholar]
- Giustarini, L.; Chini, M.; Hostache, R.; Pappenberger, F.; Matgen, P. Flood Hazard Mapping Combining Hydrodynamic Modeling and Multi Annual Remote Sensing data. Remote Sens. 2015, 7, 14200–14226. [Google Scholar] [CrossRef] [Green Version]
- Gigović, L.; Pamučar, D.; Bajić, Z.; Drobnjak, S. Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas. Water 2017, 9, 360. [Google Scholar] [CrossRef]
- Balogun, A.-L.; Matori, A.-N.; Hamid-Mosaku, A.I. A fuzzy multi-criteria decision support system for evaluating subsea oil pipeline routing criteria in East Malaysia. Environ. Earth Sci. 2015, 74, 4875–4884. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS. J. Hydrol. 2013, 504, 69–79. [Google Scholar] [CrossRef]
- Mukerji Aditya; Chatterjee Chandranath; Raghuwanshi Narendra Singh Flood Forecasting Using ANN, Neuro-Fuzzy, and Neuro-GA Models. J. Hydrol. Eng. 2009, 14, 647–652. [CrossRef]
- Pulvirenti, L.; Pierdicca, N.; Chini, M.; Guerriero, L. An algorithm for operational flood mapping from Synthetic Aperture Radar (SAR) data using fuzzy logic. Nat. Hazards Earth Syst. Sci. 2011, 11, 529–540. [Google Scholar] [CrossRef] [Green Version]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Campolo, M.; Soldati, A.; Andreussi, P. Artificial neural network approach to flood forecasting in the River Arno. Hydrol. Sci. J. 2003, 48, 381–398. [Google Scholar] [CrossRef]
- An Artificial Neural Network Model for Flood Simulation Using GIS: Johor River Basin, Malaysia | Springer Link. Available online: https://link.springer.com/article/10.1007/s12665-011-1504-z (accessed on 21 September 2019).
- Tiwari, M.K.; Chatterjee, C. Uncertainty assessment and ensemble flood forecasting using bootstrap based artificial neural networks (BANNs). J. Hydrol. 2010, 382, 20–33. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Zeinivand, H. Flood susceptibility mapping using frequency ratio and weights-of-evidence models in the Golastan Province, Iran. Geocarto Int. 2016, 31, 42–70. [Google Scholar] [CrossRef]
- Nandi, A.; Mandal, A.; Wilson, M.; Smith, D. Flood hazard mapping in Jamaica using principal component analysis and logistic regression. Environ. Earth Sci. 2016, 75, 465. [Google Scholar] [CrossRef]
- Lee, M.J.; Kang, J.; Jeon, S. Application of frequency ratio model and validation for predictive flooded area susceptibility mapping using GIS. In 2012 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Munich, Germany, 2012; pp. 895–898. [Google Scholar]
- Evaluating the Application of the Statistical Index Method in Flood Susceptibility Mapping and Its Comparison with Frequency Ratio and Logistic Regression Methods: Geomatics, Natural Hazards and Risk. Available online: https://www.tandfonline.com/doi/full/10.1080/19475705.2018.1506509 (accessed on 31 August 2019).
- Cao, C.; Chen, J.; Zhang, W.; Xu, P.; Zheng, L.; Zhu, C. Geospatial Analysis of Mass-Wasting Susceptibility of Four Small Catchments in Mountainous Area of Miyun County, Beijing. Int. J. Environ. Res. Public Health 2019, 16, 2801. [Google Scholar] [CrossRef] [PubMed]
- Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A. Landslide Susceptibility Mapping Using Different GIS-Based Bivariate Models. Water 2019, 11, 1402. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid Integration Approach of Entropy with Logistic Regression and Support Vector Machine for Landslide Susceptibility Modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Khan, H.; Shafique, M.; Khan, M.A.; Bacha, M.A.; Shah, S.U.; Calligaris, C. Landslide susceptibility assessment using Frequency Ratio, a case study of northern Pakistan. Egypt. J. Remote Sens. Space Sci. 2019, 22, 11–24. [Google Scholar] [CrossRef]
- Kumar Samanta, R.; Bhunia, G.; Shit, P.; Pourghasemi, H.R. Flood susceptibility mapping using geospatial frequency ratio technique: A case study of Subarnarekha River Basin, India. Model. Earth Syst. Environ. 2018, 4, 395–408. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Gómez, H.; Kavzoglu, T. Assessment of shallow landslide susceptibility using artificial neural networks in Jabonosa River Basin, Venezuela. Eng. Geol. 2005, 78, 11–27. [Google Scholar] [CrossRef]
- Costache, R. Flash-flood Potential Index mapping using weights of evidence, decision Trees models and their novel hybrid integration. Stoch. Environ. Res. Risk Assess. 2019, 33, 1375–1402. [Google Scholar] [CrossRef]
- Wu, J.; Liu, H.; Wei, G.; Song, T.; Zhang, C.; Zhou, H. Flash Flood Forecasting Using Support Vector Regression Model in a Small Mountainous Catchment. Water 2019, 11, 1327. [Google Scholar] [CrossRef]
- Huang, W.; Cao, Z.; Huang, M.; Duan, W.; Ni, Y.; Yang, W. A New Flash Flood Warning Scheme Based on Hydrodynamic Modelling. Water 2019, 11, 1221. [Google Scholar] [CrossRef]
- Psomiadis, E.; Soulis, K.X.; Zoka, M.; Dercas, N. Synergistic Approach of Remote Sensing and GIS Techniques for Flash-Flood Monitoring and Damage Assessment in Thessaly Plain Area, Greece. Water 2019, 11, 448. [Google Scholar] [CrossRef]
- Dottori, F.; Martina, M.L.V.; Figueiredo, R. A methodology for flood susceptibility and vulnerability analysis in complex flood scenarios. J. Flood Risk Manag. 2018, 11, S632–S645. [Google Scholar] [CrossRef]
- Zaharia, L.; Costache, R.; Prăvălie, R.; Ioana-Toroimac, G. Mapping flood and flooding potential indices: A methodological approach to identifying areas susceptible to flood and flooding risk. Case study: The Prahova catchment (Romania). Front. Earth Sci. 2017, 11, 229–247. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Sahana, M.; Chen, C.W.; Zhu, Z.; Wang, W.; Thai Pham, B. Evaluating GIS-Based Multiple Statistical Models and Data Mining for Earthquake and Rainfall-Induced Landslide Susceptibility Using the LiDAR DEM. Remote Sens. 2019, 11, 638. [Google Scholar] [CrossRef]
- Vojtek, M.; Vojteková, J. Flood Susceptibility Mapping on a National Scale in Slovakia Using the Analytical Hierarchy Process. Water 2019, 11, 364. [Google Scholar] [CrossRef]
- Miller, V.C. A quantitative geomorphic study of drainage basin characteristics in the Clinch Mountain area, Virginia and Tennessee. J. Geology 1953, 389–402. [Google Scholar]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Batista, G.; Prati, R.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Shirzadi, A.; Shahabi, H.; Chapi, K.; Tien Bui, D.; Pham, B.; Shahedi, K.; Ahmad, B.B. A comparative study between popular statistical and machine learning methods for simulating volume of landslides. Catena 2017, 157, 213–226. [Google Scholar] [CrossRef]
- Cao, C.; Xu, P.; Wang, Y.; Chen, J.; Zheng, L.; Niu, C. Flash Flood Hazard Susceptibility Mapping Using Frequency Ratio and Statistical Index Methods in Coalmine Subsidence Areas. Sustainability 2016, 8, 948. [Google Scholar] [CrossRef]
- Li, X.; Yan, D.; Wang, K.; Weng, B.; Qin, T.; Liu, S. Flood Risk Assessment of Global Watersheds Based on Multiple Machine Learning Models. Water 2019, 11, 1654. [Google Scholar] [CrossRef]
- Mardani, M.; Mardani, H.; De Simone, L.; Varas, S.; Kita, N.; Saito, T. Integration of Machine Learning and Open Access Geospatial Data for Land Cover Mapping. Remote Sens. 2019, 11, 1907. [Google Scholar] [CrossRef]
- He, Q.; Xu, Z.; Li, S.; Li, R.; Zhang, S.; Wang, N.; Pham, B.T.; Chen, W. Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling. Entropy 2019, 21, 106. [Google Scholar] [CrossRef]
- National Engineering Handbook Hydrology Chapters | NRCS. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detailfull/national/water/manage/hydrology/?cid=STELPRDB1043063 (accessed on 8 August 2019).
- Jones, R.J.A.; Hiederer, R.; Rusco, E.; Montanarella, L. Estimating organic carbon in the soils of Europe for policy support. Eur. J. Soil Sci. 2005, 56, 655–671. [Google Scholar] [CrossRef] [Green Version]
- Tóth, B.; Weynants, M.; Nemes, A.; Makó, A.; Bilas, G.; Tóth, G. New generation of hydraulic pedotransfer functions for Europe. Eur. J. Soil Sci. 2015, 66, 226–238. [Google Scholar] [CrossRef]
- Mohsenipour, M.; Shahid, S. Estimation of Saturated Hydraulic Conductivity: A Review; Advances in Engineering Research; Nova Science Publishers Inc.: New York, NY, USA, 2016; Volume 15, Chapter 5; p. 181. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Diaconu, D.C.; Andronache, I.; Pintilii, R.D.; Brețcan, P.; Simion, A.G.; Drăghici, C.C.; Gruia, K.A.; Grecu, A.; Marin, M.; Peptenatu, D. Using Fractal Fragmentation and Compaction Index in Analysis of the Deforestation Process in Bucegi Mountains Group, Romania. Carpathian J. Earth Environ. Sci. 2019, 14, 431–438. [Google Scholar]
- Pallard, B.; Castellarin, A.; Montanari, A. A look at the links between drainage density and flood statistics. Hydrol. Earth Syst. Sci. 2009, 13, 1019–1029. [Google Scholar] [CrossRef] [Green Version]
- Diaconu, D.C.; Andronache, I.; Ahammer, H.; Ciobotaru, A.M.; Zeleňáková, M.; Dinescu, R.; Pozdnyakov, A.V.; Alekseevna Chupikova, S. Fractal drainage model—A new approach to determinate the complexity of watershed. Acta Montan. Slovaca 2017, 22, 12–21. [Google Scholar]
- Wakeley, J.; Lichvar, R.; Noble, C.; Berkowitz, J. Regional Supplement to the Corps of Engineers Wetland Delineation Manual: Alaska Region (Version 2.0); US Army Corps of Engineers, U.S Army Engineer Research and Development Center: Vicksburg, MI, USA, 2011.
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P.; et al. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Raduła, M.W.; Szymura, T.H.; Szymura, M. Topographic wetness index explains soil moisture better than bioindication with Ellenberg’s indicator values. Ecol. Indic. 2018, 85, 172–179. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences 2015, 5, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modelling with GIS; Elsevier: Pergamon, Turkey, 1994; ISBN 978-1-4831-4494-8. [Google Scholar]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.J.; Lee, J.H. A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. Catena 2014, 114, 21–36. [Google Scholar] [CrossRef]
- Peponi, A.; Morgado, P.; Trindade, J. Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling. Sustainability 2019, 11, 975. [Google Scholar] [CrossRef]
- Shiruru, K. An Introduction to Artificial Neural Network. Int. J. Adv. Res. Innov. Ideas Educ. 2016, 1, 27–30. [Google Scholar]
- Taravat, A.; Rajaei, M.; Emadodin, I.; Hasheminejad, H.; Mousavian, R.; Biniyaz, E. A Spaceborne Multisensory, Multitemporal Approach to Monitor Water Level and Storage Variations of Lakes. Water 2016, 8, 478. [Google Scholar] [CrossRef]
- Sánchez-Reolid, R.; García, A.S.; Vicente-Querol, M.A.; Fernández-Aguilar, L.; López, M.T.; Fernández-Caballero, A.; González, P. Artificial Neural Networks to Assess Emotional States from Brain-Computer Interface. Electronics 2018, 7, 384. [Google Scholar] [CrossRef]
- Wu, Q.; Lee, C.M. A Modified Leakage Localization Method Using Multilayer Perceptron Neural Networks in a Pressurized Gas Pipe. Appl. Sci. 2019, 9, 1954. [Google Scholar] [CrossRef]
- Deep Learning Multilayer Perceptron (MLP) for Flood Prediction Model Using Wireless Sensor Network Based Hydrology Time Series Data Mining—IEEE Conference Publication. Available online: https://ieeexplore.ieee.org/document/8319150 (accessed on 15 August 2019).
- Costache, R.; Tien Bui, D. Spatial prediction of flood potential using new ensembles of bivariate statistics and artificial intelligence: A case study at the Putna river catchment of Romania. Sci. Total Environ. 2019, 691, 1098–1118. [Google Scholar] [CrossRef] [PubMed]
- Castro, W.; Oblitas, J.; Santa-Cruz, R.; Avila-George, H. Multilayer perceptron architecture optimization using parallel computing techniques. PLoS ONE 2017, 12, e0189369. [Google Scholar] [CrossRef]
- Naganna, S.R.; Deka, P.C.; Ghorbani, M.A.; Biazar, S.M.; Al-Ansari, N.; Yaseen, Z.M. Dew Point Temperature Estimation: Application of Artificial Intelligence Model Integrated with Nature-Inspired Optimization Algorithms. Water 2019, 11, 742. [Google Scholar] [CrossRef]
- Allawi, M.F.; Binti Othman, F.; Afan, H.A.; Ahmed, A.N.; Hossain, M.S.; Fai, C.M.; El-Shafie, A. Reservoir Evaporation Prediction Modeling Based on Artificial Intelligence Methods. Water 2019, 11, 1226. [Google Scholar] [CrossRef]
- Improving Generalization of Artificial Neural Networks in Rainfall–Runoff Modelling/Amélioration de la Généralisation de Réseaux de Neurones Artificiels Pour la Modélisation Pluie-Débit: Hydrological Sciences Journal. Available online: https://www.tandfonline.com/doi/abs/10.1623/hysj.50.3.439.65025 (accessed on 18 September 2019).
- Gnana Sheela, K.; Deepa, S.N. Neural network based hybrid computing model for wind speed prediction. Neurocomputing 2013, 122, 425–429. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer: Berlin, Germany, 1996; ISBN 978-3-540-60505-8. [Google Scholar]
- Yang, S.; Berdine, G. The receiver operating characteristic (ROC) curve. Southwest Respir. Crit. Care Chron. 2017, 5, 34–36. [Google Scholar] [CrossRef]
- Advances in Pan-European Flood Hazard Mapping—Alfieri—2014—Hydrological Processes—Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/hyp.9947 (accessed on 21 September 2019).
- Feyen, L.; Dankers, R.; Bódis, K.; Salamon, P.; Barredo, J. Fluvial flood risk in Europe in present and future climates. Clim. Chang. 2012, 112, 47–62. [Google Scholar] [CrossRef]
- Veijalainen, N. Estimation of Climate Change Impacts on Hydrology and Floods in Finland; Aalto University: Helsinki, Finland, 2012; ISBN 978-952-60-4614-3. [Google Scholar]
- Westerhoff, R.S.; Kleuskens, M.P.H.; Winsemius, H.C.; Huizinga, H.J.; Brakenridge, G.R.; Bishop, C. Automated global water mapping based on wide-swath orbital synthetic-aperture radar. Hydrol. Earth Syst. Sci. 2013, 17, 651–663. [Google Scholar] [CrossRef] [Green Version]
- Dobbin, K.K.; Simon, R.M. Optimally splitting cases for training and testing high dimensional classifiers. BMC Med. Genom. 2011, 4, 31. [Google Scholar] [CrossRef]
- Costache, R.; Zaharia, L. Flash-flood potential assessment and mapping by integrating the weights-of-evidence and frequency ratio statistical methods in GIS environment—Case study: Bâsca Chiojdului River catchment (Romania). J. Earth Syst. Sci. 2017, 126, 59. [Google Scholar] [CrossRef]
- Martins, B.; Nunes, A.; Lourenço, L.; Velez-Castro, F. Flash Flood Risk Perception by the Population of Mindelo, S. Vicente (Cape Verde). Water 2019, 11, 1895. [Google Scholar] [CrossRef]
- Silva, P.R.B.; Makara, C.N.; Munaro, A.; Schnitzler, D.; Diaconu, D.C.; Sandu, I.; Poleto, C. Risks associated of the waters from hydric systems Urban’s: The case of the rio Barigui, south of Brazil. Rev. Chim. 2017, 68, 1834–1842. [Google Scholar]
- Zeleňáková, M.; Gaňová, L.; Purcz, P.; Horský, M.; Satrapa, L.; Blišťan, P.; Diaconu, D.C. Mitigation of the Adverse Consequences of Floods for Human Life, Infrastructure, and the Environment. Nat. Hazards Rev. 2017, 18, 05017002. [Google Scholar] [CrossRef]



| River | Area (km2) | Length (km) | Altitude (m) | Slope Mean (°) | Circularity Ratio | ||
|---|---|---|---|---|---|---|---|
| Min | Mean | Max | |||||
| Buzău | 5264 | 302 | 8 | 516 | 1250 | 4 | 0.24 |
| Bâsca Roziliei | 783 | 76 | 395 | 1110 | 1510 | 15 | 0.28 |
| Slănic | 425 | 73 | 120 | 580 | 1240 | 15 | 0.20 |
| Bâsca Chiojdului | 340 | 92 | 239 | 668 | 1340 | 26 | 0.46 |
| Câlnău | 208 | 57 | 85 | 336 | 700 | 11 | 0.29 |
| Sărățel | 187 | 32 | 141 | 444 | 900 | 24 | 0.65 |
| Flood Variable | Variable Classes | No. of Flood Points | % of Flood Points | Class Area | % of Class Area | Ratio (+) | Prediction Ratio (PR) |
|---|---|---|---|---|---|---|---|
| Slope | 25–55 | 1 | 0.59% | 201,873 | 3.39% | 0.17 | 5.84 |
| 15–25 | 15 | 8.92% | 1,093,638 | 18.39% | 0.48 | ||
| 5–15 | 29 | 17.26% | 2,282,994 | 38.40% | 0.44 | ||
| 0–50 | 123 | 73.21% | 2,366,736 | 39.80% | 1.83 | ||
| Elevation | 1019–1925 | 25 | 14.88% | 989,283 | 16.63% | 0.89 | 1.08 |
| 628–1019 | 26 | 15.47% | 1,235,414 | 20.77% | 0.74 | ||
| 255–628 | 51 | 30.35% | 1,567,088 | 26.35% | 1.51 | ||
| 1.2–255 | 66 | 39.28% | 2,153,456 | 36.22% | 1.08 | ||
| HSG | A | 30 | 17.85% | 1,289,141 | 21.68% | 0.82 | 1 |
| B | 32 | 19.04% | 1,071,383 | 18.02% | 1.05 | ||
| C | 99 | 58.92% | 3,242,969 | 54.54% | 1.08 | ||
| D | 7 | 4.16% | 341,748 | 5.74% | 0.72 | ||
| Slope aspect | North, northeast | 15 | 8.92% | 832,635 | 14% | 0.63 | 2.15 |
| Northwest, east | 18 | 10.71% | 698,426 | 16.28% | 1.05 | ||
| Flat | 89 | 52.97% | 2,065,777 | 34.74% | 1.52 | ||
| West, southeast | 19 | 11.30% | 1,103,674 | 18.56% | 0.60 | ||
| South, southwest | 27 | 16.07% | 974,729 | 16.39% | 0.98 | ||
| EaC | > 4 | 75 | 44.64% | 4,967,941 | 83.56% | 0.53 | 3.82 |
| 2.5–4 | 18 | 10.17% | 268,371 | 4.51% | 2.37 | ||
| 1–2.5 | 26 | 15.47% | 306,406 | 5.15% | 3 | ||
| 0–1 | 49 | 29.16% | 402,520 | 6.77% | 4.30 | ||
| DfR | 0–50 | 74 | 46.42% | 526,807 | 8.86% | 5.23 | 6.26 |
| 50–150 | 53 | 31.54% | 870,457 | 16.64% | 2.15 | ||
| 150–300 | 30 | 17.85% | 1,094,315 | 18.40% | 0.97 | ||
| 300–450 | 7 | 4.16% | 816,602 | 13.73% | 0.30 | ||
| 450–600 | 4 | 2.38% | 632,703 | 10.64% | 0.22 | ||
| 600–750 | - | - | 426,549 | 7.17% | - | ||
| 750–900 | - | - | 312,704 | 5.25% | - | ||
| >900 | - | - | 1,265,104 | 21.27% | - | ||
| SHC | 56–1283 | 8 | 4.76% | 352,086 | 5.92% | 0.80 | 1.41 |
| 1283–1949 | 52 | 30.95% | 2,377,777 | 39.99% | 0.77 | ||
| 1949–2668 | 40 | 23.80% | 1,376,679 | 23.15% | 1.02 | ||
| 2668–3386 | 68 | 40.47% | 1,838,699 | 30.92% | 1.30 | ||
| Land use | Broad-leaved forest, coniferous forest, mixed forest | 39 | 23.21% | 2,421,990 | 40.73% | 0.56 | 3.94 |
| Scrub and/or herbaceous vegetation | 14 | 8.33% | 281,100 | 4.72% | 1.76 | ||
| Agricultural areas, moors and heathland, arable land | 43 | 25.59% | 1,983,856 | 33.36% | 0.76 | ||
| Pastures, natural grassland, open spaces with little or no vegetation | 34 | 20.23% | 889,830 | 14.96% | 1.35 | ||
| Built-up areas | 38 | 22.61% | 368,465 | 6.19% | 3.64 | ||
| DD | 0–4.7 | 94 | 55.95% | 3,831,521 | 64.44% | 0.88 | 2.86 |
| 4.7–9.7 | 71 | 42.26% | 1,888,411 | 31.76% | 1.33 | ||
| 9.7–17 | 2 | 1.19% | 155,026 | 2.60% | 0.45 | ||
| 17–27 | 1 | 0.59% | 70,283 | 1.18% | 0.50 | ||
| PLC | (−4.03)–(−0.22) | 7 | 4.16% | 319,196 | 5.36% | 0.77 | 4.16 |
| (−0.22)–0.07 | 120 | 71.42% | 3,776,549 | 63.52% | 1.12 | ||
| 0.07–0.37 | 41 | 24.40% | 1,614,633 | 27.15% | 0.89 | ||
| 0.37–4.48 | - | - | 234,863 | 3.95% | - | ||
| TPI | (−122.8)–(−18.5) | 73 | 43.45% | 968,840 | 16.26% | 2.66 | 5.87 |
| (−18.5)–9.5 | 82 | 48.80% | 3,607,795 | 60.68% | 0.80 | ||
| 9.5–36.6 | 7 | 4.16% | 963,889 | 16.21% | 0.25 | ||
| 36.6–153.8 | 6 | 3.57% | 404,717 | 6.80% | 0.52 | ||
| TWI | (−0.36)–3.2 | 25 | 14.88% | 2,226,337 | 37.44% | 0.39 | 5.59 |
| 3.2–5.4 | 74 | 44.04% | 2,652,037 | 44.60% | 0.98 | ||
| 5.4–9.1 | 45 | 26.78% | 882,423 | 14.84% | 1.80 | ||
| 9.1–19.8 | 24 | 14.28% | 184,444 | 3.10% | 4.60 | ||
| MaP | 460–600 | 18 | 10.71% | 1,166,213 | 19.61% | 0.54 | 2.25 |
| 600–750 | 59 | 35.11% | 1,523,307 | 25.62% | 1.37 | ||
| 750–900 | 56 | 33.33% | 1,627,725 | 27.37% | 1.21 | ||
| 900–1050 | 33 | 19.64% | 1,460,019 | 24.55% | 0.79 | ||
| 1050–1162 | 2 | 1.19% | 167,977 | 2.82% | 0.42 | ||
| CI | (−100)–(−32) | 7 | 4.16% | 452,756 | 7.61% | 0.54 | 3.93 |
| (−32)–(−6.2) | 106 | 63.09% | 4,231,277 | 71.17% | 0.88 | ||
| (−6.2)–20.3 | 35 | 20.83% | 981,656 | 16.51% | 1.26 | ||
| 20.3–100 | 20 | 11.90% | 279,552 | 4.70% | 2.53 |
| Flood Variable | Variable Classes | No. of Torrential Points | % of Torrential Points | Class Area | % of Class Area | Ratio (+) | Prediction Ratio (PR) |
|---|---|---|---|---|---|---|---|
| Slope | 0–5 | 19 | 11.04% | 2,366,736 | 39.80% | 0.27 | 5.10 |
| 5–15 | 25 | 14.53% | 2,282,994 | 38.40% | 0.37 | ||
| 15–25 | 51 | 17.26% | 1,093,637 | 18.39% | 1.61 | ||
| 25–55 | 77 | 73.21% | 201,873 | 3.39% | 13.18 | ||
| PC | 0.08–3.73 | 39 | 22.67% | 970,991 | 16.33% | 1.38 | 1 |
| 0.05–0.08 | 44 | 25.58% | 1,803,190 | 30.32% | 0.84 | ||
| (−0.04)–0.05 | 39 | 22.67% | 1,939,676 | 32.62% | 0.69 | ||
| (–3.15)–(–0.04) | 50 | 29.06% | 1,231,384 | 20.71% | 1.40 | ||
| HSG | A | 14 | 8.13% | 1,289,141 | 21.68% | 0.37 | 1.79 |
| B | 49 | 28.48% | 1,071,383 | 18.02% | 1.58 | ||
| C | 98 | 56.97% | 3,242,969 | 54.54% | 1.04 | ||
| D | 11 | 6.39% | 341,748 | 5.74% | 1.12 | ||
| Slope aspect | North, northeast | 33 | 19.18% | 832,635 | 14% | 1.36 | 1.56 |
| Northwest, east | 50 | 29.06% | 698,426 | 16.28% | 1.78 | ||
| Flat | 17 | 9.88% | 2,065,777 | 34.74% | 0.28 | ||
| West, southeast | 47 | 27.32% | 1,103,674 | 18.56% | 1.47 | ||
| South, southwest | 27 | 15.69% | 974,729 | 16.39% | 0.95 | ||
| L-S | 0.03–1.78 | 21 | 12.20% | 2,668,191 | 44.87% | 0.27 | 4.19 |
| 1.78–4.93 | 37 | 21.51% | 2,150,823 | 36.17% | 0.59 | ||
| 4.93–11.2 | 100 | 58.13% | 1,076,945 | 18.14% | 3.20 | ||
| >11.2 | 14 | 8.13% | 49,282 | 0.82% | 9.81 | ||
| CN | 31–49 | 3 | 1.74% | 29,892 | 0.50% | 3.46 | 2.34 |
| 49–69 | 65 | 37.79% | 1,033,834 | 17.38% | 2.17 | ||
| 69–83 | 18 | 10.46% | 797,020 | 13.40% | 0.78 | ||
| 83–98 | 86 | 50% | 4,084,495 | 68.70% | 0.72 | ||
| CI | (–100)–(–32) | 8 | 4.65% | 452,756 | 7.61% | 0.61 | 1.85 |
| (–32)–(–6.2) | 146 | 84.88% | 4,231,277 | 71.17% | 1.19 | ||
| (–6.2)–20.3 | 15 | 8.72% | 981,656 | 16.51% | 0.52 | ||
| 20.3–100 | 3 | 1.74% | 279,552 | 4.70% | 0.37 | ||
| Land use | Broad-leaved forest, coniferous forest, mixed forest | 79 | 45.93% | 2,421,990 | 40.73% | 1.12 | 3.39 |
| Scrub and/or herbaceous vegetation | 39 | 22.67% | 281,100 | 4.72% | 4.49 | ||
| Agricultural areas, moors and heathland, arable land | 24 | 13.95% | 1,983,856 | 33.36% | 0.41 | ||
| Pastures, natural grassland, open spaces with little or no vegetation | 23 | 13.37% | 889,830 | 14.96% | 0.89 | ||
| Built-up areas | 7 | 4.06% | 368,465 | 6.19% | 0.65 | ||
| SEW | 0.0006–2.5 | 109 | 63.37% | 2,771,623 | 46.61% | 1.35 | 4.23 |
| 2.5–7.7 | 22 | 12.79% | 2,004,066 | 33.70% | 0.37 | ||
| 7.7–14.5 | 11 | 6.37% | 763,903 | 12.84% | 0.49 | ||
| 14.5–26.5 | 13 | 7.55% | 341,928 | 5.75% | 1.31 | ||
| 26.5–132.5 | 17 | 9.88% | 63,721 | 1.07% | 9.22 | ||
| DD | 0–4.7 | 116 | 67.44% | 3,831,521 | 64.44% | 1.04 | 1.83 |
| 4.7–9.7 | 54 | 31.39% | 1,888,411 | 31.76% | 0.98 | ||
| 9.7–17 | 1 | 0.58% | 155,026 | 2.60% | 0.22 | ||
| 17–27 | 1 | 0.58% | 70,283 | 1.18% | 0.49 | ||
| TPI | (–122.8)–(–18.5) | 20 | 11.62% | 968,840 | 16.26% | 0.71 | 2.93 |
| (–18.5)–9.5 | 81 | 47.09% | 3,607,795 | 60.68% | 0.77 | ||
| 9.5–36.6 | 28 | 16.27% | 963,889 | 16.21% | 1 | ||
| 36.6–153.8 | 43 | 25% | 404,717 | 6.80% | 3.67 | ||
| TWI | (–0.36)–3.2 | 120 | 69.76% | 2,226,337 | 37.44% | 1.86 | 3.32 |
| 3.2–5.4 | 37 | 21.51% | 2,652,037 | 44.60% | 0.48 | ||
| 5.4–9.1 | 14 | 8.13% | 882,423 | 14.84% | 0.54 | ||
| 9.1–19.8 | 1 | 0.58% | 184,444 | 3.10% | 0.18 | ||
| MaP | 460–600 | 10 | 5.81% | 1,166,213 | 19.61% | 0.29 | 2.96 |
| 600–750 | 19 | 11.04% | 1,523,307 | 25.62% | 0.43 | ||
| 750–900 | 51 | 29.65% | 1,627,725 | 27.37% | 1.08 | ||
| 900–1050 | 73 | 42.44% | 1,460,019 | 24.55% | 1.72 | ||
| 1050–1162 | 19 | 11.04% | 167,977 | 2.82% | 3.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popa, M.C.; Peptenatu, D.; Drăghici, C.C.; Diaconu, D.C. Flood Hazard Mapping Using the Flood and Flash-Flood Potential Index in the Buzău River Catchment, Romania. Water 2019, 11, 2116. https://doi.org/10.3390/w11102116
Popa MC, Peptenatu D, Drăghici CC, Diaconu DC. Flood Hazard Mapping Using the Flood and Flash-Flood Potential Index in the Buzău River Catchment, Romania. Water. 2019; 11(10):2116. https://doi.org/10.3390/w11102116
Chicago/Turabian StylePopa, Mihnea Cristian, Daniel Peptenatu, Cristian Constantin Drăghici, and Daniel Constantin Diaconu. 2019. "Flood Hazard Mapping Using the Flood and Flash-Flood Potential Index in the Buzău River Catchment, Romania" Water 11, no. 10: 2116. https://doi.org/10.3390/w11102116
APA StylePopa, M. C., Peptenatu, D., Drăghici, C. C., & Diaconu, D. C. (2019). Flood Hazard Mapping Using the Flood and Flash-Flood Potential Index in the Buzău River Catchment, Romania. Water, 11(10), 2116. https://doi.org/10.3390/w11102116






