Research on Hydraulic Characteristics in Diversion Pipelines under a Load Rejection Process of a PSH Station
Abstract
:1. Introduction
2. Numerical Method of Computational Model
2.1. Governing Equations
2.2. Turbulence Model
2.3. Mesh Independence Analysis
2.4. Equations Discretization and Boundary Conditions
3. Case Model
4. Results Analysis
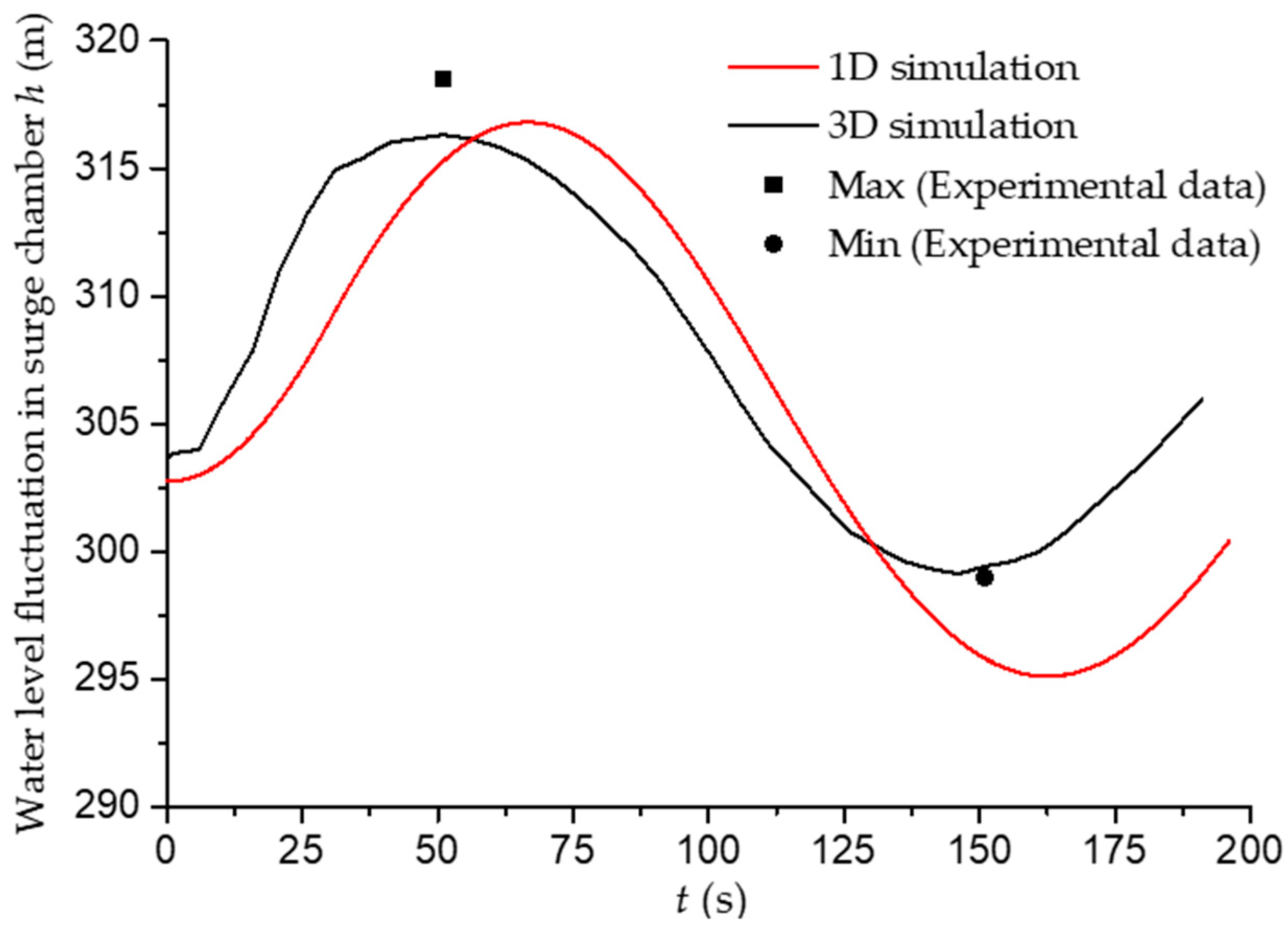
4.1. Water Level Fluctuation in Surge Chamber
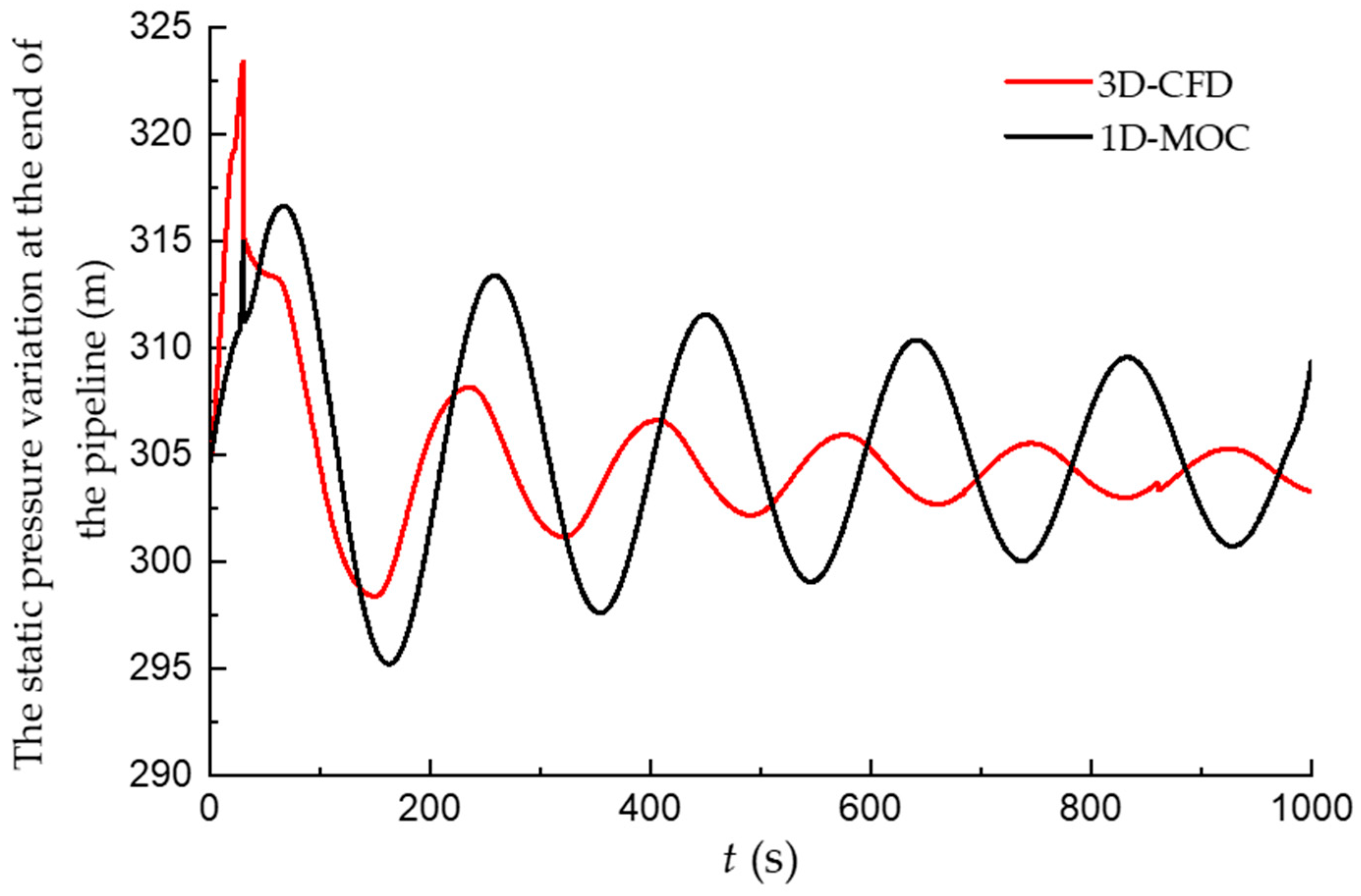
4.2. The Pressure Fluctuation at the End of Pipeline
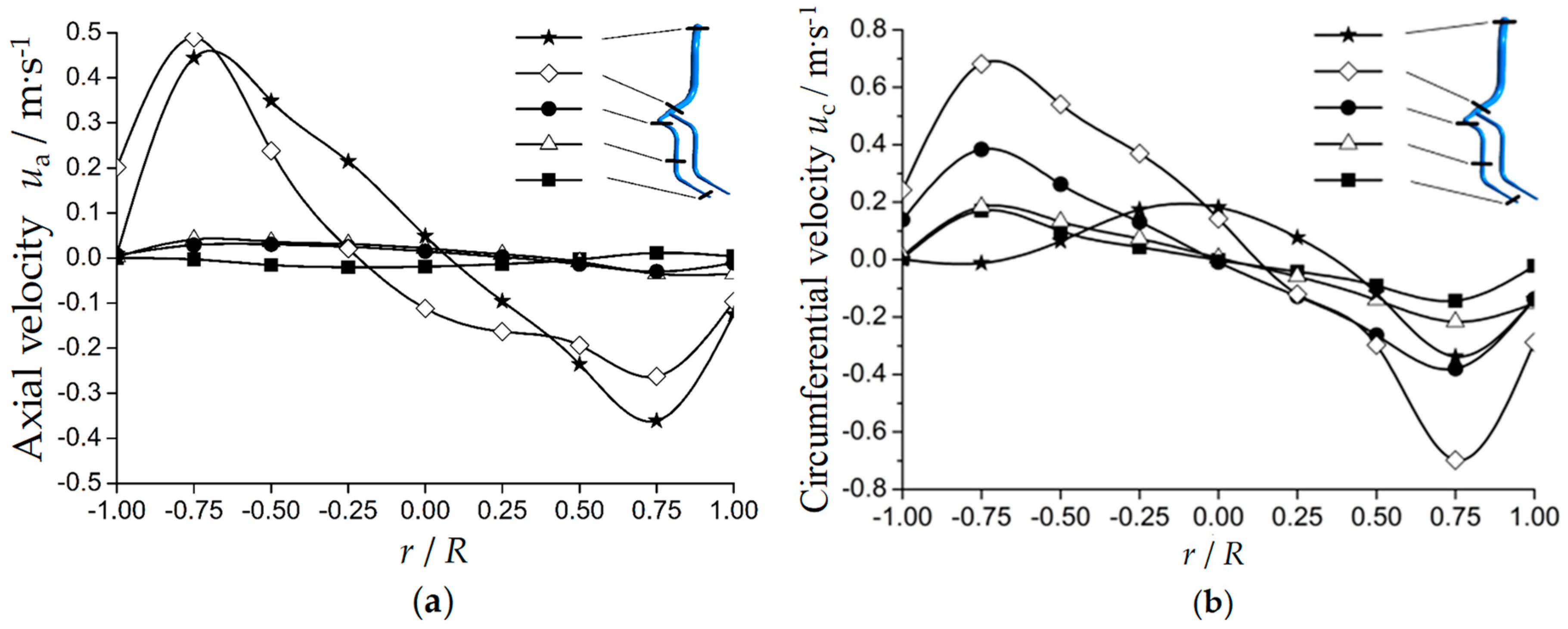
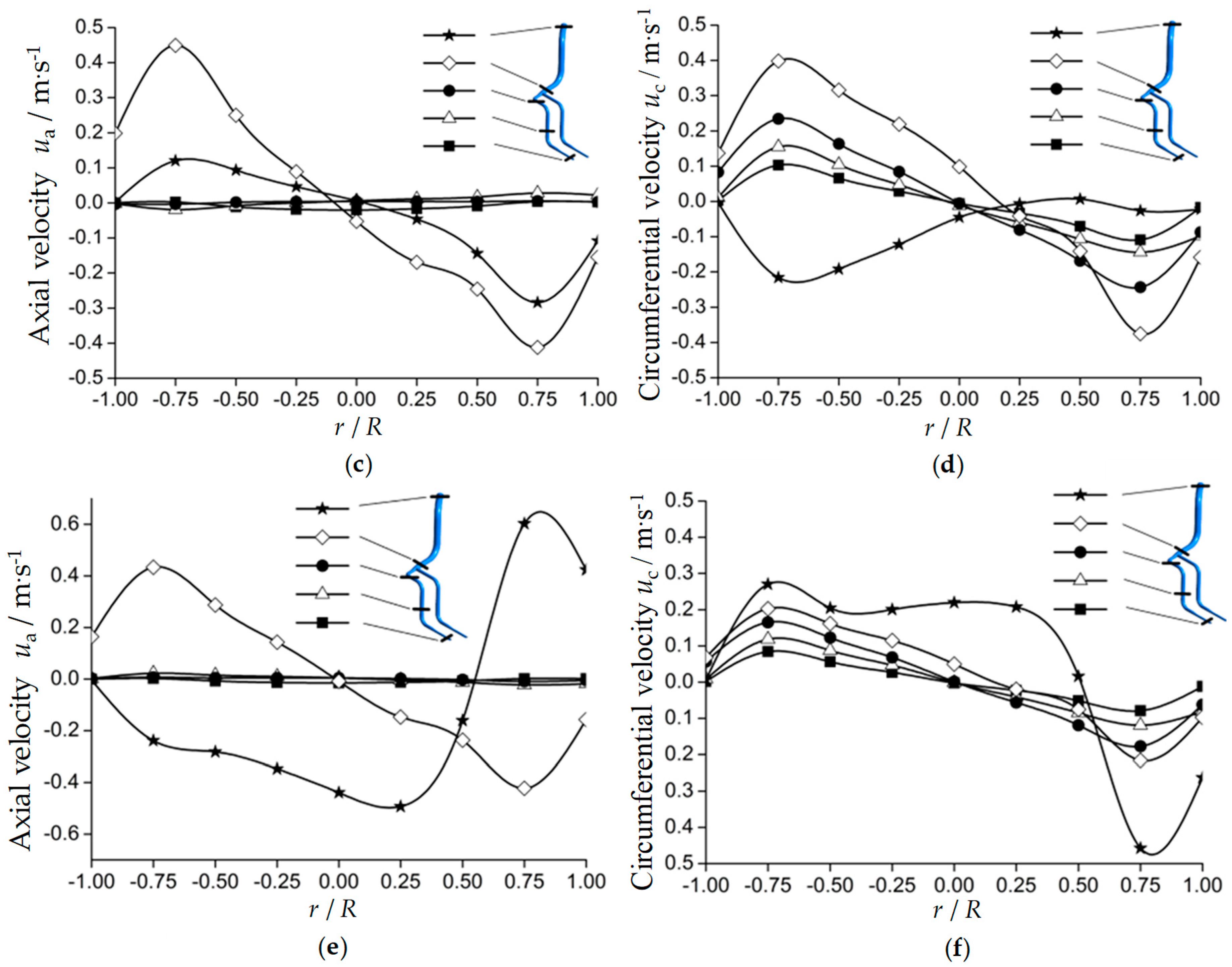
4.3. Flow Velocity Distribution at Different Cross Sections in the Pipeline
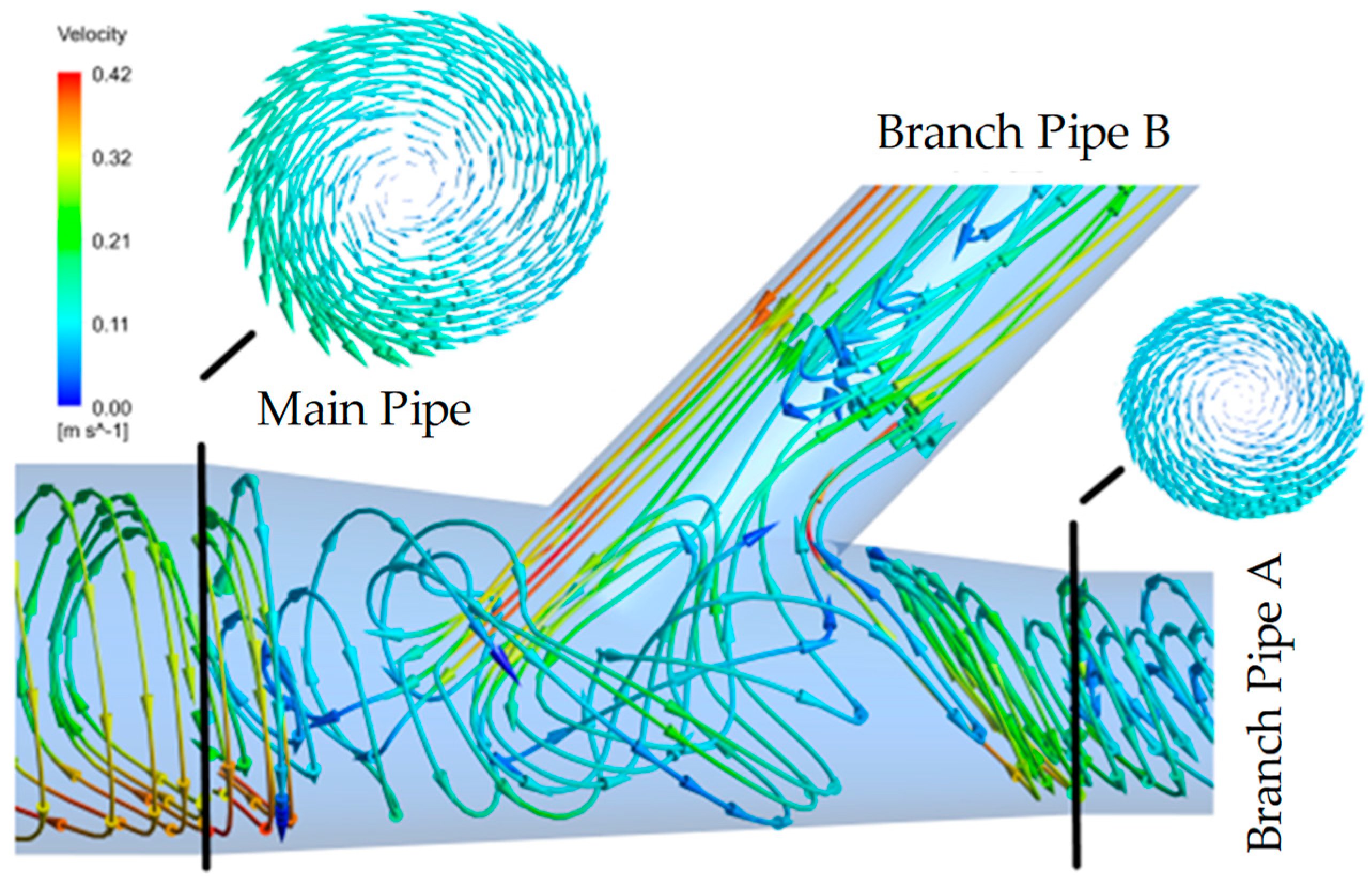
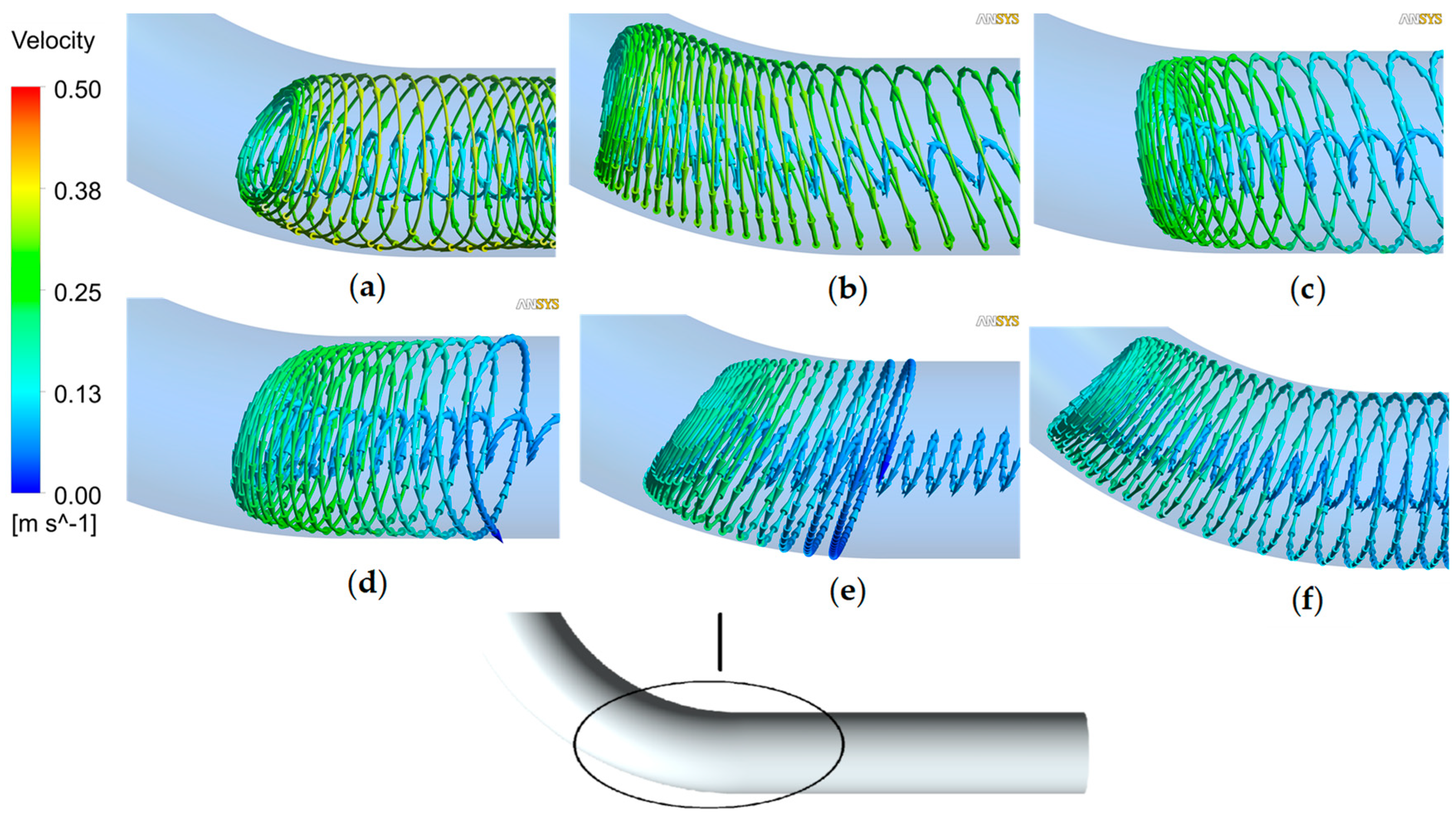
4.4. Flow Regime Analysis in the Bifurcated Pipeline
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Production of the turbulence kinetic energy | m2/s2 | |
| The phase | - | |
| Turbulence kinetic energy | m2/s2 | |
| Number of phases | - | |
| N | Number of grid cells | - |
| Pressure | Pa | |
| Axial velocity | m/s | |
| Circumferential velocity | m/s | |
| , | Velocity component | m/s |
| , | Coordinate component | m |
| Time | s | |
| Fluid density | kg/m3 | |
| Turbulent dissipation rate | m2/s3 | |
| Kinetic viscosity | Pa·s | |
| Turbulent viscosity | Pa·s | |
| The volume fraction of water phase | - | |
| The volume fraction of air phase | - | |
| Time step size | s |
Abbreviations
| 1D | One dimensional |
| 2D | Two dimensional |
| 3D | Three dimensional |
| CFD | Computational fluid dynamics |
| MOC | Method of characteristics |
| MOI | Method of implicit |
| RANS | Reynolds average Navier-Stokes |
| PAT | Pump as turbine |
| PISO | Pressure implicit with splitting of operators |
| PRESTO | PREssure STaggering Option |
| PSH | Pumped storage hydropower |
| SIMPLEC | Semi-implicit method for pressure linked equations-consistent |
| UDF | User defined function |
| VOF | Volume of fluids |
References
- Perez-Diaz, J.I.; Chazarra, M.; Garcia-Gonzalez, J.; Cavazzini, G.; Stoppato, A. Trends and challenges in the operation of pumped-storage hydropower plants. Renew. Sust. Energy Rev. 2015, 44, 767–784. [Google Scholar] [CrossRef]
- Harby, A.; Sauterleute, J.; Korpas, M.; Killingtveit, A.; Solvang, E.; Nielsen, T. Pumped Storage Hydropower; Wiley Blackwell: Hoboken, NJ, USA, 2013; pp. 597–618. [Google Scholar]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sust. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.Y.; Xu, B.B.; Patelli, E.; Tolo, S. Dynamic analysis of a pumped-storage hydropower plant with random power load. Mech. Syst. Signal Proc. 2018, 100, 524–533. [Google Scholar] [CrossRef]
- Riasi, A.; Tazraei, P. Numerical analysis of the hydraulic transient response in the presence of surge tanks and relief valves. Renew. Energy 2017, 107, 138–146. [Google Scholar] [CrossRef]
- Wan, W.Y.; Zhang, B.R. Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank. Energies 2018, 11, 16. [Google Scholar] [CrossRef]
- Chaudhry, M.H.H.; Hussaini, M.Y. Second-Order Accurate Explicit Finite-Difference Schemes for Waterhammer Analysis. J. Fluids Eng.—Trans. ASME 1985, 107, 523–529. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A Review of Water Hammer Theory and Practice. Appl. Mech. Rev. 2005, 58, 49. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.K.; Cervantes, M.J.; Dahlhaug, O.G. Experimental investigations of a model Francis turbine during shutdown at synchronous speed. Renew. Energy 2015, 83, 828–836. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, J.; Zhou, L. Hydraulic transients in the long diversion-type hydropower station with a complex differential surge tank. ScientificWorldJournal 2014, 2014, 241868. [Google Scholar] [CrossRef]
- Chen, H.X.; Zhou, D.Q.; Zheng, Y.; Jiang, S.W.; Yu, A.; Guo, Y. Load rejection transient process simulation of a Kaplan turbine model by co-adjusting guide vanes and runner blades. Energies 2018, 11, 3354. [Google Scholar] [CrossRef]
- Wen, F.; Cheng, Y.; Meng, W. Dynamic hydraulic characteristics of a prototype ball valve during closing process analysed by 3D CFD method. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bejing, China, 16–19 November 2017; p. 012115. [Google Scholar]
- Ferreira, J.; Martins, N.M.C.; Covas, D.I.C. Ball Valve Behavior under Steady and Unsteady Conditions. J. Hydraul. Eng.-ASCE 2018, 144, 12. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Soares, A.K.; Ramos, H.M.; Covas, D.I.C. CFD modeling of transient flow in pressurized pipes. Comput. Fluids 2016, 126, 129–140. [Google Scholar] [CrossRef]
- Chen, N.X.; Z., Y.J.; Tu, M.Q.; Mei, Z.Y. Study on transients and its stability in pumped storage power station under hydraulic turbulence. J. Hydraul. Eng.-ASCE 1996, 10, 7. [Google Scholar]
- Zhang, W.; Cai, F.; Zhou, J.; Hua, Y. Experimental Investigation on Air-Water Interaction in a Hydropower Station Combining a Diversion Tunnel with a Tailrace Tunnel. Water 2017, 9, 274. [Google Scholar] [CrossRef]
- Cheng, Y.G.; Li, J.P.; Yang, J.D. Free surface-pressurized flow in ceiling-sloping tailrace tunnel of hydropower plant: Simulation by VOF model. J. Hydraul. Res. 2007, 45, 88–99. [Google Scholar] [CrossRef]
- Wang, C.; Yang, J.D. Water Hammer Simulation Using Explicit-Implicit Coupling Methods. J. Hydraul. Eng.-ASCE 2015, 141, 11. [Google Scholar] [CrossRef]
- Xia, L.S.; Cheng, Y.G.; Zhou, D.Q. 3-D simulation of transient flow patterns in a corridor-shaped air-cushion surge chamber based on computational fluid dynamics. J. Hydrodyn. Ser. B 2013, 25, 249–257. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.Y.; Ou, C.Q. Simulation of flow transients in a water filling pipe containing entrapped air pocket with VOF model. Eng. Appl. Comp. Fluid Mech. 2011, 5, 127–140. [Google Scholar] [CrossRef]
- Jin, J.; Huang, G.; Nie, L.; Dong, S.; Chen, X. A multi-valve protection from water hammer in long-distance pipelines. In Proceedings of the ICMREE 2011—Proceedings 2011 International Conference on Materials for Renewable Energy and Environment, Shanghai, China, 20–22 May 2011; pp. 1835–1838. [Google Scholar]
- Dutta, P.; Saha, S.K.; Nandi, N.; Pal, N. Numerical study on flow separation in 90° pipe bend under high Reynolds number by k-ε modelling. Eng. Sci. Technol. Int. J. 2016, 19, 904–910. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.; Ramos, H. PATs Operating in Water Networks under Unsteady Flow Conditions: Control Valve Manoeuvre and Overspeed Effect. Water 2018, 10, 529. [Google Scholar] [CrossRef]
- Jing, H.X.; Zhang, D.H.; Li, G.D. Pressure variations of fluid transients in a pressurized pipeline. Fluid Dyn. Res. 2018, 50, 15. [Google Scholar] [CrossRef]
- Khan, M.; Ahmed, J.; Ahmad, L. Chemically reactive and radiative von Kármán swirling flow due to a rotating disk. Appl. Math. Mech. 2018, 39, 1295–1310. [Google Scholar] [CrossRef]
- Kabir, M.A.; Alam, M.F.; Uddin, M.A. A Numerical Study on the Effects of Reynolds Number on Blood Flow with Spiral Velocity Through Regular Arterial Stenosis. Chiang Mai J. Sci. 2018, 45, 2515–2527. [Google Scholar]
- Lin, X.H.; Jiang, S.Y.; Zhang, C.B.; Liu, X. Thermohydrodynamic Analysis of High-Speed Water-Lubricated Spiral Groove Thrust Bearing Using Cavitating Flow Model. J. Tribol.-Trans. ASME 2018, 140, 12. [Google Scholar] [CrossRef]
- Levina, G.V.; Montgomery, M.T. Tropical cyclogenesis: A numerical diagnosis based on helical flow organization. In Proceedings of the Workshop Quantised Flux in Tightly Knotted and Linked Systems, Edinburgh, UK, 3–7 December 2012. [Google Scholar]
- Zhang, B.; Wan, W.; Shi, M. Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment. Water 2018, 10, 928. [Google Scholar] [CrossRef]
- Launder, B.E.S.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 21. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Chen, H.X.; Zhang, L.G. Investigation of Pumped Storage Hydropower Power-Off Transient Process Using 3D Numerical Simulation Based on SP-VOF Hybrid Model. Energies 2018, 11, 1020. [Google Scholar] [CrossRef]
- Karim, M.M.; Prasad, B.; Rahman, N. Numerical simulation of free surface water wave for the flow around NACA 0015 hydrofoil using the volume of fluid (VOF) method. Ocean Eng. 2014, 78, 89–94. [Google Scholar] [CrossRef]
- Li, D.Y.; Wang, H.J.; Li, Z.G.; Nielsen, T.K.; Goyal, R.; Wei, X.Z.; Qin, D.Q. Transient characteristics during the closure of guide vanes in a pump turbine in pump mode. Renew. Energy 2018, 118, 973–983. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, Y.; Xie, Z.; Yang, G.; Yang, C. Numerical study on the internal flow characteristics of an axial-flow pump under stall conditions. J. Mech. Sci. Technol. 2018, 32, 4683–4695. [Google Scholar] [CrossRef]
- Fu, X.L.; Li, D.Y.; Wang, H.J.; Zhang, G.H.; Li, Z.G.; Wei, X.Z. Analysis of transient flow in a pump-turbine during the load rejection process. J. Mech. Sci. Technol. 2018, 32, 2069–2078. [Google Scholar] [CrossRef]
- Fu, L.; Wang, Y. Load shedding test and simulation analysis of hydropower station with surge shaft. Water Resour. Power 2012, 30, 4. [Google Scholar]
- Guo, W.C.; Yang, J.D.; Teng, Y. Surge wave characteristics for hydropower station with upstream series double surge tanks in load rejection transient. Renew. Energy 2017, 108, 488–501. [Google Scholar] [CrossRef]
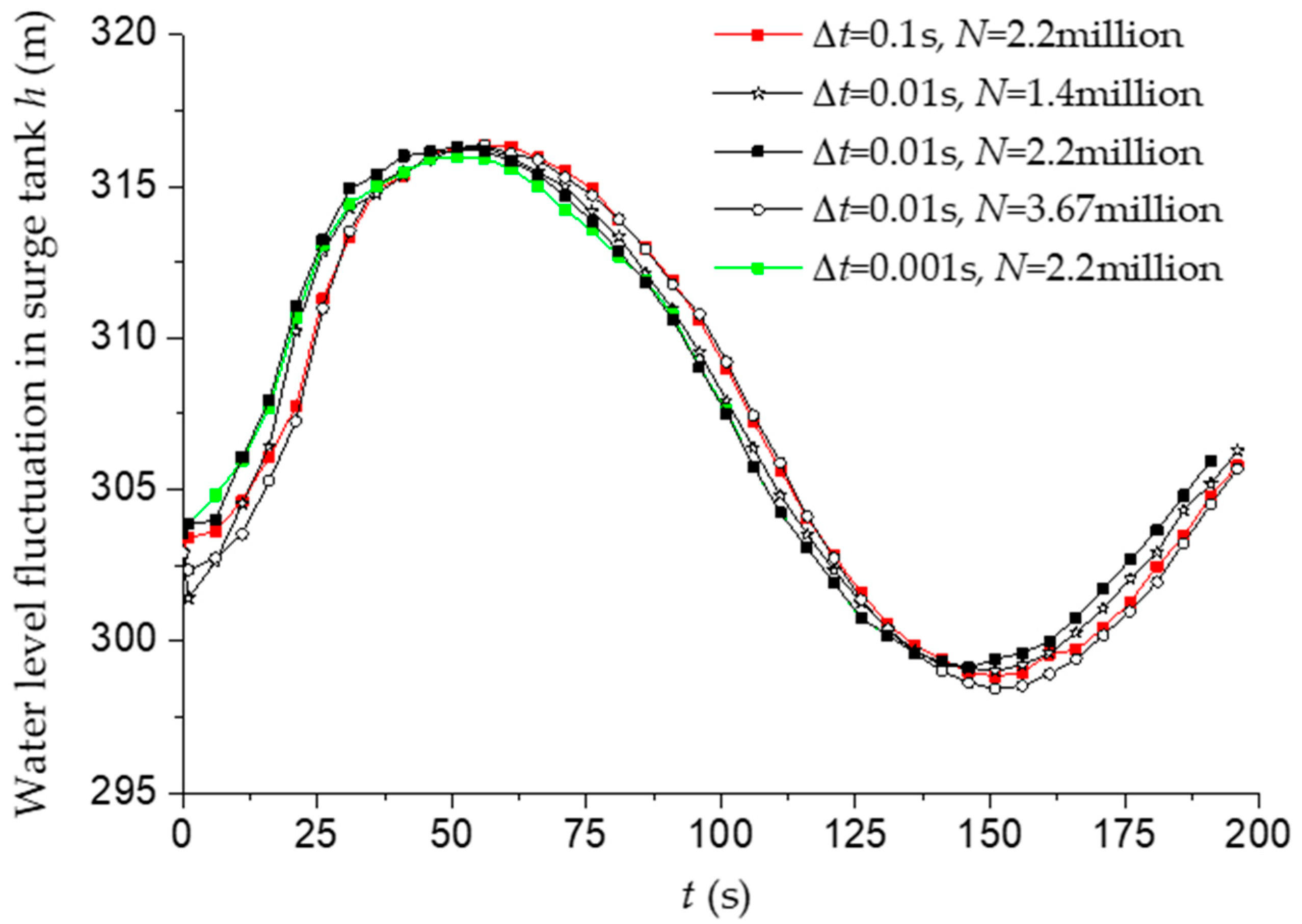
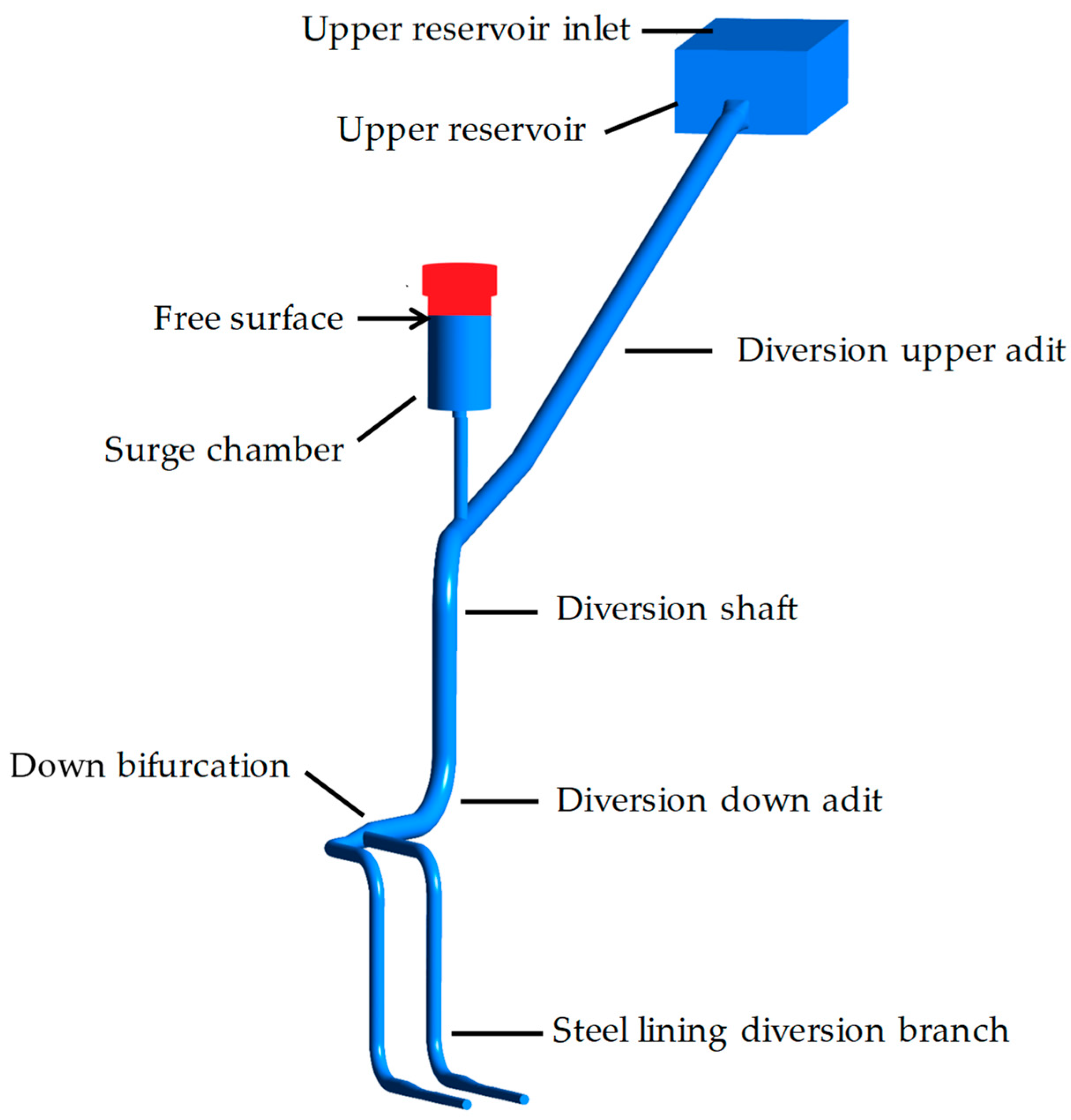

| Passages | Surge tank | Bifurcated pipe | Diversion pipe | Other region | Total |
|---|---|---|---|---|---|
| Mesh type | Tet | Hex/Tet | Hex | Hex/Tet | |
| N/104 | 90 | 20 | 100 | 10 | 220 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Chen, H.; Chen, S. Research on Hydraulic Characteristics in Diversion Pipelines under a Load Rejection Process of a PSH Station. Water 2019, 11, 44. https://doi.org/10.3390/w11010044
Zhou D, Chen H, Chen S. Research on Hydraulic Characteristics in Diversion Pipelines under a Load Rejection Process of a PSH Station. Water. 2019; 11(1):44. https://doi.org/10.3390/w11010044
Chicago/Turabian StyleZhou, Daqing, Huixiang Chen, and Shifan Chen. 2019. "Research on Hydraulic Characteristics in Diversion Pipelines under a Load Rejection Process of a PSH Station" Water 11, no. 1: 44. https://doi.org/10.3390/w11010044
APA StyleZhou, D., Chen, H., & Chen, S. (2019). Research on Hydraulic Characteristics in Diversion Pipelines under a Load Rejection Process of a PSH Station. Water, 11(1), 44. https://doi.org/10.3390/w11010044






