Development of a Maximum Entropy-Archimedean Copula-Based Bayesian Network Method for Streamflow Frequency Analysis—A Case Study of the Kaidu River Basin, China
Abstract
:1. Introduction
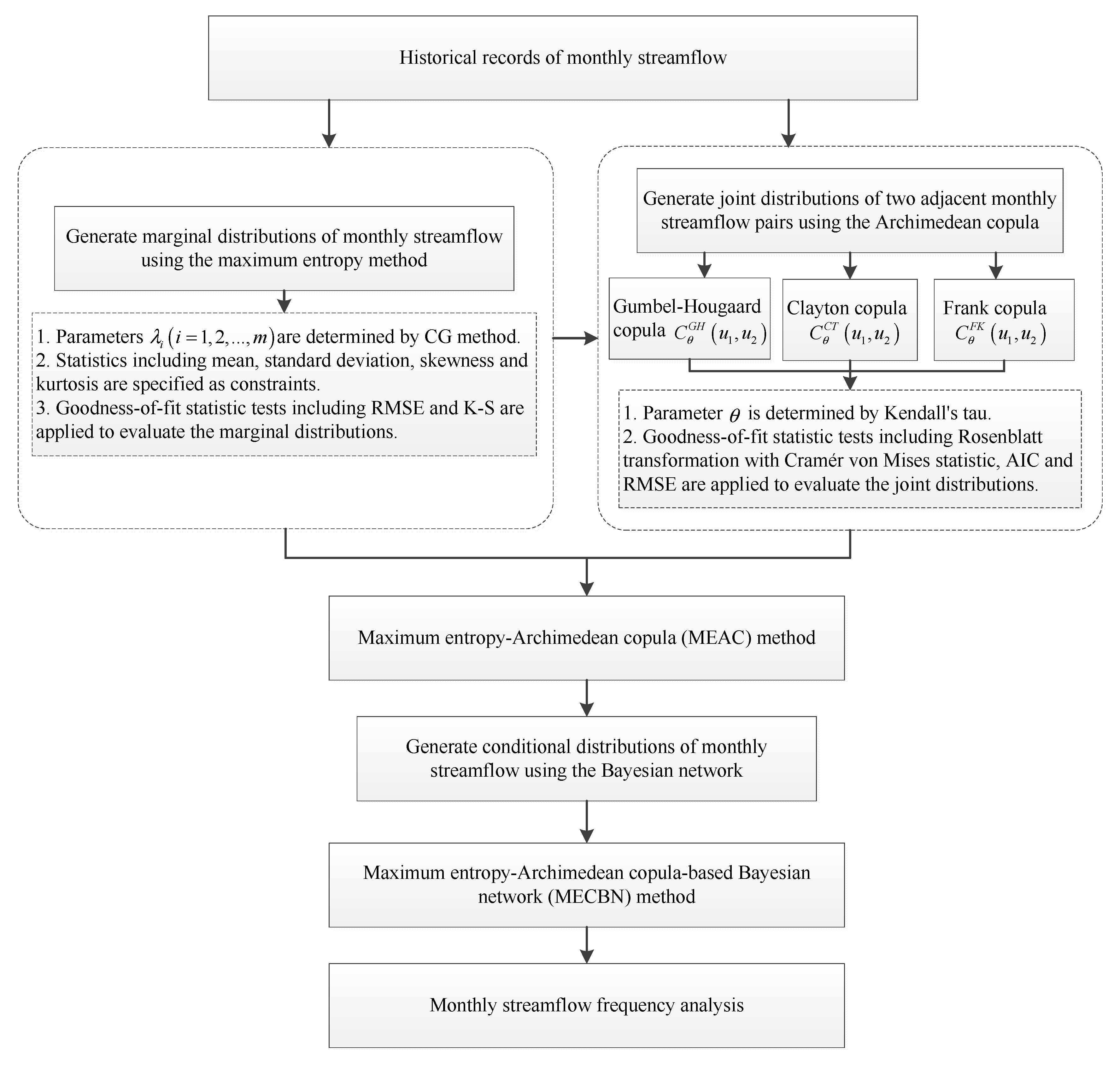
2. Methodology
2.1. Maximum Entropy Method
2.2. Archimedean Copula
2.3. Maximum Entropy-Archimedean Copula Method
2.4. Maximum Entropy-Archimedean Copula-Based Bayesian Network
3. Study Area and Measures
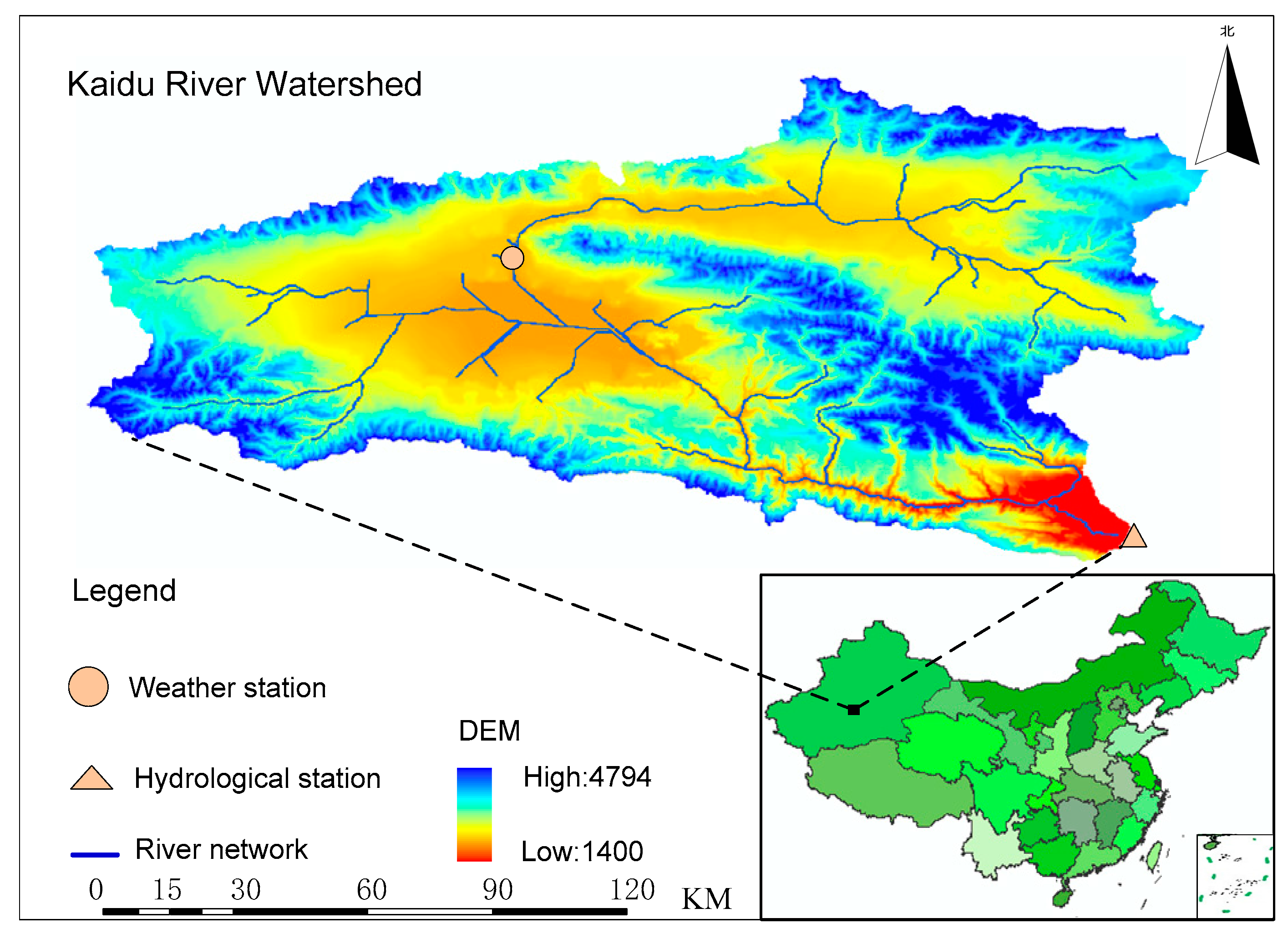
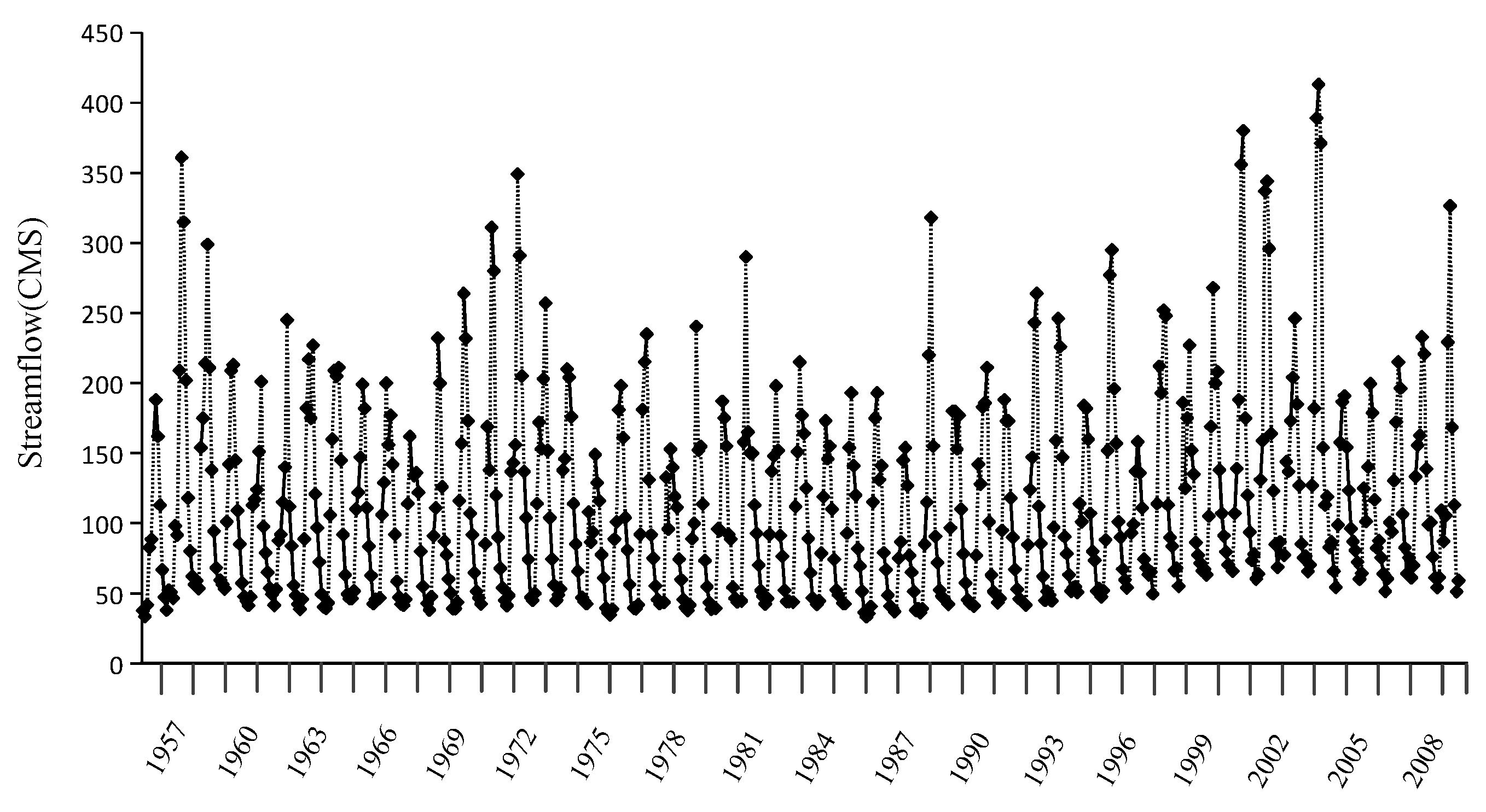
3.1. Study Area
3.2. Dependence Measures
3.3. Goodness-of-Fit (GOF)
4. Results and Discussion
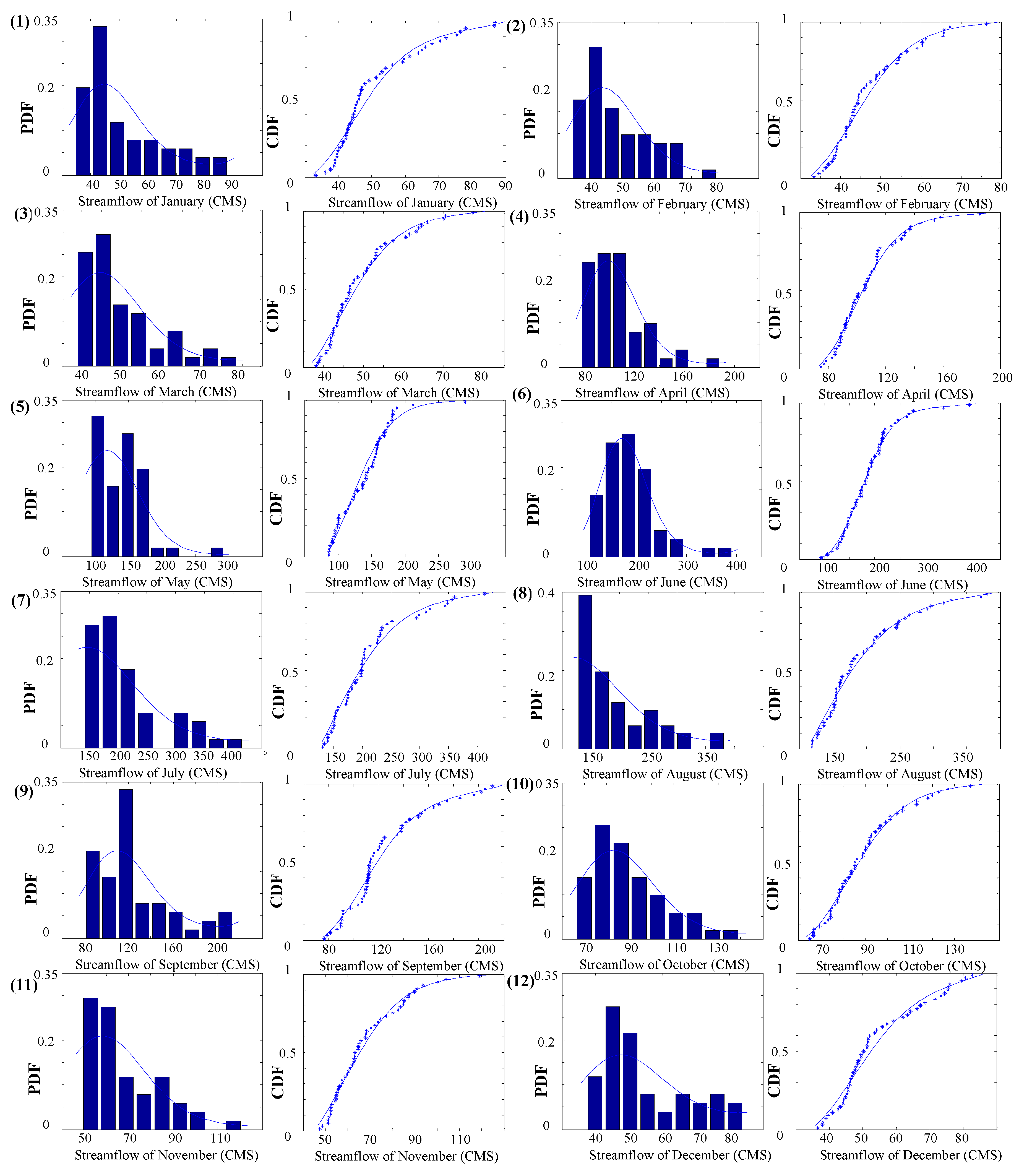
4.1. Marginal Distributions
4.2. Joint Distributions
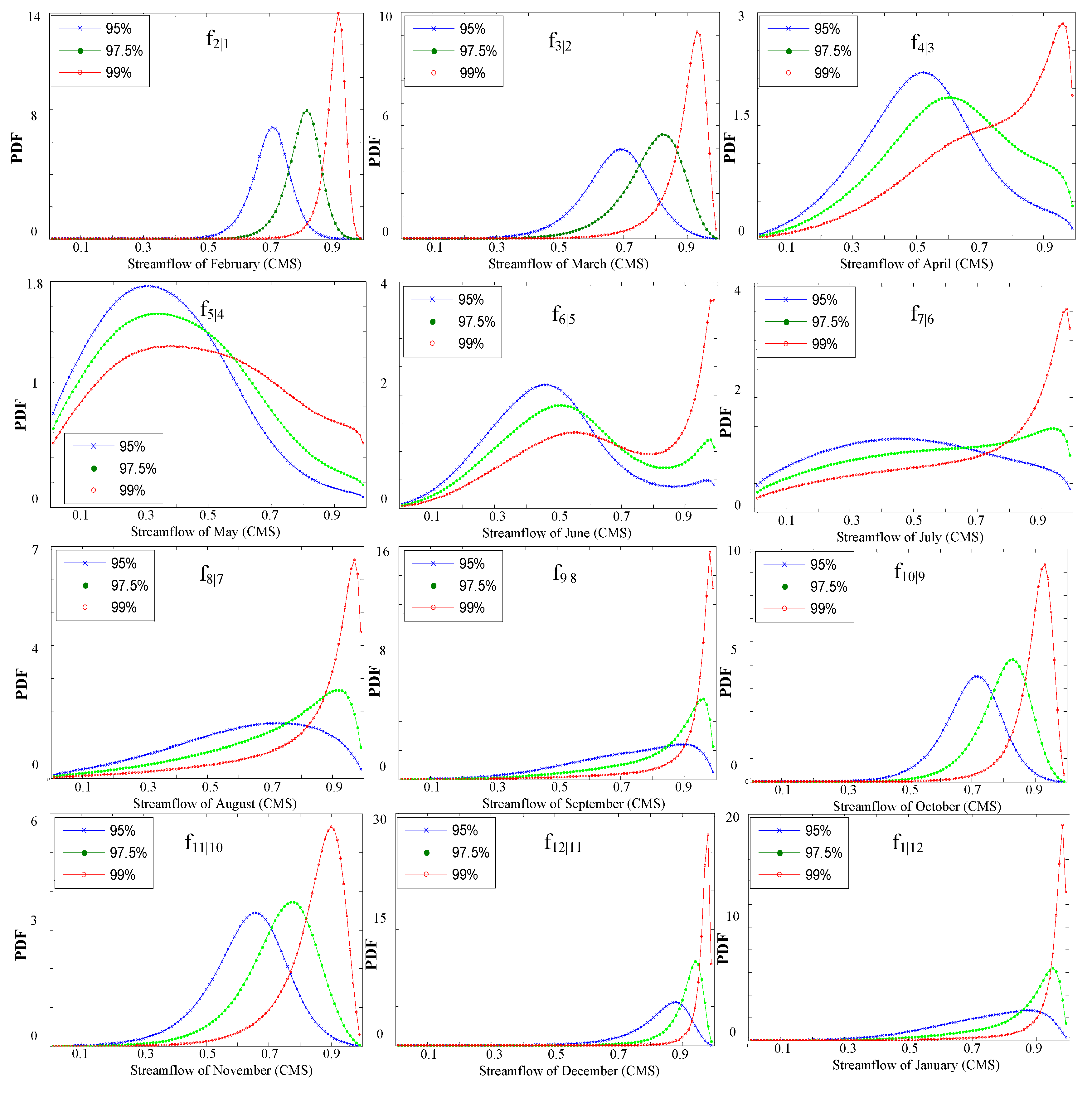
4.3. Conditional Distributions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, Q.; Huang, G.H.; Liu, Z.F.; Fan, Y.R.; Li, W. Inexact fuzzy two-stage programming for water resources management in an environment of fuzziness and randomness. Stoch. Environ. Res. Risk Assess. 2012, 26, 261–280. [Google Scholar] [CrossRef]
- Huang, G.H.; Cohen, S.J.; Yin, Y.Y.; Bass, B. Incorporation of inexact dynamic optimization with fuzzy relation analysis for integrated climate change impact study. J. Environ. Manag. 1996, 48, 45–68. [Google Scholar] [CrossRef]
- Cheng, G.H.; Huang, G.H.; Dong, C.; Baetz, B.W.; Li, Y.P. Interval recourse linear programming for resources and environmental systems management under uncertainty. J. Environ. Inform. 2017, 30, 119–136. [Google Scholar] [CrossRef]
- Huang, Y.; Qin, X.S. A pseudospectral collocation approach for flood inundation modelling with random input fields. J. Environ. Inform. 2017, 30, 95–106. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Nie, S.L.; Liu, L. Inexact multistage stochastic integer programming for water resources management under uncertainty. J. Environ. Manag. 2008, 88, 93–107. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.R.; Huang, G.H.; Baetz, B.W.; Li, Y.P.; Huang, K. Development of a copula-based particle filter (CopPF) approach for hydrologic data assimilation under consideration of parameter interdependence. Water Resour. Res. 2017, 53, 4850–4875. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.W.; Huang, G.H.; Huang, K.; Zhou, X. A PCM-based stochastic hydrological model for uncertainty quantification in watershed systems. Stoch. Environ. Res. Risk Assess. 2015, 29, 915–927. [Google Scholar] [CrossRef]
- Chen, B.; Li, P.; Wu, H.J.; Husain, T.; Khan, F. MCFP: A monte carlo simulation-based fuzzy programming approach for optimization under dual uncertainties of possibility and continuous probability. J. Environ. Inform. 2017, 29, 88–97. [Google Scholar] [CrossRef]
- Han, J.C.; Huang, G.H.; Zhang, H.; Li, Z.; Li, Y.P. Bayesian uncertainty analysis in hydrological modeling associated with watershed subdivision level: A case study of SLURP model applied to the Xiangxi River watershed, China. Stoch. Environ. Res. Risk Assess. 2014, 28, 973–989. [Google Scholar] [CrossRef]
- Pastori, M.; Udías, A.; Bouraoui, F.; Bidoglio, G. A multi-objective approach to evaluate the economic and environmental impacts of alternative water and nutrient management strategies in Africa. J. Environ. Inform. 2017, 29, 16–28. [Google Scholar] [CrossRef]
- Jordan, Y.C.; Ghulam, A.; Chu, M.L. Assessing the impacts of future urban development patterns and climate changes on total suspended sediment loading in surface waters using Geoinformatics. J. Environ. Inform. 2014, 24, 65–79. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G.H.; Fan, Y.R.; Xu, J.L. Hydrologic Risk Analysis for Nonstationary Streamflow Records under Uncertainty. J. Environ. Inform. 2016, 26, 41–51. [Google Scholar]
- Kong, X.M.; Huang, G.H.; Li, Y.P.; Fan, Y.R.; Zeng, X.T.; Zhu, Y. Inexact copula-based stochastic programming method for water resources management under multiple uncertainties. J. Water Resour. Plan. Manag. 2018, 144, 04018069. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, G.H.; Zhang, Y.; Li, Y.P. Uncertainty quantification for multivariate eco-hydrological risk in the Xiangxi River within the Three Gorges Reservoir Area in China. Engineering 2018, 4, 617–626. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.W.; Huang, G.H.; Huang, K.; Li, Y.P.; Kong, X.M. Bivariate hydrologic risk analysis based on a coupled entropy-copula method for the Xiangxi River in the Three Gorges Reservoir area, China. Theor. Appl. Climatol. 2016, 125, 381–397. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.W.; Huang, G.H.; Li, Y.P.; Huang, K.; Li, Z. Hydrologic risk analysis in the Yangtze River basin through coupling Gaussian mixtures into copulas. Adv. Water Resour. 2016, 88, 170–185. [Google Scholar] [CrossRef]
- Asztalos, J.R.; Kim, Y. Lab-Scale Experiment and model study on enhanced digestion of wastewater sludge using bioelectrochemical systems. J. Environ. Inform. 2017, 29, 98–109. [Google Scholar] [CrossRef]
- Kong, X.M.; Huang, G.H.; Fan, Y.R.; Li, Y.P.; Zeng, X.T.; Zhu, Y. Risk analysis for water resources management under dual uncertainties through factorial analysis and fuzzy random value-at-risk. Stoch. Environ. Res. Risk Assess. 2017, 31, 1–16. [Google Scholar] [CrossRef]
- Kong, X.M.; Huang, G.H.; Fan, Y.R.; Li, Y.P. A duality theorem-based algorithm for inexact quadratic programming problems: Application to waste management under uncertainty. Eng. Optim. 2016, 48, 562–581. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U. Spatial scaling in a changing climate: A hierarchical Bayesian model for non-stationary multi-site annual maximum and monthly streamflow. J. Hydrol. 2010, 383, 307–318. [Google Scholar] [CrossRef]
- Erro, J.; Lόpez, J.J. Regional frequency analysis of annual maximum streamflow in Gipuzkoa (Spain). Geophys. Res. Abstr. 2012, 14, 8274. [Google Scholar]
- Schnier, S.; Cai, X.M. Prediction of regional streamflow frequency using model tree ensembles. J. Hydrol. 2014, 517, 298–309. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.H.; Singh, V.P.; Xiao, M.Z.; Xu, C.Y. Flood frequency under the influence of trends in the Pearl River basin, China: Changing patterns, causes and implications. Hydrol. Process. 2015, 29, 1406–1417. [Google Scholar] [CrossRef]
- Chan, T.U.; Hart, B.T.; Kennard, M.J.; Pusey, B.J.; Shenton, W.; Douglas, M.M.; Valentine, E.; Patel, S. Bayesian network models for environmental flow decision making in the Daly River, Northern Territory, Australia. River Res. Appl. 2012, 28, 283–301. [Google Scholar] [CrossRef]
- Nagarajan, K.; Krekeler, C.; Slatton, K.C.; Graham, W.D. A scalable approach to fusing spatiotemporal data to estimate streamflow via a Bayesian network. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3720–3732. [Google Scholar] [CrossRef]
- Mediero, L.; Santillán, D.; Garrote, L. Flood quantile estimation at ungauged sites by Bayesian networks. Geophys. Res. Abstr. 2012, 14, 11998. [Google Scholar]
- Zhang, D.; Yan, X.P.; Yang, Z.L.; Wall, A.; Wang, J. Incorporation of formal safety assessment and Bayesian network in navigational risk estimation of the Yangtze River. Reliab. Eng. Syst. Saf. 2013, 118, 93–105. [Google Scholar] [CrossRef]
- D’Addabbo, A.; Refice, A.; Pasquariello, G. A Bayesian network approach to perform SAR/InSAR data fusion in a flood detection problem. Proc. SPIE 2014, 9224, 9244. [Google Scholar]
- Madadgar, S.; Moradkhani, H. A Bayesian framework for probabilistic seasonal drought forecasting. J. Hydrometeorol. 2013, 14, 1685. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Spatio-temporal drought forecasting within Bayesian networks. J. Hydrol. 2014, 512, 134–146. [Google Scholar] [CrossRef]
- Kong, X.M.; Huang, G.H.; Fan, Y.R.; Li, Y.P. Maximum entropy-Gumbel-Hougaard copula method for simulation of monthly streamflow in Xiangxi River, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 833–846. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Entropy-based parameter estimation for extended three-parameter Burr III distribution for low-flow frequency analysis. Trans. ASABE 2009, 52, 1193–1202. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.C. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Genest, C.; MacKay, J. The joy of copulas: Bivariate distributions with uniform marginal (Com: 87V41 P248). Am. Stat. 1986, 40, 280–283. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Wang, C.X.; Li, Y.P.; Zhang, J.L.; Huang, G.H. Assessing parameter uncertainty in semi-distributed hydrological model based on type-2 fuzzy analysis—A case study of Kaidu River. Hydrol. Res. 2015. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Li, Y.P.; Huang, G.H.; Liu, T. A fuzzy-based simulation method for modelling hydrological processes under uncertainty. Hydrol. Process. 2010, 24, 3718–3732. [Google Scholar] [CrossRef]
- Fu, A.H.; Chen, Y.N.; Li, W.H.; Li, B.F.; Yang, Y.H.; Zhang, S.H. Spatial and temporal patterns of climate variations in the Kaidu River Basin of Xinjiang, Northwest China. Quat. Int. 2013, 311, 117–122. [Google Scholar] [CrossRef]
- Poulin, A.; Huard, D.; Favre, A.C.; Pugin, S. Importance of tail dependence in bivariate frequency analysis. J. Hydrol. Eng. 2007, 12, 394–403. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisions of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
| Month | ||||
|---|---|---|---|---|
| 1 | −6.78 | 16.35 | −1.14 | −7.60 |
| 2 | −6.34 | 13.51 | 0.39 | −5.47 |
| 3 | −4.27 | 12.13 | −0.62 | −4.89 |
| 4 | −8.62 | 19.32 | 2.04 | −10.77 |
| 5 | −3.83 | 10.90 | 5.20 | −8.47 |
| 6 | −13.78 | 26.80 | 5.40 | −17.66 |
| 7 | −1.12 | 7.93 | −1.07 | −3.26 |
| 8 | −0.28 | 6.29 | −0.53 | −3.07 |
| 9 | −7.05 | 14.75 | 1.53 | −8.55 |
| 10 | −6.57 | 12.78 | 1.53 | −5.80 |
| 11 | −3.29 | 9.95 | 0.27 | −3.98 |
| 12 | −4.73 | 10.39 | −0.99 | −3.82 |
| Month | RMSE | K–S test | |
|---|---|---|---|
| p-Value | |||
| 1 | 2.28 | 0.135 | 0.145 |
| 2 | 1.46 | 0.099 | 0.347 |
| 3 | 1.20 | 0.081 | 0.490 |
| 4 | 2.31 | 0.074 | 0.546 |
| 5 | 8.62 | 0.100 | 0.340 |
| 6 | 5.06 | 0.055 | 0.706 |
| 7 | 10.28 | 0.086 | 0.447 |
| 8 | 5.41 | 0.058 | 0.684 |
| 9 | 4.44 | 0.096 | 0.371 |
| 10 | 1.52 | 0.054 | 0.722 |
| 11 | 1.82 | 0.087 | 0.436 |
| 12 | 2.06 | 0.107 | 0.290 |
| Month | Gumbel-Hougaard | Frank | Clayton | |||
|---|---|---|---|---|---|---|
| p-Value | p-Value | p-Value | ||||
| 1–2 | 34.03 | 0.383 | 32.30 | 0.782 | 35.79 | 0.053 |
| 2–3 | 33.89 | 0.368 | 32.31 | 0.762 | 35.28 | 0.063 |
| 3–4 | 32.62 | 0.552 | 32.46 | 0.667 | 32.40 | 0.063 |
| 4–5 | 34.31 | 0.303 | 34.22 | 0.408 | 37.56 | 0.023 |
| 5–6 | 33.83 | 0.437 | 33.32 | 0.612 | 33.43 | 0.068 |
| 6–7 | 33.15 | 0.542 | 32.93 | 0.662 | 33.96 | 0.048 |
| 7–8 | 33.53 | 0.482 | 33.00 | 0.672 | 33.20 | 0.093 |
| 8–9 | 33.27 | 0.507 | 32.38 | 0.752 | 33.46 | 0.088 |
| 9–10 | 34.70 | 0.288 | 32.53 | 0.697 | 36.36 | 0.043 |
| 10–11 | 33.39 | 0.527 | 32.47 | 0.722 | 34.08 | 0.078 |
| 11–12 | 32.49 | 0.637 | 32.16 | 0.752 | 33.63 | 0.083 |
| 12–1 | 33.39 | 0.437 | 32.34 | 0.792 | 34.15 | 0.063 |
| Month | Gumbel–Hougaard | Frank | ||
|---|---|---|---|---|
| AIC | RMSE | AIC | RMSE | |
| 1–2 | −311.52 | 0.0462 | −202.87 | 0.1342 |
| 2–3 | −321.77 | 0.0418 | −223.97 | 0.1091 |
| 3–4 | −347.22 | 0.0329 | −284.88 | 0.0601 |
| 4–5 | −327.10 | 0.0397 | −326.69 | 0.0399 |
| 5–6 | −341.56 | 0.0345 | −325.32 | 0.0404 |
| 6–7 | −360.95 | 0.0285 | −320.81 | 0.0422 |
| 7–8 | −341.83 | 0.0344 | −277.97 | 0.0643 |
| 8–9 | −321.79 | 0.0418 | −224.64 | 0.1084 |
| 9–10 | −338.00 | 0.0357 | −257.98 | 0.0782 |
| 10–11 | −358.19 | 0.0293 | −239.11 | 0.0941 |
| 11–12 | −299.66 | 0.0520 | −215.47 | 0.1186 |
| 12–1 | −294.01 | 0.0549 | −229.85 | 0.1030 |
| Month | Spearman’s Rho | Kendall’s Tau | Upper Tail Dependence Coefficient |
|---|---|---|---|
| 1–2 | 0.931 | 0.784 | 0.838 |
| 2–3 | 0.856 | 0.678 | 0.750 |
| 3–4 | 0.541 | 0.392 | 0.476 |
| 4–5 | 0.292 | 0.180 | 0.235 |
| 5–6 | 0.435 | 0.312 | 0.389 |
| 6–7 | 0.410 | 0.280 | 0.353 |
| 7–8 | 0.595 | 0.435 | 0.521 |
| 8–9 | 0.716 | 0.527 | 0.612 |
| 9–10 | 0.853 | 0.678 | 0.750 |
| 10–11 | 0.753 | 0.603 | 0.683 |
| 11–12 | 0.856 | 0.691 | 0.761 |
| 12–1 | 0.775 | 0.597 | 0.678 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, X.; Zeng, X.; Chen, C.; Fan, Y.; Huang, G.; Li, Y.; Wang, C. Development of a Maximum Entropy-Archimedean Copula-Based Bayesian Network Method for Streamflow Frequency Analysis—A Case Study of the Kaidu River Basin, China. Water 2019, 11, 42. https://doi.org/10.3390/w11010042
Kong X, Zeng X, Chen C, Fan Y, Huang G, Li Y, Wang C. Development of a Maximum Entropy-Archimedean Copula-Based Bayesian Network Method for Streamflow Frequency Analysis—A Case Study of the Kaidu River Basin, China. Water. 2019; 11(1):42. https://doi.org/10.3390/w11010042
Chicago/Turabian StyleKong, Xiangming, Xueting Zeng, Cong Chen, Yurui Fan, Guohe Huang, Yongping Li, and Chunxiao Wang. 2019. "Development of a Maximum Entropy-Archimedean Copula-Based Bayesian Network Method for Streamflow Frequency Analysis—A Case Study of the Kaidu River Basin, China" Water 11, no. 1: 42. https://doi.org/10.3390/w11010042
APA StyleKong, X., Zeng, X., Chen, C., Fan, Y., Huang, G., Li, Y., & Wang, C. (2019). Development of a Maximum Entropy-Archimedean Copula-Based Bayesian Network Method for Streamflow Frequency Analysis—A Case Study of the Kaidu River Basin, China. Water, 11(1), 42. https://doi.org/10.3390/w11010042







