Effect of Aluminium Salt Dosing on Activated Sludge Settleability Indicators: A New Settleability Model Development
Abstract
1. Introduction
- ZSV = zone settling velocity (m/h)
- X = activated sludge concentration (g/L)
- = sludge settleability constant (m/h)
- k = sludge settleability constant (L/g).
2. Materials and Methods
2.1. Sludge Sampling and Analysis
2.2. Settlometer Tests
2.3. Data Analysis
3. Model Development and Model Validity for Al3+ Dosed Sludge
3.1. New Model Calibration to Include Al3+ Dosing Parameter
- A = Activity (the number of unstable nuclei remaining), Bq
- = Original number of unstable nuclei, Bq
- e = Constant = 2.718
- λ = Decay constant,
- t = time, s
- ZSV = Actual settling velocity (m/h)
- () Al = Maximum settling velocity (m/h) for Al3+ dosed sludge
- () Al = Empirical Al3+ dosed sludge settling parameter relating to sludge compaction
- () Al = Empirical Al3+ dosing constant related to stokes settling velocity
- () Al = Empirical Al3+ dosing constant related sludge compaction
- () Al = Al3+ dosing concentration (mg/L)
- (X) = Al3+ dosed MLSS concentration (mg/L)
- = Empirical aluminium dosed activated sludge settling parameter related to sludge compaction (L/g)
- = Maximum settling velocity for Al3+ dosed activated sludge related to stokes settling velocity (m/h)
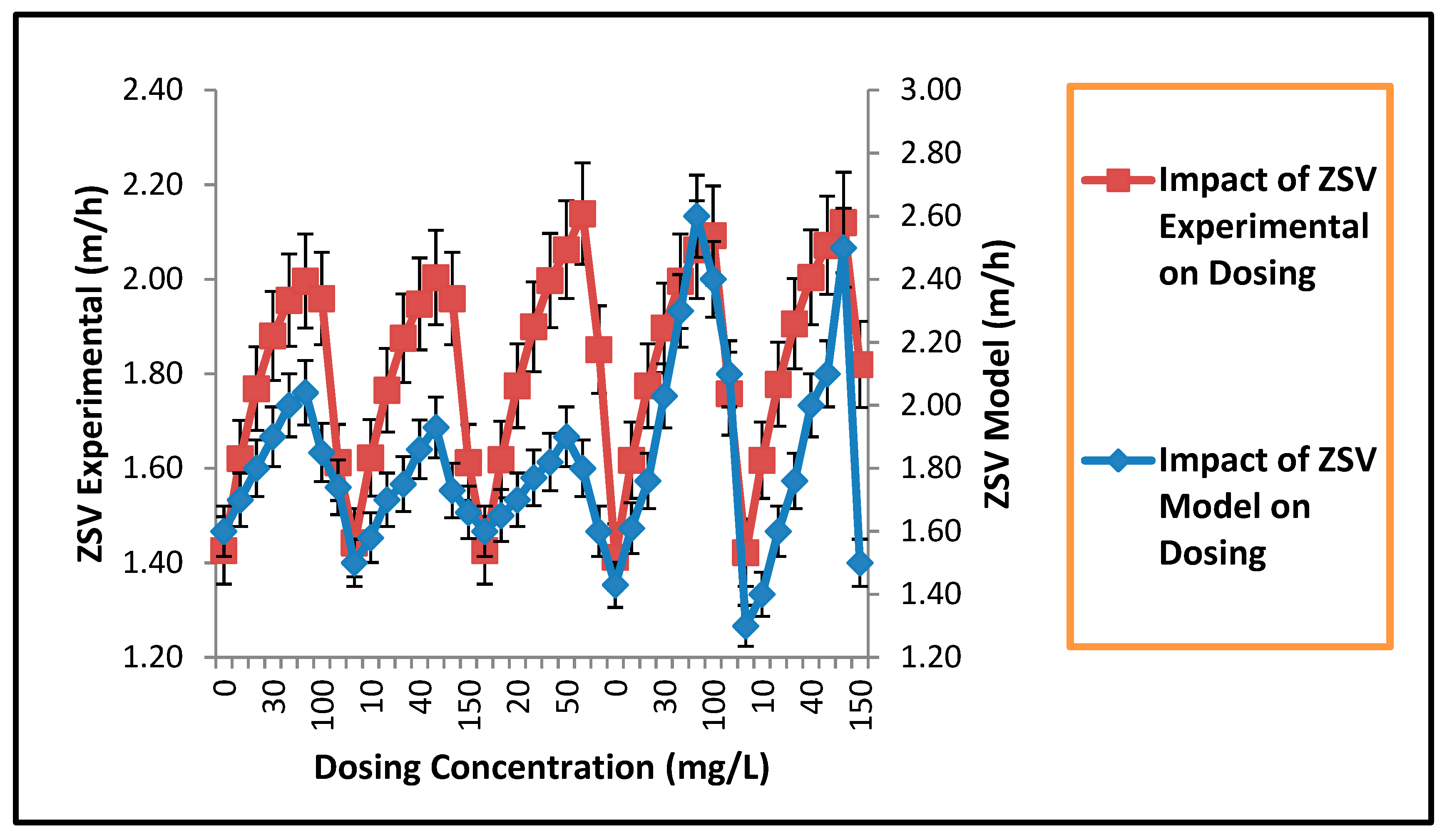
3.2. Validation of Novel Model for Impact of Al3+ Dosing on ZSV and SSVI
Novel ZSV Model
3.3. Summary and Perspectives
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Al | Aluminium |
| ASP | Activated sludge plant |
| CI | Confidence interval |
| CDAS | Chemically dosed activated sludge |
| Empirical chemical dosing constant related to stokes settling velocity | |
| Empirical chemical dosing constant related sludge compaction | |
| DF | Degree of freedom |
| DSVI | Diluted sludge volume index, mL/g |
| Aluminium dosing concentration (mg/L) | |
| ESS | Effluent suspended solid |
| EPS | Extracellular polymeric substances |
| EN | Effluent nitrogen |
| EP | Effluent phosphorus (EP) |
| FST | Final settling tank |
| F | F-test statistics |
| FFT | Full flow treatment |
| H | Sludge height, cm |
| k | Vesilind sludge settleablity constant |
| K | Dick and Young sludge settleability constant |
| Empirical settling parameter relating to sludge compaction | |
| MLD | Mega litres per day |
| MLSS | Mixed liquor suspended solids, g/L |
| R2 | Coefficient of determination |
| SSVI | Stirred specific volume Index, mL/g |
| SVI | Sludge volume index, mL/g |
| SS | Suspended colids |
| SSD | Sum of squared deviation |
| Vesilind sludge parameter related to settling velocity (m/h) | |
| Dick and Young sludge parameter related to settling velocity (m/h) | |
| WWTP | Wastewater treatment plant |
| WRc | Water Research Council |
| X | Activated sludge concentration, g/L |
| Alum dosed MLSS concentration, g/L | |
| α | Significance level |
| ZSVO | Maximum zone settling velocity (m/h) |
| ZSV | Actual zone settling velocity (m/h) |
References
- Wilfert, P.; Kumar, P.S.; Korving, L.; Witkamp, G.J.; van Loosdrecht, M.C.M. The relevance of phosphorus and iron chemistry to the recovery of phosphorus from wastewater: A review. Environ. Sci. Technol. 2015, 49, 9400–9414. [Google Scholar] [CrossRef]
- Haandel, A.C.V.; Lubbe, J.G.M.V. Handbook of Biological Wastewater Treatment: Design and Optimisation of Activated Sludge System, 2nd ed.; IWA Publishing: London, UK, 2012. [Google Scholar]
- Ojo, P.; Ifelebuegu, A.O. The Impact of Alum on the Bulking of a Full scale Activated Sludge Plant. Environ. Eng. 2016, 3, 53–57. [Google Scholar]
- Zou, J.; Zhang, L.; Wang, L.; Li, Y. Enhancing phosphorus release from waste activated sludge containing ferric or aluminium phosphates by EDTA addition during anaerobic fermentation process. Chemosphere 2017, 171, 601–608. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.; Meng, X.; Song, Y.; Terracciano, A. Effect of phosphate releasing in activated sludge on phosphorus removal from municipal wastewater. Environ. Sci. 2018, 67, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Yin, F.; Xu, Y.; Yu, H. A force-based mechanistic model for describing activated sludge settling process. Water Res. 2017, 127, 118–126. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M.K. Dynamic one-dimensional modelling of secondary settling tanks and design impacts of sizing decisions. Water Res. J. 2014, 50, 160–170. [Google Scholar] [CrossRef]
- François, P.; Locatelli, F.; Laurent, J.; Bekkour, K. Experimental study of activated sludge batch settling velocity profile. Flow Measur. Instrum. J. 2016, 48, 112–117. [Google Scholar] [CrossRef]
- Heikal, H.A.M.; El Baz, A.R.; El-Hafiz, A.A.; Farghaly, S.M. Study the Performance of Circular Clarifier in Existing Potable Water Treatment Plant by Computational Fluid Dynamics; International Water Resources Association: Paris, France, 2017. [Google Scholar]
- Zhang, D.J.; Li, Z.L.; Lu, P.L.; Zhang, T.; Xua, D.Y. A method for characterizing the complete settling process of activated sludge. Water Res. 2006, 40, 2637–2644. [Google Scholar] [CrossRef] [PubMed]
- Mancell-Egala, W.A.S.K.; Kinnear, D.J.; Jones, K.L.; Clippeleir, H.D.; Takacs, I.; Murthy, S.N. Limit of stokesian settling concentration characterizes sludge settling velocity. Water Res. 2016, 90, 100–110. [Google Scholar] [CrossRef]
- Ramin, E.; Wagner, D.S.; Yde, L.; Binning, P.J.; Rasmussen, M.R.; Mikkelsen, P.S.; Plosz, B.G. A new settling velocity model to describe secondary sedimentation. Water Res. 2014, 55, 447–458. [Google Scholar] [CrossRef]
- Ekama, G.A.; Barnard, J.L.; Gunthert, F.W.; Krebs, P.; McCorquadale, J.A.; Parker, D.S.; Wahlberg, E.J. Secondary Settling Tanks, Theory, Modelling, Design and Operation; Scientific Report No 6; International Association of Water Quality (IAWQ): London, UK, 1997. [Google Scholar]
- Tchobanoglous, G.; Burton, F.L.; Stensel, H.D. Wastewater Engineering: Treatment and Reuse, 4th ed.; McGraw-Hill Science: New York, NY, USA, 2003. [Google Scholar]
- Jung, K.W.; Hwang, M.J.; Ahn, K.H.; Ok, Y.S. Kinetic study on phosphate removal from aqueous solution by biochar derived from peanut shell as renewable adsorptive media. Int. J. Environ. Sci. Technol. 2015, 12, 3363–3372. [Google Scholar] [CrossRef]
- Ghawi, A.G.; Kris, J. A Computational Fluid Dynamics Model of Flow and Settling in Sedimentation Tanks. Appl. Comput. Fluid Dyn. J. 2012, 2, 19–34. [Google Scholar]
- Ghawi, A.G.; Kris, J. Improvement Performance of Secondary Clarifiers by a Computational Fluid Dynamics Model. Slovak J. Civ. Eng. 2011, 19, 1–11. [Google Scholar] [CrossRef]
- WEF-Water Environment Federation. Clarifier Design WEF Manual of Practice No. FD-8, 2nd ed.; McGraw-Hill: New York, NY, USA, 2005; Available online: http://www.assettler.com/COKTURME%20TANKLARI%20TASARIMI.pdf> (accessed on 20 May 2015).
- Ojo, P.; Ifelebuegu, A.O. The Impact of Aluminium Salt for Chemical Phosphorus Removal on the Settleability of Activated Sludge. Environments 2018, 5, 88. [Google Scholar] [CrossRef]
- Wilen, B.M.; Jin, B.; Lant, P. The influence of key constituents in activated sludge on surface and flocculating properties. Water Res. 2003, 37, 127–2139. [Google Scholar] [CrossRef]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 148, 166–176. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M.K. Research advances and challenges in one-dimensional modelling of secondary settling Tanks: A critical review. Water Res. J. 2014, 65, 40–63. [Google Scholar] [CrossRef]
- Torfs, E.; Balemans, S.; Locatelli, F.; Diehl, S.; Bürger, R.; Laurent, J.; François, P.; Nopens, I. On constitutive functions for hindered settling velocity in 1-D settler models: Selection of appropriate model structure. Water Res. 2017, 110, 38–47. [Google Scholar] [CrossRef]
- Vesilind, P.A. Theoretical considerations: Design of prototype thickeners from batch settling tests. J. Water Sew. Works 1968, 115, 302–307. [Google Scholar]
- Dick, R.I.; Young, K.W. Analysis of thickening performance of final settling tanks. In Proceedings of the 27th Industrial Waste Conference, Lafayette, IN, USA, 2–4 May 1972. [Google Scholar]
- Takács, I.; Patry, G.G.; Nolasco, D. A dynamic model of the clarification-thickening process. Water Res. J. 1991, 25, 1263–1271. [Google Scholar] [CrossRef]
- Dupont, R.; Dahl, C. A one-dimensional model for a secondary settling tank including density current and short-circuiting. Water Sci. Technol. 1995, 31, 215–224. [Google Scholar] [CrossRef]
- Cho, S.; Colin, F.; Sardin, M.; Prost, C. Settling velocity model of activated sludge. Water Res. J. 1993, 27, 1237–1242. [Google Scholar] [CrossRef]
- Zhang, Y.; Grassia, P.; Martin, A.; Usher, S.P.; Scales, P.J. Designing thickeners by matching hindered settling and gelled suspension zones in the presence of aggregate densification. Chem. Eng. Sci. 2015, 134, 297–307. [Google Scholar] [CrossRef]
- Guyonvarch, E.; Ramin, E.; Kulahci, M.; Plosz, B.G. ICFD: Interpreted Computational Fluid Dynamics—Degeneration of CFD to one-dimensional advection-dispersion models using statistical experimental design—The secondary clarifier. Water Res. 2015, 83, 396–411. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R.; Diehl, S.; Faras, S.; Nopens, I.; Torfs, E. A consistent modelling methodology for secondary settling tanks: A reliable numerical method. Water Sci. Technol. 2013, 68, 192–208. [Google Scholar] [CrossRef] [PubMed]
- De Clercq, J. Batch and Continuous Settling of Activated Sludge: In-depth Monitoring and 1D Compression Modelling. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2006. [Google Scholar]
- De Clercq, J.G.U.; Nopens, I.G.U.; Defrancq, J.; Vanrolleghem, P. Extending and calibrating a mechanistic hindered and compression settling model for activated sludge using in-depth batch experiments. Water Res. J. 2008, 42, 781–791. [Google Scholar] [CrossRef]
- Schuler, A.J.; Jang, H. Causes of variable biomass density and its effects on settleability in full-scale biological wastewater treatment systems. Environ. Sci. Technol. 2007, 41, 1675–1681. [Google Scholar] [CrossRef]
- Schuler, A.J.; Jang, H. Microsphere addition for the study of biomass properties and density effects on settleability in biological wastewater treatment systems. Water Res. 2007, 41, 2163–2170. [Google Scholar] [CrossRef]
- White, Settling of Activated Sludge, Technical Report TR11; WRC: Stevanhage, UK, 1975.
- MCR-Process & Technology 2008 Stiro-Settlometer. Available online: http://www.mcrpt.com/english/pdf/manuel_stiro.pdf > (accessed on 10 February 2014).
- Schuler, A.J.; Jang, H. Density effects on activated sludge zone settling velocities. Water Res. J. 2007, 41, 1814–1822. [Google Scholar] [CrossRef]
- Vaerenbergh, E.V. Numerical computation of secondary settler area using batch settling data. Tribune Cebedeau 1980, 33, 369–374. [Google Scholar]
- Wahlberg, E.J.; Keinath, T.M. Development of settling flux curves using SVI. J. Water Pollut. Control Fed. 1988, 60, 2095–2100. [Google Scholar] [CrossRef]
- Giokas, D.; Diagger, G.T.; Sperling, M.V.; Kim, Y.; Paraskevas, A. Comparison and evaluation of empirical zone settling velocity parameters based on sludge volume index using unified settling characteristics database. J. Water Res. 2003, 37, 3821–3836. [Google Scholar] [CrossRef]
- Daigger, G.T. Development of refined clarifier operating diagrams using an updated settling characteristics database. J. Water Environ. Res. 1995, 67, 95–100. [Google Scholar] [CrossRef]
- Pitman, A.R. Settling properties of extended aeration sludge. J. Water Pollut. Control Fed. 1980, 52, 524–536. [Google Scholar]
- Pitman, A.R. Operation of biological nutrient removal plants: In Theory, Design and Operation of Nutrient Removal Activated Sludge Processes; Water Research Commission: Pretoria, South Africa, 1984. [Google Scholar]
- Ekama, G.A.; Marais, G.V.R. Sludge Settleability and Secondary Settling and Design Procedures. Water Pollut. Control 1986, 87, 101–113. [Google Scholar]
- Koopman, B.; Cadee, K. Prediction of thickening capacity using diluted sludge volume index. Water Res. 1983, 17, 1427–1431. [Google Scholar] [CrossRef]
- Lakehal, D.; Krebs, P.; Krijgsman, J.; Rodi, W. Computing shear flow and sludge blanket in secondary clarifiers. J. Hydraul. Eng. 1999, 125, 253–262. [Google Scholar] [CrossRef]
- Dupont, R.; Henze, M. Modelling of the secondary clarifier combined with the activated sludge model no. 1. Water Sci. Technol. 1992, 25, 285–300. [Google Scholar] [CrossRef]
- Lyn, D.A.; Stamou, A.I.; Rodi, W. Density currents and shear induced flocculation in sedimentation tanks. Hydraul. Eng. 1992, 118, 849–867. [Google Scholar] [CrossRef]
- Otterpohl, R.; Freund, M. Dynamic models for clarifiers of activated sludge plants with dry and wet weather flows. Water Sci. Technol. 1992, 26, 1391–1400. [Google Scholar] [CrossRef]
- Mazzolani, G.; Pirozzi, F.; d’Antonoi, G. A generalized settling approach in the numerical modelling of sedimentation tanks. Water Sci. Technol. 1998, 38, 95–102. [Google Scholar] [CrossRef]
- Smollen, M.; Ekama, G.A. Comparison of empirical settling velocity equations in flux theory for secondary settling tanks: South Africa. Water Sci. Technol. 1984, 10, 175–184. [Google Scholar]
- Tuntoolavest, M.; Grady, C.P.L.J. Effect of activated sludge operational conditions on sludge thickening characteristics. Water Pollut. Control Fed. 1980, 54, 1112–1117. [Google Scholar]
- Catunda, P.F.C.; Van Haandel, A.C.; Araujo, L.S.; Vilar, A. Determination of the Settleability of Activated Sludge; The 15th Congress of the Brazilian Sanitary Engineering Organisation: Belem, Brazil, 1989. [Google Scholar]
- Catunda, P.F.C.; Van Haandel, A.C. Activated sludge settling-part I: Experimental determination of settling characteristics. Water 1992, 18, 165–172. [Google Scholar]
- Bürger, R.; Careaga, J.; Diehl, S.; Ryan, M.; Zambrano, J. Estimating the hindered-settling flux function from a batch test in a cone. Chem. Eng. Sci. 2018, 192, 244–253. [Google Scholar] [CrossRef]
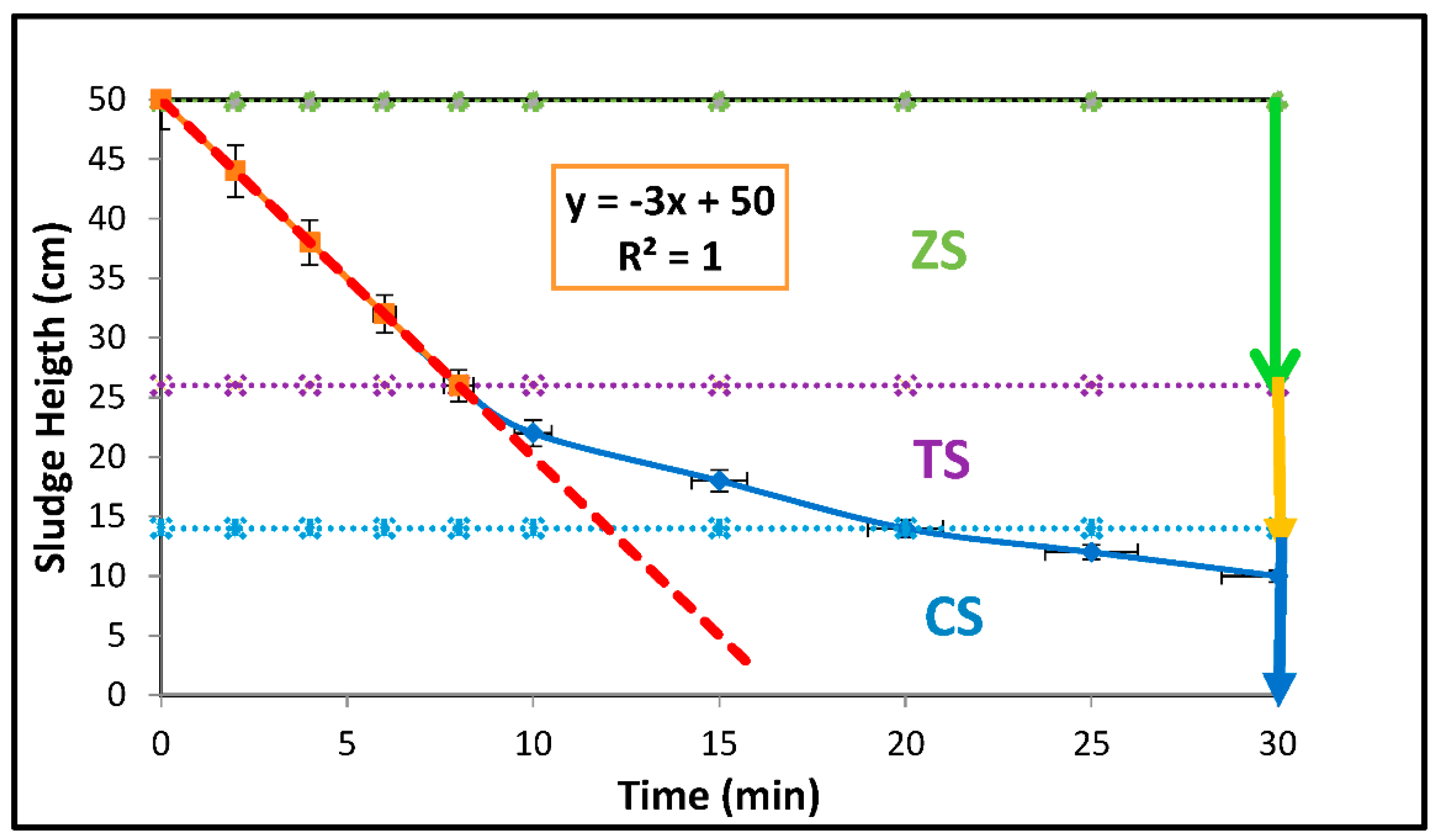
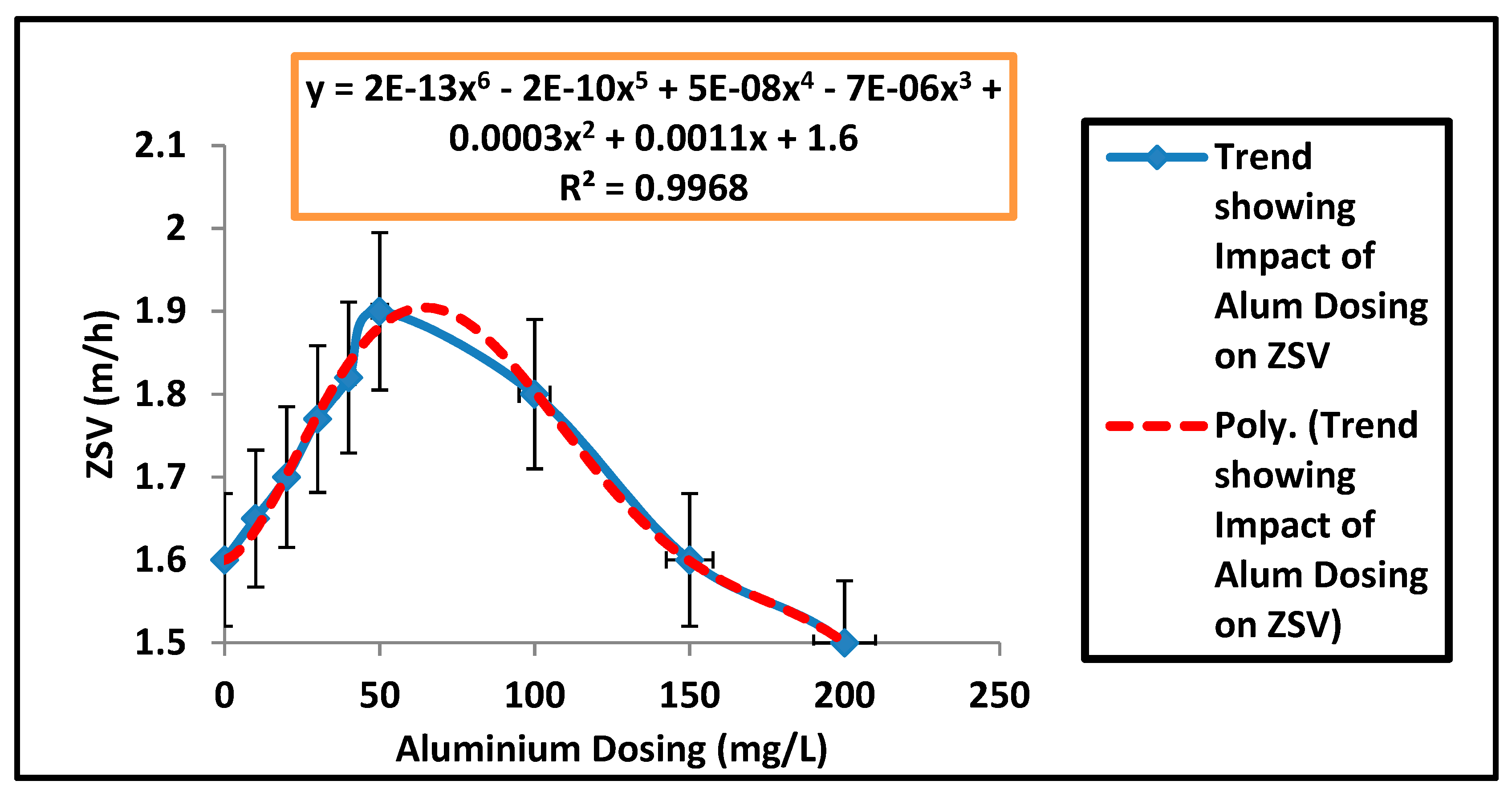
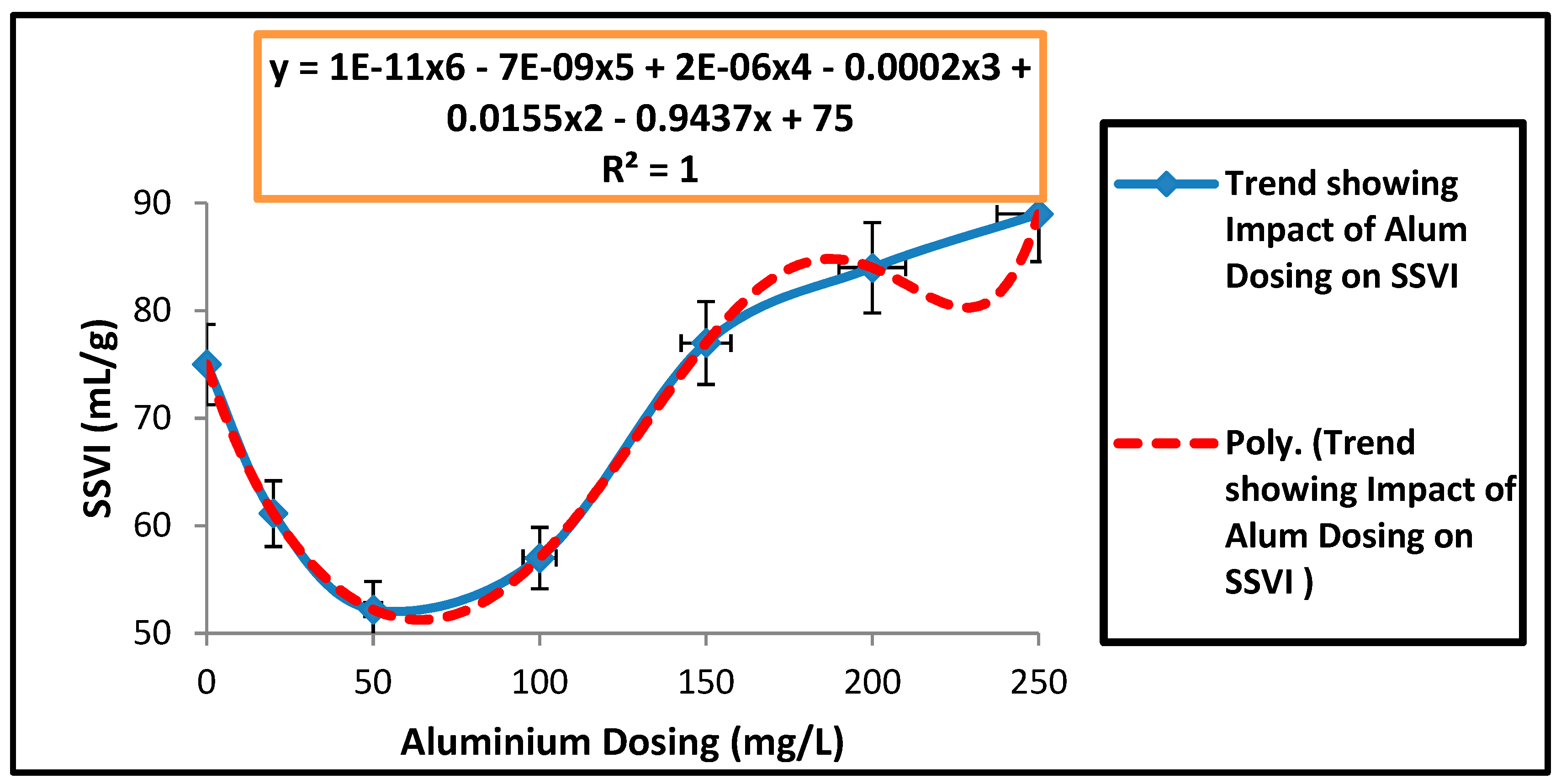
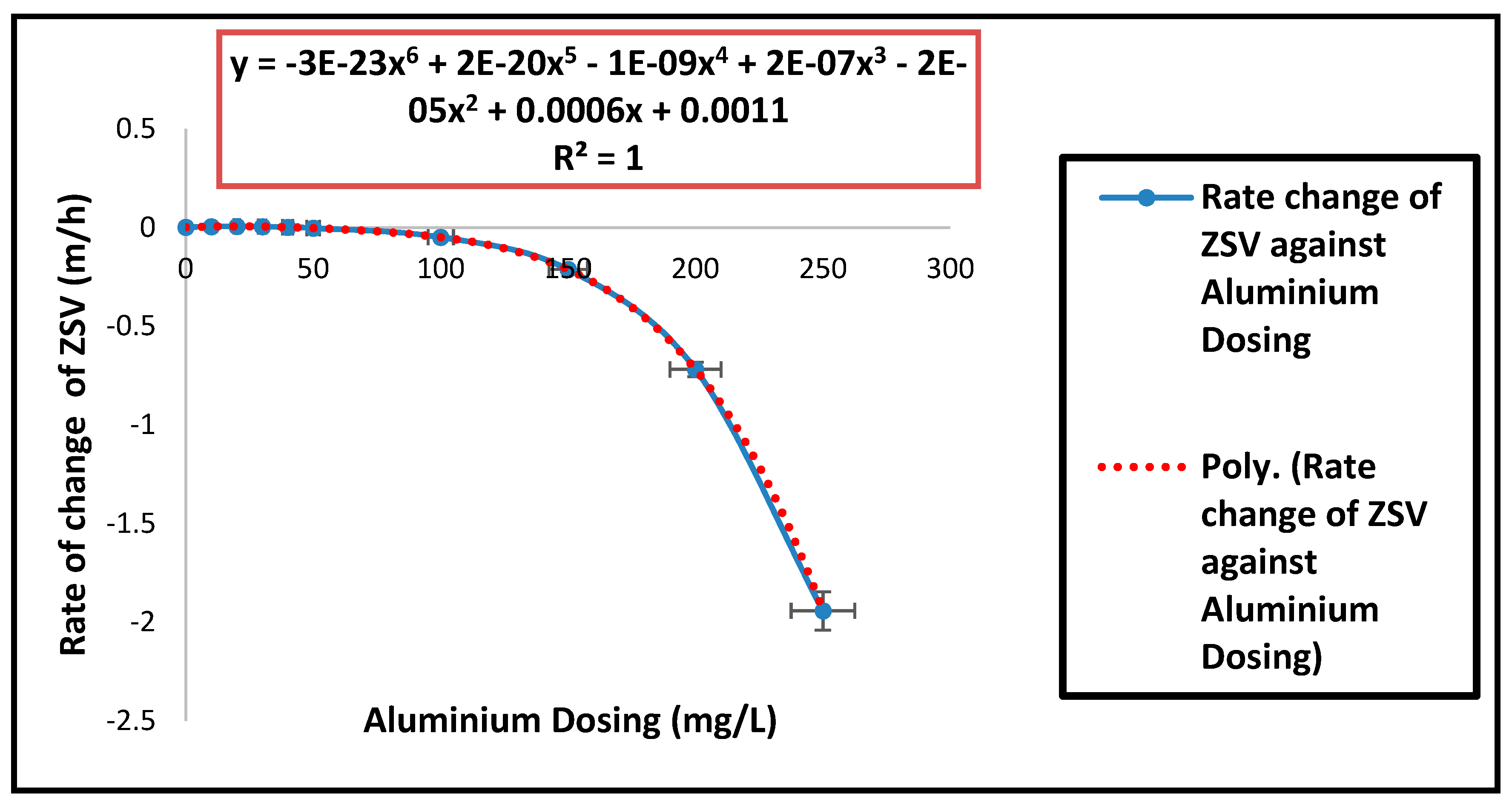
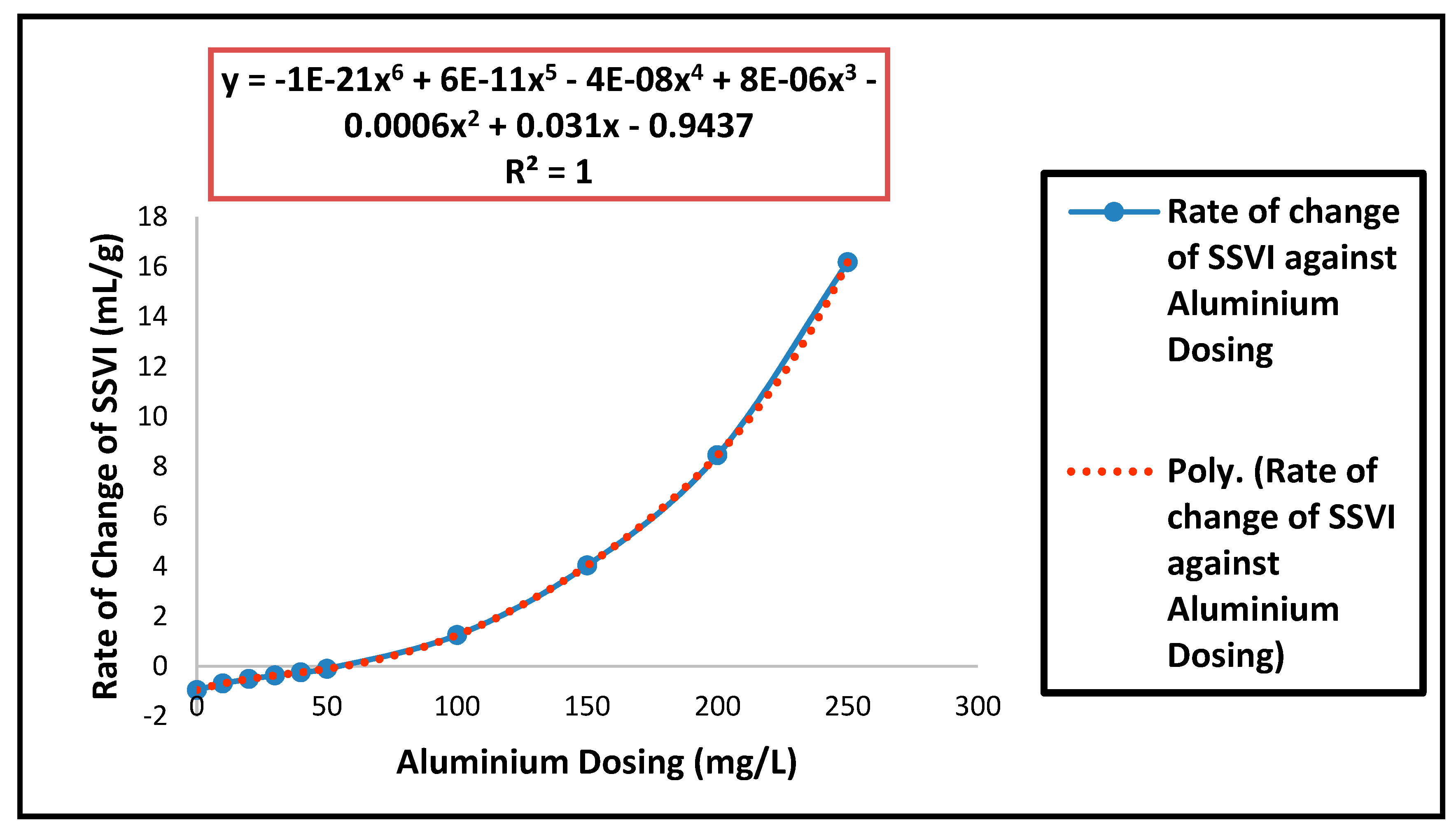
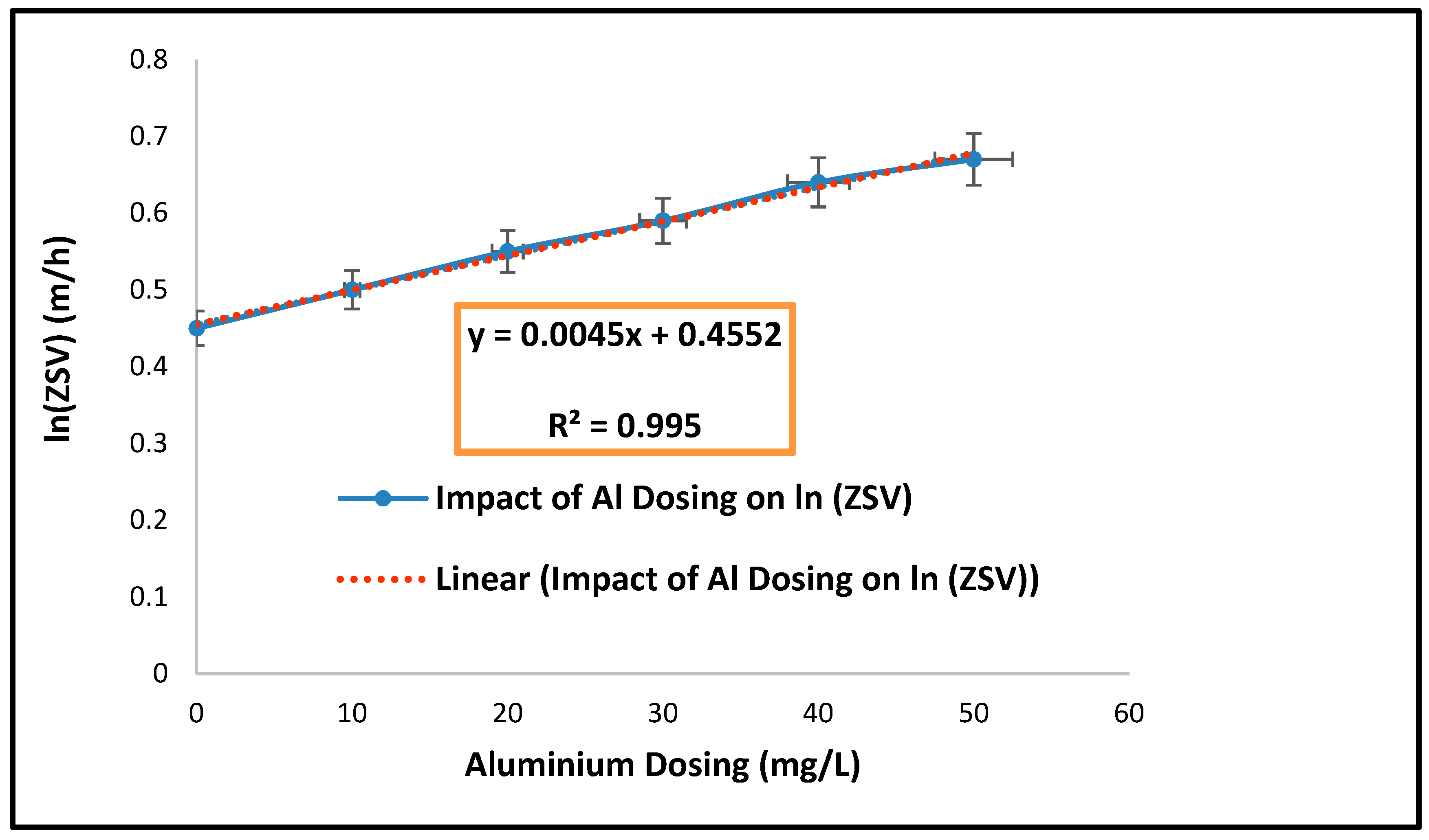
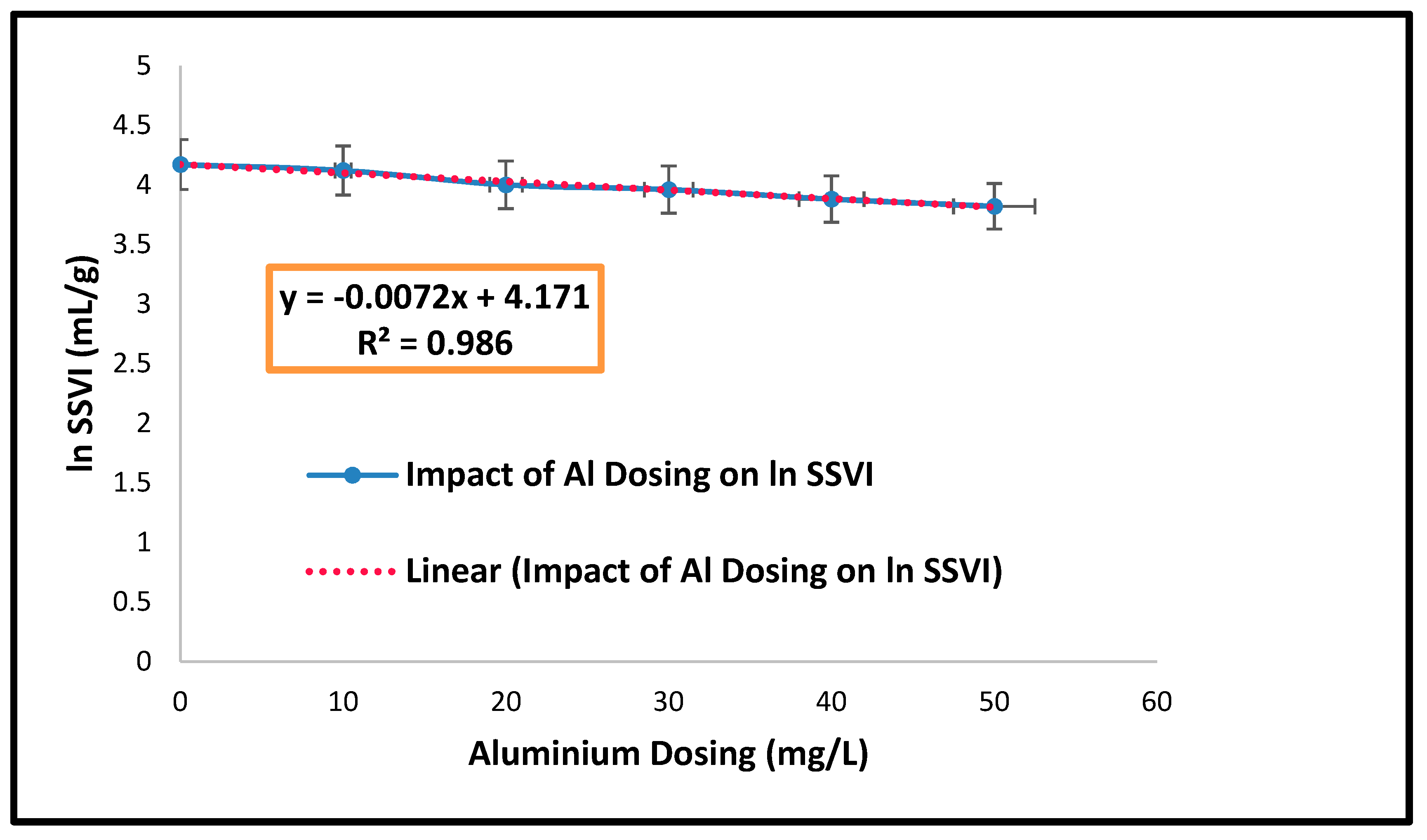
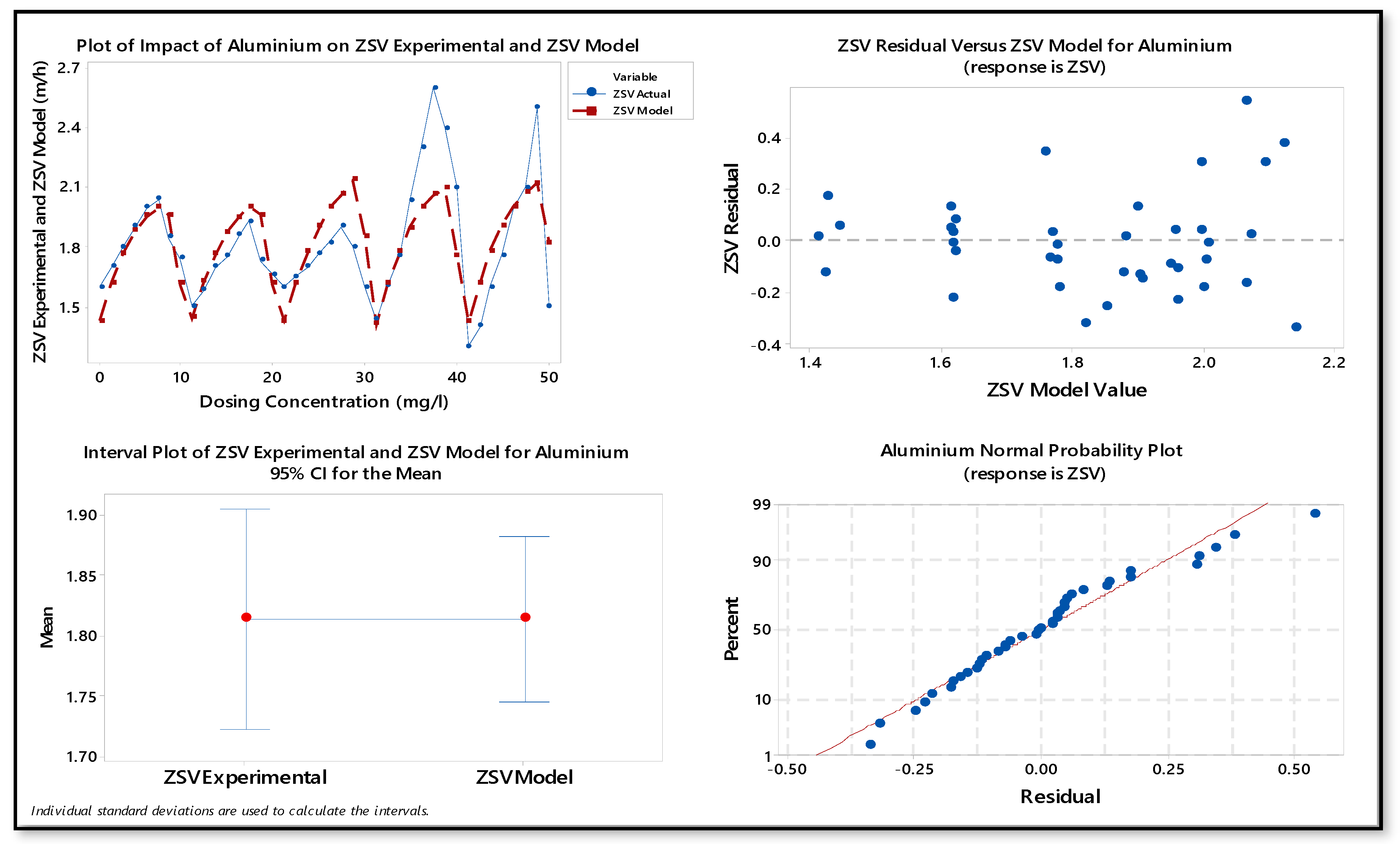
| Parameters | Estimated Values |
|---|---|
| ZSVo | 1.377 |
| Co | 0.026 |
| Kd | −0.02 |
| Ck | −0.0023 |
| DF | 36 |
| lack of fit test | 30 |
| SS | 1.14664 |
| MS | 0.01559 |
| F | 0.82 |
| P-Value | 0.675 |
| α | 0.05 |
| R2 | 0.993 |
| SSD | 0.334 |
| MLSS (g/L) | ZSV (m/h) | ZSV Model (m/h) | Al-Dosing (mg/L) | SD | Residual | Squared Residual | Squared ZSV |
|---|---|---|---|---|---|---|---|
| 2.50 | 0.47 | 0.37 | 0.00 | 9.77 | 1.74 | 3.02 | 0.22 |
| 2.76 | 0.53 | 0.48 | 10.00 | 2.15 | 7.95 | 6.32 | 0.28 |
| 2.85 | 0.59 | 0.56 | 20.00 | 6.88 | 3.13 | 9.82 | 0.35 |
| 2.94 | 0.62 | 0.62 | 30.00 | 2.00 | 1.98 | 3.91 | 0.38 |
| 3.04 | 0.67 | 0.66 | 40.00 | 1.04 | 4.41 | 1.95 | 0.45 |
| 3.15 | 0.71 | 0.68 | 50.00 | 8.20 | 4.36 | 1.90 | 0.50 |
| 3.30 | 0.62 | 0.68 | 100.00 | 4.08 | −1.09 | 1.20 | 0.38 |
| 3.50 | 0.56 | 0.52 | 150.00 | 1.25 | 1.28 | 1.63 | 0.31 |
| 2.84 | 0.41 | 0.38 | 0.00 | 1.02 | 5.77 | 3.33 | 0.17 |
| 2.90 | 0.46 | 0.48 | 10.00 | 5.43 | −4.23 | 1.79 | 0.21 |
| 2.96 | 0.52 | 0.56 | 20.00 | 1.68 | −6.53 | 4.26 | 0.27 |
| 3.00 | 0.56 | 0.62 | 30.00 | 3.42 | −1.25 | 1.57 | 0.31 |
| 3.10 | 0.62 | 0.66 | 40.00 | 1.26 | −8.79 | 7.73 | 0.38 |
| 3.11 | 0.67 | 0.69 | 50.00 | 2.28 | −7.38 | 5.45 | 0.45 |
| 3.30 | 0.55 | 0.68 | 100.00 | 1.79 | −2.29 | 5.26 | 0.30 |
| 3.50 | 0.51 | 0.52 | 150.00 | 2.15 | 4.75 | 2.26 | 0.26 |
| 2.50 | 0.47 | 0.37 | 0.00 | 9.77 | 1.74 | 3.02 | 0.22 |
| 2.60 | 0.50 | 0.48 | 10.00 | 2.55 | 3.16 | 9.97 | 0.25 |
| 2.65 | 0.53 | 0.57 | 20.00 | 1.51 | −7.48 | 5.60 | 0.28 |
| 2.70 | 0.57 | 0.63 | 30.00 | 3.95 | −1.30 | 1.68 | 0.32 |
| 2.73 | 0.60 | 0.68 | 40.00 | 6.68 | −1.77 | 3.15 | 0.36 |
| 2.80 | 0.64 | 0.71 | 50.00 | 5.50 | −1.62 | 2.64 | 0.41 |
| 2.90 | 0.59 | 0.77 | 100.00 | 3.13 | −3.39 | 1.15 | 0.35 |
| 3.10 | 0.47 | 0.65 | 150.00 | 3.36 | −2.51 | 6.32 | 0.22 |
| 2.20 | 0.36 | 0.37 | 0.00 | 2.50 | 1.79 | 3.22 | 0.13 |
| 2.50 | 0.48 | 0.48 | 10.00 | 1.80 | −7.15 | 5.10 | 0.23 |
| 2.65 | 0.60 | 0.57 | 20.00 | 9.72 | −1.48 | 2.19 | 0.36 |
| 2.73 | 0.71 | 0.63 | 30.00 | 6.17 | 1.33 | 1.77 | 0.50 |
| 2.74 | 0.83 | 0.68 | 40.00 | 2.22 | 3.04 | 9.24 | 0.69 |
| 2.80 | 0.96 | 0.71 | 50.00 | 6.05 | 5.38 | 2.89 | 0.92 |
| 3.00 | 0.88 | 0.75 | 100.00 | 1.79 | 3.07 | 9.45 | 0.77 |
| 3.25 | 0.74 | 0.61 | 150.00 | 1.82 | 3.42 | 1.17 | 0.55 |
| 2.40 | 0.26 | 0.37 | 0.00 | 1.19 | −1.21 | 1.48 | 0.07 |
| 2.50 | 0.36 | 0.48 | 10.00 | 1.54 | −2.17 | 4.72 | 0.13 |
| 2.55 | 0.47 | 0.57 | 20.00 | 1.03 | −1.78 | 3.16 | 0.22 |
| 2.62 | 0.57 | 0.64 | 30.00 | 4.45 | −1.46 | 2.13 | 0.32 |
| 2.68 | 0.68 | 0.69 | 40.00 | 2.80 | −4.22 | 1.80 | 0.46 |
| 2.75 | 0.78 | 0.72 | 50.00 | 3.75 | 2.79 | 7.78 | 0.61 |
| 2.94 | 0.91 | 0.76 | 100.00 | 2.29 | 3.80 | 1.44 | 0.83 |
| 3.15 | 0.68 | 0.64 | 150.00 | 1.83 | −3.20 | 1.02 | 0.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojo, P.; Ifelebuegu, A.O. Effect of Aluminium Salt Dosing on Activated Sludge Settleability Indicators: A New Settleability Model Development. Water 2019, 11, 179. https://doi.org/10.3390/w11010179
Ojo P, Ifelebuegu AO. Effect of Aluminium Salt Dosing on Activated Sludge Settleability Indicators: A New Settleability Model Development. Water. 2019; 11(1):179. https://doi.org/10.3390/w11010179
Chicago/Turabian StyleOjo, Peter, and Augustine Osamor Ifelebuegu. 2019. "Effect of Aluminium Salt Dosing on Activated Sludge Settleability Indicators: A New Settleability Model Development" Water 11, no. 1: 179. https://doi.org/10.3390/w11010179
APA StyleOjo, P., & Ifelebuegu, A. O. (2019). Effect of Aluminium Salt Dosing on Activated Sludge Settleability Indicators: A New Settleability Model Development. Water, 11(1), 179. https://doi.org/10.3390/w11010179





