CMADS-Driven Simulation and Analysis of Reservoir Impacts on the Streamflow with a Simple Statistical Approach
Abstract
1. Introduction
2. Methods
2.1. The Coupled Land Surface-Hydrological Model System (Noah LSM-HMS)
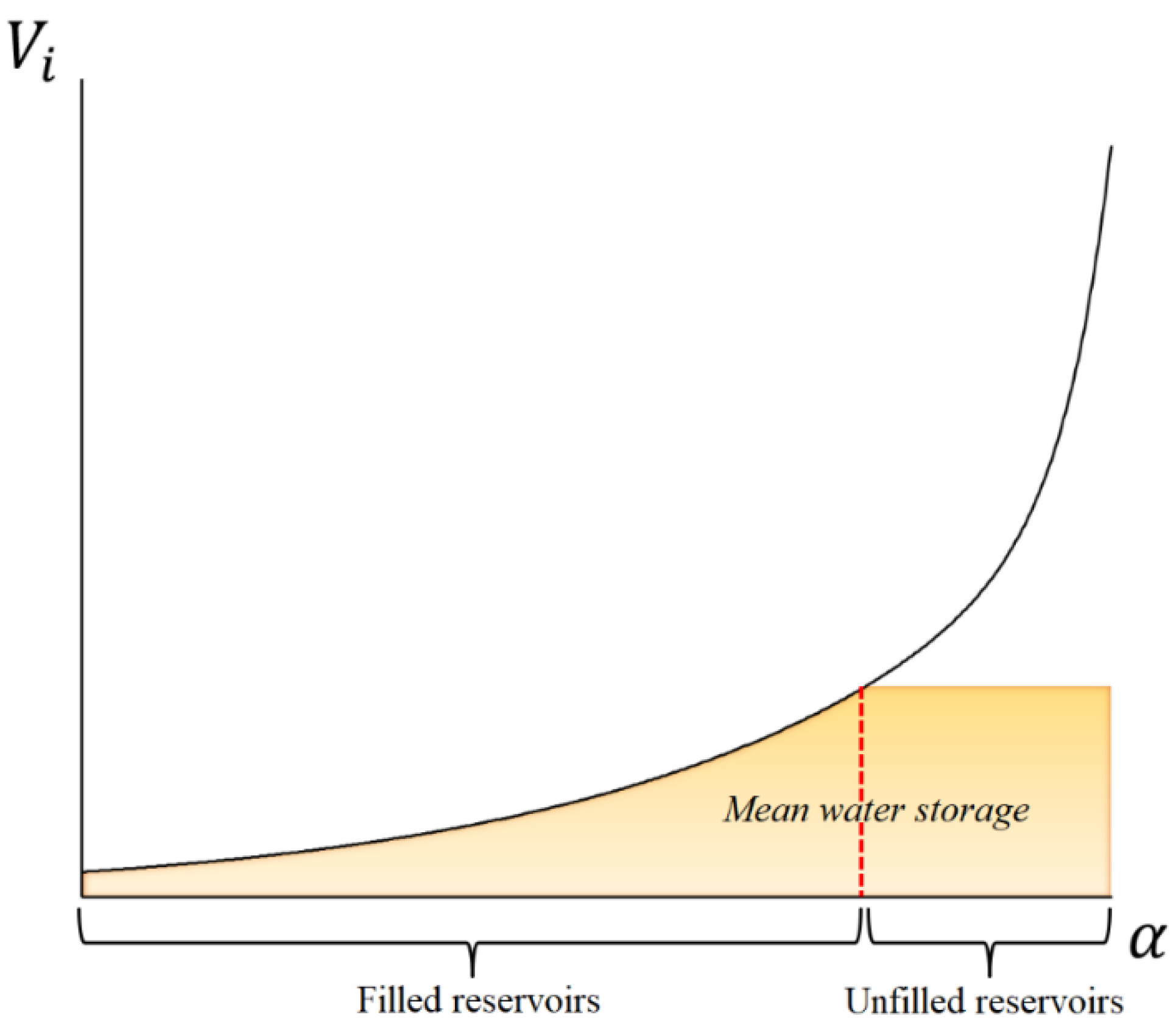
2.2. Reservoir Modelling
2.3. Module Integration
2.4. Performance Indexes
3. Case Study and Data
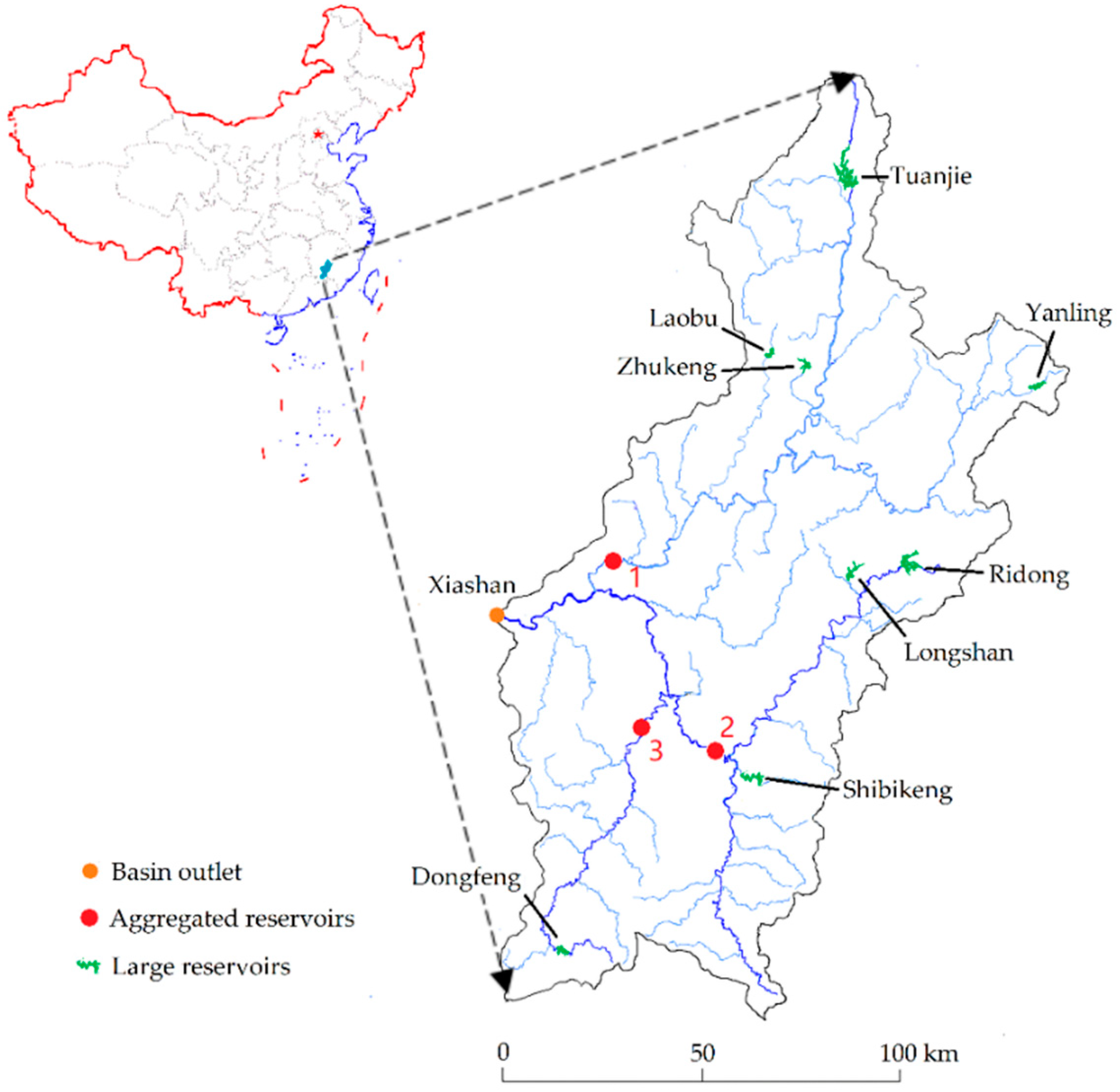
3.1. Study Area
3.2. Model Setup
- The aggregated reservoir can be placed in the proximity of the convergence point between the mainstream and the tributary or between two tributaries so that each tributary is a sub-basin and most of the small reservoirs in the entire basin can be included.
- The number and location of aggregated reservoirs or sub-basins should be in conformity to data availability, so that the sum of the reservoir capacity for each sub-basin can be known.
3.3. Data Input
4. Results and Discussions
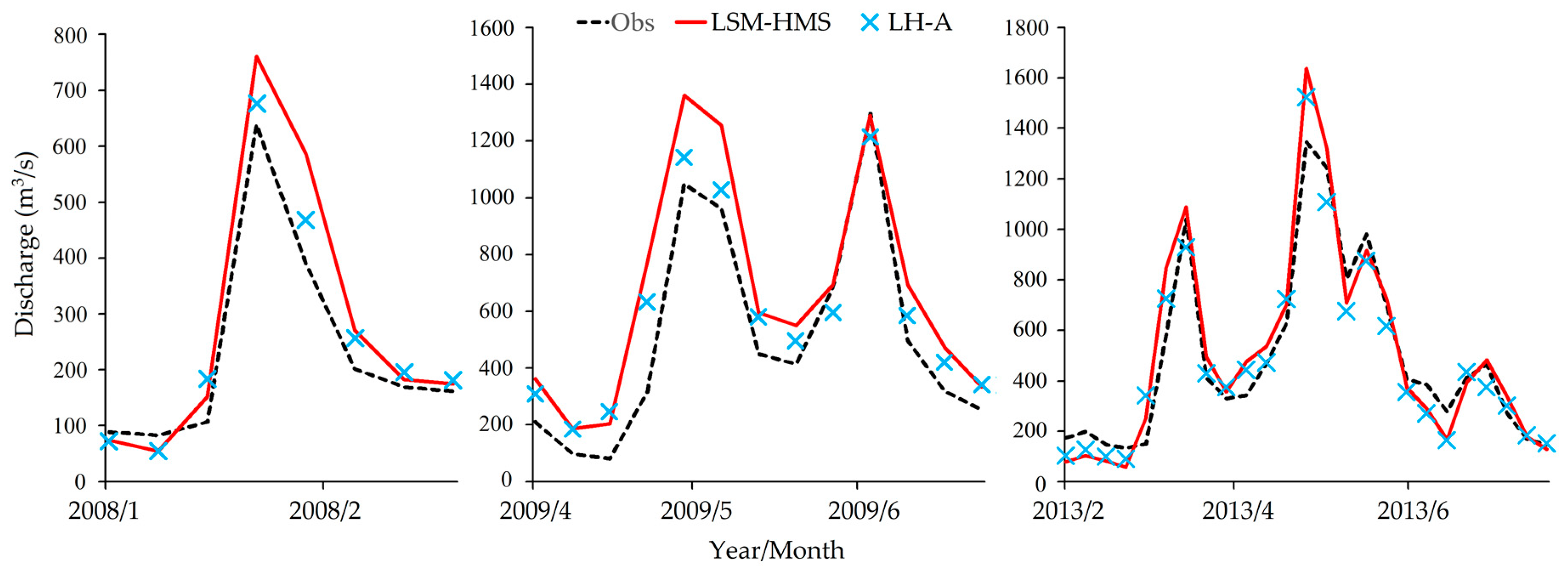
4.1. Calibration and Evaluation of the Model
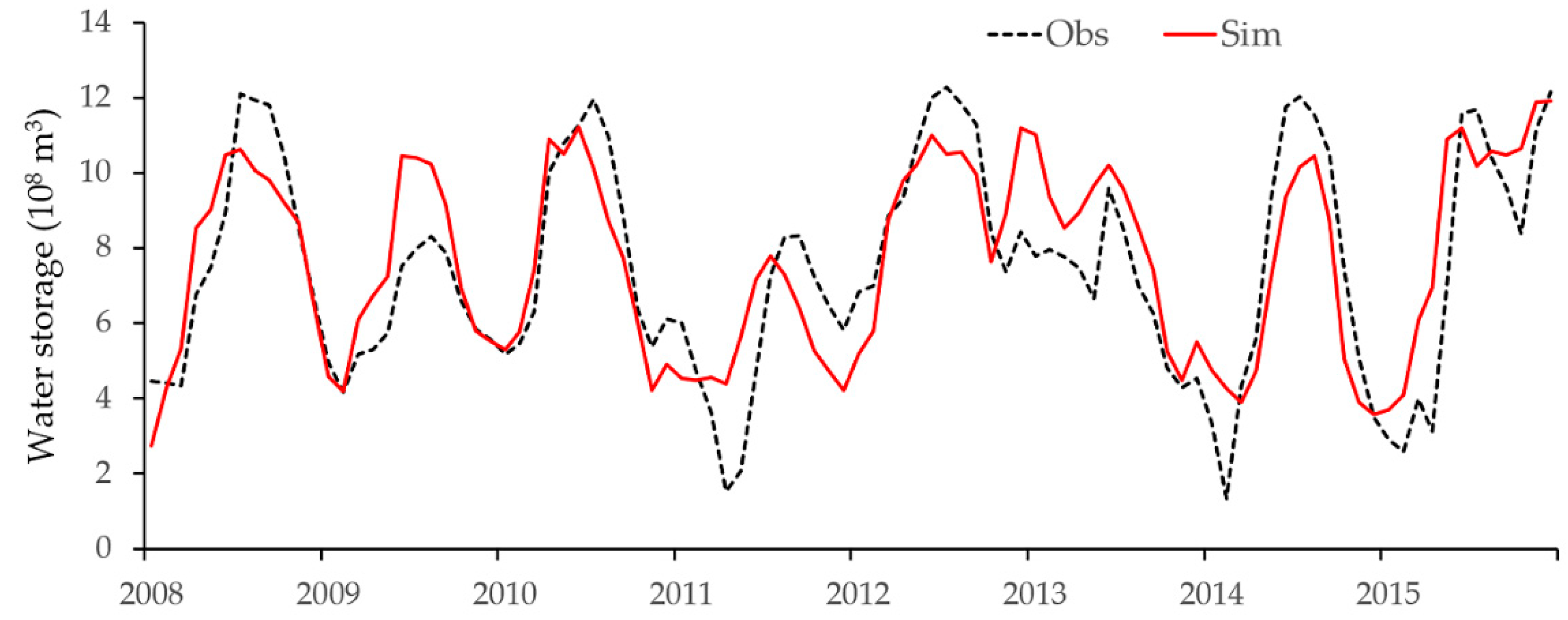
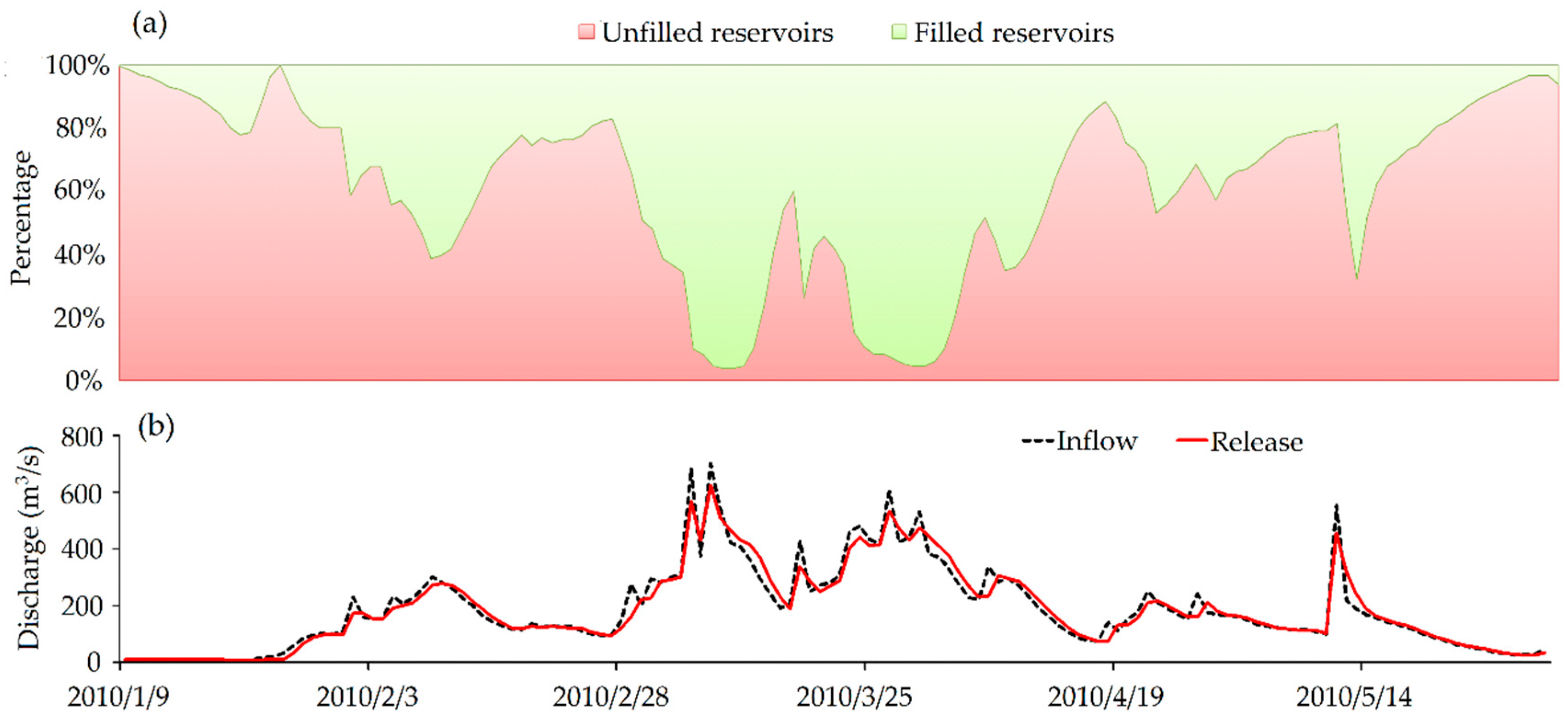
4.1.1. Reservoir Module
4.1.2. LSM-HMS and the Integrated Model
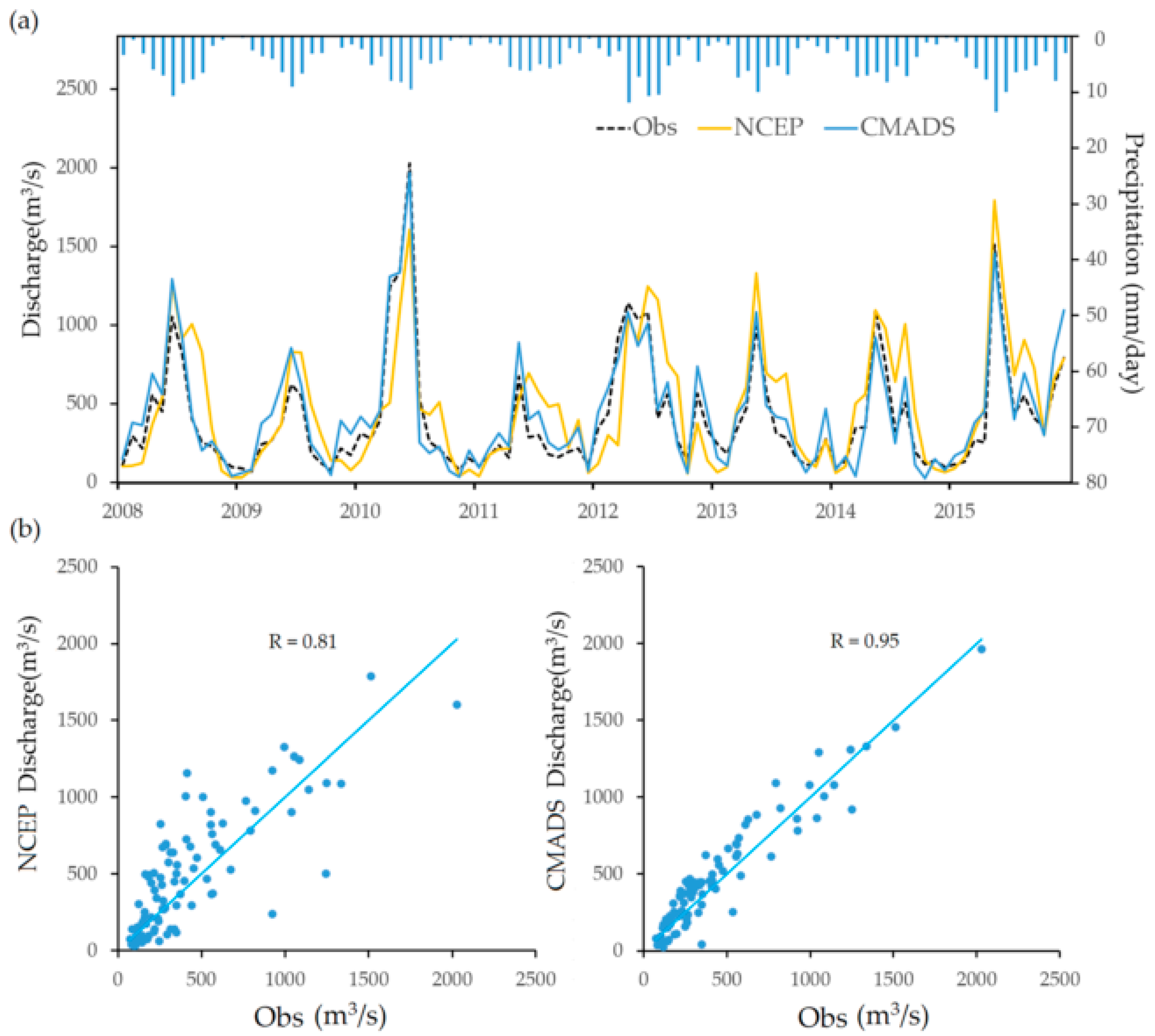
4.2. Evaluation of CMADS against NCEP Database
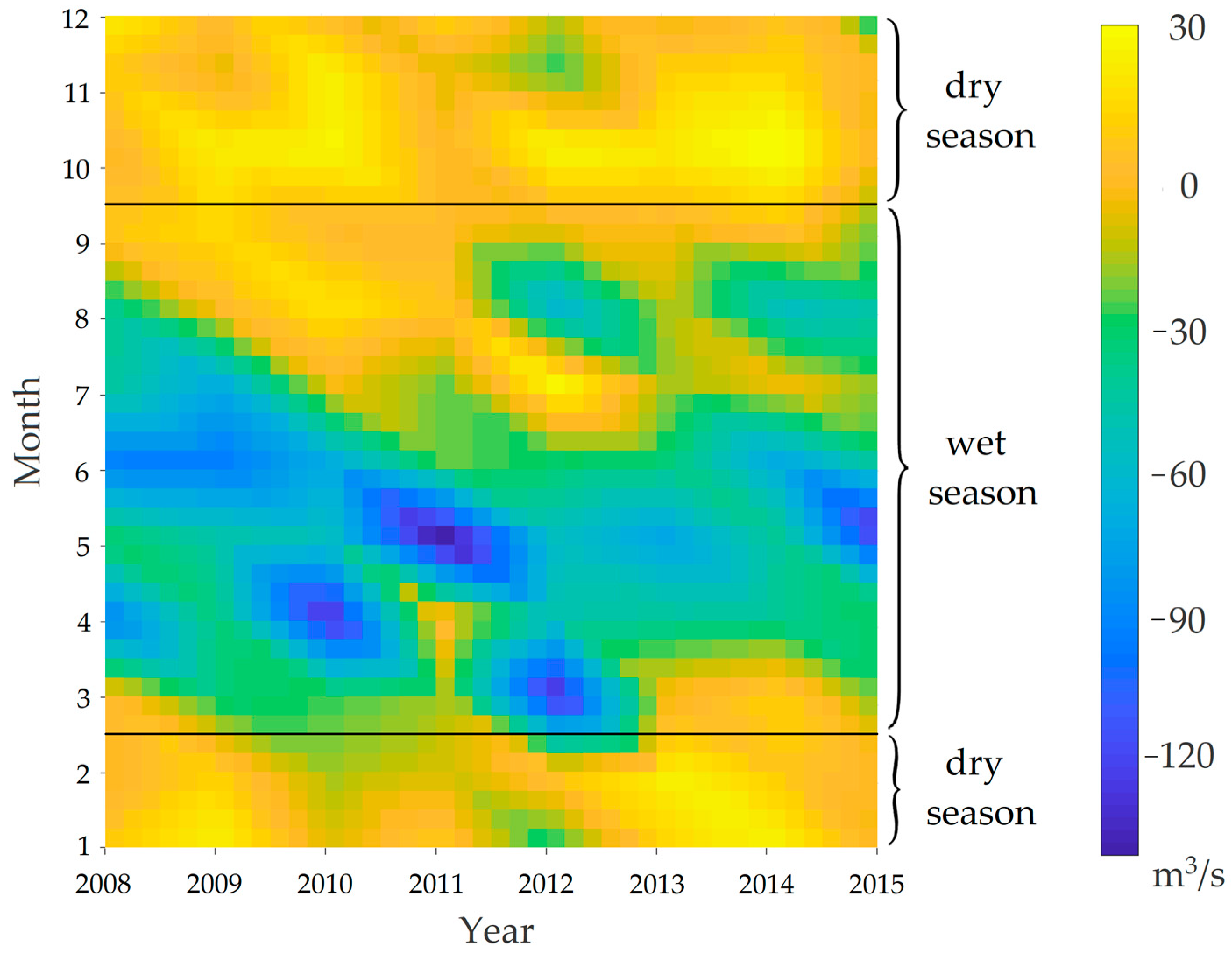
4.3. Effects of Reservoirs on Streamflow
5. Conclusions
- CMADS can serve as a high-quality meteorological database for the coupled land surface-hydrological model. CMADS-driven LSM-HMS generally have a much better performance than NCEP-driven LSM-HMS.
- The reservoir module can depict the annual and interannual variation in the water storage well for both large and small reservoirs. The integrated model yields improved simulation results at a significant level with the incorporation of reservoirs.
- Both large reservoirs and small reservoirs have a similar effect in reducing the floods in wet seasons and increasing the flow in dry seasons. Although small reservoirs are not primarily intended for flood mitigation, a large group of small reservoirs can indirectly reduce the local floods by up to 2.5% in a monthly level.
- The error of LSM-HMS is related to the input data and grid resolution as well as input parameter error. With a finer modelling resolution, the error is expected to be reduced. The simplification of the reservoir representation and the operation rule is also considered to be a source of error.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Karthikeyan, R.; Bai, Z.; Wang, J. Spatial and temporal variability of temperature, precipitation, and streamflow in upper sang-kan basin, china. Hydrol. Process. 2018, 31, 279–295. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Marhaento, H.; Booij, M.J.; Rientjes, T.H.M.; Hoekstra, A.Y. Attribution of changes in the water balance of a tropical catchment to land use change using the SWAT model. Hydrol. Process. 2017, 31, 2029–2040. [Google Scholar] [CrossRef]
- Mateo, C.M.; Hanasaki, N.; Komori, D.; Tanaka, K.; Kiguchi, M.; Champathong, A.; Sukhapunnaphan, T.; Dai Yamazaki, D.; Oki, T. Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models. Water. Resour. Res. 2015, 50, 7245–7266. [Google Scholar] [CrossRef]
- Deng, C.; Liu, P.; Liu, Y.; Wu, Z.; Wang, D. Integrated hydrologic and reservoir routing model for real-time water level forecasts. J. Hydrol. Eng. 2014, 20, 05014032. [Google Scholar] [CrossRef]
- Mushtaq, S.; Dawe, D.; Hafeez, M. Economic evaluation of small multi-purpose ponds in the Zhanghe irrigation system, China. Agric. Water. Manag. 2007, 91, 61–70. [Google Scholar] [CrossRef]
- Potter, K.W. Small-scale, spatially distributed water management practices: Implications for research in the hydrologic sciences. Water. Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Christensen, N.S.; Lettenmaier, D.P. A multimodel ensemble approach to assessment of climate change impacts on the hydrology and water resources of the Colorado River Basin. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3727–3770. [Google Scholar] [CrossRef]
- VanRheenen, N.T.; Wood, A.W.; Palmer, R.N.; Lettenmaier, D.P. Potential implications of PCM climate change scenarios for Sacramento–San Joaquin River Basin hydrology and water resources. Clim. Chang. 2004, 62, 257–281. [Google Scholar] [CrossRef]
- Hanasaki, N.; Kanae, S.; Oki, T. A reservoir operation scheme for global river routing models. J. Hydrol. 2006, 327, 22–41. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H.; Naz, B.S.; Kao, S.C.; Voisin, N. Integrating a reservoir regulation scheme into a spatially distributed hydrological model. Adv. Water. Resour. 2016, 98, 16–31. [Google Scholar] [CrossRef]
- Güntner, A.; Krol, M.S.; Araújo, J.C.D.; Bronstert, A. Simple water balance modelling of surface reservoir systems in a large data-scarce semiarid region/Modélisation simple du bilan hydrologique de systèmes de réservoirs de surface dans une grande région semi-aride pauvre en données. Hydrol. Sci. J. 2014, 49. [Google Scholar] [CrossRef]
- Cao, M.; Zhou, H.; Zhang, C.; Zhang, A.; Li, H.; Yang, Y. Research and application of flood detention modeling for ponds and small reservoirs based on remote sensing data. Sci. China Tech. Sci. 2011, 54, 2138–2144. [Google Scholar] [CrossRef]
- Deitch, M.J.; Merenlender, A.M.; Feirer, S. Cumulative effects of small reservoirs on streamflow in Northern Coastal California catchments. Water Resour. Manag. 2013, 27, 5101–5118. [Google Scholar] [CrossRef]
- Magilligan, F.J.; Nislow, K.H. Changes in hydrologic regime by dams. Geomorphology 2005, 71, 61–78. [Google Scholar] [CrossRef]
- Salamon, P.; Feyen, L. Assessing parameter, precipitation, and predictive uncertainty in a distributed hydrological model using sequential data assimilation with the particle filter. J. Hydrol. 2009, 376, 428–442. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, J.; Xu, T.; Croke, B.; Jakeman, A.; Song, Y.; Yang, Q.; Lei, X.; Liao, W. Applicability Assessment and Uncertainty Analysis of Multi-Precipitation Datasets for the Simulation of Hydrologic Models. Water 2018, 10, 1611. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, J.; Yang, M. Application of SWAT Model with CMADS Data to Estimate Hydrological Elements and Parameter Uncertainty Based on SUFI-2 Algorithm in the Lijiang River Basin, China. Water 2018, 10, 742. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Shi, C.; Wu, Y.; Ji, X. Establishment and Evaluation of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS). Water 2018, 10, 1555. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Wu, Y.; Long, A.; Wang, J.; Shi, C.; Ji, X. Investigating spatiotemporal changes of the land-surface processes in Xinjiang using high-resolution CLM3.5 and CLDAS: Soil temperature. Sci. Rep. 2017, 7, 13286. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Meng, X.; Dan, L.; Liu, Z. Energy balance-based SWAT model to simulate the mountain snowmelt and runoff—Taking the application in Juntanghu watershed (China) as an example. J. Mt. Sci. 2015, 12, 368–381. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Lei, X.; Cai, S.; Wu, H. Hydrological Modeling in the Manas River Basin Using Soil and Water Assessment Tool Driven by CMADS. Teh. Vjesn. 2017, 24, 525–534. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y. Parameter Uncertainty Analysis of the SWAT Model in a Mountain Loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Liu, J.; Shanguan, D.; Liu, S.; Ding, Y. Evaluation and Hydrological Simulation of CMADS and CFSR Reanalysis Datasets in the Qinghai-Tibet Plateau. Water 2018, 10, 513. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Cai, S.; Zhang, X.; Leng, G.; Lei, X.; Shi, C.; Liu, S.; Shang, Y. The China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) Application in China: A Case Study in Heihe River Basin. Pearl River 2016, 37, 1–9. [Google Scholar]
- Gao, X.; Zhu, Q.; Yang, Z.; Wang, H. Evaluation and Hydrological Application of CMADS against TRMM 3B42V7, PERSIANN-CDR, NCEP-CFSR, and Gauge-Based Datasets in Xiang River Basin of China. Water 2018, 10, 1225. [Google Scholar] [CrossRef]
- Yuan, F.; Kunstmann, H.; Yang, C.; Yu, Z.; Ren, L.; Fersch, B.; Xie, Z. Development of a coupled land-surface and hydrology model system for mesoscale hydrometeorological simulations. In New Approaches to Hydrological Prediction in Data-Sparse Regions, Proceedings of Symposium HS.2 at the Joint Convention of the International Association of Hydrological Sciences (IAHS) and The International Association of Hydrogeologists (IAH), Hyderabad, India, 6–12 September 2009; IAHS Press: Wallingford, UK, 2009. [Google Scholar]
- Wagner, S.; Fersch, B.; Yuan, F.; Yu, Z.; Kunstmann, H. Fully coupled atmospheric-hydrological modeling at regional and long-term scales: Development, application, and analysis of WRF-HMS. Water Resour. Res. 2016, 52, 3187–3211. [Google Scholar] [CrossRef]
- Yu, Z.; Pollard, D.; Cheng, L. On continental-scale hydrologic simulations with a coupled hydrologic model. J. Hydrol. 2006, 331, 110–124. [Google Scholar] [CrossRef]
- Yang, C. Research on Coupling Land Surface-Hydrology Model and Application. Ph.D. Thesis, Hohai University, Nanjing, China, 2009. [Google Scholar]
- Yang, C.; Lin, Z.; Yu, Z.; Hao, Z.; Liu, S. Analysis and simulation of human activity impact on streamflow in the Huaihe River basin with a large-scale hydrologic model. J. Hydrometeorol. 2010, 11, 810–821. [Google Scholar] [CrossRef]
- Yang, C.; Yu, Z.; Hao, Z.; Zhang, J.; Zhu, J. Impact of climate change on flood and drought events in Huaihe River Basin, China. Hydrol. Res. 2012, 43, 14–22. [Google Scholar] [CrossRef]
- Malveira, V.T.C.; Araújo, J.C.D.; Güntner, A. Hydrological impact of a high-density reservoir network in semiarid northeastern Brazil. J. Hydrol. Eng. 2011, 17, 109–117. [Google Scholar] [CrossRef]
- Lv, M.; Hao, Z.; Lin, Z.; Ma, Z.; Lv, M.; Wang, J. Reservoir operation with feedback in a coupled land surface and hydrologic model: A case study of the Huai River Basin, China. J. Am. Water Resour. Assoc. 2016, 52, 168–183. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- The China Meteorological Assimilation Driving Datasets for the SWAT model (CMADS). Available online: http://www.cmads.org (accessed on 25 October 2018).
- NOAA Earth System Research Laboratory. Available online: https://www.esrl.noaa.gov (accessed on 26 October 2018).
- USGS EROS Archive-Digital ElevationHYDRO1K. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-hydro1k (accessed on 1 October 2018).


| Aggregated Reservoir | Storage Capacity (108 m3) | Average Water Demand | |
|---|---|---|---|
| Non-Irrigation Period (m3/s) | Irrigation Period (m3/s) | ||
| 1 | 2.52 | 1.7 | 3.2 |
| 2 | 0.93 | 0.9 | 1.8 |
| 3 | 0.80 | 0.8 | 1.5 |
| Parameters | Input Value | Parameters | Input Value |
|---|---|---|---|
| Streambed conductivity | 0.90 s−1 | Porosity | ×1.0 |
| Manning’s roughness | 0.07 | Wilting point | ×1.0 |
| Saturated hydraulic conductivity | ×1.0 | Aquifer thickness | ×1.0 |
| Index | LSM-HMS | LH-L | LH-A | Difference (%) | ||
|---|---|---|---|---|---|---|
| LH-L/LSM-HMS | LH-A/LH-L | LH-A/LSM-HMS | ||||
| WBI | 1.08 | 1.05 | 1.03 | −2.8 | −1.9 | −4.6 |
| R | 0.95 | 0.95 | 0.96 | 0 | 1.0 | 1.0 |
| NSE | 0.89 | 0.90 | 0.91 | 1.1 | 1.1 | 2.2 |
| Probability of the paired t-Test | <0.01 * | <0.01 * | <0.01 * | |||
| Reservoir | Averaged Monthly Maximum | Averaged Monthly Minimum | ||||
|---|---|---|---|---|---|---|
| Inflow (m3/s) | Outflow (m3/s) | Difference (%) | Inflow (m3/s) | Outflow (m3/s) | Difference (%) | |
| Tuanjie | 100.0 | 87.4 | −12.6 | 1.6 | 2.5 | 56.3 |
| Yanling | 47.0 | 45.0 | −4.3 | 1.2 | 1.3 | 8.3 |
| Ridong | 33.8 | 27.9 | −17.5 | 1.2 | 0.7 | −41.7 |
| Longshan | 13.9 | 11.5 | −17.3 | 0.1 | 0.1 | 0.0 |
| Shibikeng | 25.4 | 11.8 | −53.5 | 0.3 | 0.3 | 0.0 |
| Zhukeng | 15.4 | 12.7 | −17.5 | 0.2 | 0.3 | 50.0 |
| Laobu | 15.9 | 14.1 | −11.3 | 0.1 | 0.2 | 100.0 |
| Dongfeng | 24.6 | 22.7 | −7.7 | 0.4 | 0.7 | 75.0 |
| AR† 1 | 1323.2 | 1289.6 | −2.5 | 20.3 | 20.4 | 0.0 |
| AR† 2 | 402.8 | 390.7 | −3.0 | 6.2 | 7.0 | 12.9 |
| AR† 3 | 210.1 | 208.8 | −0.7 | 2.3 | 2.8 | 21.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, N.; Yang, M.; Meng, X.; Liu, X.; Wang, Z.; Wang, H.; Yang, C. CMADS-Driven Simulation and Analysis of Reservoir Impacts on the Streamflow with a Simple Statistical Approach. Water 2019, 11, 178. https://doi.org/10.3390/w11010178
Dong N, Yang M, Meng X, Liu X, Wang Z, Wang H, Yang C. CMADS-Driven Simulation and Analysis of Reservoir Impacts on the Streamflow with a Simple Statistical Approach. Water. 2019; 11(1):178. https://doi.org/10.3390/w11010178
Chicago/Turabian StyleDong, Ningpeng, Mingxiang Yang, Xianyong Meng, Xuan Liu, Zhaokai Wang, Hao Wang, and Chuanguo Yang. 2019. "CMADS-Driven Simulation and Analysis of Reservoir Impacts on the Streamflow with a Simple Statistical Approach" Water 11, no. 1: 178. https://doi.org/10.3390/w11010178
APA StyleDong, N., Yang, M., Meng, X., Liu, X., Wang, Z., Wang, H., & Yang, C. (2019). CMADS-Driven Simulation and Analysis of Reservoir Impacts on the Streamflow with a Simple Statistical Approach. Water, 11(1), 178. https://doi.org/10.3390/w11010178







