Using a Hydrologic Model to Assess the Performance of Regional Climate Models in a Semi-Arid Watershed in Brazil
Abstract
1. Introduction
2. Materials and Methods
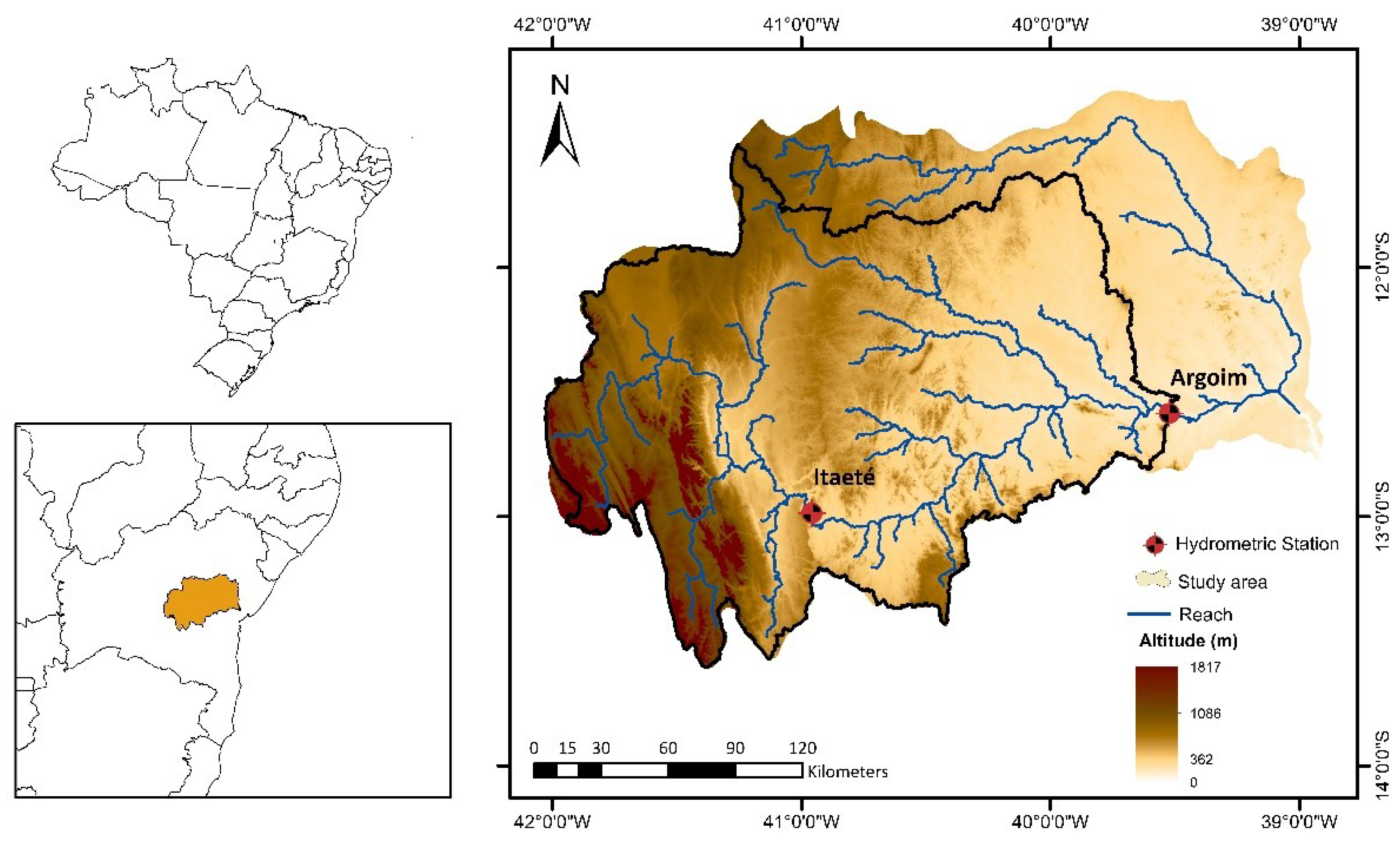
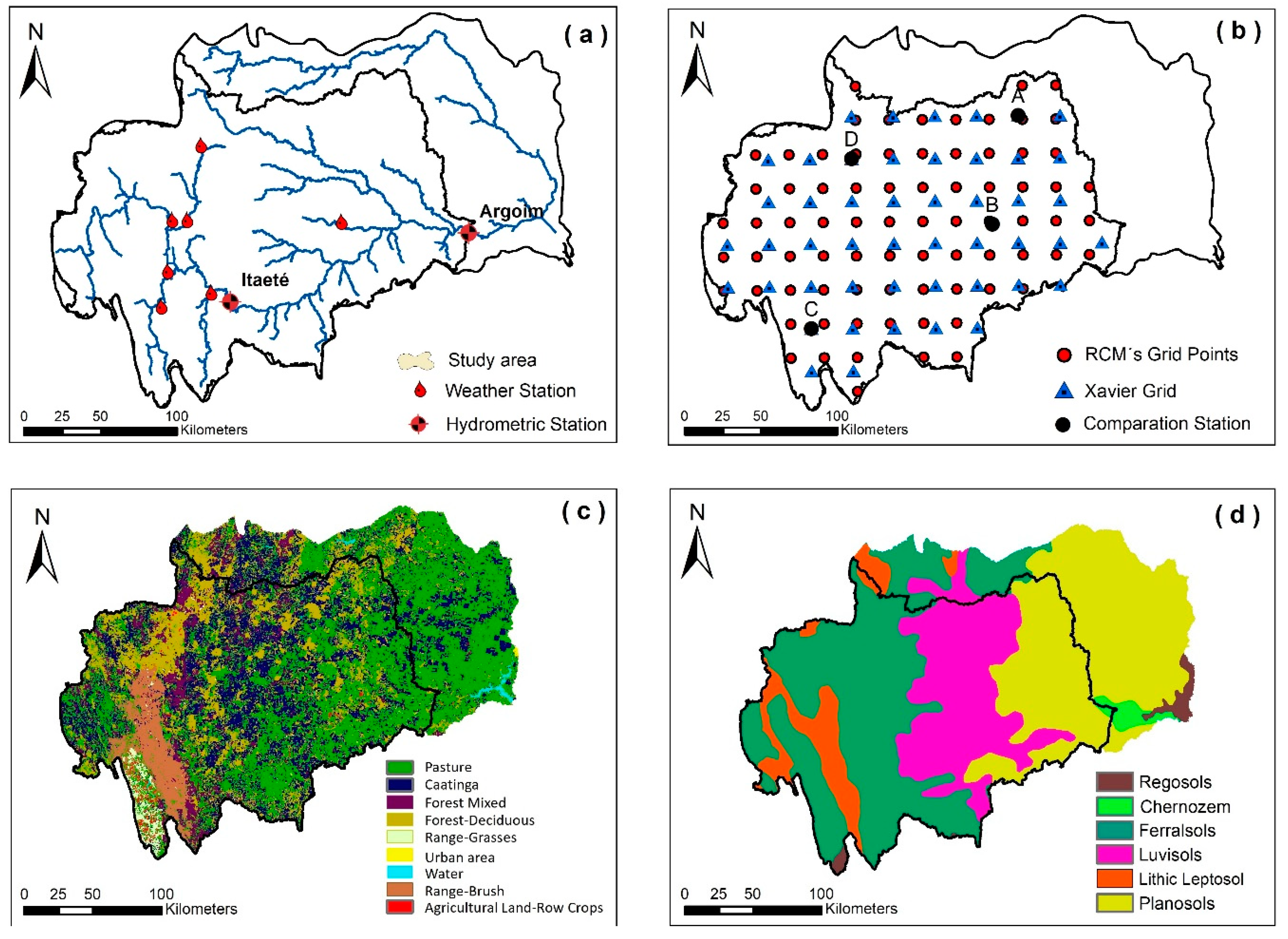
2.1. Study Area
2.2. Soil and Water Assessment Tool
2.2.1. Model Description
2.2.2. Model Setup, Calibration and Validation
2.3. Climate Change Projection
2.3.1. Regional Climate Model and Scenarios
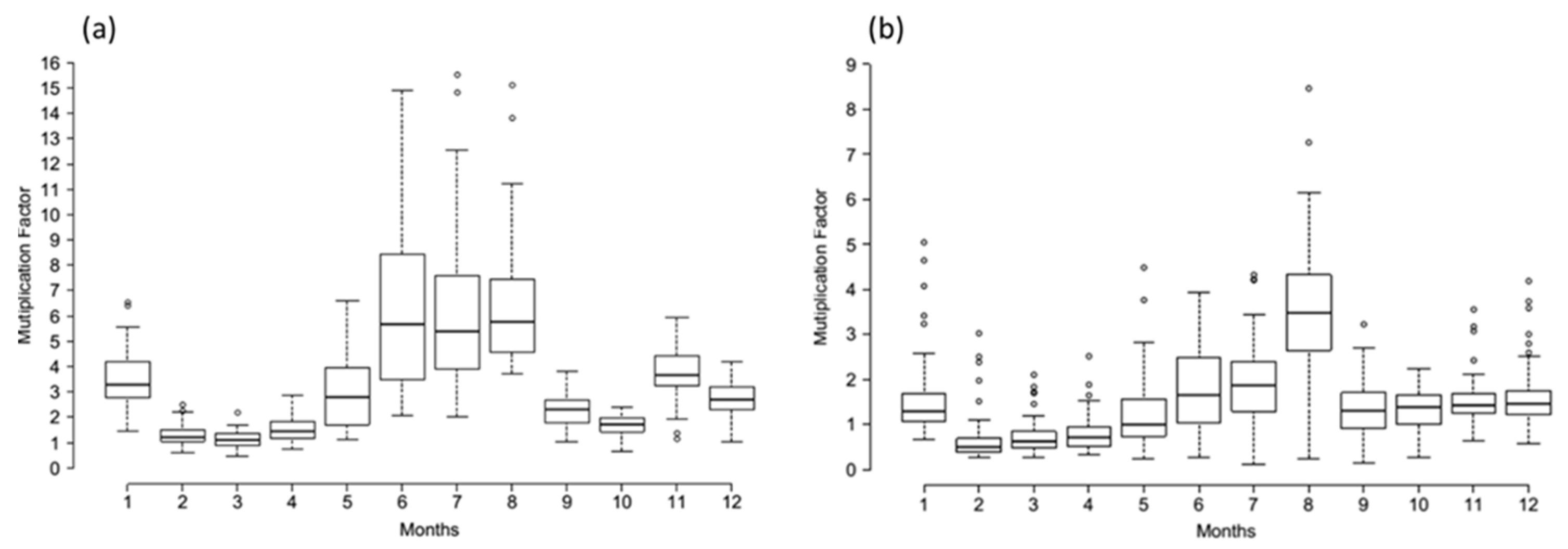
2.3.2. Bias Correction
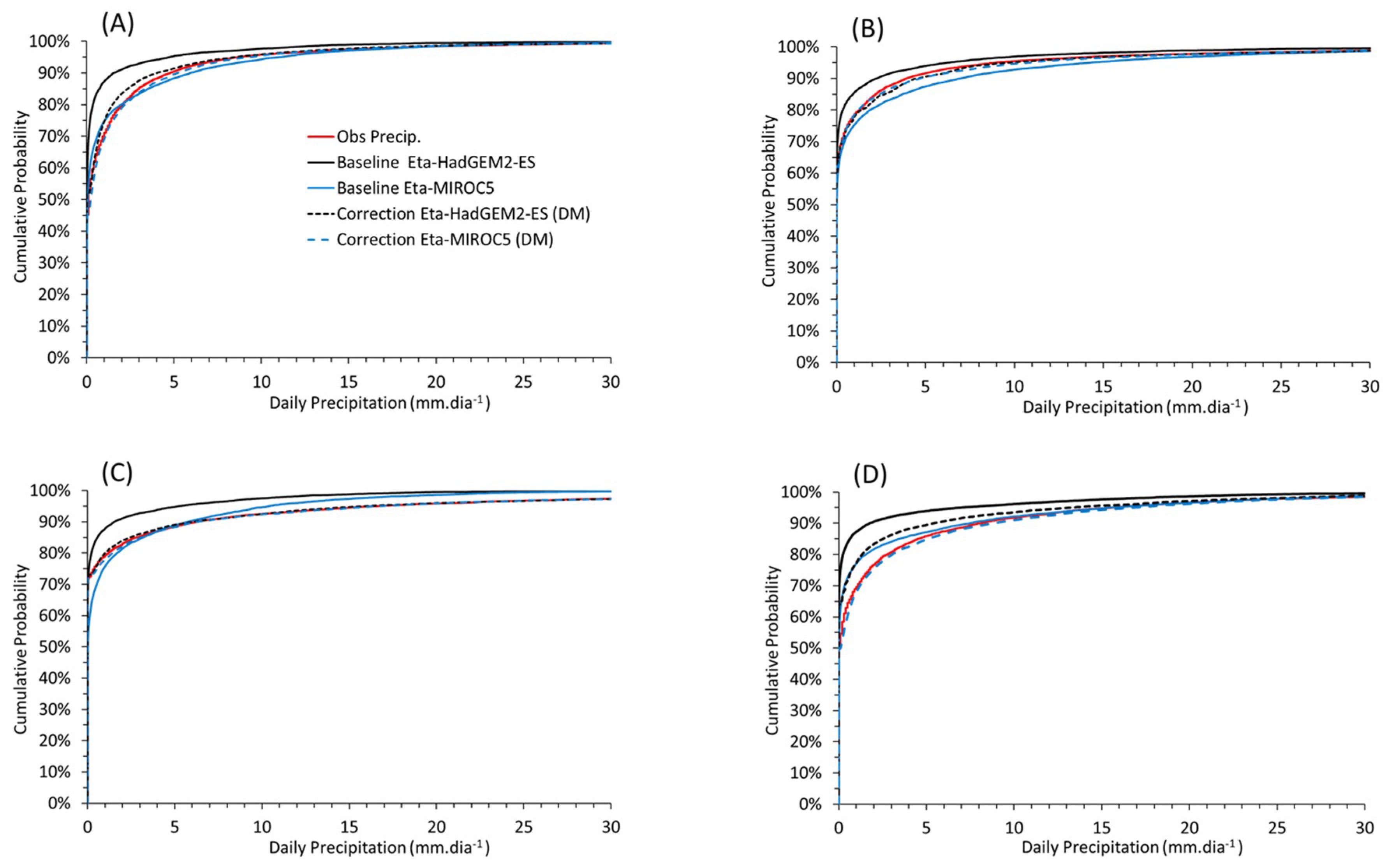
2.3.3. Evaluation of Bias Correction Methods
3. Results and Discussion
3.1. Model Calibration and Validation
3.2. Climate Projections
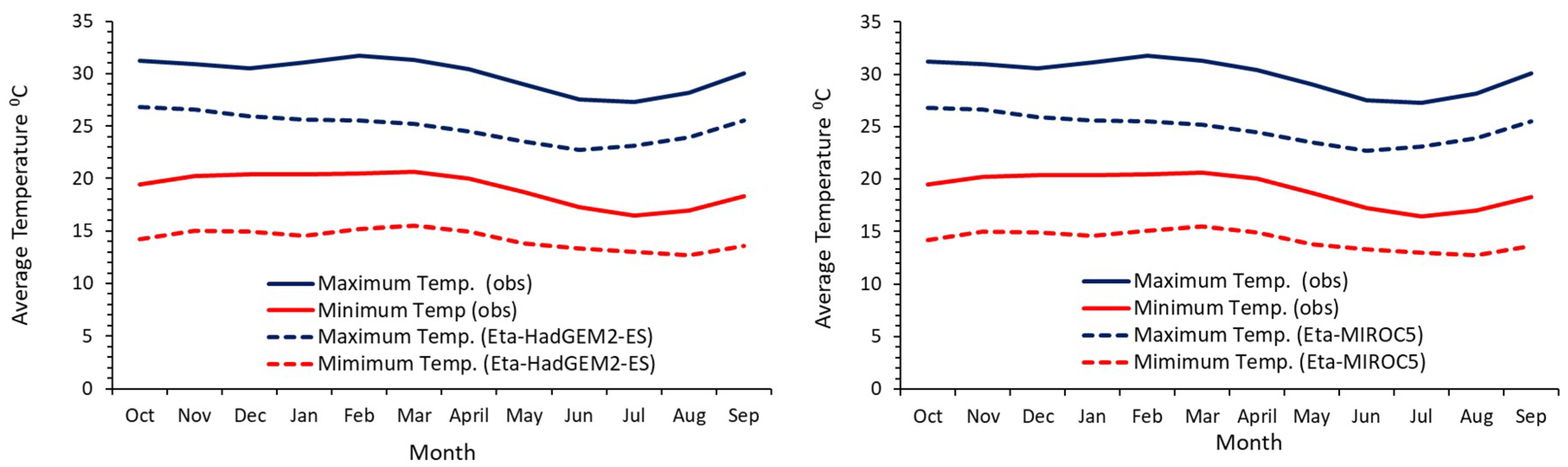
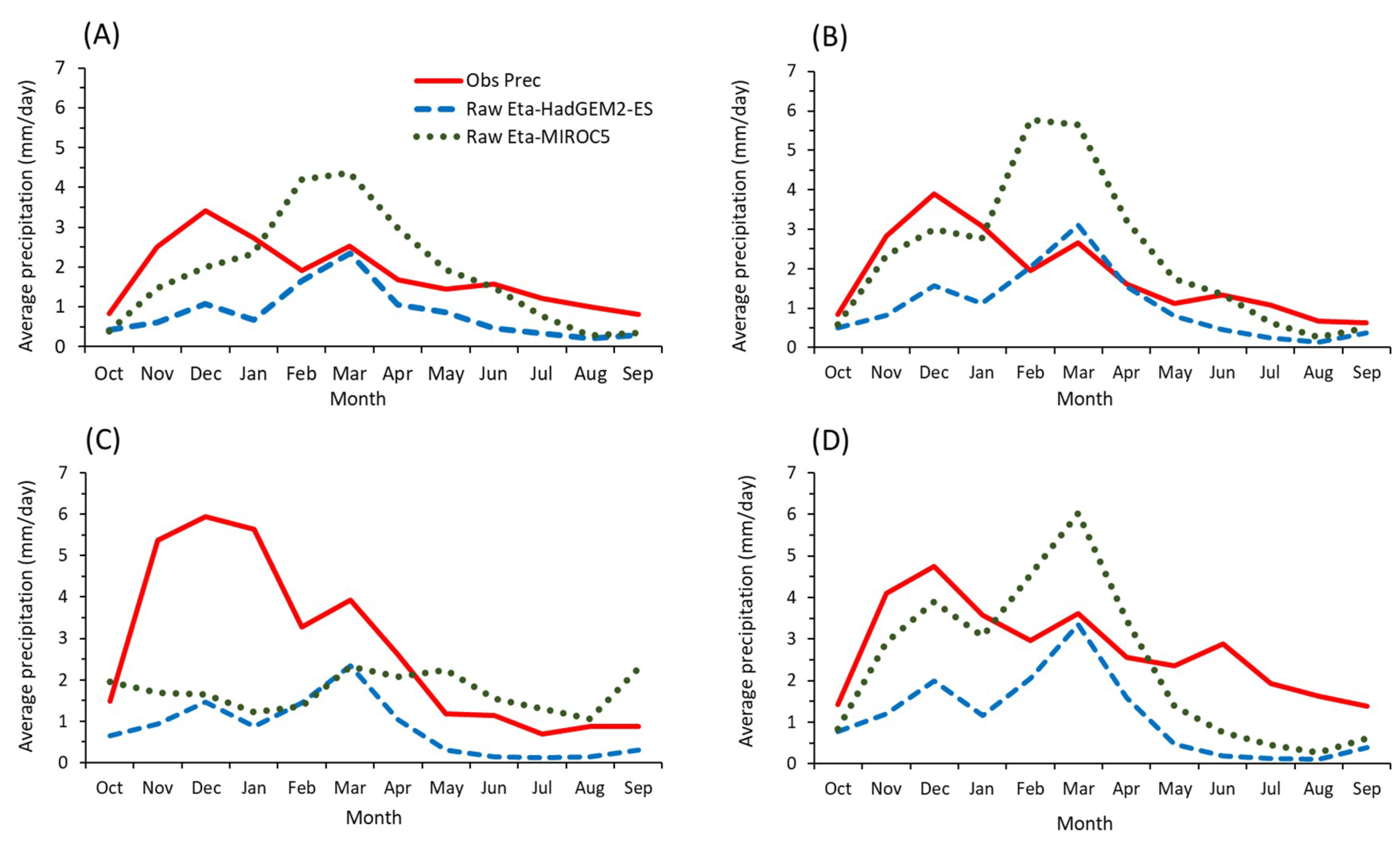
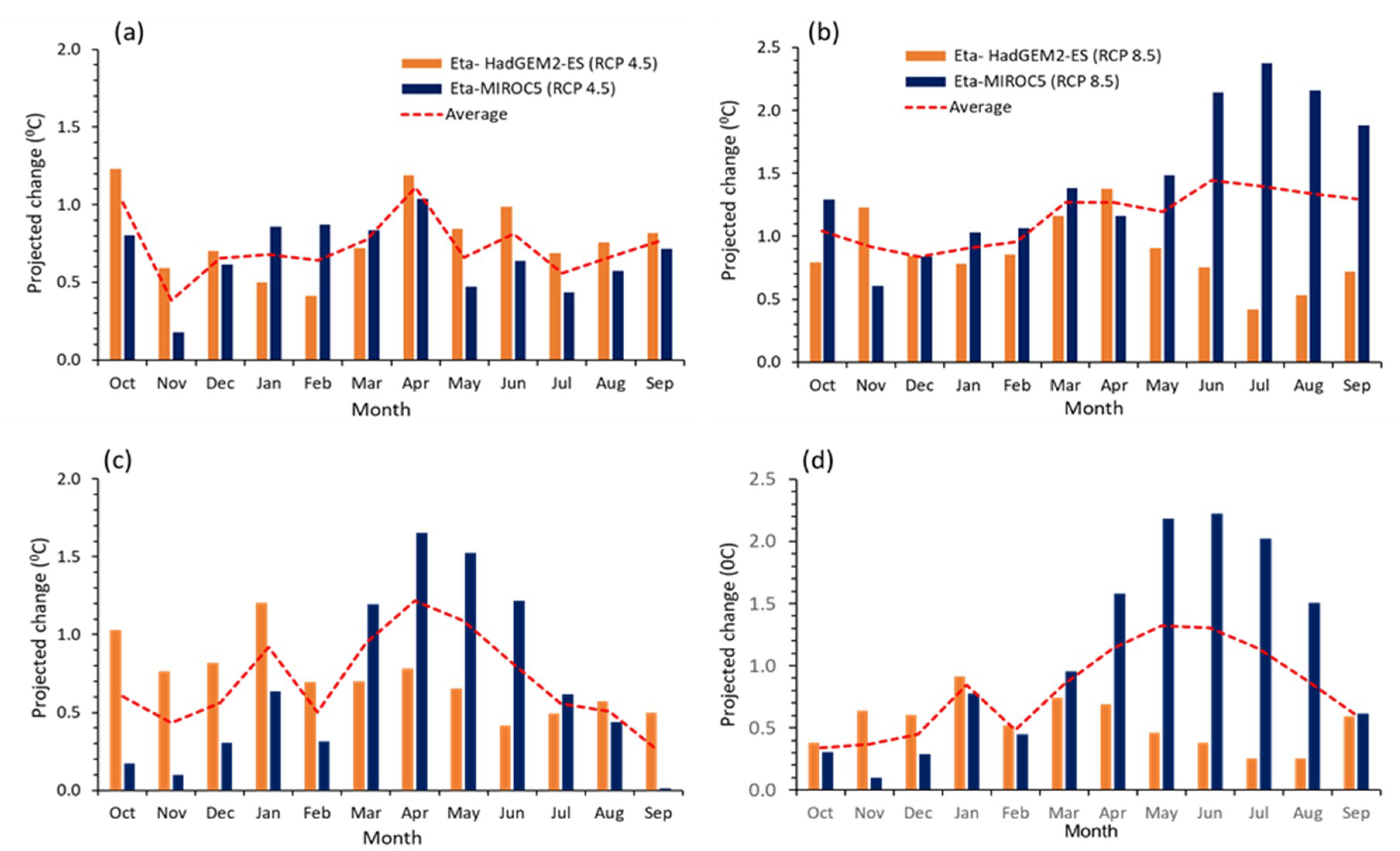
3.2.1. Raw Projections for the Baseline Period
3.2.2. Corrected Climate Projections
Corrected Temperature Projections by Linear Scaling
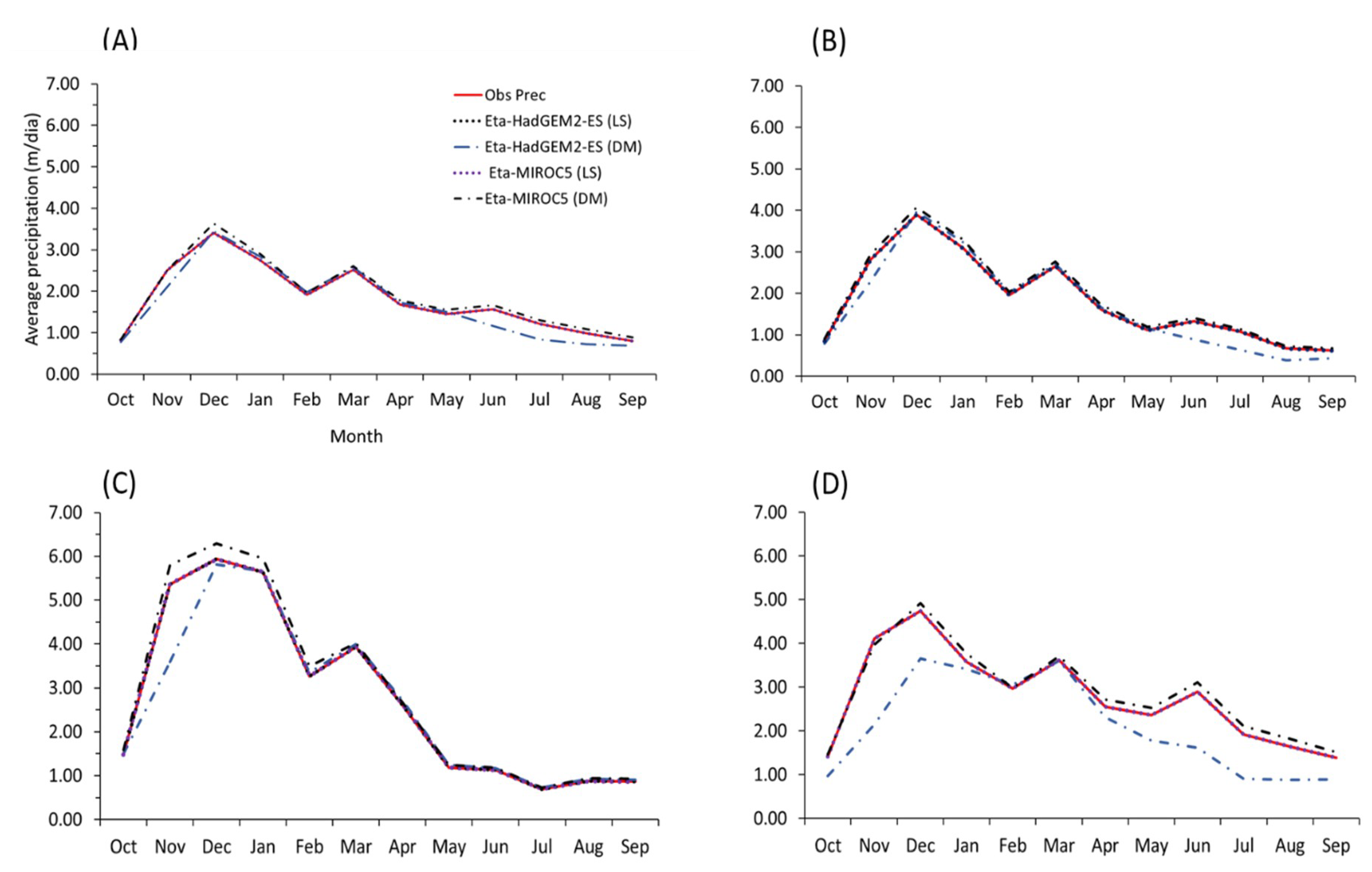
Corrected Precipitation Projections by Linear Scaling and Distribution Mapping
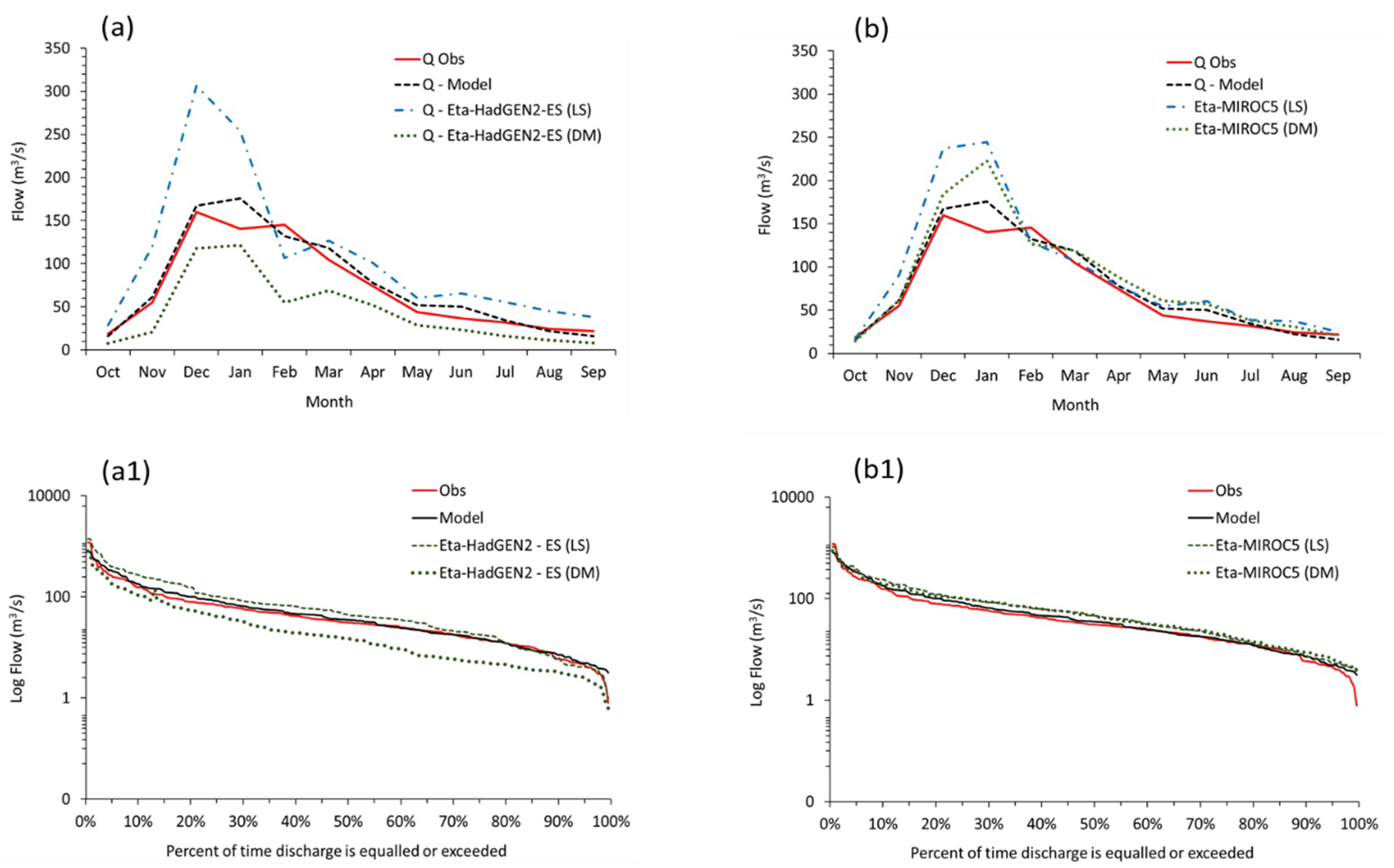
3.3. Effect of Bias Correction on the Baseline Streamflow
3.4. Climate Change Impact on Streamflow
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J. Impacts of climate change on streamflows under rcp scenarios: A case study in xin river basin, china. Atmospheric Res. 2016, 178–179, 521–534. [Google Scholar] [CrossRef]
- Mishra, Y.; Nakamura, T.; Babel, M.S.; Ninsawat, S.; Ochi, S. Impact of climate change on water resources of the bheri river basin, nepal. Water 2018, 10, 220. [Google Scholar] [CrossRef]
- Taye, M.T.; Willems, P.; Block, P. Implications of climate change on hydrological extremes in the blue nile basin: A review. J. Hydrol. Reg. Stud. 2015, 4, 280–293. [Google Scholar] [CrossRef]
- Almeida, C.; Ramos, T.B.; Segurado, P.; Branco, P.; Neves, R.; Oliveira, R.P. Water quantity and quality under future climate and societal scenarios: A basin-wide approach applied to the Sorraia River, Portugal. Water 2018, 10, 1186. [Google Scholar] [CrossRef]
- Jiménez Cisneros, B.; Oki, T.; Arnell, N.W.; Benito, G.; Cogley, J.G.; Doll, P.; Jiang, T.; Mwakalila, S.S. Freshwater resources. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 229–269. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Brazilian Institute of Geography and Statistics (IBGE). Available online: https://ww2.ibge.gov.br/home/estatistica/populacao/censo2010/ (accessed on 15 April 2017).
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, duration and severity of drought in the semiarid northeast brazil region. Int. J. Clim. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Alvala, R.C.S.; Cunha, A.P.; Brito, S.; Moraes, O.L.L. Climatic characteristics of the 2010-2016 drought in the semiarid northeast brazil region. Anais da Academia Brasileira de Ciências 2018, 90, 1973–1985. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, X.; Yao, H.; Lin, B. Improved calibration scheme of swat by separating wet and dry seasons. Ecol. Model. 2015, 301, 54–61. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.-P.; Fu, G. Uncertainties in swat extreme flow simulation under climate change. J. Hydrol. 2014, 515, 205–222. [Google Scholar] [CrossRef]
- Santos, A.M.; Galvincio, J.D.; Moura, M.S.B. Mudanças climáticas e o escoamento superficial na bacia hidrográfica do rio goiana—Pernambuco. Investigaciones Geográficas, Boletín del Instituto de Geografía 2013, 2013, 51–65. [Google Scholar]
- Kwon, H.H.; de Assis de Souza Filho, F.; Block, P.; Sun, L.; Lall, U.; Reis, D.S., Jr. Uncertainty assessment of hydrologic and climate forecast models in northeastern brazil. Hydrol. Process. 2012, 26, 3875–3885. [Google Scholar] [CrossRef]
- Githui, F.; Gitau, W.; Mutua, F.; Bauwens, W. Climate change impact on swat simulated streamflow in western kenya. Int. J. Clim. 2009, 29, 1823–1834. [Google Scholar] [CrossRef]
- De Mello, E.L.; Oliveira, F.A.; Pruski, F.F.; Figueiredo, J.C. Efeito das mudanças climáticas na disponibilidade hídrica da bacia hidrográfica dio rio paracatu. Engenharia Agrícola 2008, 28, 635–644. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Su, F.G.; Hao, Z.C.; Xu, C.Y.; Yu, Z.B.; Wang, L.; Tong, K. Impact of projected climate change on the hydrology in the headwaters of the yellow river basin. Hydrol. Process. 2015, 29, 4379–4397. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Krysanova, V.; Donnelly, C.; Gelfan, A.; Gerten, D.; Arheimer, B.; Hattermann, F.; Kundzewicz, Z.W. How the performance of hydrological models relates to credibility of projections under climate change. Hydrol. Sci. J. 2018, 63, 696–720. [Google Scholar] [CrossRef]
- Santos, C.A.S.; Almeida, C.; Ramos, T.B.; Rocha, F.A.; Oliveira, R.; Neves, R. Using a hierarchical approach to calibrate swat and predict the semi-arid hydrologic regime of northeastern brazil. Water 2018, 10, 1137. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.C.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool Theoretical Documentation. Version 2000; TR-192, Technical Report; Texas Water Resources Institute: College Station, TX, USA, 2002. [Google Scholar]
- KlemeŠ, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Chou, S.C.; Lyra, A.; Mourão, C.; Dereczynski, C.; Pilotto, I.; Gomes, J.; Bustamante, J.; Tavares, P.; Silva, A.; Rodrigues, D.; et al. Evaluation of the eta simulations nested in three global climate models. Am. J. Clim. Chang. 2014, 03, 438–454. [Google Scholar] [CrossRef]
- Chou, S.C.; Lyra, A.; Mourão, C.; Dereczynski, C.; Pilotto, I.; Gomes, J.; Bustamante, J.; Tavares, P.; Silva, A.; Rodrigues, D.; et al. Assessment of climate change over south america under rcp 4.5 and 8.5 downscaling scenarios. Am. J. Clim. Chang. 2014, 03, 512–527. [Google Scholar] [CrossRef]
- Collins, W.J.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Halloran, P.; Hinton, T.; Hughes, J.; Jones, C.D.; Joshi, M.; Liddicoat, S.; et al. Development and evaluation of an earth-system model–Hadgem2. Geosci. Model Dev. 2011, 4, 1051–1075. [Google Scholar] [CrossRef]
- Watanabe, M.; Suzuki, T.; O’ishi, R.; Komuro, Y.; Watanabe, S.; Emori, S.; Takemura, T.; Chikira, M.; Ogura, T.; Sekiguchi, M.; et al. Improved climate simulation by miroc5: Mean states, variability, and climate sensitivity. J. Clim. 2010, 23, 6312–6335. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool. Theoretical Documentation. Version 2009; Technical Report No.406; Texas Water Resources Institute: Forney, TX, USA, 2011. [Google Scholar]
- Awotwi, A.; Kumi, M.; Jansson, P.E.; Yeboah, F.; Nti, I.K. Predicting hydrological response to climate change in the white volta catchment, west africa. J. Earth Sci. Clim. Chang. 2015, 6, 1–7. [Google Scholar]
- Monteith, J.L. Evaporation and the Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- United States Department of Agriculture. Estimation of direct runoff from storm rainfall. In National Engineering Handbook; United States Department of Agriculture: Washington, DC, USA, 2004. [Google Scholar]
- Bontemps, S.; Defourny, P.; Radoux, J.; Bogaert, E.V.; Lamarche, C.; Achard, F.; Mayaux, P.; Boettcher, M.; Brockmann, C.; Kirches, G.; et al. Globcover 2009: Product Description and Validation Report 18 February 2011. Available online: http://due.esrin.esa.int/files/GLOBCOVER2009_Validation_Report_2.2.pdf (accessed on 24 August 2018).
- Embrapa. Solo Brasileiro Agora Tem Mapeamento Digital. Available online: https://www.embrapa.br/web/portal/busca-de-noticias/-/noticia/2062813/solo-brasileiro-agora-tem-mapeamento-digital (accessed on 24 August 2018).
- Silva, R.M.; Medeiros, I.C. Análise hidrossedimentológica em ambiente sig usando o modelo swat. Revista Internacional de Ciencia y Tecnología de la Información Geográfica 2014, 14, 211–231. [Google Scholar]
- De Santana, S.O.; dos Santos, R.D.; Gomes, I.A.; de Jesus, R.M.; de Araujo, Q.R.; Mendonça, J.R.; Calderano, S.B.; Faria Filho, A.F. Solos da região sudeste da bahia: Atualização da legenda de acordo com o sistema brasileiro de classificação de solos; Embrapa Solos: Rio de Janeiro, Brazil, 2002. [Google Scholar]
- Xavier, F.V. Contribuições metodológicas ao estudo da produção e distribuição espacial de sedimentos na bacia hidrográfica do rio manso, utilizando o modelo avswat. Master’s Thesis, Universidade Federal de Mato Grosso, Cuiabá, Brazil, 2009. [Google Scholar]
- Mercuri, E.G.F.; Deppe, F.; Lohmann, M.; Simões, K. Metodologia da geração de dados de entrada e aplicação do modelo swat para bacias hidrográficas brasileiras. In Anais XIV Simpósio Brasileiro de Sensoriamento Remoto; Instituto Nacional De Pesquisas Espaciais: Natal, Brasil, 2009; pp. 4773–4780. [Google Scholar]
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Daily gridded meteorological variables in brazil (1980–2013). Int. J. Clim. 2015, 2644–2659. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Bosshard, T.; Kotlarski, S.; Schär, C. Local Scenarios at Daily Resolution for Emission Scenarios a2 and rcp3pd, ch2011 Extension Series No. 1; Zurich, Switzerland, 2015; p. 12. Available online: https://www.ch2011.ch/pdf/CH2011plus_No1_Bosshard2015.pdf (accessed on 14 January 2019).
- Lenderink, G.; Buishand, A.; Deursen, W. Estimative of future discharges of the river rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Nie, W.; Yuan, Y.; Kepner, W.; Erickson, C.; Jackson, M. Hydrological impacts of mesquite encroachment in the upper san pedro watershed. J. Arid Environ. 2012, 82, 147–155. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in china. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2011, 112, 449–468. [Google Scholar] [CrossRef]
- De Oliveira, V.A.; de Mello, C.R.; Viola, M.R.; Srinivasan, R. Assessment of climate change impacts on streamflow and hydropower potential in the headwater region of the grande river basin, southeastern brazil. Int. J. Clim. 2017, 37, 5005–5023. [Google Scholar] [CrossRef]
- Alvarenga, L.A.; Mello, C.R.; Colombo, A.; Cuartas, L.A.; Chou, S.C. Hydrological responses to climate changes in a headwater watershed. Ciência E Agrotecnologia 2016, 40, 647–657. [Google Scholar] [CrossRef]
| Parameter | Description and Units | Default | Calibrated Value |
|---|---|---|---|
| GW_DELAY | Groundwater Delay (days) | 0–500 | 31–365 |
| GW_REVAP | Revaporation coefficient (-) | 0.02–0.2 | 0.02–0.2 |
| GW_RCHRG_DP | Deep aquifer recharge (mm) | 0–1 | 0.05–0.25 |
| Mgt1_CN2 | SCS runoff curve number for moisture condition II (-) | 35–98 | 45–78 |
| HRU_SLSOIL | Hillslope length (m) | 0–150 | 0–85 |
| SOL_AWC | Available water capacity of the soil layer (mm/mm soil) | 0.075–0.40 | 0.1–0.30 |
| SOL_Z | Soil depth (mm) | - | 500–3000 |
| SOL_K | Saturated hydraulic conductivity (mm/h) | - | 2–35 |
| CH_K2 | hydraulic conductivity of channel (mm/h) | 0.01–500 | 0.01–1.5 |
| Location | Discharge Average (m3/s) | Statistic | Performance | ||||
|---|---|---|---|---|---|---|---|
| Approach | Observed | Simulated | PBIAS | RSR | R2 | Moriasi et al. (2007) | |
| Itaeté | Calibration | 48.18 | 46.13 | 4.2 | 0.40 | 0.85 | Very good |
| Validation | 56.96 | 59.4 | −5.0 | 0.39 | 0.86 | Very good | |
| Argoim | Calibration | 65.89 | 67.08 | −2.0 | 0.39 | 0.88 | Very good |
| Validation | 72.7 | 83.28 | −14.0 | 0.32 | 0.80 | Very good | |
| Statistic Parameters | Model (m3/s) | Eta-HadGEM2-ES | Eta-MIROC5 | ||||
|---|---|---|---|---|---|---|---|
| Baseline | LS | DM | Baseline | LS | DM | ||
| Minimum flow | 3.1 | 0.01 | 0.98 | 0.62 | 3.3 | 4.2 | 3.9 |
| Maximum flow | 826.4 | 288.50 | 1391.0 | 792.9 | 549.5 | 1047.5 | 889.8 |
| Average flow | 77.0 | 15.67 | 109.0 | 44.3 | 88.6 | 93.1 | 85.3 |
| Q10 | 182.5 | 38.12 | 277.6 | 109.5 | 200.5 | 238.7 | 203.0 |
| Q90 | 8.5 | 1.0 | 13.4 | 6.5 | 10.26 | 10.0 | 8.4 |
| Month | October | November | December | January | February | March | April | May | June | July | August | September | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline Model * | 28.05 | 51.63 | 110.41 | 112.07 | 126.42 | 175.46 | 153.30 | 97.00 | 73.68 | 55.39 | 41.64 | 38.73 | |
| Baseline LS * | 16.71 | 90.44 | 237.14 | 244.38 | 128.35 | 106.93 | 77.92 | 54.42 | 60.25 | 38.41 | 36.90 | 24.87 | |
| Baseline DM * | 14.13 | 61.09 | 184.25 | 222.87 | 126.56 | 119.01 | 87.97 | 60.95 | 57.20 | 37.85 | 30.94 | 20.88 | |
| % change discharge under RCP 4.5 (2020–2040) | |||||||||||||
| Eta-MIROC5 | LS | 14% | 40% | −35% | −2% | 7% | −14% | −4% | −5% | −32% | −27% | −33% | −31% |
| Eta-MIROC5 | DM | 362% | 264% | 90% | 153% | 228% | 213% | 219% | 229% | 186% | 233% | 212% | 242% |
| % change discharge under RCP 8.5 (2020–2040) | |||||||||||||
| Eta-MIROC5 | LS | −75% | −54% | −49% | −48% | −46% | −61% | −67% | −64% | −73% | −72% | −71% | −69% |
| Eta-MIROC5 | DM | 186% | 84% | 76% | 89% | 160% | 135% | 124% | 136% | 116% | 146% | 126% | 149% |
| Baseline Model * | 4.24 | 3.16 | 30.45 | 16.12 | 15.93 | 50.59 | 34.27 | 11.65 | 8.04 | 5.88 | 4.06 | 3.52 | |
| Baseline LS * | 28.52 | 119.79 | 306.71 | 253.88 | 106.92 | 126.71 | 101.09 | 60.11 | 65.69 | 55.47 | 45.24 | 38.23 | |
| Baseline DM * | 7.84 | 20.54 | 117.81 | 121.51 | 55.28 | 68.64 | 52.08 | 28.44 | 23.25 | 16.23 | 11.50 | 8.20 | |
| % change discharge under RCP 4.5 (2020–2040) | |||||||||||||
| Eta-HadGEM2-ES | LS | −72% | −60% | −82% | −69% | −43% | −61% | −71% | −69% | −55% | −65% | −61% | −74% |
| Eta-HadGEM2-ES | DM | −91% | −86% | −91% | −77% | −50% | −71% | −83% | −81% | −77% | −79% | −77% | −81% |
| % change discharge under RCP 8.5 (2020–2040) | |||||||||||||
| Eta-HadGEM2-ES | LS | −45% | 9% | −81% | −80% | −70% | −90% | −94% | −84% | −42% | 18% | 419% | −20% |
| Eta-HadGEM2-ES | DM | −41% | 4% | −83% | −80% | −62% | −87% | −92% | −77% | −63% | −44% | 256% | 17% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, C.A.S.; Rocha, F.A.; Ramos, T.B.; Alves, L.M.; Mateus, M.; Oliveira, R.P.d.; Neves, R. Using a Hydrologic Model to Assess the Performance of Regional Climate Models in a Semi-Arid Watershed in Brazil. Water 2019, 11, 170. https://doi.org/10.3390/w11010170
Santos CAS, Rocha FA, Ramos TB, Alves LM, Mateus M, Oliveira RPd, Neves R. Using a Hydrologic Model to Assess the Performance of Regional Climate Models in a Semi-Arid Watershed in Brazil. Water. 2019; 11(1):170. https://doi.org/10.3390/w11010170
Chicago/Turabian StyleSantos, Carlos A. S., Felizardo. A. Rocha, Tiago B. Ramos, Lincoln M. Alves, Marcos Mateus, Rodrigo Proença de Oliveira, and Ramiro Neves. 2019. "Using a Hydrologic Model to Assess the Performance of Regional Climate Models in a Semi-Arid Watershed in Brazil" Water 11, no. 1: 170. https://doi.org/10.3390/w11010170
APA StyleSantos, C. A. S., Rocha, F. A., Ramos, T. B., Alves, L. M., Mateus, M., Oliveira, R. P. d., & Neves, R. (2019). Using a Hydrologic Model to Assess the Performance of Regional Climate Models in a Semi-Arid Watershed in Brazil. Water, 11(1), 170. https://doi.org/10.3390/w11010170








