Influence of Landscape Structures on Water Quality at Multiple Temporal and Spatial Scales: A Case Study of Wujiang River Watershed in Guizhou
Abstract
1. Introduction
2. Materials and Methods
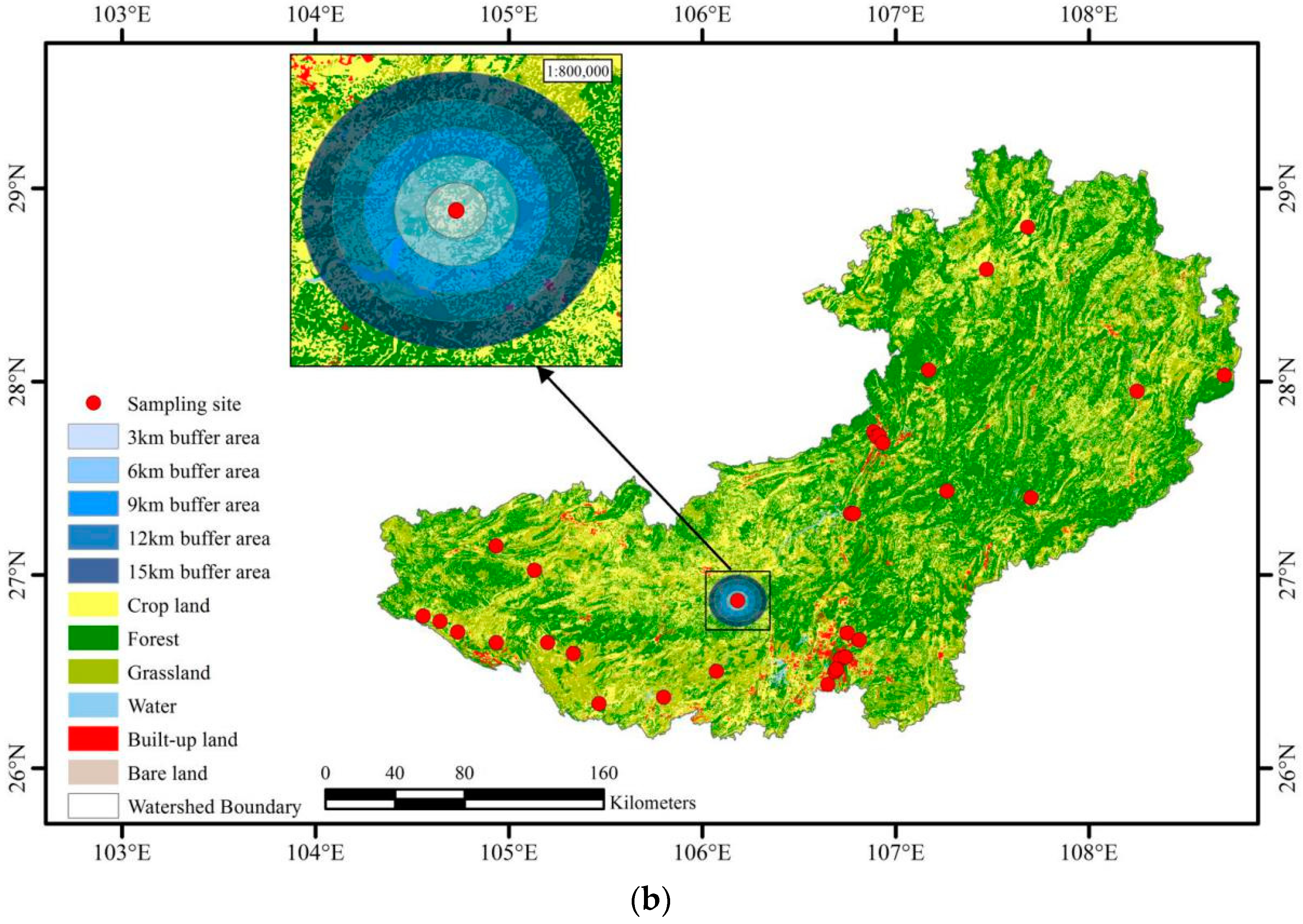
2.1. Study Area
2.2. Water Sampling and Analysis
2.3. Spatial Data
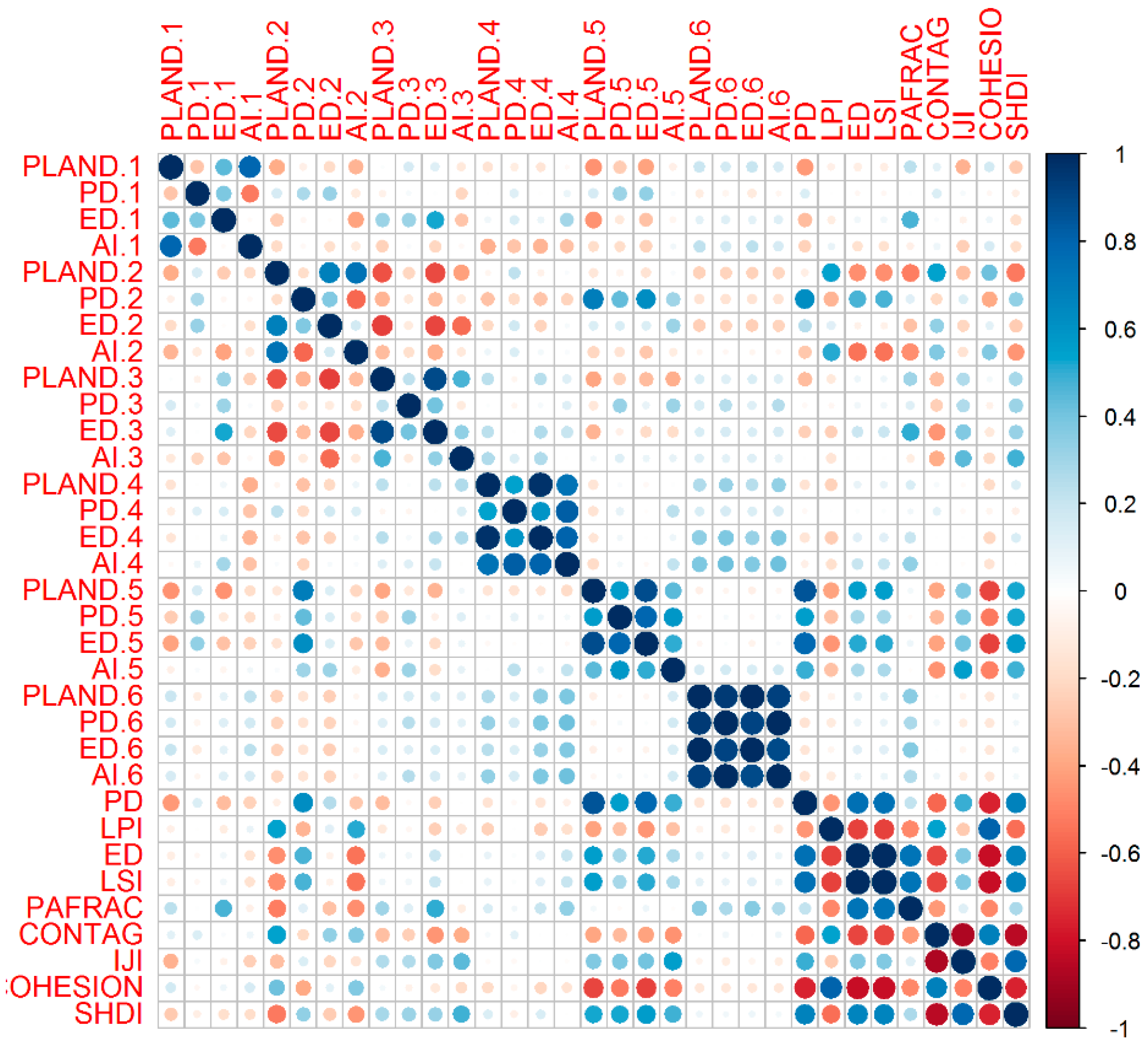
2.4. Statistical Analysis
3. Results
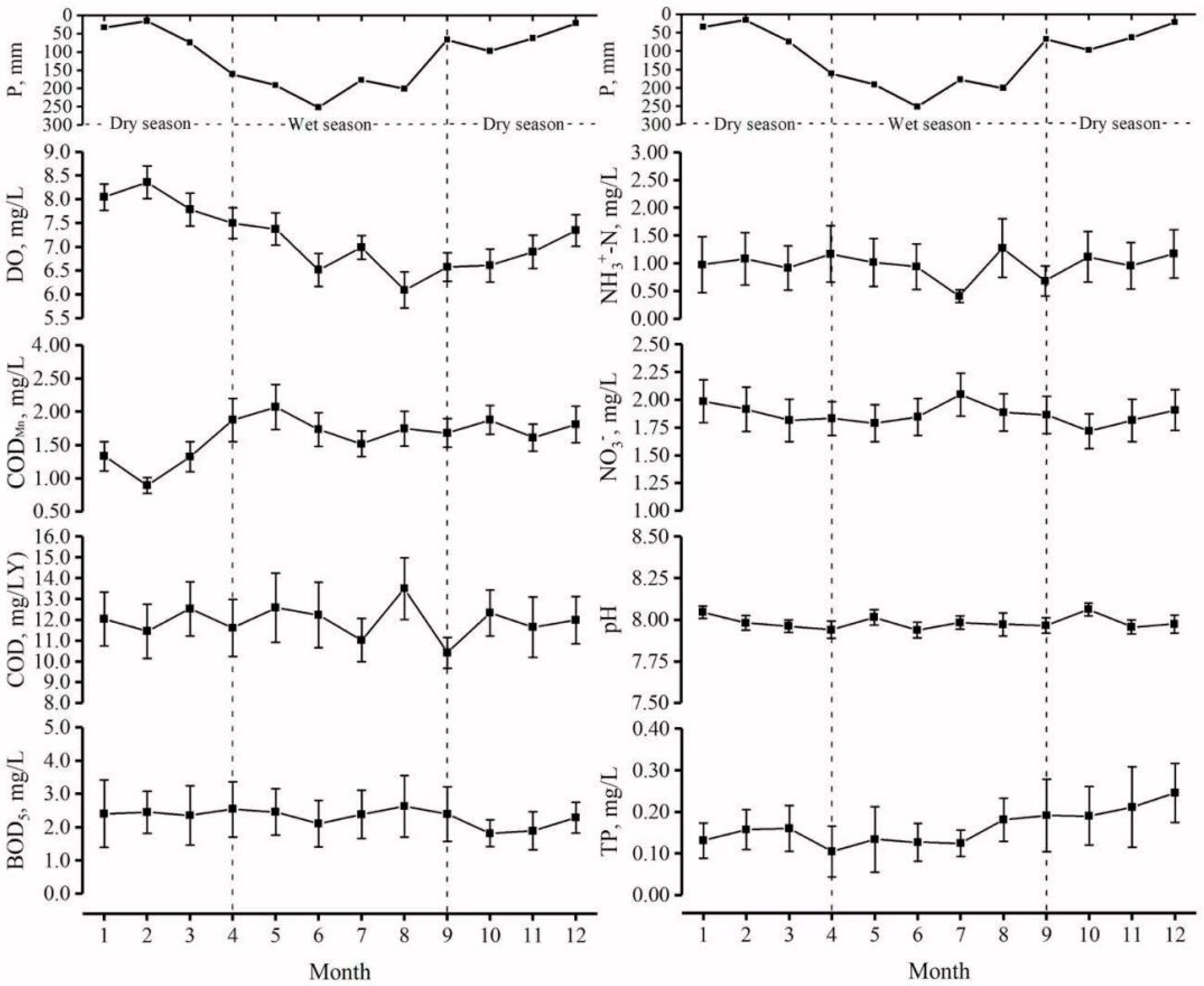
3.1. Spatial and Seasonal Variations of Water Contaminant
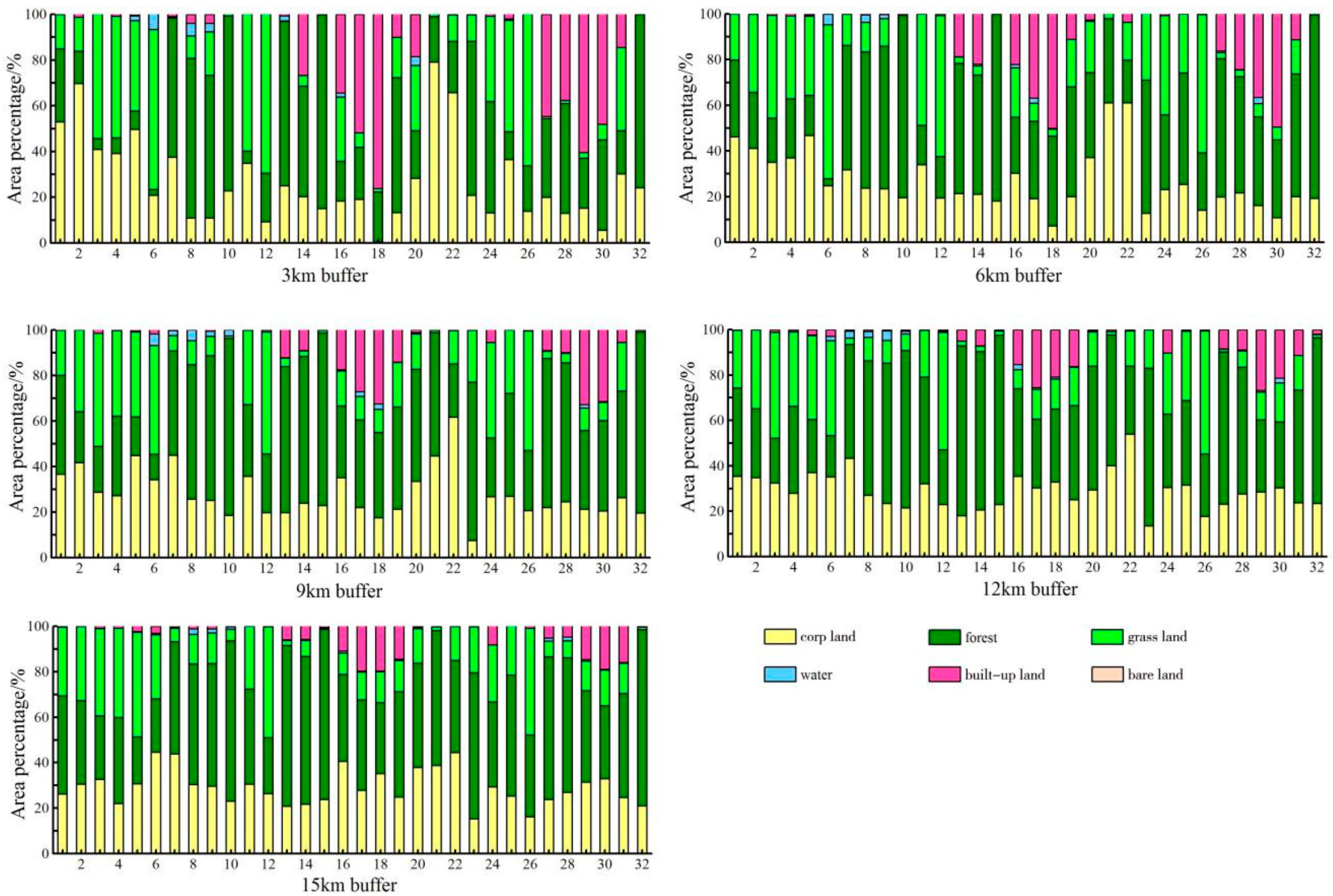
3.2. Characteristics of Landscape Composition in Different Buffer Zones
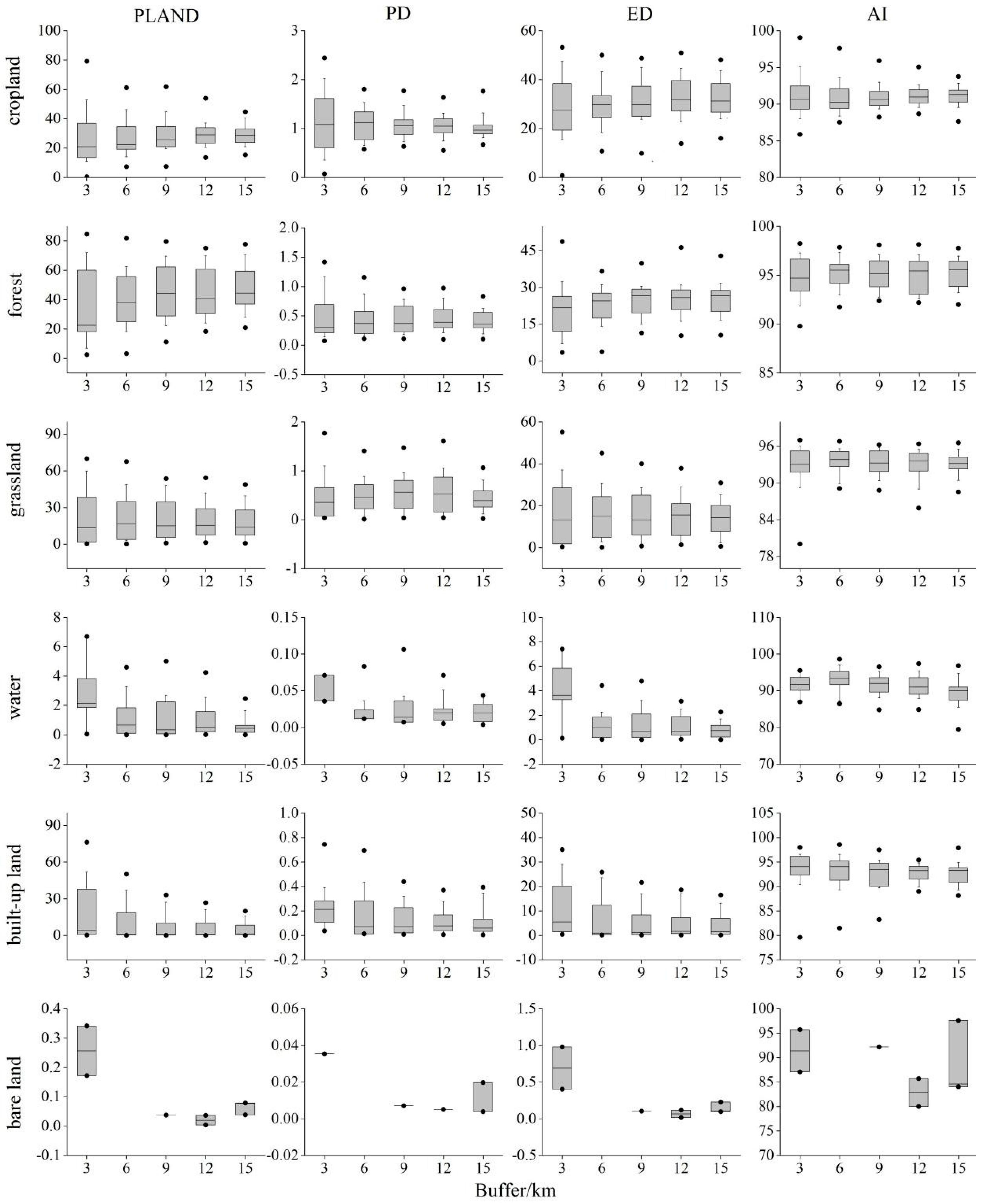
3.3. Characteristics of Landscapes at Class-Level in Different Buffer Zones
3.4. Characteristics of Landscapes at Landscape Level across Buffer Zones
3.5. Linkages between Water Contaminants and Landscape Metrics across Buffer Zone Scales Based on PLSR
4. Discussion
4.1. Seasonal Effects of Water Quality
4.2. Dominant Landscape Metrics at Class Level Affect Water Quality across Seasons and Buffer Zones
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, R.; Wang, G.; Zhang, Q.; Zhang, Z. Multi-scale analysis of relationship between landscape pattern and urban river water quality in different seasons. Sci. Rep. 2016, 6, 25250. [Google Scholar] [CrossRef]
- Lu, D.; Mao, W.; Yang, D.; Zhao, J.; Xu, J. Effects of land use and landscape pattern on PM2. 5 in Yangtze River Delta, China. Atmos. Pollut. Res. 2018, 9, 705–713. [Google Scholar] [CrossRef]
- Akasaka, M.N.; Mitsuhashi, H.; Kadono, Y. Effects of land use on aquatic macrophyte diversity and water quality of ponds. Freshw. Biol. 2010, 55, 909–922. [Google Scholar] [CrossRef]
- Tu, J.; Xia, Z.G.; Clarke, K.C.; Frei, A. Impact of urban sprawl on water quality in eastern Massachusetts, USA. Environ. Manag. 2007, 40, 183–200. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Wu, J.; Peng, S. Assessing the effects of landscape pattern on river water quality at multiple scales: A case study of the Dongjiang River watershed, China. Ecol. Indic. 2012, 23, 166–175. [Google Scholar] [CrossRef]
- Allan, J.D. Landscapes and Riverscapes: The Influence of Land Use on Stream Ecosystems. Ann. Rev. Ecol. Evol. Syst. 2004, 35, 257–284. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Wang, Y.; Guo, X.; Lu, S. Analysis of point source pollution and water environmental quality variation trends in the Nansi Lake basin from 2002 to 2012. Environ. Sci. Pollut. Res. 2016, 23, 4886–4897. [Google Scholar] [CrossRef]
- DeFries, R.; Eshleman, K.N. Land-use change and hydrologic processes: A major focus for the future. Hydrol. Process. 2004, 18, 2183–2186. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Q.; Liu, G. Influences of watershed landscape composition and configuration on lake-water quality in the Yangtze River basin of China. Hydrol. Process. 2012, 26, 570–578. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, H. The Impacts of Spatiotemporal Landscape Changes on Water Quality in Shenzhen, China. Int. J. Environ. Res. Public Health 2018, 15, 1038. [Google Scholar] [CrossRef]
- Putro, B.; Kjeldsen, T.R.; Hutchins, M.G.; Miller, J. An empirical investigation of climate and land-use effects on water quantity and quality in two urbanising catchments in the southern United Kingdom. Sci. Total Environ. 2016, 548, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Pratt, B.; Chang, H. Effects of land cover, topography, and built structure on seasonal water quality at multiple spatial scales. J. Hazard. Mater. 2012, 209, 48–58. [Google Scholar] [CrossRef]
- Tong, S.T.Y.; Chen, W. Modeling the relationship between land use and surface water quality. J. Environ. Manag. 2002, 66, 377–393. [Google Scholar] [CrossRef]
- Shi, P.; Zhang, Y.; Li, Z.; Xu, G. Influence of land use and land cover patterns on seasonal water quality at multi-spatial scales. CATENA 2017, 151, 182–190. [Google Scholar] [CrossRef]
- Bu, H.; Meng, W.; Zhang, Y.; Wang, J. Relationships between land use patterns and water quality in the Taizi River basin, China. Ecol. Indic. 2014, 41, 187–197. [Google Scholar] [CrossRef]
- Sliva, L.; Williams, D.D. Buffer zone versus whole catchment approaches to studying land use impact on river water quality. Water Res. 2001, 35, 3462–3472. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, W.; Pickett, S.T.; Li, W.; Han, L. Spatial-Temporal Variations of Water Quality and Its Relationship to Land Use and Land Cover in Beijing, China. Int. J. Environ. Res. Public Health 2016, 13, 449. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Shen, Z.; Chen, L. Assessing how spatial variations of land use pattern affect water quality across a typical urbanized watershed in Beijing, China. Landsc. Urban Plan. 2018, 176, 51–63. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Y.; Xu, Y.; Wang, Y.; Han, L. Spatial hydrological responses to land use and land cover changes in a typical catchment of the Yangtze River Delta region. CATENA 2018, 170, 305–315. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, J.; Wang, X. Recognizing the Relationship between Spatial Patterns in Water Quality and Land-Use/Cover Types: A Case Study of the Jinghe Oasis in Xinjiang, China. Water 2018, 10, 646. [Google Scholar] [CrossRef]
- Lee, S.W.; Hwang, S.J.; Lee, S.B.; Hwang, H.S.; Sung, H.C. Landscape ecological approach to the relationships of land use patterns in watersheds to water quality characteristics. Landsc. Urban Plan. 2009, 92, 80–89. [Google Scholar] [CrossRef]
- Tudesque, L.; Tisseuil, C.; Lek, S. Scale-dependent effects of land cover on water physico-chemistry and diatom-based metrics in a major river system, the Adour-Garonne basin (South Western France). Sci. Total Environ. 2014, 466, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Smart, R.P.; Soulsby, C.; Cresser, M.S.; Wade, A.J.; Townend, J.; Billett, M.F.; Langan, S. Riparian zone influence on stream water chemistry at different spatial scales: A GIS-based modelling approach, an example for the Dee, NE Scotland. Sci. Total Environ. 2001, 280, 173–193. [Google Scholar] [CrossRef]
- Mcgarigal, K.; Marks, B.J. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; General Technical Report PNW-GTR-351; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1995.
- McGarigal, K.; Cushman, S.A.; Ene, E. FRAGSTATS v4: Spatial Pattern Analysis Program for Categorical and Continuous Maps. Computer Software Program Produced by the Authors at the University of Massachusetts, Amherst. 2012. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 12 December 2015).
- Shen, Z.; Hou, X.; Li, W.; Aini, G. Relating landscape characteristics to non-point source pollution in a typical urbanized watershed in the municipality of Beijing. Landsc. Urban Plan. 2014, 123, 96–107. [Google Scholar] [CrossRef]
- Chen, Q.; Mei, K.; Dahlgren, R.A.; Wang, T. Impacts of land use and population density on seasonal surface water quality using a modified geographically weighted regression. Sci. Total Environ. 2016, 572, 450–466. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Jiang, Y.; Liu, Q.; Hou, Z.; Liao, J.; Fu, L.; Peng, Q. Influences of the land use pattern on water quality in low-order streams of the Dongjiang River basin, China: A multi-scale analysis. Sci. Total Environ. 2016, 551, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Shen, W.; Sun, W.; Tueller, P. Empirical patterns of the effects of changing scale on landscape metrics. Landsc. Ecol. 2002, 17, 761–782. [Google Scholar] [CrossRef]
- Guo, Q.H.; Ma, K.M.; Yang, L.; He, K. Testing a dynamic complex hypothesis in the analysis of land use impact on lake water quality. Water Resour. Manag. 2010, 24, 1313–1332. [Google Scholar] [CrossRef]
- Shen, Z.; Hou, X.; Li, W.; Anni, G.; Chen, L.; Gong, Y. Impact of landscape pattern at multiple spatial scales on water quality: A case study in a typical urbanised watershed in China. Ecol. Indic. 2015, 48, 417–427. [Google Scholar] [CrossRef]
- de Mello, K.; Valente, R.A.; Randhir, T.O.; Dos Santos, A.C.O. Effects of land use and land cover on water quality of low-order streams in Southeastern Brazil: Watershed versus riparian zone. CATENA 2018, 167, 130–138. [Google Scholar] [CrossRef]
- Li, S.; Gu, S.; Tan, X.; Zhang, Q. Water quality in the upper Han River basin, China: The impacts of land use/land cover in riparian buffer zone. J. Hazard. Mater. 2009, 165, 317–324. [Google Scholar] [CrossRef] [PubMed]
- O’Driscoll, C.; O’Connor, M.; de Eyto, E.; Asam, Z. Creation and functioning of a buffer zone in a blanket peat forested catchment. Ecol. Eng. 2014, 62, 83–92. [Google Scholar] [CrossRef]
- Correll, D.L. Principles of planning and establishment of buffer zones. Ecol. Eng. 2005, 24, 433–439. [Google Scholar] [CrossRef]
- Uriarte, M.; Yackulic, C.B.; Lim, Y.; Arce-Nazario, J.A. Influence of land use on water quality in a tropical landscape: A multi-scale analysis. Landsc. Ecol. 2011, 26, 1151–1164. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, M.O.; de Souza, A.L.T.; Moschini, L.E.; de Oliveira, A.K. Influence of watershed land use and riparian characteristics on biological indicators of stream water quality in southeastern Brazil. Agric. Ecosyst. Environ. 2016, 216, 333–339. [Google Scholar] [CrossRef]
- Liu, R.; Xu, F.; Zhang, P.; Yu, W. Identifying non-point source critical source areas based on multi-factors at a basin scale with SWAT. J. Hydrol. 2016, 533, 379–388. [Google Scholar] [CrossRef]
- Li, S.; Xia, X.; Tan, X.; Zhang, Q. Effects of catchment and riparian landscape setting on water chemistry and seasonal evolution of water quality in the upper Han River basin, China. PLoS ONE 2013, 8, e53163. [Google Scholar] [CrossRef]
- Ai, L.; Shi, Z.H.; Yin, W.; Huang, X. Spatial and seasonal patterns in stream water contamination across mountainous watersheds: Linkage with landscape characteristics. J. Hydrol. 2015, 523, 398–408. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, J.; Wang, Y. Application of partial least squares regression in detecting the important landscape indicators determining urban land surface temperature variation. Landsc. Ecol. 2018, 33, 1–13. [Google Scholar] [CrossRef]
- Pérezenciso, M.; Tenenhaus, M. Prediction of clinical outcome with microarray data: A partial least squares discriminant analysis (PLS-DA) approach. Hum. Genet. 2003, 112, 581–592. [Google Scholar]
- Burgués, J.; Marco, S. Multivariate estimation of the limit of detection by orthogonal partial least squares in temperature-modulated MOX sensors. Anal. Chim. Acta 2018, 1019, 49. [Google Scholar] [CrossRef] [PubMed]
- Alabri, Z.K.; Hussain, J.; Mabood, F.; Rehman, N.U.; Ali, L.; Al-Harrasi, A.; Hamaed, A.; Khan, A.L.; Rizvi, T.S.; Jabeen, F.; et al. Fluorescence spectroscopy-partial least square regression method for the quantification of quercetin in Euphorbia masirahensis. Measurement 2018, 121, 355–359. [Google Scholar] [CrossRef]
- Carrascal, L.M.; Galván, I.; Gordo, O. Partial least squares regression as an alternative to current regression methods used in ecology. Oikos 2009, 118, 681–690. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Li, X. Correlation analysis between the spatial characteristics of land use/cover- landscape pattern and surface-water quality in the Ebinur Lake area. Acta Ecol. Sin. 2017, 37, 7438–7452. (In Chinese) [Google Scholar]
- Griffith, J.A. Geographic Techniques and Recent Applications of Remote Sensing to Landscape-Water Quality Studies. Water Air Soil Pollut. 2002, 138, 181–197. [Google Scholar] [CrossRef]
- Hong, C.; Lin, G.; Kang, W. The effects of sloping landscape features on water quality in the upper and middle reaches of the Chishui River Watershed. Geogr. Res. 2018, 37, 704–716. [Google Scholar]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- James, G.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Temnerud, J.; Düker, A.; Karlsson, S.; Allard, B. Landscape scale patterns in the character of natural organic matter in a Swedish boreal stream network. Hydrol. Earth Syst. Sci. 2009, 6, 1567–1582. [Google Scholar] [CrossRef]
- Liu, P.; Cheng, J.; Liu, X.N.; Chen, Z.; Wu, Z. Characteristics of output of non-point source pollution with rainfall runoff in typical agricultural watershed of Liuxi River Valley. J. Ecol. Rural Environ. 2008, 21, 237–252. [Google Scholar]
- Yue, J. Spatial-temporal trends of water quality and its influence by land use:A case study of the main rivers in Shenzhen. Adv. Water Sci. 2006, 17, 359–364. (In Chinese) [Google Scholar]
- Xiaolong, W.; Jingyi, H.; Ligang, X.; Qi, Z. Spatial and seasonal variations of the contamination within water body of the Grand Canal, China. Environ. Pollut. 2010, 158, 1513–1520. [Google Scholar] [CrossRef] [PubMed]
- Wei, O.; Skidmore, A.K.; Toxopeus, A.G.; Hao, F. Long-term vegetation landscape pattern with non-point source nutrient pollution in upper stream of Yellow River basin. J. Hydrol. 2010, 389, 373–380. [Google Scholar]
- Wang, P.; Qi, S.; Chen, B. Influence of land use on river water quality in the Ganjiang basin WANG Peng, QI Shuhua chen bo. Acta Ecol. Sin. 2015, 35, 4326–4337. (In Chinese) [Google Scholar]
- White, M.D.; Greer, K.A. The effects of watershed urbanization on the stream hydrology and riparian vegetation of Los Peñasquitos Creek, California. Landsc. Urban Plan. 2006, 74, 125–138. [Google Scholar] [CrossRef]
- Wilson, C.; Weng, Q. Assessing Surface Water Quality and Its Relation with Urban Land Cover Changes in the Lake Calumet Area, Greater Chicago. Environ. Manag. 2010, 45, 1096–1111. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Lin, L.; Yang, K.; Liu, Q. Influences of land use on water quality in a reticular river network area: A case study in Shanghai, China. Landsc. Urban Plan. 2015, 137, 20–29. [Google Scholar] [CrossRef]
- Yu, S.; Xu, Z.; Wu, W.; Zuo, D. Effect of land use types on stream water quality under seasonal variation and topographic characteristics in the Wei River basin, China. Ecol. Indic. 2016, 60, 202–212. [Google Scholar] [CrossRef]
- Xia, P.; Kong, X.; Yu, L. Effects of land-use and landscape pattern on nitrogen and phosphorus exports in Caohai wetland watershed. J. Environ. Sci. 2016, 36, 2983–2989. (In Chinese) [Google Scholar]
- Yan, W.; Yin, C.; Tang, H. Nutrient Retention by Multipond Systems: Mechanisms for the Control of Nonpoint Source Pollution. J. Environ. Qual. 1998, 27, 1009–1017. [Google Scholar] [CrossRef]
- Yin, C.; Zhao, M.; Jin, W.; Lan, Z. A multi-pond system as a protective zone for the management of lakes in China. Hydrol. Biol. 1993, 251, 321–329. [Google Scholar] [CrossRef]
- Ji, D.; Wen, Y.; Wei, J.; Zhang, F. Relationships between landscape spatial characteristics and surface water quality in the Liu Xi River watershed. Acta Ecol. Sin. 2015, 35, 246–253. (In Chinese) [Google Scholar]
- Ouyang, W.; Hao, F.H.; Skidmore, A.K.; Groen, T.A. Integration of multi-sensor data to assess grassland dynamicsin a Yellow River sub-watershed. Ecol. Indic. 2012, 18, 163–170. [Google Scholar] [CrossRef]
- Galbraith, L.M.; Burns, C.W. Linking Land-use, Water Body Type and Water Quality in Southern New Zealand. Landsc. Ecol. 2007, 22, 231–241. [Google Scholar] [CrossRef]
- Uuemaa, E.; Roosaare, J.; Ülo, M. Scale dependence of landscape metrics and their indicatory value for nutrient and organic matter losses from catchments. Ecol. Indic. 2005, 5, 350–369. [Google Scholar] [CrossRef]
- Li, Y.; Qureshi, S.; Kappas, M. On the relationship between landscape ecological patterns and water quality across gradient zones of rapid urbanization in coastal China. Ecol. Model. 2015, 318, 100–108. [Google Scholar] [CrossRef]



| NH3+-N | spectrophotometric method with salicylic acid; |
| DO | iodine quantity method; |
| CODMn | acidic (alkaline) potassium permanganate method; |
| COD | dichromate method; |
| BOD5 | dilution and inoculation method |
| NO3− | phenol disulfonic acid spectrophotometry |
| TP | ammonium molybdate spectrophotometric method |
| pH | PH-40A portable PH acidity meter |
| Index | Description | Calculation |
|---|---|---|
| Patch density (PD) | Number of patches per unit area (unit: n/100 ha) | a b |
| Edge density (ED) | Total length of all edge segments per hectare for the considered landscape/class (unit: m/ha) | b b |
| Aggregation index (AI) | Degree of dispersion of the patches equals the number of like adjacencies involving the corresponding class (unit: %) | AI = a |
| Percent of landscape (PLAND) | Event when the entire image is comprised of a single patch. | |
| Contagion index (CONTAG) | Tendency of land use types to be aggregated (unit: %) | |
| Shannon’s diversity index (SHDI) | Patch diversity in landscape (no unit) | |
| Landscape shape index (LSI) | Sum of the landscape boundary divided by the square root of the total landscape area (no unit) | |
| Interspersion and juxtaposition index (IJI) | Measurement of the extent to which patch types are interspersed. | |
| Perimeter-area fractal dimension (PAFRAC) | PAFRAC is meaningful if the log-log relationship between perimeter and area is linear over the full range of patch sizes. | |
| Patch cohesion index (COHESION) | Patch cohesion index measures the physical connectedness of the corresponding patch type. |
| DO | CODMn | COD | BOD5 | NH3+-N | NO3− | TP | ||
|---|---|---|---|---|---|---|---|---|
| 3 km | ED.5 | −0.098 | ||||||
| ED a | −0.013 | −0.016 | ||||||
| LSI a | −0.050 | |||||||
| CONTAG a | 0.017 | |||||||
| COHESION | 0.047 | |||||||
| 6 km | PLAND.5 a | 0.046 | 0.031 | |||||
| ED.5 a | 0.005 | −0.031 | ||||||
| PD | −0.003 | |||||||
| CONTAG a | 0.027 | |||||||
| 9 km | ED.2 a | −0.01 | −0.064 | |||||
| PD | −0.004 | |||||||
| LPI | 0.049 | |||||||
| CONTAG a | 0.035 | 0.035 | ||||||
| COHESION a | 0.033 | 0.0326 | ||||||
| SHDI | −0.001 | −0.0012 | ||||||
| 12 km | ED.3 | −0.001 | ||||||
| AI.5 a | 0.031 | −0.011 | ||||||
| CONTAG | 0.005 | |||||||
| 15 km | ED.1 a | 0.007 | −0.05 | |||||
| AI.2 a | −0.001 | 0.01 | ||||||
| PD.3 a | −0.002 | |||||||
| ED.3 | −0.001 | |||||||
| PD | −0.003 | |||||||
| ED a | 0.02 | −0.061 | −0.006 | |||||
| LSI a | 0.004 | −0.024 | −0.002 | |||||
| CONTAG a | −0.056 | 0.037 | ||||||
| COHESION | −0.036 | 0.0228 | 0.022 |
| DO | CODMn | COD | BOD5 | NH3+-N | NO3− | TP | ||
|---|---|---|---|---|---|---|---|---|
| 6 km | AI.4 a | 0.01 | ||||||
| AI.5 a | 0.013 | −0.070 | −0.030 | |||||
| 9 km | PLAND.1 a | 0.003 | −0.015 | −0.008 | −0.003 | |||
| ED.1 a | 0.023 | −0.025 | −0.018 | −0.013 | ||||
| ED.3 | −0.003 | |||||||
| AI.3 | −0.002 | |||||||
| AI.4 a | −0.007 | 0.009 | 0.036 | 0.019 | 0.008 | |||
| 12 km | ED.1 a | −0.037 | −0.128 | −0.058 | ||||
| AI.2 | 0.0141 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Ren, X.; Yang, Z.; Long, H.; Xiao, J. Influence of Landscape Structures on Water Quality at Multiple Temporal and Spatial Scales: A Case Study of Wujiang River Watershed in Guizhou. Water 2019, 11, 159. https://doi.org/10.3390/w11010159
Xu G, Ren X, Yang Z, Long H, Xiao J. Influence of Landscape Structures on Water Quality at Multiple Temporal and Spatial Scales: A Case Study of Wujiang River Watershed in Guizhou. Water. 2019; 11(1):159. https://doi.org/10.3390/w11010159
Chicago/Turabian StyleXu, Guoyu, Xiaodong Ren, Zhenhua Yang, Haifei Long, and Jie Xiao. 2019. "Influence of Landscape Structures on Water Quality at Multiple Temporal and Spatial Scales: A Case Study of Wujiang River Watershed in Guizhou" Water 11, no. 1: 159. https://doi.org/10.3390/w11010159
APA StyleXu, G., Ren, X., Yang, Z., Long, H., & Xiao, J. (2019). Influence of Landscape Structures on Water Quality at Multiple Temporal and Spatial Scales: A Case Study of Wujiang River Watershed in Guizhou. Water, 11(1), 159. https://doi.org/10.3390/w11010159





