Pump-as-Turbine Selection Methodology for Energy Recovery in Irrigation Networks: Minimising the Payback Period
Abstract
:1. Introduction
2. Materials and Methods
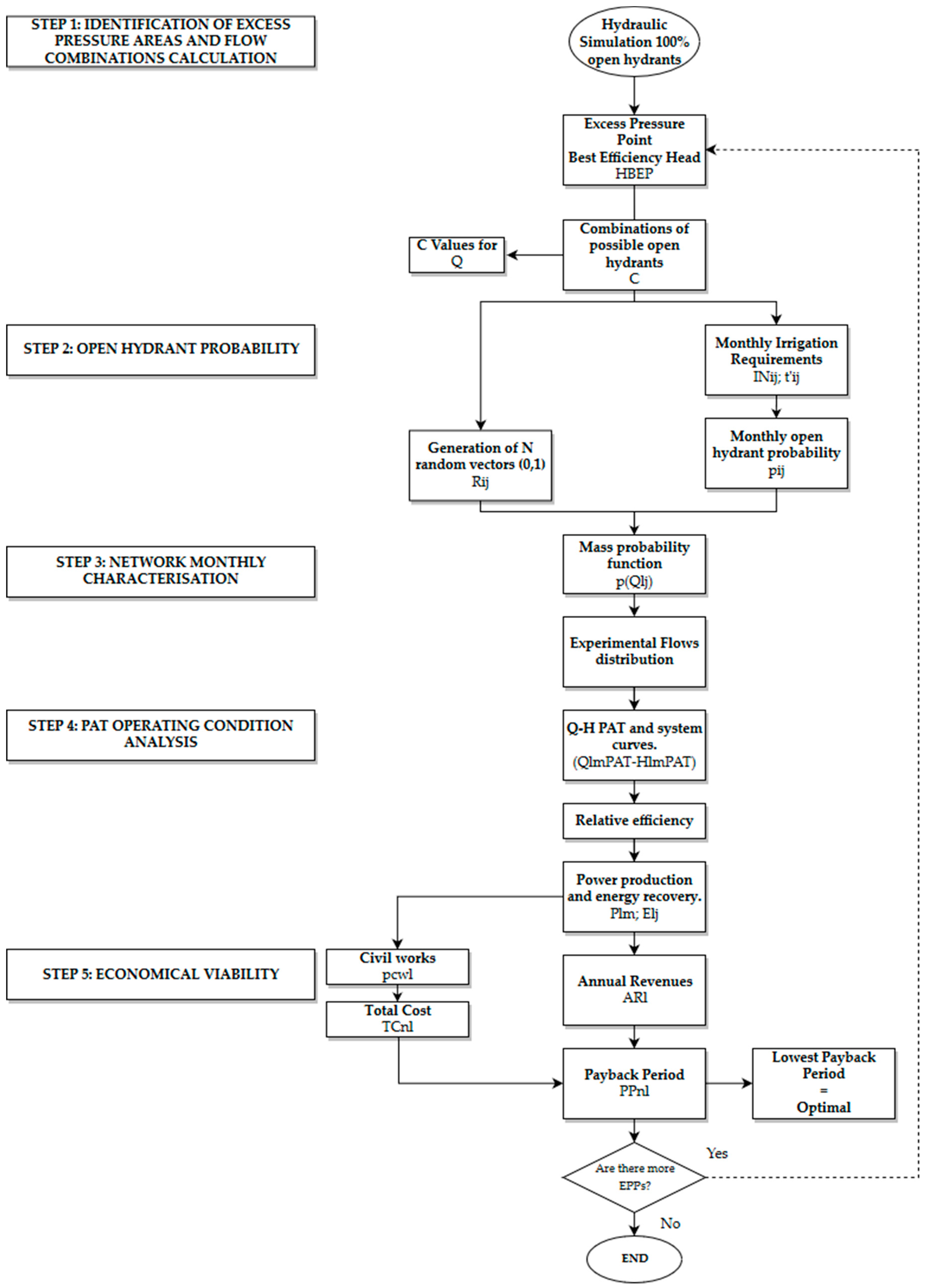
2.1. Methodology
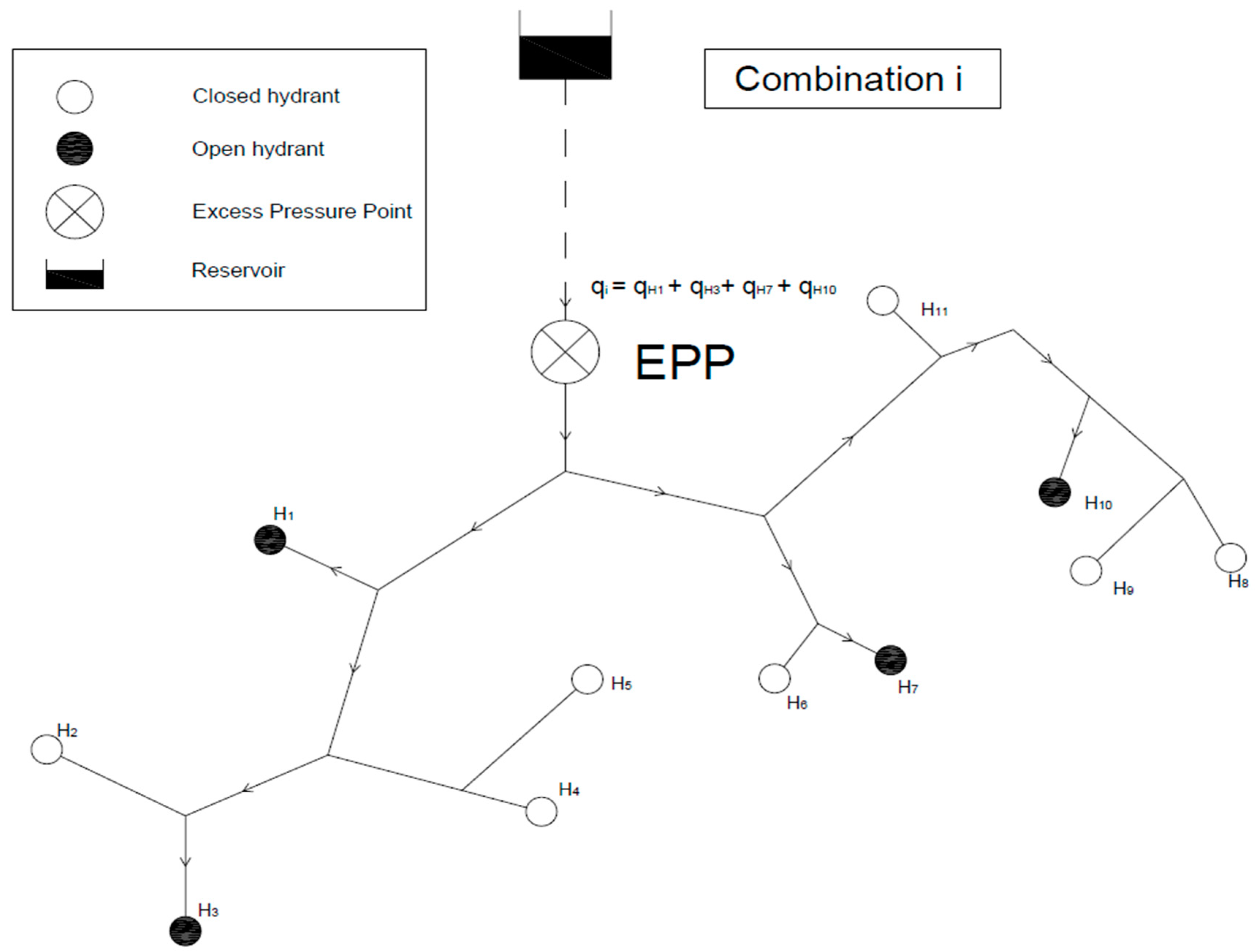
2.1.1. Location of Excess Pressure Points and Calculation of Downstream Open/Closed Hydrants Combinations
2.1.2. Open Hydrant Probability Calculation
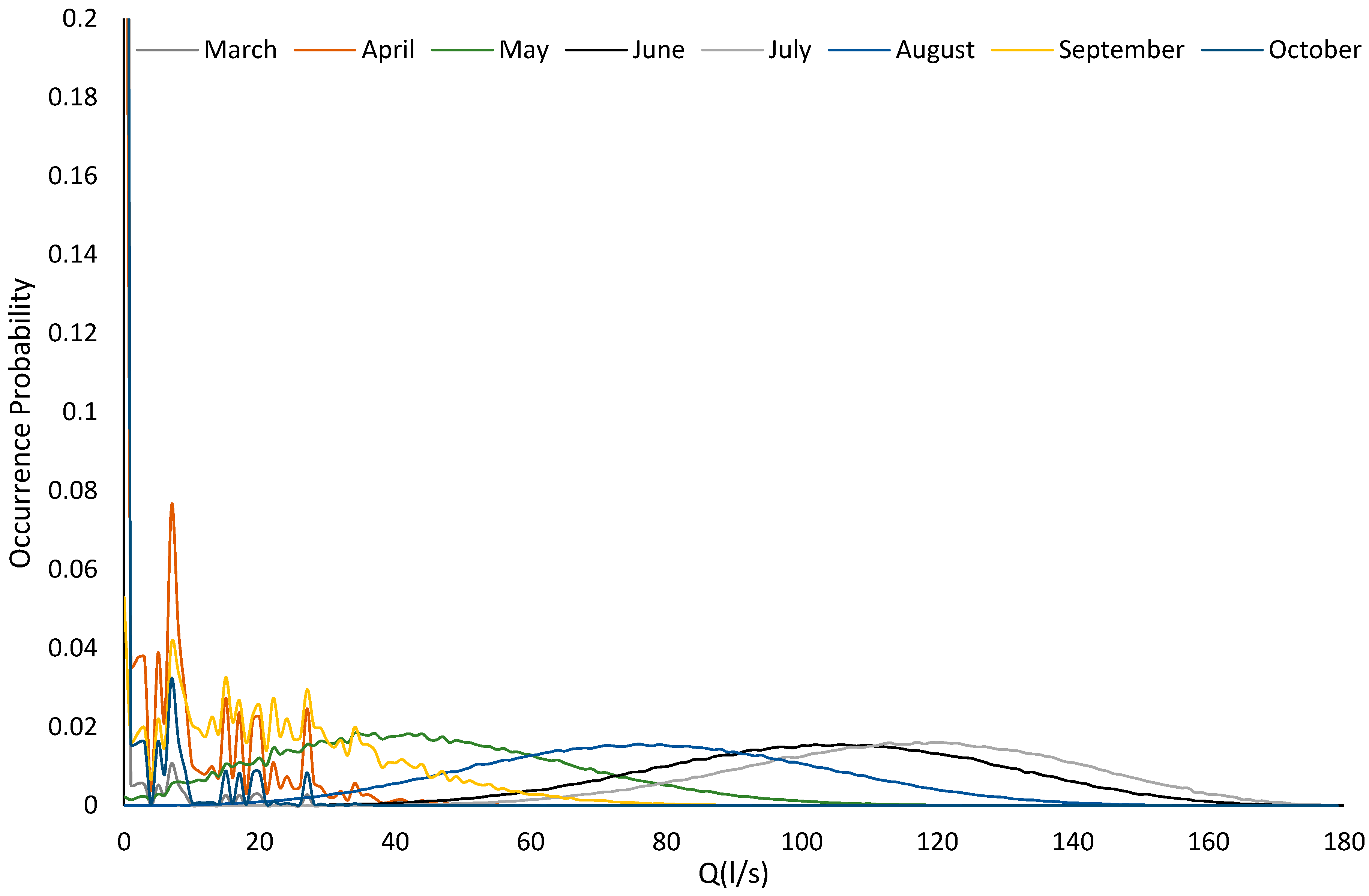
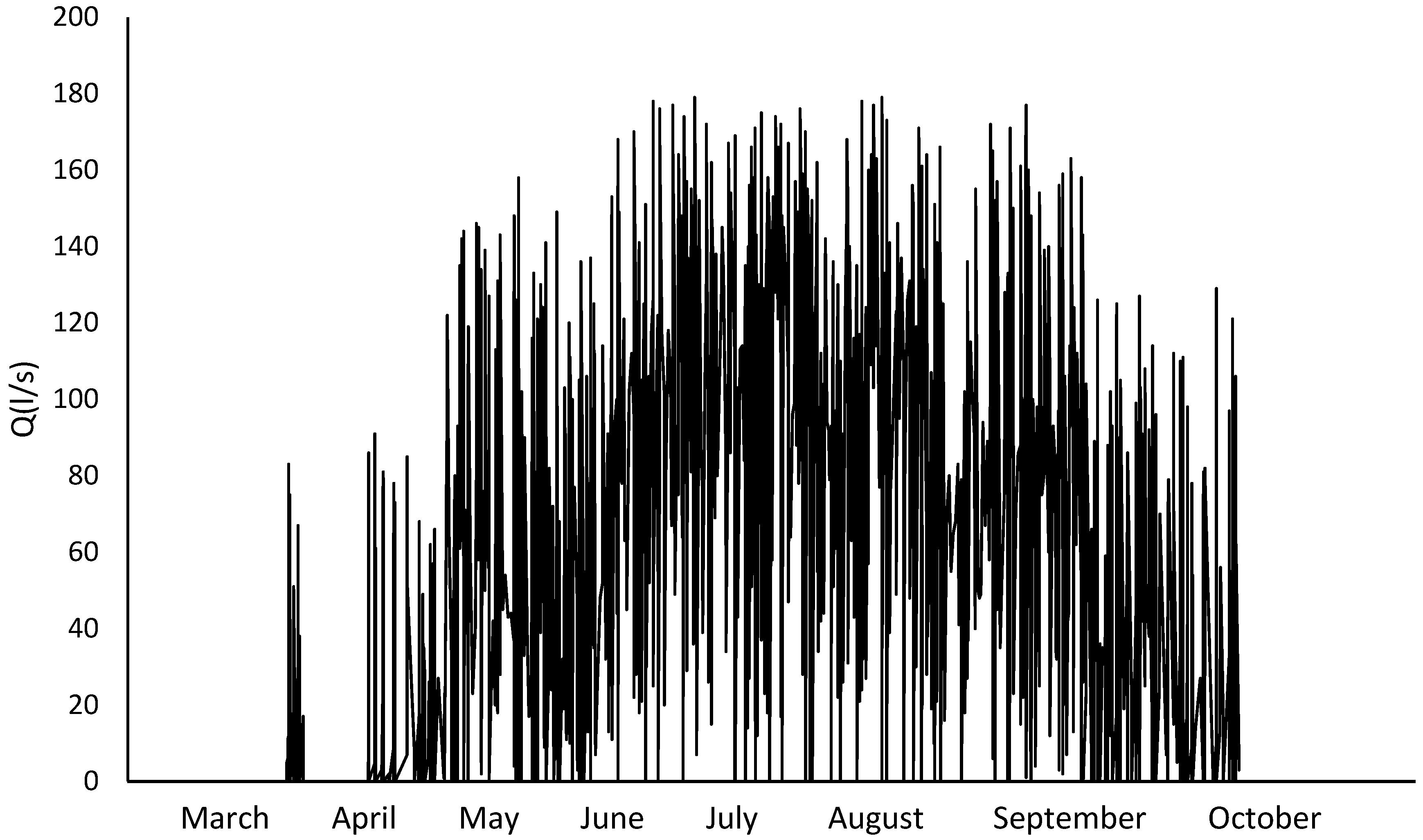
2.1.3. Monthly Characterisation of the Network: Mass Probability Function, Calculation
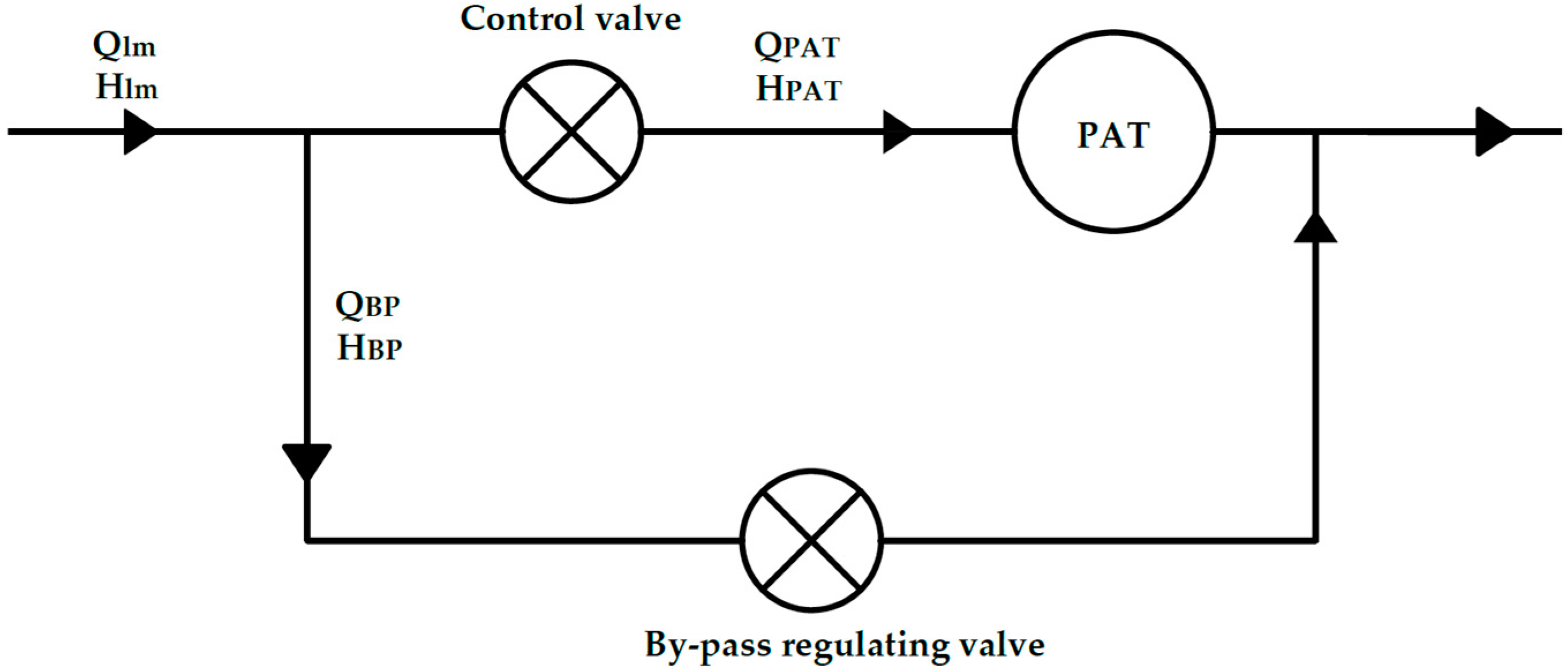
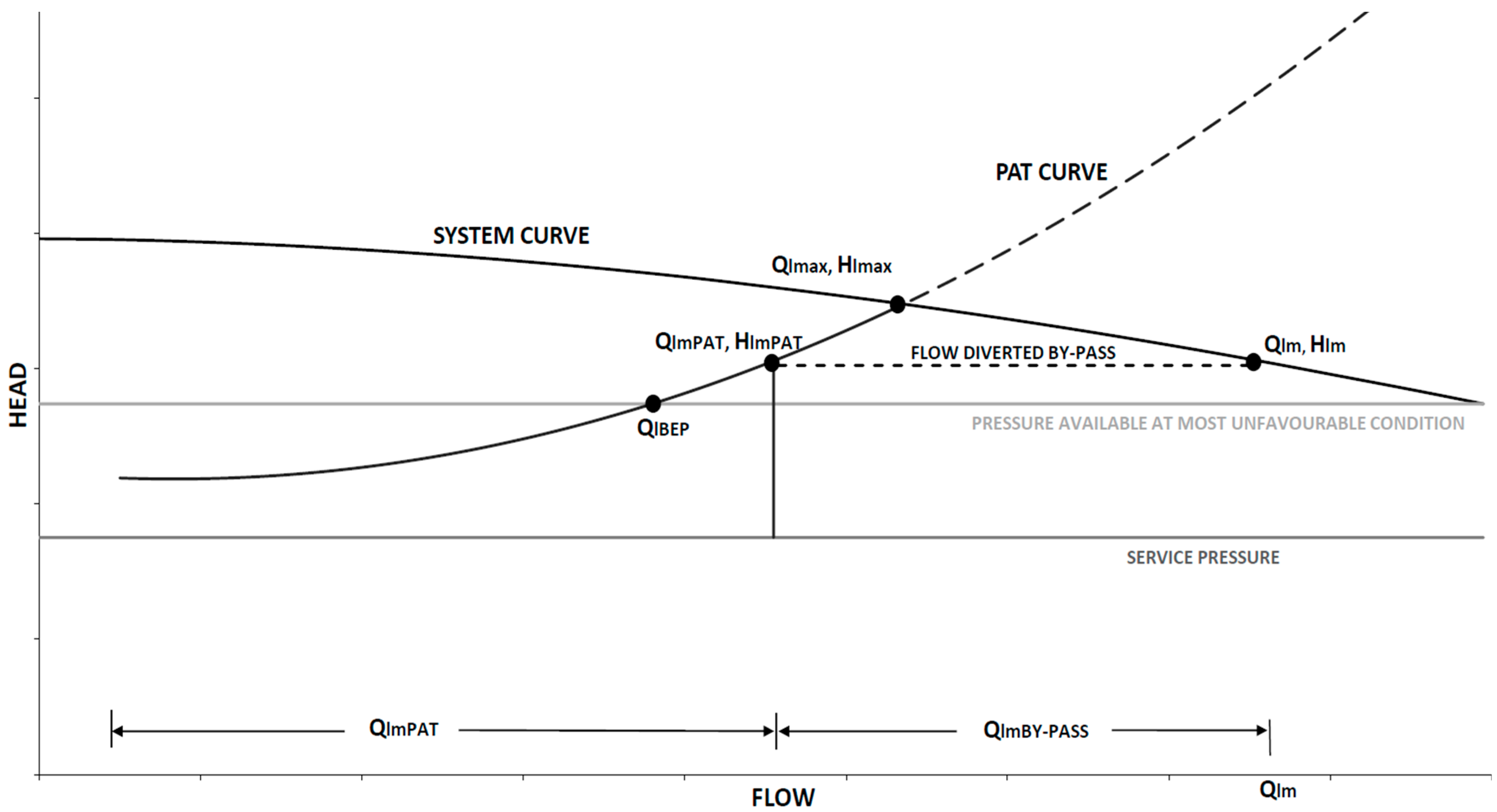
2.1.4. PAT Operating Conditions Analysis
- (i)
- (ii)
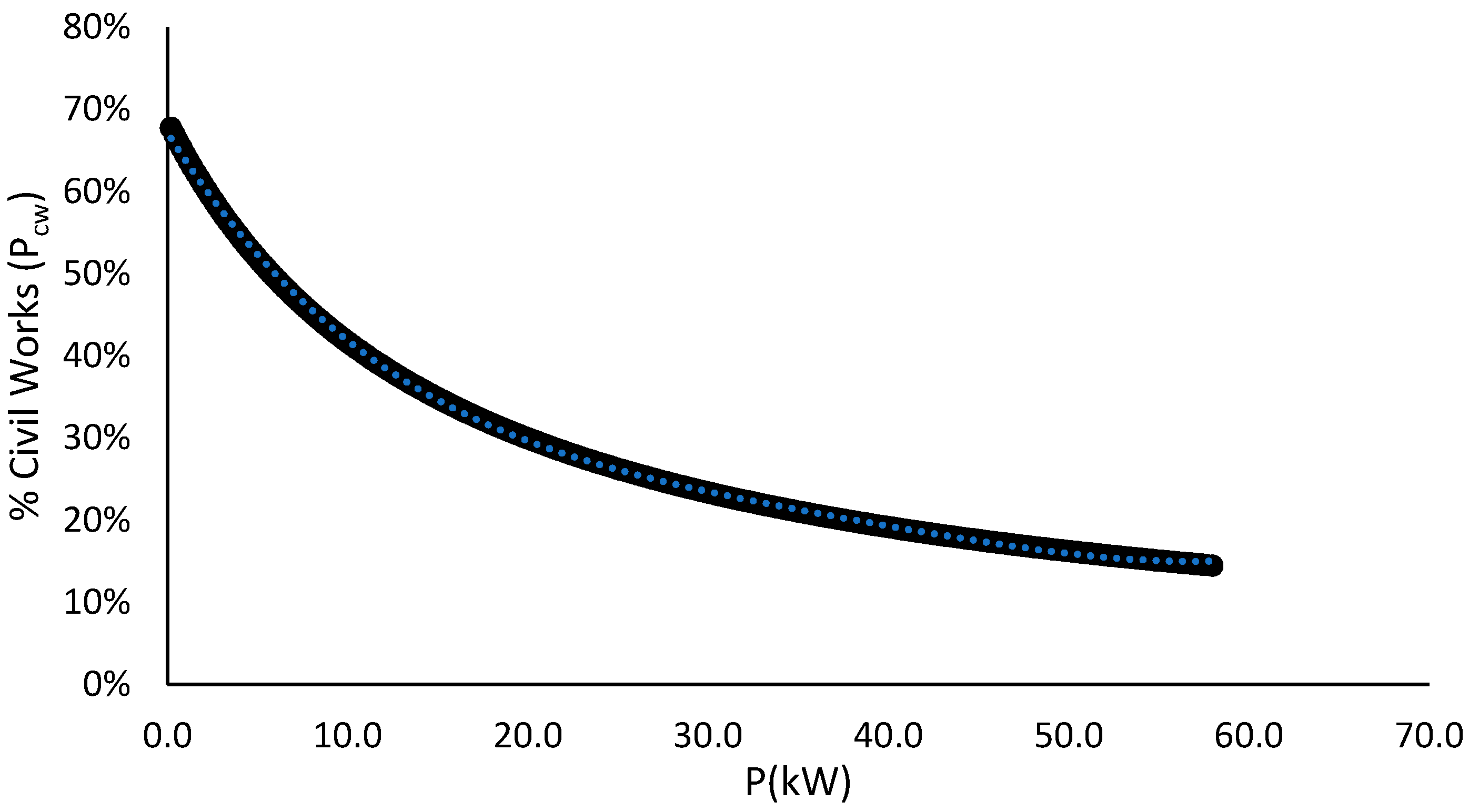
2.1.5. Economic Viability
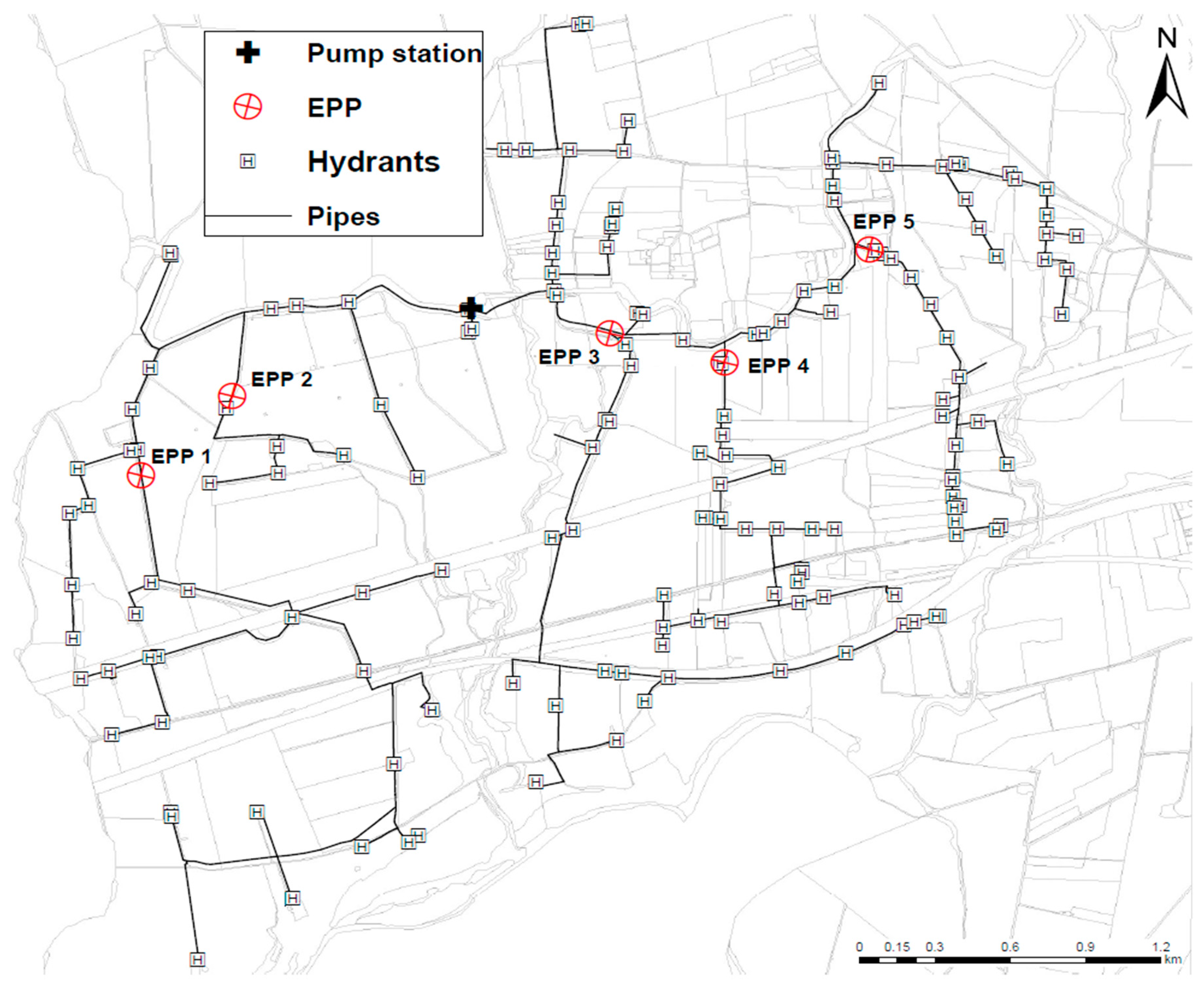
2.2. Study Area
3. Results
3.1. Location of Excess Pressure Areas and Calculation of Downstream Open/Closed Hydrant Combinations
3.2. Open Hydrant Probability Calculation
3.3. Monthly Characterisation of the Network: Mass Probability Function, Calculation
3.4. PAT Operating Conditions Analysis
3.5. Economic Viability
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Random scenario | |
| Annual revenues generated for the installation designed for the flow l | |
| Bernoulli Trial | |
| Combinations of downstream open hydrants | |
| Total cost for a PAT with n magnetic polar pairs generator installation for the flow l | |
| Monthly days | |
| Monthly experimental volumes | |
| Monthly energy recovered in the scenario l | |
| Best efficiency point head | |
| Head recovered for flow m in scenario l | |
| Monthly water requirements per hydrant | |
| Number of simulations | |
| Number of downstream hydrants | |
| Monthly number of repeating times of the flow value l | |
| Monthly open hydrant probability | |
| Power for the scenario produced for the inlet flow m in the scenario l | |
| Mass probability function | |
| Monthly mass probability function of the flow value l | |
| Percentage of civil works in the total installation cost | |
| Payback period for an PAT installation design for the flow l with a generator with n polar pairs | |
| Design flow of the network | |
| Maximum flow running in the pipe EPP studied | |
| Value of the flow in scenario l | |
| Random variable Flow | |
| BEP flow value in scenario l | |
| Flow running through the PAT when m flow is demanded in the scenario l | |
| Monthly random vector [0-1] | |
| Monthly energy tariff | |
| Monthly hydrant irrigation time required | |
| Monthly hydrant water availability | |
| Maximum PAT performance | |
| Relative performance of the flow value m in the PAT designed for flow value l | |
| Water specific weight | |
| Sub-indexes | |
| Hydrant sub-index | |
| Month sub-index | |
| Flow values for main scenarios sub-index | |
| Flow values for relative scenarios sub-index | |
| Generator magnetic polar pair sub-index | |
Appendix A
| Civil Works | |||||
|---|---|---|---|---|---|
| CW.1 | Manual trench excavation (20 × 2 × 1.5 m) | m3 | 76 | 49.45 | 3758.20 |
| CW.2 | Bypass: Supply + fixing 300 mm ductile iron pipes | lm | 18 | 96.35 | 1734.30 |
| CW.3 | Reinforced concrete slab 10 cm | m2 | 8 | €16.2 | €129.8 |
| CW.4 | Protection House: Concrete blocks (40 × 20 × 10 cm) supply and fixing (4 × 2 × 2.5 m) | m2 | 30 | €41.78 | €1253.40 |
| CW.5 | Manual backfilling: Same material excavation | m3 | 76 | €3.54 | €269.04 |
| Total | €7144.78 | ||||
References
- Nogueira, M.; Perrella, J. Energy and hydraulic efficiency in conventional water supply systems. Renew. Sustain. Energy Rev. 2014, 30, 701–714. [Google Scholar] [CrossRef]
- Copeland, C.; Carter, N.T. Energy-Water Nexus: The Water Sector’s Energy Use; Congressional Research Service: Washington, DC, USA, 2017.
- Lofman, D.; Petersen, M.; Bower, A. Water, Energy and Environment Nexus: The California Experience. Int. J. Water Resour. Dev. 2002, 18, 73–85. [Google Scholar] [CrossRef]
- Rodríguez-Díaz, J.A.; Pérez-Urrestarazu, L.; Camacho-Poyato, E.; Montesinos, P. The paradox of irrigation scheme modernization: More efficient water use linked to higher energy demand. Span. J. Agric. Res. 2011, 9, 1000–1008. [Google Scholar] [CrossRef]
- Navarro Navajas, J.M.; Montesinos, P.; Camacho-Poyato, E.; Rodríguez-Díaz, J.A. Impacts of irrigation network sectoring as an energy saving measure on olive grove production. J. Environ. Manag. 2012, 111, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Moreno, M.; Corcoles, J.; Tarjuelo, J.; Ortega, J. Energy efficiency of pressurised irrigation networks managed on-demand and under a rotation schedule. Biosyst. Eng. 2010, 107, 349–363. [Google Scholar] [CrossRef]
- Fernández García, I.; Rodríguez Díaz, J.A.; Camacho Poyato, E.; Montesinos, P. Optimal operation of pressurized irrigation networks with several supply sources. Water Resour. Manag. 2013, 27, 2855–2869. [Google Scholar] [CrossRef]
- Pardo, M.A.; Manzano, J.; Cabrera, E.; García-Serra, J. Energy audit of irrigation networks. Biosyst. Eng. 2013, 115, 89–101. [Google Scholar] [CrossRef]
- Jimenez-Bello, M.A.; Royuela, A.; Manzano, J.; Prats, A.G.; Martínez-Alzamora, F. Methodology to improve water and energy use by proper irrigation scheduling in pressurised networks. Agric. Water Manag. 2015, 149, 91–101. [Google Scholar] [CrossRef]
- Mérida García, A.; Fernández García, I.; Camacho Poyato, E.; Montesinos Barrios, P.; Rodríguez Díaz, J.A. Coupling irrigation scheduling with solar energy production in a smart irrigation management system. J. Clean. Prod. 2018, 175, 670–682. [Google Scholar] [CrossRef]
- Power, C.; Coughlan, P.; McNabola, A. The applicability of hydropower technology in wastewater treatment plants. In Proceedings of the International Water Association World Congress on Water, Climate and Energy, Dublin, Ireland, 13–18 May 2012. [Google Scholar]
- Carravetta, A.; del Giudice, G.; Fecarotta, O.; Ramos, H. Energy production in water distribution networks: A PAT design strategy. Water Res. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Carravetta, A.; del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 1, 411–424. [Google Scholar] [CrossRef]
- Corcoran, L.; Coughlan, P.; McNabola, A. Energy recovery potential using micro hydropower in water supply networks in the UK & Ireland. Water Sci. Technol. 2013, 13, 552–560. [Google Scholar] [CrossRef]
- Ramos, H.M.; Borga, A.; Simão, M. New design solutions for low-power energy production in water pipe systems. Water Sci. Eng. 2009, 4, 69–84. [Google Scholar]
- Carravetta, A.; Fecarotta, O.; Del Giudice, G.; Ramos, H. Energy recovery in water systems by PATs: A comparisons among the different installation schemes. Procedia Eng. 2014, 70, 275–284. [Google Scholar] [CrossRef]
- Power, C.; McNabola, A.; Coughlan, P. Development of an evaluation method for hydropower energy recovery in wastewater treatment plants: Case studies in Ireland and the UK. Sustain. Energy Technol. Assess. 2014, 7, 166–177. [Google Scholar] [CrossRef]
- Power, C.; McNabola, A.; Coughlan, P. Micro-hydropower energy recovery at waste-water treatment plants: Turbine selection and optimization. J. Energy Eng. 2016, 1, 143. [Google Scholar] [CrossRef]
- Novara, D.; Carravetta, A.; McNabola, A.; Ramos, H.M. A cost model for Pumps As Turbines in run-of-river and in-pipe energy recovery micro-hydropower applications. J. Water Res. Plan. Manag. 2019. under review. [Google Scholar]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower potential in water distribution networks: Pressure control by PATs. Water Resour. Manag. 2015, 29, 699–714. [Google Scholar] [CrossRef]
- Lydon, T.; Coughlan, P.; McNabola, A. Pump-as-turbine: Characterization as an energy recovery device for the water distribution network. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- García Morillo, J.; McNabola, A.; Camacho, E.; Montesinos, P.; Rodríguez Díaz, J.A. Hydropower energy recovery in pressurized irrigation networks: A case of study of an Irrigation District in the South of Spain. Agric. Water Manag. 2018, 204, 17–27. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Modelling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study. Water 2016, 8, 234. [Google Scholar] [CrossRef]
- Perez-Sanchez, M.; Sanchez-Romero, F.J.; Ramos, H.M.; Lopez-Jimenez, P.A. Optimization Strategy for Improving the Energy Efficiency of Irrigation Systems by Micro Hydropower: Practical Application. Water 2017, 9, 799. [Google Scholar] [CrossRef]
- Tarragó, E.F.; Ramos, H. Micro-Hydro Solutions in Alqueva Multipurpose Project (AMP) towards Water-Energy-Environmental Efficiency Improvements. Bachelor’s Thesis, Universidade de Lisboa, Lisboa, Portugal, 2015. [Google Scholar]
- Rodríguez-Díaz, J.A.; Camacho-Poyato, E.; López-Luque, R. Model to Forecast Maximum Flows in On-Demand Irrigation Distribution Networks. J. Irrig. Drain. Eng. 2007, 133, 222–231. [Google Scholar] [CrossRef]
- Clément, R. Calcul des débits das les réseaux d’irigation fonctionant a la demande. La Houille Blanche 1966, 20, 553–576. [Google Scholar] [CrossRef]
- Monserrat, J.; Poch, R.; Colomer, M.A.; Mora, F. Analysis of Clément’s first formula for irrigation distribution networks. J. Irrig. Drain. Eng. 2004, 130, 99–105. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Lamaddalena, N.; Sagardoy, J.A. Performance Analysis of On-demand Pressurized Irrigation Systems; Irrigation and Drainage Paper 59; FAO: Rome, Italy, 2000. [Google Scholar]
- Olkin, I.; Gleser, L.J.; Derman, C. Probability Models and Applications, 1st ed.; Macmillan: New York, NY, USA, 1980. [Google Scholar]
- Barbarelli, S.; Amelio, M.; Florio, G. Experimental activity at test rig validating correlations to select pumps running as turbines in microhydro plants. Energy Convers. Manag. 2017, 149, 781–797. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 290, 800–807. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. A model for the extrapolation of the characteristic curves of Pumps as Turbines from a datum Best Efficiency Point. Energy Convers. Manag. 2018, 174, 1–7. [Google Scholar] [CrossRef]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Messineo, A.; Milici, B.; Napoli, E.; Notaro, V.; Puleo, V.; Scopa, A. Energy recovery in water distribution networks. Implementation of pumps as turbine in a dynamic numerical model. Proc. Eng. 2014, 70, 439–448. [Google Scholar] [CrossRef]
- Fernández García, I.; Rodríguez Díaz, J.A.; Camacho Poyato, E.; Montesinos, P.; Berbel, J. Effects of modernization and medium-term perspectives on water and energy use in irrigation districts. Agric. Syst. 2014, 131, 56–63. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET. Users Manual; US Environmental Protection Agency (EPA): Cincinnati, OH, USA, 2000.
- LUMIOS. Available online: https://www.esios.ree.es/es/lumios?rate=rate1&start_date=03-09-2018T14:02&end_date=04-09-2018T14:02 (accessed on 7 May 2018).
- Lydon, T.; Coughlan, P.; McNabola, A. Pressure management and energy recovery in water distribution networks: Development of design and selection methodologies using three pump-as-turbine case studies. Renew. Energy 2017, 114, 1038–1050. [Google Scholar] [CrossRef]
- CYPE Ingenieros, S.A. Generador de Precios de la Construcción. Spain. Available online: http://www.generadordeprecios.info/ (accessed on 15 April 2018).
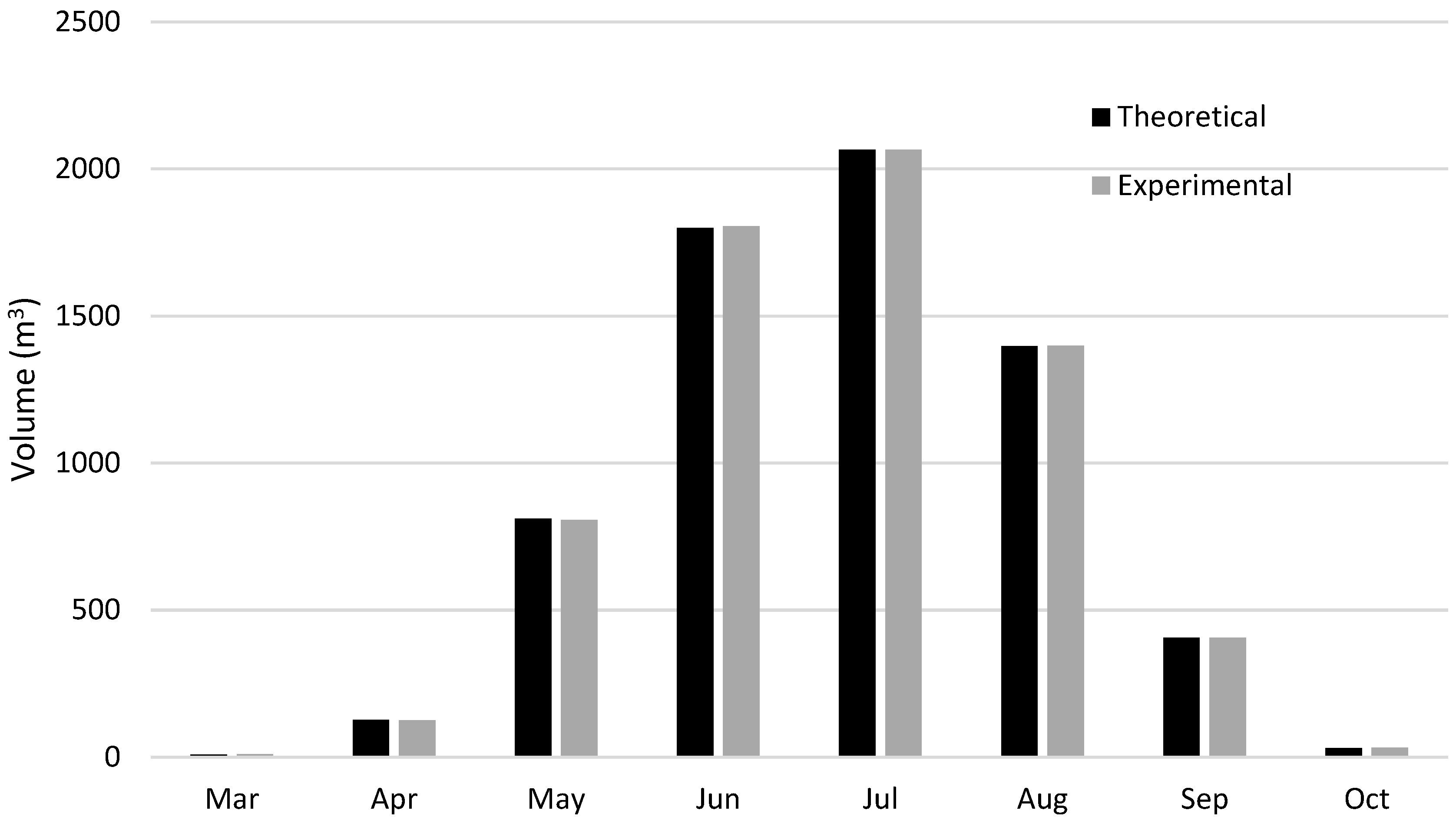
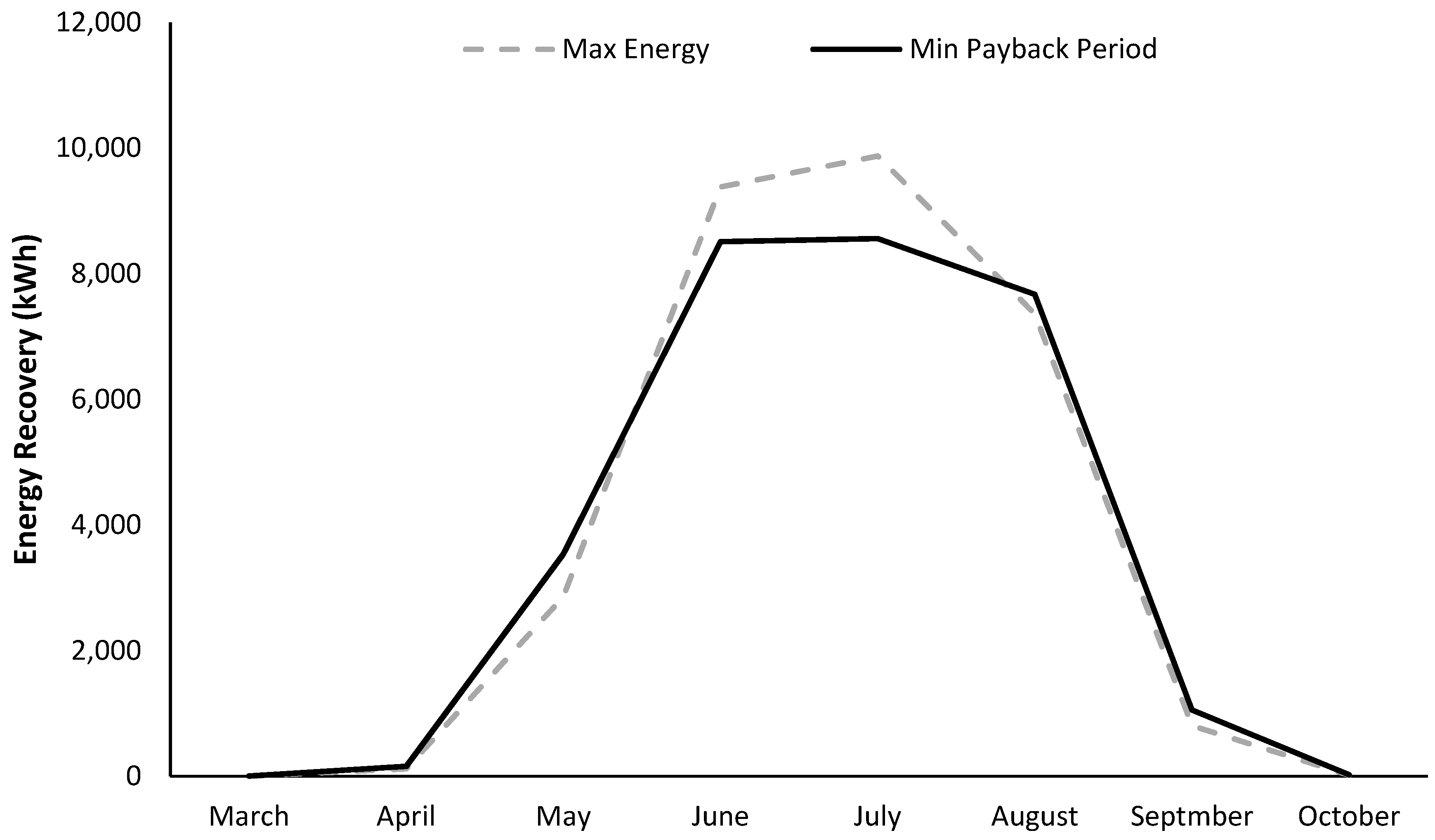
| Crop | Surface Percentage | Monthly Open Hydrant Probability (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| March | April | May | June | July | August | September | October | ||
| Citrus | 56 | 0.3 | 4.1 | 14.7 | 25.5 | 28.1 | 24.4 | 13.0 | 1.0 |
| Maize | 32 | 0.0 | 0.0 | 7.6 | 23.8 | 26.7 | 14.6 | 0.0 | 0.0 |
| Cotton | 9 | 0.0 | 0.0 | 1.8 | 6.0 | 7.1 | 4.2 | 0.0 | 0.0 |
| Sunflower | 3 | 0.0 | 0.0 | 1.1 | 2.5 | 2.4 | 0.3 | 0.0 | 0.0 |
| Total (%) | 100 | 0.3 | 4.1 | 25.2 | 57.8 | 64.3 | 43.5 | 13.0 | 1.0 |
| EPP | Downstream Hydrants | Flow Values | Q Range (l/s) | Bernoulli Trials | Total Simulations |
|---|---|---|---|---|---|
| 1 | 23 | 8,388,608 | 0–297 | 17,000,000 | 204,000,000 |
| 2 | 5 | 32 | 0–82 | 15,000 | 180,000 |
| 3 | 21 | 2,097,152 | 0–179 | 5,000,000 | 60,000,000 |
| 4 | 26 | 67,108,864 | 0–101 | 140,000,000 | 1,680,000,000 |
| 5 | 21 | 2,097,152 | 0–75 | 5,000,000 | 60,000,000 |
| EPP | Optimal Scenario | BEP Flow (l/s) | BEP Power (kW) | Polar Pairs | Cost (€) | Energy (MWh) | PP (Years) |
|---|---|---|---|---|---|---|---|
| 1 | 2,743,236 | 88 | 9.1 | 1 | 16,438 | 40.8 | 3.5 |
| 2 | 13 | 39 | 2.9 | 2 | 12,339 | 6.9 | 15.8 |
| 3 | 631,784 | 54 | 5.8 | 2 | 14,207 | 29.5 | 4.2 |
| 4 | 30,122,847 | 46 | 4.5 | 2 | 13,352 | 11.1 | 10.6 |
| 5 | 1,051,433 | 36 | 2.8 | 2 | 12,278 | 5.6 | 19.4 |
| Total | - | - | 25.1 | - | 68,614 | 93.9 | 6.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crespo Chacón, M.; Rodríguez Díaz, J.A.; García Morillo, J.; McNabola, A. Pump-as-Turbine Selection Methodology for Energy Recovery in Irrigation Networks: Minimising the Payback Period. Water 2019, 11, 149. https://doi.org/10.3390/w11010149
Crespo Chacón M, Rodríguez Díaz JA, García Morillo J, McNabola A. Pump-as-Turbine Selection Methodology for Energy Recovery in Irrigation Networks: Minimising the Payback Period. Water. 2019; 11(1):149. https://doi.org/10.3390/w11010149
Chicago/Turabian StyleCrespo Chacón, Miguel, Juan Antonio Rodríguez Díaz, Jorge García Morillo, and Aonghus McNabola. 2019. "Pump-as-Turbine Selection Methodology for Energy Recovery in Irrigation Networks: Minimising the Payback Period" Water 11, no. 1: 149. https://doi.org/10.3390/w11010149
APA StyleCrespo Chacón, M., Rodríguez Díaz, J. A., García Morillo, J., & McNabola, A. (2019). Pump-as-Turbine Selection Methodology for Energy Recovery in Irrigation Networks: Minimising the Payback Period. Water, 11(1), 149. https://doi.org/10.3390/w11010149








