Simulation of Flow and Agricultural Non-Point Source Pollutant Transport in a Tibetan Plateau Irrigation District
Abstract
1. Introduction
2. Materials and Methods
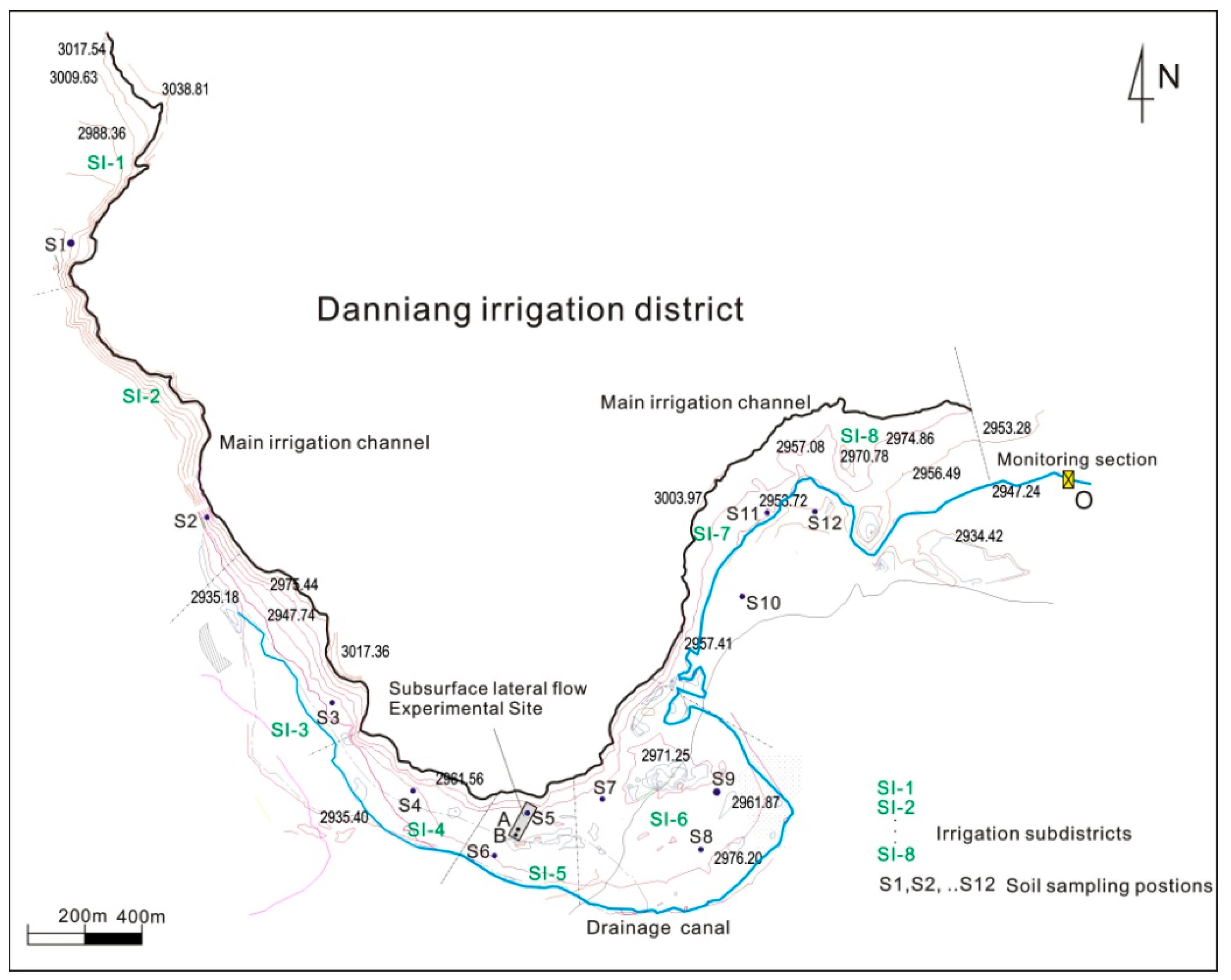
2.1. Study Area
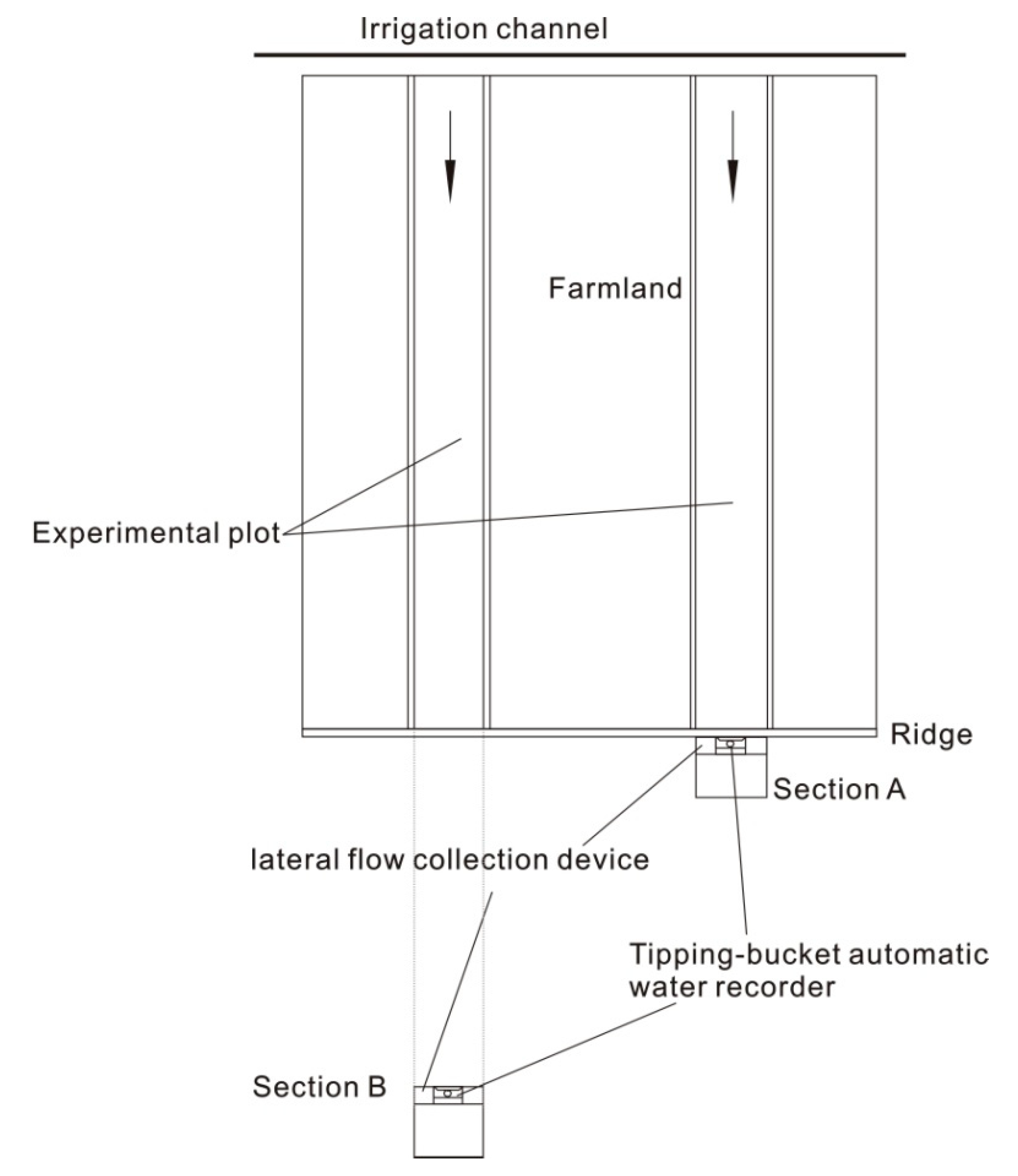
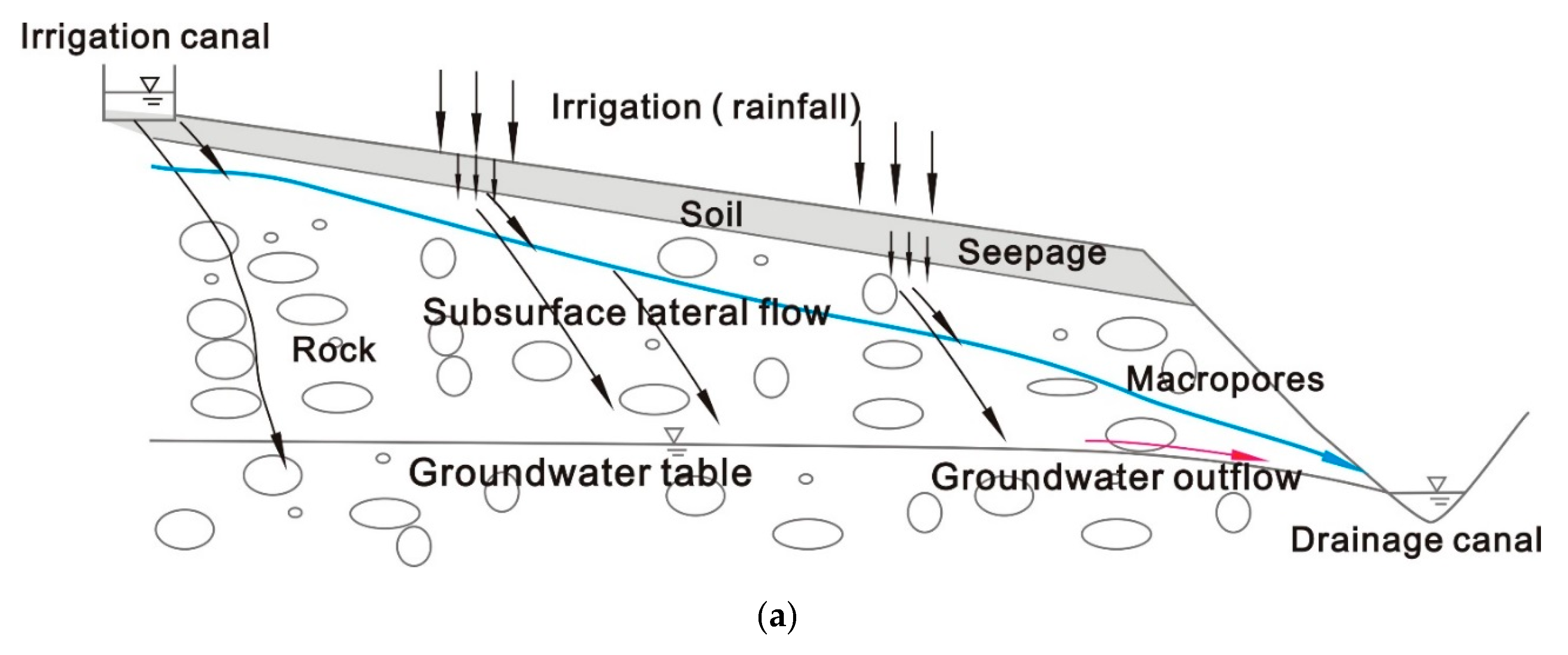
2.2. Monitoring Hydrological and ANPS Pollution Transport and Transformation Processes in the Soil and Rock
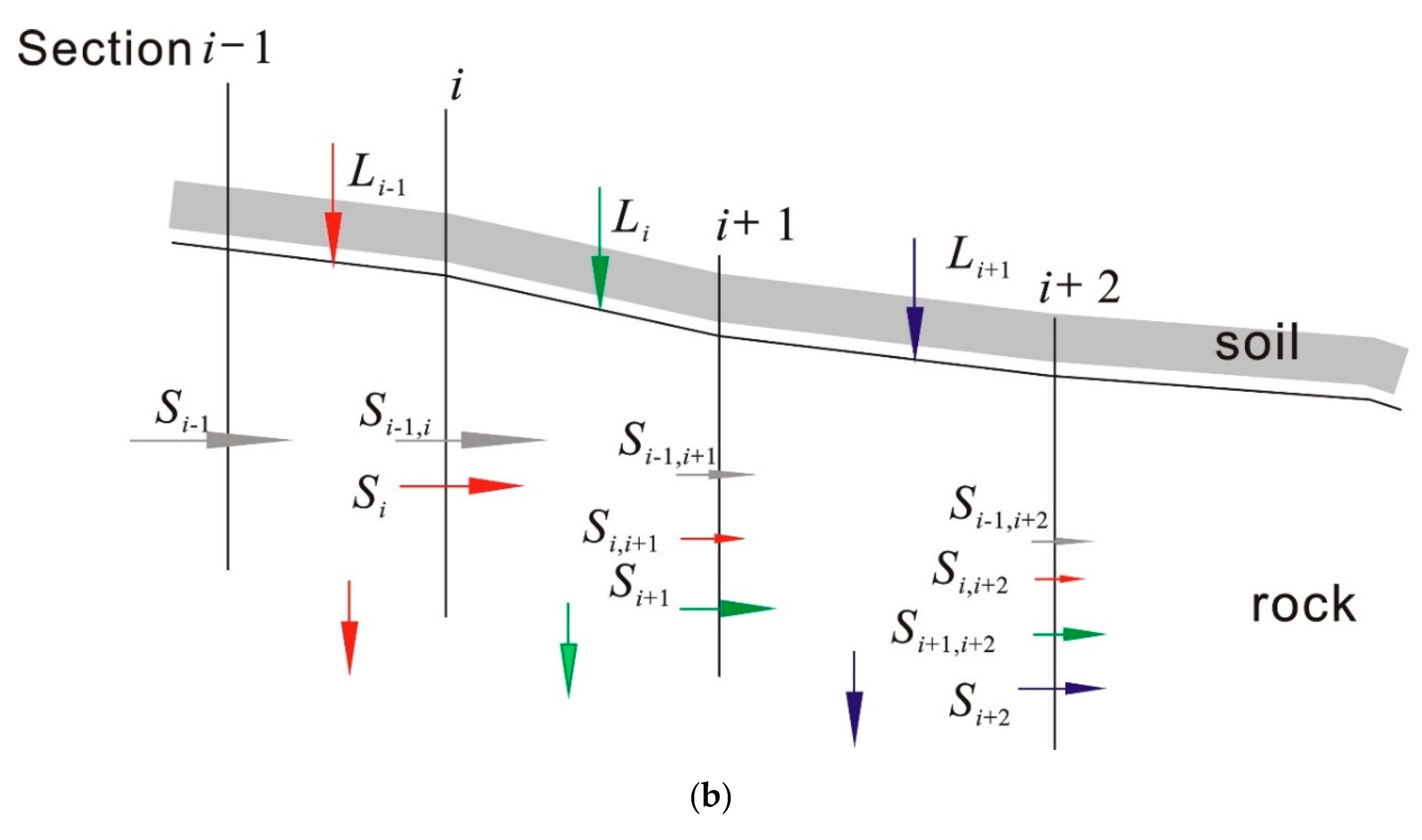
2.3. Simulation of Hydrological and ANPS Pollution Transport Processes in the Plateau Irrigation District
2.4. Calibration of Model Parameters
2.5. Sobol’s Sensitivity Analysis
3. Results
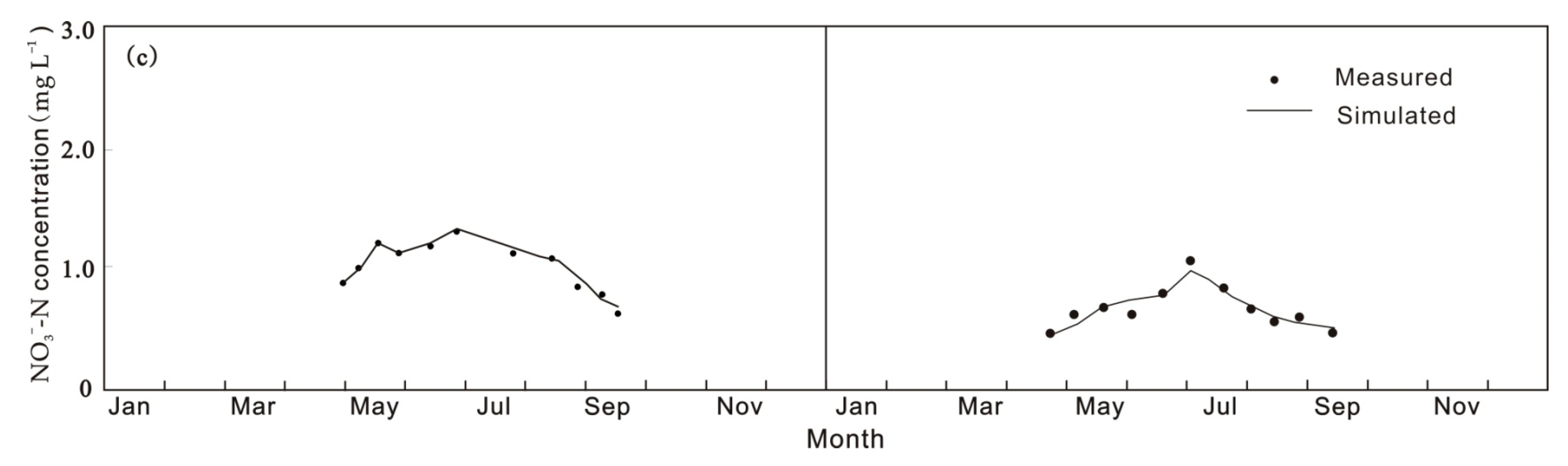
3.1. Characterization of Flow and NH4+-N and NO3−-N Transport
3.2. Simulation of ANPS Pollutant Transport and Transformation Processes
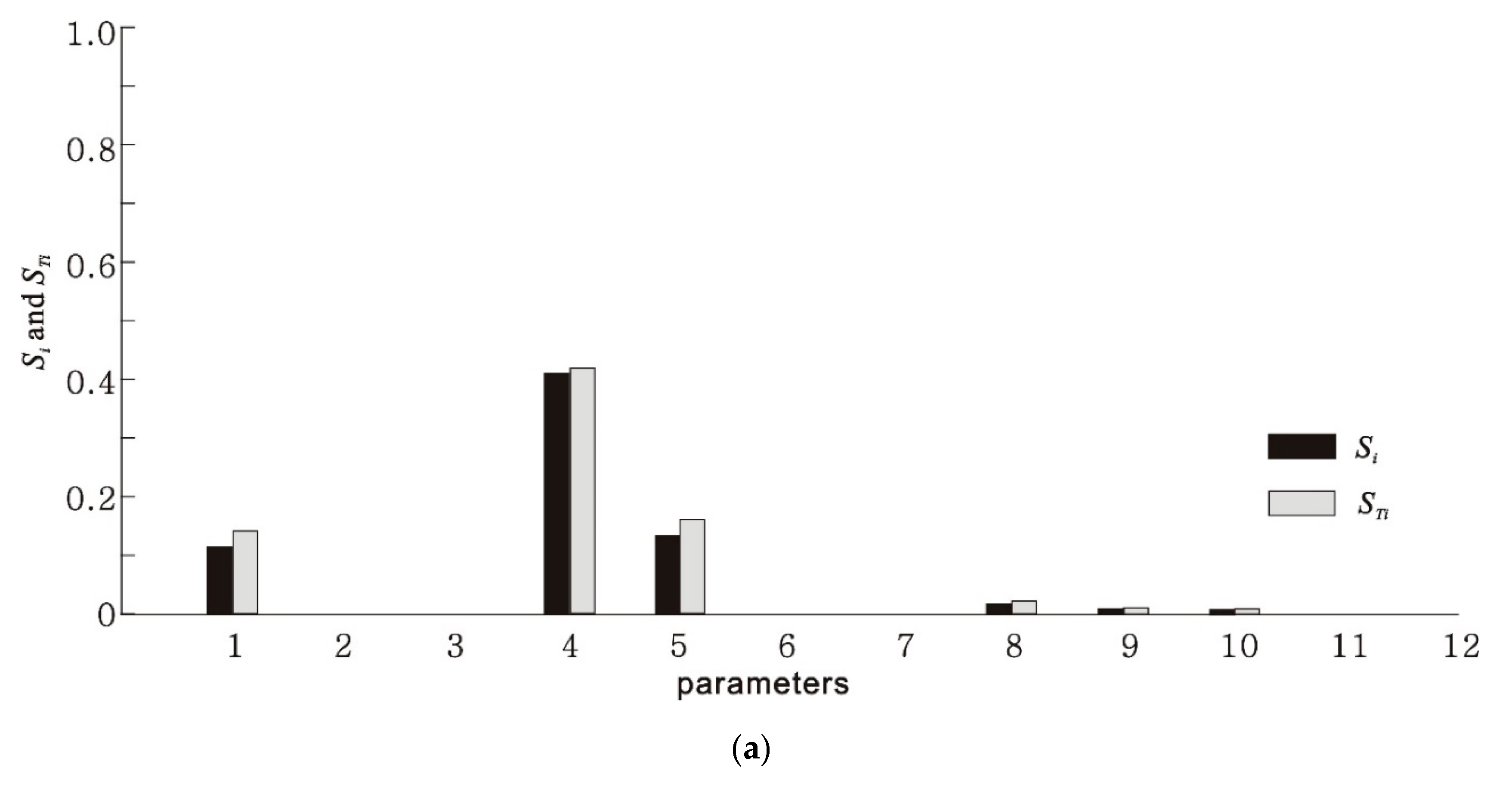
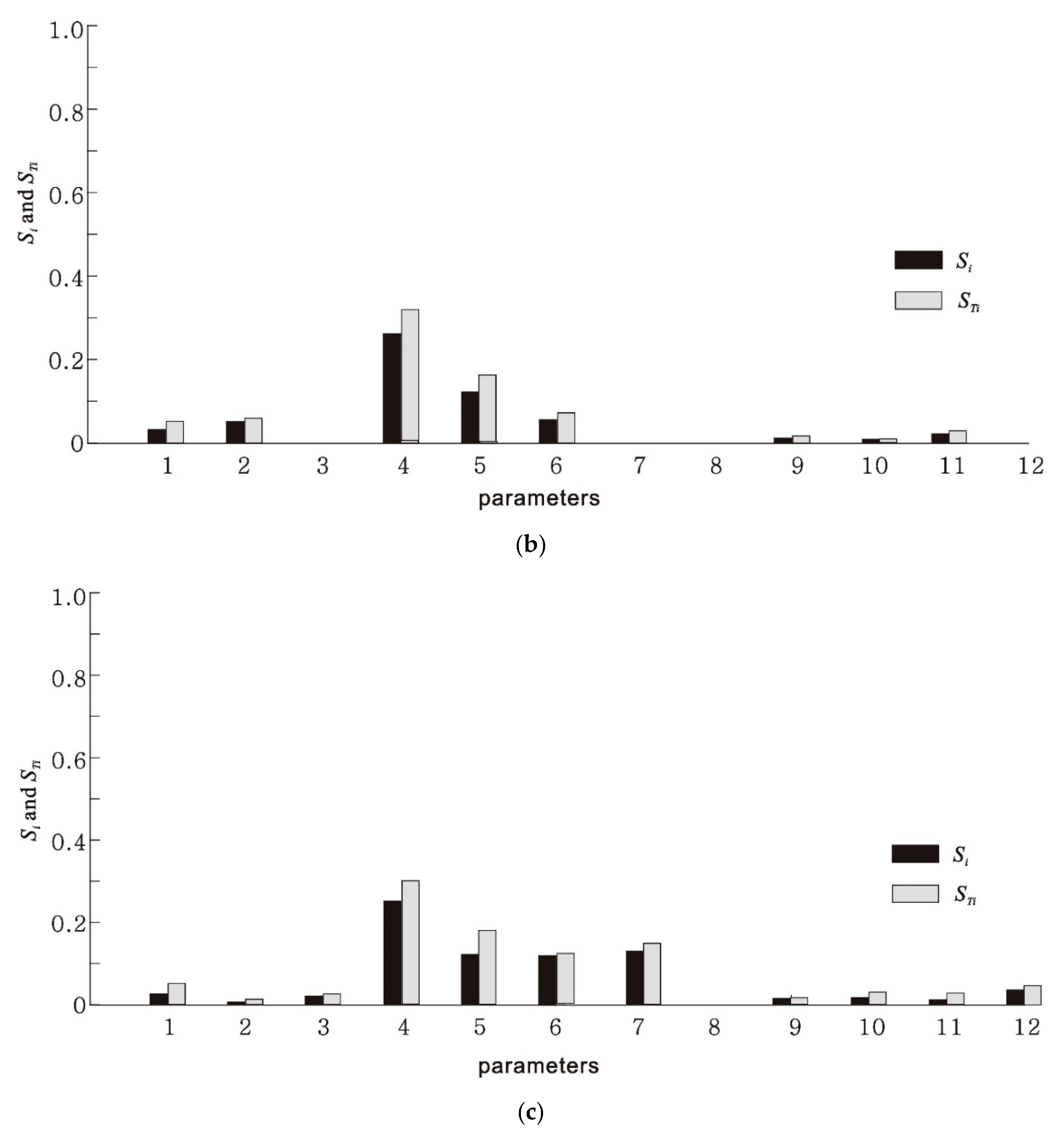
3.3. Sensitivity Evaluation of Model Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ibrikci, H.; Cetin, M.; Karnez, E.; Flügel, W.A.; Ryan, J. Irrigation-induced nitrate losses assessed in a Mediterranean irrigation district. Agric. Water Manag. 2015, 148, 223–231. [Google Scholar] [CrossRef]
- Jiménez-Aguirre, M.T.; Isidoro, D. Hydrosaline Balance in and Nitrogen Loads from an irrigation district before and after modernization. Agric. Water Manag. 2018, 208, 163–175. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, R.; Chen, H. Drainage-process analyses for agricultural non-point-source pollution from irrigated paddy systems. J. Irrig. Drain. Eng.-ASCE 2014, 15, 1943–4774. [Google Scholar] [CrossRef]
- Ogden, F.L.; Julien, P.Y. CASC2D: A two-dimensional, physically based, Hortonian hydrologic model. In Mathematical Models of Small Watershed Hydrology and Applications; Singh, V.P., Frevert, D.K., Eds.; Water Resources Publications: Highlands Ranch, CO, USA, 2002; Chapter 4; pp. 69–112. [Google Scholar]
- Borah, D.K.; Xia, R.J.; Bera, M. DWSM—A Dynamic Watershed Simulation Model. In Mathematical Models of Small Watershed Hydrology & Applications; Water Resources Publications: Highlands Ranch, CO, USA, 2002; pp. 113–166. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual Version 2000; GSWRL Report 02-02; BRC Report 02-06; TR-192; Texas Water Resources Institute: College Station, TX, USA, 2002. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Čerkasova, N.; Umgiesser, G.; Ertürk, A. Development of a hydrology and water quality model for a large transboundary river watershed to investigate the impacts of climate change—A SWAT application. Ecol. Eng. 2018, 124, 99–115. [Google Scholar] [CrossRef]
- Xie, X.; Cui, Y. Development and test of SWAT for modeling hydrological processes in irrigation districts with paddy rice. J. Hydrol. 2011, 396, 61–71. [Google Scholar] [CrossRef]
- Lee, S.B.; Yoon, C.G.; Jung, K.W. Comparative evaluation of runoff and water quality using HSPF and SWMM. Water Sci. Technol. 2010, 62, 1401–1409. [Google Scholar] [CrossRef]
- Chahinian, N.; Tournoud, M.G.; Perrin, J.L. Flow and nutrient transport in intermittent rivers: A modelling case-study on the Vene River using SWAT 2005. Hydrol. Sci. J. 2011, 192, 143–159. [Google Scholar] [CrossRef]
- Lucadamo, L.; De Filippis, A.; Mezzotero, A.; Vizza, S.; Gallo, L. Biological and chemical monitoring of some major Calabrian (Italy) Rivers. Environ. Monit. Assess. 2007, 146, 453–471. [Google Scholar] [CrossRef]
- Howarth, R.W. Coastal nitrogen pollution: A review of sources and trends globally and regionally. Harmful Algae 2008, 8, 14–20. [Google Scholar] [CrossRef]
- Kroeze, C.; Bouwman, L.; Seitzinger, S. Modeling global nutrient export from watersheds. Curr. Opin. Environ. Sustain. 2012, 4, 195–202. [Google Scholar] [CrossRef]
- Zhou, T.; Wu, J.; Peng, S. Assessing the effects of landscape pattern on river water quality at multiple scales: A case study of the Dongjiang River watershed. China Ecol. Indic. 2012, 23, 166–175. [Google Scholar] [CrossRef]
- Pollock, D.W.; Kookana, R.S.; Correll, R.L. Integration of the pesticide impact rating index with a geographic information system for the assessment of pesticide impact on water quality. Water Air Soil Pollut. Focus 2005, 5, 67–88. [Google Scholar] [CrossRef]
- Watanabe, T.; Kimura, M.; Asakawa, S. Dynamics of methanogenic archaeal communities based on rRNA analysis and their relation to methanogenic activity in Japanese paddy field soils. Soil Biol. Biochem. 2007, 39, 2877–2887. [Google Scholar] [CrossRef]
- Dechmi, F.; Burguete, J.; Skhiri, A. SWAT application in intensive irrigation systems: Model modification, calibration and validation. J. Hydrol. 2012, 470–471, 227–238. [Google Scholar] [CrossRef]
- Abdelwahab, O.M.M.; Ricci, G.F.; De Girolamo, A.M.; Gentile, F. Modelling soil erosion in a Mediterranean watershed: Comparison between SWAT and AnnAGNPS models. Environ. Res. 2018, 166, 363–376. [Google Scholar] [CrossRef] [PubMed]
- Belcher, K.W.; Boehm, M.M.; Fulton, M.E. Agroecosystem sustainability: A system simulation model approach. Agric. Syst. 2004, 79, 225–241. [Google Scholar] [CrossRef]
- Franceschini, S.; Tsai, C.W. Assessment of uncertainty sources in water quality modeling in the Niagara River. Adv. Water Resour. 2010, 33, 493–503. [Google Scholar] [CrossRef]
- Wang, K.; Lin, Z.; Zhang, R. Impact of phosphate mining and separation of mined materials on the hydrology and water environment of the Huangbai River basin, China. Sci. Total Environ. 2016, 543, 347–356. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–417. [Google Scholar]
- Zhang, C.; Chu, J.; Fu, G. Sobol’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China. J. Hydrol. 2013, 480, 58–68. [Google Scholar] [CrossRef]
- Massmann, C.; Wagener, T.; Holzmann, H. A new approach to visualizing time-varying sensitivity indices for environmental model diagnostics across evaluation time-scales. Environ. Model. Softw. 2014, 51, 190–194. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Shibata, H.; Urakawa, R.; Toda, H.; Inagaki, Y.; Tateno, R. Changes in nitrogen transformation in forest soil representing the climate gradient of the Japanese archipelago. J. For. Res. 2011, 16, 374–385. [Google Scholar] [CrossRef]
- Urakawa, R.; Shibata, H.; Kuroiwa, M. Effects of freeze thaw cycles resulting from winter climate change on soil nitrogen cycling in ten temperate forest ecosystems throughout the Japanese archipelago. Soil Biol. Biochem. 2014, 74, 82–94. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, R.; Sheng, F. Characterizing heterogeneous processes of water flow and solute Transport in soils using multiple tracer experiments. Vadose Zone J. 2013, 12, 1712–1717. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I—A discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- BIPM, IEC, IFCC, ISO, IUPAC, IUPAP and OIML. Guide to the Expression of Uncertainty in Measurement (GUM); International Organization for Standardization: Geneva, Switzerland, 1995; ISBN 92-67-10188-9. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Ju, X.; Zhang, C. Nitrogen cycling and environmental impacts in upland agricultural soils in North China: A review. J. Integr. Agric. 2017, 16, 2848–2862. [Google Scholar] [CrossRef]
- Huang, T.; Ju, X.; Yang, H. Nitrate leaching in a winter wheat-summer maize rotation on a calcareous soil as affected by nitrogen and straw management. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Gu, L.; Liu, T.; Zhao, J.; Dong, S.; Liu, P.; Zhang, J.; Zhao, B. Nitrate leaching of winter wheat grown in lysimeters as affected by fertilizers and irrigation on the North China Plain. J. Integr. Agric. 2015, 14, 374–388. [Google Scholar] [CrossRef]
- Diez, J.A.; Roman, R.; Caballero, R.; Caballero, A. Nitrate leaching from soils under a maize-wheat-maize sequence, two irrigation schedules and three types of fertilisers. Agric. Ecosyst. Environ. 1997, 65, 189–199. [Google Scholar] [CrossRef]
- Nossent, J.; Nossent, J.; Sarrazin, F.; Pianosi, F.; van Griensven, A.; Wagener, T.; Bauwens, W. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model. Environ. Model. Softw. 2017, 91, 210–222. [Google Scholar]
- Marc, J.R.; Jan, K. Tree-based ensemble methods for sensitivity analysis of environmental models: A performance comparison with Sobol and Morris techniques. Environ. Model. Softw. 2018, 107, 245–266. [Google Scholar]
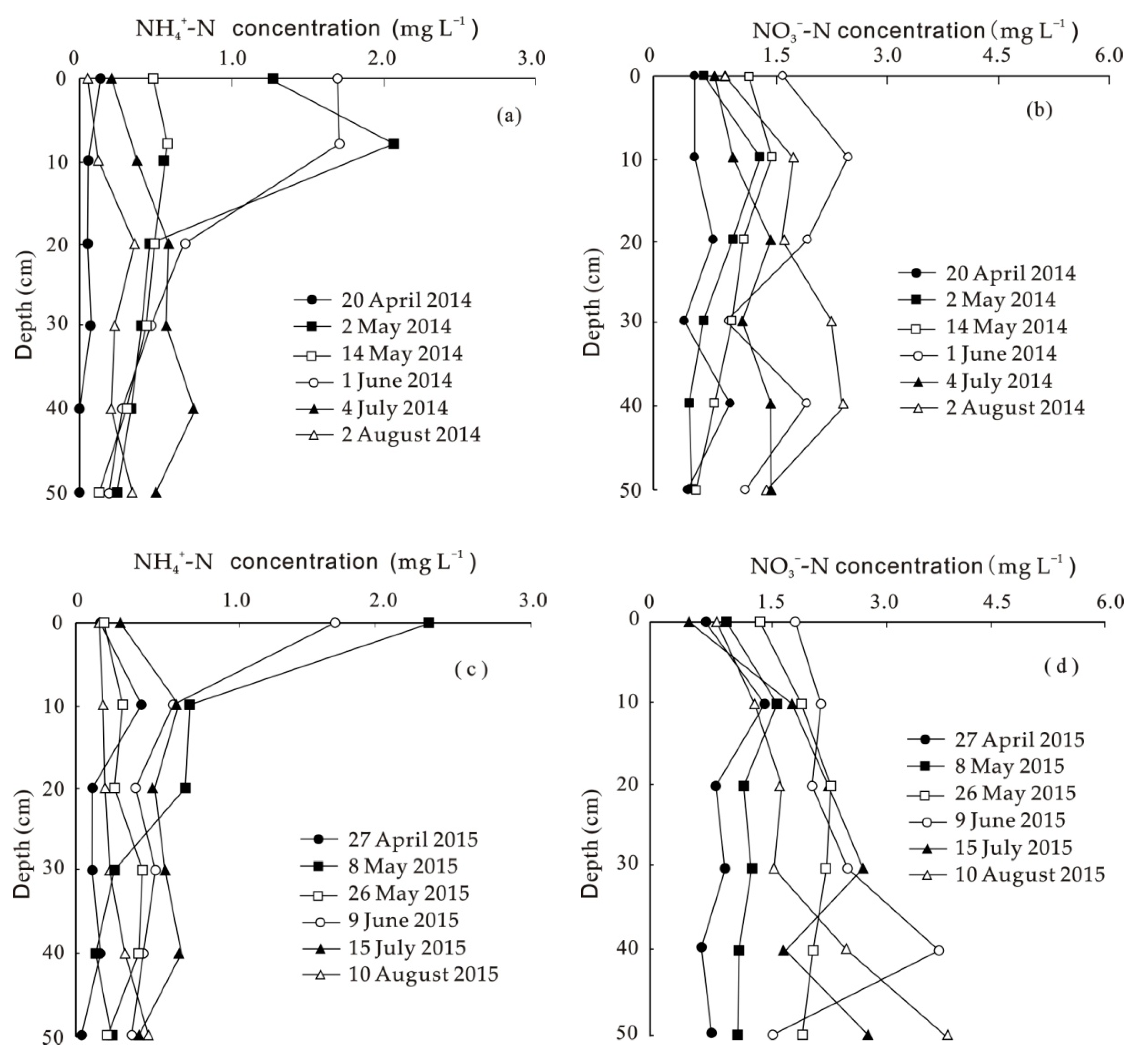
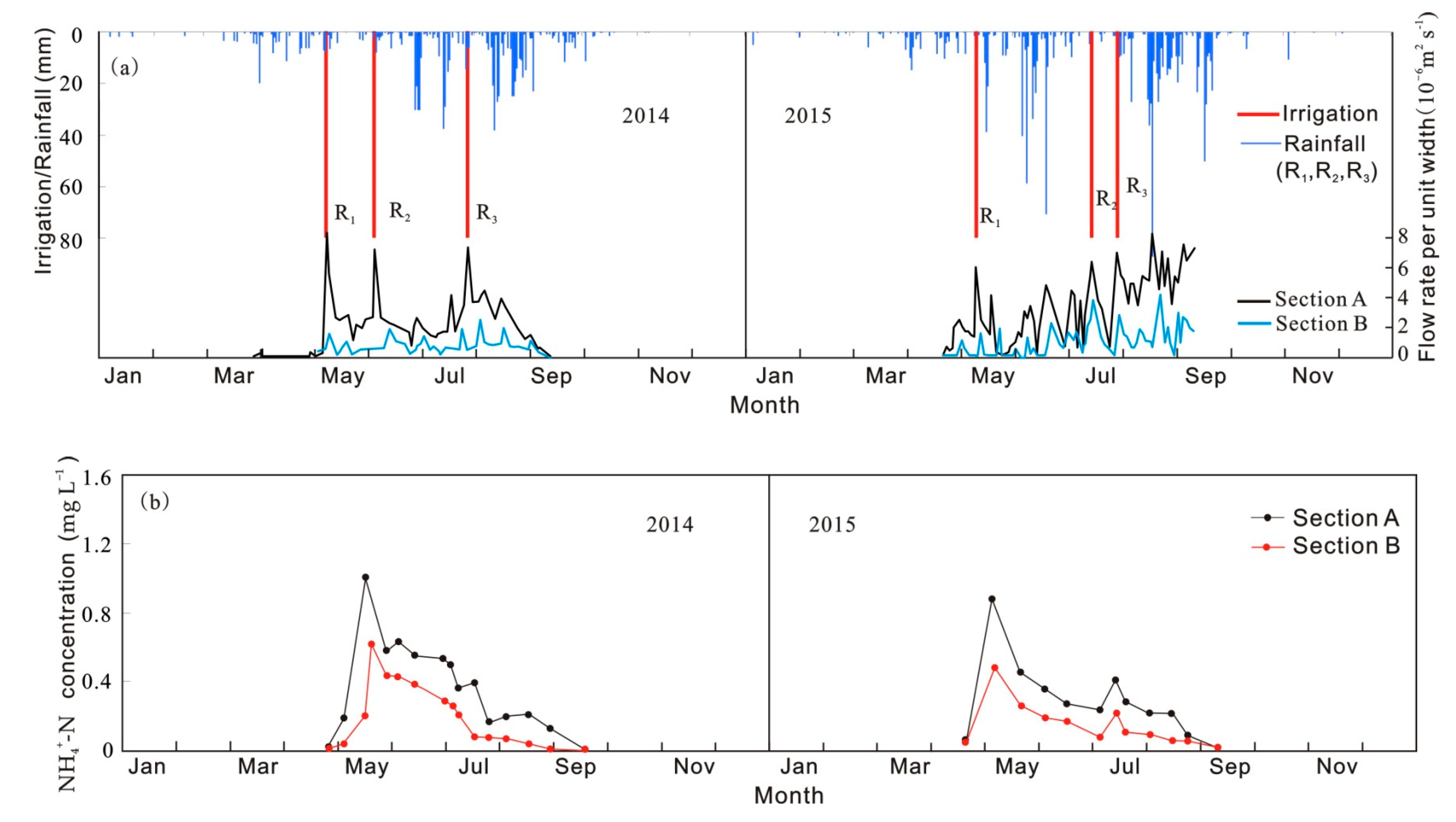
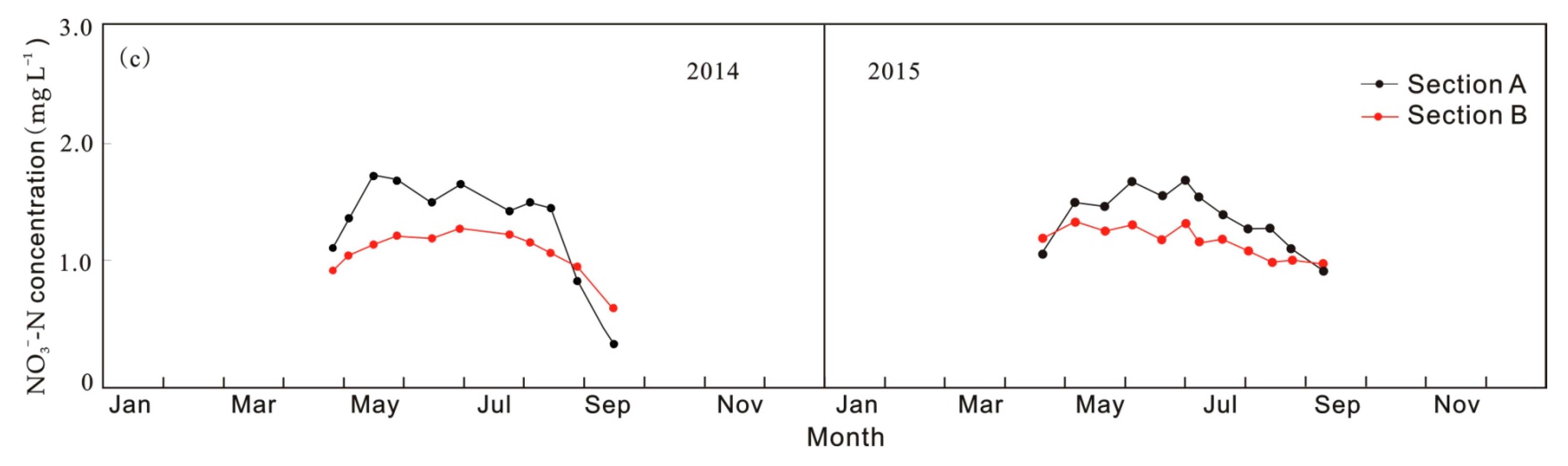
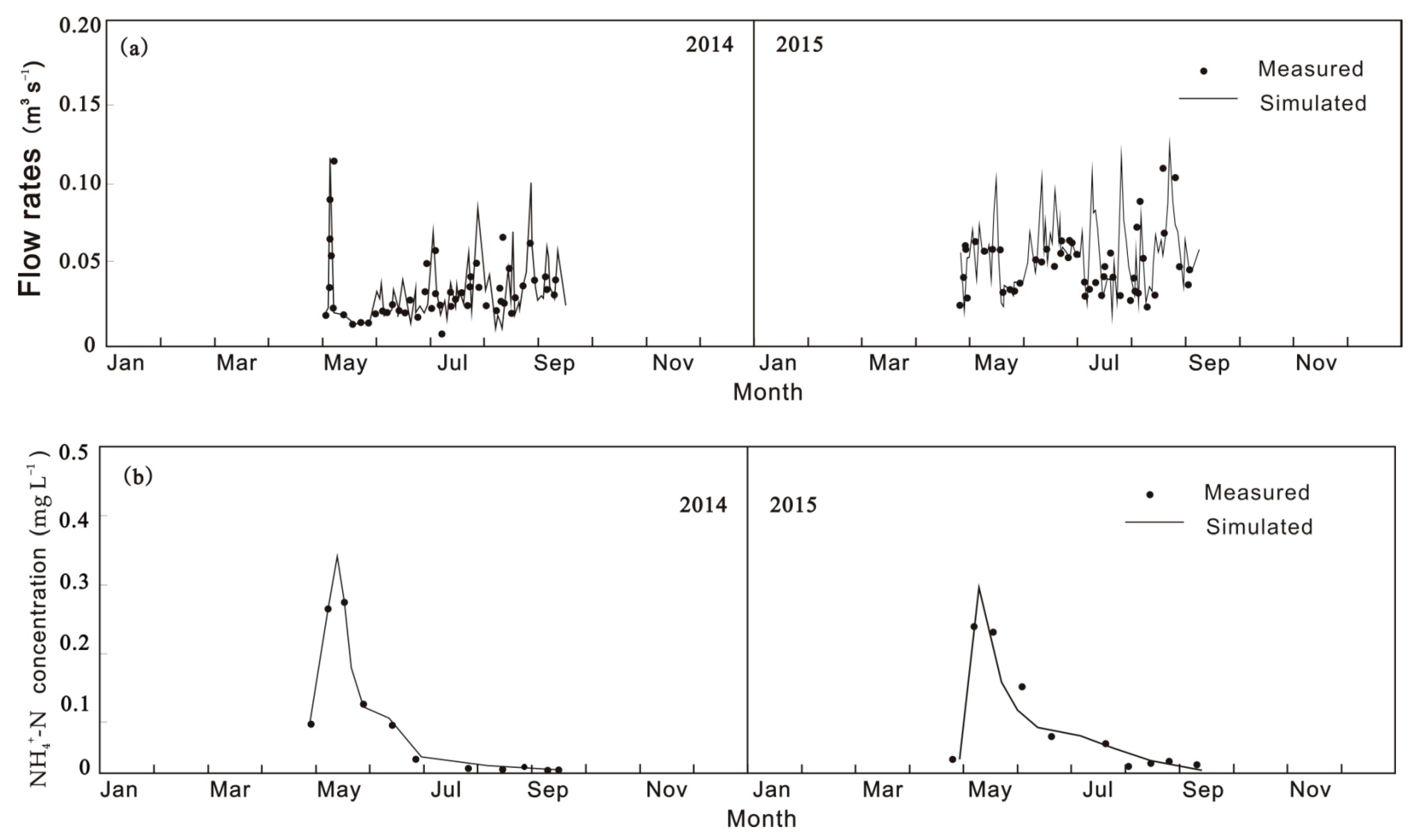
| Depth (cm) | Clay (%) | Sand (%) | Silt (%) | Bulk Density (g/cm3) | |||
|---|---|---|---|---|---|---|---|
| Mean ± STD a | Max/Min b | Mean ± STD | Max/Min | Mean ± STD | Max/Min | Max/Min | |
| 0–10 | 12.4 ± 4.3 | 17.3/10.6 | 53.6 ± 2.3 | 55.4/47.0 | 24.7 ± 4.6 | 28.6/16.4 | 0.98/1.32 |
| 20–30 | 12.9 ± 9.6 | 20.4/10.1 | 55.0 ± 8.7 | 57.9/47.4 | 27.1 ± 0.9 | 30.0/22.0 | 1.20/1.42 |
| 30–40 | 10.4 ± 7.7 | 14.8/9.4 | 52.3 ± 4.1 | 61.3/48.2 | 27.3 ± 3.9 | 31.0/23.0 | 1.24/1.48 |
| 40–50 | 11.8 ± 6.3 | 19.4/7.3 | 52.4 ± 3.6 | 54.9/45.6 | 27.8 ± 5.6 | 33.8/21.5 | 1.22/1.38 |
| 50+ | 0 | 0 | 100.0 ± 0.0 | 100/100 | 0 | 0 | 1.36/1.40 |
| Chemical | Sowing and Tilling Stages | Jointing and Heading Stages | Flowering and Filling Stages | |||
|---|---|---|---|---|---|---|
| Mean | Max/Min a | Mean | Max/Min | Mean | Max/Min | |
| 2014 | ||||||
| NH4+-N | 6.14 × 10−6 | 9.78 × 10−5/3.30 × 10−6 | 4.24 × 10−6 | 1.01 × 10−4/1.77 × 10−6 | 2.11 × 10−6 | 8.94 × 10−6/1.57 × 10−6 |
| NO3−-N | 3.25 × 10−6 | 5.14 × 10−5/1.07 × 10−6 | 3.44 × 10−5 | 5.78 × 10−4/1.21 × 10−5 | 8.60 × 10−6 | 1.84 × 10−5/3.39 × 10−6 |
| 2015 | ||||||
| NH4+-N | 7.44 × 10−6 | 1.26 × 10−4/0.54 × 10−6 | 3.99 × 10−6 | 7.93 × 10−5/1.15 × 10−6 | 2.02 × 10−6 | 4.64 × 10−6/1.33 × 10−6 |
| NO3−-N | 3.18 × 10−6 | 8.74 × 10−5/2.21 × 10−6 | 4.04 × 10−5 | 6.48 × 10−4/2.04 × 10−5 | 7.54 × 10−5 | 1.02 × 10−4/5.48 × 10−5 |
| No. | Brief Description (Unit) | Calibrated | Minimum | Maximum |
|---|---|---|---|---|
| 1 | Seepage from soil into rock (mm day−1), LE | -a | 1.4 | 12.6 |
| 2 | NH4+-N concentration in the soil water(mg L−1) | - | 0.4 | 6.2 |
| 3 | NO3−-N concentration in the soil water(mg L−1) | - | 1.8 | 8.4 |
| 4 | α, parameter in Equation (3) | 1.554 | 1.00 | 2.05 |
| 5 | β, parameter in Equation (3) | 0.0182 | 0.0020 | 0.110 |
| 6 | NH4+-N transformation rate in the lateral flow in the rock (day−1) | 0.142 | 0.102 | 0.20 |
| 7 | NO3−-N transformation rate in the lateral flow in the rock (day−1) | 0.171 | 0.144 | 0.224 |
| 8 | Ksat, parameter in Equation (6) (m s−1) | 3.42 × 10−5 | 3.08 × 10−5 | 3.94 × 10−5 |
| 9 | µ, parameter in Equation (6) | 0.15 | 0.12 | 0.18 |
| 10 | L, parameter in Equation (6) (m) | 240 | 200 | 280 |
| 11 | NH4+-N transformation rate in the surface drainage (day−1) | 0.11 | 0.09 | 0.14 |
| 12 | NO3−-N transformation rate in the surface drainage (day−1) | 0.09 | 0.06 | 0.13 |
| Flow rate and Chemical Concentrations | NSE | rRMSE (%) | FE | FB |
|---|---|---|---|---|
| Flow rate | 0.791 | 5.132 | 0.2014 | 0.031 |
| NH4+-N concentration | 0.701 | 8.364 | 0.2466 | 0.048 |
| NO3−-N concentration | 0.644 | 7.532 | 0.3172 | −0.051 |
| Growing Stages | Water (104 m3 km−1) | NH4+-N Mass (kg km−1 ) | NO3−-N Mass (kg km−1) | ||||
|---|---|---|---|---|---|---|---|
| Seepage | Transformation | Discharge | Seepage | Transformation | Discharge | ||
| Sowing and tilling stages | 2.16 | 2.550 | 5.71 | 7.74 | 43.8 | 4.91 | 9.77 |
| Jointing and heading stages | 3.64 | 2.386 | 3.29 | 6.42 | 84.2 | 11.90 | 22.45 |
| Flowering and filling stages | 3.87 | 0.492 | 0. 64 | 0.98 | 74.5 | 9.77 | 14.42 |
| Total | 9.67 | 5.428 | 9.64 | 15.14 | 202.5 | 26.58 | 46.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhou, Z.; Wang, K.; Xu, C. Simulation of Flow and Agricultural Non-Point Source Pollutant Transport in a Tibetan Plateau Irrigation District. Water 2019, 11, 132. https://doi.org/10.3390/w11010132
Li Y, Zhou Z, Wang K, Xu C. Simulation of Flow and Agricultural Non-Point Source Pollutant Transport in a Tibetan Plateau Irrigation District. Water. 2019; 11(1):132. https://doi.org/10.3390/w11010132
Chicago/Turabian StyleLi, Yuqing, Zuhao Zhou, Kang Wang, and Chongyu Xu. 2019. "Simulation of Flow and Agricultural Non-Point Source Pollutant Transport in a Tibetan Plateau Irrigation District" Water 11, no. 1: 132. https://doi.org/10.3390/w11010132
APA StyleLi, Y., Zhou, Z., Wang, K., & Xu, C. (2019). Simulation of Flow and Agricultural Non-Point Source Pollutant Transport in a Tibetan Plateau Irrigation District. Water, 11(1), 132. https://doi.org/10.3390/w11010132






