Next Article in Journal
Decontamination of Arsenic in Actual Water Samples by Calcium Containing Layered Double Hydroxides from a Convenient Synthesis Method
Next Article in Special Issue
The Optimal Width and Mechanism of Riparian Buffers for Storm Water Nutrient Removal in the Chinese Eutrophic Lake Chaohu Watershed
Previous Article in Journal
Water Quality Prediction Method Based on IGRA and LSTM
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 10
Issue 9
10.3390/w10091149
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

First-Principles Study on the Migration of Heavy Metal Ions in Ice-Water Medium from Ulansuhai Lake

by
Chi Sun
1,
Changyou Li
1,*,
Jianjun Liu
2,
Xiaohong Shi
1,
Shengnan Zhao
1,
Yong Wu
3 and
Weidong Tian
1
1
College of Water Conservancy and Civil Engineering, Inner Mongolia Agricultural University, Hohhot 010018, China
2
Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 200000, China
3
College of Resources and Environment, Henan Agricultural University, Zhengzhou 450002, China
*
Author to whom correspondence should be addressed.
Water 2018, 10(9), 1149; https://doi.org/10.3390/w10091149
Submission received: 19 July 2018 / Revised: 23 August 2018 / Accepted: 24 August 2018 / Published: 28 August 2018
(This article belongs to the Special Issue Lake and River Restoration: Method, Evaluation and Management)
Browse Figures
Versions Notes

Abstract

:
Energy is a fundamental driver that causes material movement. It is important to discover changes in energy by studying the internal mechanism of pollutant migration between system components during the freezing process. To explore the migration mechanism of heavy metal ions (HMIs) from ice to water in a lake, we carried out a laboratory freezing experiment and simulated the distribution and migration of HMIs (Fe, Cu, Mn, Zn, Pb, Cd, and Hg) under different conditions. Then, we analyzed the use of energy by first-principle calculations. The results showed that HMIs are more stable in an aqueous environment than in an ice environment. For the same HMI, the binding energy in water is smaller than that in ice. Hence, the HMIs migrated from ice to water as the lake was freezing. The ability of different kinds of heavy metals to migrate from ice to water is related to their binding energy in ice. The concentrations of HMIs in ice are positively correlated with their binding energies. This study investigated the migration characteristics and mechanisms of HMIs in the process of lake freezing.

1. Introduction

In aqueous ecosystems, substances migrate, transform, and are metabolized. At present, there is much research at home and abroad on the processes and mechanisms of material transfer and transformation, but most of these focus on the liquid water phase [1,2]. The increase in ice media due to freezing has an important influence on the migration of chemical substances. Research on the ice-water media involved in changes in lake environments and pollutants in multi-media environments has drawn much attention [3]. Lakes of the world that are located in high latitudes undergo a freeze-thaw cycle every year, and their environmental characteristics are obviously different from those of other lakes. Ice bodies play an important role in the environmental impact on the lakes during ice growth. Therefore, it is very important to study the distribution and migration mechanism of pollutants in the ice-water environment of cold regions.
The solute release into liquid water during freezing in an artificial environment has been extensively studied in various fields, such as technology, chemical analysis, food, medicine [4,5,6,7], and pollutant removal. In particular, freezing enrichment technology is used in industry to purify solutions [8]. In natural water, salt is redistributed from ice to water when the ocean freezes [9]. In recent years, there have been many investigations into the migration of pollutants from ice to water in lakes. Wang [10] found that the concentrations of Cr, Hg, and As varied widely between ice and water. In some parts of the lake, the amount of As in the water under the ice was more than ten times higher than in the ice. By simulating the migration of heavy metals in the ice-water medium, Lv [11] determined that the migration coefficients of heavy metals in ice-water systems were 0.12–0.84, also showing that heavy metals migrated from ice to water during freezing. Liu et al. [12] concluded that during the ice growth period in Ulansuhai Lake, Hg concentrations increased in the water first during the freezing process, then the dynamic equilibrium of the Hg between the water and sediments became upset, and finally a portion of the Hg migrated to the sediments, as a result of the difference in the equilibrium gradient. Based on the above studies, the migration and distribution of pollutants from ice to water in ice-water systems were obtained. The question is why do pollutants exhibit such a pattern of behavior? We all know that migration is a form of movement and that energy is the fundamental cause of material movement. Therefore, the freezing process must be accompanied by changes in energy. Finding the change of energy in this process is important to study the internal mechanism of pollutant migration in the lake ice-water media during the freezing period.
Lake water is a natural electrolyte solution. After freezing in a lake, there will be both ice and liquid water. In this study, we think of ice and water as two materials. These two materials are calculated from the perspective of solid state physics and quantum chemistry and analyzed to investigate the energy changes of pollutants in ice and water systems. This change of energy and the determination of the stability of contaminants in ice and water systems will involve a first-principles study. First-principles is usually associated with computation, when there are no other experimental, empirical, or semi-empirical parameters in the calculations that inform the program of which atoms are in use and where they are located. As the basis for evaluating things, first principles and empirical parameters represent the two extremes. First-principles can simulate the periodic structure, and it is independent of any empirical parameters that can solve the system of a ground state electronic structure and properties, while it is also a way to design materials. The research focus of first-principles is on the prediction of alloying effects in the processing of metals, the choice of atom positions, and the effects of electronic structures and properties on surfaces and interface layers [13,14,15,16,17]. Therefore, it is necessary to introduce first-principles calculations in the study of the transport mechanism of pollutants in lake ice-water media.
Inevitably, there is a difference in energy between lake pollutants that have migrated to water from ice. It is necessary to obtain the pollutant energy values in the most stable state in each media using the first-principles to explore the energy change of the pollutants in the freezing process. First of all, the morphology of pollutants in ice and water media should be determined using first-principles to calculate the energy. Water molecules in the liquid state, do not exist in the form of individual molecules, but in the form of a dimer, trimer, or tetrahedron [18]. There are at least 13 types of ice that have been characterized. Ice, such as frost and snow, which are exposed to daily life, are termed ice-Ih [19,20], while pure ice is a crystalline structure containing a tetrahedron [21]. Therefore, the structure of water and ice is important in establishing the microstructural model.
Lake freezing in natural conditions is a macroscopic and complex process. The complexity is mainly reflected in three aspects: (1) types of pollutants; (2) forms of contaminants; and (3) external environmental conditions. These factors have resulted in hardly any studies of the mechanism of pollutant migration from the perspective of energy. In this study, simulated lake freezing experiments conducted in the laboratory can control the environmental conditions and the types and forms of pollutants into individual variables, such that the migration mechanism of heavy metal ions can be explored in-depth. In this work, we focused on the migration of HMIs from ice to water in the course of the lake freezing using simulation experiments. First-principles were applied to calculate the binding energy in the different media in the ice-water system. This topic is important to better understand the mechanisms of lake ecosystems in cold regions, especially during the course of climate change.

2. Materials and Methods

2.1. Study Site

Ulansuhai Lake (40°36′–41°03′ N, 108°43′–108°57′ E) is on the Inner Mongolian Plateau, in the interior of Inner Mongolia, China. Its surface area is 283 km2. It usually enters the freezing period from November to April of the next year. The average thickness of the ice over many years is 0.63 m. It is the only drainage channel for local farmland, industrial waste water, and domestic sewage [22]. Every year, about 5 × 108 m3 of water is abstracted from the lake for farm irrigation, while 2 × 108 m3 of industrial waste water and sanitary waste with lead, mercury, arsenic, chromium, cadmium, and other heavy metals are discharged into it [23]. During the ice-covered period, the concentrations of heavy metals in the water are greater than that of the open water period. In particular, the concentrations of Hg in water during winter exceed the standard for III-type water quality, and the concentrations in the lake inlet region exceed the standard for V-type water quality [11]. For example, in January 2017, concentrations of heavy metals (Cu, Fe, Mn, Zn, Pb, Cd, and Hg) in the lake water were 1–3 (mean = 1.67) times higher than those in November 2016.

2.2. Experiment

2.2.1. Simulation Experiment Device

In order to simulate the top-down freezing process of water in natural lakes, a one-dimensional, unidirectional ice simulator was used (Figure 1). The experimental apparatus consisted of one cylinder within another, with the intervening space filled with insulating material. The inner cylinder holds the experimental sample. The insulation is meant to prevent heat loss from the side and bottom of the water column, ensuring that the cooling starts at the top (identical to freezing in natural lakes). The column body can be independently removed, not only for cleaning but also for easy removal of the formed ice. A piston was provided near the bottom to buffer pressure from expansion during the freezing, which otherwise could cause damage to the experimental instrument. To simulate the cold weather during which the lake freezes over, the experiment was carried out in a low-temperature storage.

2.2.2. Experimental Design and Methods

The freezing conditions of the indoor experimental simulation were designed based on the data for Ulansuhai Lake during the freezing period over many years. Water samples from this lake were not used during the field experiment work. Because the interaction of various pollutants and ions in the natural lake is complicated, it is hard to control the conditions for the types and concentrations of each ion. Therefore the characteristics of lake water were only used as a guide for the design of the experiment. Heavy metals exist in various forms in the lake water environment as simple ions and metal complexes [24]. Different forms exhibit unique chemical behaviors and play different roles in the aquatic environment of lakes. Zhao [25] used the geochemical software (PHREEQC, U.S. Geological Survey, Reston, VA, USA) to study the existence of heavy metals in Ulansuhai Lake. Simple ion heavy metals are the dominant form in Ulansuhai Lake. Therefore, the experimental design for this study only considered simple ion heavy metals in the microscopic simulation. The common heavy metals in Ulansuhai Lake (Cu, Fe, Mn, Zn, Pb, Cd, and Hg) were selected to prepare the water samples, using ultrapure water (resistivity: 18.2 MΩ·cm) and primary standards for each heavy metal (Table 1). Cl− is the dominant anion in the water of Ulansuhai Lake. The average concentration of the whole lake is 750.6 mg/L. The hydrochemical type of the lake is [Cl]NaIII and the TDS is more than 1000 mg/L. It belongs to high salinity brackish water [26]. In our experiment, water of V type and 10,000 μg/L was prepared according to the standard materials (Sample number in Table 1). The concentration of standard materials is 1000 µg/mL with the medium of C(HNO3) = 1.0 mol/L. We stepwise diluted it using ultrapure water by the standard materials. Water quality is a V-type in Ulansuhai Lake based on measured data over many years. Hence, we prepared the experimental samples according to V type. In order to study the migration of heavy metal ions under the same initial concentration conditions, and easily and accurately detect the ions concentration, we set the initial concentration to 10,000 µg/L. Each water sample of 2 L was prepared in the simulator. The freezing temperatures were set as −15 °C and −25 °C in the laboratory. According to the statistical results of the temperature data of Ulansuhai Lake from 1977–2015, the average low temperature is about −22.2 °C during the lake freezing period, so the experiment was designed with a freezing temperature of −25 °C; the average temperature is about −13.9 °C, so the experiment was designed with a freezing temperature of −15 °C. According to the ‘Environmental quality standards of surface water’ [27], Ulansuhai Lake has a V-type water quality [28] based on data measured over many years. To reduce the experimental error, the initial concentrations of these heavy metals in the water samples were all set as the maximum values allowed for V-type water, while the other initial concentrations were 10,000 μg/L (Table 1). The pH values of 5, 7, and 11 were chosen to represent acidic, neutral, and alkaline conditions, respectively. The limits for iron and manganese are in the supplementary items of surface water sources for the centralized drinking water standard in China. The devices were assembled, placed in the freezer, and taken out when the ice was about 1/3 of the total volume (which matches the ice: water ratio in Ulansuhai Lake during the freezing period; i.e., 1/3 to 1/2, [29]). After measuring the ice thickness, the ice was placed in separate containers to melt. For all water samples, the heavy metal concentrations were tested in triplicate according to the ‘Water and Wastewater monitoring analysis method’ [30]. The samples were first digested and underwent other appropriate pre-treatments. Then, the concentrations of Fe, Cu, Zn, Pb, Cd, and Mn were measured in a graphite oven-atomic absorption spectrometer, while those of Hg were measured with a double-channel atomic fluorescence spectrometer. The simulation experiments were completed in the laboratory of the National Position Observation Research Station of the Ulansuhai Wetland System in Inner Mongolia, China. In this study, water samples from this lake were not used during the experiment. But the setting up of simulated experimental conditions was based on the water environment characteristics of Ulansuhai Lake. Although the water environmental conditions of Ulansuhai Lake were used as a reference in the experiment design, the results can be applied to other lakes with a long freezing period. The lakes in high altitude areas of China have common characteristics of 4–7 months freezing period, and the ice thickness about 0.5–1.5 m, and environmental average temperature below −20 °C during the freezing period, which is the same as other lakes in North Europe [31].
The heavy metal concentrations were measured in each layer of ice and the underlying water. To study the changes in the distribution of heavy metals in the ice-water system under different conditions, the distribution coefficient (K) was calculated individually for each heavy metal as the ratio between the mean concentration in the three ice layers (CS) and that of the underlying water (CL).
K = C S / C L

2.3. Calculation

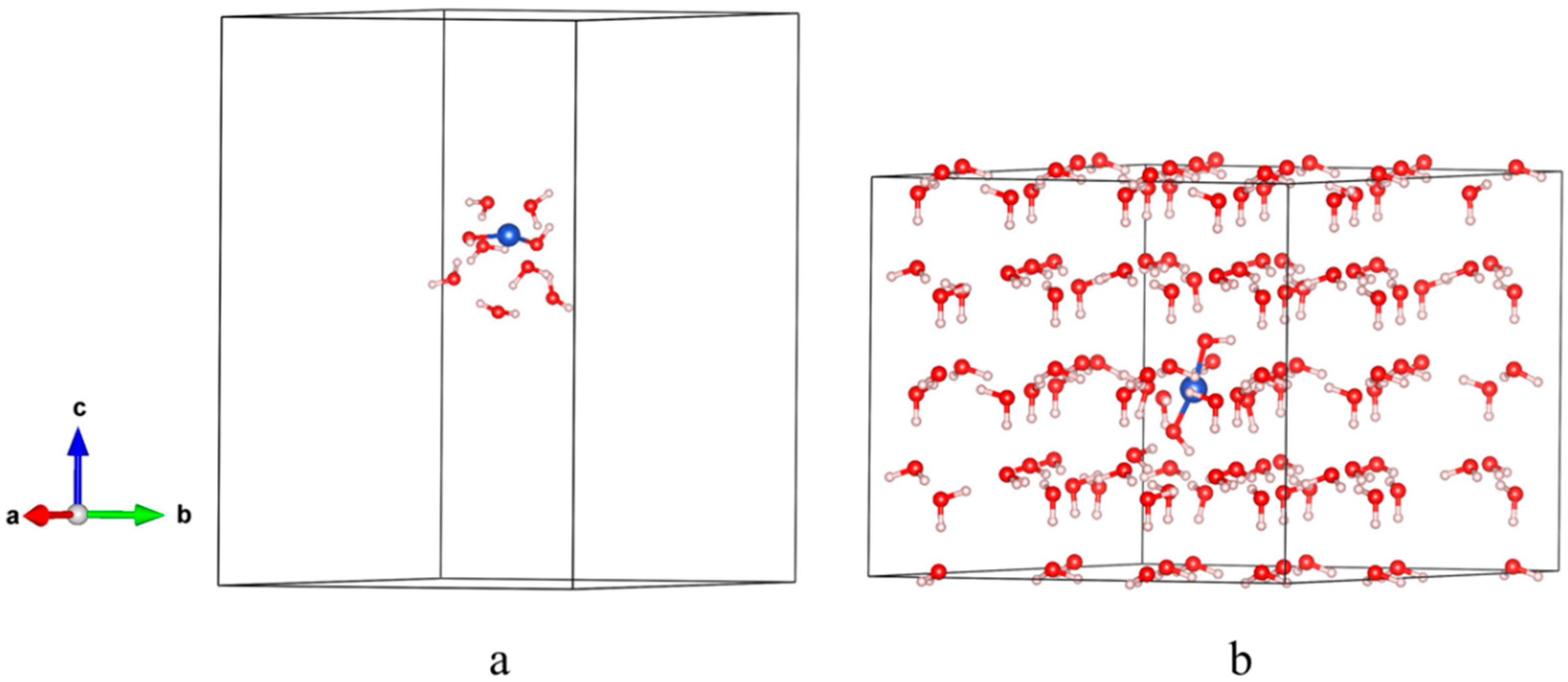
2.3.1. Microstructure Model

Choosing Cu2+ is just an example for introducing model setup. The models of other divalent heavy metal ions are basically similar to Cu2+. The only difference is the change of hydration number of ions in the water environment. Water system model: HMIs are surrounded by a number of water molecules [32]. The hydrated metal ions are formed because the strong action of the electric field near the ions causes the partial solvent water molecules to be arranged around them. Water molecules surround the metal ions with a hydration layer in a certain sequence around the metal ions according to Frank and Wen [33]. The water molecules and ions are bounded in firm combinations. The water molecules in the first hydration layer lose a translational degree of freedom, often accompanied by ions moving together. The number of molecules does not vary relative to temperature. The hydration numbers of a set of HMIs were determined by the 1H nuclear magnetic resonance method according to Swift and Sayre [34]. Therefore, when establishing the water system model in the case of Cu2+, firstly, two OH− were simulated near Cu2+ in order to balance positive and negative charges in a liquid system and optimize the cluster structure, and then five H2O were simulated around the Cu2+ in the first hydration layer. In addition, two H2O were simulated to surround and fix the two OH−. Figure 2a illustrates a model in the liquid phase, where the H2O outside the first hydration layer were not considered in the model because the H2O of the second hydration layer were acting weakly and were in a disordered structure.
Ice system model: Compared to liquid water, whose microstructural arrangement is disordered, solid ice has an organized order. The structure of ice is a tetrahedral formation with hexagonal rings. Each hydrogen atom is connected with two oxygen atoms, which are bounded by covalent bonds and hydrogen bonds, respectively [35]. Ice exhibits different configurations at different temperatures and pressures. There are 13 configurations discovered up to the present. According to the temperature and pressure conditions, lake ice occurs as ice-Ih [20,36]. A single crystal cell of ice-Ih is expanded into a 2 × 2 × 2 super pure ice cell structure. Depending on the state of most of the contaminants in the ice, they occur in bubbles or channels [3]. Thus, when we established the model, a hole was set up in the ice. In order to determine the structure of HMIs in ice with the lowest energy, the cluster structure of HMIs and two OH− were placed in the middle of the two H2O layers, and replacing the positions of one, two or three H2O in one layer. After optimizing these four structures, the energy of each whole system was calculated. Finally, the lowest energy was found to be the structure that replaced the position of one H2O in the center of the super pure ice cell. Figure 2b is the optimizing model for Cu2+ in ice. Based on the above established model of Cu2+ in the water and ice environments, several other heavy metal models were found to be similar.

2.3.2. Binding Energy Calculation Method

The definition of binding energy is the energy released by a single atom (system) into the corresponding material with which it has become bound. The more energy released, the more stable the material, and vice versa. The binding energies of HMIs in an ice body and a water body can be calculated. The stability of HMIs in the two media can be assessed by the size of the binding energies, which can reveal the mechanism of migration of HMIs in ice and water media. The first-principles calculations were performed at the Institute of Integrated Computational Materials Research Centre, Shanghai Institute of Ceramics, Chinese Academy of Sciences.
The DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP) [37,38] with the Perdew-Burk-Ernzerh parameterization of the generalized gradient approximation (GGA) adopted for the exchange correlation potential [39]. An energy cut off of 400 eV was consistently used in our calculations. The atomic positions are fully relaxed with the conjugate gradient procedure until the residual forces vanished within 0.05 eV/A. The standard of energy convergence is 10−5 eV/A 2 × 2 × 1 Monkhorst–Pack k-point was used to sample the surface Brillouin zone.
To compare the binding energy of HMIs in ice-water systems, two models of ice and water were established. The calculation formula for the binding energies was:
E = [E(M) + E(H)] − E(M + H)
In the calculation formula of the liquid (or solid) state system, E(M + H) is the energy of the equilibrium geometry when the contaminant molecule M and the liquid water (or solid state) molecule H form the interaction system, and E(M) and E(H) are the equilibrium geometry energies when M and H molecules exist individually.

3. Results

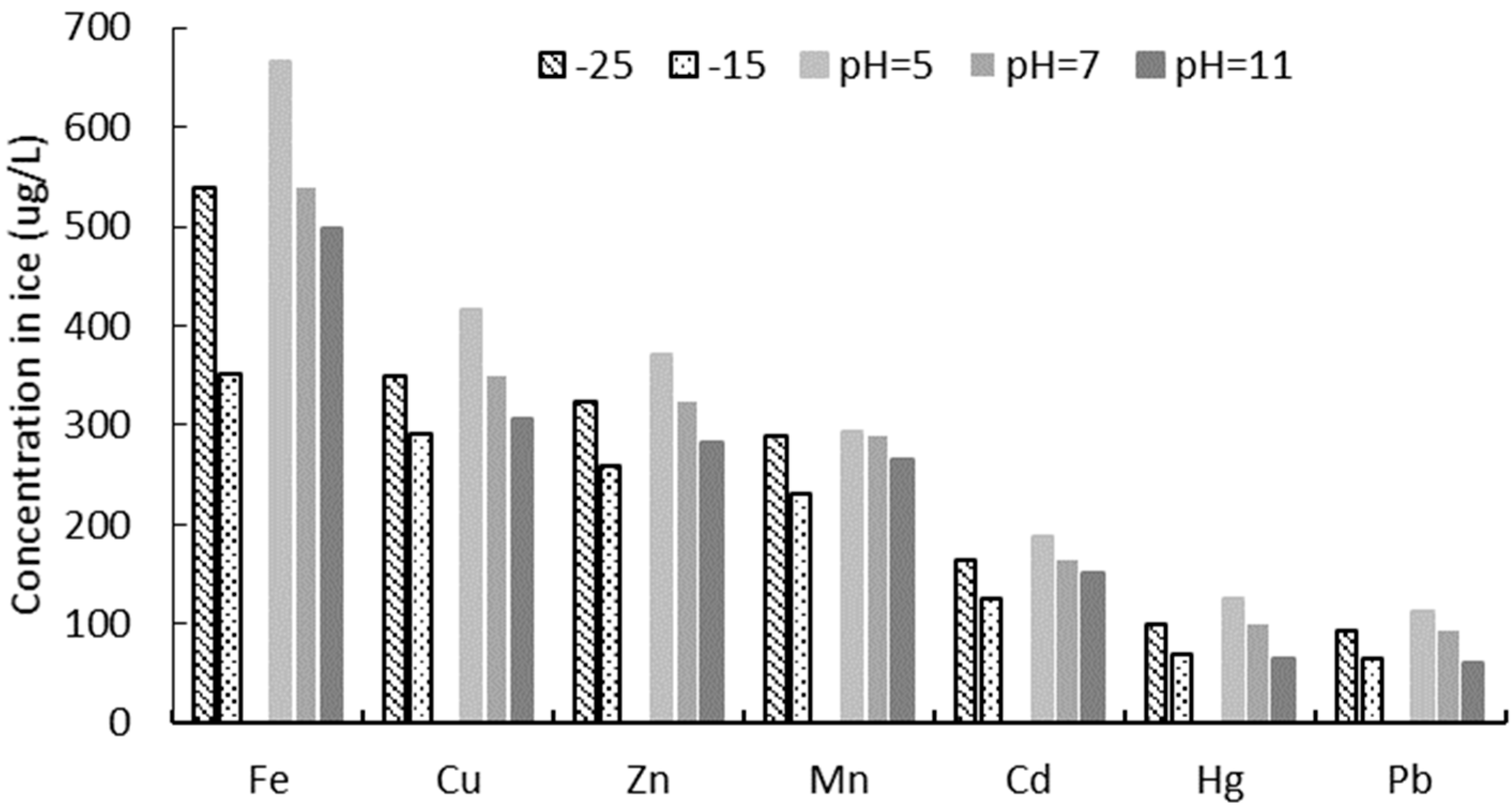
3.1. The Distribution and Transfer of HMIs in Ice and Water

The concentrations of the different HMIs in ice and water were obtained based on the lake freezing simulation experiments. If the temperature is −25 °C and −15 °C, the other two conditions are kept same, which are the pH is 7 and the initial concentration is 10,000 μg/L. If the pH is 5 or 11, the other two conditions are kept the same; temperature is −25 °C and the initial concentration is 10,000 μg/L. If the initial concentration is V-type or 10,000 μg/L, the other two conditions are the same; the temperature is −25 °C and the pH is 7. Figure 3 shows the concentrations of HMIs in the ice medium. At the same condition, the concentrations of HMIs in ice were in the following order: Fe > Cu > Mn > Zn > Cd > Hg > Pb. The results were calculated according to Equation (1) and the distribution coefficients (K) are given in Table 2. Regardless of whether the temperature is −25 °C or −15 °C, the pH is 5 or 11, or the initial concentration is V-type or 10,000 μg/L, the concentration in ice is less than the initial concentration of the solution before freezing, and significantly less than the concentration in the water under ice. This indicates that HMIs migrate from ice to water when the lake is freezing, and are released during the freezing. At the same condition, the concentrations of HMIs in ice were in the following order: Fe > Cu > Mn > Zn > Cd > Hg > Pb. This result is consistent with the result of Lv Hongzhou, who did indoor simulation of Ulansuhai Lake [11,12]. From Figure 3, the concentration in ice under acidic condition is greater than that under alkaline. This result is consistent with the result of Wang Shuang, that the concentration of heavy metals in ice is acidic > neutral > alkaline according to the simulation of frozen Ulansuhai Lake [10]. Under the specific conditions of high concentration of heavy metals and high pH, the Ulansuhai Lake is easier to concentrate in surface sediments.

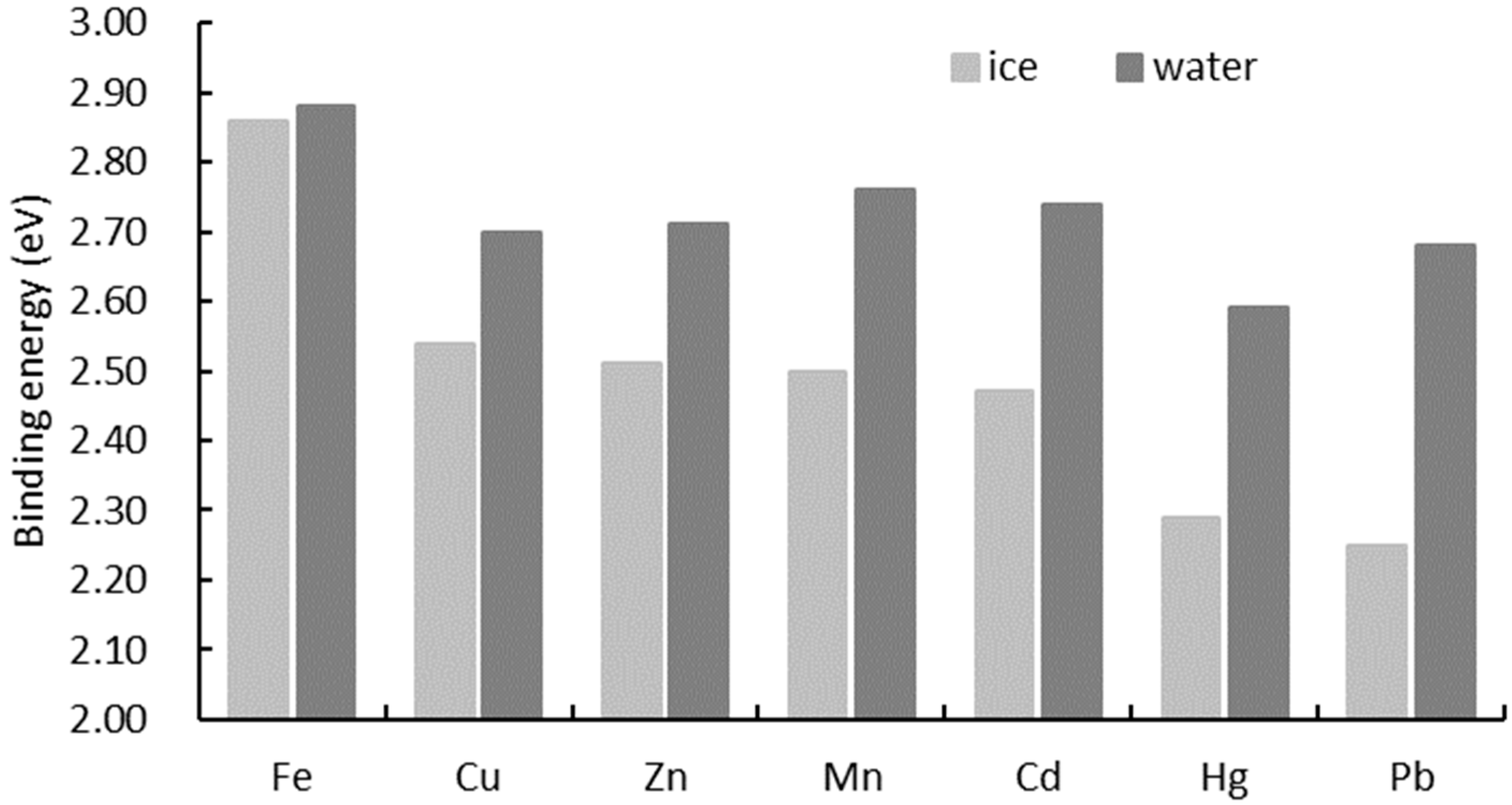
3.2. Energy of HMIs in Ice and Water

The results were calculated according to Equation (2), and the binding energy calculation process is shown in Table 3. The binding energies of HMIs were also calculated, as shown in Figure 4. It can be seen that the binding energies of the different heavy metals in water are greater than those in ice. In order to verify the results, we calculated the hydrogen bond energy of Ih-ice according to the first principle, and obtained the hydrogen bond energy of 0.276 eV, which is similar to the result (6.87 kcal/mol = 0.268 eV) of Liu Yi by the AIM method [40]. Therefore, the binding energy calculated based on this method is reliable.

4. Discussion

It can be seen from the experimental results of simulating lake freezing that the concentration in water under ice is much greater than that in ice, no matter whether the temperature of freezing is different or the initial concentration is different. Therefore, lake pollutants migrate to the water under ice during freezing. The movement of this migration results from changes in energy, so we discuss the mechanism from three aspects: structural stability, binding energy, and ionic radius.

4.1. Mechanism of HMIs Migration in Ice and Water

4.1.1. Stability of HMIs in Ice and Water

Based on the liquid phase model and solid phase model, we find that the HMIs in water are tightly surrounded by water molecules. Those water molecules are in a relatively free state. That means the binding energy of HMIs that combine with H2O is relatively high. However, HMIs remain in the ice without enough surrounding free H2O when the solution begins freezing. At this time, Cu2+ will interact with H2O and form an opening in the regular ice structure, as the binding energies of HMIs are relatively lower. Therefore, the micro-model also shows that HMIs are more stable in the water media than in the ice media. On the other hand, based on the calculated binding energies, the binding energy of the same HMI in water is larger than that in ice.

4.1.2. Binding Energy of HMIs in Ice and Water

Lake freezing is the process of changing from the single medium of water to the multiple media of ice-water. The process described from the molecular viewpoint is a complex process. However, this study captured two states, the state of HMIs in the aqueous medium and in the ice medium. According to the results shown in Figure 3, the binding energy in water was greater than that in ice for the same HMI. From an energy point of view, when the lake is freezing, the ice medium increases. For the two-media system, HMIs are more likely to exist in the relatively more stable aqueous environment. Therefore, the concentrations of HMIs in water are greater than those in ice. Therefore, HMIs migrate from ice to water when freezing.

4.2. Mechanism of Different HMIs in Ice

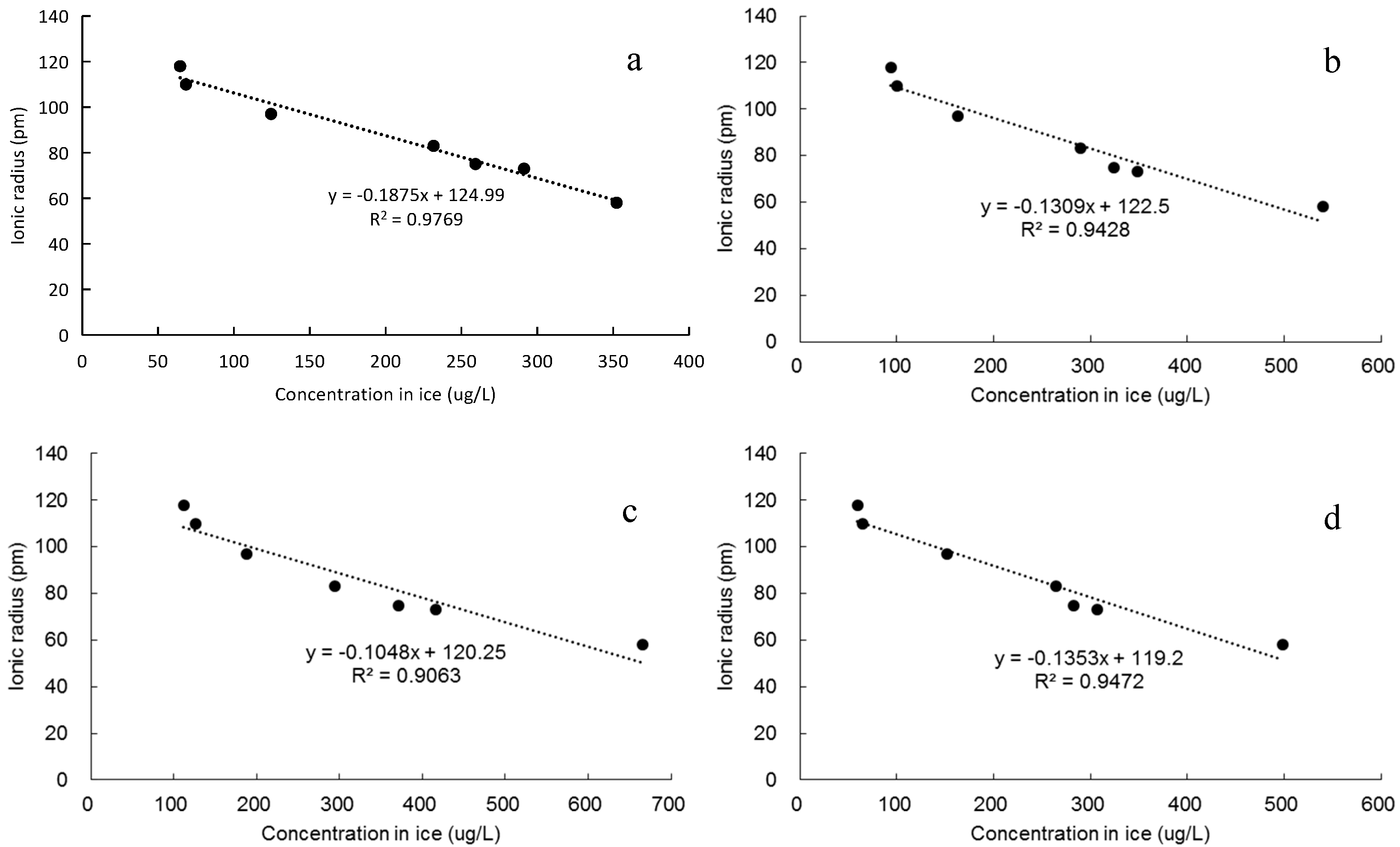
4.2.1. Effect of Ionic Radius on Concentration in Ice

Under the same temperature and initial concentration, the heavy metals have different behaviors in ice. For ions of the same charge, the larger the ionic radius, the weaker its influence on the water structure. Similarly, among ions with similar ionic radii, those with higher charges affect the water structure less. Taken together, the higher the charge density of the ion, the greater its influence on the water structure [41]. The heavy metal ions selected in this study all promote molecular association (i.e., stronger hydration and lower mobility of solute in the solution; [42]). Based on the relationship between concentration in ice and ionic radius, as shown in Figure 5, we find that when a single environmental factor changes, the concentrations of different heavy metals in the ice body are negatively correlated with their ionic radius. With an increase in ionic radius, the charge density decreases, and the influence on the structure of water is weakened. The effect of hydration on promoting the association of water molecules is also weakened, and therefore the solute mobility is lower. In contrast, under the same conditions, the concentrations of ionic pollutants in the ice gradually decreases with increasing ionic radius.

4.2.2. Effect of Binding Energy on Concentration in Ice

According to the results of the experimental freezing under different conditions, the concentration trends of HMIs in ice were the same regardless of the different external conditions. It can be seen that the migration capacities of HMIs from ice to water were independent of changes in the external conditions. In order to explore the reasons for the concentration distribution of HMIs in ice, the binding energies of the different HMIs in ice were calculated. The results showed that the trends in the concentrations of the HMIs in ice were the same. The differences among the concentrations of different HMIs in ice results from the different binding capacity of the HMIs. As shown in Figure 3 and Figure 4, Fe3+ has the highest binding energy in ice among the heavy metals, such that the concentrations of Fe3+ in the ice were higher than those of the other HMIs. The binding energy of Pb2+ in ice was the lowest and its concentrations were also less. The binding energy of heavy metal ions in ice is related to the characteristic of ions. Fe loses three electrons to form Fe3+, so there are three OH−, forming a neutral cluster around Fe3+. The cluster is held more firmly by H2O in the ice structure, so the binding energy between Fe3+ and ice is the largest in these seven kinds of heavy metal ions. Therefore, ion concentration remains larger in ice. Compared with other divalent heavy metal ions, the atoms with larger radii have a longer interaction distance with H2O and a weaker interaction force, so the binding energy with ice is smaller. The concentration of H2O in ice is relatively smaller when freezing. Figure 6 shows the relationship between concentration in ice and binding energy in ice, and under these four conditions the concentration of different heavy metals in the ice body are positively correlated with their binding energies.
The molecular model of heavy metal ions in an ice and water body was established based on first principles, which allowed the binding energy for each ion to be determined. The phenomenon of heavy metal pollutants concentrating in the lower bottom water during the frozen period was fully explained from the energy viewpoint, which is the main driver of the migration. The results reflect the interdisciplinary nature of the research methods, and provide a theoretical basis and ability to predict changes in the behavior of heavy metals in lakes during periods of freezing.

5. Conclusions

Above all, we aim to clarify the migration mechanism of HMIs from ice to water, when lakes are freezing from the perspective of energy change. HMIs are stable in a lower energy state, similar to all materials. They are more stable in an aqueous environment than in an ice environment. For the same HMI, the binding energy in water is smaller than that in ice. Thus HMIs migrate from ice to water when the lake is freezing. The ability of different HMIs to migrate from ice to water is related to the binding energies in ice. The concentrations of HMIs in ice are positively correlated with their binding energies.

6. Implications and Future Research

In our future research, we intend to study the relationship of the binding energies and concentration values of HMIs. Based on these relationships, we can predict the contents of some heavy metals in ice bodies and water bodies during periods of freezing. Using an equation to describe the relationships, we can not only reduce the field workload during freezing periods, but we can also check the agreement between the measured and predicted values and test the theoretical reliability of this experimental study.

Author Contributions

Data curation, C.S., X.S., S.Z. and W.T.; Formal analysis, Y.W.; Methodology, C.S., S.Z. and Y.W.; Software, C.S. and J.L.; Writing-original draft, C.S.; Writing-review & editing, C.L. and X.S.

Funding

This research was funded by the National Natural Science Foundation of China (Grant Nos.s 51339002, 51669022, 51509133, 51569019).

Acknowledgments

We are grateful for assistance with the Institute of Integrated Computational Materials Research Centre, Shanghai Institute of Ceramics, Chinese Academy of Sciences and the laboratory of the National Position Observation Research Station of the Ulansuhai Wetland System in Inner Mongolia, China.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Chen, A.; Zeng, G.; Zhang, J.; Lu, L.; Chen, M.; Xu, P. Global landscape of total organic carbon, nitrogen and phosphorus in lake water. Sci. Rep. 2015, 5, 15043. [Google Scholar] [CrossRef] [PubMed]
  2. Yu, J.; Fan, C.; Zhong, J.; Zhang, Y.; Wang, C.; Lei, Z. Evaluation of in situ simulated dredging to reduce internal nitrogen flux across the sediment-water interface in lake Taihu, China. Environ. Pollut. 2016, 214, 866–877. [Google Scholar] [CrossRef] [PubMed]
  3. Zhang, Y.; Li, C.Y.; Shi, X.H.; Chao, L.I. The migration of total dissolved solids during natural freezing process in Ulansuhai Lake. J. Arid. Land 2012, 4, 85–94. [Google Scholar] [CrossRef]
  4. Bengtsson, L. Mixing in ice-covered lakes. Hydrobiologia 1996, 322, 91–97. [Google Scholar] [CrossRef]
  5. Fedotov, V.I.; Cherepanov, N.V.; Tyshko, K.P. Some features of the growth, structure and metamorphism of East Antarctic landfast sea ice. In Antarctic Sea Ice: Physical Processes, Interactions and Variability; Jeffries, M.O., Ed.; American Geophysical Union: Washington, DC, USA, 2013; pp. 343–354. [Google Scholar]
  6. Baker, R.A. Trace organic contaminant concentration by freezing-IV: Ionic effects. Water Res. 1970, 4, 559–573. [Google Scholar] [CrossRef]
  7. Huige, N.J.J.; Thijssen, H.A.C. Production of large crystals by continuous ripening in a stirrer tank. J. Cryst. Growths 1972, 13–14, 483–487. [Google Scholar] [CrossRef]
  8. Muller, M.; Sekoulov, I. Waste water reuse by freeze concentration with falling film reactor. Water Sci. Technol. 1992, 26, 1475–1482. [Google Scholar] [CrossRef]
  9. Weeks, W. Sea ice: The potential of remote sensing. Oceanus 1981, 24, 39–48. [Google Scholar]
  10. Wang, S. Study on Distribution Law and Laboratory Simulation Experiment of Heavy Metals during the Icebound Season in Wulansuhai Lake; Inner Mongolia Agriculture University: Inner Mongolia, China, 2012. (In Chinese) [Google Scholar]
  11. Lv, H.Z. Studies on Pollutant Distribution in Ice-Water System of Ulansuhai Lake; Inner Mongolia Agriculture University: Inner Mongolia, China, 2015. (In Chinese) [Google Scholar]
  12. Liu, Y.; Li, C.Y.; Anderson, B.; Zhang, S.; Shi, X.H.; Zhao, S.N. A modified QWASI model for fate and transport modeling of mercury between the water-ice-sediment in Lake Ulansuhai. Chemosphere 2017, 176, 117–124. [Google Scholar] [CrossRef] [PubMed]
  13. Zhao, L.; Sun, Y.; Li, Y.G.; Meng, X.F.; Song, Q.L. First-principles studies of the effects of microalloy elements on Fe/Al interface. J. At. Mol. Phys. 2007, 24, 853–857. (In Chinese) [Google Scholar]
  14. Hu, X.L.; Zhang, Y.; Lu, G.H.; Wang, T.M.; Xiao, P.H.; Yin, P.G.; Xu, H.B. Effect of impurity on structure and mechanical properties of NiAl intermetallics: A first-principles study. Intermetallics 2009, 17, 358–364. [Google Scholar] [CrossRef]
  15. Xu, Q.C.; Ven, A.V. First-principles investigation of migration barriers and point defect complexes in B2-NiAl. Intermetallics 2009, 17, 319–329. [Google Scholar] [CrossRef]
  16. Wei, H.; Liang, J.J.; Sun, B.Z.; Zheng, Q.; Sun, X.F.; Peng, P.; Yao, X.; Dargusch, M.S. Site preference of Re in NiAl and valence band structure of NiAl containing Re: First-principles study and photoelectron spectrum. Appl. Phys. Lett. 2009, 94, 1731–1756. [Google Scholar]
  17. Kogita, T.; Kohyama, M.; Kido, Y. Structure and dynamics of NiAl(110) studied by high-resolution ion scattering combined with density functional calculations. Phys. Rev. B 2009, 80, 308–310. [Google Scholar] [CrossRef]
  18. Tu, T.S.; Fang, H.P. The microstructure of liquid water. J. Phys. Chem. 2010, 39, 79–84. (In Chinese) [Google Scholar]
  19. Zhou, P. A Theoretical Calculated Investigation on Hydrogen Bonding Clusters of Water-Ammonia Molecules; Shandong Normal University: Shandong, China, 2008. (In Chinese) [Google Scholar]
  20. Michalarias, I.; Beta, I.; Ford, R.; Ruffle, S.; Li, J.C. Inelastic neutron scattering studies of water in DNA. Appl. Phys. A 2002, 74, s1242–s1244. [Google Scholar] [CrossRef]
  21. Isakov, S.V.; Moessner, R.; Sondhi, S.L.; Tennant, D.A. Analytical theory for proton correlations in common water ice Ih. Phys. Rev. B 2015, 91, 245152. [Google Scholar] [CrossRef]
  22. Wu, Y.; Li, C.Y.; Zhang, C.F.; Shi, X.H.; Bourque, C.P.A.; Zhao, S.N. Evaluation of the applicability of the SWAT model in an arid piedmont plain oasis. Water Sci. Technol. 2016, 73, 1341–1348. [Google Scholar] [CrossRef] [PubMed]
  23. Zhao, S.N.; Shi, X.H.; Li, C.Y.; Zhang, S.; Sun, B.; Wu, Y.; Zhao, S.X. Diffusion flux of phosphorus nutrients at the sediment-water interface of the Ulansuhai Lake in northern China. Water Sci. Technol. 2017, 75, 1455–1465. [Google Scholar] [CrossRef] [PubMed]
  24. Ye, S.Y.; Sun, J.C.; Jiang, C.Y. Current situation and advances in hydrogeochemical researches. Acta Geosci. Sin. 2002, 23, 477–482. (In Chinese) [Google Scholar]
  25. Zhao, S.N. Enviromental Geochemistry of Heavy Metal and Modelling Analysis of Their Speciation for Ulansuhai Lake in Inner Mongolia; Inner Mongolia Agriculture University: Inner Mongolia, China, 2013. (In Chinese) [Google Scholar]
  26. Cui, F.L.; Li, C.Y.; Shi, X.H.; Shi, Y.Q.; Fu, X.J. Seasonal changing characteristics of the major ions in Ulansuhai Lake. J. Arid. Land Resour. Environ. 2013, 8, 137–142. [Google Scholar]
  27. Environment Quality Standards for Surface Water; GB3838-2002; State Environmental Protection Administration of the People’s Republic of China: Beijing, China, 2002. (In Chinese)
  28. Li, W.P.; Xu, J.; Yu, L.H.; Han, P.J.; Zhao, Z.; Jing, J. Distribution characteristics of nutrients and phytoplankton in Ulansuhai Lake during the icebound season. Ecol. Environ. Sci. 2014, 23, 1007–1013. (In Chinese) [Google Scholar]
  29. Yang, F.; Li, C.Y.; Leppäranta, M.; Shi, X.H.; Zhao, S.N.; Zhang, C.F. Notable increases in nutrient concentrations in a shallow lake during seasonal ice growth. Water Sci. Technol. 2016, 74, 2773–2783. [Google Scholar]
  30. The State Environmental Protection Administration the Water and Wastewater Monitoring Analysis Method Editorial Board. Water and Wastewater Monitoring Analysis Method, 4th ed.; China Environmental Science Press: Beijing, China, 2002; pp. 38–47. (In Chinese) [Google Scholar]
  31. Sergey, K.; Mikhail, N. Lake ladoga ice phenology: Mean condition and extremes during the last 65 years. Hydrol. Process. 2011, 25, 2859–2867. [Google Scholar]
  32. Wang, W.H.; Zhao, L.; Yan, B. Effects of ions on structure of liquid water. Chemistry 2010, 73, 491–498. (In Chinese) [Google Scholar]
  33. Frank, H.S.; Wen, W.Y. Ion-solvent interaction. Structural aspects of ion-solvent interaction in aqueous solutions: A suggested picture of water structure. Discuss. Faraday Soc. 1957, 24, 133–140. [Google Scholar] [CrossRef]
  34. Swift, T.J.; Sayre, W.G. Determination of hydration numbers of cations in aqueous solution by means of proton NMR. J. Chem. Phys. 1966, 44, 3567–3574. [Google Scholar] [CrossRef]
  35. Goto, A.; Hondoh, T.; Mae, S. The electron density distribution in ice Ih determined by single-crystal X-ray diffractometry. J. Chem. Phys. 1990, 93, 1412–1417. [Google Scholar] [CrossRef]
  36. Petrenko, V.F.; Whitworth, R.W. Physics of Ice; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
  37. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
  38. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1998, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  40. Liu, Y. Atoms-in-Molecules Molecular-Dynamics Study of Ion-Water Bonding of K+ Solvation in Water; North University of China: Taiyuan, China, 2010. (In Chinese) [Google Scholar]
  41. Wang, W.H.; Zhao, L.; Yan, B.; Tan, X.; Qi, Y.; He, B. Effects of concentration and freeze-thaw on the first hydration shell structure of Zn2+ ions. J. Tianjin Univ. 2011, 17, 381–385. (In Chinese) [Google Scholar] [CrossRef]
  42. Marcus, Y. Effect of ions on the structure of water: Structure making and breaking. Chem. Rev. 2009, 109, 1346–1370. [Google Scholar] [CrossRef] [PubMed]
Water 10 01149 g001 550
Figure 1. Device for unidirectionally simulating the freezing of lake water.
Figure 1. Device for unidirectionally simulating the freezing of lake water.
Water 10 01149 g001
Water 10 01149 g002 550
Figure 2. (a) The model of Cu2+ in the aqueous environment. (b) The model of Cu2+ in the ice environment (a represents x-axis, b represents y-axis, c represents z-axis; the blue atom is Cu, the red atoms are O, the grey atoms are H).
Figure 2. (a) The model of Cu2+ in the aqueous environment. (b) The model of Cu2+ in the ice environment (a represents x-axis, b represents y-axis, c represents z-axis; the blue atom is Cu, the red atoms are O, the grey atoms are H).
Water 10 01149 g002
Water 10 01149 g003 550
Figure 3. The heavy mental concentrations in ice under different conditions.
Figure 3. The heavy mental concentrations in ice under different conditions.
Water 10 01149 g003
Water 10 01149 g004 550
Figure 4. Binding energies of HMIs in ice and water.
Figure 4. Binding energies of HMIs in ice and water.
Water 10 01149 g004
Water 10 01149 g005 550
Figure 5. The relationship between concentration in ice and ionic radius ((a) T = −25 °C, pH = 7, initial concentration is 10,000 μg/L; (b) T = −15 °C, pH = 7, initial concentration is 10,000 μg/L; (c) pH = 5, T = −25 °C, initial concentration is 10,000 μg/L; (d) pH = 11, T = −25 °C, initial concentration is 10,000 μg/L).
Figure 5. The relationship between concentration in ice and ionic radius ((a) T = −25 °C, pH = 7, initial concentration is 10,000 μg/L; (b) T = −15 °C, pH = 7, initial concentration is 10,000 μg/L; (c) pH = 5, T = −25 °C, initial concentration is 10,000 μg/L; (d) pH = 11, T = −25 °C, initial concentration is 10,000 μg/L).
Water 10 01149 g005
Water 10 01149 g006 550
Figure 6. The relationship between concentration in ice and binding energy in ice ((a) T = −25 °C, pH = 7, initial concentration is 10,000 μg/L; (b) T = −15 °C, pH = 7, initial concentration is 10,000 μg/L; (c) pH = 5, T = −25 °C, initial concentration is 10,000 μg/L; (d) pH = 11, T = −25 °C, initial concentration is 10,000 μg/L).
Figure 6. The relationship between concentration in ice and binding energy in ice ((a) T = −25 °C, pH = 7, initial concentration is 10,000 μg/L; (b) T = −15 °C, pH = 7, initial concentration is 10,000 μg/L; (c) pH = 5, T = −25 °C, initial concentration is 10,000 μg/L; (d) pH = 11, T = −25 °C, initial concentration is 10,000 μg/L).
Water 10 01149 g006
Table
Table 1. Concentration values of the standard materials and the initial concentrations (mg/L).
Table 1. Concentration values of the standard materials and the initial concentrations (mg/L).
Standard MaterialsSample NumberC1C2
CuGSB04-1725-20041.010.0
FeGSB04-1726-20043.010.0
MnGSB04-1736-20040.110.0
ZnGSB04-1761-20040.110.0
PbGSB04-1742-20040.110.0
CdGSB04-1721-20040.0110.0
HgGSB04-1729-20040.00110.0
Table
Table 2. The distribution coefficients (K) of heavy metals under different conditions.
Table 2. The distribution coefficients (K) of heavy metals under different conditions.
HMIsT = −25 °CT = −15 °CpH = 5pH = 11V-Type10,000 µg/L
Fe0.0370.0240.0450.0340.0610.037
Cu0.0240.0200.0280.0210.1050.024
Zn0.0220.0170.0250.0190.0170.022
Mn0.0190.0160.0200.0180.0130.019
Cd0.0110.0080.0130.0100.1180.011
Hg0.0070.0050.0080.0040.0550.007
Pb0.0060.0040.0070.0040.0100.006
Table
Table 3. Binding energy calculation process (eV).
Table 3. Binding energy calculation process (eV).
Heavy MetalsE(M)Calculation in IceCalculation in Water
E (M + H)E (H)E (M + H)E (H)
Fe−28.09−1268.80−1237.85−118.12−87.15
Cu−16.10−1256.49−1237.85−105.95−87.15
Zn−15.41−1255.76−1237.85−105.27−87.15
Mn−18.98−1259.33−1237.85−108.89−87.15
Cd−14.10−1254.42−1237.85−103.99−87.15
Hg−13.50−1253.64−1237.85−103.24−87.15
Pb−17.63−1257.73−1237.85−107.46−87.15

Share and Cite

MDPI and ACS Style

Sun, C.; Li, C.; Liu, J.; Shi, X.; Zhao, S.; Wu, Y.; Tian, W. First-Principles Study on the Migration of Heavy Metal Ions in Ice-Water Medium from Ulansuhai Lake. Water 2018, 10, 1149. https://doi.org/10.3390/w10091149

AMA Style

Sun C, Li C, Liu J, Shi X, Zhao S, Wu Y, Tian W. First-Principles Study on the Migration of Heavy Metal Ions in Ice-Water Medium from Ulansuhai Lake. Water. 2018; 10(9):1149. https://doi.org/10.3390/w10091149

Chicago/Turabian Style

Sun, Chi, Changyou Li, Jianjun Liu, Xiaohong Shi, Shengnan Zhao, Yong Wu, and Weidong Tian. 2018. "First-Principles Study on the Migration of Heavy Metal Ions in Ice-Water Medium from Ulansuhai Lake" Water 10, no. 9: 1149. https://doi.org/10.3390/w10091149

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop