Abstract
The current study investigates an improved version of Least Square Support Vector Machines integrated with a Bat Algorithm (LSSVM-BA) for modeling the dissolved oxygen (DO) concentration in rivers. The LSSVM-BA model results are compared with those obtained using M5 Tree and Multivariate Adaptive Regression Spline (MARS) models to show the efficacy of this novel integrated model. The river water quality data at three monitoring stations located in the USA are considered for the simulation of DO concentration. Eight input combinations of four water quality parameters, namely, water temperature, discharge, pH, and specific conductance, are used to simulate the DO concentration. The results revealed the superiority of the LSSVM-BA model over the M5 Tree and MARS models in the prediction of river DO. The accuracy of the LSSVM-BA model compared with those of the M5 Tree and MARS models is found to increase by 20% and 42%, respectively, in terms of the root-mean-square error. All the predictive models are found to perform best when all the four water quality variables are used as input, which indicates that it is possible to supply more information to the predictive model by way of incorporation of all the water quality variables.
1. Introduction
Assessment of river water quality is a challenging issue in field environmental modeling. Among the river water quality parameters, dissolved oxygen (DO) is a critical one for decision-makers in management of water quality and river ecology [1]. The level of DO concentration within a water body (e.g., river and lake) is very important for aquatic organisms (e.g., fish and plants) as low and high values of DO are harmful for the aquatic environment [2]. DO is released within a river through diffusion or aeration processes and by photosynthesis of plants such as algae and phytoplankton [3]. The sources for supplying DO are limited and, therefore, the conscious management of water quality is very important for maintaining the DO level in water bodies [4].
The DO concentration in a river depends on many biotic/abiotic parameters such as the amount of aquatic plants, nutrient concentrations, streamflow discharge, specific conductance, pH, and water temperature [5], as well as their complex interactions [6]. Physical-based models such as QUAL2K [7] and Water Quality Analysis Simulation Program WASP [8] are generally used to mimic these physical processes in a simplified manner for the prediction of DO. However, the physically based models developed using deterministic equations often fail to predict DO concentration with reasonable accuracy. This is due to several causes: (1) knowledge of many of the biotic/abiotic processes responsible for DO concentration in water bodies is still not clear and the data/information required for modeling many of the interactions are difficult to acquire; (2) many of the biotic/abiotic processes are highly nonlinear and cannot be described perfectly with mathematical equations and (3) hydro-biological data are often prone to errors which cause high uncertainties in prediction [9,10]. However, it has been noticed that many of these processes follow a stochastic behavior. The DO concentration in water bodies changes with time with a sequential relationship between two consecutive values. This encouraged the development of stochastic models in which statistical methods are used to find a relationship between input and output.
The DO concentration in a water body fluctuates on an annual, monthly, daily, or even hourly scale with respect to the water temperature and other features of the water body [4]. Studying the daily and hourly fluctuations of DO concentration might be of interest for particular water bodies with shallow water depth as the concentration of DO fluctuates significantly within a very short period due to high dynamics of physical, chemical, and biological processes in water bodies with shallow depth [9,10]. On the other hand, fluctuation of DO concentration in a river is not significant at the hourly or daily scale. Furthermore, the monthly DO concentration provides seasonal variation of this important water quality parameter which is more useful for management of river water quality and ecology. Therefore, models have been developed in this study for the prediction of the monthly concentration of DO in river.
Regression models are most widely used for modeling stochastic behavior of DO concentration in water bodies [5,11]. Zounemat-Kermani and Scholz (2014) used stepwise regression for the selection of influential parameters for prediction of DO concentration. Khan and Valeo (2015) introduced fuzzy linear regression to predict DO from abiotic factors [5]. Li et al. (2017) employed linear regression for estimation of DO from multiple water quality parameters [12]. However, the capability of conventional regression-based models is limited in simulating highly nonlinear and nonstationary behavior. The time series of DO concentration is often found to be highly stochastic in nature, which is not possible to simulate using conventional regression models. With the advances of artificial intelligence (AI)-based methods, the application of AI in the development of stochastic models has gained significant attention. In recent years, a large number of AI approaches such as artificial neural networks (ANNs), support vector machines (SVMs), fuzzy methods, and model trees (MTs) have been widely used for prediction of different hydrological phenomena such as rainfall [13,14], temperature [15,16], evaporation [17], streamflow [18,19,20], and water demand [21]. Despite various limitations, the AI-based models have been found to provide hydrological prediction in an efficient way. The AI-based models have simple structure and a low number of mathematical parameters but can consider a large number of predictors. The computational time of AI-based models is much less compared with physical-based models. Furthermore, the AI-based approaches have been found to be highly adaptable to different hydrological and ecological conditions [19]. All these traits give the AI techniques great potential for the modeling of river DO concentration [20].
The AI techniques used for modeling DO concentration can be broadly divided into four groups [22,23]: (i) ANN [1,12,24,25,26,27,28,29,30,31,32,33]; (ii) SVM [22,34,35,36,37]; (iii) fuzzy logic [5,38,39,40,41] and (iv) heuristic models [37,42,43,44,45]. Among these, the ANN-based models have been most widely utilized compared with others for the prediction of river DO concentration. Heddam [33] utilized a generalized regression neural network (GRNN) for predicating DO concentration. He compared the performance of GRNN with multiple linear regressions (MLR) and showed the better prediction capability of GRNN compared with MLR. Nemati et al. [43] compared the performance of an adaptive neuro-fuzzy inference system (ANFIS) and genetic programming (GP) for prediction of DO concentration in a river in Hong Kong and found ANFIS to be more efficient compared with GP in predicting DO concentration. Mohammadpour et al. [45] used a feedforward backpropagation neural network (BPNN) for the prediction of DO concentration. They improved the model performance through optimization of BPNN parameters using particle swarm optimization (PSO) and compared the results with those obtained using SVM. Based on the root mean square error (RMSE) values, they reported that ANN-PSO has higher prediction capability than SVM. Heddam [32] compared the performance of a multilayer perceptron neural network (MPNL) with SVM and least square SVM (LSSVM) for the estimation of river DO concentration and showed superior performance of MPNL compared with SVM and LSSVM. Ay and Kisi [28] and Akkoyunlu et al. [27] used multilayer perceptron neural networks (MLPNNs) and radial basis function neural networks (RBFNNs) to predict DO concentration in USA and Turkey, respectively, and showed their efficiency. Bayram et al. [29] compared the regression and teaching–learning-based optimization approaches to estimate DO concentration in Turkey by employing temperature of air and water as predictors and indicated improvement in model performance through optimization. Kisi et al. [42] assessed the performance of MLPNN, GP, and ANFIS in predicting DO concentration and showed that GP is more capable than others in terms of prediction accuracy.
Besides ANNs, SVMs have also been extensively employed for prediction of river DO concentration [46,47,48]. Liu et al. [34] optimized the parameters of SVM using PSO to develop an SVM-PSO model for the prediction of DO concentration. They compared the results of SVM-PSO with those of ANN and GP and reported better performance of SVM-PSO. Liu et al. [35] improved the accuracy of LSSVM in the prediction of DO concentration by developing an LSSVM-PSO model and showed that the LSSVM-PSO is more accurate than LSSVM in prediction of DO concentration. Malek et al. (2014) assessed the performance of SVM in the prediction of DO concentration in two different lakes in Malaysia and reported that SVM models using dichotomized values of DO can provide high prediction accuracy [49]. Jadhav et al. compared the performance of LSSVM and GP for estimation of DO concentration in a lake in India and reported similar capabilities of both GP and LSSVM in prediction [37]. An excellent employment of LSSVM for prediction of DO in crab ponds of China was conducted by [50]; the authors found higher accuracy of LSSVM compared with RBFNN. Recently, a new study compared the performance of LSSVM, multivariate adaptive regression splines (MARS), and M5 model trees in the prediction of DO concentration and reported the performance of LSSVM as being very close to that of MARS [51].
The studies revealed the superiority of different AI methods in predicting DO concentration under different environmental conditions. Most of the SVM-based approaches revealed LSSVM as a useful method for estimation of the water quality parameters. However, all the studies reported that the efficiency of LSSVM models significantly depends on the values of the kernel (σ) and regularization (γ) parameters. These hyper-parameters can be considered as decision variables and should be determined accurately by optimization algorithms for better performance of LSSVM models. A number of studies employed different optimization techniques for estimation of optimum values of LSSVM parameters including heuristic optimization approaches such as GA [52,53,54], PSO [34,55,56,57,58,59], and Colony [60,61] algorithms. In this study, the hyper-parameters of LSSVM were optimized using the Bat algorithm (BA). The proposed hybrid metaheuristic LSSVM-BA algorithm is used for the prediction of DO concentration. The BA has been widely utilized for parameter optimization of the model used in forecasting climatological variables [62,63] and reservoir operation [64,65]. The studies reported BA as an efficient optimization technique. Therefore, it is expected that optimization of LSSVM parameters using BA would significantly improve the prediction capability of LSSVM and the LSSVM-BA model can be used for better prediction of DO concentration in water bodies.
The main objective of this study is to evaluate the capability of the hybrid metaheuristic LSSVM-BA model in the estimation of monthly DO concentration at three locations of the USA, which has been previously investigated using different AI-based approaches [24,32,33]. The results obtained using LSSVM-BA are compared with those obtained using M5 and MARS. M5 and MARS have been used for the comparison of the performance of LSSVM-BA as they have been found to be highly efficient in the prediction of hydrological variables in a number of recent studies [51,66]. Heddam and Kisi (2018) employed both MARS and M5 for the prediction of DO concentration at the same locations to compare their performance with LSSVM [51]. Therefore, comparison of performance of LSSVM-BA with MARS and M5 will help to assess the improvement of the performance of LSSVM after integration with BA.
2. Materials and Methods
2.1. LSSVM
LSSVM [59] is an edited version of SVM [67]. The SVM acts based on a set of quadratic programming problems [68] while the LSSVM acts based on linear programming and linear equations to improve the performance of the SVM. A nonlinear mapping function is used in LSSVM (Figure 1) which is based on following Equations (1) and (2) [69]:
where is a nonlinear function used for the mapping of the input variables to a higher-dimensional space, wT is the weight vector, and b is the bias term. The values of b and wT are computed using the following cost function:
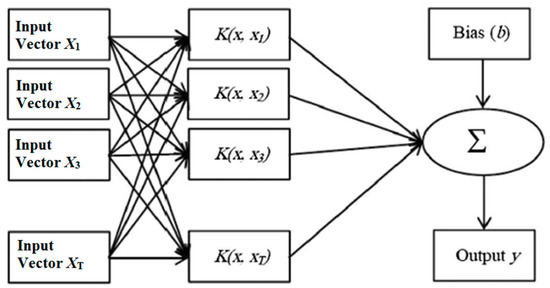
Figure 1.
Diagram showing the structure of a typical Least Square Support Vector Machine (LSSVM) model.
The following constraints are considered for the cost function:
where γ is the regularization parameter; N is the number of datapoints; xi and yi are the parameters which are defined as input parameter (pH, temperature, depth sensor, and other parameters) and output parameter (DO concentration), respectively; and is the residual vector for the input data. A kind of convex optimization problem is generated based on Equations (3) and (4) which is solved by the Lagrange Multipliers method based on the following equation:
where is the Lagrange Multiplier and the following equation is computed based on the partial derivative of Equation (5) with consideration of [69]:
The kernel function is defined based on the following equation:
Then, Equation (7) is inserted into Equation (6) and the following equation is generated:
There are several kinds of kernel functions which can be used. Previous studies showed that the radial basis function has the better performance [24] and, thus, it is used in this study:
The σ and γ are important parameters which have a significant impact on the final results. In the present study, the values of these parameters are inserted into the bat algorithm as decision variables in order to obtain the optimum values.
2.2. Bat Algorithm
The bat generates a loud sound which is returned back through reflection from surrounding objects including its prey. Based on this echolocation ability, the bat can identify its prey. The following assumptions are considered in the bat algorithm [70]:
- All bats use the echolocation ability for the identification of prey based on received sounds from the surroundings.
- Each bat has random velocity () at the position and the loudness, wavelength, and frequency of received sounds are , , and , respectively.
- The loudness varies from a large positive value to a minimum value.
The bats have the pulsation rate which varies from 0 to 1, where 0 means the pulsation rate has reached its minimum, while 1 means it has reached its maximum. The velocity, frequency, and position values for bats are updated based on the following Equations (10)–(12):
where, is the position at time t − 1, is a random vector between 0 and 1, is the minimum frequency, is the maximum frequency, is the best location for bats, t means time step, and indicates the velocity for bats. Then, local search based on a random walk is considered based on the following equation:
where A(t) is loudness and is a random number between −1 and 1.
The loudness and pulsation rate are updated at each level. When the bats find the prey, the loudness value decreases and the pulsation rate increases based on Equation (14):
where and are constant parameters.
2.3. LSSVM-BA Algorithm
- The bats’ positions are considered as decision variables and the values of
and are the LSSVM parameters which need to be optimized based on an objective function such as RMSE estimated from simulated DO and measured DO values. The improvement of LSSVM in the current study is done based on the following steps:
- The initial values for the random parameters in the bat algorithm and and parameters are initialized in the first level.
- A counter number is considered for this level, such as in Figure 2.
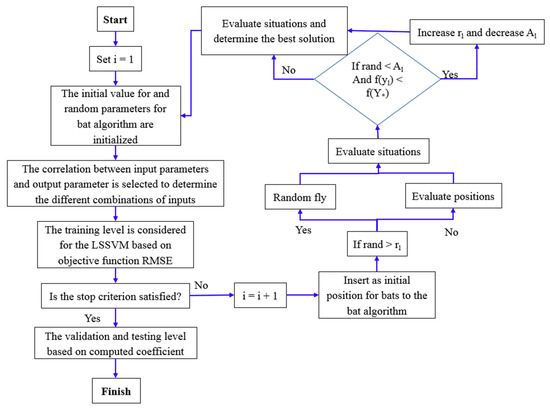 Figure 2. The flowchart showing the LSSVM–Bat Algorithm (BA) algorithm.
Figure 2. The flowchart showing the LSSVM–Bat Algorithm (BA) algorithm. - The kind of kernel function and the inputs and output are selected and the correlation between inputs and output is measured to determine the effective combination of inputs.
- The model is trained, and the performance of the method is evaluated based on objective function such as RMSE.
- The stop criterion is checked and if it is satisfied, the algorithm is shifted to the validation and testing phases and the results based on extracted parameters of and are considered for making a decision on the continuation of the method.
- The values of and as initial positions of bats are inserted into the bat algorithm. In fact, they are considered as decision variables.
- If rand > rl is considered, the positions based on objective functions are evaluated; otherwise, the random fly is considered and shifted to the next level.
- If rand < Al and f(yl) < f() is considered, the rl is increased and Al is decreased; otherwise, the bats’ situations are evaluated and switched to next level.
- One number is added to the counter and then switched to the third level.
The simulation process for the modeling of DO concentration is considered for the first level. Then, the objective function is computed, and the convergence criteria are checked. The unknown parameters are added to the bat algorithm as decision variables and, subsequently, the objective function is computed. The unknown values of the parameters are considered as bats’ positions. There are two constraints in this level. The least DO with its minimum and maximum values, which are considered as the lower and upper bounds of the computed value of DO, are supplied to the model. The model computes the value of DO based on these constraints. If these constraints cannot be satisfied, the penalty functions are applied on the objective function of the bat algorithm so that the algorithm understands not to exit from the permissible domain. Therefore, the model acts for different conditions so that the application of the constraints can produce reliable results in critical conditions.
2.4. M5 Tree
One of the successful models in simulation applications in water engineering and hydrology is M5 [66,69,71]. The M5 tree acts based on tree classification [72], which can be used for generating relationships between independent and dependent variables. This model is a combination of linear regression and a tree model which can be used for any kind of qualitative or quantitative data. The domain of data in the M5 model is divided into subsets which are known as leaves. The linear regression equation is given to leaves in contrast to the tree regression model which gives numerical labels to the subsets. The model can predict the continuous variables well. Each decision-making tree has a structure like a tree which including roots, branches, nodes, and leaves. The root as the first node is located in the upper section and the chain of branches and nodes reaches to the leaves. Each node is considered as a predicative variable. The generation of the model is considered based on two levels. The decision tree is generated based on the standard deviation reduction (SDR) criterion in the child node with the branching of data:
where T is number of samples in each node, is the number of subsets which is generated based on splitting of each node, sd is the standard deviation, and SDR is the reduced standard deviation. The model selects the branch which has the least SDR. The classification process in the tree can cause a larger structure due to a large number of generations of branches. The second level is known as pruning, which substitutes the subtrees with the linear regression function, pruning the big tree; the tree model divides the sample space among the subtrees and a tree region model is generated in each subtree.
2.5. Multivariate Adaptive Regression Spline (MARS)
The MARS is a simple tool which is widely used for hydrological simulations for better accuracy [69,73,74]. The structure of MARS before modeling is not specific and, thus, it is a nonparametric model. This method can model the nonlinear relationship between predicator variables and an objective decision. In fact, this method divides the data into subsets and then fits the functions as a basis function which corresponds with the complexity of data. Adaptive regression for the model is based on the following equation:
where is the dependent variable, is a constant term, is the basis function, is the coefficient of the Mth basis function, and m is the number of the nonzero terms or the terms by which the basis functions are divided in these nodes.
The first level of the model is related to the forward stage. The model starts from a constant term and then the basis functions are added to this term gradually. The model adds the basis functions which can decrease RMSE. The forward stage causes overfitting of data, which means that the model fits data which have been involved in the modeling process, but does not provide a good fit for the data which have not participated in the modeling process. When the model can have a good fit for all data, the backward stage is considered for the modeling process. In fact, the backward stage means the pruning of the basis functions which have the least effect in the modeling process. Thus, the determinant of such models is computed based on the generalized cross validation (GCV):
where M is the number of basis functions, N is the number of datapoints, is the true value at , is the forecasted value, and c is the complexity function. The value is a complexity penalty which is computed based on following equation:
where d is the penalizing factor.
3. Case Study
Three stations located in Washington County (USGS 14206950), Summit County (USGS 10133800), and New Jersey (USGS 01463500) of the USA are considered as the case study (Figure 3). The water quality data recorded at those three stations for the period January 2002 to December 2016 were extracted from the United States Geological Survey (USGS) website (USGS, 2017). In fact, data for several water quality monitoring stations are available on the USGS website that could be used for the development of model. Nevertheless, the data for all the water quality parameters are not available or not reliable for the selected duration at most of the stations. In addition, as can be observed from Figure 3, the three selected stations are located at different regions which can allow us to examine the performance of the proposed models under different geographical and climatic conditions. Furthermore, Heddam and Kisi (2018) developed a model for the prediction of DO concentration at the same stations [51]. In order to carry out a rational comparison with the previous research findings, the proposed models are developed for the prediction of DO concentration at the same selected stations.
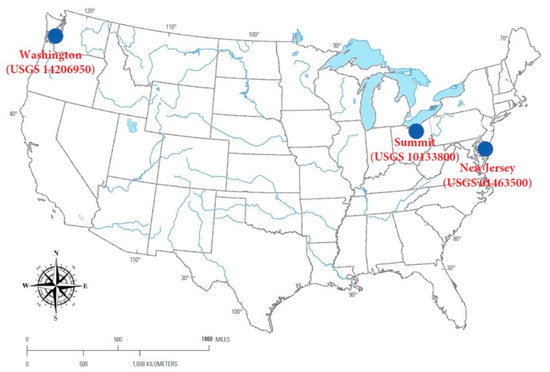
Figure 3.
The locations of the three case study sites in Washington (USGS 14206950), Summit (USGS 10133800), and New Jersey (USGS 01463500), USA.
The observed data were divided into three sets for the training (2002–2010), validation (2011–2013), and testing (2014–2016) of the models at USGS 10133800 and USGS 01463500, while data for the period 2003–2010 was used for training at USGS 14206950 as data are available only from 2003 at this station. More details of the geographical information and historical data division for the training, validation, and testing of the model are given in Table 1. The water quality parameters including water temperature (WT), discharge (Q, cfs), pH (sd, unit), specific conductance (SC, µS/cm), and DO (mg/lit) are used in the present study. Table 2 shows the statistical information of the water quality parameters. The Pearson coefficient based on the following equation is used to measure the correlation of different parameters with DO:
where cov is the covariance between quantitative X and Y; and are the standard deviations of X and Y, respectively; and are the averages of X and Y, respectively; and is the expectation value.

Table 1.
Geographical information and division of historical data into the training, validation, and testing periods.

Table 2.
The statistical properties of the water quality variables used in this study at the three investigated monitoring stations.
The studied variables should be normalized to have the same scale so that the mean equals 0 and the standard deviation equals 1. The Z score method is used for this issue [75]:
where is the normalized parameter, is the mean value, and is the standard deviation.
The following indices are used for the evaluation of the different models:
where : observed DO, : average of observed DO, : predicated value of DO, : average predicated value of DO, N: number of datapoints, MAE: mean absolute error, RMSE: root-mean-square error, and R: determination of coefficient [76,77].
4. Results and Discussion
4.1. The Correlations between DO and Other Water Quality Parameters
Table 3 presents the correlation coefficient between DO and other water quality parameters. The highest correlation of DO is found with WT followed by SC at all three monitoring stations. The least value of correlation coefficient at all three stations was found for pH. Different input combinations were constructed based on the correlation analysis presented in Table 3. Table 4 shows different input combinations based on four water quality parameters, namely, WT, SC, Q, and pH. Two combinations are considered without WT to determine the effectiveness of other parameters in the absence of WT in predicting DO. Besides this, two combinations of three variables and one combination of four variables were suggested for investigating the optimum input variables for prediction of DO.

Table 3.
The correlation coefficients between DO and other water quality parameters.

Table 4.
The input combinations used for the development of prediction models.
4.2. Sensitivity Analysis of Bat Algorithm Parameters
The root-mean-square error is considered as the objective function for the evaluation of results. The evolutionary nature-inspired algorithms have parameters with random natures and, thus, sensitivity analysis is necessary to determine the accurate values of these parameters. The parameter values are varied, and the sensitivity of the parameters is computed against the variations of the objective function. When the RMSE is selected as the objective function, the aim of the problem is to minimize the objective function to compute the best value of different parameters. The first combination of inputs is selected for the explanation of the sensitivity analysis. The results of the sensitivity analysis using other input combinations are not provided in order to avoid repetition.
An important point to report here is that there are some parameters such as the maximum frequency, minimum frequency, and loudness that drive bats in the optimized path. The decision variables are bats’ positions or unknown parameters of LSSVM. The parameters such as maximum frequency, minimum frequency, or loudness are mathematical or physical parameters that lead the bats or solution to the best position or best solution. Therefore, these parameters adjust the sounds and the bats are led to the best position for finding the food (or the best solution).
Table 5 shows the results of sensitivity analysis of the bat algorithm at all the three investigated water quality monitoring stations. The population size for the bat algorithm was varied from 20 to 80. The objective function was found to have the least value (0.882 mg/lit) for the population size 60 at the USGS 14206950 station. The minimum frequency was varied from 0.1 to 0.4 and the best value was obtained as 0.2. The maximum frequency was varied between 0.30 and 0.90 and the least value (0.882 mg/lit) of the objective function was found for 0.7 Hz. The least value of the objective function was found for the maximum loudness of 5 dB. The maximum number for the basis function for the MARS model at all the stations is considered as 130. The backward stage based on the condition of the problem and inputs are considered for tree pruning in order to have the maximum pruning. The M5 Tree model does not require any user-defined parameters. The process continues for the M5 Tree model until the SDR value is smaller than the expected value. All the methods have the same complexity, in terms of computation time.

Table 5.
The sensitivity of the parameters of the bat algorithm at the three investigated water quality monitoring stations.
4.3. Modeling River Dissolved Oxygen Concentration
Table 6 shows the performance of the different predictive models with different input combinations over the training, validation, and testing phases at USGS 14206950 station. The least values of the absolute error are found for the first input combination for all the predictive models (LSSVM-BA, M5 Tree, and MARS). This indicates that it is possible to supply more information to the predictive model through incorporation of all the predictors. The worst performance is noticed for LSSVM-BA 4 and LSSVM-BA 5 models during the training phase. Better performance of LSSVM-BA compared with M5 Tree and MARS models is found consistently for all the input combinations.

Table 6.
The performance indicators of the predictive models during training/validation/testing phases at USGS 14206950.
The least values of RMSE and MAE are found for the LSSVM-BA 1 during training (0.672 and 0.425 mg/lit), validation (0.689 and 0.912 mg/lit), and testing (0.882 and 0.588 mg/lit). The first input combination is also found to be best in terms of correlation. The results in Table 6 demonstrate the significance of WT in the prediction of DO. The LSSVM-BA 1 showed enhancement over M5 Tree 1 and MARS 1 by 20% and 42% in terms of RMSE and 13% and 45% in terms of MAE, respectively, during the testing phase. This clearly indicates the capability of the integrative model (LSSVM-BA) and the potential of the nature-inspired algorithm for tuning LSSVM parameters.
Table 7 shows the performance of the LSSVM-BA, M5 Tree, and MARS models in prediction of DO at USGS 10133800 station during all the modeling phases. From Table 7, it is clear that LSSVM-BA performed better compared with the M5 tree and MARS. This can be elaborated through the results of RMSE and MAE. The least values of RMSE and MAE are achieved for the LSSVM-BA 1 during model training (0.712 and 0.525 mg/lit), validation (0.745 and 0.597 mg/lit), and testing (0.892 and 0.888 mg/lit). The performance of the LSSVM-BA model is evaluated against the best results obtained using M5 Tree and MARS models. The prediction accuracy of LSSVM-BA model is found to improve in term of RMSE and MAE by 27% and 27.4%, and by 32% and 27.5% for M5 Tree and MARS models, respectively. The eighth input combination (LSSVM-BA 8), i.e., with two inputs, WT and SC, is found to have a performance close to that of the best input combination (LSSVM-BA 1). This indicates an alternative in the case of limited data. In such a condition, WT and SC only can be used for the development of a DO prediction model.

Table 7.
The performance of the predictive models during training/validation/testing at USGS 10133800 station.
It is worthwhile to validate the current research with the literature. The comparison of the results with those obtained in other studies showed that the LSSVM-BA can decrease RMSE in model prediction by about 5–11% compared with classical SVM [36]. There are some critical observations of Table 7. For example, all the three predictive models behave differently for the 5th input combination. The reason for this is the uncertainty and low correlation of DO with the input. With respect to this, a Bayesian method is considered for measuring the uncertainty of model parameters and their effect on DO [57]. The results showed that the pH has the least weight or most uncertainty among all the parameters. Thus, incorporation of more parameters does not guarantee the successful performance of the models.
Table 8 shows the performance of LSSVM-BA, M5 Tree, and MARS models during different modeling phases at USGS 01463500 station. Based on the statistical results presented in Table 8, the LSSVM-BA accomplishes the best results over the other models. The best results in term of RMSE and MAE are achieved for the first input combination and LSSVM-BA model during all the modeling phases. The best RMSE and MAE are found to be 0.814 and 0.545 mg/lit during training, 0.823 and 0.697 mg/lit during validation, and 0.895 and 0.889 mg/lit during testing. The evaluation of the proposed LSSVM-BA model compared with the best results obtained using the M5 Tree and MARS models during the testing phase revealed the better prediction accuracy of LSSVM-BA in terms of RMSE and MAE by 27.4% and 27.7% and 31.7% and 28.2% over the M5 Tree and MARS models.

Table 8.
The performance of the predictive models during training/validation/testing at USGS 01463500 station.
In general, the results of the three investigated stations are found to collaborate well with previous findings. Heddam and Kisi et al. (2017) showed that the regression methods without accurate estimation of some unknown parameters in their structure have a weaker performance compared with other AI methods such as ANN. Hence, the regression methods can be improved by the optimization of model parameters [77,78,79]. Other studies in the literature have also showed that the application of regression models with heuristic methods can improve model performance [80].
The performance of the models was also investigated using a scatter plot of observed and simulated values of DO concentration. Figure 4, Figure 5 and Figure 6 shows the scatter plots for all the three stations during three modeling phases (i.e., training, validation, and testing). In general, the proposed integrative model displays a better correlation performance compared with the M5 Tree and MARS models. A closer examination revealed that the prediction was excellent for the whole range of DO values (0.10–24.8 mg/lit) at USGS 14206950 station. Relatively lower performance for the DO concentrations between 6.5–7.9 and 9.7–11.18 mg/lit is observed at USGS 10133800 station, particularly during the testing phase. This can be justified through the lack of the input attribute information at this particular station. Besides this, the concentration of dissolved oxygen may be affected by other environmental influences at this station. Relatively better performance in prediction of all values of DO concentration (5.4–16.9 mg/lit) is observed at USGS 01463500 station.
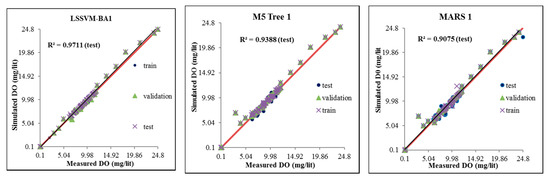
Figure 4.
Scatter plot of observed and simulated DO concentration by three predictive models during model training, validation, and testing at USGS 14206950.
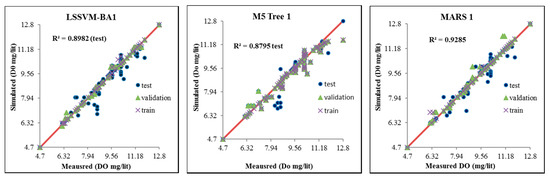
Figure 5.
Scatter plot of observed and simulated DO concentration by three predictive models during model training, validation, and testing at USGS 10133800.
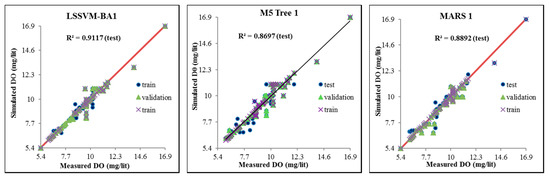
Figure 6.
Scatter plot of observed and simulated DO concentration by three predictive models during model training, validation, and testing at USGS 01463500.
5. Conclusions
Water quality is a major concern in water resource management. Among several water quality variables, DO is the main concern in term of aquatic environment and ecology. The magnitude of DO relies on several other water quality variables and interactions among the variables, and, thus, the modeling of DO is an interesting but complex topic in environmental science. A novel modeling strategy based on integration of a nature-inspired algorithm with LSSVM was proposed in this study for the prediction of DO at three river water quality monitoring stations located in the USA. The results were compared with those obtained using MT5 and MARS models. The overall findings of the study are as follows:
- The performance of LSSVM-BA 1 was found to be best among all the models based on higher correlation (see Figure 4) and lower RMSE and MAE compared with the other models at all three stations (see Table 6, Table 7 and Table 8). For instance, LSSVM-BA 1 for the USGS 14206950 station showed better accuracy by 3.1%, 11%, 45%, 40%, 27%, 28%, and 29% than the LSSVM-BA 2, LSSVM-BA 3, LSSVM-BA 4, LSSVM-BA 5, LSSVM-BA 6, LSSVM-BA 7, and LSSVM-BA 8 models.
- The MARS 1 and M5 Tree 1 models showed the lowest RMSE and MAE among all the MARS and M5 Tree models at all three stations during all three modeling phases (training, validation, and testing).
- The fourth and the fifth input combinations (without the WT parameter) showed the worst performance among all the input combinations at all the three stations at all the three modeling phases, which indicates the importance of WT in prediction of DO.
- All three predictive models (LSSVM, MARS, and M5 Tree) showed relatively better performance when only WT and SC were used as input at two stations, namely, USGS 10133800 and USGS 01463500, which indicates that WT and SC can be used for reasonable prediction of DO when other water quality data are not available.
Overall, the results showed better performance of the LSSVM-BA model compared with other models. As further research, the nature-inspired algorithms used in the current research can be considered for the improvement of other methods such as ANN and ANFIS. Furthermore, the performance of LSSVM-BA against those improved models can be evaluated to find the best model for river DO prediction. In addition, the improved models can be used for the prediction of daily or hourly DO concentration in shallow water bodies to show their efficacy in prediction of DO concentration under different environmental conditions.
Author Contributions
Conceptualization, Ahmed El-Shafie; Methodology, Mohammad Ehteram; Software, Mohammad Ehteram; Validation, Zaher Mundher Yaseen and Ahmad Sharafati; Formal Analysis, Nadhir Al-Ansari; Investigation, Nadhir Al-Ansari; Data Curation, Mohammad Ehteram; Writing-Original Draft Preparation, Mohammad Ehteram and Ahmad Sharafati; Writing-Review & Editing, Shamsuddin Shahid; Visualization, Zaher Mundher Yaseen; Supervision, Ahmed El-Shafie.
Funding
The research was funded by the Universiti Teknologi Malaysia GUP grant No. 19H44.
Acknowledgments
The authors thank the reviewers and editors for their significant comments to improve the paper context.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Šiljić Tomić, A.; Antanasijević, D.; Ristić, M.; Perić-Grujić, A.; Pocajt, V. A linear and non-linear polynomial neural network modeling of dissolved oxygen content in surface water: Inter- and extrapolation performance with inputs’ significance analysis. Sci. Total Environ. 2018, 610–611, 1038–1046. [Google Scholar] [CrossRef] [PubMed]
- Post, C.J.; Cope, M.P.; Gerard, P.D.; Masto, N.M.; Vine, J.R.; Stiglitz, R.Y.; Hallstrom, J.O.; Newman, J.C.; Mikhailova, E.A. Monitoring spatial and temporal variation of dissolved oxygen and water temperature in the Savannah River using a sensor network. Environ. Monit. Assess. 2018, 190, 272. [Google Scholar] [CrossRef] [PubMed]
- Boyd, C.E.; Torrans, E.L.; Tucker, C.S. Dissolved Oxygen and Aeration in Ictalurid Catfish Aquaculture. J. World Aquac. Soc. 2018, 49, 7–70. [Google Scholar] [CrossRef]
- Reeder, W.J.; Quick, A.M.; Farrell, T.B.; Benner, S.G.; Feris, K.P.; Tonina, D. Spatial and Temporal Dynamics of Dissolved Oxygen Concentrations and Bioactivity in the Hyporheic Zone. Water Resour. Res. 2018. [Google Scholar] [CrossRef]
- Khan, U.T.; Valeo, C. Comparing a Bayesian and fuzzy number approach to uncertainty quantification in short-term dissolved oxygen prediction. J. Environ. Inform. 2017, 30, 1–16. [Google Scholar] [CrossRef]
- He, J.; Chu, A.; Ryan, M.C.; Valeo, C.; Zaitlin, B. Abiotic influences on dissolved oxygen in a riverine environment. Ecol. Eng. 2011, 37, 1804–1814. [Google Scholar] [CrossRef]
- Chapra, S.C.; Pelletier, G.J.; Tao, H. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality: Documentation and Users Manual; Civil and Environmental Engineering Dept., Tufts University: Medford, MA, USA, 2003. [Google Scholar]
- Wool, T.A.; Ambrose, R.B.; Martin, J.L.; Comer, E.A.; Tech, T. Water quality analysis simulation program (WASP). 2006. Available online: https://www.epa.gov/ceam/water-quality-analysis-simulation-program-wasp (accessed on 22 August 2018).
- Ahmed, A.A.M. Prediction of dissolved oxygen in Surma River by biochemical oxygen demand and chemical oxygen demand using the artificial neural networks (ANNs). J. King Saud Univ.—Eng. Sci. 2017, 29, 151–158. [Google Scholar] [CrossRef]
- Cox, B.A. A review of dissolved oxygen modelling techniques for lowland rivers. Sci. Total Environ. 2003, 314, 303–334. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Scholz, M. Modeling of Dissolved Oxygen Applying Stepwise Regression and a Template-Based Fuzzy Logic System. J. Environ. Eng. 2014. [Google Scholar] [CrossRef]
- Li, X.; Sha, J.; Wang, Z. A comparative study of multiple linear regression, artificial neural network and support vector machine for the prediction of dissolved oxygen. Hydrol. Res. 2017, 48, 1214–1225. [Google Scholar] [CrossRef]
- Kuok, K.K.; Kueh, S.M.; Chiu, P.C. Bat optimisation neural networks for rainfall forecasting: Case study for Kuching city. J. Water Clim. Chang. 2018. [Google Scholar] [CrossRef]
- Sulaiman, J.; Wahab, S.H. Heavy Rainfall Forecasting Model Using Artificial Neural Network for Flood Prone Area. In IT Convergence and Security 2017; Springer: Singapore, 2018; pp. 68–76. [Google Scholar]
- Shank, D.B.; Hoogenboom, G.; McClendon, R.W. Dewpoint temperature prediction using artificial neural networks. J. Appl. Meteorol. Climatol. 2008, 47, 1757–1769. [Google Scholar] [CrossRef]
- Radhika, Y.; Shashi, M. Atmospheric temperature prediction using support vector machines. Int. J. Comput. Theory Eng. 2009, 1, 55. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. M5 model tree based modelling of reference evapotranspiration. Hydrol. Process. 2009, 23, 1437–1443. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support Vector Regression for Rainfall-Runoff Modeling in Urban Drainage: A Comparison with the EPA’s Storm Water Management Model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; De Marinis, G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water 2017, 9, 2. [Google Scholar] [CrossRef]
- Liu, Y.; Sang, Y.-F.; Li, X.; Hu, J.; Liang, K. Long-Term Streamflow Forecasting Based on Relevance Vector Machine Model. Water 2016, 9, 9. [Google Scholar] [CrossRef]
- Candelieri, A. Clustering and support vector regression for water demand forecasting and anomaly detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Ji, X.; Shang, X.; Dahlgren, R.A.; Zhang, M. Prediction of dissolved oxygen concentration in hypoxic river systems using support vector machine: A case study of Wen-Rui Tang River, China. Environ. Sci. Pollut. Res. 2017, 24, 16062–16076. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Yin, H.; Chapra, S.C.; Zhou, Q. Modelling dissolved oxygen depression in an urban river in China. Water 2017, 9, 520. [Google Scholar] [CrossRef]
- Heddam, S.; Kisi, O. Extreme learning machines: A new approach for modeling dissolved oxygen (DO) concentration with and without water quality variables as predictors. Environ. Sci. Pollut. Res. 2017, 24, 16702–16724. [Google Scholar] [CrossRef] [PubMed]
- Keshtegar, B.; Heddam, S. Modeling daily dissolved oxygen concentration using modified response surface method and artificial neural network: A comparative study. Neural Comput. Appl. 2017, 1–12. [Google Scholar] [CrossRef]
- Liu, S.; Yan, M.; Tai, H.; Xu, L.; Li, D. Prediction of dissolved oxygen content in aquaculture of Hyriopsis Cumingii using Elman neural network. 2011. Available online: https://link.springer.com/chapter/10.1007/978-3-642-27275-2_57 (accessed on 22 August 2018).
- Akkoyunlu, A.; Altun, H.; Cigizoglu, H.K. Depth-integrated estimation of dissolved oxygen in a lake. J. Environ. Eng. 2011, 137, 961–967. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Modeling of dissolved oxygen concentration using different neural network techniques in Foundation Creek, El Paso County, Colorado. J. Environ. Eng. 2011, 138, 654–662. [Google Scholar] [CrossRef]
- Bayram, A.; Uzlu, E.; Kankal, M.; Dede, T. Modeling stream dissolved oxygen concentration using teaching–learning based optimization algorithm. Environ. Earth Sci. 2015, 73, 6565–6576. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, J.; Yu, H.; Zhen, Z.; Li, D. Three-dimensional short-term prediction model of dissolved oxygen content based on pso-bpann algorithm coupled with kriging interpolation. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Diamantopoulou, M.J.; Antonopoulos, V.Z.; Papamichail, D.M. Cascade correlation artificial neural networks for estimating missing monthly values of water quality parameters in rivers. Water Resour. Manag. 2007, 21, 649–662. [Google Scholar] [CrossRef]
- Heddam, S. Use of optimally pruned extreme learning machine (OP-ELM) in forecasting dissolved oxygen concentration (DO) several hours in advance: A case study from the Klamath River, Oregon, USA. Environ. Process. 2016, 3, 909–937. [Google Scholar] [CrossRef]
- Heddam, S. Generalized regression neural network (GRNN)-based approach for colored dissolved organic matter (CDOM) retrieval: Case study of Connecticut River at Middle Haddam Station, USA. Environ. Monit. Assess. 2014, 186, 7837–7848. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Xu, L.; Li, D.; Li, Q.; Jiang, Y.; Tai, H.; Zeng, L. Prediction of dissolved oxygen content in river crab culture based on least squares support vector regression optimized by improved particle swarm optimization. Comput. Electron. Agric. 2013, 95, 82–91. [Google Scholar] [CrossRef]
- Liu, S.; Xu, L.; Jiang, Y.; Li, D.; Chen, Y.; Li, Z. A hybrid WA–CPSO-LSSVR model for dissolved oxygen content prediction in crab culture. Eng. Appl. Artif. Intell. 2014, 29, 114–124. [Google Scholar] [CrossRef]
- Mohammadpour, R.; Shaharuddin, S.; Chang, C.K.; Zakaria, N.A.; Ghani, A.A.; Chan, N.W. Prediction of water quality index in constructed wetlands using support vector machine. Environ. Sci. Pollut. Res. 2014, 6208–6219. [Google Scholar] [CrossRef] [PubMed]
- Jadhav, M.S.; Khare, K.C.; Warke, A.S. Water Quality Prediction of Gangapur Reservoir (India) Using LS-SVM and Genetic Programming. Lakes Reserv. Res. Manag. 2015, 20, 275–284. [Google Scholar] [CrossRef]
- Ranković, V.; Radulović, J.; Radojević, I.; Ostojić, A.; Čomić, L. Prediction of dissolved oxygen in reservoirs using adaptive network-based fuzzy inference system. J. Hydroinform. 2012, 14, 167–179. [Google Scholar] [CrossRef]
- Heddam, S. Modeling hourly dissolved oxygen concentration (DO) using two different adaptive neuro-fuzzy inference systems (ANFIS): A comparative study. Environ. Monit. Assess. 2014, 186, 597–619. [Google Scholar] [CrossRef] [PubMed]
- Heddam, S. Modelling hourly dissolved oxygen concentration (DO) using dynamic evolving neural-fuzzy inference system (DENFIS)-based approach: Case study of Klamath River at Miller Island Boat Ramp, OR, USA. Environ. Sci. Pollut. Res. 2014, 21, 9212–9227. [Google Scholar] [CrossRef] [PubMed]
- Ay, M.; Kişi, Ö. Estimation of dissolved oxygen by using neural networks and neuro fuzzy computing techniques. KSCE J. Civ. Eng. 2017, 21, 1631–1639. [Google Scholar] [CrossRef]
- Kisi, O.; Akbari, N.; Sanatipour, M.; Hashemi, A.; Teimourzadeh, K.; Shiri, J. Modeling of dissolved oxygen in river water using artificial intelligence techniques. J. Environ. Inform. 2013, 22, 92–101. [Google Scholar] [CrossRef]
- Nemati, S.; Fazelifard, M.H.; Terzi, Ö.; Ghorbani, M.A. Estimation of dissolved oxygen using data-driven techniques in the Tai Po River, Hong Kong. Environ. Earth Sci. 2015, 74, 4065–4073. [Google Scholar] [CrossRef]
- Khani, S.; Rajaee, T. Modeling of Dissolved Oxygen Concentration and Its Hysteresis Behavior in Rivers Using Wavelet Transform-Based Hybrid Models. CLEAN—Soil Air Water 2017, 45. [Google Scholar] [CrossRef]
- Mehdipour, V.; Memarianfard, M.; Homayounfar, F. Application of gene expression programming to water dissolved oxygen concentration prediction. Int. J. Hum. Cap. Urban. Manag. 2017, 2, 39–48. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, N.; Gupta, S. Support vector machines in water quality management. Anal. Chim. Acta 2011, 703, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Tan, G.; Yan, J.; Gao, C.; Yang, S. Prediction of water quality time series data based on least squares support vector machine. Procedia Eng. 2012, 31, 1194–1199. [Google Scholar] [CrossRef]
- Granata, F.; De Marinis, G. Machine learning methods for wastewater hydraulics. Flow Meas. Instrum. 2017, 57, 1–9. [Google Scholar] [CrossRef]
- Malek, S.; Mosleh, M.; Syed, S.M. Dissolved oxygen prediction using support vector machine. Int. J. Bioeng. Life Sci. 2014, 8, 46–50. [Google Scholar]
- Yu, H.; Chen, Y.; Hassan, S.; Li, D. Dissolved oxygen content prediction in crab culture using a hybrid intelligent method. Sci. Rep. 2016. [Google Scholar] [CrossRef] [PubMed]
- Heddam, S.; Kisi, O. Modelling daily dissolved oxygen concentration using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Zhu, X.; Ma, S.; Xu, Q. A WD-GA-LSSVM model for rainfall-triggered landslide displacement prediction. J. Mt. Sci. 2018, 15, 156–166. [Google Scholar] [CrossRef]
- Rostami, A.; Baghban, A. Application of a supervised learning machine for accurate prognostication of higher heating values of solid wastes. Energy Sources Part. A Recov. Util. Environ. Eff. 2018, 40, 558–564. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Nazari, M.A.; Mahian, O.; Ghasempour, R. A proposed model to predict thermal conductivity ratio of Al2O3/EG nanofluid by applying least squares support vector machine (LSSVM) and genetic algorithm as a connectionist approach. J. Therm. Anal. Calorim. 2018, 1–11. [Google Scholar] [CrossRef]
- Huan, J.; Cao, W.; Qin, Y. Prediction of dissolved oxygen in aquaculture based on EEMD and LSSVM optimized by the Bayesian evidence framework. Comput. Electron. Agric. 2018, 150, 257–265. [Google Scholar] [CrossRef]
- Wang, P.; Liu, C.; Li, Y. Estimation method for ET0 with PSO-LSSVM based on the HHT in cold and arid data-sparse area. Clust. Comput. 2018, 1–10. [Google Scholar] [CrossRef]
- Wu, Y.-H.; Shen, H. Grey-related least squares support vector machine optimization model and its application in predicting natural gas consumption demand. J. Comput. Appl. Math. 2018, 338, 212–220. [Google Scholar] [CrossRef]
- Zhao, H.; Huang, G.; Yan, N. Forecasting Energy-Related CO2 Emissions Employing a Novel SSA-LSSVM Model: Considering Structural Factors in China. Energies 2018, 11, 781. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, Y.; Liu, J.; Wei, H.; Zhao, J.; Liao, R. A novel model based on wavelet LS-SVM integrated improved PSO algorithm for forecasting of dissolved gas contents in power transformers. Electr. Power Syst. Res. 2018, 155, 196–205. [Google Scholar] [CrossRef]
- Li, Y.; Yang, P.; Wang, H. Short-term wind speed forecasting based on improved ant colony algorithm for LSSVM. Clust. Comput. 2018, 1–7. [Google Scholar] [CrossRef]
- Niu, D.; Li, S.; Dai, S. Comprehensive Evaluation for Operating Efficiency of Electricity Retail Companies Based on the Improved TOPSIS Method and LSSVM Optimized by Modified Ant Colony Algorithm from the View of Sustainable Development. Sustainability 2018, 10, 860. [Google Scholar] [CrossRef]
- Li, W.K.; Wang, W.L.; Li, L. Optimization of water resources utilization by multi-objective moth-flame algorithm. Water Resour. Manag. 2018, 1–14. [Google Scholar] [CrossRef]
- Lotfinejad, M.M.; Hafezi, R.; Khanali, M.; Hosseini, S.S.; Mehrpooya, M.; Shamshirband, S. A comparative assessment of predicting daily solar radiation using bat neural network (BNN), generalized regression neural network (GRNN), and neuro-fuzzy (NF) system: A case study. Energies 2018, 11, 1188. [Google Scholar] [CrossRef]
- Ehteram, M.; Karami, H.; Farzin, S. Reservoir optimization for energy production using a new evolutionary algorithm based on multi-criteria decision-making models. Water Resour. Manag. 2018, 32, 2539–2560. [Google Scholar] [CrossRef]
- Ehteram, M.; Mousavi, S.F.; Karami, H.; Farzin, S.; Singh, V.P.; Chau, K.; El-Shafie, A. Reservoir operation based on evolutionary algorithms and multi-criteria decision-making under climate change and uncertainty. J. Hydroinform. 2018. [Google Scholar] [CrossRef]
- Kisi, O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Dibike, Y.B.; Velickov, S.; Solomatine, D.; Abbott, M.B. Model induction with support vector machines: Introduction and applications. J. Comput. Civ. Eng. 2001, 15, 208–216. [Google Scholar] [CrossRef]
- Yaseen, Z.; Kisi, O.; Demir, V. Enhancing long-term streamflow forecasting and predicting using periodicity data component: Application of artificial intelligence. Water Resour. Manag. 2016. [Google Scholar] [CrossRef]
- Bolouri-Yazdeli, Y.; Bozorg Haddad, O.; Fallah-Mehdipour, E.; Mariño, M.A. Evaluation of real-time operation rules in reservoir systems operation. Water Resour. Manag. 2014, 28, 715–729. [Google Scholar] [CrossRef]
- Keshtegar, B.; Piri, J.; Kisi, O. A nonlinear mathematical modeling of daily pan evaporation based on conjugate gradient method. Comput. Electron. Agric. 2016, 127, 120–130. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Sharda, V.N.; Prasher, S.O.; Patel, R.M.; Ojasvi, P.R.; Prakash, C. Performance of Multivariate Adaptive Regression Splines (MARS) in predicting runoff in mid-Himalayan micro-watersheds with limited data. Hydrol. Sci. J.—J. Des. Sci. Hydrol. 2008, 53, 1165–1175. [Google Scholar] [CrossRef]
- Kisi, O. Modeling reference evapotranspiration using three different heuristic regression approaches. Agric. Water Manag. 2016, 169, 162–172. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model. 2002. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ghareb, M.I.; Ebtehaj, I.; Bonakdari, H.; Ravinesh, D.; Siddique, R.; Heddam, S.; Yusif, A. Rainfall pattern forecasting using novel hybrid intelligent model based ANFIS-FFA. Water Resour. Manag. 2018, 32, 105–122. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ebtehaj, I.; Bonakdari, H.; Deo, R.C.; Mehr, A.D.; Hanna, W.; Wan, M.; Diop, L.; El-shafie, A.; Singh, V.P. Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. J. Hydrol. 2017, 554, 263–276. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Fu, M.; Wang, C.; Hanna, W.; Wan, M.; Deo, R.C.; El-shafie, A. Application of the Hybrid Artificial Neural Network Coupled with Rolling Mechanism and Grey Model Algorithms for Streamflow Forecasting over Multiple Time Horizons. Water Resour. Manag. 2018, 32, 1883–1899. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Deo, R.C.; Yaseen, Z.M.; Kashani, M.H. Pan evaporation prediction using a hybrid multilayer perceptron-firefly algorithm (MLP-FFA) model: Case study in North Iran. Theor. Appl. Climatol. 2018, 133, 1119–1131. [Google Scholar] [CrossRef]
- Fahimi, F.; Yaseen, Z.M.; El-shafie, A. Application of soft computing based hybrid models in hydrological variables modeling: A comprehensive review. Theor. Appl. Climatol. 2016, 1–29. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).