Monthly Rainfall-Runoff Modeling at Watershed Scale: A Comparative Study of Data-Driven and Theory-Driven Approaches
Abstract
1. Introduction
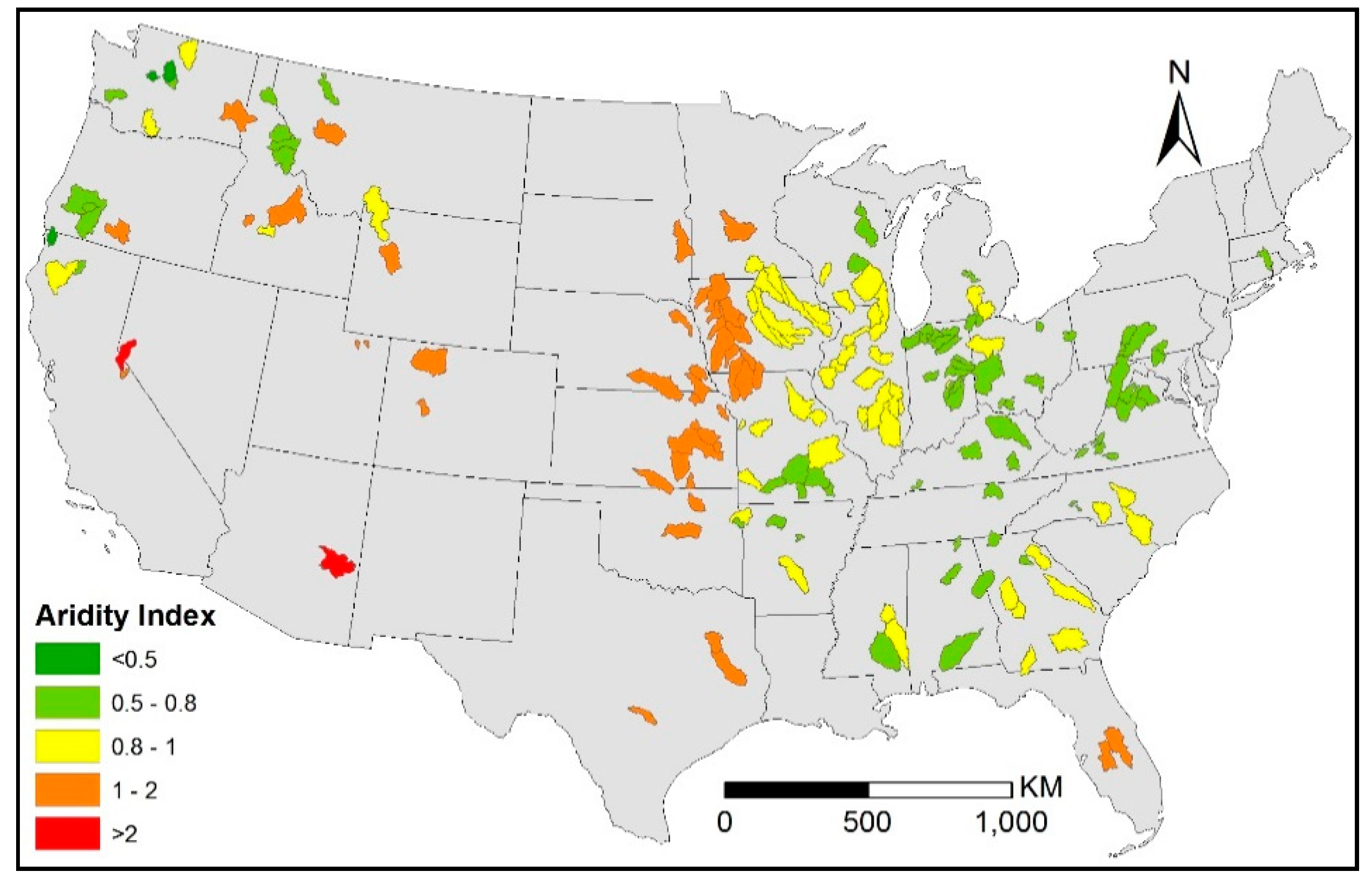
2. Study Watersheds and Data Sources
3. Methodology
3.1. Theory-Driven Conceptual Hydrologic Model
3.2. Data-Driven Method
3.3. Comparative Study, Sensitivity Analysis, and Uncertainty Analysis
4. Results
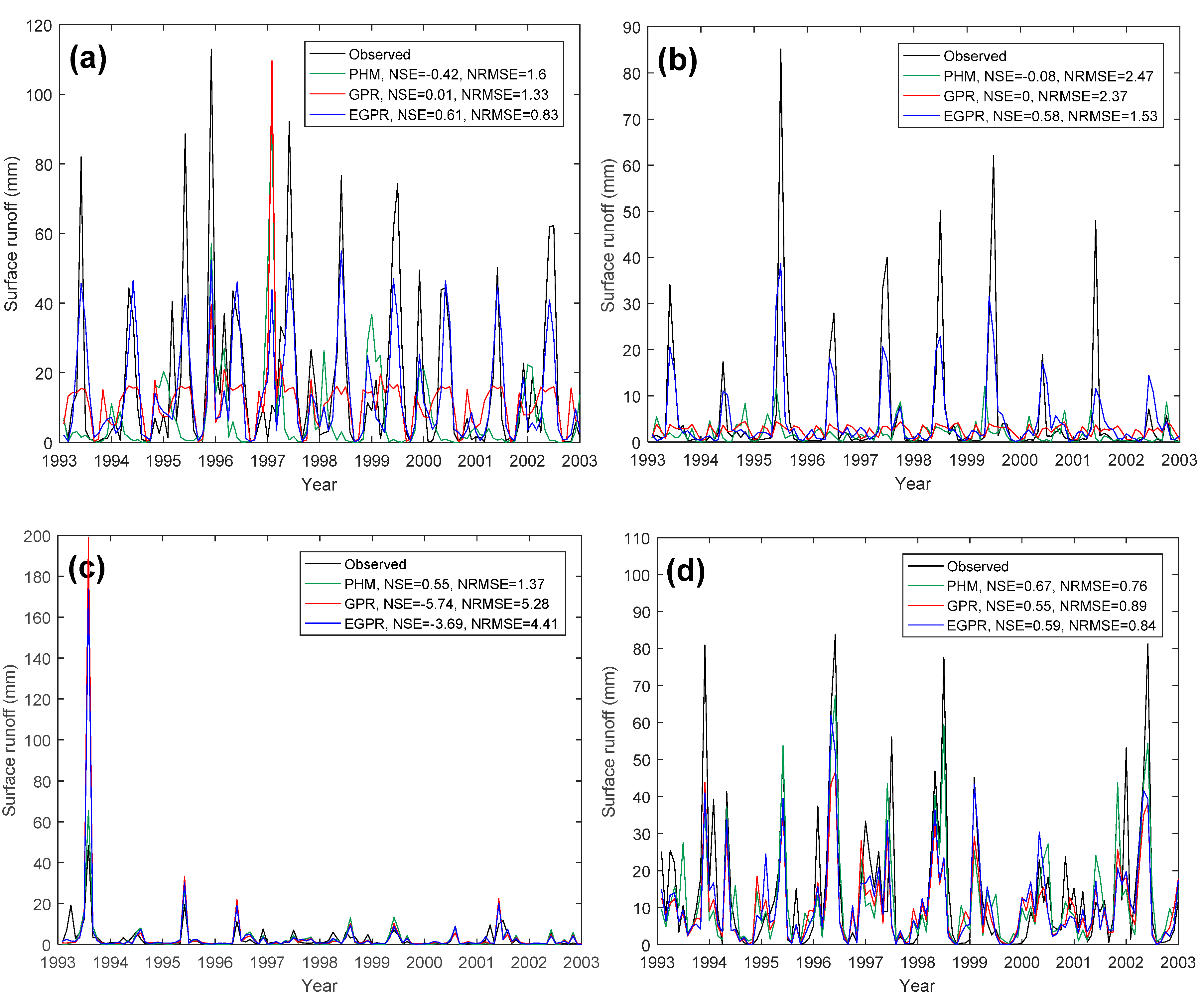
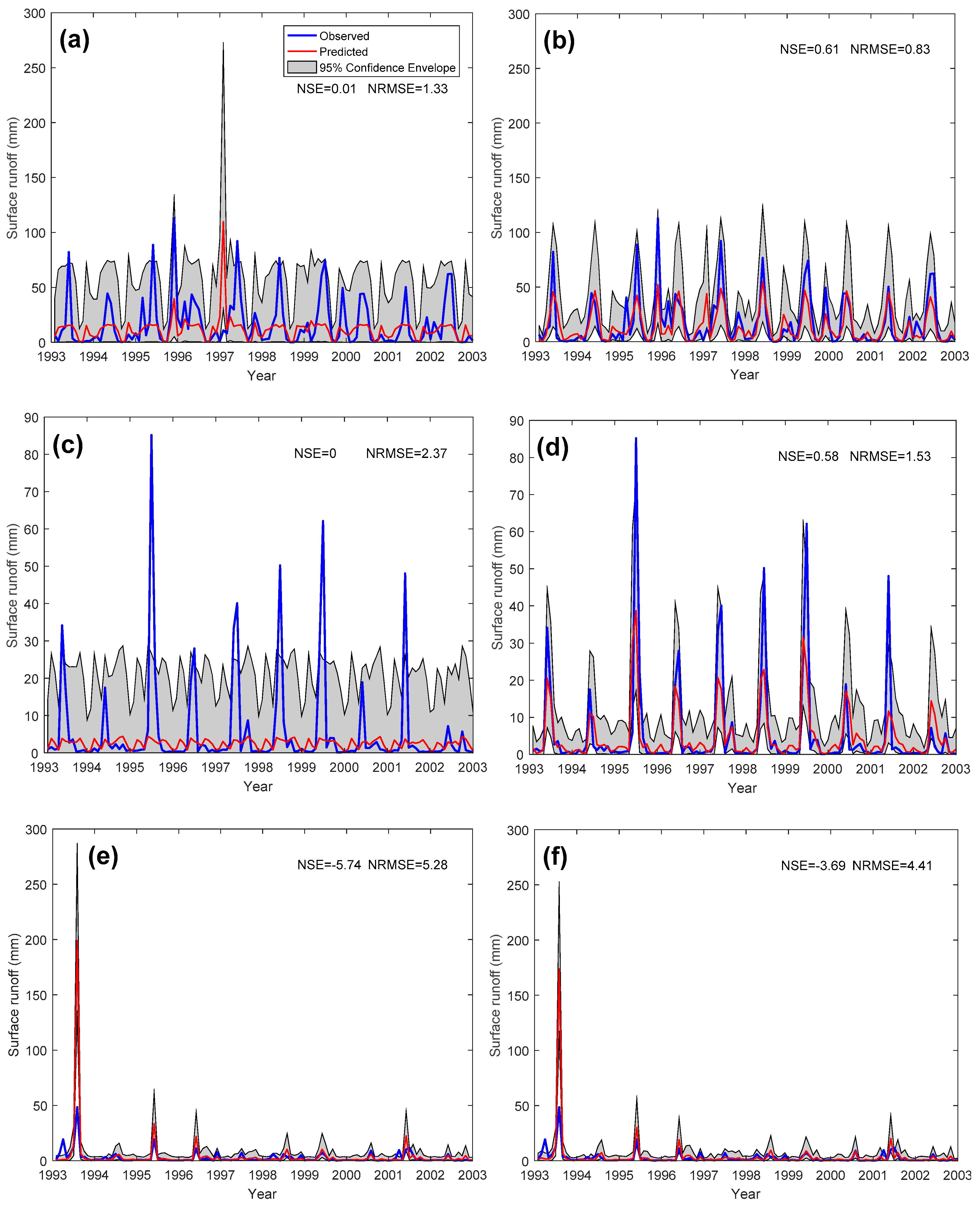
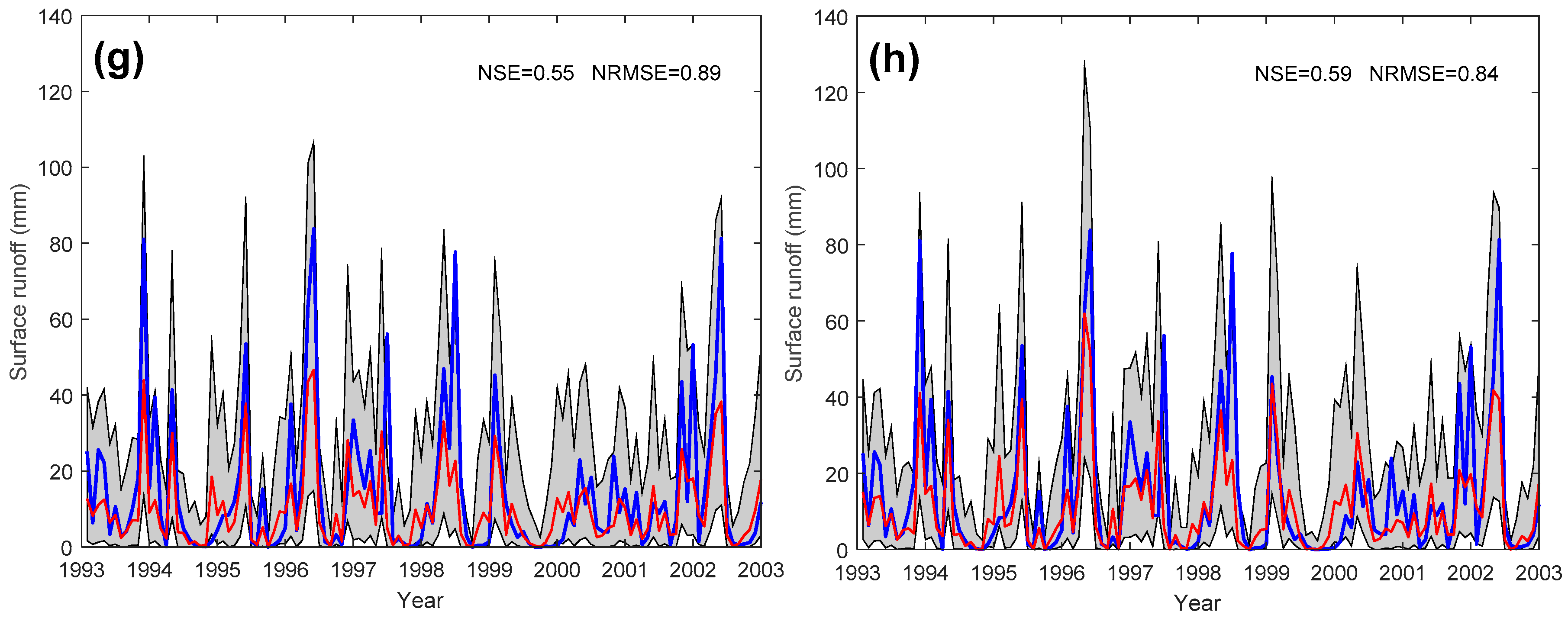
4.1. Model Performance of PHM and GPR
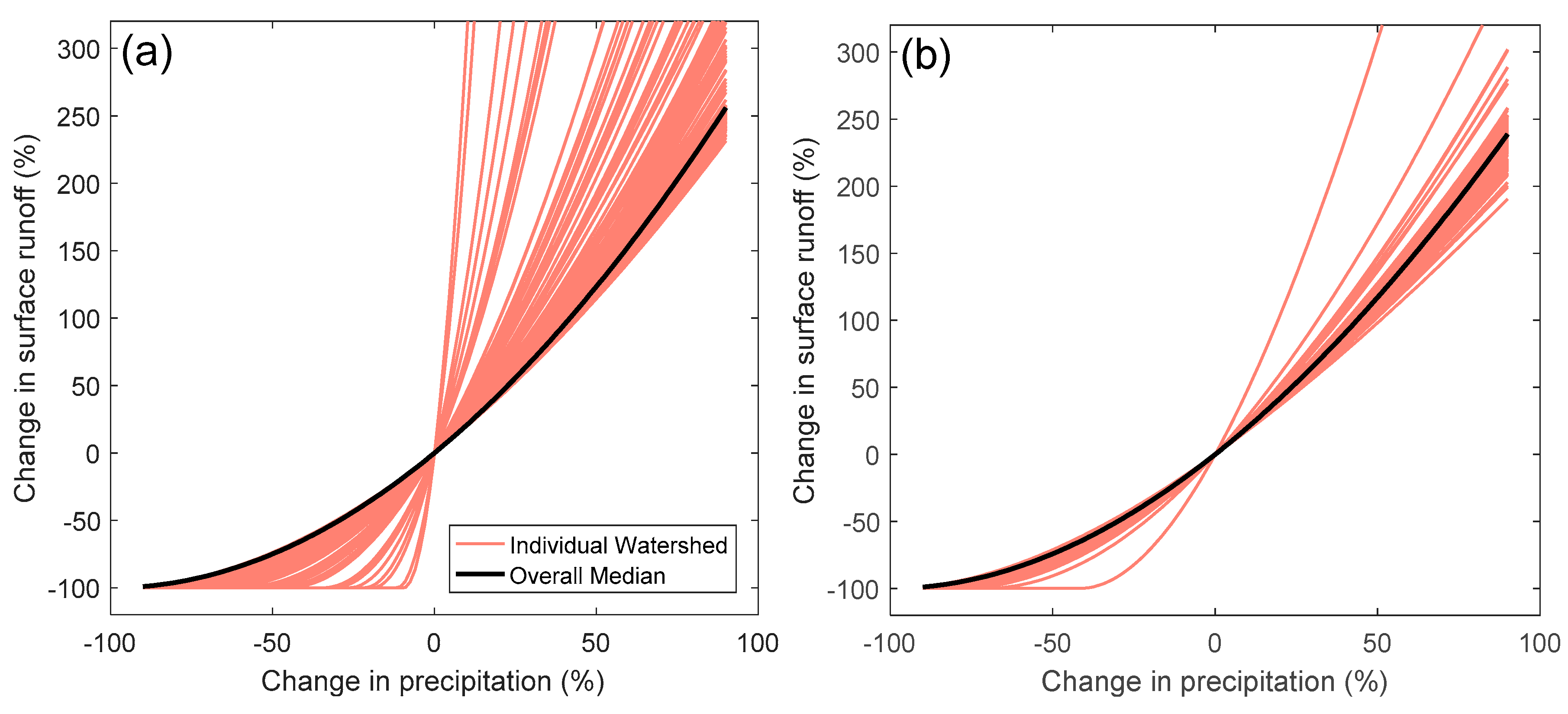
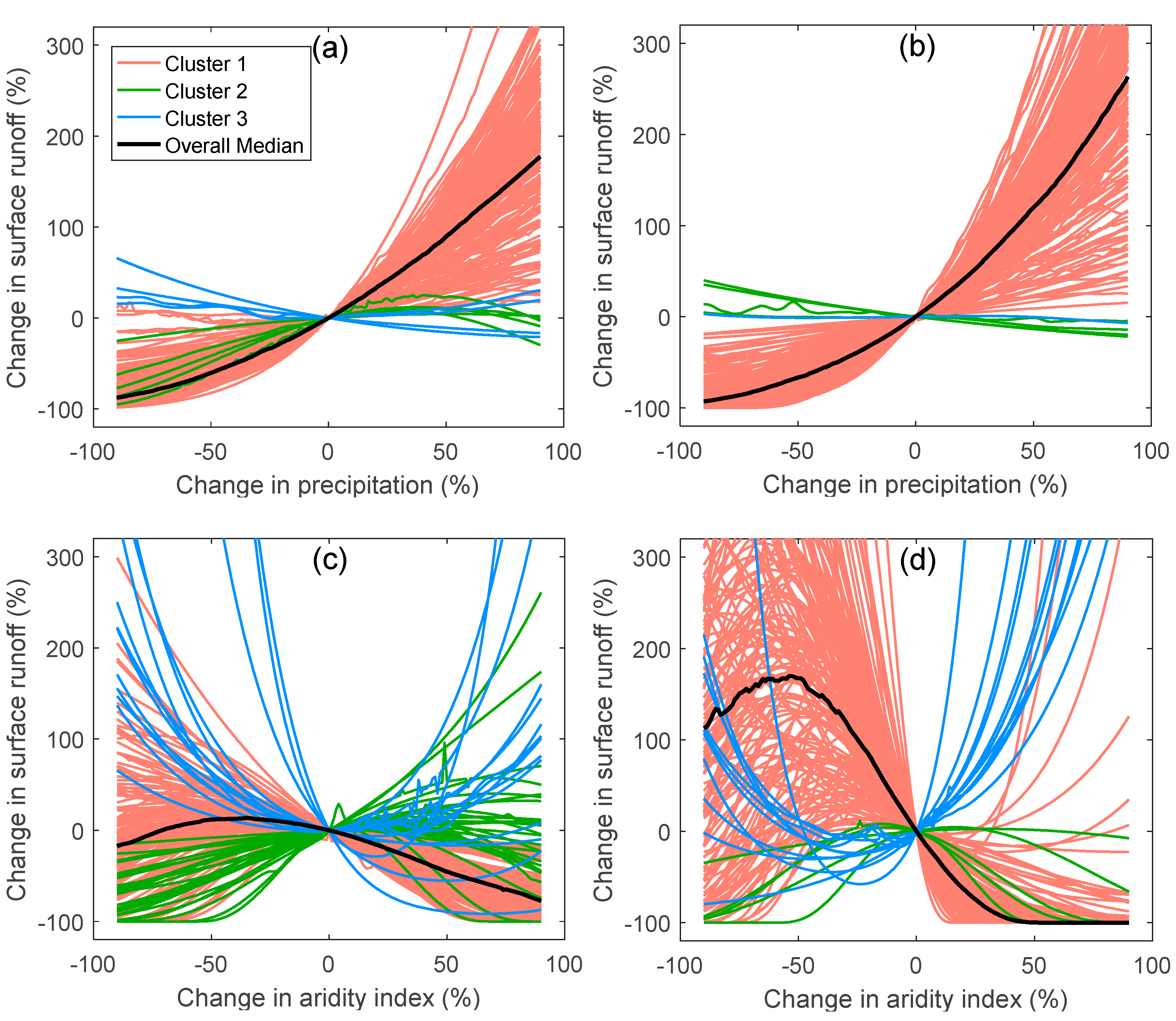
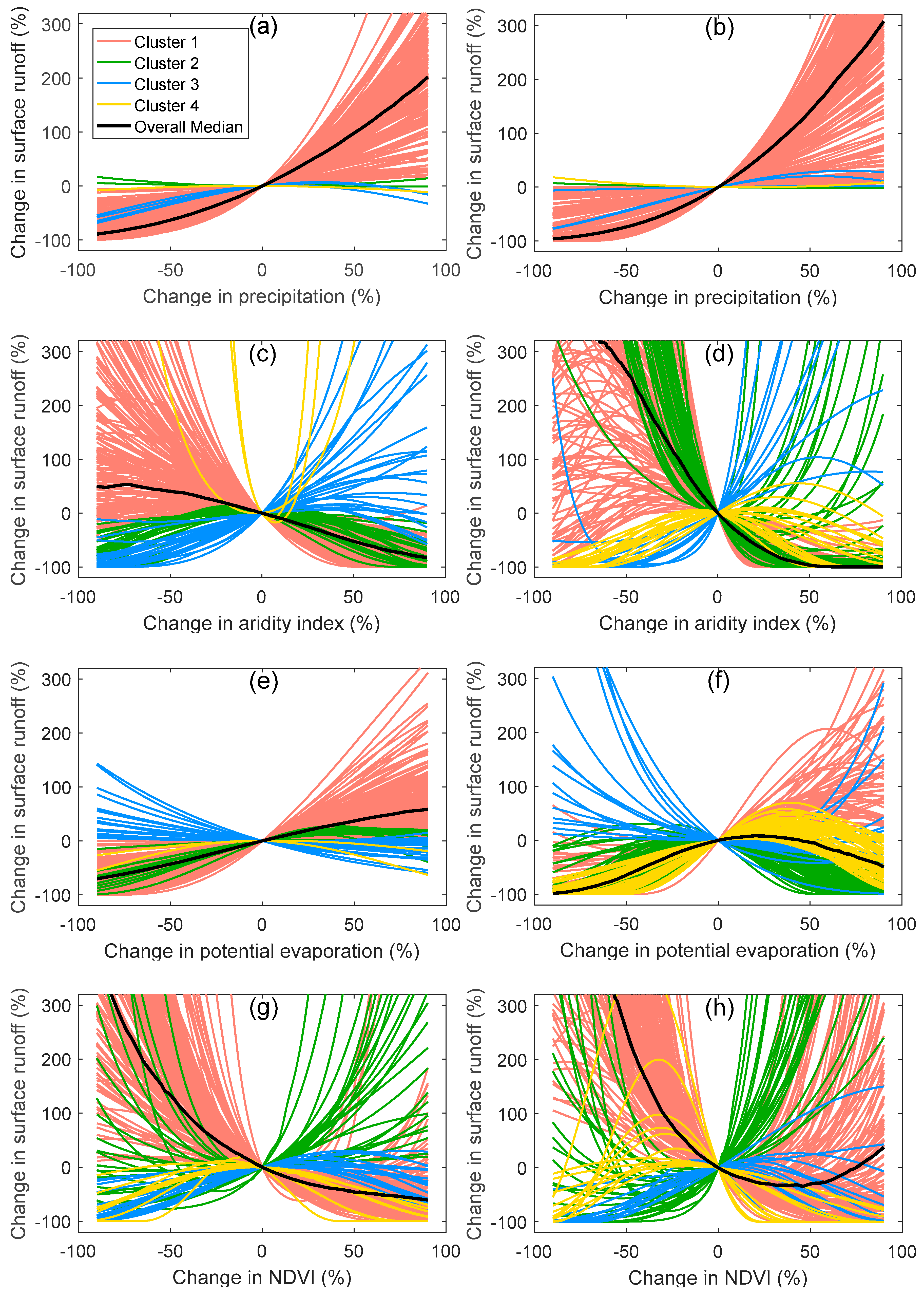
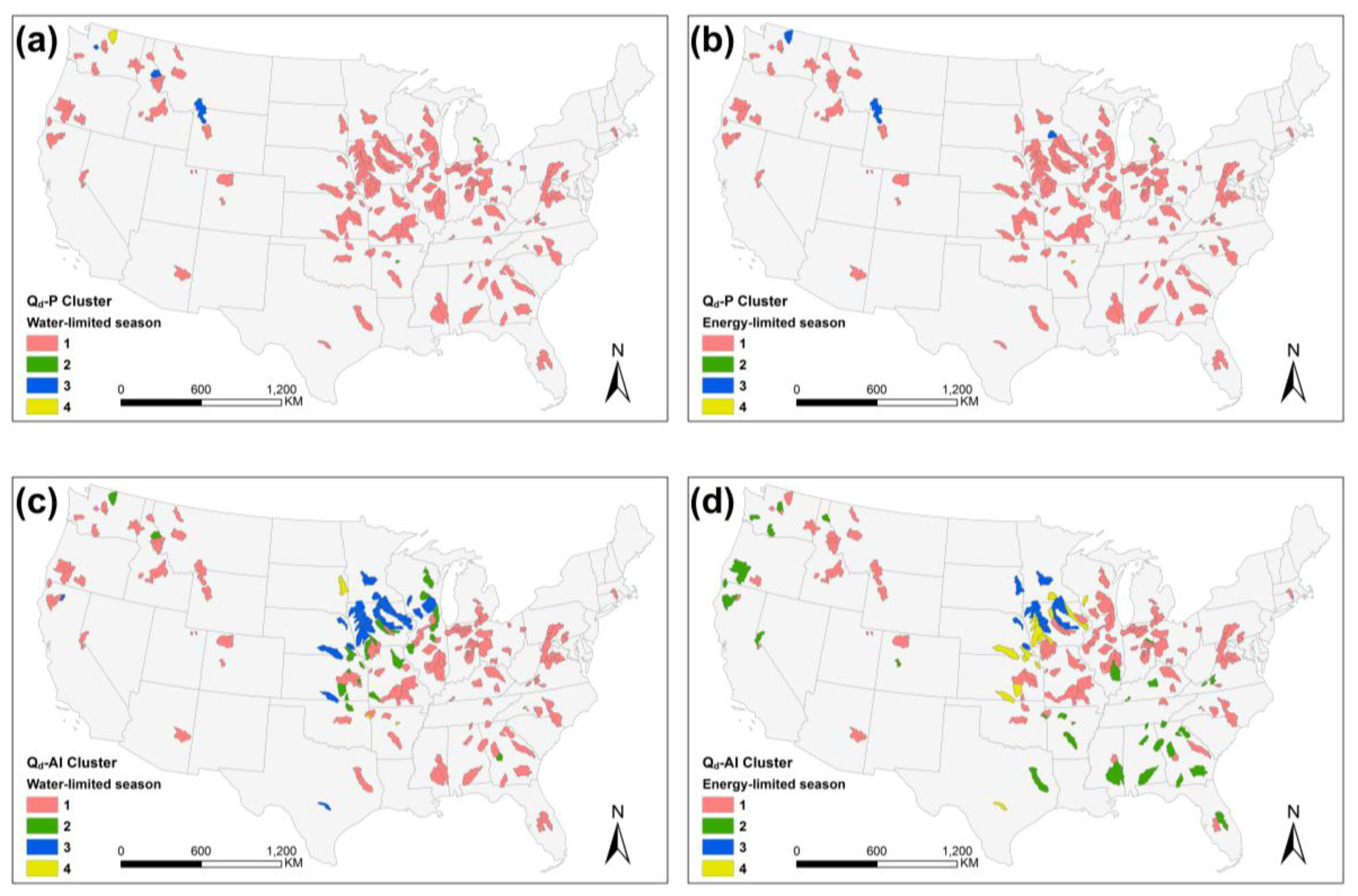
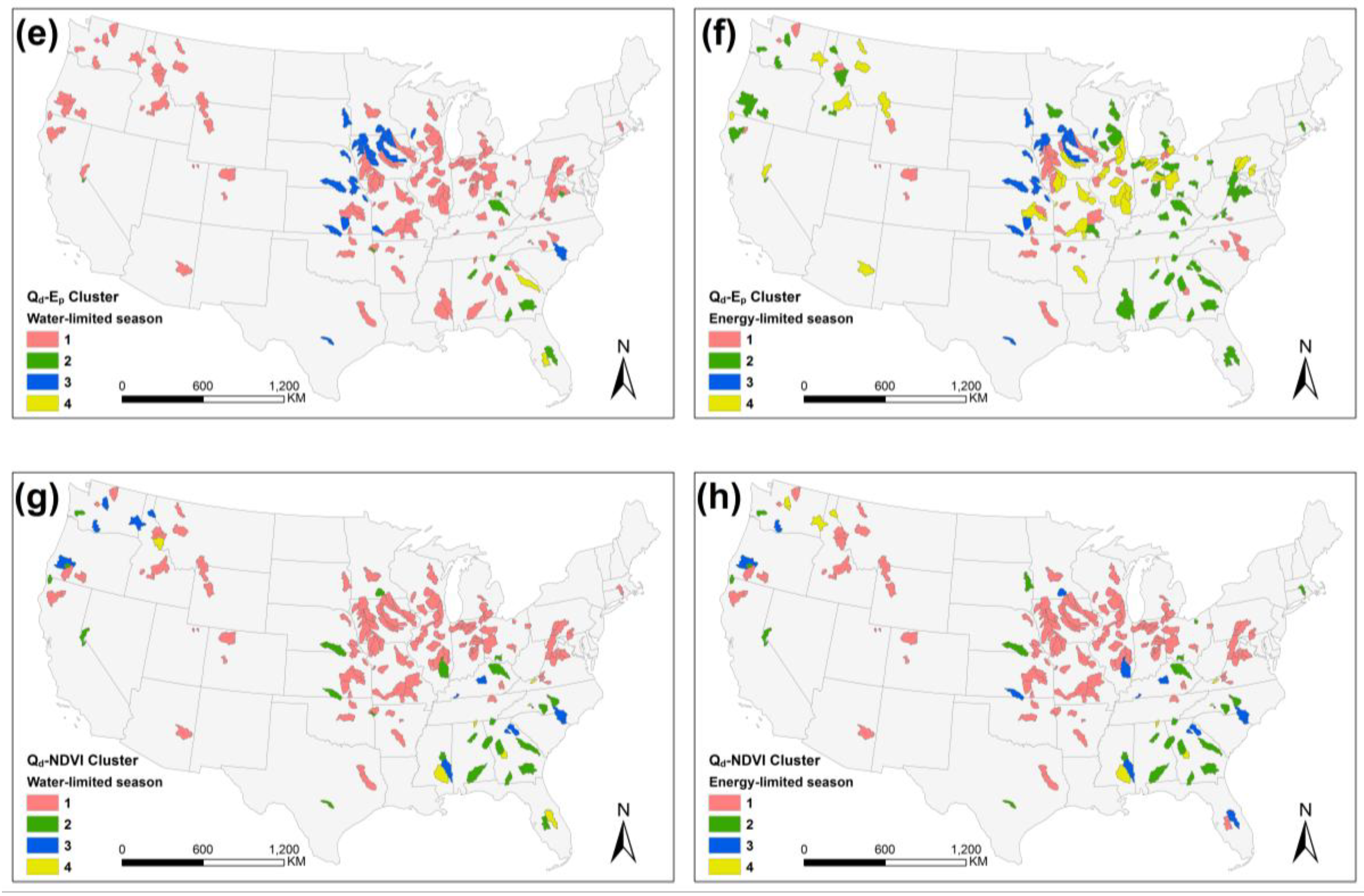
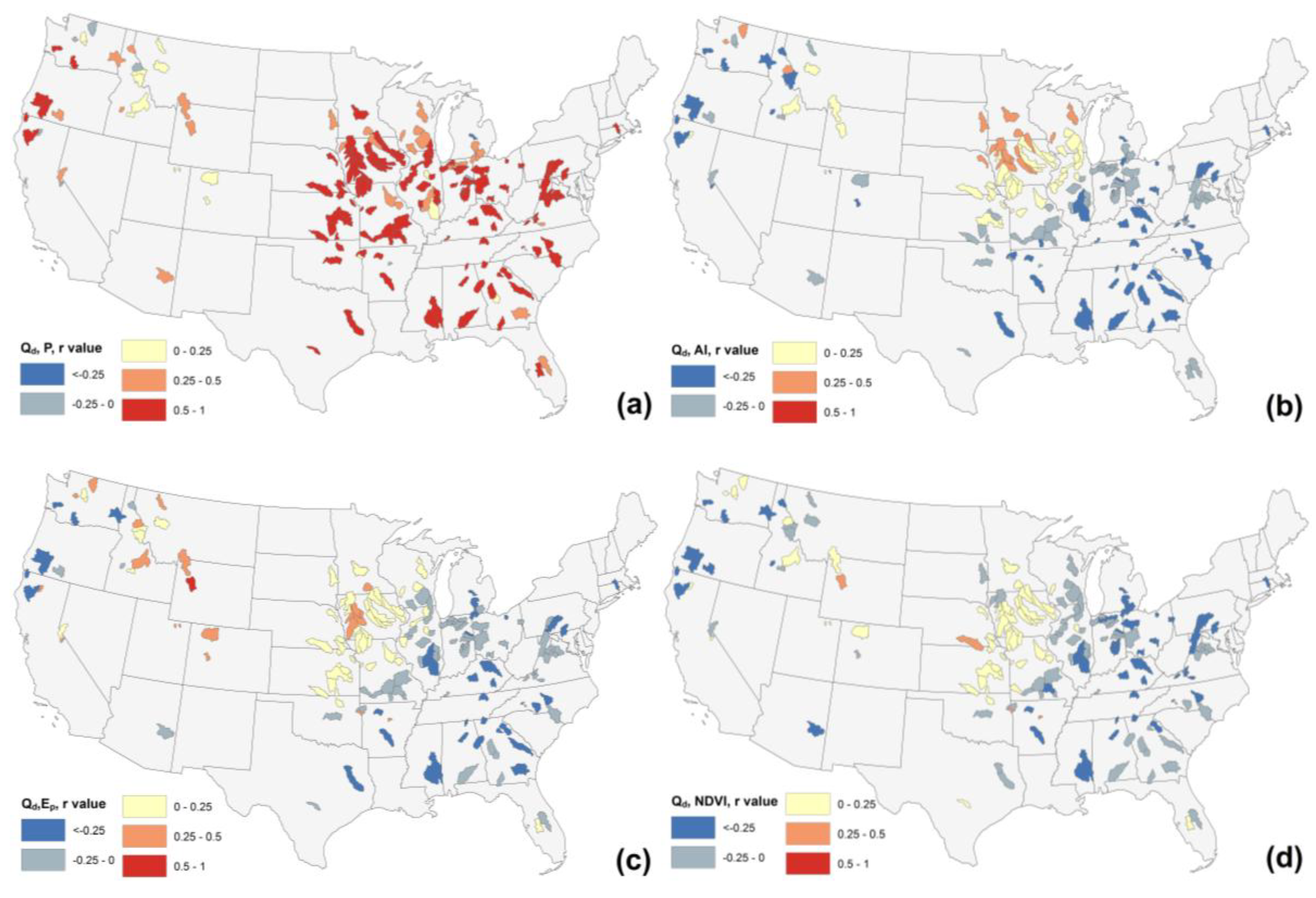
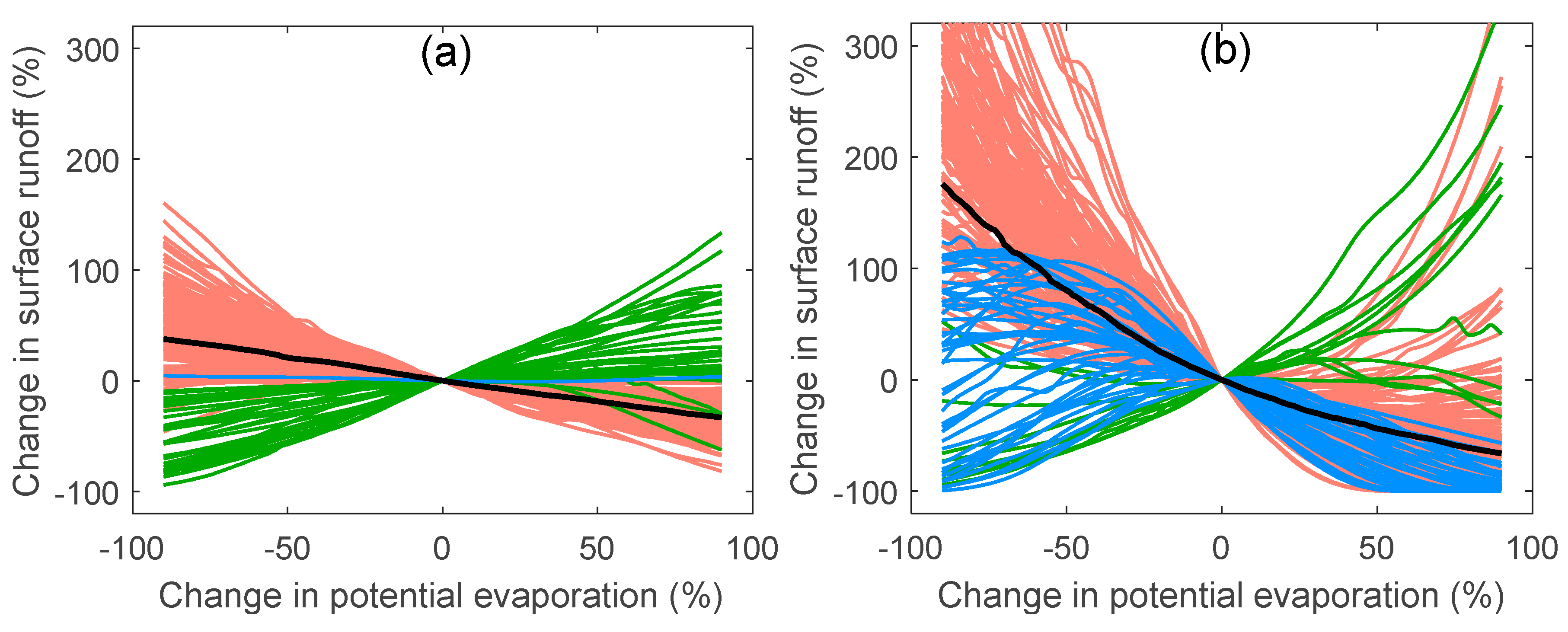
4.2. Sensitivity Analysis
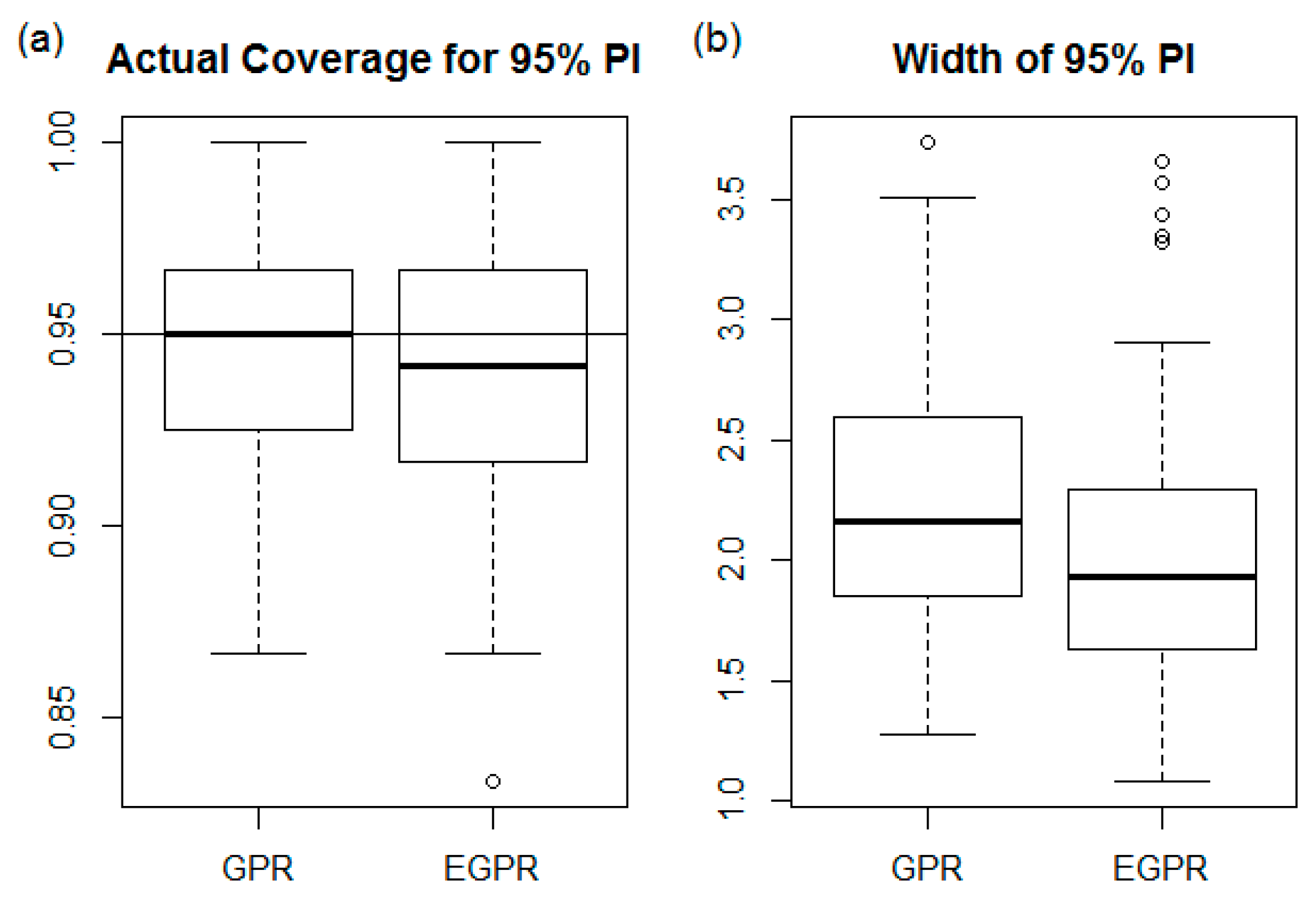
4.3. Uncertainty Analysis
5. Discussion
5.1. Model Performance Comparison
5.2. Physical Interpretation of Sensitivity Analysis Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–123. [Google Scholar] [CrossRef]
- Babovic, V. Data mining in hydrology. Hydrol. Process. 2005, 19, 1511–1515. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resources variables: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 1: Concepts and methodology. Hydrol. Earth Syst. Sci. 2010, 14, 1931–1941. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 2: Application. Hydrol. Earth Syst. Sci. 2010, 14, 1943–1961. [Google Scholar] [CrossRef]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.W.; Mount, N.J.; See, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Prog. Phys. Geogr. 2012, 36, 480–513. [Google Scholar] [CrossRef]
- Genton, M.G. Classes of kernels for machine learning: A statistics perspective. J. Mach. Learn. Res. 2001, 2, 299–312. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006; ISBN 026218253X. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; The MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann Publishers: Burlington, MA, USA, 2016. [Google Scholar]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian Process Regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Mount, N.J.; Maier, H.R.; Toth, E.; Elshorbagy, A.; Solomatine, D.; Chang, F.; Abrahart, R.J. Data-driven modelling approaches for socio-hydrology: Opportunities and challenges within the Panta Rhei Science Plan. Hydrol. Sci. J. 2016, 61, 1192–1208. [Google Scholar] [CrossRef]
- Mount, N.J.; Abrahart, R.J. Load or concentration, logged or unlogged? Addressing ten years of uncertainty in neural network suspended sediment prediction. Hydrol. Process. 2011, 25, 3144–3157. [Google Scholar] [CrossRef]
- Sudheer, K.P. Knowledge extraction from trained neural network river flow models. J. Hydrol. Eng. 2005, 10, 264–269. [Google Scholar] [CrossRef]
- Nouraini, V.; Fard, M.S. Sensitivity analysis of the artificial neural network outputs in simulation of the evaporation process at different climatologic regines. Adv. Eng. Softw. 2012, 47, 127–146. [Google Scholar] [CrossRef]
- Dawson, C.W.; Mount, N.J.; Abrahart, R.J.; Louis, J. Sensitivity analysis for comparison, validation and physical legitimacy of neural network-based hydrological models. J. Hydroinform. 2014, 16, 407–418. [Google Scholar] [CrossRef]
- Kingston, G.B.; Maier, H.R.; Lambert, M.F. Calibration and validation of neural networks to ensure physically plausible hydrological modeling. J. Hydrol. 2005, 314, 158–176. [Google Scholar] [CrossRef]
- Mount, N.J.; Dawson, C.W.; Abrahart, R.J. Legitimising data-driven models: Exemplification of a new data-driven mechanistic modelling framework. Hydrol. Earth Syst. Sci. 2013, 17, 2827–2843. [Google Scholar] [CrossRef]
- Anctil, F.; Perrin, C.; Andréassian, V. Impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. Environ. Model. Softw. 2004, 19, 357–368. [Google Scholar] [CrossRef]
- Toth, E.; Brath, A. Multistep ahead streamflow forecasting: Role of calibration data in conceptual and neural network modeling. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Sivapalan, M. Assessing the impact of climate variability on catchment water balance and vegetation cover. Hydrol. Earth Syst. Sci. 2012, 16, 43–58. [Google Scholar] [CrossRef]
- Wang, D.; Alimohammadi, N. Responses of annual runoff, evaporation, and storage change to climate variability at the watershed scale. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Chen, X.; Alimohammadi, N.; Wang, D. Modeling interannual variability of seasonal evaporation and storage change based on the extended Budyko framework. Water Resour. Res. 2013, 49, 6067–6078. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D. Modeling seasonal surface runoff and base flow based on the generalized proportionality hypothesis. J. Hydrol. 2015, 527, 367–379. [Google Scholar] [CrossRef]
- Duan, Q.; Schaake, J.; Andreassian, V.; Franks, S.; Goteti, G.; Gupta, H.V.; Gusev, Y.M.; Habets, F.; Hall, A.; Hay, L.; et al. The Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base flow and recession analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nermani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.; Pak, E.W.; Mahoney, R.; Vermote, E.; El Saleous, N. An extended AVHRR 8-km NDVI data set compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Wang, D.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in Darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef]
- USA Department of Agriculture Soil Conservation Service (USDA SCS). National Engineering Handbook, Section 4: Hydrology; S. Government Printing Office: Washington, DC, USA, 1985.
- Chen, X.; Wang, D.; Tian, F.; Sivapalan, M. From channelization to restoration: Sociohydrologic modeling with changing community preferences in the Kissimmee River Basin, Florida. Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer Science & Business Media: Berlin, Germany, 1999. [Google Scholar]
- Sanso, B.; Forest, C.E. Uncertainty quantification: Statistical calibration of climate system properties. J. R. Stat. Soc. Ser. C 2009, 58, 485–503. [Google Scholar] [CrossRef]
- Olson, R.; Sriver, R.; Chang, W.; Haran, M.; Urban, N.M.; Keller, K. What is the effect of unresolved internal climate variability on climate sensitivity estimates? J. Geophys. Res. Atmos. 2013, 118, 4348–4358. [Google Scholar] [CrossRef]
- Chang, W.; Haran, M.; Olson, R.; Keller, K. Fast dimension-reduced climate model calibration and the effect of data aggregation. Ann. Appl. Stat. 2014, 8, 649–673. [Google Scholar] [CrossRef]
- McNeall, D.J.; Challenor, P.G.; Gattiker, J.R.; Stone, E.J. The potential of an observational data set for calibration of a computationally expensive computer model. Geosci. Model Dev. 2013, 6, 1715–1728. [Google Scholar] [CrossRef]
- Chang, W.; Applegate, P.J.; Haran, M.; Keller, K. Probabilistic calibration of a Greenland Ice Sheet model using spatially-resolved synthetic observations: Toward projections of ice mass loss with uncertainties. Geosci. Model Dev. 2014, 7, 1933–1943. [Google Scholar] [CrossRef]
- Chang, W.; Haran, M.; Applegate, P.J.; Pollard, D. Calibrating an ice sheet model using high-dimensional binary spatial data. J. Am. Stat. Assoc. 2016, 111, 57–72. [Google Scholar] [CrossRef]
- Chang, W.; Haran, M.; Applegate, P.J.; Pollard, D. Improving ice sheet model calibration using paleoclimate and modern data. Ann. Appl. Stat. 2016, 10, 2274–2302. [Google Scholar] [CrossRef]
- Pollard, D.; Chang, W.; Haran, M.; Applegate, P.J.; DeConto, R. Large ensemble modeling of last deglacial retreat of the West Antarctic Ice Sheet: Comparison of simple and advanced statistical techniques. Geosci. Model Dev. 2016, 9, 1697–1723. [Google Scholar] [CrossRef]
- Williams, C.K.I. Computation with Infinite Neural Networks. Neural Comput. 1998, 10, 1203–1216. [Google Scholar] [CrossRef]
- Nychka, D.W. Spatial-Process Estimates as Smoothers. In Smoothing and Regression: Approaches, Computation, and Application; Schimek, M.G., Ed.; Wiley: New York, NY, USA, 2000; pp. 393–424. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef][Green Version]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 1. Background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- May, R.J.; Maier, H.R.; Dandy, G.C.; Fernando, T.M.K.G. Non-linear variable selection for artificial neural networks using partial mutual information. Environ. Model. Softw. 2008, 23, 1312–1326. [Google Scholar] [CrossRef]
- May, R.J.; Dandy, G.C.; Maier, H.R. Review of Input Variable Selection Methods for Artificial Neural Networks; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Galelli, S.; Castelletti, A. Tree-based iterative input variable selection for hydrological modelling. Water Resour. Res. 2013, 49, 4295–4310. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H.C. Influence of lag time on event-based rainfall-runoff modeling using the data driven approach. J. Hydrol. 2012, 438, 223–233. [Google Scholar] [CrossRef]
- He, J.; Valeo, C.; Chu, A.; Neumann, N.F. Prediction of event-based stormwater runoff quantity and quality by ANNs developed using PMI-based input selection. J. Hydrol. 2011, 400, 10–23. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Thomas, H.A. Final Report: Improved Methods for National Water Assessment. Water Resources Contract: WR15249270; Harvard Water Resources Group: Cambridge, MA, USA, 1981. [Google Scholar]
- Bergström, S. The HBV Model: Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1992. [Google Scholar]
- Martinez, G.F.; Gupta, H.V. Toward improved identification of hydrological models: A diagnostic evaluation of the “abcd” monthly water balance model for the conterminous United States. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting using conceptual models part Ⅰ—A discussion of principles. J. Hydrol. 1970, 10, 280–290. [Google Scholar] [CrossRef]
- Montero, P.; Vilar, J. TSclust: An R Package for Time Series Clustering. J. Stat. Softw. 2014, 62, 1–43. [Google Scholar] [CrossRef]
- Golay, X.; Kollias, S.; Stoll, G.; Meier, D.; Valavanis, A.; Boesiger, P. A new correlation based fuzzy logic clustering algorithm for fMRI. Magn. Reson. Med. 1998, 40, 249–260. [Google Scholar] [CrossRef] [PubMed]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Wang, D.; Wu, L. Similarity of climate control on base flow and perennial stream density in the Budyko framework. Hydrol. Earth Syst. Sci. 2013, 17, 315–324. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]



| Model | NSE | NRMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| <0 | 0–0.5 | 0.5–0.9 | 0.9–1 | Mean | 0–0.5 | 0.5–1 | 1–2 | >2 | Mean | |
| PHM | 30 | 79 | 94 | 0 | 0.38 | 0 | 94 | 103 | 6 | 1.14 |
| GPR | 19 | 84 | 100 | 0 | 0.39 | 1 | 100 | 94 | 8 | 1.15 |
| EGPR | 6 | 57 | 139 | 1 | 0.52 | 3 | 124 | 72 | 4 | 1.01 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, W.; Chen, X. Monthly Rainfall-Runoff Modeling at Watershed Scale: A Comparative Study of Data-Driven and Theory-Driven Approaches. Water 2018, 10, 1116. https://doi.org/10.3390/w10091116
Chang W, Chen X. Monthly Rainfall-Runoff Modeling at Watershed Scale: A Comparative Study of Data-Driven and Theory-Driven Approaches. Water. 2018; 10(9):1116. https://doi.org/10.3390/w10091116
Chicago/Turabian StyleChang, Won, and Xi Chen. 2018. "Monthly Rainfall-Runoff Modeling at Watershed Scale: A Comparative Study of Data-Driven and Theory-Driven Approaches" Water 10, no. 9: 1116. https://doi.org/10.3390/w10091116
APA StyleChang, W., & Chen, X. (2018). Monthly Rainfall-Runoff Modeling at Watershed Scale: A Comparative Study of Data-Driven and Theory-Driven Approaches. Water, 10(9), 1116. https://doi.org/10.3390/w10091116





