Adaptation of an Existing Intake Structure Caused by Increased Sediment Level
Abstract
1. Introduction
1.1. General
1.2. Project-Related Background
- further stabilisation and protection of the vertical trash racks
- new trash racks using only the upper three field of the intake
- no limitation in the operation of the HPP (as far as it is possible)
- all works have to be done under water (saturation diving)
2. Materials and Methods
2.1. Overview
- Preliminary numerical simulation to test first assumptions and prepare the scale model test (Section 2.4).
- Validation with the scale model test and comparison of the two main geometry variations for the new trash rack structure (Section 2.2 and Section 3.2)
- Further optimisation including refinement in the structure and additional load cases (Section 3.3)
2.2. Trash Rack Options
2.3. Numerics
2.4. Scale Model Test
3. Results
3.1. Overview
3.2. Comparison Scale Model Test and Numerics—Validation
3.2.1. Local Head Loss
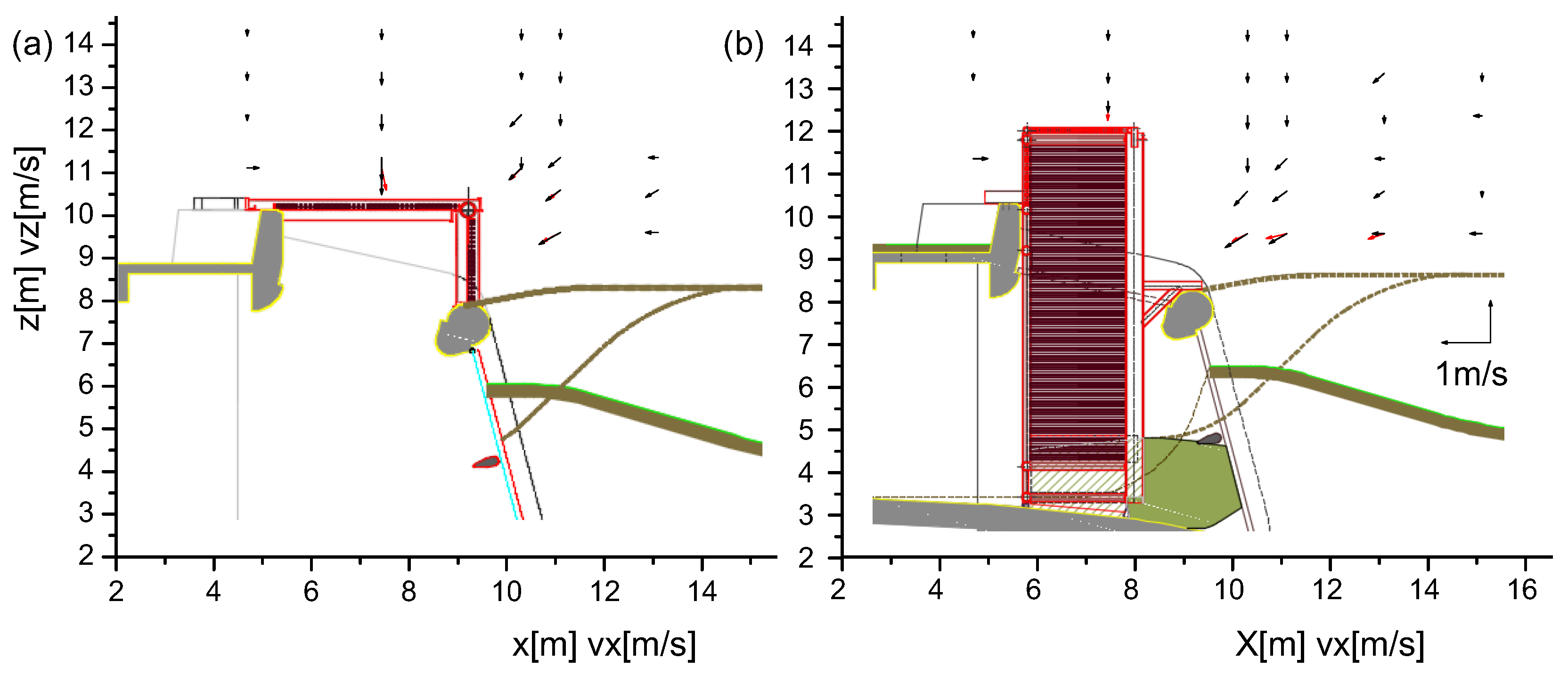
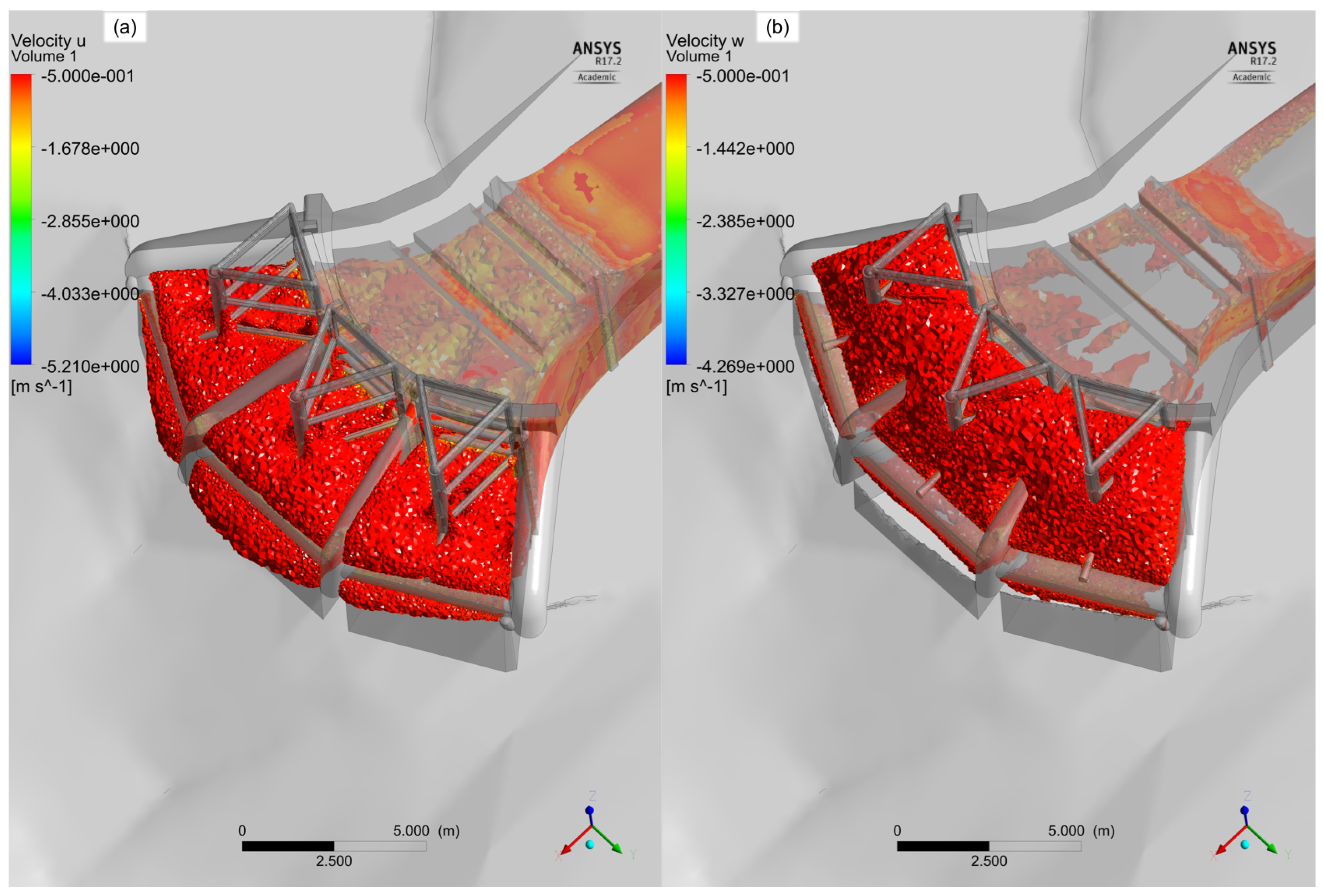
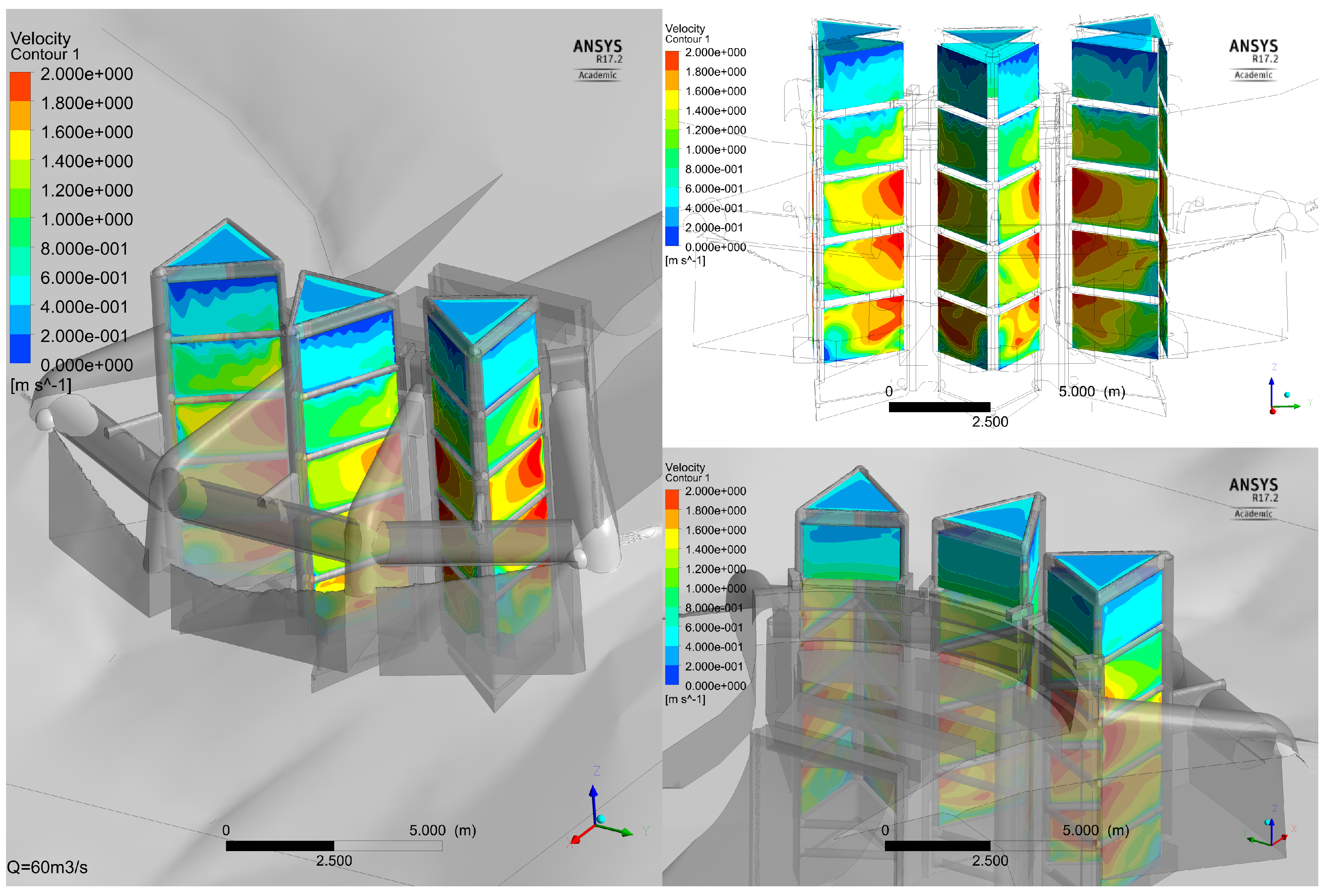
3.2.2. Velocity Distribution
3.3. Final Geometry
4. Discussion
- limitation to an essentially needed reservoir size for the intake
- exclusion of the full water height as a needed degree of freedom for the investigation (simplification of the water height regulation to a very long fixed overflow)
- vital input for the design of the inflow condition
- localisation of the measurement cross section for the local head loss measurement
- proof of the negligibly of the submerged measurement instrument on the results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| A | = area (m) |
| = kinetic energy (Joule) | |
| F | = Froude number (–) |
| g | = gravity acceleration (m · s) |
| h | = head (m) |
| = head loss (m) | |
| Q | = discharge (m · s) |
| u | = velocity in x-direction (m · s) |
| v | = velocity in y-direction (m · s) |
| w | = velocity in z-direction (m · s) |
| z | = elevation (m) |
| = kinetic energy correction factor (–) | |
| = evaluation factor of the angle in the velocity vector (–) | |
| = scale factor (–) | |
| = mass density of water ≈ 997 (kg m) |
References
- Johnson, P.L. Hydro-Power Intake Design Considerations. J. Hydraul. Eng. 1988, 114, 651–661. [Google Scholar] [CrossRef]
- Khan, L.A.; Wicklein, E.A.; Rashid, M.; Ebner, L.L.; Richards, N.A. Computational fluid dynamics modeling of turbine intake hydraulics at a hydropower plant. J. Hydraul. Res. 2004, 42, 61–69. [Google Scholar] [CrossRef]
- Gabl, R.; Innerhofer, D.; Achleitner, S.; Righetti, M.; Aufleger, M. Evaluation criteria for velocity distributions in front of bulb hydro turbines. Renew. Energy 2018, 121, 745–756. [Google Scholar] [CrossRef]
- Huber, B.; Kampel, I. Air entraining vortices in hydraulic model test and CFD-simulation valued at two case studies. WasserWirtschaft 2017, 107, 33–38. [Google Scholar] [CrossRef]
- Mulligan, S.; De Cesare, G.; Casserly, J.; Sherlock, R. Understanding turbulent free-surface vortex flows using a Taylor-Couette flow analogy. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Park, I.; Kim, H.-J.; Seong, H.; Rhee, D.S. Experimental Studies on Surface Vortex Mitigation Using the Floating Anti-Vortex Device in Sump Pumps. Water 2018, 10, 441. [Google Scholar] [CrossRef]
- Sarkardeh, S.; Reza Zarrati, A.; Jabbari, E.; Marosi, M. Numerical simulation and analysis of flow in a reservoir in the presence of vortex. Eng. Appl. Comp. Fluid 2014, 8, 598–608. [Google Scholar] [CrossRef]
- Taştan, K.; Yildirim, N. Effects of Intake Geometry on the Occurrence of a Free-Surface Vortex. J. Hydraul. Eng. 2018, 144, 04018009. [Google Scholar] [CrossRef]
- Yang, J.; Liu, T.; Bottacin-Busolin, A.; Lin, C. Effects of intake-entrance profiles on free-surface vortices. J. Hydraul. Res. 2014, 52, 523–531. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Estévez, A.; Guardo, A.; Coussirat, M. Failures due to ingested bodies in hydraulic turbines. Eng. Fail. Anal. 2011, 18, 464–473. [Google Scholar] [CrossRef]
- Böttcher, H.; Unfer, G.; Zeiringer, B.; Schmutz, S.; Aufleger, M. Fischschutz und Fischabstieg–Kenntnisstand und aktuelle Forschungsprojekte in Österreich [Fish protection and downstream migration: Current state of knowledge and research projects in Austria]. Österreichische Wasser- und Abfallwirtschaft 2015, 67, 299–306. [Google Scholar] [CrossRef]
- Raynal, S.; Courret, D.; Chatellier, L.; Larinier, M.; David, L. An experimental study on fish-friendly trashracks—Part 1. Inclined trashracks. J. Hydraul. Res. 2013, 51, 56–66. [Google Scholar] [CrossRef]
- Raynal, S.; Chatellier, L.; Courret, D.; Larinier, M.; David, L. An experimental study on fish-friendly trashracks—Part 2. Angled trashracks. J. Hydraul. Res. 2013, 51, 67–75. [Google Scholar] [CrossRef]
- Wang, Y.; Politano, M.; Ho, H.C.; Muste, M.; Michell, F.; Stallings, J. Assessment of ice plugging of a cooling water intake by a numerical model. J. Hydraul. Res. 2014, 52, 81–92. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Farahani, A. Sustainably Managing Reservoir Storage: Ancient Roots of a Modern Challenge. Water 2018, 10, 117. [Google Scholar] [CrossRef]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Chamoun, S.; De Cesare, G.; Schleiss, A.J. Managing reservoir sedimentation by venting turbidity currents: A review. Int. J. Sediment Res. 2016, 31, 195–204. [Google Scholar] [CrossRef]
- Huang, C.-C.; Lai, J.-S.; Lee, F.-Z.; Tan, Y.-C. Physical Model-Based Investigation of Reservoir Sedimentation Processes. Water 2018, 10, 352. [Google Scholar] [CrossRef]
- Jenzer Althaus, J.M.I.; Cesare, G.D.; Schleiss, A.J. Sediment Evacuation from Reservoirs through Intakes by Jet-Induced Flow. J. Hydraul. Eng. 2015, 141, 04014078. [Google Scholar] [CrossRef]
- Müller, M.; De Cesare, G.; Schleiss, A.J. Experiments on the effect of inflow and outflow sequences on suspended sediment exchange rates. Int. J. Sediment Res. 2017, 32, 155–170. [Google Scholar] [CrossRef]
- Nomura, S.; Hitomi, J.; De Cesare, G.; Takeda, Y.; Yamamoto, Y.; Sakaguchi, H. Sediment mass movement of a particle-laden turbidity current based on ultrasound velocity profiling and the distribution of sediment concentration. Geol. Soc. Lond. Spec. Publ. 2018, 477. [Google Scholar] [CrossRef]
- De Cesare, G.; Schleiss, A.; Hermann, F. Impact of turbidity currents on reservoir sedimentation. J. Hydraul. Eng. 2001, 127, 6–16. [Google Scholar] [CrossRef]
- Epely-Chauvin, G.; De Cesare, G.; Schwindt, S. Numerical modelling of plunge pool scour evolution in non-cohesive sediments. Eng. Appl. Comp. Fluid 2014, 8, 477–487. [Google Scholar] [CrossRef][Green Version]
- Haun, S.; Kjærås, H.; Løvfall, S.; Olsen, N.R.B. Three-dimensional measurements and numerical modelling of suspended sediments in a hydropower reservoir. J. Hydrol. 2013, 479, 180–188. [Google Scholar] [CrossRef]
- Oehy, C.D.; Schleiss, A.J. Control of Turbidity Currents in Reservoirs by Solid and Permeable Obstacles. J. Hydraul. Eng. 2007, 133, 637–648. [Google Scholar] [CrossRef]
- Bonalumi, M.; Anselmetti, F.S.; Kaegi, R.; Wüest, A. Particle dynamics in high-Alpine proglacial reservoirs modified by pumped-storage operation. Water Resour. Res. 2011, 47, W09523. [Google Scholar] [CrossRef]
- Müller, M.; De Cesare, G.; Schleiss, A.J. Continuous Long-Term Observation of Suspended Sediment Transport between Two Pumped-Storage Reservoirs. J. Hydraul. Eng. 2014, 140, 05014003. [Google Scholar] [CrossRef]
- Müller, M.; De Cesare, G.; Schleiss, A.J. Flow field in a reservoir subject to pumped-storage operation—In situ measurement and numerical modeling. J. Appl. Water Eng. Res. 2016. [Google Scholar] [CrossRef]
- Hager, W.H.; Boes, R.M. Hydraulic structures: A positive outlook into the future. J. Hydraul. Res. 2014, 52, 299–310. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, H.; Liu, J.; Sun, B.; Tian, Y. Numerical investigation of flow in a vertical pipe inlet/outlet with a horizontal anti-vortex plate: Effect of diversion orifices height and divergence angle. Eng. Appl. Comp. Fluid 2018, 12, 182–194. [Google Scholar] [CrossRef]
- Gems, B.; Mazzorana, B.; Hofer, T.; Sturm, M.; Gabl, R.; Aufleger, M. 3-D hydrodynamic modelling of flood impacts on a building and indoor flooding processes. Nat. Hazards Earth Syst. Sci. 2016, 16, 1351–1368. [Google Scholar] [CrossRef]
- Lauffer, H. Das Kaunertalkraftwerk. Österreichische Wasserwirtschaft; Springer: New York, NY, USA, 1968. [Google Scholar]
- Oehy, C.D.; De Cesare, G.; Schleiss, A.J. Effect of inclined jet screen on turbidity current. J. Hydraul. Res. 2010, 48, 81–90. [Google Scholar] [CrossRef]
- Obendorfer, R.; Hofer, B.; Bol, A. Underwater maintenance works in the Gepatsch reservoir. Hydropower Dams 2018, 25, 64–73. [Google Scholar]
- Nan, D.; Shigemitsu, T.; Zhao, S. Investigation and Analysis of Attack Angle and Rear Flow Condition of Contra-Rotating Small Hydro-Turbine. Energies 2018, 11, 1806. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Li, Z.; Nielsen, T.K.; Goyal, R.; Wei, X.; Qin, D. Transient characteristics during the closure of guide vanes in a pump-turbine in pump mode. Renew. Energy 2018, 118, 973–983. [Google Scholar] [CrossRef]
- Yang, J.; Pavesi, G.; Liu, X.; Xie, T.; Liu, J. Unsteady flow characteristics regarding hump instability in the first stage of a multistage pump-turbine in pump mode. Renew. Energy 2018, 127, 377–385. [Google Scholar] [CrossRef]
- Castillo, L.; García, J.; Carrillo, J. Influence of Rack Slope and Approaching Conditions in Bottom Intake Systems. Water 2017, 9, 65. [Google Scholar] [CrossRef]
- Carrillo, J.; García, J.; Castillo, L. Experimental and numerical modelling of bottom intake racks with circular bars. Water 2018, 10, 605. [Google Scholar] [CrossRef]
- Andersson, A.G.; Andreasson, P.; Lundström, T.S. CFD-modelling and validation of free surface flow during spilling of reservoir in down-scale model. Eng. Appl. Comp. Fluid 2013, 7, 159–167. [Google Scholar] [CrossRef]
- Cao, P.; Wang, Y.; Kang, C.; Li, G.; Zhang, X. Investigation of the role of non-uniform suction flow in the performance of water-jet pump. Ocean Eng. 2017, 140, 258–269. [Google Scholar] [CrossRef]
- Gabl, R.; Righetti, M. Design criteria for a type of asymmetric orifice in a surge tank using CFD. Eng. Appl. Comp. Fluid 2018, 12, 397–410. [Google Scholar] [CrossRef]
- Putra, R.A.; Schäfer, T.; Neumann, M.; Lucas, D. CFD studies on the gas-liquid flow in the swirl generating device. Nucl. Eng. Des. 2018, 332, 213–225. [Google Scholar] [CrossRef]
- Renno, C.; Petito, F.; Accarino, M.L. Thermal Model in ANSYS for a Comparison Between two Configurations of a Concentrating Photovoltaic System. Heat Transf. Eng. 2018. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Proceedings of the Fourth International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003. [Google Scholar]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Bermúdez, M.; Cea, L.; Puertas, J.; Conde, A.; Martín, A.; Baztán, J. Hydraulic model study of the intake-outlet of a pumped-storage hydropower plant. Eng. Appl. Comp. Fluid 2012, 11, 483–495. [Google Scholar] [CrossRef]
- Yang, J.; Andreasson, P.; Högström, C.-M.; Teng, P. The Tale of an Intake Vortex and Its Mitigation Countermeasure: A Case Study from Akkats Hydropower Station. Water 2018, 10, 881. [Google Scholar] [CrossRef]
- Gabl, R.; Achleitner, S.; Neuner, J.; Aufleger, M. Accuracy analysis of a physical scale model using the example of an asymmetric orifice. Flow Meas. Instrum. 2014, 36, 36–46. [Google Scholar] [CrossRef]
- Idelchik, I.E. Handbook of Hydraulic Resistance Coefficients of Local Resistance and of Friction; U.S. Department of Commerce National Technical Information service (NTIS): Springfield, VA, USA, 1960.
- Ward-Smith, A.J. Internal Fluid Flow—The Fluid Dynamics of Flow in Pipes and Ducts; Clarendon Press: Oxford, UK, 1980. [Google Scholar]
- Gou, J.; Su, X.; Yuan, X. Adaptive mesh refinement method-based large eddy simulation for the flow over circular cylinder at ReD = 3900. Int. J. Computat. Fluid Dyn. 2018. [Google Scholar] [CrossRef]
- Albayrak, I.; Kriewitz, C.R.; Hager, W.H.; Boes, R.M. An experimental investigation on louvres and angled bar racks. J. Hydraul. Res. 2018, 46, 59–75. [Google Scholar] [CrossRef]
- Böttcher, H.; Gabl, R.; Ritsch, S.; Aufleger, M. Experimental study of head loss through an angled fish protection system. In Proceedings of the 4th IAHR Europe Congress, Liege, Belgium, 27–29 July 2016; Dewals, B., Ed.; CRC Press: Liege, Belgium, 2016; pp. 637–642. [Google Scholar]
- Meusburger, H. Energy Loss at Trashracks in Hydroelectric Power Stations [Energieverluste an Einlaufrechen von Flusskraftwerken]. Mitteilungen der Versuchsanstalt fur Wasserbau, Hydrologie und Glaziologie an der Eidgenossischen Technischen Hochschule Zurich. 2002. Available online: https://www.researchgate.net/publication/292544074_Energy_loss_at_trashracks_in_hydroelectric_power_stations (accessed on 10 August 2018).
- Gao, F.; Zhao, L.; Boufadel, M.C.; King, T.; Robinson, B.; Conmy, R.; Miller, R. Hydrodynamics of oil jets without and with dispersant: Experimental and numerical characterization. Appl. Ocean Res. 2017, 68, 77–90. [Google Scholar] [CrossRef]
- Dargahi, B. Flow characteristics of bottom outlets with moving gates. J. Hydraul. Res. 2010, 48, 476–482. [Google Scholar] [CrossRef]



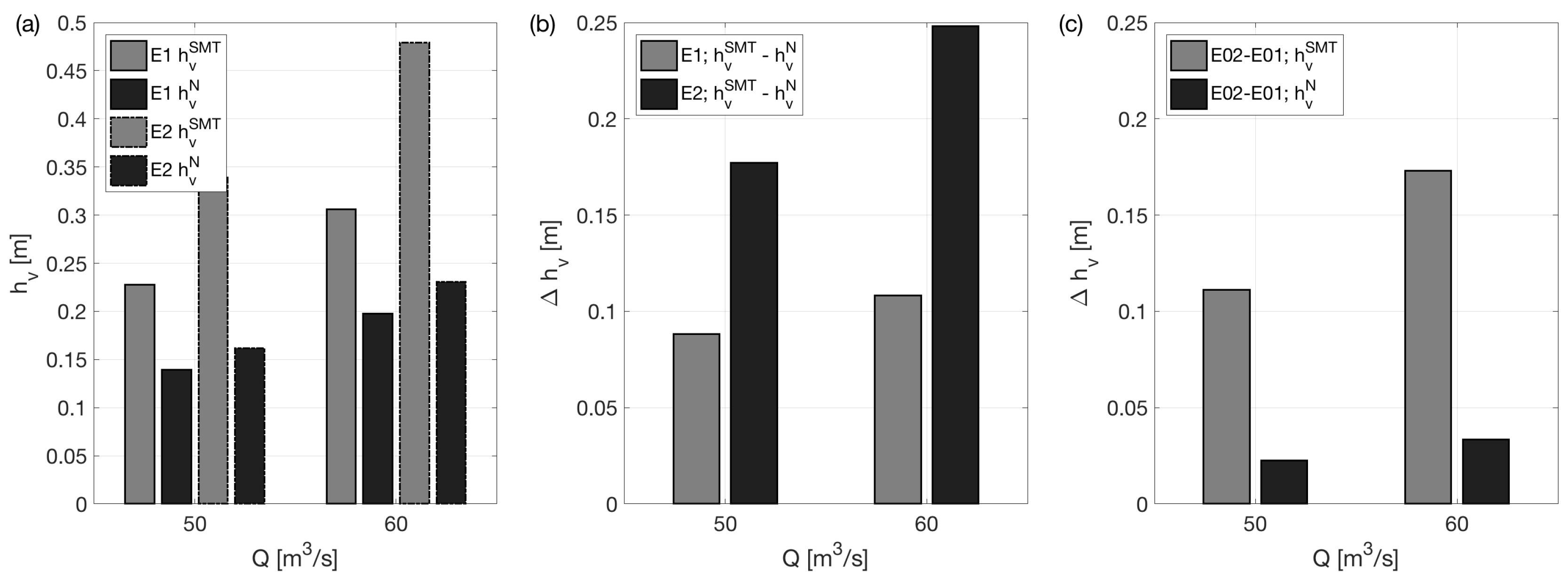

| Q () | E01 | E02 | E02-E01 | |||
|---|---|---|---|---|---|---|
| 60 | 50 | 60 | 50 | 60 | 50 | |
| (m) | 0.306 | 0.228 | 0.479 | 0.339 | 0.173 | 0.111 |
| (m) | 0.197 | 0.139 | 0.231 | 0.162 | 0.033 | 0.022 |
| (m) | 0.178 | 0.125 | 0.213 | 0.150 | 0.036 | 0.025 |
| (m) | 0.108 | 0.088 | 0.248 | 0.177 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabl, R.; Gems, B.; Birkner, F.; Hofer, B.; Aufleger, M. Adaptation of an Existing Intake Structure Caused by Increased Sediment Level. Water 2018, 10, 1066. https://doi.org/10.3390/w10081066
Gabl R, Gems B, Birkner F, Hofer B, Aufleger M. Adaptation of an Existing Intake Structure Caused by Increased Sediment Level. Water. 2018; 10(8):1066. https://doi.org/10.3390/w10081066
Chicago/Turabian StyleGabl, Roman, Bernhard Gems, Florian Birkner, Bernhard Hofer, and Markus Aufleger. 2018. "Adaptation of an Existing Intake Structure Caused by Increased Sediment Level" Water 10, no. 8: 1066. https://doi.org/10.3390/w10081066
APA StyleGabl, R., Gems, B., Birkner, F., Hofer, B., & Aufleger, M. (2018). Adaptation of an Existing Intake Structure Caused by Increased Sediment Level. Water, 10(8), 1066. https://doi.org/10.3390/w10081066








