Threshold Based Footprints (for Water)
Abstract
1. Introduction
2. Materials and Methods
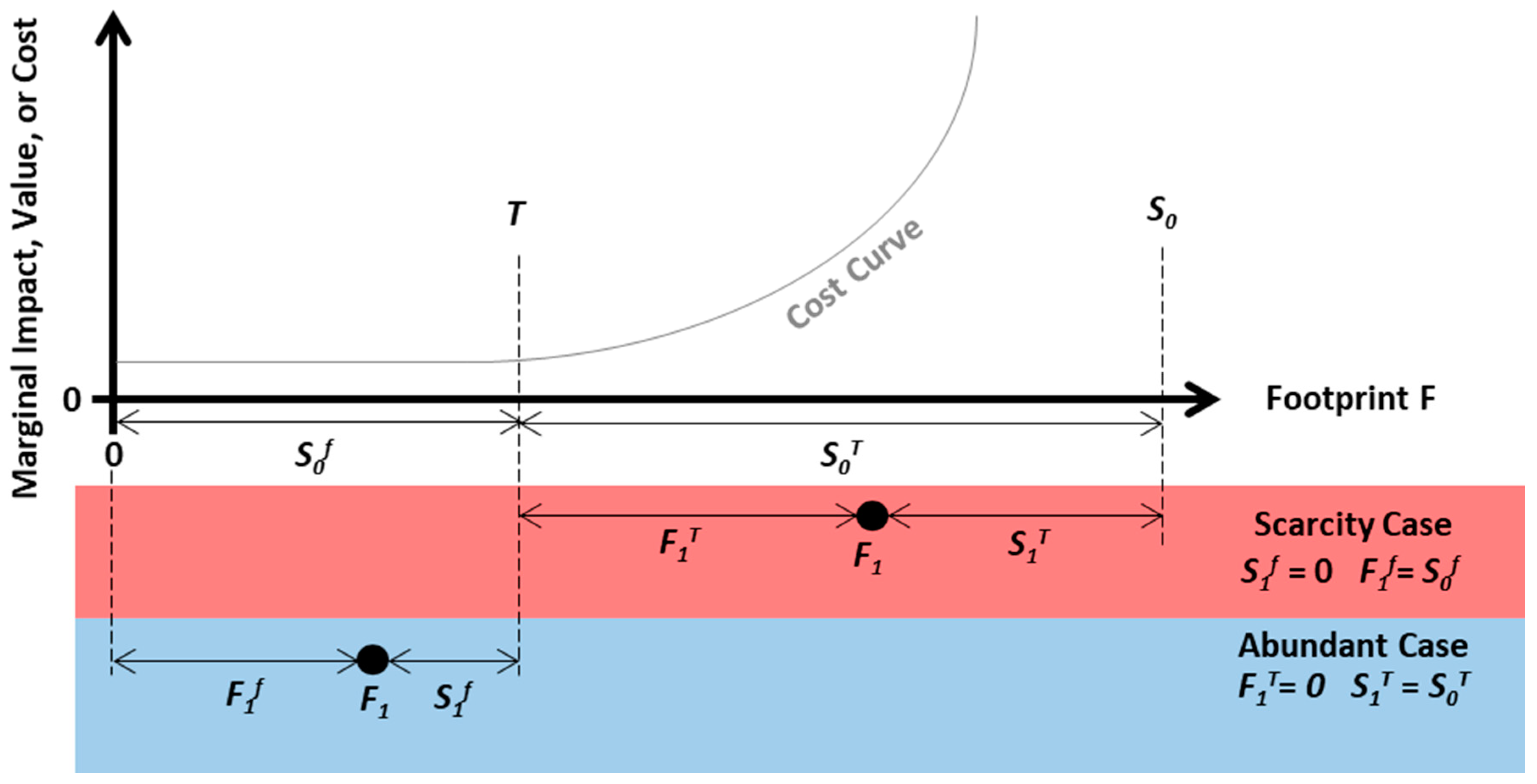
2.1. Mathematics of a Threshold-Based Footprint
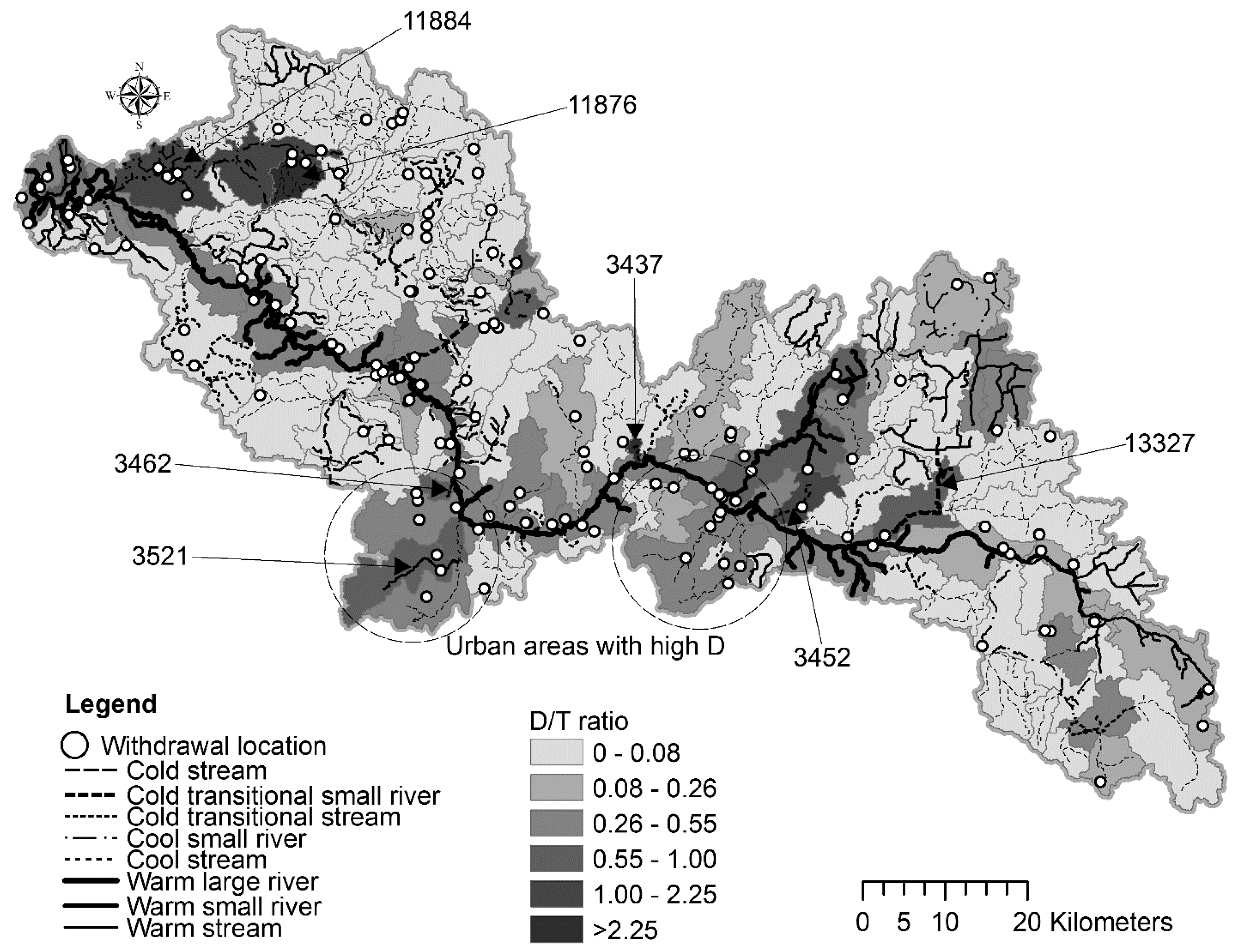
2.2. Application of the Threshold Concept to Water Footprints and Impact Metrics
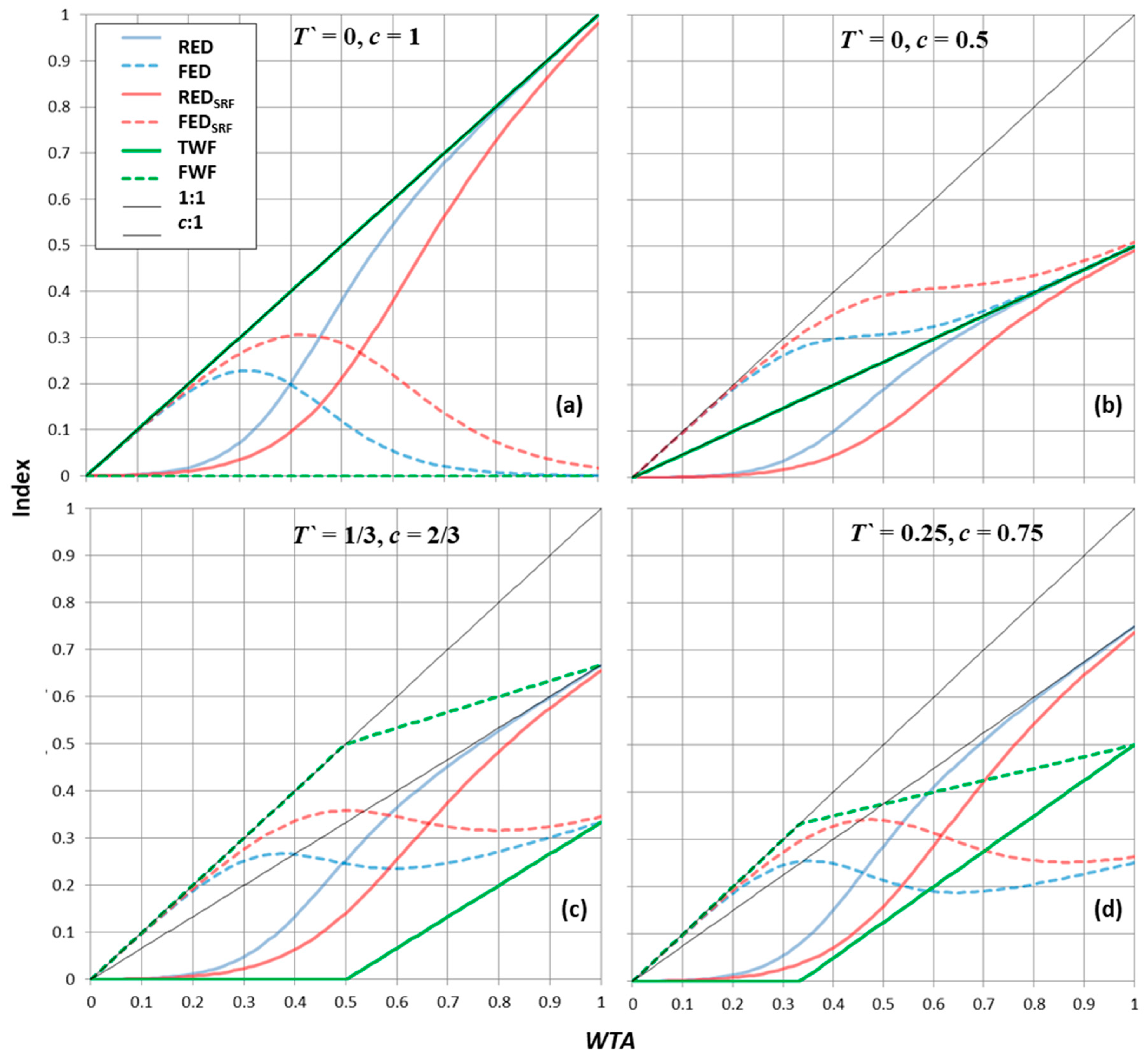
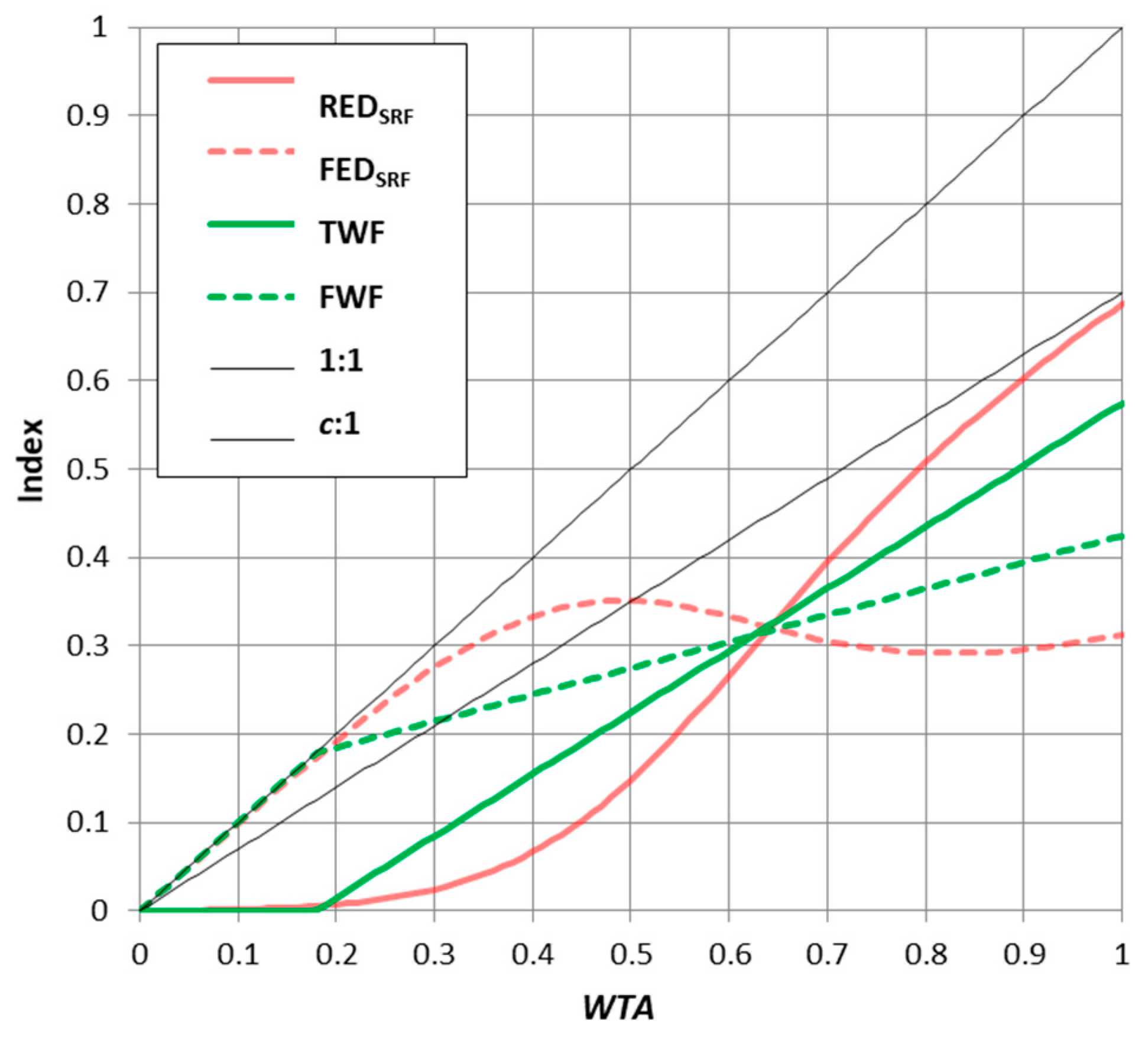
3. Results
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Various Threshold-Based Water Scarcity and Stress Indices
Appendix B. The Economic Interpretation of FT
References
- Liu, J.; Dietz, T.; Carpenter, S.R.; Folke, C.; Alberti, M.; Redman, C.L.; Schneider, S.H.; Ostrom, E.; Pell, A.N.; Lubchenco, J.; et al. Coupled human and natural systems. Ambio 2007, 36, 639–649. [Google Scholar] [CrossRef]
- Cohen, S. We Need to Accelerate the Development of Sustainability Metrics. Available online: https://www.whu.edu/en/faculty-research/entrepreneurship-and-innovation-group/chair-of-entrepreneurship-i/sustainability-blog/measuring-sustainability-the-need-for-precise-metrics/ (accessed on 30 July 2018).
- Marten, S.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; van de Koppel, J.; van de Leemput, I.A.; Levin, S.A.; van Nes, E.H; et al. Anticipating critical transitions. Science 2012, 338, 344–348. [Google Scholar]
- Walker, B.; Holling, C.S.; Carpenter, S.R.; Kinzing, A. Resilience, adaptability, and transformability in socio-ecological systems. Ecol. Soc. 2004, 9, 5. [Google Scholar] [CrossRef]
- RA/SFI. Thresholds and Alternate States in Ecological and Social–Ecological Systems; Resilience Alliance report #183; Resilience Alliance and Santa Fe Institute: Santa Fe, NM, USA, 2009. [Google Scholar]
- Couttenier, M.; Soubeyran, R. Drought and Civil War in Sub-Saharan Africa; Working Paper no.21; Paris School of Economics: Paris, France, 2011. [Google Scholar]
- Duarte, C.M.; Agusti, S.; Agawin, N.S.R. Response of a Mediterranean phytoplankton community to increased nutrient inputs: A mesocosm experiment. Mar. Ecol. Prog. Ser. 2000, 195, 61–70. [Google Scholar] [CrossRef]
- Solimini, A.G.; Cardoso, A.C.; Heiskanen, A.-S. Indicators and Methods for the Ecological Status Assessment under the Water Framework Directive; #EUR-22314-EN; European Commission Joint Research Centre Institute for Environment and Sustainability: Ispra, Italy, 2006. [Google Scholar]
- Lawn, P.A. An assessment of the valuation methods used to calculate the Index of Sustainable Economic Welfare (ISEW), Genuine Progress Indicator (GPI), and Sustainable Net Benefit (SNBI). Environ. Dev. Sustain. 2005, 7, 185–208. [Google Scholar] [CrossRef]
- Wang, L.Z.; Lyons, J.; Kanehl, P. Impacts of urbanization on stream habitat and fish across multiple spatial scales. Environ. Manag. 2001, 28, 255–266. [Google Scholar] [CrossRef]
- Steinman, A.D.; Nicholas, J.R.; Seelbach, P.W.; Allan, J.W.; Ruswick, F. Science as a fundamental framework for shaping policy discussions regarding the use of groundwater in the State of Michigan: A case study. Water Policy 2011, 13, 69–86. [Google Scholar] [CrossRef]
- Reeves, H.W.; Hamilton, D.A.; Seelbach, P.W.; Asher, A.J. Ground-Water-Withdrawal Component of the Michigan Water-Withdrawal Screening Tool; United States Geological Survey Scientific Investigations Report 2009–5003; United States Geological Survey: Reston, VA, USA, 2009; p. 36.
- Swartz, W.; Sala, E.; Tracey, S.; Watson, R.; Pauly, D. The Spatial Expansion and Ecological Footprint of Fisheries (1950 to Present). PLoS ONE 2010, 5, e15143. [Google Scholar] [CrossRef] [PubMed]
- EPA. Clean Water Act Sec. 303(d), 33 U.S.C. § 1313(d); EPA: Washington, DC, USA, 1972. [Google Scholar]
- EPA. Water Quality Planning and Management; Code of Federal Regulations, 40 CFR 130.7.; EPA: Washington, DC, USA, 1992. [Google Scholar]
- Richter, B.D.; Mathews, R.; Harrison, D.L.; Wigington, R. Ecologically sustainable water management: Managing river flows for ecological integrity. Ecol. Appl. 2003, 13, 206–224. [Google Scholar] [CrossRef]
- Sayre, N.F. The Genesis, History, and Limits of Carrying Capacity. Ann. Assoc. Am. Geogr. 2008, 98, 120–134. [Google Scholar] [CrossRef]
- Rees, W.E.; Wackernagel, M. Ecological Footprints and Appropriated Carrying Capacity: Measuring the Natural Capital Requirements of the Human Economy; Jansson, A., Folke, C., Hammer, M., Costanza, R., Eds.; Island Press: Washington, DC, USA, 1994. [Google Scholar]
- Ehrlich, P.R.; Holdren, J.P. Impact of Population Growth. Science 1971, 171, 1212–1217. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Reichert, P.; Abbaspour, K.C.; Zehnder, A.J.B. A water resources threshold and its implications for food security. Environ. Sci. Technol. 2003, 37, 3048–3054. [Google Scholar] [CrossRef] [PubMed]
- Galli, A.; Wiedmann, T.; Ercin, E.; Knoblauch, D.; Ewing, B.; Giljum, S. Integrating Ecological, Carbon and Water footprint into a “Footprint Family” of indicators: Definition and role in tracking human pressure on the planet. Ecol. Indic. 2012, 16, 100–112. [Google Scholar] [CrossRef]
- Perez-Dominguez, R.; Maci, S.; Courrat, A.; Borja, A.; Neto, J.; Elliott, M. Review of Fish-Based Indices to Assess Ecological Quality Condition in Transitional Waters; Available online: http://www.wiser.eu/download/D4.4-1.pdf (accessed on 30 July 2018).
- Zhang, Y.; Singh, S.; Bakshi, B.R. Accounting for ecosystem services in life cycle assessment, Part I: A critical review. Environ. Sci. Technol. 2010, 44, 2232–2242. [Google Scholar] [CrossRef] [PubMed]
- Fiksel, J.; Bruins, R.; Gatchett, A.; Gilliland, A.; Ten Brink, M. The triple value model: A systems approach to sustainable solutions. Clean Technol. Environ. Policy 2014, 16, 691–702. [Google Scholar] [CrossRef]
- Palmer, M.A.; Lettenmaier, D.P.; Poff, N.L.; Postel, S.L.; Richter, B.; Warner, R. Climate change and river ecosystems: Protection and adaptation options. Environ. Manag. 2009, 44, 1053–1068. [Google Scholar] [CrossRef] [PubMed]
- Poff, N.L.; Richter, B.D.; Arthington, A.H.; Bunn, S.E.; Naiman, R.J.; Kendy, E.; Acreman, M.; Apse, C.; Bledsoe, B.P.; Freeman, M.C.; et al. The ecological limits of hydrologic alteration (ELOHA): A new framework for developing regional environmental flow standards. Freshw. Biol. 2010, 55, 147–170. [Google Scholar] [CrossRef]
- Postel, S.; Richter, B.D. Rivers for Life: Managing Water for People and Nature; Island Press: Washington, DC, USA, 2003; ISBN 978-1559634441. [Google Scholar]
- Witmer, M.C.H.; Cleij, P. Water Footprint: Useful for Sustainability Policies; #500007001; PBL Netherlands Environmental Assessment Agency: The Hague, The Netherlands, 2012. [Google Scholar]
- Tharme, R.E. A global perspective on environmental flow assessment: Emerging trends in the development and application of environmental flow methodologies for rivers. River Res. Appl. 2003, 19, 397–442. [Google Scholar] [CrossRef]
- Postel, S.L. Entering an Era of Water Scarcity: The Challenges Ahead. Ecol. Appl. 2000, 10, 941–948. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Wiedmann, T.O. Humanity’s unsustainable environmental footprint. Science 2014, 344, 1114–1117. [Google Scholar] [CrossRef] [PubMed]
- Falkenmark, M. Water and sustainability: A reappraisal. Environment 2008, 50, 4–16. [Google Scholar] [CrossRef]
- Meadows, D.H.; Meadows, D.H.; Randers, J.; Behrens, W.W., III. The Limits to Growth: a report to the Club of Rome. Available online: http://www.donellameadows.org/wp-content/userfiles/Limits-to-Growth-digital-scan-version.pdf (accessed on 30 July 2018).
- Hussen, A. Principles of Environmental Economics and Sustainability: An Integrated Economic and Ecological Approach, 3rd ed.; Routledge: Abingdon, UK, 2012. [Google Scholar]
- Brown, A.; Matlock, M.D. A Review of Water Scarcity Indices and Methodologies. White Pap. 2011, 106, 19. [Google Scholar]
- Gini, C. Variabilità e mutabilità. In Memorie di Metodologica Statistica; Pizetti, E., Salvemini, T., Eds.; Libreria Eredi Virgilio Veschi: Rome, Italy, 1955. [Google Scholar]
- Jackson, L.E.; Kurtz, J.C.; Fisher, W.S. Evaluation Guidelines for Ecological Indicators; #EPA/620/R-99/005; U.S. Environmental Protection Agency: Washington, DC, USA, 2000.
- Samhouri, J.F.; Levin, P.S.; Ainsworth, C.H. Identifying Thresholds for Ecosystem-Based Management. PLoS ONE 2010, 5, e8907. [Google Scholar] [CrossRef] [PubMed]
- Richter, B.D.; Warner, A.T.; Meter, J.L.; Lutz, K. A collaborative and adaptive process for developing environmental flow recommendations. River Res. Appl. 2006, 22, 297–318. [Google Scholar] [CrossRef]
- Richter, B.D.; Davis, M.M.; Apse, C.; Konrad, C. A presumptive standard for environmental flow protection. River Res. Appl. 2012, 28, 1312–1321. [Google Scholar] [CrossRef]
- Wiedmann, T.; Barrett, J. A Review of the Ecological Footprint Indicator—Perceptions and Methods. Sustainability 2010, 2, 1645–1693. [Google Scholar] [CrossRef]
- Solanes, M.; Gonzalez-Villarreal, F. The Dublin Principles for Water as Reflected in a Comparative Assessment of Institutional and Legal Arrangements for Integrated Water Resources Management; Global Water Partnership: Stockholm, Sweden, 1999. [Google Scholar]
- Glennon, R. Unquenchable; Island Press: Washington, DC, USA, 2010. [Google Scholar]
- Ruddell, B.L.; Adams, E.A.; Rushforth, R.; Tidwell, V.C. Embedded resource accounting for coupled natural-human systems: An application to water resource impacts of the western US electrical energy trade. Water Resour. Res. 2014, 50, 7957–7972. [Google Scholar] [CrossRef]
- Rushforth, R.R.; Adams, E.A.; Ruddell, B.L. Generalizing ecological, water and carbon footprint methods and their worldview assumptions using Embedded Resource Accounting. Water Resour. Ind. 2013, 1, 77–90. [Google Scholar] [CrossRef]
- Kates, R.W.; Clark, W.C.; Corell, R.; Hall, J.M.; Jaeger, C.C.; Lowe, I.; McCarthy, J.J.; Schellnhuber, H.J.; Bolin, B.; Dickson, N.M.; et al. Sustainability Science. Science 2001, 292, 641–642. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Finkbeiner, M. Water footprinting: How to address water use in life cycle assessment? Sustainability 2010, 2, 919–944. [Google Scholar] [CrossRef]
- Berger, M.; Finkbeiner, M. Methodological Challenges in Volumetric and Impact-Oriented Water Footprints. J. Ind. Ecol. 2012, 17, 79–89. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K.; Aldaya, M.M.; Mekonnen, M.M. The Water Footprint Assessment Manual: Setting the Global Standard; Water Footprint Network; Earthscan Publishing: Oxford, UK, 2011. [Google Scholar]
- Pfister, S.; Bayer, P.; Koehler, A.; Hellweg, S. Environmental Impacts of Water Use in Global Crop Production: Hotspots and Trade-Offs with Land Use. Environ. Sci. Technol. 2011, 45, 5761–5768. [Google Scholar] [CrossRef] [PubMed]
- Pfister, S.; Koehler, A.; Hellweg, S. Assessing the environmental impacts of freshwater consumption in LCA. Environ. Sci. Technol. 2009, 43, 4098–4104. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and flow regulation of the world’s large river systems. Science 2005, 308, 405–408. [Google Scholar] [CrossRef] [PubMed]
- Ridoutt, B.; Pfister, S. A revised approach to water footprinting to make transparent the impacts of consumption and production on global freshwater scarcity. Glob. Environ. Chang. 2010, 20, 113–120. [Google Scholar] [CrossRef]
- Chenoweth, J.; Hadjikakou, M.; Zoumides, C. Review article: Quantifying the human impact on water resources: A critical review of the water footprint concept. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 9389–9433. [Google Scholar] [CrossRef]
- Kounina, A.; Margni, M.; Bayart, J.; Boulay, A.; Berger, M.; Bulle, C.; Frischknecht, R.; Koehler, A.; Mila i Canals, L.; Motoshita, M.; et al. Review of methods addressing freshwater use in life cycle inventory and impact assessment. Int. J. Life Cycle Assess. 2013, 18, 707–721. [Google Scholar] [CrossRef]
- Mila i Canals, L.; Chenoweth, J.; Chapagain, A.; Orr, S.; Anton, A.; Clift, R. Assessing freshwater use in LCA: Part I—Inventory modelling and characterization factors for the main impact pathways. Int. J. Life Cycle Assess. 2008, 14, 28–42. [Google Scholar] [CrossRef]
- Pfister, S.; Ridoutt, B.G. Water footprint: Pitfalls on common ground. Environ. Sci. Technol. 2013, 48, 4. [Google Scholar] [CrossRef] [PubMed]
- ISO (2014), ISO 14046:2014(en): Environmental Management—Water Footprint—Principles, Requirements and Guidelines. Available online: https://www.iso.org/obp/ui/#iso:std:iso:14046:ed-1:v1:en (accessed on 30 July 2018).
- Mubako, S.T.; Ruddell, B.L.; Mayer, A.S. Relationship between water withdrawals and freshwater ecosystem water scarcity quantified at multiple scales for a Great Lakes watershed. J. Water Resour. Plan. Manag. 2013, 139, 671–681. [Google Scholar] [CrossRef]
- Zorn, T.G.; Seelbach, P.W.; Rutherford, E.S.; Wills, T.C.; Cheng, S.T.; Wiley, M.J. A Regional-Scale Habitat Suitability Model to Assess the Effects of Flow Reduction on Fish Assemblages in Michigan Streams; Fisheries Research Report 2089; Michigan Department of Natural Resources: Ann Arbor, MI, USA, 2008. [Google Scholar]
- Pacific Institute. Exploring the Case for Corporate Context-Based Water Targets. 2017. Available online: https://www.ceowatermandate.org/files/context-based-targets.pdf (accessed on 28 June 2018).
- Alliance for Water Stewardship. The AWS International Water Stewardship Standard. 2014. Available online: http://a4ws.org/wp-content/uploads/2017/04/AWS-Standard-Full-v-1.0-English.pdf (accessed on 28 June 2018).
- Wichelns, D. Virtual water and water footprints offer limited insight regarding important policy questions. Int. J. Water Resour. Dev. 2010, 26, 639–651. [Google Scholar] [CrossRef]
- Hanemann, W.M. Chapter 4: The economic conception of water. In Water Crisis: Myth or Reality; Rogers, P.P., Llamas, M.R., Martinez-Cortina, L., Eds.; Taylor & Francis Group: Oxford, UK, 2006; pp. 61–91. [Google Scholar]
- Hoekstra, A.Y.; Mekonnen, M.M.; Chapagain, A.K.; Mathews, R.E.; Richter, B.D. Global monthly water scarcity: Blue water footprints versus blue water availability. PLoS ONE 2012, 7, e32688. [Google Scholar] [CrossRef] [PubMed]
- Zetland, D. The End of Abundance: Economic Solutions to Water Scarcity; Aguanomics Press: Mission Viejo, CA, USA, 2011; ISBN 978-0615469737. [Google Scholar]
- Fang, K.; Heijungs, R.; de Snoo, G.R. Understanding the complementary linkages between environmental footprints and planetary boundaries in a footprint–boundary environmental sustainability assessment framework. Ecol. Econ. 2015, 114, 218–226. [Google Scholar] [CrossRef]
- Heistermann, M. HESS Opinions: A planetary boundary on freshwater use is misleading. Hydrol. Earth Syst. Sci. 2017, 21, 3455–3461. [Google Scholar] [CrossRef]
- Verones, F.; Pfister, S.; Hellweg, S. Quantifying Area Changes of Internationally Important Wetlands Due to Water Consumption in LCA. Environ. Sci. Technol. 2013, 47, 9799–9807. [Google Scholar] [CrossRef] [PubMed]
| RED | RED SRF | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| c | T` | RMSE | Peak FED | @ WTA | Notes | T` | RMSE | Peak FED | @ WTA | Notes |
| 0 | - | 0 | 1 | 1 | - | 0 | 1 | 1 | ||
| 0.1 | 0.010 | 0.008 | 0.900 | 1 | 0.018 | 0.009 | 0.902 | 1 | ||
| 0.2 | 0.019 | 0.016 | 0.800 | 1 | 0.036 | 0.018 | 0.804 | 1 | ||
| 0.3 | 0.029 | 0.024 | 0.700 | 1 | 0.054 | 0.027 | 0.705 | 1 | ||
| 0.4 | 0.038 | 0.032 | 0.600 | 1 | 0.071 | 0.036 | 0.607 | 1 | ||
| 0.5 | 0.048 | 0.040 | 0.500 | 1 | 0.089 | 0.045 | 0.509 | 1 | ||
| 0.6 | 0.058 | 0.048 | 0.401 | 0.4 | FED local maxima | 0.107 | 0.054 | 0.411 | 0.54 | FED local maxima |
| 0.7 | 0.067 | 0.056 | 0.301 | 0.37 | FED local maxima | 0.125 | 0.064 | 0.351 | 0.49 | FED local maxima |
| 0.8 | 0.077 | 0.064 | 0.248 | 0.34 | FED local maxima | 0.143 | 0.073 | 0.333 | 0.46 | FED local maxima |
| 0.9 | 0.086 | 0.072 | 0.238 | 0.33 | FED local maxima | 0.161 | 0.082 | 0.319 | 0.44 | |
| 1 | 0.096 | 0.080 | 0.228 | 0.31 | 0.179 | 0.091 | 0.306 | 0.42 | ||
| 1 | 0.000 | 0.122 | 0.228 | 0.31 | 0.000 | 0.190 | 0.306 | 0.42 | ||
| RMSE/c = 0.08 | RMSE/c = 0.09 | |||||||||
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruddell, B.L. Threshold Based Footprints (for Water). Water 2018, 10, 1029. https://doi.org/10.3390/w10081029
Ruddell BL. Threshold Based Footprints (for Water). Water. 2018; 10(8):1029. https://doi.org/10.3390/w10081029
Chicago/Turabian StyleRuddell, Benjamin L. 2018. "Threshold Based Footprints (for Water)" Water 10, no. 8: 1029. https://doi.org/10.3390/w10081029
APA StyleRuddell, B. L. (2018). Threshold Based Footprints (for Water). Water, 10(8), 1029. https://doi.org/10.3390/w10081029




