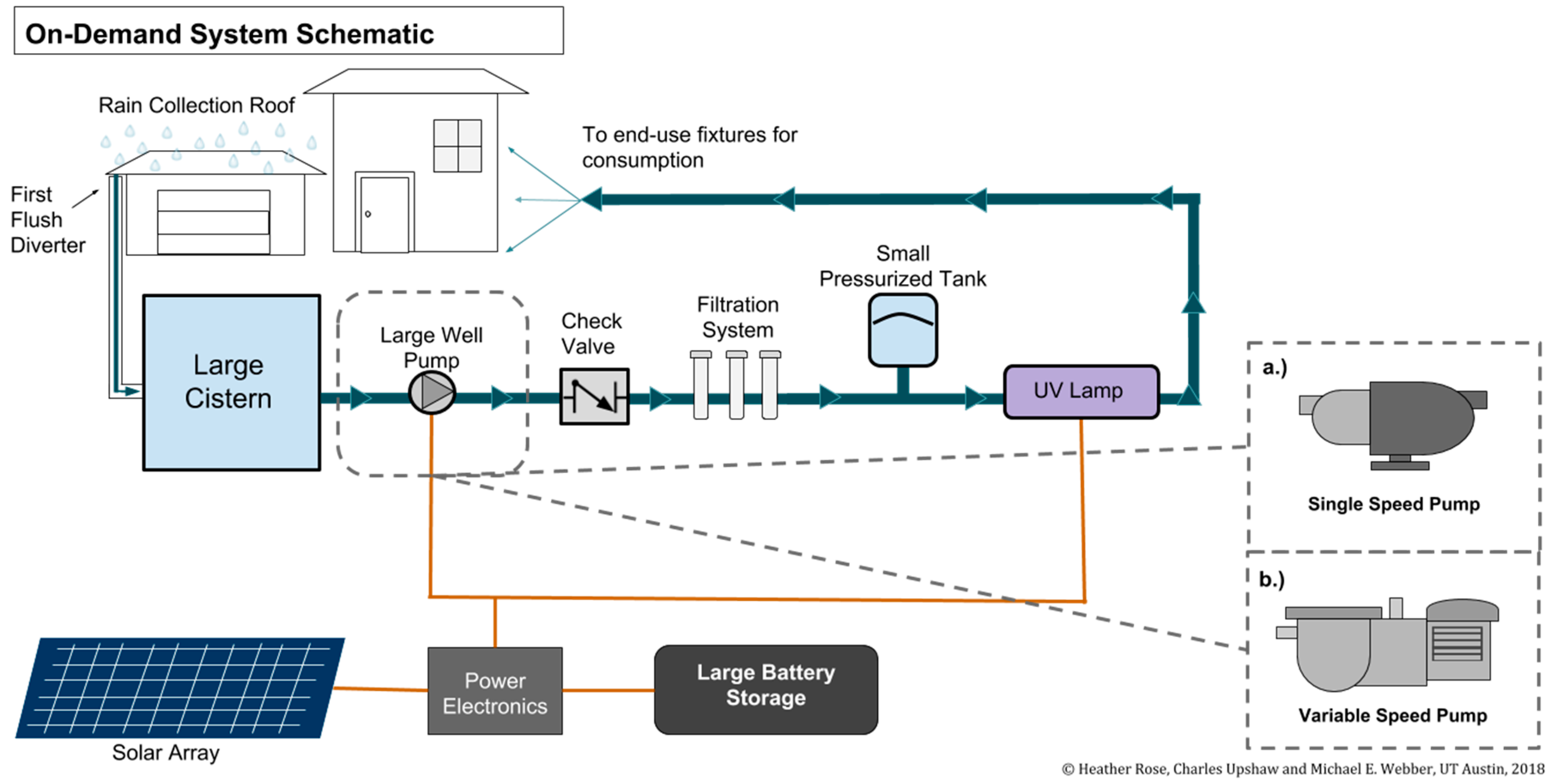
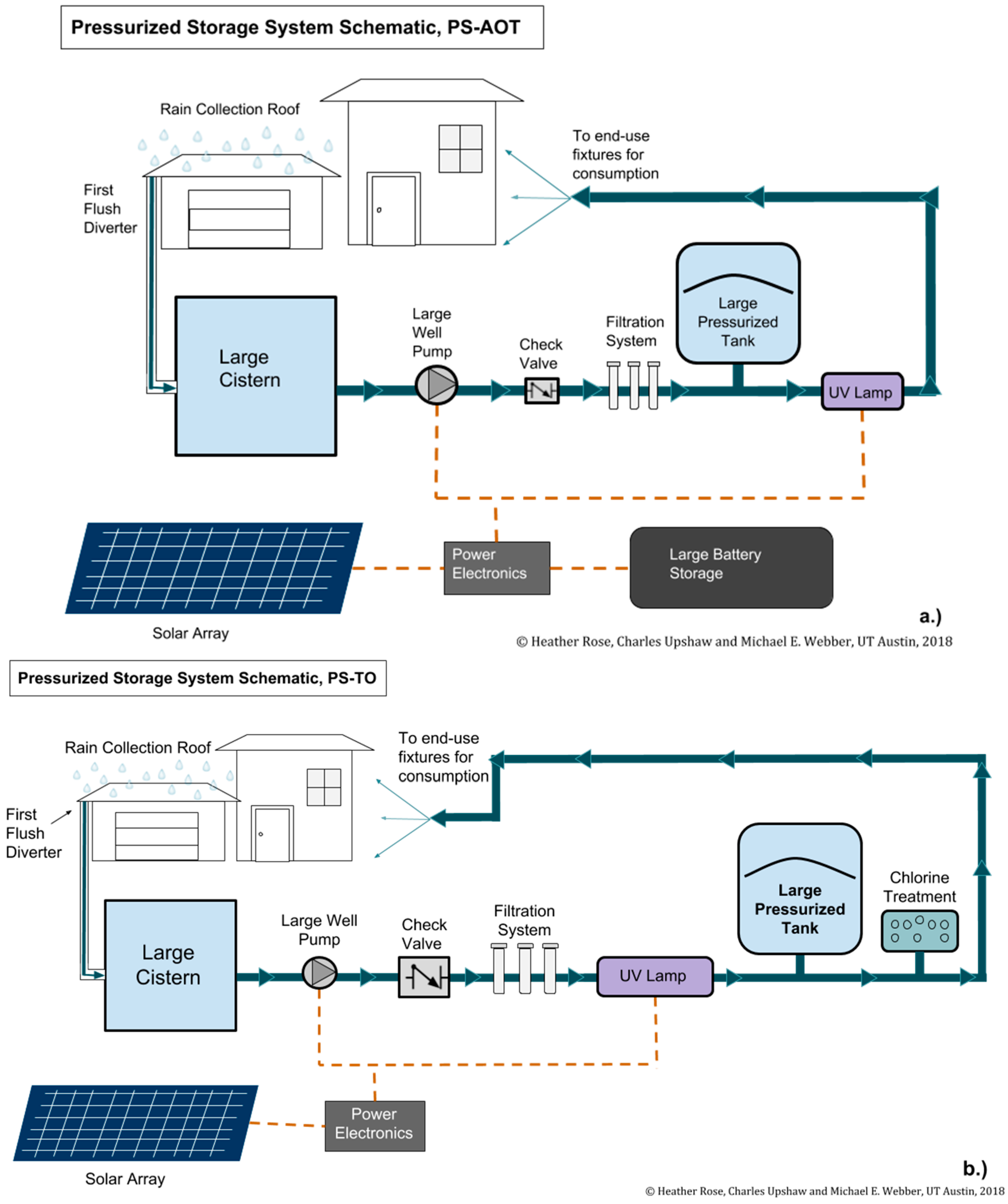
4.1. System Energy Analysis
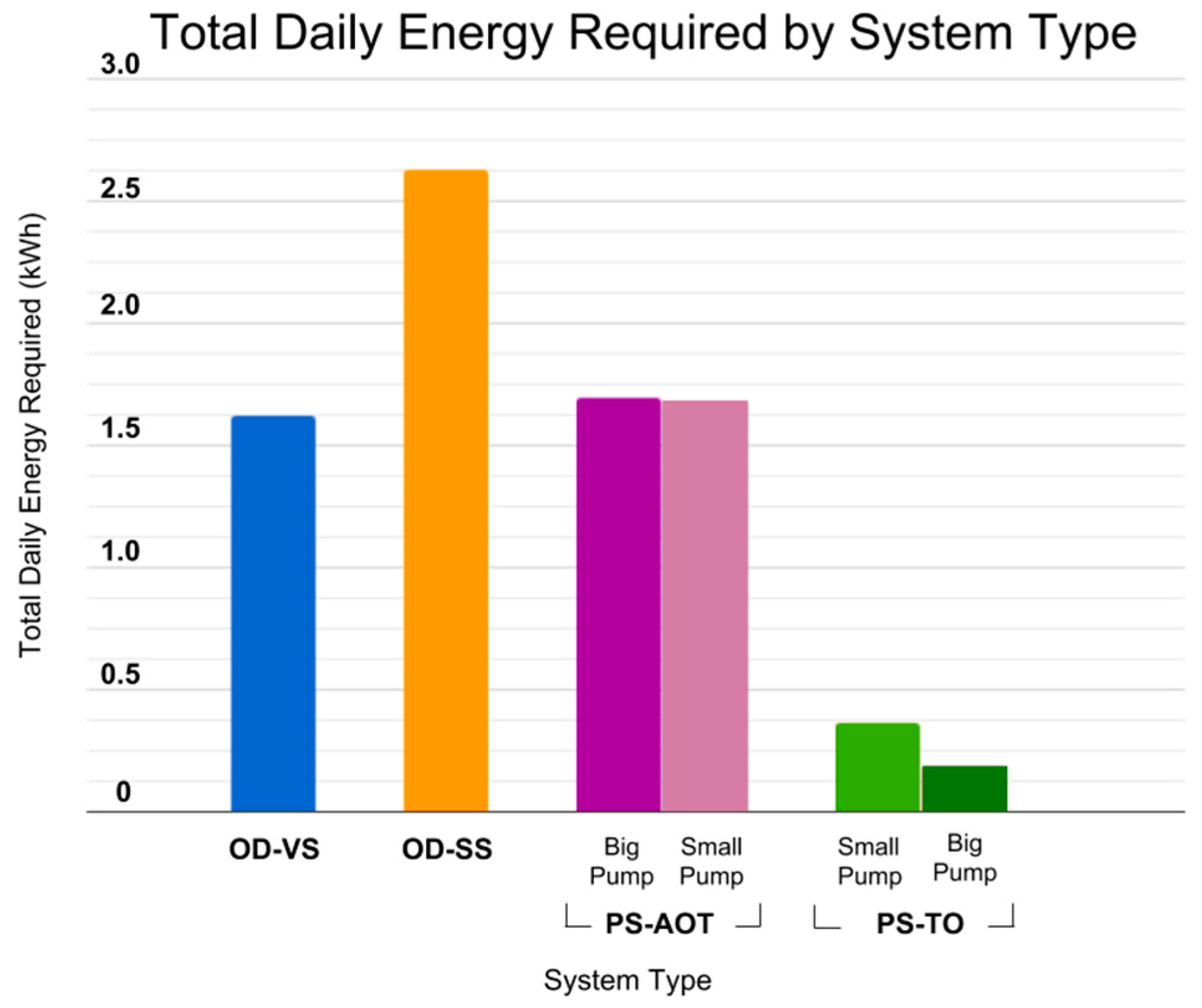
From our analysis, we found the OD-SS required the highest total daily energy requirement of 2.63 kWh/day. The OD-VS and the PS-AOT systems had similar maximum energy requirements of 1.65 and 1.69 kWh per day, respectively. The PS-TO system had the lowest daily energy requirements, ranging from 0.19 to 0.36 kWh per day based on assigned pumping time and pump size. See
Figure 3 below.
4.1.1. Empirical On-Demand System (OD-SS)
For the OD-SS system, we found the total daily energy requirement was 2.63 kWh, which is 60% more than that of the OD-VS system. The maximum power needed for the OD-SS system was 0.62 kW when only considering steady state power (startup power demand can spike 10–25% higher). We think these values are much more representative of the actual energy requirements for an on-demand system as it models the real-world dilemma of pump over-sizing. When purchasing a pump, one must size for a maximum flow rate in order to prevent pump failure. However, pumps are designed to perform at maximum efficiency when operating at higher flow rates. As seen from the Residential End Uses of Water 2016 data [
7], flow rates are relatively low compared to pump capacity. This over capacity of the pump results in more energy consumption because the excess pressurization is throttled at the tap (or other end-use), wasting much of the energy put into pressurizing the water.
4.1.2. Variable-Speed Pump On-Demand System (OD-VS)
We found the total daily energy requirement for the OD-VS system was 1.65 kWh per day, while the maximum power needed was 0.180 kW (when considering a peak flow rate of 4.5 GPM [
15]). Our variable speed on-demand pump model was based on theoretical pump power equations, with flow rates averaged from the uses each hour, pressure drop simplified to a quadratic system curve, and efficiency coefficients made constant for simplification. This equation calculates the power needed to deliver water at the calculated flow rate and pressure drop, but it does not capture the potential inefficiencies of very low part-load operation nor the potential increase in power for delivering significantly higher volumes of water. These shortcomings in modeling pump performance have been identified by Ward in 2012 [
6] and others, but this method is useful for providing a generalized order of magnitude estimate for the power demand and energy consumption for an on-demand variable speed system. Keeping these simplifications in mind, we still estimate that there could be significant energy savings by using a variable speed pump instead of a single speed pump for residential rainwater systems.
4.1.3. Pressurized Storage, UV On-Demand Treatment System (PS-AOT)
For the PS-AOT system, we found the daily energy required for small, medium, and large sized pumps ranged from 1.67 to 1.69 kWh. The main power consumer in this system is the UV lamp, requiring 1.55 kWh of energy per day. Conversely, the energy required for pumping was only 0.12–0.14 kWh per day. The pump power requirements for this system ranged from 0.03 to 0.19 kW depending on the designated flow rate and pump size. We can see in this system that while there are savings from operating a smaller pump for a longer period of time (thus reducing frictional pressure drop), these relative savings are dwarfed by the energy needs of the always-on treatment system. The relative differences between the larger, faster pump and the smaller, slower pump are system-dependent, and there could be no savings from the smaller pump if the system is static pressure dominated.
4.1.4. Pressurized Storage, UV Once a Day Treatment (PS-TO)
For the PS-TO system, we found that the total energy requirements varied by assigned treatment time and pump size (0.19–0.36 kWh for treatment times between 0.75 and 4 h). Interestingly, in this system configuration, the scenario with the small pump consumes the most energy because the longer fill duration means the UV lamp is on for hours longer, which swamps the lower pumping energy savings. We see significant energy savings for the largest pump size, despite higher pumping energy, due to the shorter time-period that the UV lamp is in operation. When comparing the PS-TO system to the PS-AOT, we see significant energy savings across the board due to only operating the UV lamp while pumping the water into the pressurized tank.
It should be noted that treating water before storing it comes with a risk of contamination. If the tank is not emptied completely on a regular basis, residual water that was treated days before could remain in the tank, allowing residual biologic contaminants to slowly build to a level that is no longer safe for consumption. This risk of contamination is why RWH systems typically position the UV treatment last in the assembly before delivery to a house plumbing [
2]. It should also be noted that UV lamps have a “warm up time” before they reach full treatment capacity. Therefore, using this configuration on its own, without a means to properly periodically flush the pressure tank, and/or without a secondary residual treatment system (e.g., chlorine or ozone), should be limited to applications where non-potable water is suitable.
4.1.5. Power and Energy Storage Requirements between Systems
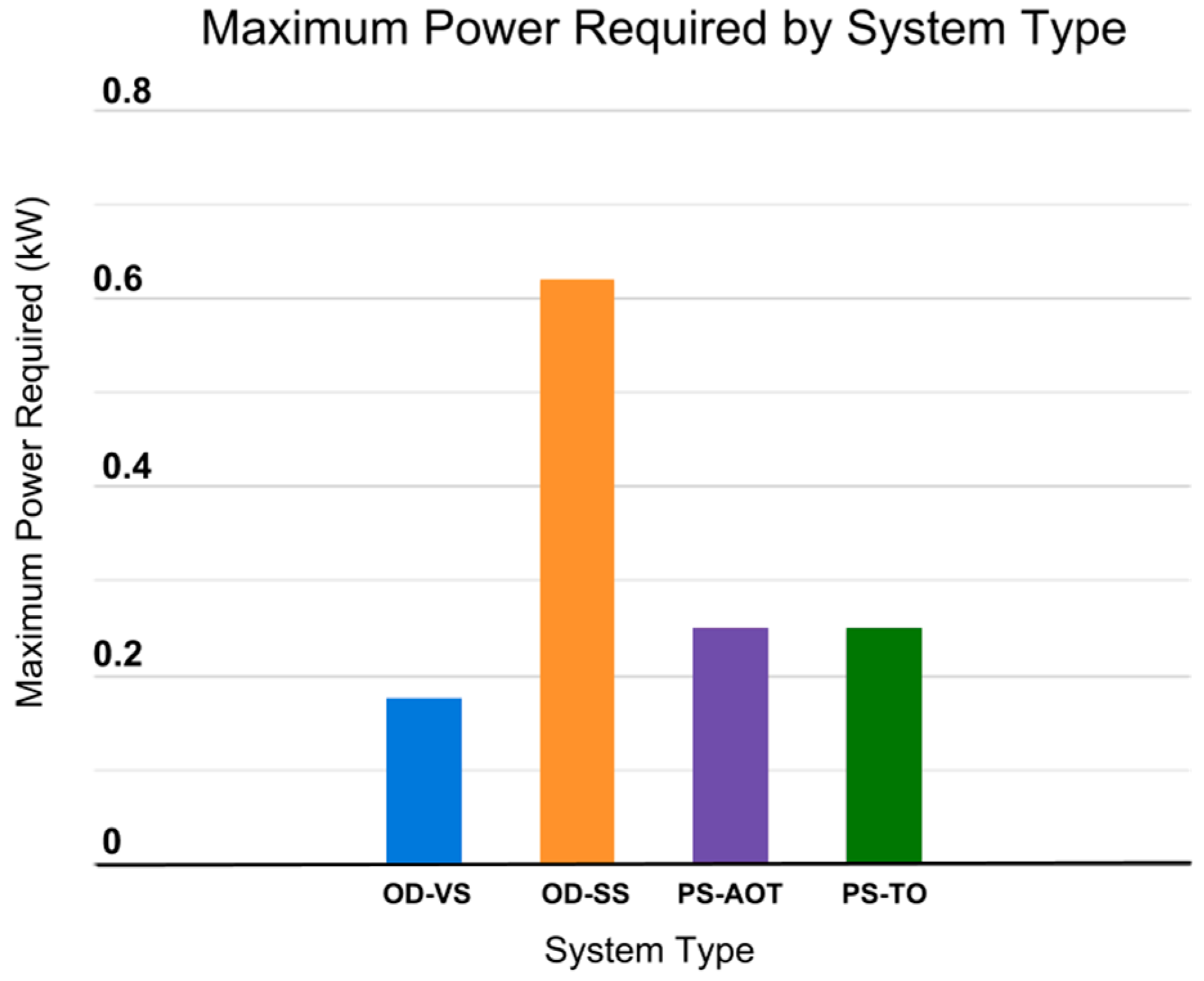
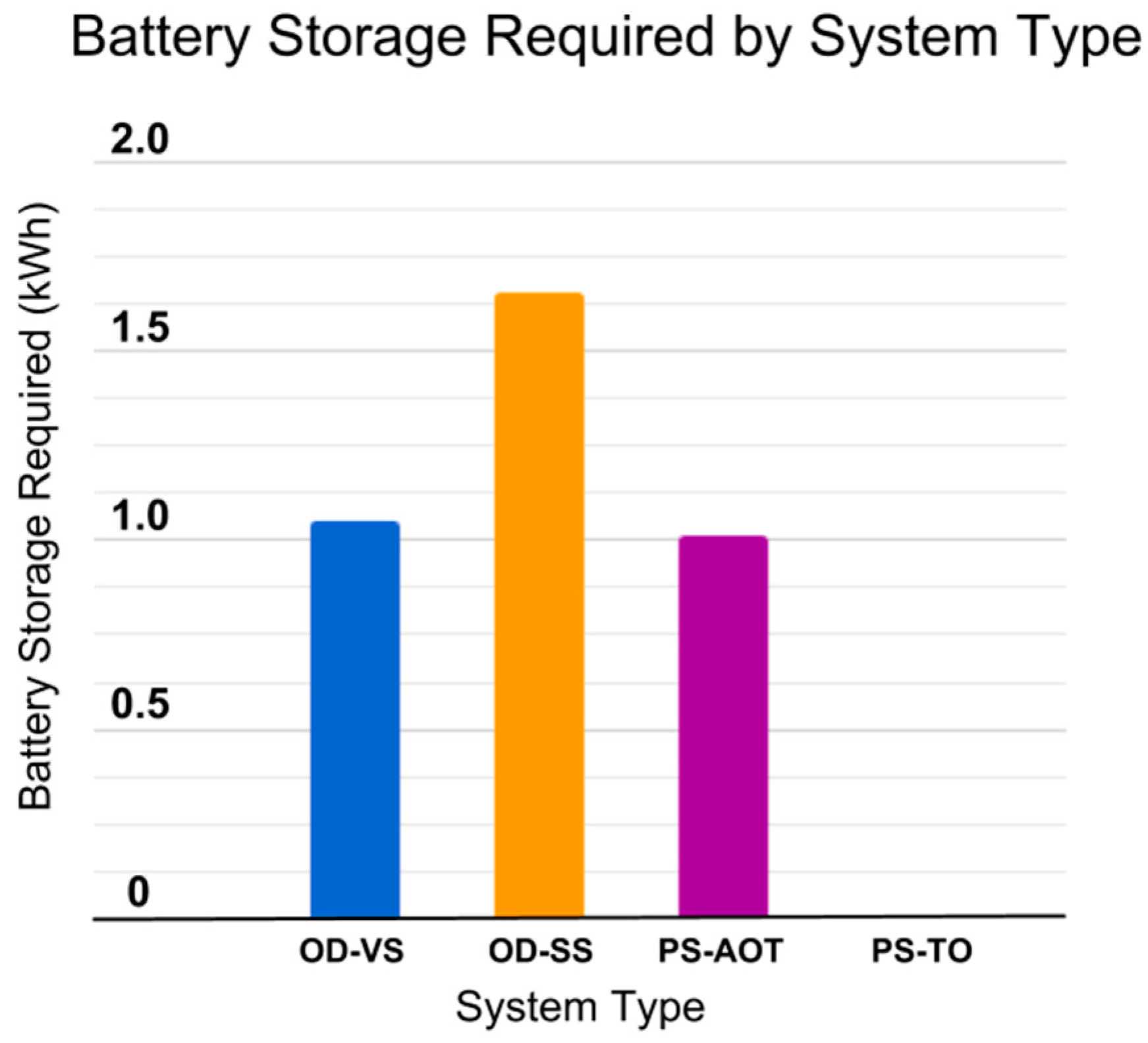
Comparing these four system configurations, we can see a significant difference in PV capacity and battery storage requirements between systems. The OD-SS system has a maximum power requirement of 0.62 kW and to run this system at night requires a minimum battery storage of 1.65 kWh per day. In comparison, the OD-VS system requires a maximum power of 0.18 kW and to run this system at night requires a minimum of 1.07 kWh of battery storage.
By comparison, the PS-AOT and the PS-TO models both have a maximum power requirement of 0.25 kW. The PS-AOT system requires a battery storage of 1.01 kWh per day to power the UV lamp at night, whereas the PS-TO system does not require any additional battery storage as both pumping and treatment occur during daylight hours using solar energy. See
Figure 4 and
Figure 5 below for a comparison of required Power and Battery Storage between systems.
Overall, these results show that the battery storage requirements for the OD-SS system is the highest due to the combined energy needed to run an over-sized pump and treat water on demand. The OD-VS and PS-AOT systems’ battery storage requirements are relatively similar due to the UV lamp energy being the main driver for energy consumption in both scenarios.
4.2. System Cost Analysis
From our analysis, the OD-SS system is the most expensive. We believe that this is due to the extra energy requirements of a single speed, oversized pump that operates at a higher energy capacity than necessary. We can see the OD-VS and the PS-AOT systems are similar in price range, despite having different system configurations. The PS-AOT system requires pressurized tanks, in the 100+ gallon capacity range, mostly accounting for the difference in price between the OD-VS and the PS-AOT systems.
From our analysis, the least expensive system is the PS-TO system. This system saves a lot of energy because water is only pumped and treated once per day, removing the necessity for battery storage all together. In addition, because water is pumped once per day, at a designated flow rate, a single speed appropriately sized pump can be used, significantly reducing costs.
Comparing these systems via our analysis, we can see the biggest driver for cost is the amount of PV energy and battery storage required for each system. In fact, battery storage alone makes up for 39% of the OD-SS system’s cost requirements, 42% of the OD-VS system’s cost requirements, and 30% of the PS-AOT system’s cost requirements. The extra cost of the large pressurized tank for the PS systems seemed to affect total cost the least. This being said, systems with lower energy demand can significantly reduce costs by reducing the need for large PV arrays and battery storage.
The best value system, by far, is the PS-TO system, because of its very low energy requirements. Because this system has a set flow rate chosen by the operator, a significantly smaller (and less expensive) single speed pump can be used. In addition, the PV array can be sized appropriately (only providing power for items actively in use), which significantly reduces cost.
Although the PS-TO system is the most energy and cost effective of the four systems, there is always a risk of contamination with stored water as discussed above. For this reason, we recommend adding a secondary treatment directly before consumption (such as chlorine, reverse osmosis, etc.)
It should be noted that the above cost analyses only consider the prices based on energy, power and flow rate capacities. When pricing out a system, it is very unlikely that items such as battery banks, PV arrays and UV lamps will be available at the exact capacities described in this analysis. Due to market demand, additional costs should be anticipated for battery banks, PV arrays and UV lamps at higher than necessary capacities. However, the purpose of this analysis was not to provide comprehensive system cost estimates, but rather to analyze the relative differences in cost between these system configurations to get an understanding of the underlying driving factors.
Additionally, it also should be noted that this analysis only considers upfront capital costs. Further analysis would need to be conducted to investigate the additional operational and maintenance costs of replacing pumps, batteries, PV arrays and tanks as they degrade over time. This analysis does not consider the long-term loss in energy efficiency due to battery life cycles and solar panel degradation. The more the battery and solar panel are used, the less life cycles remain, contributing to loss in efficiency. Further analysis would need to be conducted to see how great of a contributor this loss in efficiency would be.
This analysis only considers costs for the energy consuming components of a rainwater harvesting system for the purpose of comparing costs between system types. Further analysis would need to be conducted to estimate costs of cisterns, filters, pipes, etc. that are also required components of any complete rainwater harvesting system [
2].
For safety, we recommend having the ability to create an On-Demand treatment and delivery system in case more water is consumed than was treated and stored. In addition, homes should always have access to municipal water supply in case of malfunction, water contamination or water shortages.