Abstract
Long and continuous series of precipitation in a high temporal resolution are required for several purposes, namely, urban hydrological applications, design of flash flood control structures, etc. As data of the temporally required resolution is often available for short period, it is advantageous to develop a precipitation model to allow for the generation of long synthetic series. A stochastic model is applied for this purpose, involving an alternating renewal process (ARP) describing a system consisting of spells that can take two possible states: wet or dry. Stochastic generation of rainfall time series using ARP models is straight forward for single site simulation. The aim of this work is to present an extension of the model to spatio-temporal simulations. The proposed methodology combines an occurrence model to define in which locations rainfall events occur simultaneously with a multivariate copula to generate synthetic events. Rainfall series registered in different regions of Germany are used to develop and test the methodology. Results are compared with an existing method in which long independent time series of rainfall events are transformed to spatially dependent ones by permutation of their order. The proposed model shows to perform as a satisfactory extension of the ARP model for multiple sites simulations.
1. Introduction
Stochastic modeling of precipitation aims at conceptually representing the natural process through some mathematical relationships in order to generate synthetic series that reproduce the statistical properties of observations. Synthetic series are used for different purposes, e.g., planning and design, deriving long extended time series or regionalization of rainfall to areas without measurements. Among the existing precipitation models, the following types can be found: data driven generators (e.g., resampling [1,2] and disaggregation [3,4,5]), time series models (e.g., Markov chains [6]), and event-based methods [7,8,9], such as point and cluster process-based (e.g., Neyman-Scott [10,11,12,13], Barlett-Lewis [14,15,16,17,18,19,20]) or alternating renewal models [21,22,23,24].
The spatio-temporal scale of the model is determined by the hydrological application, and modeling becomes more challenging for high resolutions. Precipitation in a sub-hourly temporal resolution is a key input for several purposes, namely rainfall erosivity quantification, optimization of design and operation of urban drainage systems, flash flood control structures, etc. Point or single-site models are useful when the spatial variability of precipitation is low and/or in cases in which a uniform representation is sufficient. Multi-point models are able to simultaneously generate time series at different sites while preserving temporal and spatial cross-correlation of the process. Many examples of multi-site models can be found in the literature; however, most of them are based on monthly, weekly, and up to daily time scales. For finer time resolutions, some of the models become complex and the parameters increase drastically. Furthermore, their performance declines as a result of the difficulty to reproduce historical properties. Nevertheless, some models for simulating rainfall on sub-daily temporal resolution and at several sites simultaneously are available, and therefore an overview of some of them is included here.
An event based model is proposed by [9] consisting of rain cells (single events) and storms (clustering of cells). The model shows a good performance is reproducing extreme events for different temporal scales. However it is complex, many information and stepwise analysis are required, and adaptation to new case studies and interpretation is not straight-forward.
The authors of [10,12,25] present and apply a model based on a Neyman-Scott process combined with a generator of spatial circular raincells to simulate rainfall up to a 1 min time resolution. As a very high number of parameters is involved, a calibration module is provided to speed up their estimation. The model shows good performance in reproducing daily extreme values for single stations. Tarpanelli et al. [13] describe a simpler approach also based on Neyman-Scott model but combined with a rearrangement algorithm that is able to reproduce hourly and daily extremes. The method is simple to interpret and apply. However, as the rearranging is based on the hourly time series, it is not clear whether the structure of the storms is conserved within this process, which is very important in applications that involve fast response hydrological systems.
Haberlandt et al. [24] propose a method to simulate rainfall in multiple stations based on a single-site alternating renewal process (ARP). The model generates independent precipitation time series for several locations, and is then combined with a multi-site resampling procedure to reproduce the spatial dependence structure of rainfall by reordering the events. Extreme values show to be well reproduced for short durations, whereas a systematic overestimation is obtained for long durations.
Many of these models are able to simulate rainfall up to one hour time resolution. However, many applications require a finer resolution and therefore an extra disaggregation model is required. Licznar et al. [4] present a stochastic model to disaggregate spatio-temporal data into fine temporal resolutions. The model involves a moderate number of parameters and is validated based on simulations of network flows showing a good performance. Another disaggregation model based on daily data combined with posterior resampling of events is presented by [5], resulting is a good performance in reproducing hourly extreme values, whereas sub-hourly extremes are overestimated.
Simultaneous simulation of precipitation at multiple sites involves several variables that could be modeled jointly. Multivariate models are capable of including the interdependencies between correlated variables. These models can be constructed by combining two components, the marginals describing each of the involved variables and a copula describing the dependence structure among them, resulting in a very flexible frame in multivariate modeling. Copulas are multivariate distribution functions whose marginals are all uniform. Multivariate copulas have not been used for hydrology applications as often as bivariate ones. The increase of dimensionality makes the application and interpretation of results more complicated. Some applications using three-dimensional copulas include the modeling of rainfall events [26,27,28,29], flood events [30,31,32,33], occurrence of floods in different tributaries [34,35,36], sediment transport [37], and droughts [38,39,40]. Additionally, the use of four dimensions can be found in studies related with modeling of rainfall events [20], daily evapotranspiration [41] and sea storms [42]. The application of highly dimensional models should be able to reproduce the complete dependence structure of the variables describing the phenomena. Recent research introduces pair-copula constructions to build flexible multivariate distributions called Vine copulas [43]. Some hydrological applications based on these copulas can be found in the works [8,20,44,45,46,47].
The overview of the existing literature reveals some limitations of the available models to simulate rainfall in multiple sites. Several of these methods need to be further combined with other models to provide time series of precipitation, especially if the following aspects are targeted: (i) continuity, (ii) high temporal resolution, and (iii) in multiple sites. Data driven methods are limited to observed attributes, like patterns of rainfall and the length of the observation period. Multi-site models are usually complex, hard to interpret and involve several stages of simulation, which result in many parameters, especially for applications that require high temporal resolutions. Copulas have shown to efficiently mimic joint behavior of event characteristics. However, their application for continuous modeling has been limited.
Therefore, the objective of this work is to contribute to the possibility of obtaining long rainfall series for multiple sites that can properly reproduce different characteristics of the observations, whilst keeping the model as simple as possible. For this reason a model based on an alternating renewal process is extended here for multiple sites. The model has been applied by [23] for modeling rainfall in single sites and was shown to be efficient for high temporal resolution applications. The model is considered easy to interpret and to transfer to new regions of interest. Furthermore, as it is event based, the number of parameters is not affected by the temporal resolution. The following questions are to be addressed in this work:
- Is an extension of the Alternating Renewal based process model to a multi-site application feasible?
- Is the proposed extension able to reproduce both average event properties and extreme event statistics of observed rainfall in a high temporal resolution?
- How is the proposed model performing compared to the current practice?
- Are copulas efficient tools for modeling continuous precipitation in a high temporal resolution?
It is the aim of this work to address these questions by developing a stochastic continuous precipitation model for simulating long time series of rainfall in a high temporal resolution. The application of the model for multi-sites is to be assessed.
2. Materials and Methods
2.1. Methods
2.1.1. Alternating Renewal Process
The precipitation model presented in this work is based on the theory of an alternating renewal process. This process is a continuous-time stochastic one that cycles through two possible states defined as rainfall and no-rainfall. Consequently, rainfall is modeled as events and involves two structures that complement each other: external and internal. The external structure involves the variables describing the durations of the wet and dry spells (WSD and DSD) and variables that consider the amount and intensity of rainfall falling during the wet spells (WSA and WSI). The renewal process has a precondition that these variables are independent and identically distributed (IID).The distribution of rainfall within the wet spells is described by the internal structure and involves the following variables: intensity of peak and time of occurrence of the peak (WSPeak and WSTpeak). The different components of the model are presented in Figure 1.
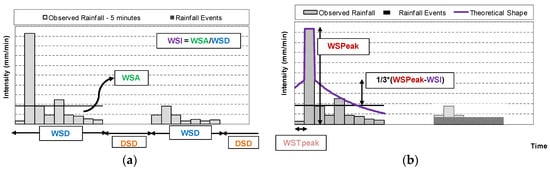
Figure 1.
Components of the (a) external and (b) internal structures of the precipitation model.
Observed rainfall consists of measurements performed on a regular basis, for example every 5 min. Therefore, some thresholds must be set to identify events from the continuous time series. At first, the minimum time between wet spells to consider events as independent needs to be set. Here, 5 min are selected, meaning that a volume of precipitation different to zero is observed in all time steps within the wet spell. This threshold omits any intra-event gaps, which, according to [48], can lead to strong biases in WSI and WSD if they are extensive. However, this threshold results in some cases in which the autocorrelation of event variables are significantly different from zero, especially for the WSD, failing the precondition of IID variables. Further discussion regarding this shortcoming can be found in [49]. Second the minimum volume for an event to be considered as relevant is set to 1 mm. Only these events are included in the multi-site model, the discarded ones, referred to as small events, are implemented into the time series in a different way and uniformly for all stations.
Probability (marginal) distributions are fitted to DSD, WSD, WSA, WSI, and WSPeak for each station. WSTpeak values are modeled using a uniform distribution which results in values between 0 and 1 that are multiplied by the total duration (WSD) to derive the location of the peak intensity. The correlation between WSA and WSD is significant. Additionally, their ratio, i.e., WSI, is significantly correlated with the WSPeak. These dependence structures are included in the model by multivariate functions called copulas. Eventually, the external and internal structures are linked by a bivariate copula model used to simulate peak intensities conditioned on pairs of WSA-WSD. The internal structure is modeled by a mixture of two exponential functions described by a single parameter and estimated for each event. The marginal distributions describing variables involved in the external structure include a total of 10 parameters. These parameters are estimated for events belonging to different seasons separately. The internal structure involves a total of eight parameters estimated for all seasons together. Furthermore, for the external structure the parameters are specific for each station, whereas for the internal structure these parameters are invariant for all stations within a region.
As the novelty of this work is the extension of the ARP to multi-sites the following subsections will focus on the details related with this contribution. The development focuses on the external structure of the model. Therefore, further features related with definition and modeling of the internal structure and small events can be found in [23], which applies the same model but for single stations.
2.1.2. Multivariate Synthesis of Rainfall Events
The proposed method consists of a number of subsequent steps. First an occurrence model is involved to generate the occurrence of rainfall events in a single or several stations simultaneously (Section Occurrence Model). Then a wet spell model generates pseudo values of WSA and WSD either for one station using bivariate copulas or for several stations using Vine copulas (Section Multivariate Wet Spell Model). Consequently pseudo values are bias corrected and transformed to real values by using probability distributions fitted to all events registered in each station. Thereafter, dry spells are introduced by a dry spell model into the time series for one of the stations and adjusted for the surrounding ones (Section Multivariate Dry Spell Model). In the last step the continuous series of events are converted to time series, i.e., with equidistant time steps.
The method requires the identification of events that occur simultaneously in several stations. For this purpose events are determined based on continuous time series for each station. Thereafter the temporal occurrence of events is compared between sites to define the events occurring isolated and those extending to several stations. The starting time step and length (WSD) are used to define events occurring simultaneously in several stations. A moving window of ±a × WSD is applied at the starting of each event to define whether events are classified as occurring simultaneously with events registered in other stations. a is a value that allows for some flexibility in the definition of simultaneous events and can change for different types of events. In this work a constant value of 1.5 is taken for all events. Events are then separated according to the simultaneous occurrence in 1, 2, 3, …, k stations.
The spatio-temporal structure of rainfall events is affected by topography, orography, coastal influences and the type of storm according to the season [50]. As stated by these authors, intense storms have an elliptical shaped field influence, whereas long lasting duration storms show a multi-cellular shape. Therefore rainfall events are additionally separated into different seasons according to the nature of physical processes causing them.
Occurrence Model
This part of the model is set up to simulate long time series of events occurring in 1, 2, 3, …, k stations simultaneously based on observed percentages. Percentages of events occurring in 1, 2, 3, …, k stations along with percentage of events occurring at each of the stations are included within this model to estimate their probabilities of occurrence. For a case study involving three stations a long time series describing events occurring in one, two, or three stations is randomly generated based on the probabilities of occurrence of each case and then events are assigned to each station according to the respective probabilities of occurrence. The outcome is a time series of event occurrences consisting of 0 s and 1 s that are assigned to each of the stations, with 0 meaning no event and 1 meaning event occurring at a particular station, an example is presented in Table 1.

Table 1.
Example of short time series resulting from occurrence model for a three stations case.
Events extended to all stations are indicated with a number 3 in the first line of Table 1. The multi-site model must guarantee that these events occur in the same temporal period of the final synthetic time series. Events extended to all stations in two sequential steps of the analysis are defined as “consecutive” (see e.g., columns 3–4 and 10–11 of Table 1, marked with italic). From the rest of the events, the cases defined as “longest” are identified. An example of these events is marked with a red box (Table 1). These events correspond to the case with the highest number of events to be introduced when all stations are compared within a period delimited by events extended to all stations (i.e., between columns 4 and 10). This classification of events will be used later when the DSD is addressed (Section Multivariate Dry Spell Model).
Once the long time series of occurrence of events is generated, the next step is to assign event characteristics to the different occurrences. For this purpose, and using the previously presented example, three different multivariate models are used for generating time series of events occurring at either one, two, or three stations. The procedure is applied to each season separately.
Multivariate Wet Spell Model
Vine copulas are used to simulate pseudo-pairs of WSA and WSD for different locations simultaneously, resulting in spatially correlated time series of events. These models consist of decomposition of multivariate probability densities into bivariate copulas. Thus the method presents the advantage of using two-dimensional models for which a well-investigated variety of families is available. Modeling multiple variables by pair-copulas results in high flexibility to reproduce different dependence structures [51]. Furthermore there are several possible Vine structures which are constructed by specifying the order of the involved variables and their pair-wise dependencies. Two special Vine structure specifications are the so called drawable or D-Vine and canonical or C-Vine [47]. Vines are conceptualized as trees consisting of nodes (univariate random variables) and edges (bivariate copulas). In the D-Vine case each tree is a path and every node is connected to at most two edges, whereas a C-Vine structure assigns one node to each tree that is connected to all other nodes by the maximal number of edges [51].
The use of these copulas for an n-dimensional application requires the decomposition of the problem into products of pairs, i.e., bivariate, copula densities, and marginal densities. The pair-copula construction is defined by [43,52,53,54], and the density is represented as
where the first double product of the equation corresponds to pair copula densities (conditional and unconditional pairs), whereas the third product, i.e., the fk, represents the marginal densities of the n variables. If four variables are involved in the analysis, the density is presented as
where c14|23, c13|2, and c24|3 are conditional pairs, c12, c23, and c34 are unconditional pairs, and f1, f2, f3, and f4 are marginal densities of each of the variables. A graphical representation of this structure is shown in Figure 2, which includes a nested set of trees used to depict the decomposition. The Vine tree structure [53] indicates the order of dependency of the variables for a regular Vine structure.
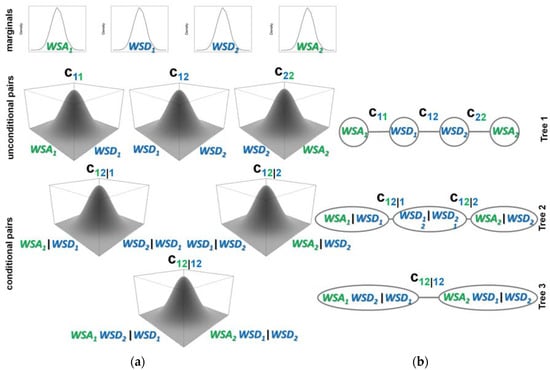
Figure 2.
Example of components of a Vine copula to model events occurring simultaneously in two stations. (a) Marginal densities, unconditional and conditional pair copula densities (under N(0, 1) margins for visualization). (b) Vine tree structure.
A Vine copula model is set up for each group of events classified as occurring in 1, 2, 3, …, k stations. Therefore, the models range from 2-variate for events occurring in one station, i.e., for modeling WSA and WSD, to up to 2 × k-variate for events occurring in k stations simultaneously, as the WSA and WSD for each of the k stations are considered. The example presented in Figure 2 involves two stations and therefore four variables. Moreover, the structure of the Vine trees is set up to guarantee that the first step contains the copulas modeling the pairs of WSA and WSD for each of the stations, i.e., these pairs are unconditionally modeled as can be depicted from the C11 and C22 bivariate models in Figure 2. The dependence structure between WSDs from both stations is as well modeled in this first tree (C12). For the case presented in Figure 2, which involves two stations, the structure defines the model as a D-Vine as every node is connected to at most two edges. For a case involving three stations, the structure is specified in a different way. The structure again guarantees that the WSA and WSD are modeled unconditionally for each of the stations with bivariate models C11, C22 and C33. The dependences between WSDs are as well unconditionally modeled in this first tree. However, as there are three stations involved, the WSD corresponding to one of the stations is connected to the WSD of the other two stations (e.g., C12 and C13) in addition to the WSA (e.g., C11). One of the nodes is therefore connected to three edges.
Once the structure is defined, Brechmann et al. [51] summarize the following sequential steps to set up a Vine copula model: Selection of appropriate pair-copula families (unconditional and conditional pairs) by information criteria such as Akaike Information Criterion [55,56] and estimation of the corresponding parameter for each family by statistical inference (Maximum Likelihood method).
As was mentioned, a Vine copula model is set up for each group of events classified as occurring in 1, 2, 3, …, k stations. The copulas are used to simulate pseudo values that need to be back transformed to the real space. Marginal distributions are fitted to WSA and WSD involving all events registered by each station. The inclusion of all events guarantees a more robust fitting. Furthermore, this procedure results in a gain of robustness if regionalization of the model is of interest (it is not the aim to address this issue here). The transformation of pseudo values to the real space requires some correction as the first correspond to sub-sample of events whereas the marginals represent the whole data set.
A Bias Correction is used for this purpose which aims to correct the probabilities resulting from the different subsamples, i.e., groups of events based on occurrences in different stations, to the sample including all events. It is likely that an event classified as isolated is characterized by low values of WSD and WSA, and therefore low probabilities associated to these values, whereas an event extended to several stations will most likely have a long duration and high volume and thus high probabilities if all events are included. A Bias Correction is defined for each station by comparing the complete time series of events with the events belonging to the different groups, i.e., events occurring at 1, 2, …, k stations.
The analysis and synthesis presented in this work are performed using R [57] a free software environment for statistical computing. The simulations are accomplished with the aid of the following packages: Lmomco [58], Copula [59,60,61,62], CVine [51], and VineCopula [63].
Multivariate Dry Spell Model
The duration of dry spells is not significantly correlated to variables characterizing wet spell. Therefore they are introduced into the model randomly using probability distributions fitted to DSD. Nevertheless, the generation of long time series of DSD for the different stations must guarantee that events occurring in two or three stations are temporally matching. For this purpose and in order to assure that events modeled as occurring simultaneously in several stations will appear in the same temporal period, the DSD are generated stochastically for one of the stations and thereafter estimated for the rest of the stations to match the total duration between events including the WSDs. The station used for DSD generation changes for the different steps of calculation. DSD are incorporated in two different ways according to their classification as “consecutive” or “longest” explained in Section Occurrence Model. From the observed time series DSD are divided into these two groups and probability distributions are fitted to the ensemble of “consecutive” events considering all stations together and to the “longest” events for each station separately.
The resulting time series of the occurrence model defines the distribution and station to be used for randomly introducing values of DSD. As an example for Table 1, in column 3 a DSD from the distribution “consecutive” will be introduced for one of the three stations, which is selected randomly. This way, the total duration between these events extended to all stations is defined. Thereafter, the DSD for the other two stations is assigned according to their WSD (which results from the Vine copula) to fulfill the total duration.
Another case corresponds to a period delimited by events extended to all stations with many events in between. In this case the DSD distribution fitted to “longest” events is used for generating random values of DSD. An example of this case is shown in Table 1 for events occurring between columns 4 and 10. In this example Station C would be used for introducing random values of DSD as it has the highest number of events within the delimited period, i.e., four events. The DSDs corresponding to the rest of the stations are then introduced randomly but in this cases conditioned to the total duration between events occurring in all stations for that period. The described methodology results in a continuous time series of events i.e., wet spells followed by dry spells for each of the involved stations.
Limitations of the Model
The proposed method relies on the definition of rainfall events as occurring isolated or simultaneously in several stations. The assumption for defining events is therefore an important feature. In this work a minimum duration between events of 5 min was assumed, and only events with volume equal or greater than 1 mm are included in the multisite modeling. Furthermore a fixed value of 1.5 was applied for defining the moving window to compare events in different stations and classify them as isolated or simultaneous. This fixed value could vary according to the type of event or to the distance between stations to account for the movement of the storm from one station to the next and to the temporal lag between rainfall registered in different locations.
The model could be applied to data sets involving many stations; however a limitation would be the length of data available in several stations simultaneously for setting it up. The total number of observed events must be divided into sub-samples according to the number of involved stations and cases of occurrence. Furthermore rainfall events are separated into different seasons according to the nature of physical processes causing them.
2.1.3. Alternative Method: Simulated Annealing
An alternative method is used to compare and assess the performance of the proposed methodology. This method is based on simulated annealing and is explained and applied to hourly rainfall time series by [24]. The method consists of two steps. First, a temporal stochastic synthesis of rainfall is performed in different stations as single sites. The model presented by [23] is used for this purpose. The simultaneous synthesis of WSA and WSD is done using the regional empirical copula, which is described in the mentioned publication. In the second step, the rainfall events from the different stations are resampled to reproduce the spatial dependency among the stations according to the distance between them.
The resampling consists of a non-linear discrete optimization based on Simulated Annealing, and the aim is to minimize an objective function that takes into account the difference of spatial dependency structure between observed and simulated time series. Three different spatial consistency measures are taken into account, namely probability of bivariate rainfall occurrence, correlation between rainfall intensities and continuity measure, and weights of each measure within the objective function. For more details, the reader may refer to [24].
2.1.4. Assessment Criteria for Performance
The synthetic rainfall should be able to reproduce the spatial dependence structure of the rainfall process. Different measures are used for evaluating the performance of the model and comparing observed and synthetic rainfall series. The measures are based on each individual station or on areal time series estimated using all stations involved in the multi-site synthesis.
Three different bivariate criteria are used to evaluate the spatial consistency by comparing the 5-min time series of continuous rainfall from two sites. The first criterion is a continuity measure, which expresses the ratio of expected amount of rainfall at one station (i) for time steps without rainfall at the neighboring station (j) to the expected amount in i from time steps with rainfall in j [64]. The lower the values the higher the interrelation between stations. The ratio is calculated as follows:
where E(.) is the expectation operator, and zi and zj are the 5-min rainfall time series at stations i and j. The second criterion is the Pearson’s coefficient of correlation applied to time steps for which rainfall is registered in both stations.
where cov(.) is the covariance and Var(.) is the variance operator. High values of correlation indicate high interrelation between stations. The third criterion is the Log-odds ratio [65]. This measure takes into account the probabilities of either rain or no-rain in two stations simultaneously and is calculated as follows:
where p11i,j, p00i,j, p10i,j and p01i,j are the joint probabilities of rain (1) or no-rain (0) at stations i and j, i.e., p11i,j indicates the probability of rain at both stations. These probabilities are calculated by the number of time steps for each of the cases over the total number of time steps. The Log-odds ratio takes into account the probabilities of either rain or no-rain in two stations simultaneously. High values of this ratio indicate high spatial interrelation between two stations, as for the correlation coefficient.
Measures based on event characteristics focus on events identified from the continuous time series and compare their basic statistics, like mean, standard deviation, skewness, and kurtosis. Final time series for single stations and additionally based on areal precipitation are used here. The areal precipitation consists of spatially averaged rainfall amount over the region. Each of the involved stations is assigned an area of influence within the region by a simple Thiessen polygon method.
The performance of the model for different temporal scales is as well evaluated based on long time series (observed and synthetic, both for single stations and areal) which are aggregated to different temporal resolutions (5 min, 1 h, 6 h, and 1 day). Thereafter, wet time steps are identified for each time series using the following thresholds for defining a time step as wet: 0.01 mm (5 min), 0.1 mm (1 and 6 h) and 1 mm (1 day). Basic statistics like mean, variance, intermittence, and temporal persistence are evaluated.
Extreme values are of main interest for many applications. Therefore these events are evaluated based on intensity duration frequency curves (IDF). The curves are constructed by univariate rainfall frequency analysis from spatially observed and synthetic time series based on moving windows of different durations (from 5 up to 1440 min) and for the return periods of 1, 5, and 10 years. The analysis is performed according to the German design guidelines [66], i.e., fitting the time series to Gumbel distributions for the different durations. The areal precipitation time series are used for the extreme value analysis.
Deviations between observed and simulated results are calculated as relative percentages for each station (Equation (6)) or as errors averaged over all stations, i.e., relative standard error (Equation (7)). These errors are computed as
where N is the total number of stations, Zi* and Zi are simulated and observed characteristics respectively (e.g., moments, extreme values with a duration associated to a return period). Positive errors resulting from Equation (6) indicate overestimation by synthetic series.
2.2. Study Area and Data
Stations located in different regions in Germany are used for developing and validating the proposed model. The available information is provided by the German National Weather Service (Deutscher Wetterdienst DWD) and corresponds to stations belonging to a network of automated weather stations that is operating since the mid 1990s. The precipitation is measured every 5 min. Precipitation in Germany occurs all year round, and events can be separated into two seasons [67]: convective dominated type or Summer (April to September) and stratiform dominated type or Winter (October to March).
A total of eight groups of stations located in the north (Lower Saxony, NS) and in the south (Baden Württemberg, BAWU) are used for evaluating the model. The stations are selected based on the length of data available for a common period within each group. The groups of stations consist of either two or three stations located at distances ranging from 11 up to 59 km. Some basic information about the stations as well as their location can be found in Figure 3 and Table 2. The available time series with rainfall registered in all stations for each case study range from 8 to up to 19 years. The case studies corresponding to NS indicate greater distance between the stations and therefore bigger areas involved for the evaluation based on areal precipitation (see red circles in Figure 3).
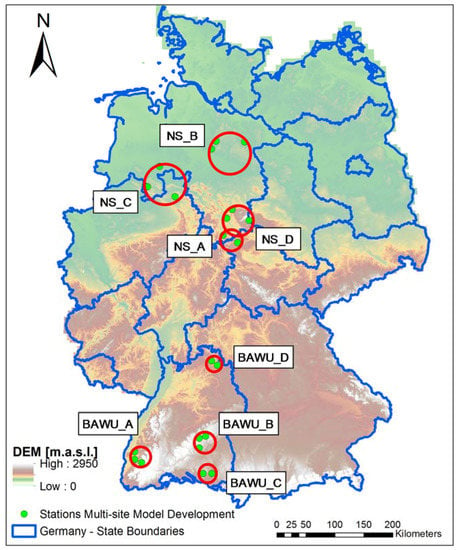
Figure 3.
Location of rain gauge stations and groups used for developing the model. The red circles indicate the areas involved for each case.

Table 2.
Attributes of rainfall stations used for model development.
The areal precipitation is estimated including all stations involved for each case study. Observed and synthetic time series from multiple stations (two or three) are used and the Thiessen polygon is applied for this purpose. In the case of two stations, the areal rainfall is just the average of the two time series. For cases involving three stations, the proportion of area assigned to each station ranges from 0.22 to 0.43 with a median value of 0.34. The total areas corresponding to each case are shown as red circles in Figure 3.
The extreme values assessment is also based on the areal precipitation. An additional data set of IDF curves provided by KOSTRA DWD-2000 [68] is included in this evaluation. These curves are commonly used by engineers in the study region for dimensioning hydraulic structures involved in sewer systems. KOSTRA consists of an atlas of regionalized values of extreme rainfall amounts associated to different durations and return periods. The amounts are provided on a raster for all Germany with cell sizes of 8.45 km × 8.45 km. These extremes are then distributed within the durations, i.e., disaggregated into 5 min intervals, using an Euler type 2 model in which the peak intensity is located at one third of the total duration of the event (for details see [50]). The average between rasters included in the area of interest must be calculated. As KOSTRA was developed on a point basis, the application of these values on an areal basis requires some reduction factors. These factors are provided based on the area and duration [69]. As the areas included in the mentioned publication reach a maximum of 1000 km2, reduction factors are extrapolated for bigger areas, i.e., for three out of the eight cases, by simple linear regressions. The reduction factors used for the different case studies are presented in Figure 4. Note that for events with durations of 5 min the Reduction Factor values corresponding to 15 min are taken, since this is the minimum available duration.
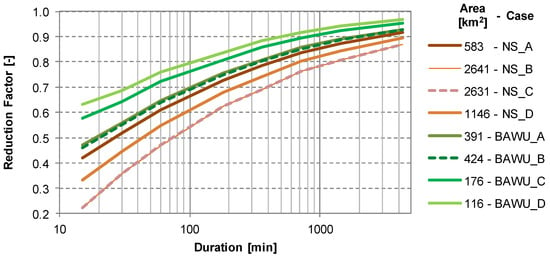
Figure 4.
KOSTRA reduction factors for the different case studies.
3. Results and Discussion
3.1. Model Set Up
3.1.1. Identification of Events Occurring Simultaneously
The 8 case studies are used to identify events and classify them as isolated or as occurring in several stations. In Table 3 the percentage of events occurring in either one, two, or three stations simultaneously are presented in the first three lines, whereas the percentage of events in each of the stations are presented in the following three lines. As some of the cases include no more than two stations, the corresponding cells are marked with a “-”. As can be seen most of the events (50–78%) correspond to isolated ones, i.e., registered in one station. Another feature is that for the BAWU cases the percentages of events registered in two or three stations are higher than for the NS cases. This is due to the fact that the stations in BAWU are closer to each other with distances ranging from 12 to 23 km (see Table 2), whereas for the NS cases these distances range from 15 to 60 km. Additionally Table 3 depicts that the percentage of events registered in each of the stations is close to balanced. All these percentages are included within the Occurrence Model to generate a long time series of rainfall occurrence and the attribution of the events to the different involved stations. The total number of available events for the isolated cases has a median of 907 (with a minimum of 613 and maximum of 1947), for events registered in two stations 380 (min./max. 243/690) and for events occurring in 3 stations a median of 227 (min./max. 141/405).

Table 3.
Percentages of observed events occurring in several stations simultaneously (1, 2, 3) and in each of the stations (A, B, C) for different seasons and case studies.
The events classified as occurring in one, two, or three stations are used for estimating Kendall’s Tau correlations between different event characteristics. The resulting values for all case studies are presented in Figure 5. Correlation between WSA and WSD is stronger for events occurring during winter compared to summer (see left plot). This correlation is stronger for events observed in several stations and weaker for isolated events. As depicted from the right plot and in contrast to WSD, WSA shows weaker correlations when pairs of stations are compared and there is no evident difference between summer and winter events. The aim of the Vine copula model is to reproduce all these correlations.
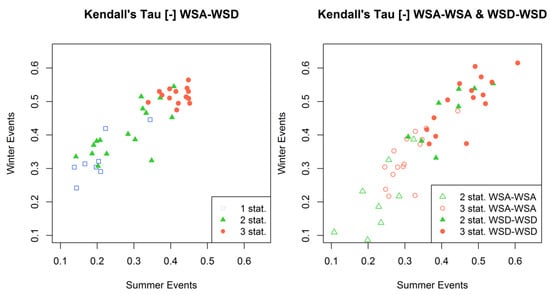
Figure 5.
Dependence between event characteristics according to their occurrence in one, two, or three stations simultaneously for all cases.
3.1.2. Modeling of Events Occurring Simultaneously
The following step of calculation involves the analysis of events occurring in either one, two, or three stations for setting up the Vine copula models. As explained in the Methods section, the Vine copulas are used to mimic the correlations involving WSA and WSD for several stations. For events occurring in only one station, the Vine copula consists of one tree with one bivariate model, as only one pair of variables is involved: WSA-WSD. These pairs suggest some asymmetry with respect to the main diagonal, so that one variable cannot be exchanged by the second one, i.e., C(u,v) ≠ C(v,u); therefore some of the pairs of points cannot be captured by symmetric copulas. Tawn copulas [70] are able to model asymmetric behavior and are therefore used to model all isolated events.
For events occurring in two and three stations simultaneously, four and six variables are involved, i.e., the WSA and WSD corresponding to each of the involved stations. As was mentioned, the pre-defined tree structures for events occurring in two or three stations guarantee that pairs of WSA-WSD for each of the stations are directly modeled in the first step of simulation. Based on the pre-defined tree structures, different copula families and parameters are selected and estimated for each study case and season separately in a sequential way. Many different families are chosen for the different structures of the tree. The bivariate copulas selected to model the WSA-WSD for each of the involved stations are in more than half of the cases the Tawn copulas, followed by Clayton [71]. For the WSD-WSD, the t copula was selected for more than 40% of the cases, followed by the Gumbel, Frank, and Frank-Joe [70]. For the rest of the cases, i.e., excluding the first tree, the conditional models include different copulas with Independent, Gaussian, Gumbel, and Frank [71] accounting for around 70% of the selected families. A test developed by [72] is applied to assess the goodness of fit of the different Vine copulas. The authors propose a test of equality between two dependence structures estimated based on empirical copulas. The test is applied for each fitted Vine copula and therefore only for cases involving two and three stations. As the test compares empirical copulas, it was applied 10 times (10 simulations from the fitted Vine copulas) for each case and the median of resulting p-values are presented in Table 4. Resulting p-values equal or higher than 0.05 indicate that the null hypothesis of equal dependence structure is not rejected at a 5% level. The p-values indicate a rejection of the test only for two cases: NS_A (2 stations) and BAWU_A (3 stations), both cases summer events. The rest of the cases indicate a good agreement between dependence structures of observed and fitted Vine copulas.

Table 4.
Goodness of fit of Vine copula models as p-values for different seasons and case studies.
In Figure 6, observed (upper triangular matrix) and modeled (lower triangular matrix) pairs of pseudo-characteristics of summer events occurring in three stations for the BAWU_B case are presented. Pairs of pseudo-values are visualized using hexagon binning, which is a form of bivariate histogram that shows the join-structure of big samples. The number of points falling within each hexagon is counted, and a color ramp is used to show the proportion of points, light-colored hexagons indicate less points, whereas dark indicates a higher concentration of pairs. These plots are done using the hexbin R package [73]. Pairs of WSA-WSD observed in each of the stations suggest non-exchangeable behavior that is well reproduced by the Vine model (see pairs highlighted with red boxes). Overall joint structures between pairs of variables are properly modeled by the Vine copula as can be inferred from Kendall’s Tau coefficients from upper and lower triangular matrixes.
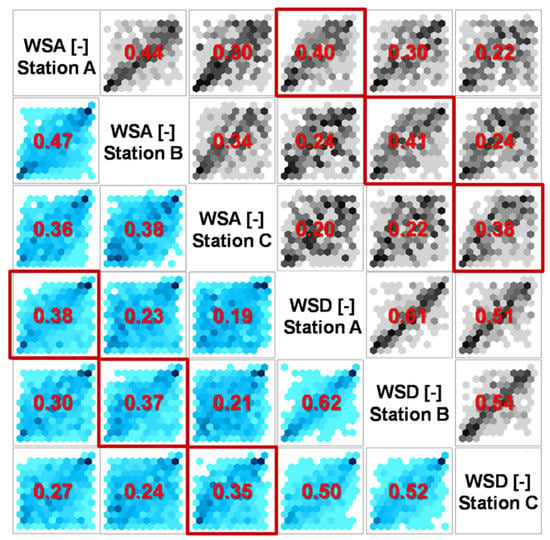
Figure 6.
Pairs of pseudo-values of summer events occurring in three stations simultaneously for the BAWU_B case (Kendall’s Tau in red). Upper triangular matrix: Observed. Lower triangular matrix: Synthetic.
The Vine copulas are used for generating random samples of pseudo-characteristics that need to be back transformed to the real space by the marginal distributions. The resulting pseudo-values correspond to events occurring in either one, two, or three stations. The probability distributions describing WSA and WSD are fitted to the whole sample of events registered in each of the stations. Therefore the back transformation is performed using an additional bias correction aiming to transform the pseudo-value from a subsample corresponding to say an event occurring in only one station to the sample including all events.
Figure 7 (left plot) shows the cumulative distributions of WSD corresponding to events classified as occurring in 1, 2 or 3 stations along with the distribution considering all events together observed during summer in BAWU_A case. As can be seen the WSD describing events occurring in 3 stations (red points) are, for similar frequencies, longer than the ones occurring in 1 or 2 stations. This is logical since events lasting longer, i.e., with longer WSD, are expected to be registered by several stations. The bias correction is performed based on the probability distribution of all stations involved in each case study together and a curve for correction is provided for each of the number of stations involved. If for example a Vine copula modeling events in one station yields a pseudo-WSD value of 0.5, a value of 0.3 should be used to convert it to actual WSD (as can be inferred from the green curve of the middle plot in Figure 7). On the other hand, if a copula fitted to events occurring in 3 stations generates a pseudo-WSD of 0.5, then a value of 0.7 should be used (see red curve of the same plot) when the pseudo-value is to be transformed using the marginal distribution.
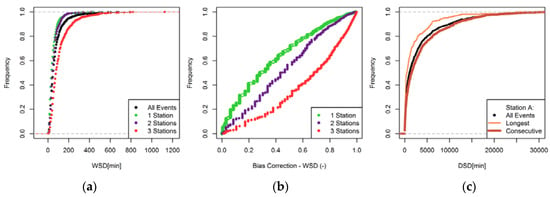
Figure 7.
(a) Cumulative distributions of WSD, (b) bias correction of WSD, and (c) cumulative distributions of DSD for summer events corresponding to BAWU_A case.
The right plot in Figure 7 shows the different type of distributions used for introducing the DSD into the model. As can be seen the distribution corresponding to “longest” events represent cases that have lower durations, whereas the “consecutive” ones have on average longer durations compared to all events. This is logical as the events identified as “longest” correspond to the cases in which the highest number of events are observed compared to the other involved stations (see Section Occurrence Model and red box in Table 1). This definition results in the exclusion of long DSD and the shift of the distribution to the left.
3.2. Evaluation of Results
Both the Vine copula model and SA provide long time series of event characteristics for each of the stations involved in the multi-site synthesis. These time series are thereafter transformed into 5-min continuous series by applying the internal structure model independently for each station and introducing the small events uniformly for all stations. The final synthetic time series consist of 100 years of rainfall and are compared with observations. Some of the evaluations are based on single stations and others on areal precipitation.
3.2.1. Spatial Consistency Measures
The two synthetic time series are used for estimating different spatial consistency measures, i.e., based on single stations and compared in a pair-wise way. Some results are shown in Figure 8. The values estimated from the observed time series are included in red (triangles and curve). Note that the small events (WSA < 1 mm) were excluded from these time series, as they were not involved in the multisite synthesis. It can be seen that the SA is better reproducing the continuity measure; whereas the correlation is better reproduced by the Vine copula. The Log-odds and p11 are underestimated by both models. However, the Vine copula outperforms the SA as the results are closer to observed ones. Overall, the Vine copula appears to reproduce these measures better, even though they are not directly involved within the model set up, as in the case for the SA optimization criteria. Thus, these values are validating the results from the Vine Copula model. Note that the application of SA to hourly data resulted in better reproduction of these measures, especially for the correlation [24].
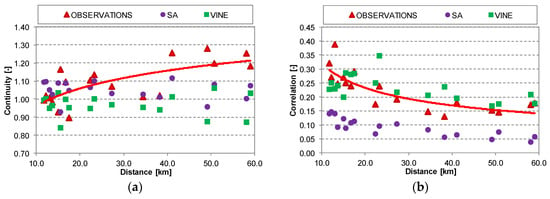
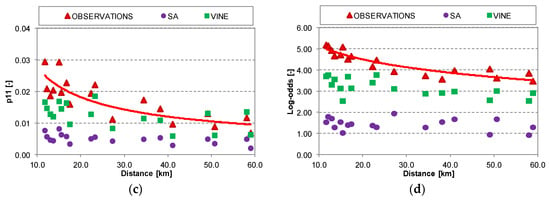
Figure 8.
Bivariate spatial consistency measures of observed and simulated time series, small events are excluded: (a) Continuity measure; (b) Pearson’s coefficient of correlation; (c) Joint probability of rain in both stations; (d) Log-odds ratio.
3.2.2. Event Based Measures
The capability of the models to reproduce different event characteristics is additionally evaluated. Different moments are considered and ranges of errors for the first order moment and different rainfall characteristics are presented in Figure 9.
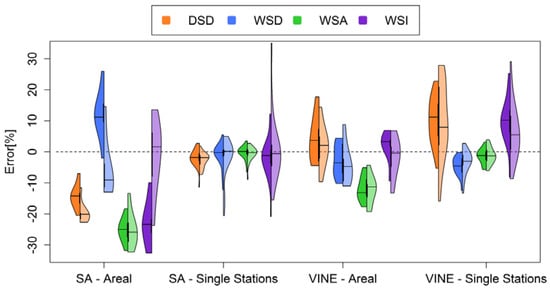
Figure 9.
Errors of mean values of event characteristics based on areal and single sites resulting from two models used for multisite synthesis for summer (left plots of violins) and winter (right plots of violins) events for all stations.
The comparison based on single stations indicates that the SA model is reproducing the first order moments in an acceptable way, as the errors are around zero for all stations. This was expected as the SA is using the single site model for simulating events that are only resampled, so the final results should be similar. For the model based on Vine copulas the single stations results show some deviations. The mean value of DSD is overestimated for most of the stations, whereas the WSD and WSA are slightly underestimated and their range of errors are much lower indicating acceptable results. The WSD results in higher underestimation compared to WSA, and this combination results in an overestimation of WSI for most of the stations. The overestimation of the DSD is a result of the way the dry spells are introduced after the long time series of events occurring in either one, two, or three stations are simulated. On the other hand even if the WSA and WSD are not directly modeled from a probability distribution as in the SA case the resulting values are acceptable. Event identification based on areal precipitation shows very different results compared with single sites. These results indicate the outperformance of the Vine Copula model over the SA for most event characteristics. The Vine copula delivers very acceptable errors for all characteristics except for the WSA, for which mean values are systematically underestimated. SA on the other hand underestimates both DSD and WSA for all cases and deviations are higher.
Further interpretation of the areal time series indicates that the Vine Copula underestimates the total seasonal rainfall as a result of underestimation of mean values of WSA. For the SA, even if this underestimation is stronger, it is compensated with the underestimation of DSD, i.e., an overestimation of number of rainfall events per year, resulting in an acceptable value of total seasonal rainfall (not shown here).
Results for different moments are presented as RSE in Table 5 (see Equation (7)) based on areal precipitation for all cases and the two models for comparison. Errors appear to increase as the order of the moment evaluated increases as would be expected. The Vine Copula model shows for most of the characteristics and moments lower errors compared to the SA when areal precipitation is evaluated. SA outperforms the Vine Copula only when Skewness and Kurtosis of directly simulated variables, i.e., DSD, WSD, and WSA, are evaluated.

Table 5.
Evaluation of statistics of different variables describing the external structure of rainfall events resulting from two models for multisite synthesis based on areal precipitation and presented for all cases as RSE.
The performance of the models for different temporal resolutions is as well evaluated and presented as RSE for all stations and case studies in Table 6. Results indicate, as in the previous analysis, that SA outperforms Vine copulas for comparison based on single stations, and the opposite for areal precipitation. Only when the temporal persistence is evaluated the Vine copula indicates results that are either similar or better than the ones from SA both for single sites and areal precipitation. For most of the cases increase of temporal aggregation indicates increase of errors, an exception is the intermittence.

Table 6.
Evaluation of performance based on wet time steps for different temporal resolutions resulting from two multisite models and presented for all stations as RSE for single stations and areal precipitation.
3.2.3. Extreme Values Measures
Intensity duration frequency curves (IDFs) derived from areal precipitation for all cases are compared with the ones resulting from synthetic time series (SA and Vine Copulas) and KOSTRA (without and with reduction). Errors between IDFs derived from observations and the different considered cases are presented in Figure 10 for return periods that go up to 10 years due to the data availability. The violin-plots include errors resulting from all cases and durations that range from 5 min up to one day. It can be seen that if no reduction factor is included, KOSTRA results in a nearly consistent overestimation of the extreme values for most of the cases. The reduction factors improve the performance of KOSTRA significantly (see “KOSTRA—Reduced”), the errors are around zero, with overall some underestimation especially for low return periods. The range of errors appears to be lower for the multisite models, both showing underestimation of IDFs, but the Vine Copulas model shows median errors closer to zero.
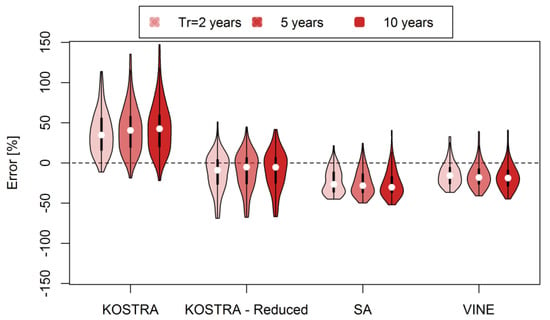
Figure 10.
Comparison of models regarding their ability to reproduce extreme events for durations ranging from 5 min to 24 h for all stations.
The IDF curves for two cases are shown in Figure 11. The shown cases correspond to the ones with biggest (NS_B) and smallest (BAWU_D) areas. The effect of the area size is clearly seen in both curves representing extreme values provided by KOSTRA (see gray continuous and dashed lines). For the NS_B case (left plots) the deviation of KOSTRA curves is more pronounced, especially for low durations, compared to the curves corresponding to BAWU_D. The total synthetic time series are partitioned into subseries with equal length of observed time series. The extreme values estimated based on the different subseries and associated to different durations and return periods are shown as symbols (circles and crosses for Vine and SA). Overall the figures show an acceptable agreement between the range of results of simulated extremes and observed ones. The extreme values represented as medians of all subseries are used for estimating the errors shown in Figure 10. The NS_B case shows deviations between observed and medians that are very similar for both models with stronger deviations for longer durations. For the BAWU_D case, the Vine copula results in lower range of deviations, especially for short durations, up to 6 h the Vine model clearly outperforms the SA.
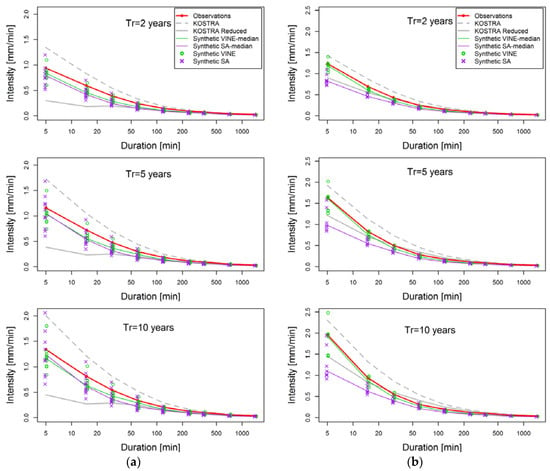
Figure 11.
Comparison of IDF curves obtained from observed, KOSTRA, KOSTRA Reduced, and simulated time series (all realizations are shown as symbols: circles for Vine and crosses for SA) for the cases: (a) NS_B corresponding to the biggest area; (b) BAWU_D involving the smallest area.
A more detailed comparison between each of the multi-site models and KOSTRA-Reduced reveals that the latter underestimates extreme values for sub-hourly durations and all return periods. These underestimations may be related to the reduction factors, which range between 0.22 and 0.56 for the corresponding durations as was shown in Figure 4. On the other hand both multi-site models show acceptable results for short durations with a slight underestimation for all stations, which is more marked as the duration increases. Summarizing, the multisite models would be preferable for low durations and KOSTRA for long ones, while Vine copulas outperform SA, as the ranges of errors are lower.
4. Conclusions
The goal of this work was to develop a stochastic model that can properly reproduce mean event properties and extreme value statistics of rainfall in a high temporal resolution for multiple locations. Consequently, the model needs to involve the temporal and spatial simulation of long continuous precipitation for several stations simultaneously. The developed method consists of an extension of the model based on alternating renewal process presented by [23] for single site simulations to multi-site applications. Therefore, it is event-based and benefits from the fact that the number of parameters is not affected by the temporal resolution. It involves several steps of calculation that are sequential, namely the occurrence model, the Vine copulas, and incorporation of dry spells. The proposed model has the advantage that it accounts for the spatial extension of events within the Occurrence model for simulating rainfall characteristics. However, the several stages of simulation involved make it complex and difficult to interpret. The multi-site model is compared to the alternative Simulated Annealing (SA) method. The performance of the models is evaluated based on different stations in Germany with high temporal resolution (5 min) data. A comparison with a common practice design strategy, in this case KOSTRA, is also included in order to discuss the advantages and limitations of the precipitation model in terms of reproducing extreme events. The main findings are the following:
- Synthetic time series are compared in a pair-wise way, i.e., every two stations, to estimate spatial consistency measures. Overall, these measures (as shown in Figure 8) are better reproduced by the Vine copula model compared to the alternative method. Furthermore, these measures are not involved within the Vine copula model, as is the case for the SA optimization criteria, so these outcomes underline the satisfactory performance of the proposed model.
- The capability of the two models to reproduce different event characteristics is additionally compared. The evaluation based on single sites depicts some deficiencies of the proposed model, however these results are improved when the evaluation is performed based on areal precipitation (see Figure 9). Overall, SA performs better for single stations but fails when the areal precipitation is considered. These results suggest that the Vine copula model is reliable in reproducing the simultaneous occurrence of rainfall in several stations, whereas the SA is unable to mimic this behavior. Unfortunately, the proposed method systematically underestimates total seasonal rainfall.
- Extreme events are evaluated by assessing Intensity Duration Frequency curves (IDFs). The proposed model shows acceptable results as the ranges of errors are smaller than the ones from the SA and KOSTRA (see Figure 10). Vine copulas outperform SA. However, these models would be preferable for short durations, and KOSTRA for long ones. The reduction factors applied to KOSTRA are provided for different durations and areas of application, though for large areas, extrapolation by simple linear regressions was necessary. These factors could be revised, as they result in the underestimation of extreme values for most of the analyzed cases. Myers and Zehr [74] present reduction factors developed for the city of Chicago that are as well provided for different return periods, with higher factors for lower return periods.
- Overall, the copula-based proposed extension of the ARP delivers satisfactory results both for the average event statistics and for the extremes. Furthermore, the model has the advantage that the number of parameters is not affected by the temporal resolution. However the model consists of several steps of simulation that follow each other and is hard to interpret, as mentioned in the literature review as one limitation of the existing models for multi-site synthesis. Moreover, the model was only applied to cases involving two and three stations. Despite the fact that it could be applied to data sets involving more stations, a limitation would be the length of data available in several stations simultaneously for setting up the different modules within the model, especially the Vine copulas. Another important aspect that is subject of further research is the regionalization of this multi-site model, i.e., setting up the model for locations without observations. Current work involves exploring the capability of the radar data, which is spatially and temporally available in very high resolutions, to extract some of the characteristic that are required for modeling rainfall in multiple sites simultaneously.
Author Contributions
Conceptualization, A.C.C.P. and U.H.; Methodology, A.C.C.P. and U.H.; Software, A.C.C.P.; Validation, A.C.C.P.; Formal Analysis, A.C.C.P.; Investigation, A.C.C.P.; Data Curation, A.C.C.P.; Writing-Original Draft Preparation, A.C.C.P.; Writing-Review & Editing, A.C.C.P. and U.H.; Visualization, A.C.C.P.; Supervision, U.H.; Funding Acquisition, U.H.
Funding
This research was funded by the German Federal Ministry of Education and Research (BMBF) grant number Förderkennzeichen 033W002A.
Acknowledgments
The authors would like to thank the colleagues Bora Shehu and Anne Fangmann for their help and useful comments. Special thanks go to Benedikt Gräler for his constructive suggestions regarding some of the explanations involving Vine copulas. The results presented in this study are part of a research project about synthetic generation of time series of precipitation for the optimal planning and operation of urban drainage systems (SYNOPSE), funded by the German Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung BMBF) who are grateful acknowledged. We are also thankful for the provision and right to use data from the German National Weather Service (Deutscher Wetterdienst DWD) and to the Open Access fund of Leibniz Universität Hannover for funding the publication of this article. The authors appreciate the constructive suggestions from the academic editor and three anonymous reviewers which helped improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
| ARP | Alternating renewal process |
| BAWU | German state of Baden Württemberg |
| C-Vine | Canonical Vine copula |
| DEM | Digital Elevation Map |
| DSD | Dry spell duration |
| D-Vine | Drawable Vine copula |
| DWD | Deutscher Wetterdienst (German National Weather Service) |
| IDF | Intensity duration frequency curves |
| IID | Independent identically distributed |
| KOSTRA | Koordinierte Starkniederschlagsregionalisierung, official German statistics of extreme precipitation |
| m.a.s.l. | Meters above sea level referred to tide gauge Amsterdam (DHHN92) |
| mNN | Meters above German Standard Zero (Normalnull) |
| NS | German state of Lower Saxony (Niedersachsen) |
| p00 | Joint probability of no-rain (0) and no-rain (0) at two stations |
| p01 | Joint probability of no-rain (0) and rain (1) at two stations |
| p10 | Joint probability of rain (1) and no-rain (0) at two stations |
| p11 | Joint probability of rain (1) and rain (1) at two stations |
| RSE | Relative standard error |
| SA | Simulated annealing |
| Tr | Return period |
| WSA | Wet spell amount |
| WSD | Wet spell duration |
| WSI | Wet spell intensity |
| WSPeak | Wet spell peak amount |
| WSTpeak | Wet spell time to peak |
References
- Bárdossy, A. Generating Precipitation Time Series Using Simulated Annealing. Water Resour. Res. 1998, 34, 1737–1744. [Google Scholar] [CrossRef]
- Beck, F. Generation of Spatially Correlated Synthetic Rainfall Time Series in High Temporal Resolution: A Data Driven Approach. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2013. [Google Scholar]
- Licznar, P.; Schmitt, T.G.; Rupp, D.E. Distributions of microcanonical cascade weights of rainfall at small timescales. Acta Geophys. 2011, 59, 1013–1043. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; Lockie, T.; Davis, M.D. A stochastic spatial-temporal disaggregation model for rainfall. Res. Lett. Inf. Math. Sci. 2004, 6, 109–122. [Google Scholar]
- Müller, H.; Haberlandt, U. Temporal rainfall disaggregation using a multiplicative cascade model for spatial application in urban hydrology. J. Hydrol. 2018, 556, 847–864. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B. Generalizations of chain-dependent processes: Application to hourly precipitation. Water Resour. Res. 1995, 31, 1331–1341. [Google Scholar] [CrossRef]
- Zhang, Z.; Switzer, P. Stochastic space-time regional rainfall modeling adapted to historical rain gauge data. Water Resour. Res. 2007, 43, W03441. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y.; Charles, S. Modelling the dependence and internal structure of storm events for continuous rainfall simulation. J. Hydrol. 2012, 464, 249–261. [Google Scholar] [CrossRef]
- Willems, P. A spatial rainfall generator for small spatial scales. J. Hydrol. 2001, 252, 126–144. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; Kilsby, C.; O’Connell, P. A space-time Neyman-Scott model of rainfall: Empirical analysis of extremes. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Burton, A.; Fowler, H.J.; Kilsby, C.G.; O’Connel, P.E. RainSim: A spatial–temporal stochastic rainfall modelling system. Environ. Model. Softw. 2008, 23, 1356–1369. [Google Scholar] [CrossRef]
- Burton, A.; Fowler, H.J.; Kilsby, C.G.; O’Connell, P.E. A stochastic model for the spatial-temporal simulation of nonhomogeneous rainfall occurrence and amounts. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Franchini, M.; Brocca, L.; Camici, S.; Melone, F.; Moramarco, T. A simple approach for stochastic generation of spatial rainfall pattern. J. Hydrol. 2012, 472, 63–76. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. A point process model for rainfall: Further developments. Proc. R. Soc. Lond. A 1988, 417, 283–298. [Google Scholar] [CrossRef]
- Verhoest, N.; Troch, P.E.; Troch, F.P. On the applicability of Bartlett–Lewis rectangular pulses models in the modeling of design storms at a point. J. Hydrol. 1997, 202, 108–120. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; Isham, V.; Onof, C. Point process models of rainfall: Developments for fine-scale structure. Proc. R. Soc. A 2007, 463, 2569–2587. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; Onof, C.; De Baets, B. A comparative copula-based bivariate frequency analysis of observed and simulated storm events: A case study on Bartlett-Lewis modeled rainfall. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Pham, M.T.; Vanhaute, W.J.; Vandenberghe, S.; De Baets, B.; Verhoest, N.E.C. A copula-based assessment of Bartlett–Lewis type of rainfall models for preserving drought statistics. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 7469–7516. [Google Scholar] [CrossRef]
- Kaczmarska, J.; Isham, V.; Onof, C. Point process models for fine-resolution rainfall. Hydrol. Sci. J. 2014, 59, 1972–1991. [Google Scholar] [CrossRef]
- Vernieuwe, H.; Vandenberghe, S.; De Baets, B.; Verhoest, N.E.C. A continuous rainfall model based on vine copulas. Hydrol. Earth Syst. Sci. 2015, 19, 2685–2699. [Google Scholar] [CrossRef]
- Haberlandt, U. Stochastic rainfall synthesis using regionalized model parameters. J. Hydrol. Eng. 1998, 3, 160–168. [Google Scholar] [CrossRef]
- Bernardara, P.; De Michele, C.; Rosso, R. A simple model of rain in time: An alternating renewal process of wet and dry states with a fractional (non-Gaussian) rain intensity. Atmos. Res. 2007, 84, 291–301. [Google Scholar] [CrossRef]
- Callau Poduje, A.C.; Haberlandt, U. Short time step continuous rainfall modeling and simulation of extreme events. J. Hydrol. 2017, 552, 182–197. [Google Scholar] [CrossRef]
- Haberlandt, U.; Ebner von Eschenbach, A.-D.; Buchwald, I. A space-time hybrid hourly rainfall model for derived flood frequency analysis. Hydrol. Earth Syst. Sci. 2008, 12, 1353–1367. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Bianucci, P.; Garrote, L.; Granados, A. The influence of the annual number of storms on the derivation of the flood frequency curve through event-based simulation. Water 2016, 8, 335. [Google Scholar] [CrossRef]
- Kao, S.; Govindaraju, R. Trivariate statistical analysis of extreme rainfall events via the Plackett family of copulas. Water Resour. Res. 2008, 44, W02415. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V. Gumbel-Hougaard copula for trivariate rainfall frequency analysis. J. Hydrol. Eng. 2007, 12, 409–419. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Statistical characterization of temporal structure of storms. Adv. Water Resour. 2006, 29, 827–842. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Design hyetograph analysis with 3-copula function. Hydrol. Sci. J. 2006, 51, 223–238. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M. Probabilistic assessment of flood risks using trivariate copulas. Theor. Appl. Climatol. 2013, 111, 341–360. [Google Scholar] [CrossRef]
- Serinaldi, F.; Grimaldi, S. Fully nested 3-copula: Procedure and application on hydrological data. J. Hydrol. Eng. 2007, 12, 420–430. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.; Beliveau, J.; Jacques, C. Metaelliptical copulas and their use in frequency analysis of multivariate hydrological data. Water Resour. Res. 2007, 43, W09401. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.; Shenglian, G.; Hao, Z.; Li, T. Flood Coincidence Risk Analysis Using Multivariate Copula Functions. J. Hydrol. Eng. 2012, 17, 742–755. [Google Scholar] [CrossRef]
- Wang, C.; Chang, N.-B.; Yeh, G.-T. Copula-based flood frequency (COFF) analysis at the confluences of river systems. Hydrol. Process. 2009, 23, 1471–1486. [Google Scholar] [CrossRef]
- Durante, F.; Salvadori, G. On the construction of multivariate extreme value models via copulas. Environmetrics 2010, 21, 143–161. [Google Scholar] [CrossRef]
- Bezak, N.; Mikoš, M.; Šraj, M. Trivariate Frequency Analyses of Peak Discharge, Hydrograph Volume and Suspended Sediment Concentration Data Using Copulas. Water Resour. Manag. 2014, 28, 2195–2212. [Google Scholar] [CrossRef]
- Ma, M.; Song, S.; Ren, L.; Jiand, S.; Song, J. Multivariate drought characteristics using trivariate Gaussian and Student t copulas. Hydrol. Process. 2013, 27, 1175–1190. [Google Scholar] [CrossRef]
- Song, S.; Singh, V. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch. Environ. Res. Risk A 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Wong, G.; Lambert, M.; Leonard, M.; Metcalfe, A. Drought Analysis using trivariate copulas conditional on climatic states. J. Hydrol. Eng. 2010, 15, 129–141. [Google Scholar] [CrossRef]
- Pham, M.T.; Vernieuwe, H.; De Baets, B.; Verhoest, N.E.C. A coupled stochastic rainfall-evapotranspiration model for hydrological impact analysis. Hydrol. Earth Syst. Sci. 2018, 22, 1263–1283. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Passoni, G.; Vezzoli, R. A multivariate model of sea storms using copulas. Coast. Eng. 2007, 54, 734–751. [Google Scholar] [CrossRef]
- Czado, C. Pair-copula constructions of multivariate copulas. In Workshop on Copula Theory and Its Applications; Jaworki, P., Durante, F., Härdle, W., Rychlik, T., Eds.; Lecture Notes in Statistics; Springer: Berlin/Heidelberg, Germany, 2010; p. 198. [Google Scholar] [CrossRef]
- Gräler, B. Modelling skewed spatial random fields through the spatial vine copula. Spat. Stat. 2014, 10, 87–102. [Google Scholar] [CrossRef]
- Xiong, L.; Yu, K.; Gottschalk, L. Estimation of the distribution of annual runoff from climatic variables using copulas. Water Resour. Res. 2014, 50, 7134–7152. [Google Scholar] [CrossRef]
- Gräler, B.; van den Berg, M.J.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; De Baets, B.; Verhoest, N.E.C. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Shafaei, M.; Fakheri-Fard, A.; Dinpashoh, Y.; Mirabbasi, R.; De Michele, C. Modeling flood event characteristics using D-vine structures. Theor. Appl. Climatol. 2017, 130, 713–724. [Google Scholar] [CrossRef]
- Gaál, L.; Molnar, P.; Szolgay, J. Selection of intense rainfall events based on intensity thresholds and lightning data in Switzerland. Hydrol. Earth Syst. Sci. 2014, 18, 1561–1573. [Google Scholar] [CrossRef]
- Callau Poduje, A.C. Spatio-temporal modeling of precipitation in a high temporal resolution for urban hydrological applications. In Mitteilungen des Instituts für Hydrologie und Wasserwirtschaft Heft 107; Institute of Hydrology and Water Resources Management: Leibniz Universität Hannover, Germany, 2018; ISSN 0343-8090. [Google Scholar]
- Bacchi, B.; Kottegoda, N.T. Identification and calibration of spatial correlation patterns of rainfall. J. Hydrol. 1995, 165, 311–348. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Schepsmeier, U. Modeling Dependence with C- and D-Vine Copulas: The R Package CDVine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef]
- Joe, H. Families of m-variate distributions with given margins and m(m − 1)/2 bivariate dependence parameters. In Distributions with Fixed Marginals and Related Topics; Rüschendorf, L., Schweizer, B., Taylor, M.D., Eds.; Institute of Mathematical Statistics: Bethesda, MD, USA, 1996. [Google Scholar]
- Bedford, T.; Cooke, R.M. Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Czado, C.; Aas, K. Truncated regular vines in high dimensions with applications to financial data. Can. J. Stat. 2012, 40, 68–85. [Google Scholar] [CrossRef]
- Dißmann, J.F.; Brechmann, E.C.; Czado, C.; Kurowicka, D. Selecting and estimating regular vine copulae and application to financial returns. Comput. Stat. Data Anal. 2013, 59, 52–69. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: https://www.R-project.org/ (accessed on 15 December 2016).
- Asquith, W. Lmomco—L-Moments, Censored L-Moments, Trimmed L-Moments, L-Comoments, and Many Distributions; R Package Version 2.2.3; Texas Tech University: Lubbock, TX, USA, 2016. [Google Scholar]
- Yan, J. Enjoy the Joy of Copulas: With a Package copula. J. Stat. Softw. 2007, 21, 1–21. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Yan, J. Modeling Multivariate Distributions with Continuous Margins Using the copula R Package. J. Stat. Softw. 2010, 34, 1–20. [Google Scholar] [CrossRef]
- Hofert, M.; Maechler, M. Nested Archimedean Copulas Meet R: The nacopula Package. J. Stat. Softw. 2011, 39, 1–20. [Google Scholar] [CrossRef]
- Hofert, M.; Kojadinovic, I.; Maechler, M.; Yan, J. Copula: Multivariate Dependence with Copulas. R Package Version 0.999-14. 2015. Available online: http://CRAN.R-project.org/package=copula (accessed on 15 December 2016).
- Schepsmeier, U.; Stoeber, J.; Brechmann, E.C.; Graeler, B.; Nagler, T.; Erhardt, T. VineCopula: Statistical Inference of Vine Copulas. R Package Version 2.0.1. 2016. Available online: https://CRAN.R-project.org/package=VineCopula (accessed on 15 December 2016).
- Wilks, D.S. Multisite generalization of a daily stochastic precipitation generation model. J. Hydrol. 1998, 210, 178–191. [Google Scholar] [CrossRef]
- Mehrotra, R.; Srikanthan, R.; Sharma, A. A comparison of three stochastic multi-site precipitation occurrence generators. J. Hydrol. 2006, 331, 280–292. [Google Scholar] [CrossRef]
- DWA. Hydraulische Bemessung und Nachweis von Entwässerungssystemen; Arbeitsblatt A 118; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e. V.: Hennef, Germany, 2006. [Google Scholar]
- Eggert, B.; Berg, P.; Haerter, J.O.; Jacob, D.; Moseley, C. Temporal and spatial scaling impacts on extreme precipitation. Atmos. Chem. Phys. 2015, 15, 5957–5971. [Google Scholar] [CrossRef]
- Bartels, H.; Dietzer, B.; Malitz, G.; Albrecht, F.M.; Guttenberger, J. KOSTRA-DWD-2000, Starkniederschlagshöhen für Deutschland (1951–2000). Technical Report, DeutscherWetterdienst—Abteilung Hydrometeorologie, Offenbach am Main, 2005. Available online: https://www.dwd.de/DE/fachnutzer/wasserwirtschaft/kooperationen/kostra/fortschreibung_pdf.pdf%3F__blob%3DpublicationFile%26v%3D3 (accessed on 20 June 2018).
- Verworn, H.R. Flächenabhängige Abminderung statistischer Regenwerte. Korresp. Wasserwirtsch. 2008, 9, 493–498. [Google Scholar]
- Tawn, J.A. Bivariate extreme value theory: Models and estimation. Biometrika 1988, 75, 397–415. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006; ISBN 9780387286594. [Google Scholar]
- Rémillard, B.; Scaillet, O. Testing for equality between two copulas. J. Multivar. Anal. 2009, 100, 377–386. [Google Scholar] [CrossRef]
- Carr, D.; Lewin-Koh, N.; Maechler, M.; Deepayan, S. Hexbin: Hexagonal Binning Routines. R Package Version 1.27.1. 2015. Available online: https://CRAN.R-project.org/package=hexbin (accessed on 15 December 2016).
- Myers, V.A.; Zehr, R.M. A Methodology for Point-to-Area Rainfall Frequency Ratio; NOAA Technical Report NWS 24; National Weather Service, NOAA, U. S. Department of Commerce: Washington, DC, USA, 1980.
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).