Quantification of Seasonal Precipitation over the upper Chao Phraya River Basin in the Past Fifty Years Based on Monsoon and El Niño/Southern Oscillation Related Climate Indices
Abstract
1. Introduction
2. Study Area and Data Analysis
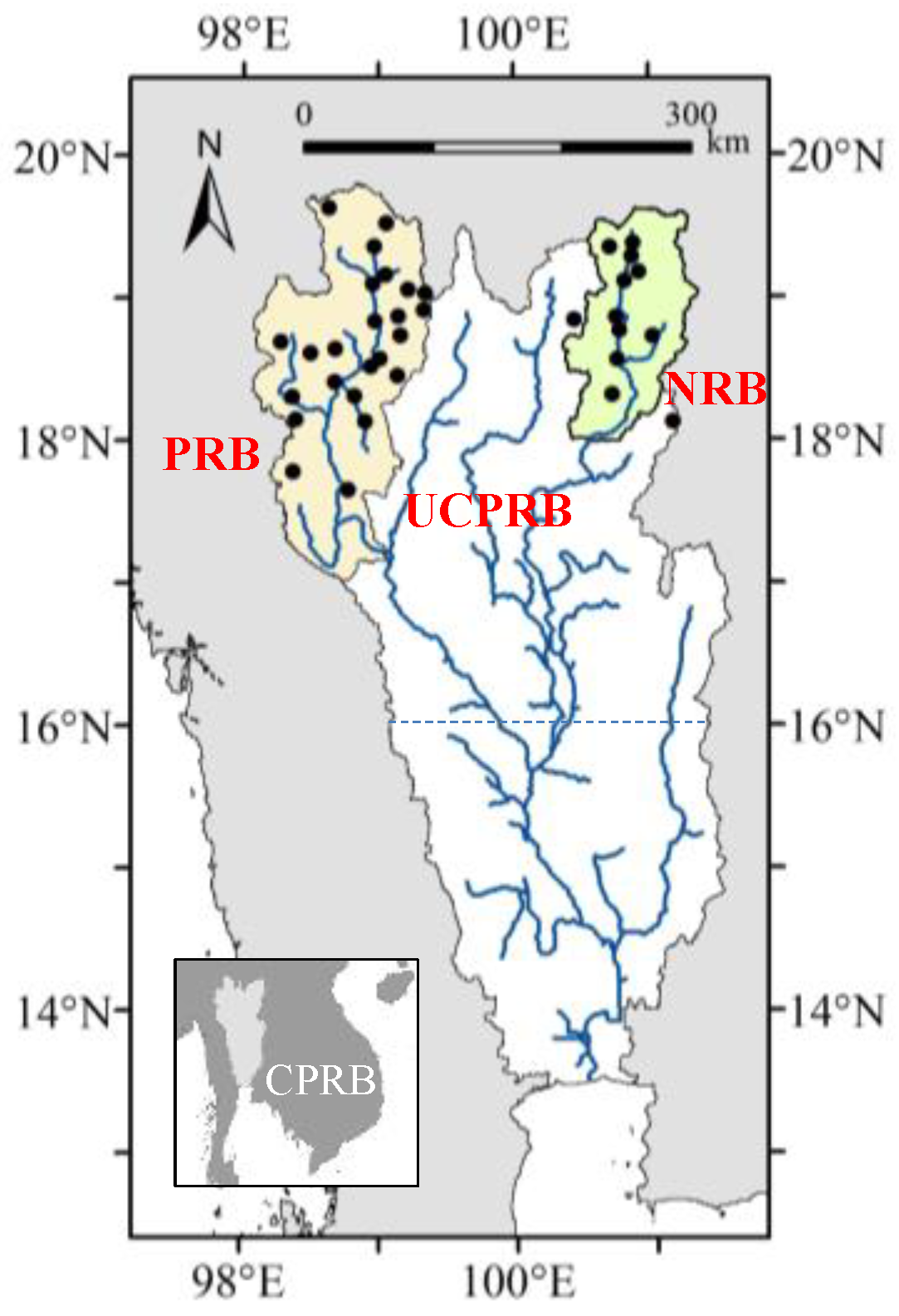
2.1. Study Area
2.2. Data Source
2.3. Overview of Data Analysis
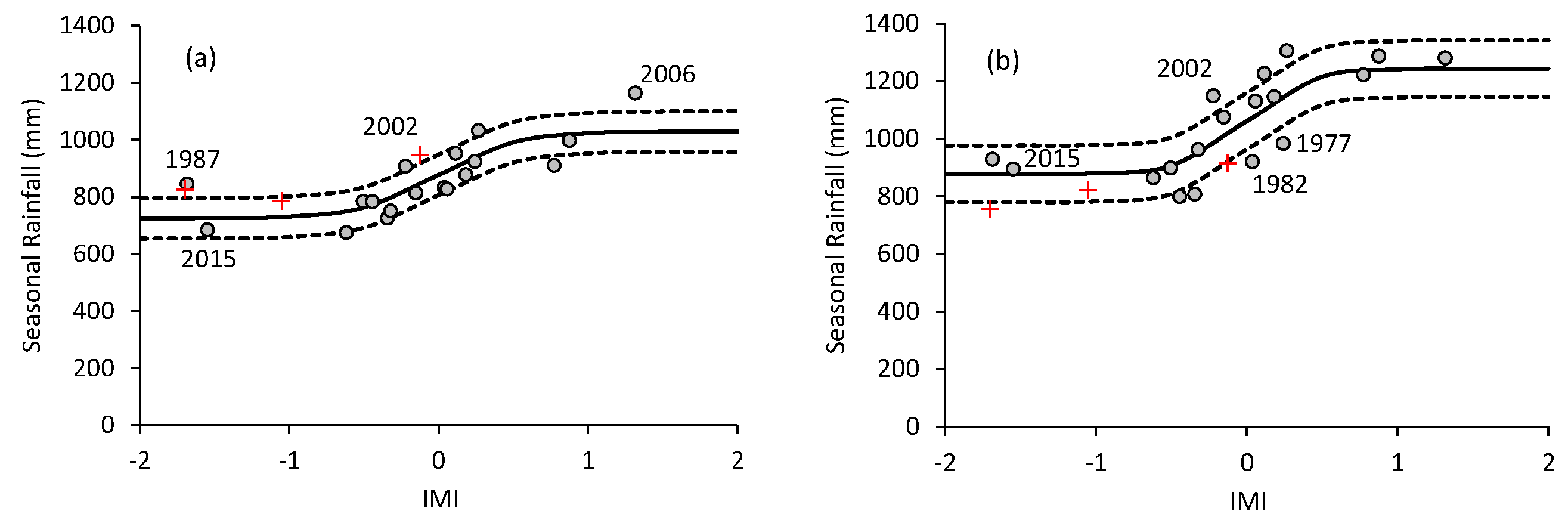
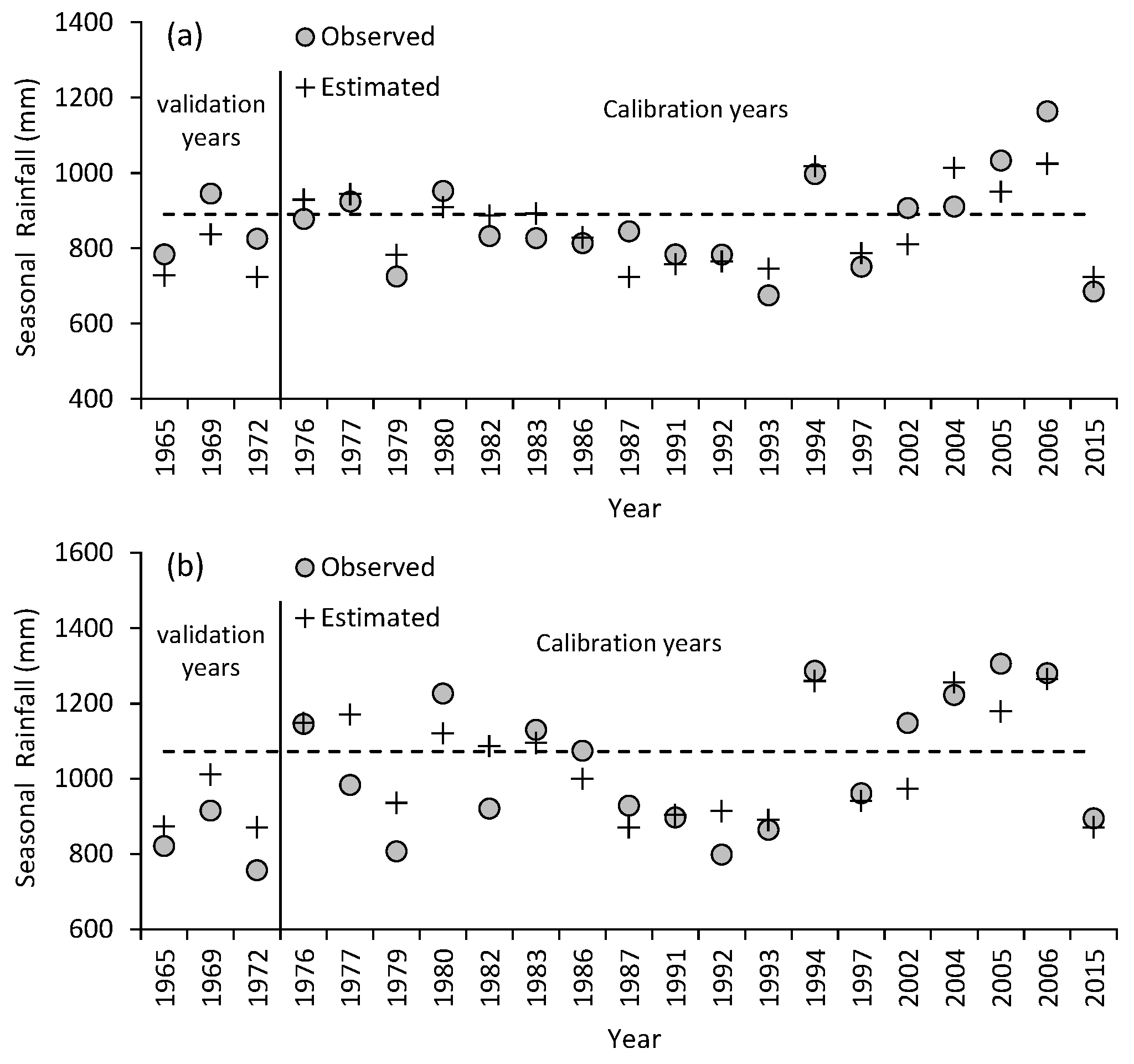
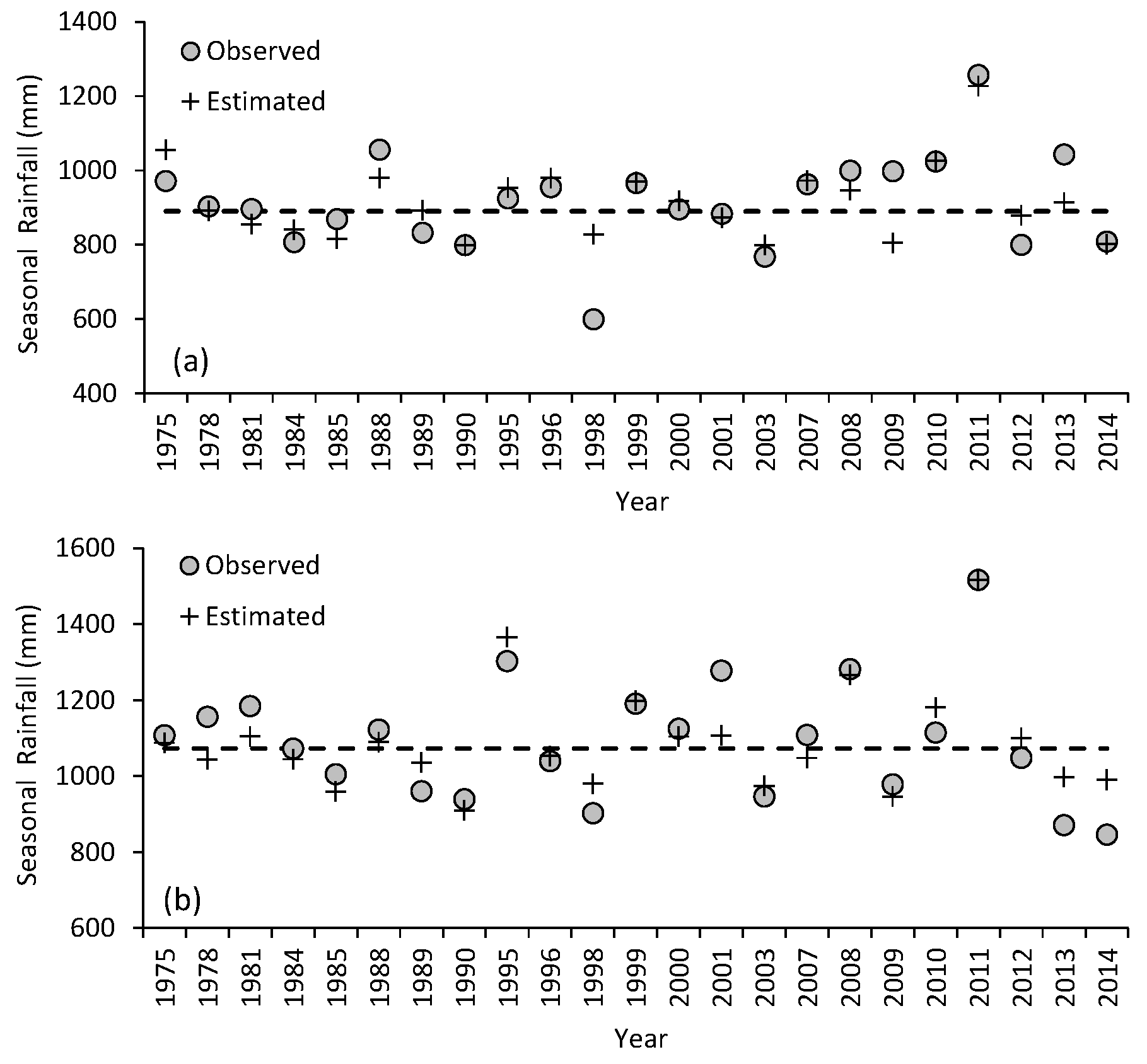
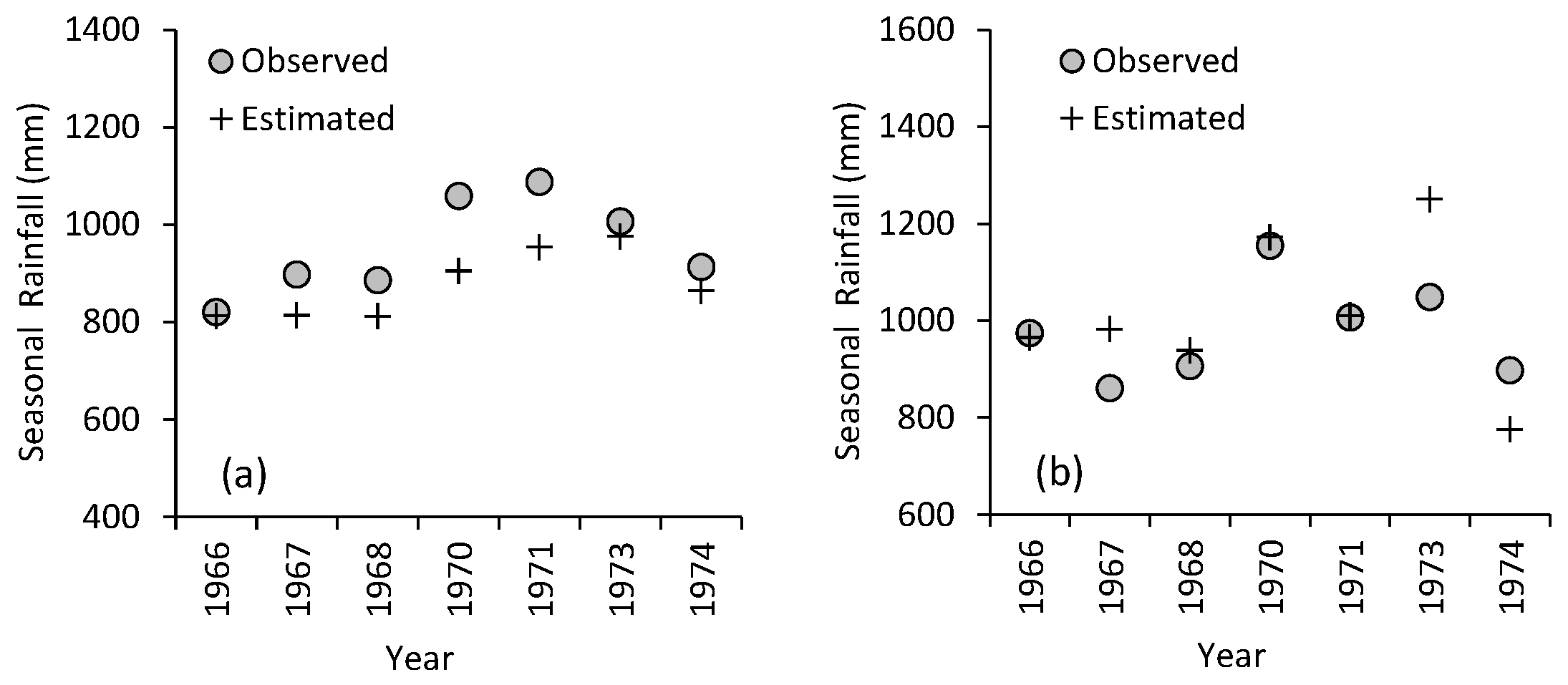
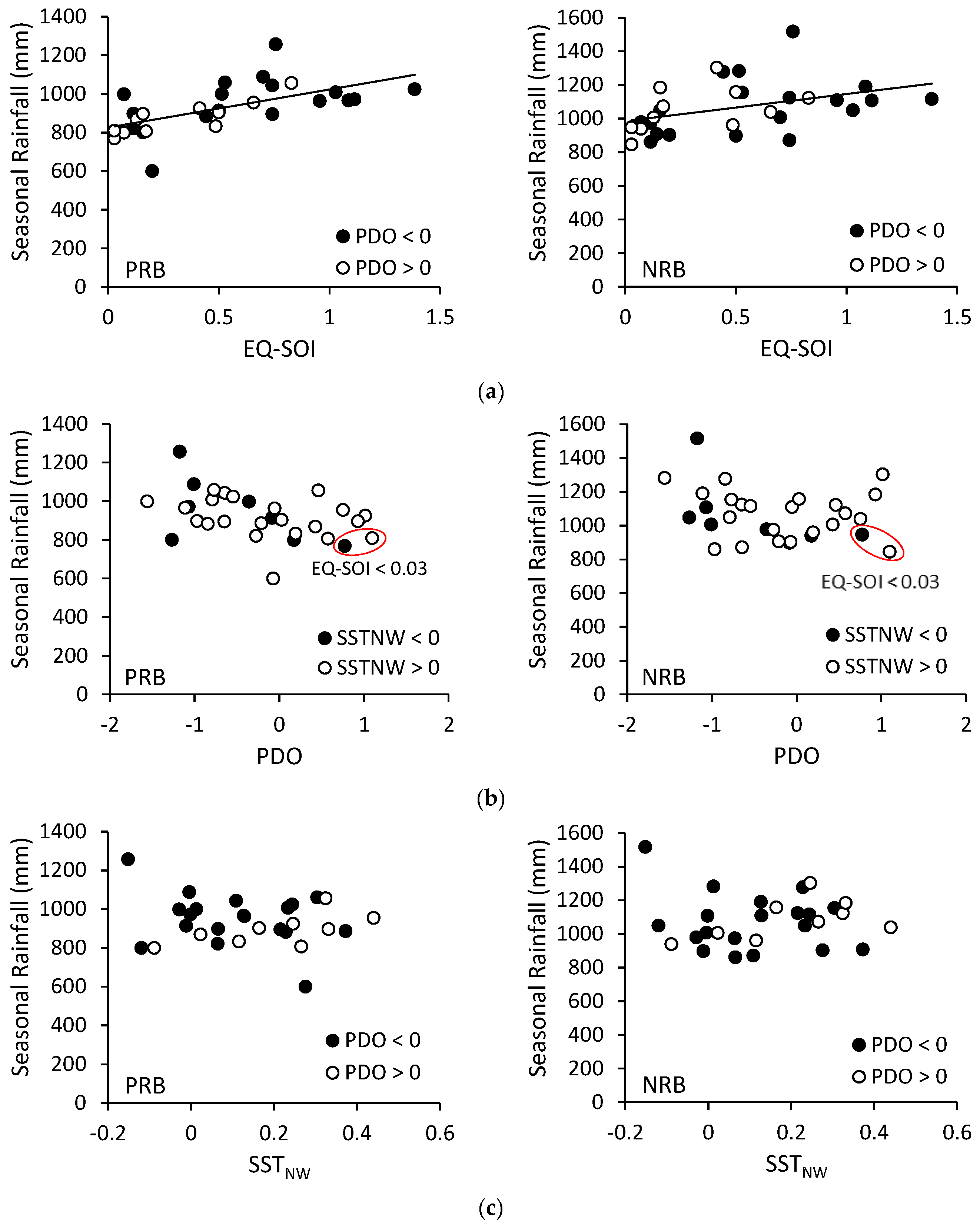
3. Results
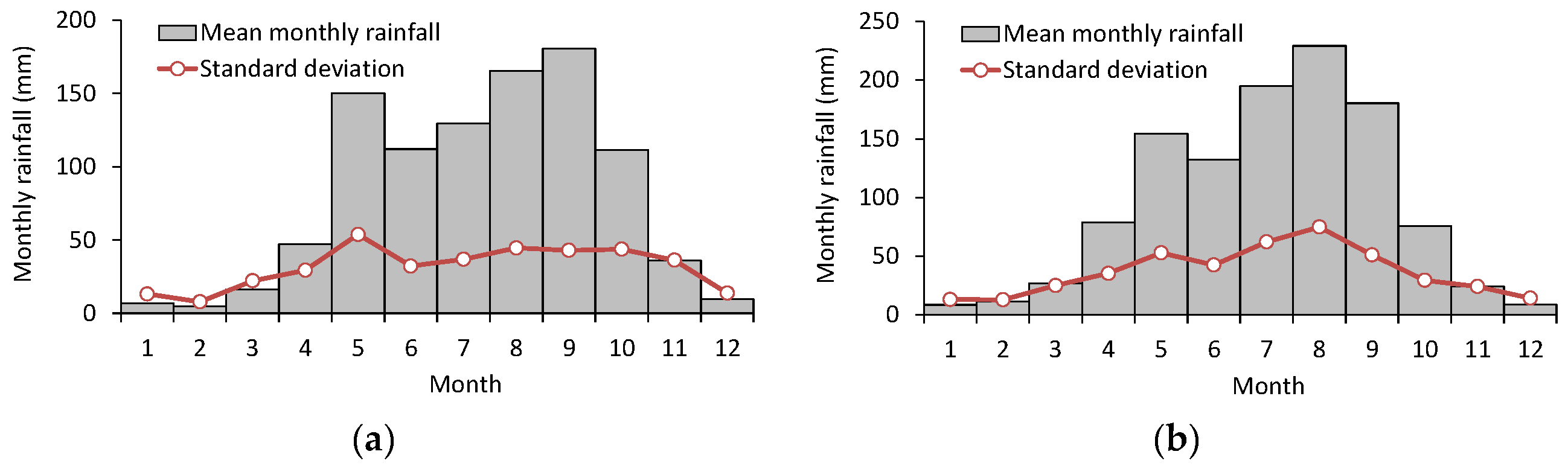
3.1. Characteristics of Rainfall and Corresponding Climate Indices
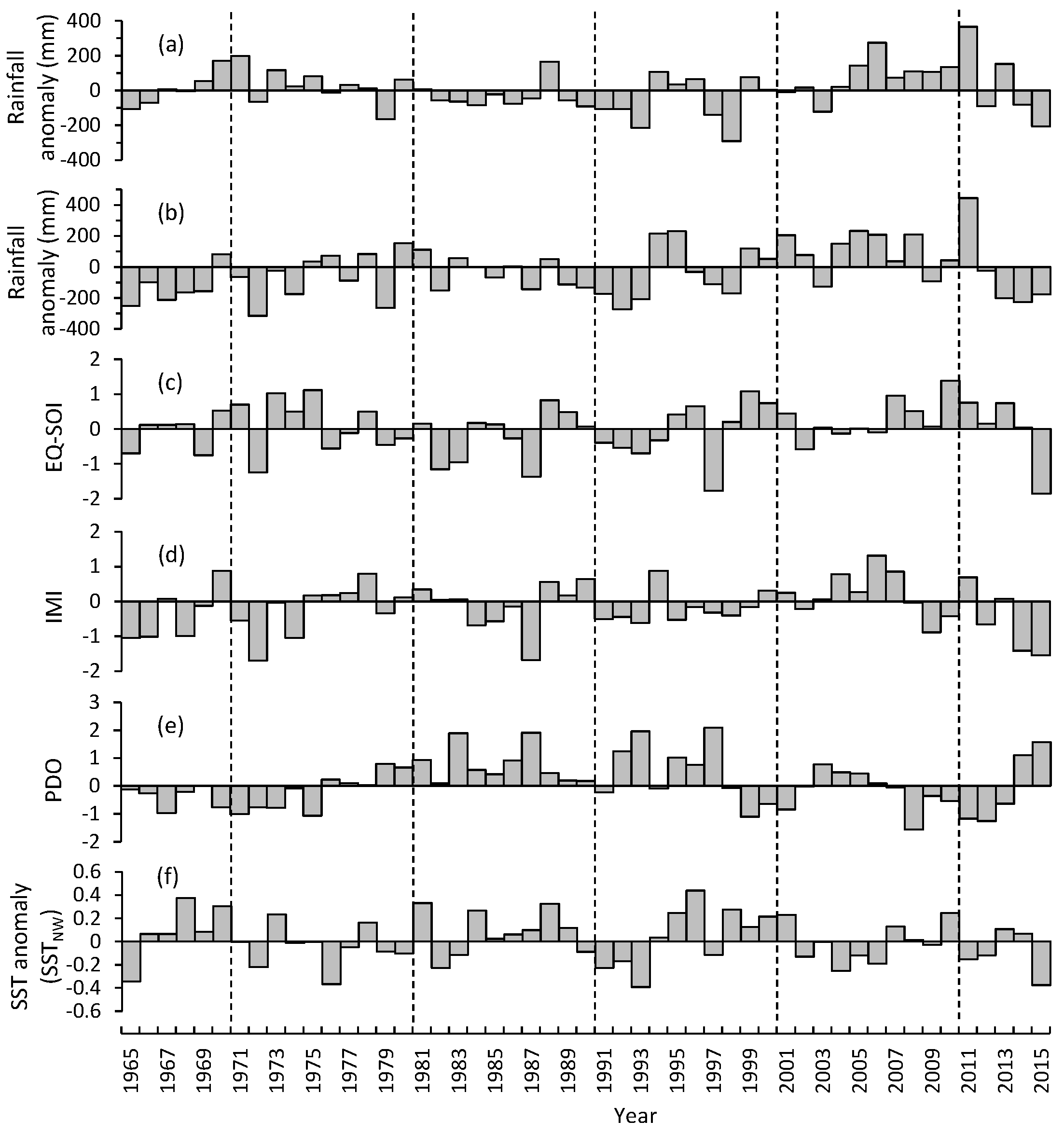
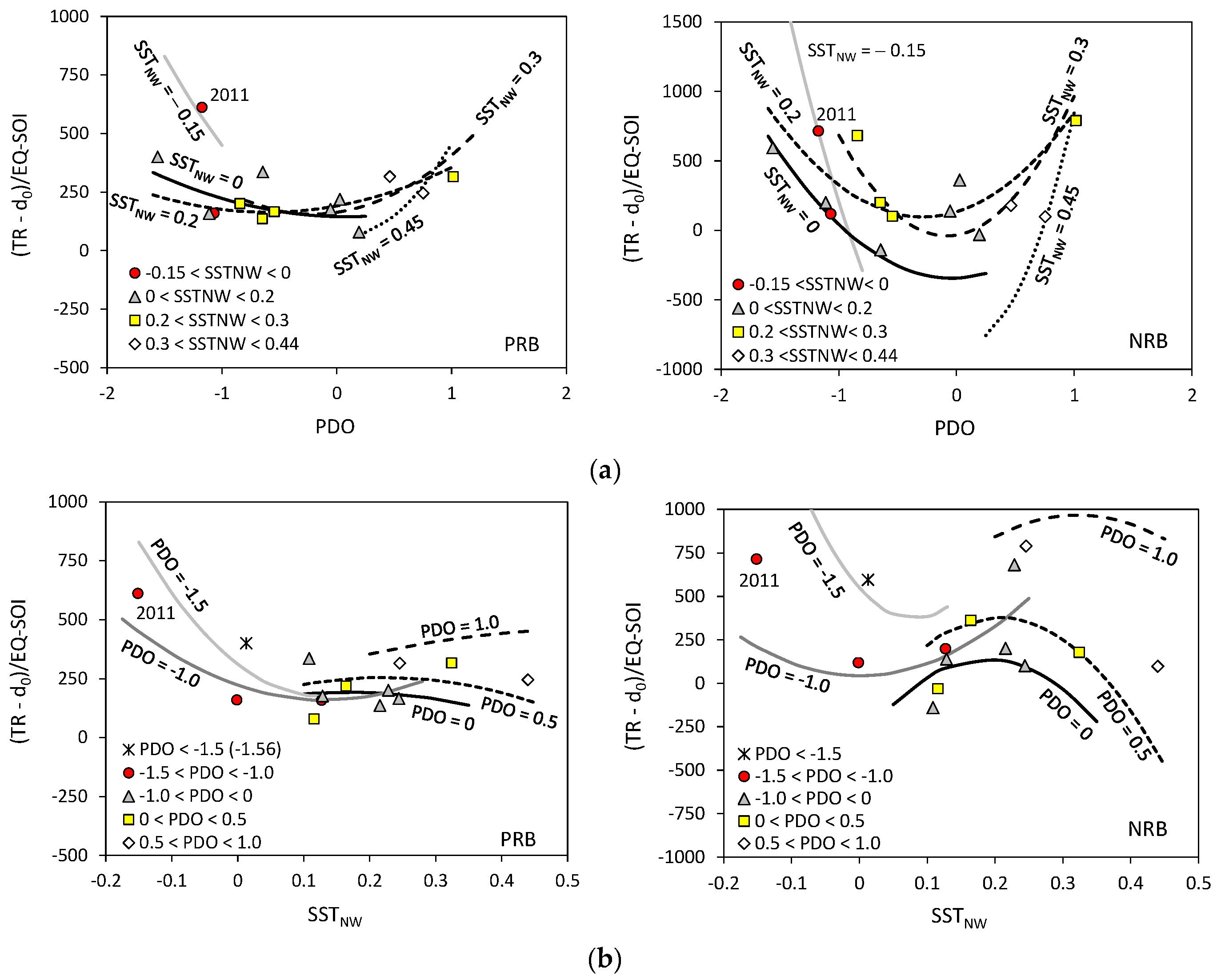
3.2. Relationship between Seasonal Rainfall and Climate Indices
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. Global Assessment Report on Disaster Risk Reduction; United Nations: Geneva, Switzerland, 2009; p. 207. ISBN 9789211320282. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. Available online: https://www.ipcc.ch/pdf/assessment-report/ar5/syr/SYR_AR5_FINAL_full_wcover.pdf (accessed on 29 April 2018).
- Miyan, M.A. Droughts in Asian Least Developed Countries: Vulnerability and sustainability. Weather Clim. Extr. 2015, 7, 8–23. [Google Scholar] [CrossRef]
- Tanoue, M.; Hirabayashi, Y.; Ikeuchi, H. Global-scale river flood vulnerability in the last 50 years. Sci. Rep. 2016, 6, 36021. [Google Scholar] [CrossRef] [PubMed]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Cai, W.; Borlace, S.; Lengaigne, M.; van Rensch, P.; Collins, M.; Vecchi, G.; Timmermann, A.; Santoso, A.; McPhaden, M.J.; Wu, L.; et al. Increasing frequency of extreme El Niño events due to greenhouse warming. Nat. Clim. Chang. 2014, 4, 111–116. [Google Scholar] [CrossRef]
- Cai, W.; Wang, G.; Santoso, A.; McPhaden, M.J.; Wu, L.; Jin, F.-F.; Timmermann, A.; Collins, M.; Vecchi, G.; Lengaigne, M.; et al. Increased frequency of extreme La Niña events under greenhouse warming. Nat. Clim. Chang. 2015, 5, 132–137. [Google Scholar] [CrossRef]
- Komori, D.; Nakamura, S.; Kiguchi, M.; Nishijima, A.; Yamazaki, D.; Suzuki, S.; Kawasaki, A.; Oki, K.; Oki, T. Characteristics of the 2011 Chao Phraya River flood in central Thailand. Hydrol. Res. Lett. 2012, 6, 41–46. [Google Scholar] [CrossRef]
- Promchote, P.; Wang, S.S.-Y.; Johnson, P.G. The 2011 Great Flood in Thailand: Climate Diagnostics and Implications from Climate Change. J. Clim. 2016, 29, 367–379. [Google Scholar] [CrossRef]
- Ueangsawat, K.; Jintrawet, A. The Impacts of ENSO Phases on the Variation of Rainfall and Stream Flow in the Upper Ping River Basin, Northern Thailand. Environ. Nat. Resour. J. 2013, 11, 97–119. [Google Scholar]
- Tsai, C.; Behera, S.K.; Waseda, T. Indo-China Monsoon Indices. Sci. Rep. 2015, 5, 8107. [Google Scholar] [CrossRef] [PubMed]
- Singhrattna, N.; Rajagopalan, B.; Clark, M.; Krishna Kumar, K. Seasonal forecasting of Thailand summer monsoon rainfall. Int. J. Climatol. 2005, 25, 649–664. [Google Scholar] [CrossRef]
- Divakar, L.; Babel, M.S.; Perret, S.R.; Das Gupta, A. Optimal allocation of bulk water supplies to competing use sectors based on economic criterion—An application to the Chao Phraya River Basin, Thailand. J. Hydrol. 2011, 401, 22–35. [Google Scholar] [CrossRef]
- Takeda, M.; Laphimsing, A.; Putthividhya, A. Dry season water allocation in the Chao Phraya River basin, Thailand. Int. J. Water Resour. Dev. 2015, 32, 321–338. [Google Scholar] [CrossRef]
- Kripalani, R.H.; Singh, S.V.; Panchawagh, N.; Brikshavana, M. Variability of the summer monsoon rainfall over Thailand—Comparison with features over India. Int. J. Climatol. 1995, 15, 657–672. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a Long-term Daily Gridded Precipitation Dataset for Asia based on a Dense Network of Rain Gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Matsumoto, J. Seasonal transition of summer rainy season over Indochina and adjacent monsoon region. Adv. Atmos. Sci. 1997, 14, 231–245. [Google Scholar] [CrossRef]
- Wang, B.; Fan, Z. Choice of South Asian summer monsoon indices. Bull. Am. Meteorol. Soc. 1999, 80, 629–638. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific decadal climate oscillation with impacts on salmon. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–362. [Google Scholar] [CrossRef] [PubMed]
- NOAA National Weather Service Climate Prediction Center. Available online: http://www.cpc.ncep.noaa.gov/data/indices/ (accessed on 29 April 2018).
- University of Hawaii, International Pacific Research Center (IPRC). Available online: http://apdrc.soest.hawaii.edu/projects/monsoon/index.html (accessed on 29 April 2018).
- Japan Meteorological Agency. Available online: http://ds.data.jma.go.jp/tcc/tcc/products/elnino/index/ (accessed on 29 April 2018).
- NOAA ESRL Physical Sciences Division. Available online: http://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/PDO/ (accessed on 29 April 2018).
- JAMSTEC. Available online: http://www.jamstec.go.jp/frsgc/research/d1/iod/iod/dipole_mode_index.html (accessed on 29 April 2018).
- Meyers, G.; McIntosh, P.; Pigot, L.; Pook, M. The years of El Niño, La Niña, and interactions with the tropical Indian Ocean. J. Clim. 2007, 20, 2872–2880. [Google Scholar] [CrossRef]
- Sen Roy, S.; Sen Roy, N. Influence of Pacific decadal oscillation and El Niño Southern oscillation on the summer monsoon precipitation in Myanmar. Int. J. Climatol. 2011, 31, 14–21. [Google Scholar] [CrossRef]
- Krishnamurthy, L.; Krishnamurthy, V. Influence of PDO on South Asian summer monsoon and monsoon–ENSO relation. Clim. Dyn. 2014, 42, 2397–2410. [Google Scholar] [CrossRef]
- Limsakul, A.; Singhruck, P. Long-term trends and variability of total and extreme precipitation in Thailand. Atmos. Res. 2016, 169, 301–317. [Google Scholar] [CrossRef]
- Hoell, A.; Funk, C. The ENSO-Related West Pacific Sea Surface Temperature Gradient. J. Clim. 2013, 26, 9545–9562. [Google Scholar] [CrossRef]
- Singhrattna, N.; Babel, M.S. Changes in summer monsoon rainfall in the Upper Chao Phraya River Basin, Thailand. Clim. Res. 2011, 49, 155–168. [Google Scholar] [CrossRef]
| Index | Definition | Data Sources |
|---|---|---|
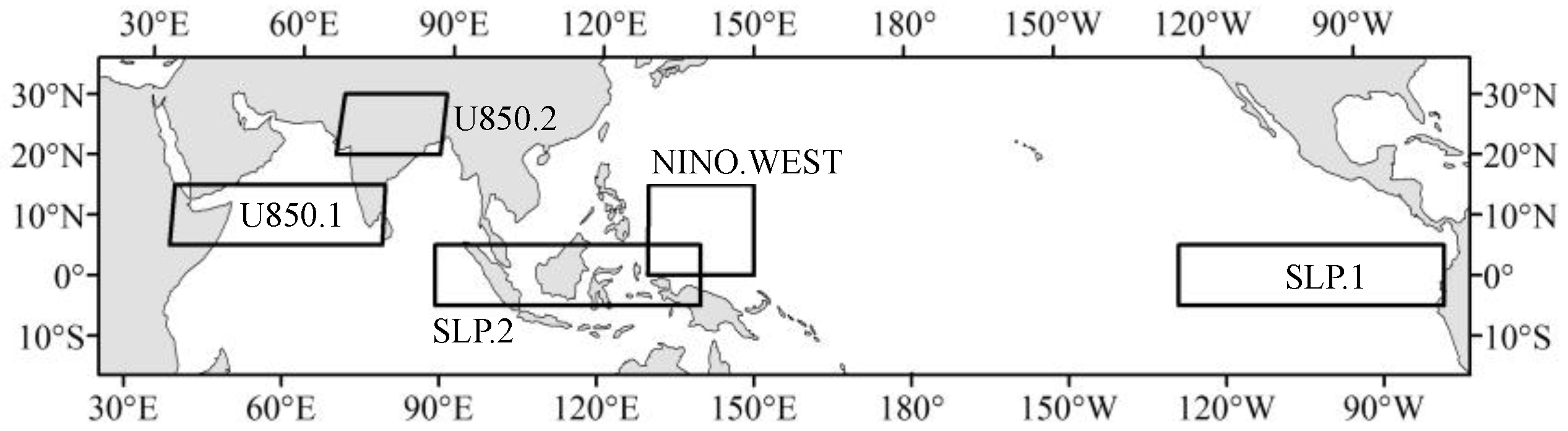
| EQ-SOI | The difference between the area-averaged sea level pressure in an area of the eastern equatorial Pacific (80° W–130° W, 5° N–5° S; indicated as SLP.1 in Figure 3) and an area over Indonesia (90° E–140° E, 5° N–5° S; SLP.2 in Figure 3) | [21] |
| IMI | The difference between the 850-hPa zonal wind in the domain of 40° E–80° E, 5° N–15° N (indicated as U850.1 in Figure 3) and that in the domain of 70° E–90° E, 20° N–30° N (U850.2 in Figure 3) | [22] |
| SST | Anomalies in sea surface temperature for the domain over | [23] |
| NINO.WEST | the western tropical Pacific (130° E–150° E, 15° N–EQ) | |
| NINO.3 | the eastern equatorial Pacific (150° W–90° W, 5° N–5° S) | |
| NINO.4 | the central equatorial Pacific (160° E–150° W, 5° N–5° S) | |
| NINO.34 | the central/eastern equatorial Pacific (170° W–120° W, 5° N–5° S) | |
| PDO | The leading principal component of the mean monthly SST in the Pacific Ocean north of 20° N [19] | [24] |
| DMI | An anomalous SST gradient between the western (50° E–70° E, 10° S–10° N) and southeastern equatorial Indian Ocean (90° E–110° E, 10° S–0° N) | [25] |
| Basin | a (mm) | b (mm) | λ |
|---|---|---|---|
| PRB | 302.4 | 723.0 | 4.107 |
| NRB | 395.1 | 870.6 | 4.734 |
| Basin | EQ-SOI < 0.0 | EQ-SOI > 0.0 | All Years | |
|---|---|---|---|---|
| PRB | r | 0.83 | 0.79 | 0.81 |
| RMSE (mm) | 69.0 | 78.4 | 74.4 | |
| NRB | r | 0.82 | 0.89 | 0.86 |
| RMSE (mm) | 95.4 | 72.1 | 83.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinouchi, T.; Yamamoto, G.; Komsai, A.; Liengcharernsit, W. Quantification of Seasonal Precipitation over the upper Chao Phraya River Basin in the Past Fifty Years Based on Monsoon and El Niño/Southern Oscillation Related Climate Indices. Water 2018, 10, 800. https://doi.org/10.3390/w10060800
Kinouchi T, Yamamoto G, Komsai A, Liengcharernsit W. Quantification of Seasonal Precipitation over the upper Chao Phraya River Basin in the Past Fifty Years Based on Monsoon and El Niño/Southern Oscillation Related Climate Indices. Water. 2018; 10(6):800. https://doi.org/10.3390/w10060800
Chicago/Turabian StyleKinouchi, Tsuyoshi, Gakuji Yamamoto, Atchara Komsai, and Winai Liengcharernsit. 2018. "Quantification of Seasonal Precipitation over the upper Chao Phraya River Basin in the Past Fifty Years Based on Monsoon and El Niño/Southern Oscillation Related Climate Indices" Water 10, no. 6: 800. https://doi.org/10.3390/w10060800
APA StyleKinouchi, T., Yamamoto, G., Komsai, A., & Liengcharernsit, W. (2018). Quantification of Seasonal Precipitation over the upper Chao Phraya River Basin in the Past Fifty Years Based on Monsoon and El Niño/Southern Oscillation Related Climate Indices. Water, 10(6), 800. https://doi.org/10.3390/w10060800




