Hazard Assessment under Multivariate Distributional Change-Points: Guidelines and a Flood Case Study
Abstract
1. Introduction
2. Materials
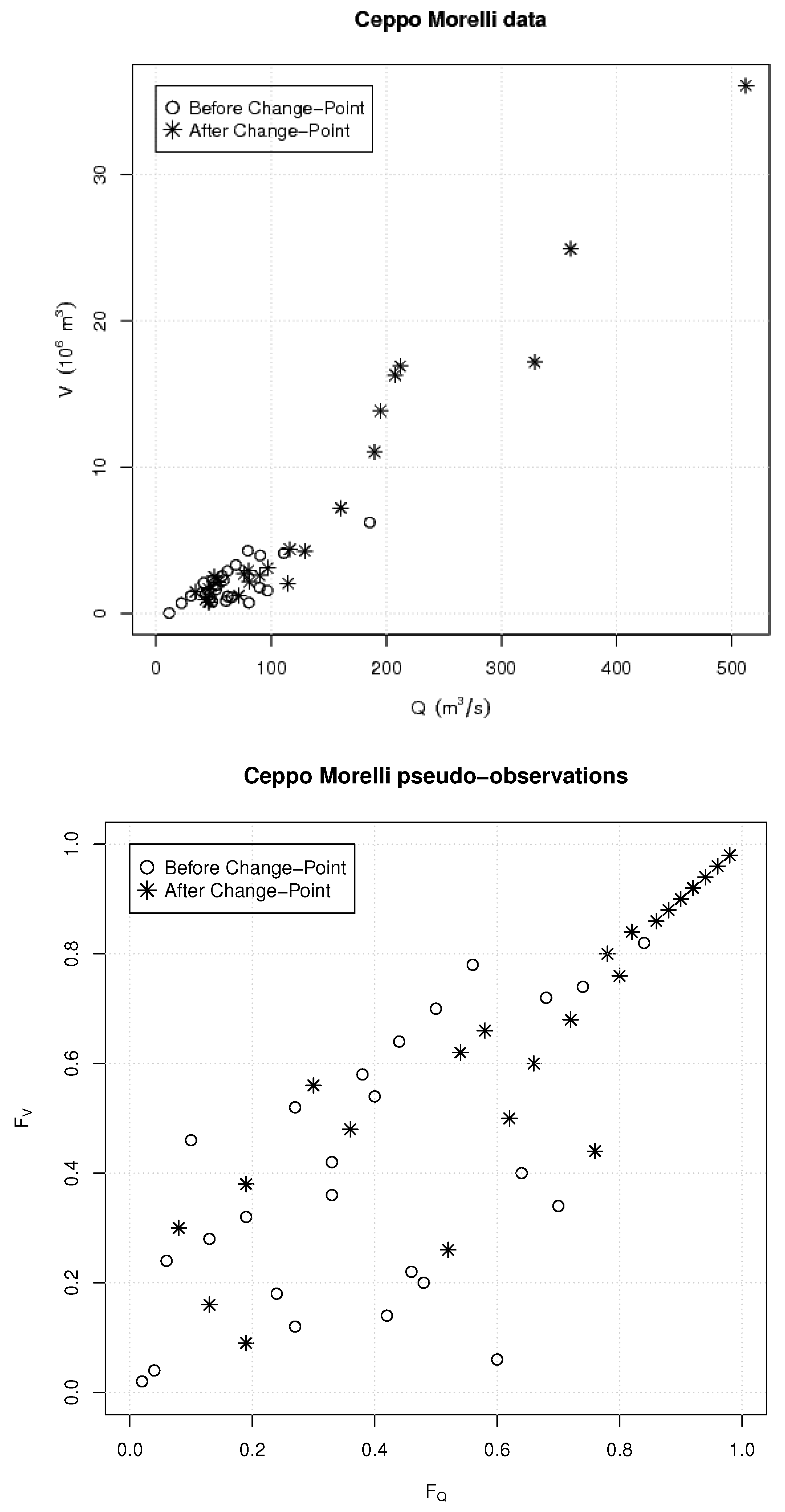
3. Methods
- changes of any of the marginal distributions s, or
- changes of the copula , or
- both of the previous cases.
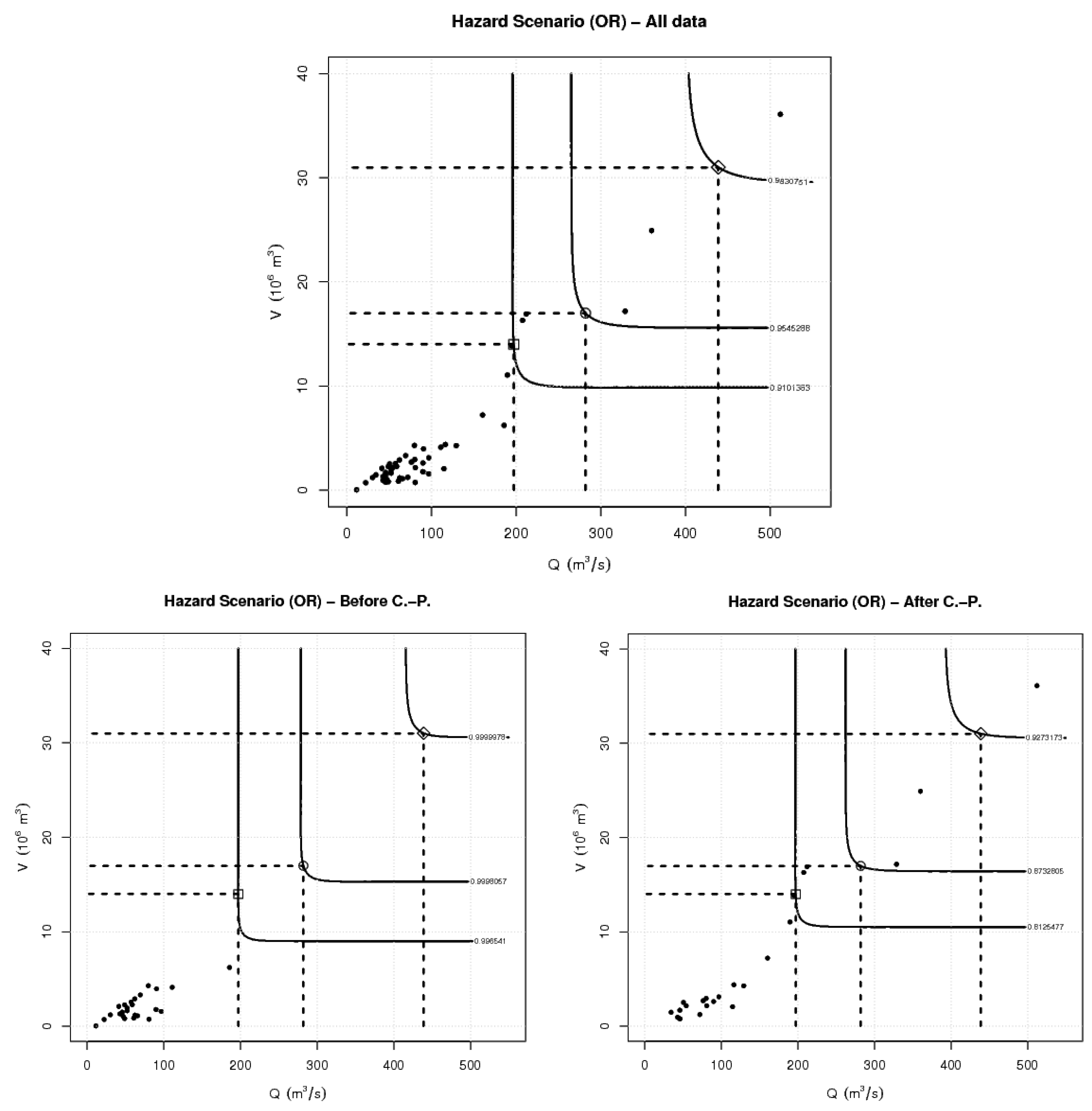
3.1. Hazard Scenarios
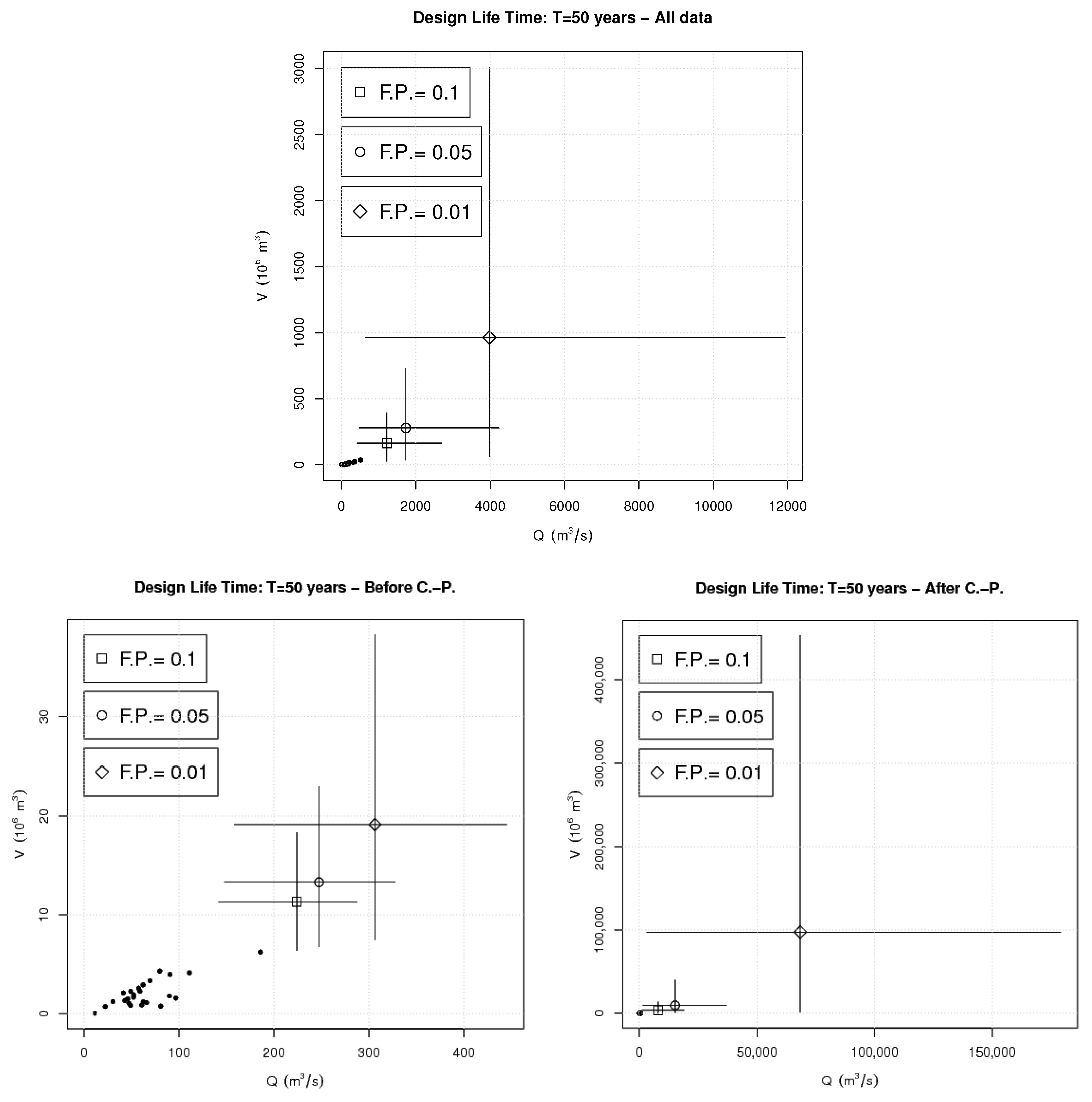
3.2. The Failure Probability Approach
4. Results and Discussion
- a change of the univariate distribution (respectively, ), or
- a change of the copula associated with , or
- both the previous instances.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Bendat, J.; Piersol, A. Random Data: Analysis and Measurement Procedures, 4st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Rao, A.; Hamed, K.; Chen, H.L. Nonstationarities in Hydrologic and Environmental Time Series, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Montanari, A.; Koutsoyiannis, D. Modeling and mitigating natural hazards: Stationarity is immortal! Water Resour. Res. 2014, 50, 9748–9756. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationarity case. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.; Kundzewicz, Z.; Lettenmaier, D.; Stouffer, R. Climate change—Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Kundzewicz, Z.; Robson, A. Detecting Trend and Other Changes in Hydrological Data. Water, World Climate Programme Data and Monitoring; Volume WMO/TD—No. 1013; World Meteorological Organization: Geneva, Switzerland, 2000. [Google Scholar]
- Kundzewicz, Z.; Robson, A. Change detection in hydrological records—A review of the methodology. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Ben Aissia, M.A.; Chebana, F.; Ouarda, T.; Roy, L.; Bruneau, P.; Barbet, M. Dependence evolution of hydrological characteristics, applied to floods in a climate change context in Quebec. J. Hydrol. 2014, 519, 148–163. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A.; Rosso, R. Bivariate statistical approach to check adequacy of dam spillway. ASCE J. Hydrol. Eng. 2005, 10, 50–57. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C.; Durante, F. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; De Michele, C. Multivariate return period calculation via survival functions. Water Resour. Res. 2013, 49, 2308–2311. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; De Michele, C.; Bernardi, M.; Petrella, L. A multivariate Copula-based framework for dealing with Hazard Scenarios and Failure Probabilities. Water Resour. Res. 2016, 52, 3701–3721. [Google Scholar] [CrossRef]
- Mediero, L.; Jimenez-Alvarez, A.; Garrote, L. Design flood hydrographs from the relationship between flood peak and volume. Hydrol. Earth Syst. Sci. 2010, 14, 2495–2505. [Google Scholar] [CrossRef]
- Gaál, L.; Szolgay, J.; Kohnová, S.; Hlavčová, K.; Parajka, J.; Viglione, A.; Merz, R.; Blöschl, G. Dependence between flood peaks and volumes: A case study on climate and hydrological controls. Hydrol. Sci. J. 2015, 60, 968–984. [Google Scholar] [CrossRef]
- Nelsen, R. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Salvadori, G.; De Michele, C.; Kottegoda, N.; Rosso, R. Extremes in Nature. An Approach Using Copulas; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2007; Volume 56. [Google Scholar]
- Durante, F.; Sempi, C. Principles of Copula Theory; CRC/Chapman & Hall: Boca Raton, FL, USA, 2016. [Google Scholar]
- De Michele, C.; Salvadori, G. A Generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas. J. Geophys. Res. 2003, 108, 4067. [Google Scholar] [CrossRef]
- Gräler, B.; van den Berg, M.J.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; Baets, B.D.; Verhoest, N.E.C. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Dutfoy, A.; Parey, S.; Roche, N. Multivariate Extreme Value Theory—A Tutorial with Applications to Hydrology and Meteorology. Depend. Model. 2014, 2. [Google Scholar] [CrossRef]
- Salas, J.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Serinaldi, F. Dismissing return periods! Stoch. Environ. Res. Risk Assess. 2015, 29, 1179–1189. [Google Scholar] [CrossRef]
- Moftakhari, H.R.; Salvadori, G.; AghaKouchak, A.; Sanders, B.F.; Matthew, R.A. Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 9785–9790. [Google Scholar] [CrossRef] [PubMed]
- Genest, C.; Favre, A. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Yan, J. Modeling multivariate distributions with continuous margins using the copula R package. J. Stat. Softw. 2010, 34, 1–20. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Yan, J.; Holmes, M. Fast large-sample goodness-of-fit tests for copulas. Stat. Sin. 2011, 21, 841–871. [Google Scholar] [CrossRef]
- Joe, H. Dependence Modeling with Copulas; Chapman & Hall/CRC: London, UK, 2014. [Google Scholar]
- Salvadori, G.; Tomasicchio, G.R.; D’Alessandro, F. Practical guidelines for multivariate analysis and design in coastal and off-shore engineering. Coast. Eng. 2014, 88, 1–14. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Hofert, M.; Kojadinovic, I.; Maechler, M.; Yan, J. Copula: Multivariate Dependence with Copulas; R Package Version 0.999-17; R Package: Vienna, Austria, 2017. [Google Scholar]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Vezzoli, R.; Salvadori, G.; De Michele, C. A distributional multivariate approach for assessing performance of climate-hydrology models. Nat. Sci. Rep. 2017, 7, 12071. [Google Scholar] [CrossRef] [PubMed]
- Chebana, F.; Ouarda, T.B.; Duong, T.C. Testing for multivariate trends in hydrologic frequency analysis. J. Hydrol. 2013, 486, 519–530. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A.; Grimaldi, S.; Lombardo, F.; Koutsoyiannis, D. One hundred years of return period: Strengths and limitations. Water Resour. Res. 2015, 51, 8570–8585. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, C.; Xu, C.Y.; Yu, K.X.; Guo, S. A framework of change-point detection for multivariate hydrological series. Water Resour. Res. 2015, 51, 8198–8217. [Google Scholar] [CrossRef]
- Ye, L.; Zhou, J.; Zeng, X.; Tayyab, M. Hydrological Mann-Kendal Multivariate Trends Analysis in the Upper Yangtze River Basin. J. Geosci. Environ. Prot. 2015, 3, 34–39. [Google Scholar] [CrossRef]
- Holmes, M.; Kojadinovic, I.; Quessy, J.F. Nonparametric tests for change-point detection à la Gombay and Horváth. J. Multivar. Anal. 2013, 115, 16–32. [Google Scholar] [CrossRef]
- Bücher, A.; Kojadinovic, I.; Rohmer, T.; Segers, J. Detecting changes in cross-sectional dependence in multivariate time series. J. Multivar. Anal. 2014, 132, 111–128. [Google Scholar] [CrossRef]
- Bücher, A.; Kojadinovic, I. A dependent multiplier bootstrap for the sequential empirical copula process under strong mixing. Bernoulli 2016, 22, 927–968. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Naveau, P. Nonparametric tests for change-point detection in the distribution of block maxima based on probability weighted moments. Extremes 2017, 20, 417–450. [Google Scholar] [CrossRef]
- Kojadinovic, I. npcp: Some Nonparametric CUSUM Tests for Change-Point Detection in Possibly Multivariate Observations; R Package Version 0.1-9.; R Package: Vienna, Austria, 2017. [Google Scholar]
- Embrechts, P.; Hofert, M. A note on generalized inverses. Math. Methods Oper. Res. 2013, 77, 423–432. [Google Scholar] [CrossRef]
- Bernardi, M.; Durante, F.; Jaworski, P.; Petrella, L.; Salvadori, G. Conditional risk based on multivariate hazard scenarios. Stoch. Environ. Res. Risk Assess. 2018, 32, 203–211. [Google Scholar] [CrossRef]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.; Mays, L.W. Applied Hydrology, 1st ed.; McGraw-Hill: Singapore, 1988. [Google Scholar]
- Kottegoda, N.; Rosso, R. Applied Statistics for Civil and Environmental Engineers; Wiley-Blackwell: Oxford, UK, 2008. [Google Scholar]
- Chebana, F.; Ouarda, T.B.M.J. Multivariate quantiles in hydrological frequency analysis. Environmetrics 2011, 22, 63–78. [Google Scholar] [CrossRef]
- Corbella, S.; Stretch, D.D. Multivariate return periods of sea storms for coastal erosion risk assessment. Nat. Hazards Earth Syst. Sci. 2012, 12, 2699–2708. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Ben Aissia, M.A.; Chebana, F.; Ouarda, T.; Roy, L.; Desrochers, G.; Chartier, I.; Robichaud, É. Multivariate analysis of flood characteristics in a climate change context of the watershed of the Baskatong reservoir, Province of Québec, Canada. Hydrol. Process 2012, 26, 130–142. [Google Scholar] [CrossRef]
- Massei, N.; Laignel, B.; Deloffre, J.; Mesquita, J.; Motelay, A.; Lafite, R.; Durand, A. Long-term hydrological changes of the Seine River flow (France) and their relation to the North Atlantic Oscillation over the period 1950–2008. Int. J. Climatol. 2010, 30, 2146–2154. [Google Scholar] [CrossRef]
- Alexander, M.; Capotondi, A.; Miller, A.; Chai, F.; Brodeur, R.; Deser, C. Decadal variability in the northeast Pacific in a physical-ecosystem model: Role of mixed layer depth and trophic interactions. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Alheit, J.; Niquen, M. Regime shifts in the Humboldt Current ecosystem. Prog. Oceanogr. 2004, 60, 201–222. [Google Scholar] [CrossRef]
- Daskalov, G. Long-term changes in fish abundance and environmental indices in the Black Sea. Mar. Ecol. Prog. Ser. 2003, 255, 259–270. [Google Scholar] [CrossRef]
- Dickson, B.; Osterhus, S. One hundred years in the Norwegian Sea. Norsk Geogr. Tidsskr. Nor. J. Geogr. 2007, 61, 56–75. [Google Scholar] [CrossRef]
- Schwing, F.; Murphree, T.; Green, P. The Northern Oscillation index (NOI): A new climate index for the northeast Pacific. Prog. Oceanogr. 2002, 53, 115–139. [Google Scholar] [CrossRef]
- Serreze, M.; Walsh, J.; Chapin, F.; Osterkamp, T.; Dyurgerov, M.; Romanovsky, V.; Oechel, W.; Morison, J.; Zhang, T.; Barry, R. Observational evidence of recent change in the northern high-latitude environment. Clim. Chang. 2000, 46, 159–207. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Vezzoli, R.; Pecora, S. Multivariate assessment of droughts: Frequency analysis and Dynamic Return Period. Water Resour. Res. 2013, 49, 6985–6994. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Multivariate real-time assessment of droughts via Copula-based multi-site Hazard Trajectories and Fans. J. Hydrol. 2014. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate Standardized Drought Index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
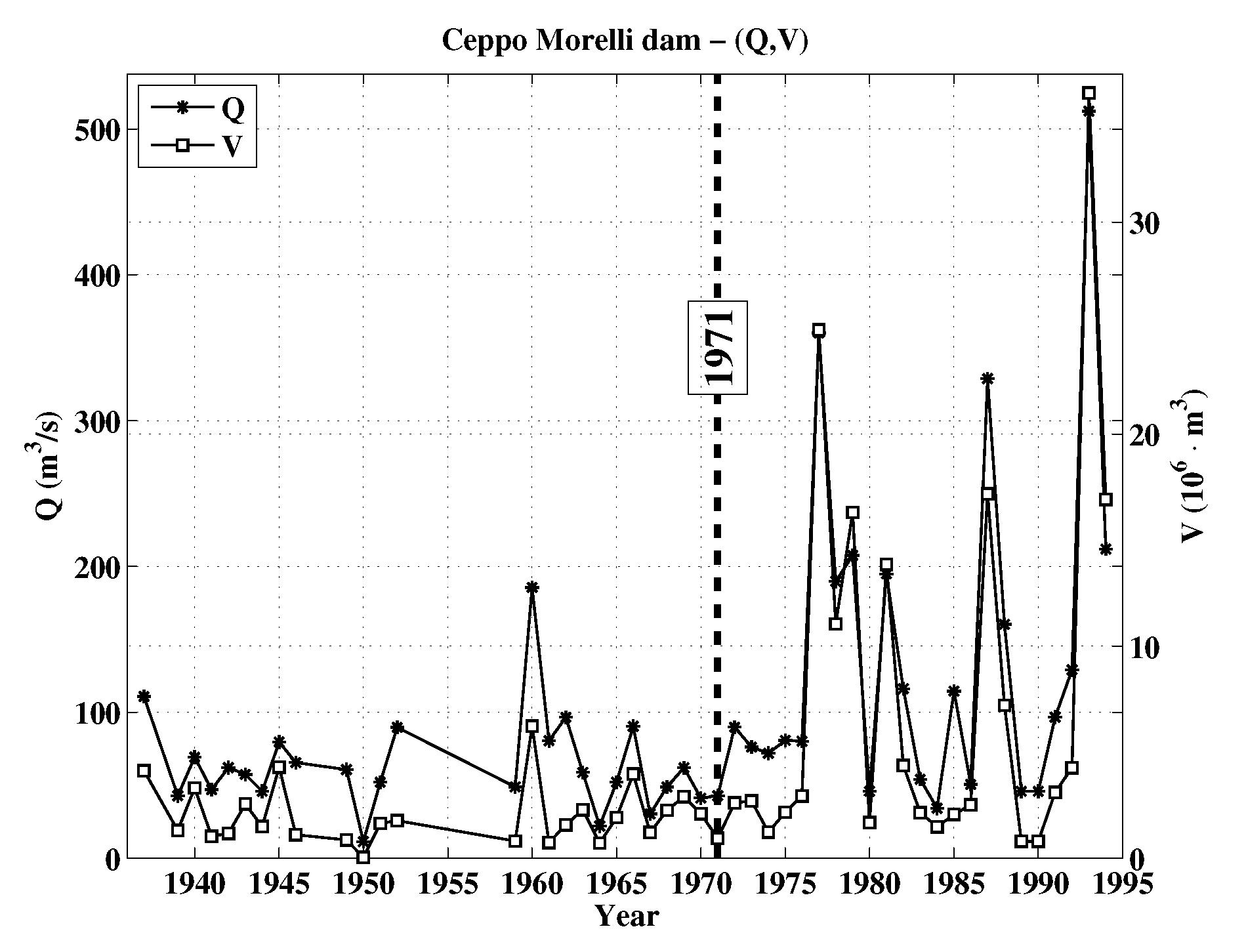


| Variable | Shape | Scale | Position | p-Value |
|---|---|---|---|---|
| All data | ||||
| Q | 0.37 | 36.21 | 59.36 | 77% |
| s.e. | 0.11 | 5.04 | 5.71 | |
| V | 0.61 | 1.52 | 1.72 | 91% |
| s.e. | 0.13 | 0.25 | 0.24 | |
| Before Change-Point | ||||
| Q | 0.02 | 24.46 | 50.05 | 87% |
| s.e. | 0.11 | 3.79 | 5.36 | |
| V | 0.12 | 0.95 | 1.39 | 99% |
| s.e. | 0.16 | 0.16 | 0.21 | |
| After Change-Point | ||||
| Q | 0.71 | 42.96 | 71.74 | 98% |
| s.e. | 0.30 | 11.75 | 10.92 | |
| V | 1.07 | 2.03 | 2.20 | 92% |
| s.e. | 0.34 | 0.67 | 0.50 | |
| All Data | Before Change-Point | After Change-Point | |
|---|---|---|---|
| 4.33 | 1.53 | 11.69 | |
| s.e. | 1.37 | 0.72 | 5.31 |
| p-Value | 9% | 47% | 44% |
| Quantile (%) | Q | V | ||
|---|---|---|---|---|
| 90% | 197 | 14 | 0.0880 | |
| 95% | 282 | 17 | 0.0453 | |
| 99% | 439 | 31 | 0.0172 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salvadori, G.; Durante, F.; De Michele, C.; Bernardi, M. Hazard Assessment under Multivariate Distributional Change-Points: Guidelines and a Flood Case Study. Water 2018, 10, 751. https://doi.org/10.3390/w10060751
Salvadori G, Durante F, De Michele C, Bernardi M. Hazard Assessment under Multivariate Distributional Change-Points: Guidelines and a Flood Case Study. Water. 2018; 10(6):751. https://doi.org/10.3390/w10060751
Chicago/Turabian StyleSalvadori, Gianfausto, Fabrizio Durante, Carlo De Michele, and Mauro Bernardi. 2018. "Hazard Assessment under Multivariate Distributional Change-Points: Guidelines and a Flood Case Study" Water 10, no. 6: 751. https://doi.org/10.3390/w10060751
APA StyleSalvadori, G., Durante, F., De Michele, C., & Bernardi, M. (2018). Hazard Assessment under Multivariate Distributional Change-Points: Guidelines and a Flood Case Study. Water, 10(6), 751. https://doi.org/10.3390/w10060751







