Uchimizu: A Cool(ing) Tradition to Locally Decrease Air Temperature

Abstract

The urban heat island effect was first described 200 years ago, but the development of ways to mitigate heat in urban areas reaches much further into the past. Uchimizu is a 17th century Japanese tradition, in which water is sprinkled around houses to cool the ground surface and air by evaporation. Unfortunately, the number of published studies that have quantified the cooling effects of uchimizu are limited and only use surface temperature or air temperature at a single height as a measure of the cooling effect. In this research, a dense three-dimensional Distributed Temperature Sensing (DTS) setup was used to measure air temperature with high spatial and temporal resolution within one cubic meter of air above an urban surface. Six experiments were performed to systematically study the effects of (1) the amount of applied water; (2) the initial surface temperature; and (3) shading on the cooling effect of uchimizu. The measurements showed a decrease in air temperature of up to 1.5 °C at a height of 2 m, and up to 6 °C for near-ground temperature. The strongest cooling was measured in the shade experiment. For water applied in quantities of 1 mm and 2 mm, there was no clear difference in cooling effect, but after application of a large amount of water (>5 mm), the strong near-ground cooling effect was approximately twice as high as when only 1 mm of water was applied. The dense measurement grid used in this research also enabled us to detect the rising turbulent eddies created by the heated surface.

1. Introduction

In the past, the Japanese water throwing tradition known as uchimizu has been used widely to cool urban surfaces and decrease the air temperature around houses and in gardens. Uchimizu (combination of uchi for hit or throw, and mizu for water) is a tradition that stems from the 17th century [1]. However, over the last 50 years, this environmental control method has lost popularity. This has been mainly caused by a rapid development in technology and by socio-economic change, causing citizens to feel that traditional methods were too laborious or low class [2]. Nowadays, Japanese megacitie,s such as Tokyo, are aiming to revive the use of uchimizu to cool the city, especially during hot summer months. Citizens practicing uchimizu in Japanese urban areas have been found to use less air-conditioning, which significantly decreases their domestic energy consumption [2]. Additionally, it was found that the level of outdoor comfort among citizens is higher in areas that applied uchimizu [3].

The comeback of uchimizu is interesting because of its claimed reduction of the Urban Heat Island (UHI) effect [4]. The UHI is a well-documented phenomenon that refers to higher temperatures within urbanized areas compared to surrounding rural areas [5]. Urban air temperatures are higher for various reasons, such as lower amounts of cooling by transpiring vegetation and evaporating water bodies, lower albedo, and increased heat production by humans, vehicles, and industries. In particular, during hotter summer months, a strong UHI is associated with increased human discomfort, energy consumption, health risks, and increased mortality rates [6,7,8]. In this research, UHI is defined as the urban canopy UHI [9].

Because one of the main causes of UHI is reduced evaporation, increasing evaporation by strategical placement of water bodies and green areas is an often used method that leads to local decrease of temperature. For example, water-retentive artificial turfs have surface temperatures up to 2 °C lower than conventional grass turfs [6], and sufficiently watered green roofs cool the ambient air environment while dry green roofs do not [10]. Although vegetated areas in cities can decrease the local air temperature by several degrees, several studies have shown that the strongest cooling effect is provided by open water bodies [11,12].

Evaporative cooling requires water as well as energy from the environment, which is extracted from the surface or the air. This latent energy flux leads to a decrease in air and surface temperatures. Practices like uchimizu tackle heat stress in two ways: (1) they decrease the mean radiant temperature to which the body is exposed by decreasing the surface temperature; and (2) they decrease the actual air temperature by extracting part of the energy necessary for the water to evaporate.

The revival of uchimizu is promoted by Japanese authorities as a “clever way to feel cool” [13,14]. Also, thanks to this initiative, research on this topic is becoming more frequent in Japan [15,16,17]. However, pavement watering as a method to cool the ambient temperature is also popular in France [4,18,19,20], and the principle is used all over the world to cool the roofs of houses [21,22,23], or, for example, the air temperature in railway stations in Japan [24].

Despite the popularity of the method, the number of published studies that have quantified the cooling effects of uchimizu is very limited. Most studies have only used measurements of the surface temperature, or the air temperature at a single height, as a measure of the cooling effect. Air temperature decreases between 1.5 and 2.3 °C were reported in these studies. Japanese studies have reported air temperature decreases of 1.5–3° [15,17], and French studies have reported decreases of 0.4–1.8° [4,18].

Experimental work has been very important for the advancement of (urban) hydrology [25], as has also been demonstrated by previous experimental work on uchimizu. A few studies focused on measuring the vertical temperature profile. Himeno et al. (2010) [16] by measuring the air temperature at four heights (0.4, 0.9, 1.5, and 1.8 m), and found that the cooling effect decreases (from 4 °C to 2 °C) with height. Slingerland (2012) [26] measured a more detailed temperature profile in Rotterdam, The Netherlands. They concluded that the air temperature profile between 0 and 2 m above a wetted ground surface is consistently 1–2 °C lower than above a dry ground. These differences in observed air temperature profiles highlight the importance of studying the reduction of air temperature decrease with increasing height above wet surfaces. High-resolution air temperature profile measurements are expected to give additional insight into the above described cooling effects of uchimizu.

In this research, a three-dimensional setup was used to measure the air temperature within one cubic meter of air, right above a wet/dry ground surface, with high spatial and temporal resolution. Several uchimizu experiments were performed under varying initial conditions. The objective of this paper was to study and understand the effects of uchimizu under different conditions, such as a varying initial ground surface temperature, shading of the pavement, and differences in the applied amount of water. Here, we provide an estimate of the cooling potential of the uchimizu technique as well as an explanation for the variability of its effectiveness under different initial conditions.

2. Methods

2.1. Field Site

This paper presents and analyzes measurements of six experiments, with varying initial air temperature, ground surface temperature, shading, and applied amount of water. The uchimizu experiments were done on a paved street in an urbanized area at the Delft University of Technology campus (51.998${}^{\circ }$ N, 4.378${}^{\circ }$ E), Delft, The Netherlands. All measurements were done on 24 August 2016 between 11:24 and 17:40 local time (LT = UTC + 2). On the 24 August, it was a sunny day with a clear sky all day long. The air temperature at 2 m varied between 27.4 and 33.0 °C, with a relative humidity between 38.5% and 51.0%, and a wind speed between 0.1 and 0.7 m/s. Global radiation was recorded at the station of the Rotterdam of the Royal Netherlands Meteorological Institute (KNMI), about 5.9 km from the measurement site.

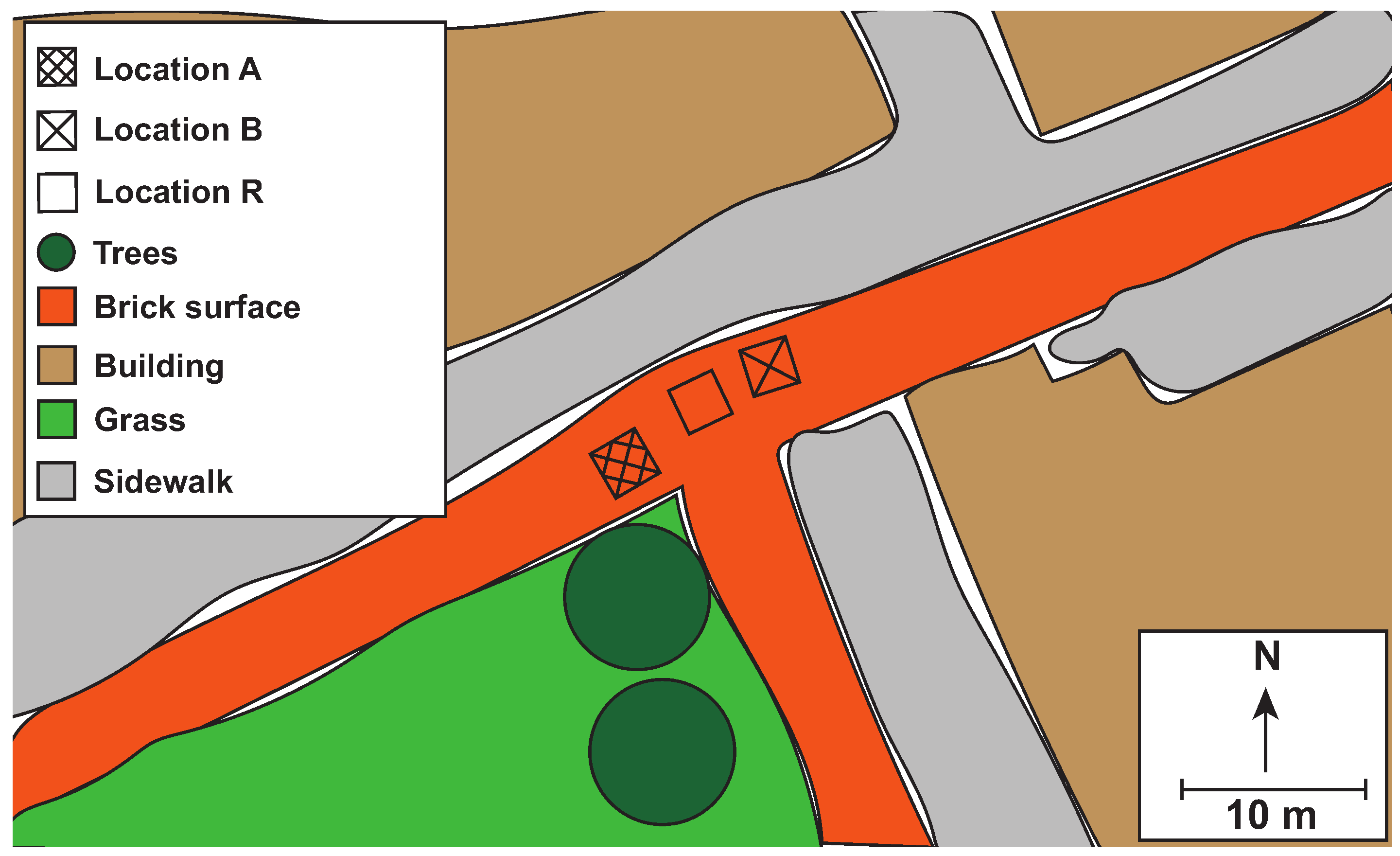
Two uchimizu measurement locations were used during this experiment (Figure 1), each 3 m × 3 m. The ground surface consisted of red bricks in a 45${}^{\circ }$ herringbone block pavement. The field site was surrounded by buildings on Northern and Eastern sides at distances of 6 m and 15 m from Location A, and 5 m and 5 m from Location B. An open field with trees was located in the southwest of the measurement locations. Location A was shaded by trees approximately between 14:00 and 16:00 LT. Location B was in full sunlight the whole day. In between Location A and B was the reference location, R. This location was uninfluenced by wetting and stayed in the sun the whole day.

Wind speed, wind gusts, relative humidity, and air temperature were measured 1.5 and 2.0 m above the ground surface using a HOBO weather station (Onset Computer Co., Bourne, MA, USA), with a measurement interval of 1 min. The resolution and accuracy of individual sensors can be found in the Supplementary Material. The wet bulb temperature T${}_W$ was calculated from observed relative humidity and air temperature. This weather station was moved together with the temperature monitoring setup from Location A to B and vice versa. Before each uchimizu experiment, the ground surface temperature was measured using an infrared temperature sensor (Testo SE & Co., Lenzkirch, Germany).

2.2. Distributed Temperature Sensing

To study changes in the temperature distribution near the paved surface during an uchimizu experiment, this study used Distributed Temperature Sensing (DTS). DTS allows precise and fast temperature measurements along the length of a glass fibre cable. This technique has, for example, been used to measure temperature at a high resolution in lakes [27,28], soils [29,30], streams [31], groundwater [32], and in the atmosphere [33]. A more detailed description of DTS can be found in [34,35].

DTS allows temperature measurements with sub-centimeter vertical measurement resolution by wrapping fiber optic cables around a coil or other construction [27]. However, as cables are often attached to the construction, this can introduce a significant error in observed air temperature values [36]. The measurement setup used in this study [37] reduced this effect by spanning cables across the construction without a physical contact between the cable and the construction anywhere in the region of interest for the temperature measurements (Figure 2).

The temperature monitoring setup consisted of a cage construction with 80 vertical bars, spanning a space of 1 m${}^3$ (1 m × 1 m × 1 m). Two bend-proof white-colored fibre optic cables (AFL, part number SR0015161001) with lengths of 1143 and 1243 m and a diameter of 1.6 mm were spanned within the cage, resulting in more than 34,000 sampling points. The cables were unequally vertically spaced, with 3 mm spacing in the lowest 120 mm of the setup, 15 mm spacing between 120 and 200 mm, 35 mm spacing between 200 and 500 mm, and 80 to 200 mm spacing in the upper 500 mm (the schematics of the setup can be found in [37]). The cables were connected to the four channels of an Ultima-S DTS device (Silixa Ltd., London, UK) with a sampling resolution of 12.5 cm and a time interval of 1 min with a 2 s integration time for each channel. More details about the used setup can be found in [37]. Double-ended calibration was used [38] to achieve high precision monitoring results.

2.3. Experiments

Six uchimizu experiments were done, with the aim of studying the influence of varying initial ground surface temperatures, shading, and applied amount of water on the cooling effect. An overview of conducted experiments is presented in

Table 1. Details of the six experiments, with starting time, location, sun or shaded, water applied, surface temperature before water application (T${}_g$), and links to videos showing the vertical evolution of temperature during each experiment.

Exp.	Time	Location	Sun/Shade	Water Applied	T${}_{\mathit{g}}$ (${}^{\circ }$C)	Link to Video
1	11:24	A	sun	1 mm	37.5 ± 1.4	https://youtu.be/SwwEf8-BNxw
2	13:21	B	sun	1 mm	40.6 ± 1.1	https://youtu.be/9oVsFIpk5Yg
3	14:33	A	shade	1 mm	36.9 ± 4.8	https://youtu.be/bIiyApdKo
4	15:29	B	sun	2 mm	42.6 ± 1.3	https://youtu.be/8WDEklxFj2U
5	16:23	A	sun	2 mm	47.7 ± 0.9	https://youtu.be/5sS6C13elTY
6	17:00	B	sun	>5 mm	41.3 ± 1.9	https://youtu.be/k8ID4dLhDxY

.

Before each measurement, the temperature monitoring setup was placed at the reference location, and the ground surface temperature was measured at nine places within the 9 m${}^2$ area of the experimental location (A or B). The values presented in Table 1 are averages of these measurements and their standard deviations. It can be seen that a wide variety of initial temperatures was covered by the six experiments. The standard deviation of the ground temperature before the third experiment was relatively high, because the surface was shaded by a tree, and therefore, the ground temperature varied depending on the instantaneous position of the shade patches.

Water was applied through pouring and was evenly distributed over the whole 9 m${}^2$ of the experimental location. This took, on average, 1.0–2.5 min. Immediately after the application of water, the temperature monitoring setup was positioned in the middle of the wet area to monitor the cooling effect of the evaporating water. To prevent water from running off from this space, a 5 mm threshold was applied around the measurement area. An experiment ended only when the ground surface was dry again, based on visual inspection. Each time a new uchimizu experiment started, the weather station was repositioned to the location of this experiment.

To investigate the influence of water on the cooling rate and change in temperature, different depths of water were applied: 1 mm (9 L), 2 mm (18 L), etc., until the whole area experienced continuous surface runoff (i.e., the amount of water was much higher than the 5 mm threshold surrounding the experimental location). Three experiments were done on Location A and three experiments on Location B (Figure 1 and Table 1). One of the experiments on Location A was done on a shaded surface to study the influence of shade. Before the beginning of this experiment, the setup was not placed on the reference location (R) but close to the measurement location, to ensure the measurements before and after uchimizu were both taken in the shade of the tree.

2.4. Energy Balance Analysis

To understand the mechanisms behind the varying initial conditions of the experiments, simple heat transfer balance calculations were done. The intent of this analysis was not to predict the precise magnitude of the decrease in air temperature, but to assess the potential effect of initial ground surface temperature on the cooling effect that uchimizu has on air temperature.

The total energy (E${}_{tot}$ (kJ/kg)) available to cool the ground (E${}_G$) and the air (E${}_A$) was calculated as the sum of energy necessary for increasing the water temperature to the observed temperature of the ground before the start of the experiment (see Table 1 for each experiment) and the energy necessary to evaporate the water.

$$E_{tot}=E_G+E_A,$$

(1a)

$$E_{tot}=m_{water}*C{p}_{water}*\Delta T+m_{water}*L,$$

(1b)

$$E_G=m_{brick}*C{p}_{clay}*(T_s-T_W),$$

(2)

where m${}_{water}$ [kg] is the mass of the applied water, Cp${}_{water}$ (4.2 kJ kg${}^{-1}$K${}^{-1}$) is the specific heat of water, $\Delta$T [K] is the temperature difference between the initial pavement temperature and the tap water (15 °C) used for the experiment, and L (2257 kJ/kg) is the latent heat of evaporation. Furthermore, m${}_{brick}$ [kg] is the mass of the brick pavement cooled by the applied amount of water, Cp${}_{clay}$ (1.381 kJ kg${}^{-1}$K${}^{-1}$), T${}_s$ [K] is the measured ground temperature, and T${}_W$ [K] is the wet bulb temperature.

To simplify the calculation, we assumed that the clay bricks were cooled first because of their higher thermal conductivity (k${}_{clay}$ = 0.48 W m${}^{-1}$K${}^{-1}$) compared to air (k${}_{air}$ = 0.03 W m${}^{-1}$K${}^{-1}$). We also assumed that the bricks were cooled uniformly in both the vertical and horizontal directions. The amount of energy necessary to cool the brick pavement to the wet bulb temperature (E${}_G$) and the total energy (E${}_{tot}$) were, therefore, calculated first and subtracted to find out how much was left to cool the air (E${}_A$). When the energy available for cooling the air was known, the change in air temperature ($\Delta$T${}_{air}$) was calculated using

$$\Delta T_{air}=\frac{E_{tot}-E_G}{m_{air}*C{p}_{air}}.$$

(3)

The air temperature change was then divided by this “ventilation coefficient” (C${}_v$ [–]) to simulate the exchange of air in the measured area (A = 1 m${}^2$).

$$C_v=U_{gust}*\frac{E_A}{k_{air}*A*\Delta T_{air}}$$

(4)

where U${}_{gust}$ [m/s] is the measured gust speed.

All variables in Equations (1)–(4) were known with exception of the mass of the clay bricks necessary to calculate E${}_G$. The density ($\rho$) of clay is 1746 kg/m${}^3$, so with known volume (V) the mass can be calculated using m = V/$\rho$. However, to what depth the bricks were cooled by the uchimizu experiment was not measured. Therefore, a range between 0.1 and 50 mm (thickness of the bricks) was prescribed, and temperature changes were calculated for each “heat infiltration depth” for the clay bricks, as well as for the air. Figure 3a shows how much cooling reached the air ($\Delta$T${}_{air}$) after a given portion of the brick was cooled down to wet bulb temperature by 1 mm of water.

Assuming that the ground was cooled to the wet bulb temperature, the energy supplied by the ground, and consequently, the amount of energy that needed to be supplied by the air, was dependent on the difference between the wet bulb temperature and the temperature of the ground. The higher the difference between T${}_s$ and T${}_W$, the more energy that was supplied by the ground and the less cooling that was left for the air. Figure 3b) shows the influence of the combination of various wet bulb temperatures (T${}_W$) and ground surface temperatures (T${}_s$) on the air temperature change ($\Delta$T${}_{air}$) resulting from the application of 1 mm of water, assuming the whole brick was cooled (50 mm). The red dots represent the measured combination of T${}_s$ and T${}_W$ at the start of each of our experiment.

Although the energy balance calculation using 1 mm of water resulted in numbers similar to those measured by previous studies [15,17,26,39], the calculated cooling effect for 2 mm and 5 mm of water was unrealistically strong (Figure 3a1). When 2 mm of water was used, the calculation predicted cooling effect was between 11 and 32 °C, and for 5 mm, the difference reached 66 to 80 °C according to the used energy balance calculation. For three reasons such a simplified energy balance approach is no longer applicable when more water is applied, as follows: (1) no additional energy has entered the system. In reality, energy was constantly being added in the form of incoming solar radiation which resulted in an increased temperature; (2) all the energy was extracted from the 1 m${}^2$ of bricks and the 1 m${}^3$ of air above. This assumption was partly addressed by introducing the ventilation coefficient (Equation (4)) which simulates the exchange of the 1 m${}^3$ of air used in the calculation; (3) all of the water evaporated. It is, however, realistic to assume that a certain amount of water infiltrated and did not contribute to the cooling. Five, or even two, millimeters of water on brick pavement by far exceeds the wetting loss of a brick pavement [40]. Hence, infiltration losses will occur. The only effect of this extra water was the cooling of the brick, according to Equation (1b).

2.5. Overview of Data Analysis Methods

Measurements taken during the six experiments on 24 August 2016 were analyzed from several perspectives. To simplify the representation of the 3D results, averages of the horizontal layers were used. In the following section, first, the general horizontal profile is discussed. The vertical profiles for the reference location and profiles after application of water were compared. The effect of incoming solar radiation on the temperature measurements was quantified, as well as the effect of the applied water on the relative humidity of the air. Four aspects of the cooling properties of uchimizu were looked into with more detail: the effect of the amount of water applied, the effect of shade, the effect of initial ground temperature, and the general spatial variability in the 3D measurements.

3. Results

3.1. Energy Balance Analysis

The energy balance analysis provided a simplified insight into some of the physical drivers, such as the effect of the initial ground surface temperatureon evaporative cooling. The calculations suggested that there might have been no cooling effect for Experiment 5 and strong cooling after the third experiment. Experiments 1, 2, 4 and 6 were expected to have similar results with cooling effects between 0 and 2 °C. Slingerland (2012) [26] showed that a high amount of water might have a larger influence than 1 mm of water on the near ground temperatures, which suggests that Experiment 6 might result in different vertical cooling profile than the other experiments.

3.2. General Findings

Figure 4 presents the recordings for the whole day, i.e., horizontal averages of temperature measured by the setup for each 1-min time step (Figure 4d,e) in relation to instantaneous weather conditions (Figure 4a–c). The solid vertical lines show the times when water distribution was finished and the setup and meteorological station repositioned to a new location. This time was considered to be the beginning of each new uchimizu experiment. The dashed vertical lines in subplots Figure 4d,e show the times when the setup was repositioned from a measurement location to the uninfluenced reference location. Since the meteorological station was not repositioned to the reference location and stayed at the original location until the beginning of a new experiment when it was moved to a new location, the dashed lines are not present in subplots Figure 4a,c. No vertical lines can be found in subplot Figure 4b, because the radiation measurements were taken from the KNMI weather station in Rotterdam. Finally, in Figure 4e, the red vertical lines depict times when the application of water began. Equal distribution of the water over the 9 m${}^2$ location took around about 1–2 min.

Figure 4e shows the average temperature profiles of several layers in the cube, with focus on the lowest three layers (13, 16, and 19 mm above the ground). For more detail, please see the cross-sections of the measurement setup for each time step of each event. Links to videos created from these cross-sections are provided in Table 1, and can be also downloaded from https://doi.org/10.5281/zenodo.182395 [41].

Temperatures measured from 200 mm up showed, in general, very small differences among the layers. This suggests that the air above this level was already relatively well mixed by turbulence. When the setup was positioned on the reference location, the temperature decreased with height. The application of water took around one minute, and the effect of uchimizu was immediately visible in the dataset from the moment the application of water started, as the reference location was in the proximity of the measurement location and the cooling effect stretched beyond the boundary of the measurement location. After re-positioning of the setup above a wet surface, the vertical profile changed. The cooling effect was the strongest for the 13 mm layer, followed by the 16 mm layer, followed by the above-lying layers.

A pocket of warm air formed above the cold layer close to the ground almost immediately after the application of water. The highest temperatures were measured between 30 and 80 mm (see videos from Table 1 for more detailed view). This pocket persisted until the end of the experiment.

The measured effect of the added water on the relative humidity (RH) was negligible. The biggest increase in RH was measured 1.5 m above the ground right after the last experiment (added water amount over 5 mm) and reached only 2.3%. Fluctuations of several percentage points were also measured above the dry reference position.

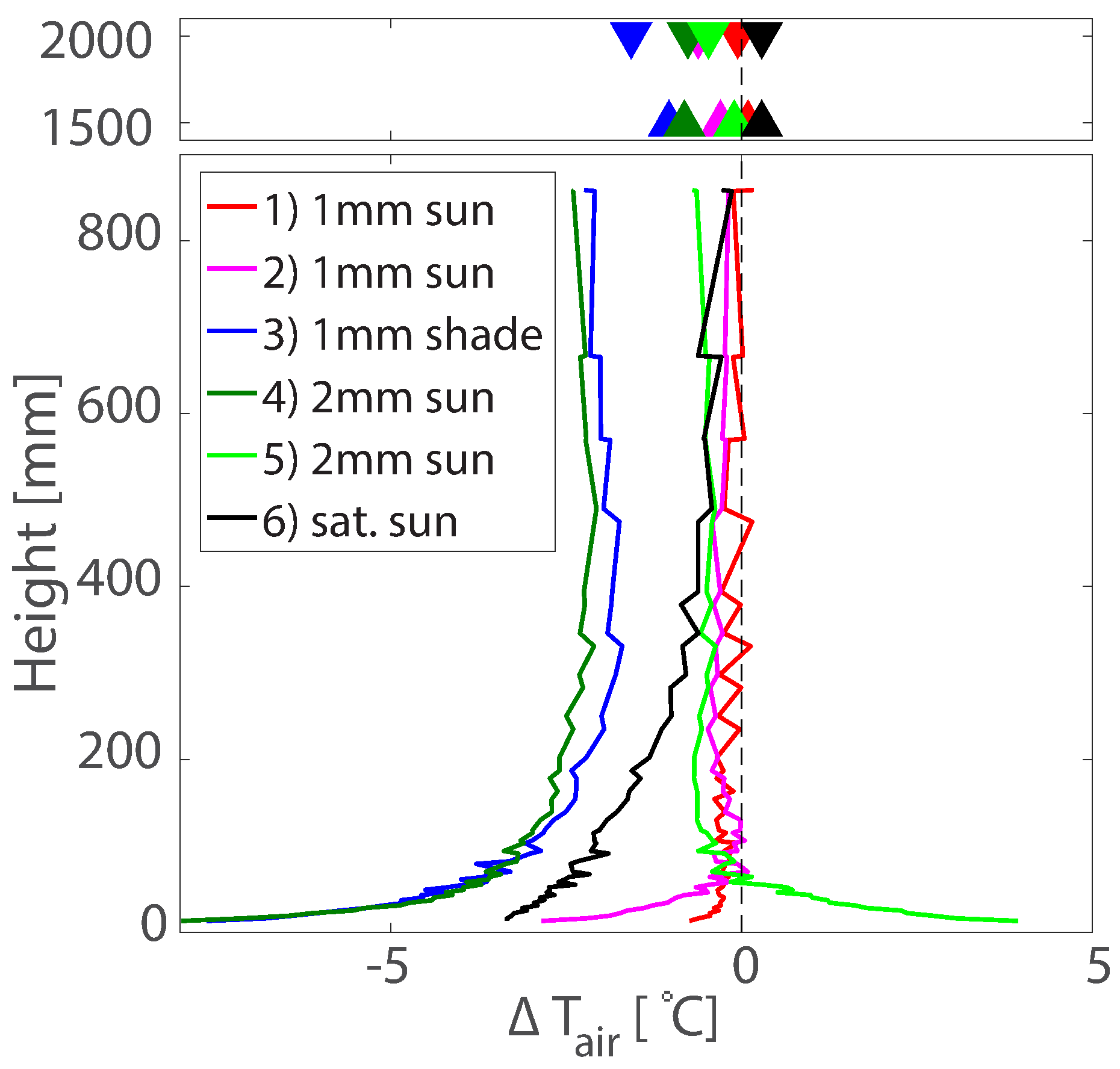
3.3. Effect of Applied Water Amount

To simplify the presentation of the data, we focused mostly on the seven chosen layers in Figure 4e) and the temperature differences before and after the application of uchimizu. Figure 5 presents the differences between the horizontal profile measured at the reference location before the uchimizu and the measurement location after uchimizu (T${}_{after}$–T${}_{before}$). The temperature difference profiles shown in the diagram are at times when the cooling effect of uchimizu reached its maximum.

The first three experiments were done with 1 mm of water. The third experiment was conducted in the shade and will be therefore discussed separately. The first experiment took place in the morning, when the initial ground temperature and global radiation were relatively low, resulting in only very weak cooling (−0.7 °C) close to the ground. The second experiment repeated the conditions of the first experiment, but now at Location B and resulted in a stronger cooling effect, especially near the ground. Near-surface cooling reached −2.9 °C, while higher layers of air experienced cooling of only about −0.3 °C, on average. The measured ground surface temperatures before the first and second experiments were 37.5 °C and 40.6 °C, respectively. After the water application, the ground surface temperature was not measured; however the air temperatures measured by the setup 13 mm above the ground reached after uchimizu were 30.2 °C and 35.0 °C for the first and second experiments, respectively.

Double the amount of water (2 mm) was used in the fourth and the fifth experiments. The temperature difference profile of the fourth experiment was very similar to the profile described in the second experiment. However, the cooling effect was stronger. Eight minutes after application of water, the temperature close to the ground dropped 8 °C compared to the situation before uchimizu. Higher up, the cooling reached −2.2 °C, on average. In contrast to that, the fifth experiment showed almost no cooling effect. The zero cooling effect after the fifth experiment was predicted by the energy balance analysis due to the high T${}_s$−T${}_W$ difference.

Figure 5 also shows an increase in the near-surface temperature by 4 °C for the fifth experiment, which was not expected. The measured increase in the near-surface temperature at the start of the fifth experiment might be explained by a large underestimation of T${}_{before}$. The initial ground temperature at Location A at the start of experiment 5 was 47.7 °C before the water was applied. Moreover, the setup was not located at the reference location for more than two minutes. This might not have been sufficient for the setup to reach equilibrium. Spruit et al. (2016) [42] showed that the response time of DTS to shock changes in temperature can be up to 1 min.

The fifth experiment cooled the pavement to approximately 38 °C but did not result in a colder layer of air close to the ground surface. As shown in Figure 4d, the lower layers of air continued to be the warmest at all times during Experiment 5, while the temperature profile inverted at least partly during all other experiments. A contributing factor for the creation of such a profile may have been the low wind speed during this experiment as it often dropped to 0 m/s (see Figure 4a).

During the sixth experiment, water was applied until continuous runoff from the area appeared. The vertical distribution of temperature change during the last experiment differed from the previous ones, especially in the lower layers. The temperature change of the lowest layer was only a decrease of 3.4 °C, which is 4.6 °C less cooling than after the fourth experiment. However, the rapid decrease in the cooling effect on the following layers was not present after this last experiment. For the first 100 mm, the temperature change decreased only by ∼0.5 °C. The uniform cooling that is typical for higher layers was reached only after ∼400 mm. The wind speed during this experiment was again very low and might have, similarly to the previous experiment, contributed to a different vertical temperature profile.

3.4. Effect of Shade

The third experiment was performed in the shade of a tree, and 1 mm of water was applied. The initial temperature of the pavement was only 36 °C. Compared to other experiments, uchimizu performed in the shade showed the strongest cooling effect on air temperature. The strongest cooling was measured close to the ground, with a temperature drop of −6.5 °C within the first two minutes, and the maximum temperature decrease, −8.3 °C, was reached at at 14:48. For the third experiment, Figure 4e shows immediate responses by all the measured layers to uchimizu.

Based on the lower T${}_s$−T${}_W$ difference, the energy balance analysis predicted this experiment to have the strongest cooling effect. This was mainly due to the lower T${}_s$ compared to other experiments. In general, shade decreases the amount of shortwave radiation that reaches the ground, which consequently leads to lower ground temperatures compared to sun-exposed locations, but it also leads to a lower amount of energy available in the system.

The results suggest that shade might increase the air cooling effect of uchimizu. Shashua-Bar et al. (2009) [43] measured an amplified cooling effect in the shade of trees for grassy areas. Their study, however, also reported an increase in temperature if the shade was provided by a mesh. Our experiment, in combination with the energy balance calculated by Equations (1) and (2), shows that, indeed, a better cooling performance is to be expected if the pavement is shaded.

3.5. Effect of Initial Ground Temperature

The effect of the initial ground temperature was predicted by the energy balance analysis to play an important role in the cooling efficiency of uchimizu. The results show that, indeed, the experiment with the lowest ground temperature (Experiment 3) resulted in the largest amount of cooling and vice versa. However, if the initial ground temperature was the only driving force, the first experiment should have resulted in almost as strong of a cooling effect as the third experiment. The initial ground temperatures of these two experiments differed only by 0.6 °C. Nonetheless, the results of the first experiment showed a very weak cooling effect, as predicted and visualized in Figure 3b, due to the low wet bulb temperature. Similarly, the fourth experiment was done on a relatively warm surface (T${}_s$ = 42.6 °C) and resulted, as expected, in strong cooling comparable to the experiment performed in the shade.

3.6. Local Variability

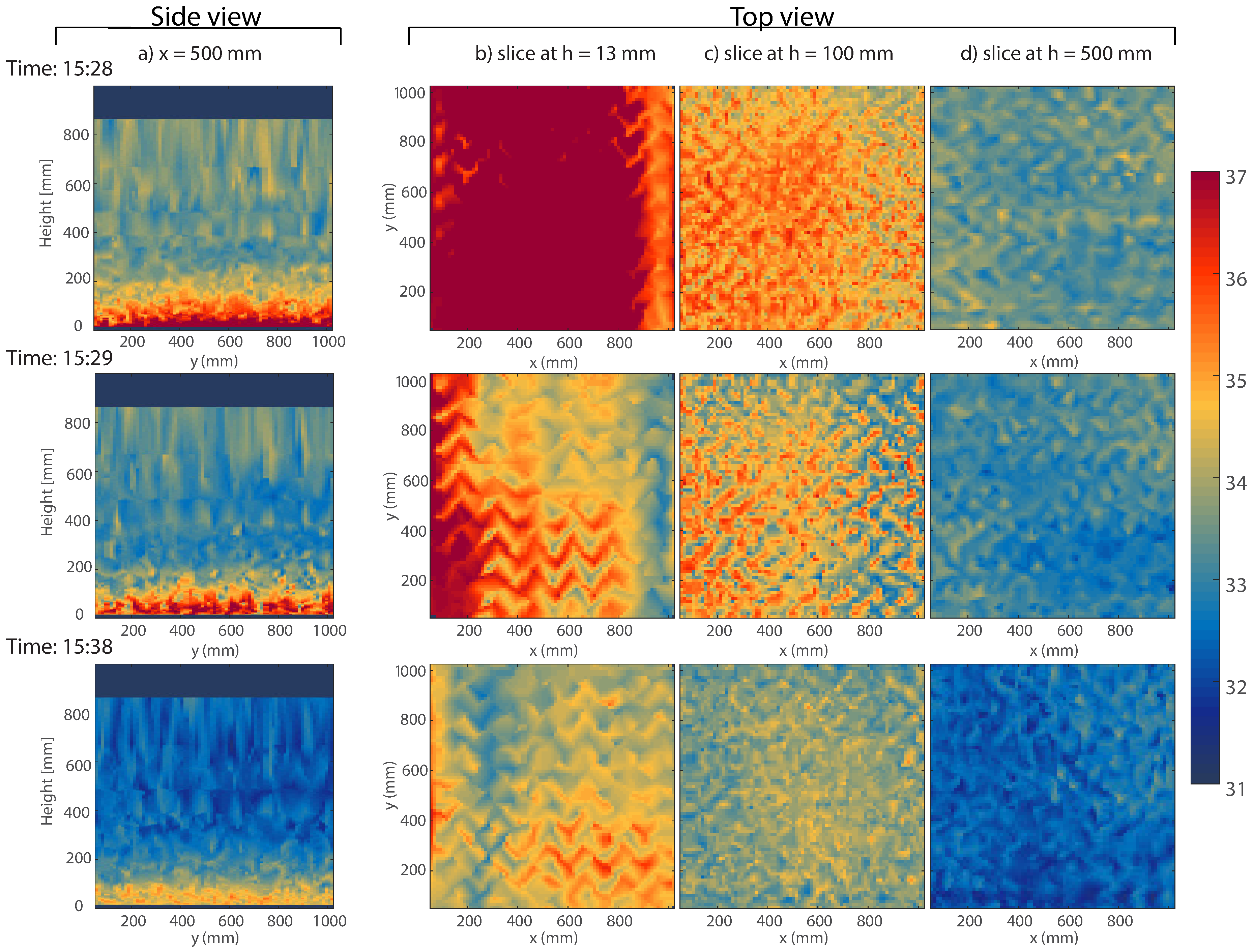
The use of the high-resolution temperature monitoring method above a wet surface during a hot summer day resulted in several interesting insights into the cooling effect of uchimizu, such as a vertical profile of rising turbulent eddies. Figure 6 allows a more detailed examination of the cooling effect of uchimizu for the fourth experiment (2 mm of water applied over a sun exposed location) than the average value profile shown in Figure 5 (dark green line). Compared to the previous figures, Figure 6 shows the absolute instantaneous values of that particular cross-section, not the averages over the whole layer (as in, for example, Figure 4d)).

Figure 6a shows three vertical cross-sections through the middle of the setup (x = 500 mm) for the fourth experiment. The top left subplot depicts the situation just before the water was applied, which means that the setup was at the reference location, and the two subplots below show the situation at 1 min and 9 min after the application of uchimizu. Especially in the lowest 200 mm of air, where the measurement resolution was highest, the creation of turbulence (eddies) can be observed. The spatial variability of the rising warm air was very well revealed by the fine resolution of the setup.

Figure 6b–d show the horizontal spatial variability of the temperature distribution before and after the fourth uchimizu experiment. The spatial variability originated primarily from the shape of the pavement. The herringbone pattern with warm bricks and colder interstices was clearly visible in the data. This influence could even be seen at 500 mm above the ground (Figure 6d).

Detailed vertical and horizontal cross-sections of the instantaneous temperature also provided an insight in the effects of insolation and shading. Figure 6b, especially at 15:29, suggests that the side of the setup where x = 0 was more exposed to sun than the side where x = 1000. This localized temperature increase was, however, only visible for the lowest layers of the set up and might partly be an artifact of an unevenly heated pavement.

4. Discussion

4.1. Discussion of Energy Balance Analysis

The results of the six uchimizu experiments were analyzed from different perspectives. Simplifying the system to a basic energy balance proved to be helpful in understanding the sensitivity to different variables, such as the wet bulb temperature or the ground surface temperature. As shown by Figure 3b, the energy balance analysis predicted low-to-no cooling effects for the fifth experiment and the strongest cooling effect for the third experiment. This was indeed what the measurement results showed. However, the energy balance analysis predicted more cooling when more water was applied. This was not confirmed by the measurements. The most likely explanation for this overestimation of the cooling effect for water amounts greater than 1 mm is the infiltration of part the water. With recorded infiltration rates of at least 10 mm/h for similar brick pavements, a significant part of the applied water can infiltrate the joints between the bricks [44] so that it is no longer available for evaporative cooling.

In our energy balance model, the dynamic properties of the atmosphere were represented simplistically. To include the effect of air exchange by wind, the ventilation coefficient was used to relate the amount of energy required to cool the air E${}_A$ with the air temperature decrease $\Delta$T${}_{air}$. Similarly, the decrease in turbulence due to the transition of the temperature of the bricks from being warmer than the air to being colder than the air, as well as the effect of entrainment and vertical wind, was not taken into account in the calculation. Instead, we continued to use the observed U${}_{gust}$ in Equation (4).

When it comes to the paving material, it was assumed that the whole brick had the same temperature as the temperature measured on the surface and that the cooling was homogeneous throughout the whole volume of the brick. In reality, it is likely that the temperature of the brick gradually changed from the surface towards deeper layers, but this difference was not monitored and was not included in the energy balance approach. Instead, the cooling was seen more as a process starting on the surface, where the water was applied, and proceeded deeper into the brick. This simplification introduced in our energy balance analysis likely led to an overestimation of the energy necessary to cool the ground.

The type of pavement seems to play an important role in the cooling effect of uchimizu. The simple energy balance analysis revealed the importance of the density and heat capacity of the paving material. Equation (2) shows a direct proportionality between the heat capacity and the energy necessary to cool the pavement. The same equation then hints at the inverse proportionality between the density and the energy (m = V/$\rho$). Surfaces with higher density and lower heat capacity, such as, for example, asphalt ($\rho$ ≈ 2000 kg/m${}^3$, Cp≈ 0.95 kJ/(kg K), might require less energy for cooling than clay bricks.

4.2. Discussion of the Experimental Setup

The construction of the setup was specially designed to capture the variation in temperature with very fine spatial resolution. However, the dense cable spacing in the set-up and the vertical bars of the walls of the cube may have led to undesired effects, such as reduced ventilation inside and at the bottom of the construction. Although the ventilation was not restricted totally, the chosen setup might, to a certain extent, have limited the effective area of cooling to that directly above the wetted ground surface. The influence of the grid is expected to have been small, since the relative volume of the optical fibre over the complete setup was only 0.4%. In the bottom 10 cm, the percentage was a bit higher at 2%. However, the cable nets could induce small-scale convection cells by the physical tendency to diffuse the temperature interface [37].

Similarly, the grid of the “walls” of the cube provided shading for the area under and behind the construction causing differences in the influence of radiation along the vertical axis of the setup. As can be seen by studying the films, this influence was relatively small. Also, in the recordings shown in the top view of Figure 6 (h = 13 mm), a colder strip due to the shading is visible at x > 800 mm. The cables within the construction might have affected the amount of incoming radiation, and therefore, the evaporative cooling. During our fieldwork campaign, it was impossible to quantify the attenuation of the incoming radiation by the setup. Future work will study this in more detail.

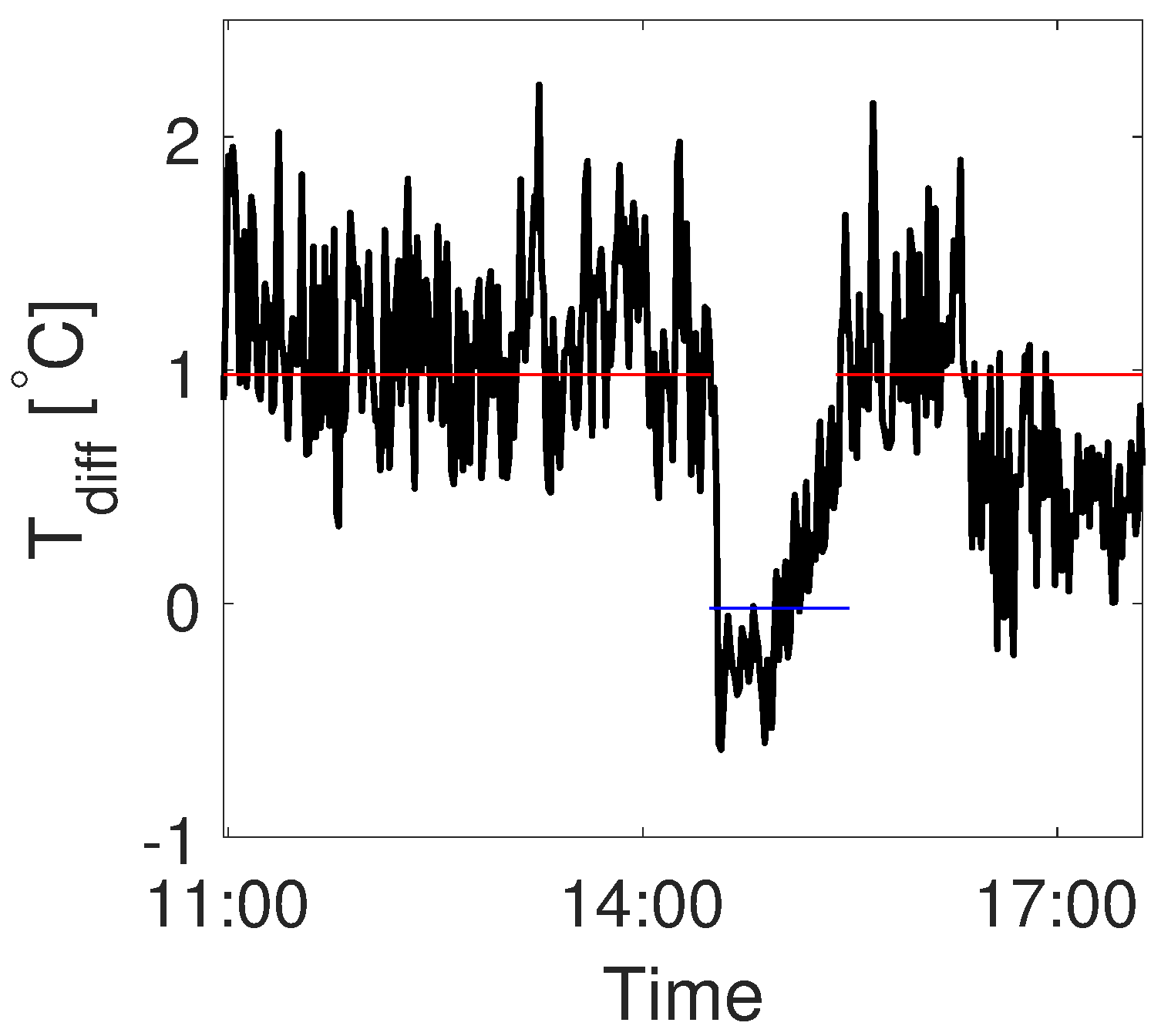
The effect of solar radiation on the temperature monitoring setup is visible from Figure 4e. As there was very small vertical variation in the temperature measured by the setup above ∼200 mm, the highest layer of the setup (yellow line in Figure 4e) should have a similar temperature to the air temperature measured at 1.5 m by the sensors with radiation shields (gray lines in Figure 4e). However, measurements taken by the shielded sensors collected up to 2 °C lower temperatures than the highest layers of the setup. This difference disappeared when the setup was in the shade (14:33 until 15:23). The differences between the measurements of the highest layer (859 mm) and the 1.5 m temperature sensor ($T_{859}$-$T_{T1500}$) for each time step are shown in Figure 7. The effect of radiation on the recorded temperatures was around 1 °C, on average, when positioned in the sun, and close to zero for measurements in the shade (−0.02 °C). Later in the afternoon (after 16:20) the effect of direct insolation on the white fibre optic cable decreased again, probably as a consequence of lower incoming solar radiation. This is in agreement with research done by [45]. They found that the effect of radiation on DTS can reach up to 2.8 °C when the values of incoming shortwave radiation are high. Although, de Jong et al. (2015) [33] showed smaller effects of solar radiation (−0.4 °C ,on average) for 1.6 mm white cable, the same one used in our uchimizu measurements, we observed an effect of up to about 1.0 to 1.5 °C.

4.3. Discussion of the Measurement Results

The amount of water applied did not show a clear relationship with the cooling effect. Applying 1 mm of water resulted in a relatively weak cooling effect, with the strongest cooling occurring near the ground. The strong cooling effect recorded after the fourth experiment using 2 mm of water, might suggest that double the amount of water leads to more cooling. However, the following experiment with 2 mm of water resulted in almost no cooling and even, an increase in temperature near the ground. The last experiment, when the surface was fully saturated by water, resulted in a slightly different profile than all previous experiments. It is possible that the amount of water influenced the thickness of the lower air layer that was experiencing stronger cooling than the higher, well-mixed air. The measured differences for small (1–2 mm) and large (>5 mm) amounts of water correspond with preliminary research done by [26]. The current evaporative cooling effect was also influenced by the temperature of the applied water (15 °C). If, for example, rain water with ambient temperature was applied, the cooling effect might be lower.

Previous studies done by [15,17,39] reported temperature decreases between 1.5 and 2.3 °C, measured at 1.2 m above the ground, and a more detailed profile done by [16] showed a cooling effect decreasing from 4 °C at 0.4 m above the ground to 2 °C at 1.8 m above the ground. Similar values were measured in our experiment, but with much higher resolution. While Himeno et al. (2010) [16] measured the effect on four levels, the setup used in this research consisted of 53 horizontal layers. Similarly, the dense measurement grid in each of these layers allowed for a detailed observation of the spatial variability in temperature caused by the unevenly heated pavement underneath.

The average values for each horizontal layer, presented in Figure 5, showed a typical profile of strong cooling close to the ground followed by constant cooling higher up. Air above 200 mm experienced a similar level of cooling for all measured horizontal layers. Nonetheless, even with stronger cooling close to the ground, the lowest layer of air (under 200 mm in Figure 6 Side view) stayed warmer than the air above. The homogeneous temperature of air above 200 mm is inconsistent with the measurements of [16], who showed variations among the measured levels. This difference might have been caused by using average values of a horizontal layer rather than using point measurements. The top view of Figure 6 shows variation by up to 1 °C for the higher layers of air (100 and 500 mm), and up to 3 °C for the layer closest to the ground. For this reason, we recommend averaging several measurement points at one level as a better estimation of the temperature change.

Uchimizu showed promising potential for mitigating the UHI at a local scale by decreasing both the air and ground temperatures. Decreasing the ground temperature lowers the mean radiant temperature (MRT) and consequently, increases human comfort. Another factor influencing human comfort is the relative humidity (RH). Higher levels of RH generally have a negative impact on human comfort. The effect of uchimizu on RH was measured to be negligible (2.3%) in the climate of The Netherlands, but implications of increasing the RH should be considered for more humid climates. Human comfort is influenced by a broad scale of factors and was not explicitly studied in this research. On the other side, in dry, urban environments, especially during heatwaves, the slight increase in RH might have an even larger positive impact on human comfort.

The brick pavement showed a distinct change in colour at the moment that all water had disappeared from the brick. This was the moment at which each experiment was stopped as further cooling was not expected. As is visible from Figure 4e, temperatures at h = 13 mm were constant by the end of each experiment and temperatures at h = 100 were already increasing. As expected, results suggested that at the end of each experiment, the near-surface temperature was still lower at the experimental location than at the reference location. The conclusion that cooling stops the moment the pavement is dry seems to be valid. Although it is not within the scope of the current paper, it would be interesting to continue monitoring after the moment the pavement runs dry to prove this and to see how quickly the temperature starts to increase again.

4.4. Outlook

The limitations and uncertainties described above show the need for further research. It was assumed that all the water evaporated. However, further research is needed to assess how much infiltrates and how much evaporates. Simultaneous measurements of a profile of areas with and without uchimizu might provide more accurate quantification of the cooling effect. Alternatively, application of uchimizu on a plot of artificial street surface on a small scale could also provide an estimate of the degree of water infiltration.

A second setup measuring simultaneously above a dry surface would also contribute to another important aspect, the duration of the cooling effect. Information about the time when the cooled surface and air warmed up again to a temperature of an uninfluenced area cannot be precisely derived from measurements of a single setup. However, the results of this research suggest that the effect lasts longer than an hour. As is visible from Figure 4e), the reference location was always warmer than the measurement location, even after a long measuring period (e.g., 13:20 until 14:20).

More measurements are also necessary to fully understand the effects of shade and initial ground temperature on uchimizu practices. The results of this study suggest that shade might enhance the cooling effect of uchimizu. Similarly, a lower ground temperature can be beneficial for cooling by uchimizu, since less energy is extracted from the ground and more from the air. Such effect, however, is only confirmed for the warmest and coldest initial ground temperatures measured in our experiment.

This research specifically focused on the temperature change within the 1 m${}^3$ of air closest to the ground. Further research should extend to areas around and above 1 m${}^3$. Further research is also needed for deeper understanding of the effect of evaporation in general and uchimizu, in particular, on UHI at the city level. The temperature decreases measured in this research showed the potential for local cooling. However, in order for uchimizu to be used over a whole city, more research needs to be done to come to a reliable estimate of the decrease in temperature and the amount of water that would be necessary to achieve this decrease. This water demand is the reason why this topic is also interesting from a water management point of view.

5. Conclusions

This research focused on quantifying the cooling effect of the traditional Japanese water throwing tradition of uchimizu on air temperature in an urban environment. The measurements showed a decrease in air temperature of up to 1.6 °C at a height of 2 m, and up to 8 °C for near-ground temperature. The highest rate of cooling was measured for the experiment performed in the shade. Stronger cooling effects were also predicted for lower initial ground temperatures, especially in combination with high wet bulb temperatures. The results of the third and fifth experiments agreed with this hypothesized effect of initial ground temperature; nonetheless, the remaining experiments did not show this relationship. For applied amounts of water of 1 mm and 2 mm, there was no clear difference in cooling effect.

We further conclude that the use of high resolution temperature monitoring setups, such as the one used in this research, can potentially lead to significant improvements in the understanding of atmospheric processes at a micro-scale. Thanks to the dense measurement grid, we were able to capture the vertical distribution of temperature over time in high detail. The fine resolution was even able to capture the rising turbulent eddies created by the heated surface.

Overall, this study sheds promising new light on a traditional cooling method. This simple water throwing method has the potential to decrease temperatures in impervious and paved parts of urban areas by using a limited amount of water. Besides its cooling effect, uchimizu practice is also an opportunity to activate awareness among citizens, and to stimulate citizen participation in solving heat stress problems and cooling energy saving. Uchimizu is a local technique with proven local effects. Application at the city scale as an UHI mitigation strategy is beyond the scope of this study but could provide interesting new insights on urban climate control and water resources management.