Indirect Damage of Urban Flooding: Investigation of Flood-Induced Traffic Congestion Using Dynamic Modeling
Abstract
:1. Introduction
2. Study Area and Models
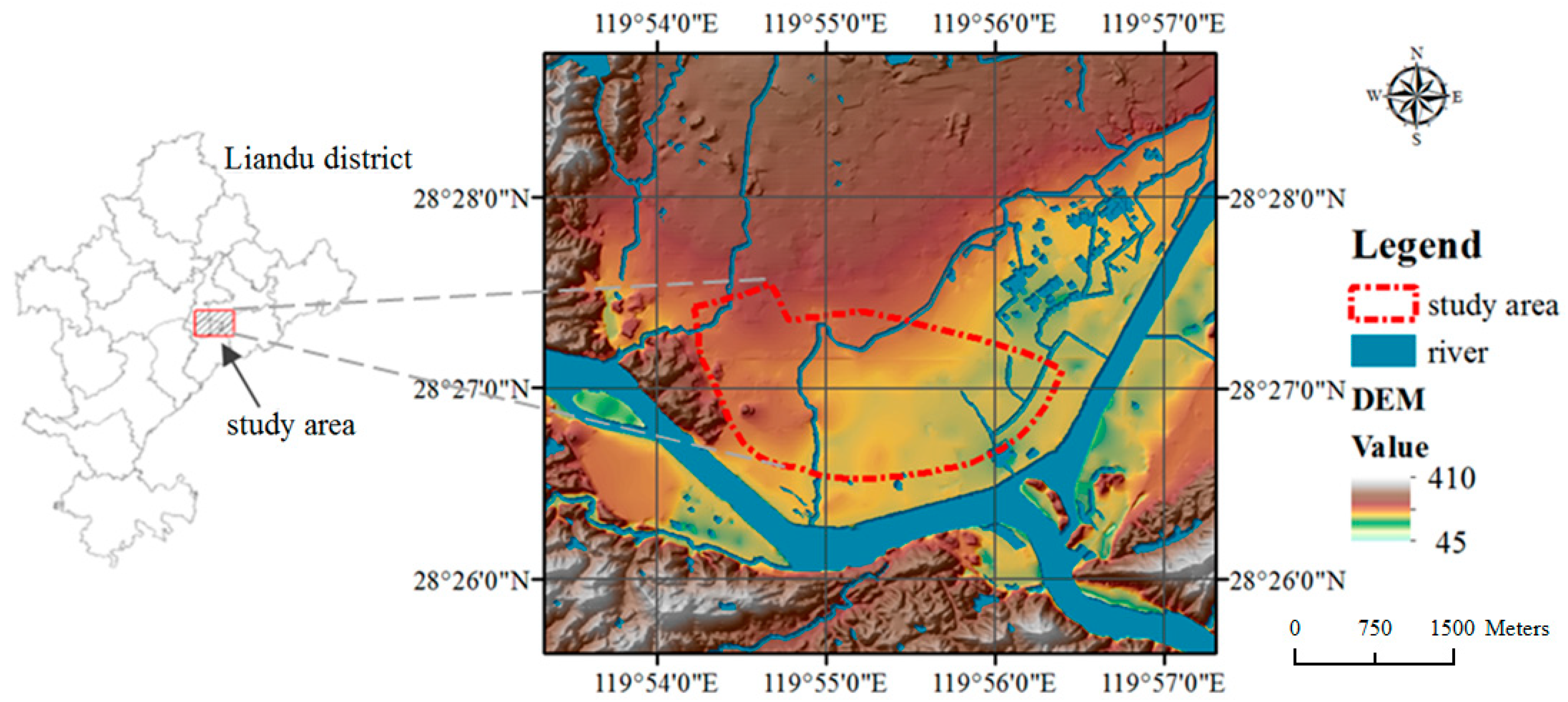
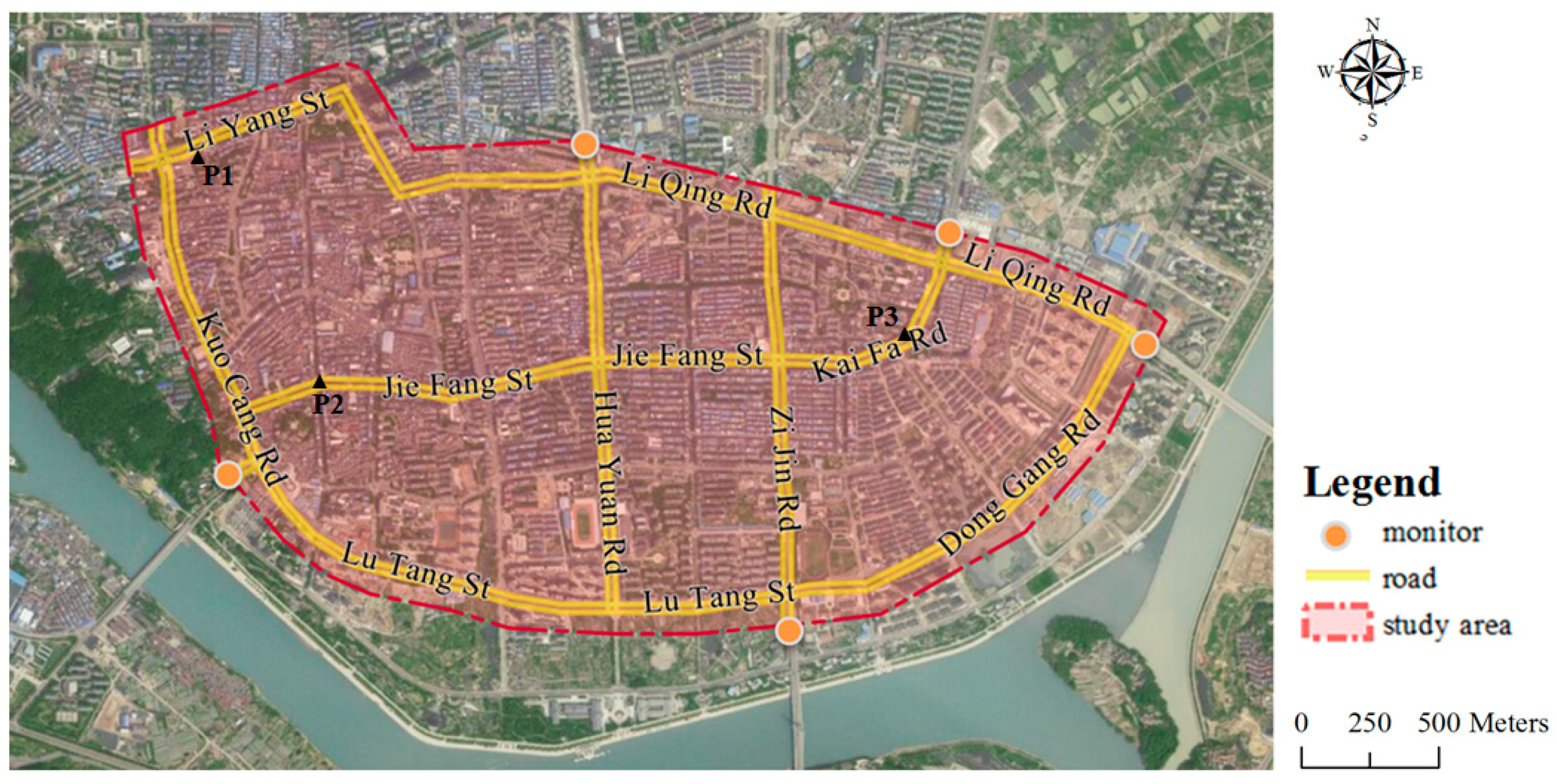
2.1. Study Area
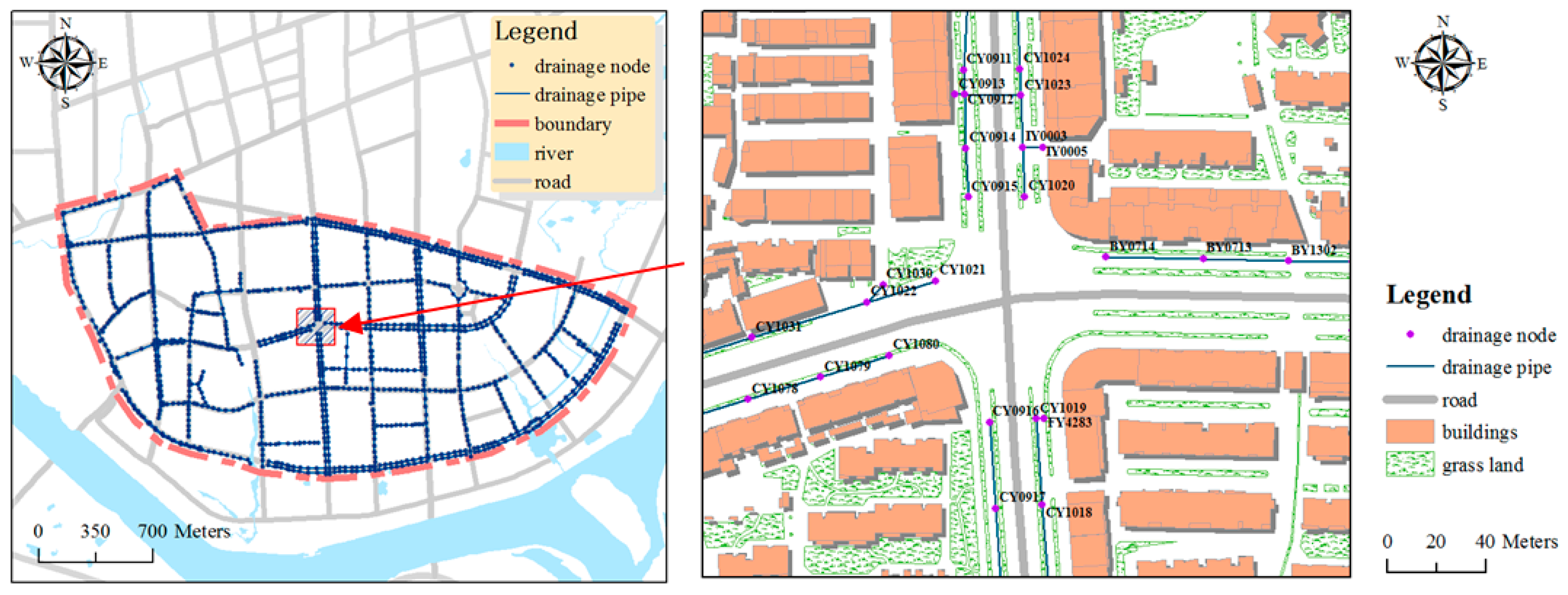
2.2. SWMM–TELEMAC2D Integrated Model
2.3. Agent-Based Model
3. Methodology
3.1. Environmental Simulation of Traffic and Flooding
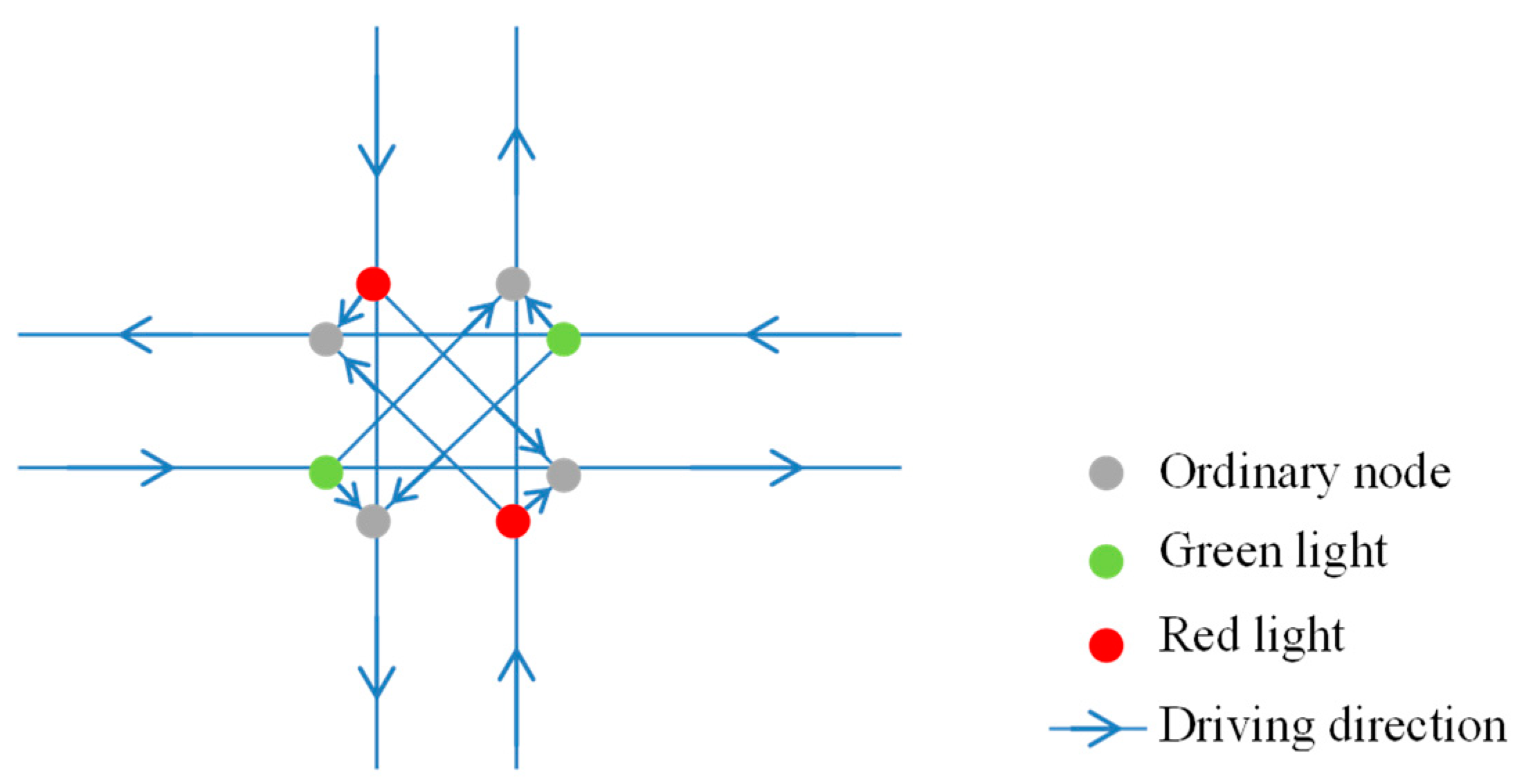
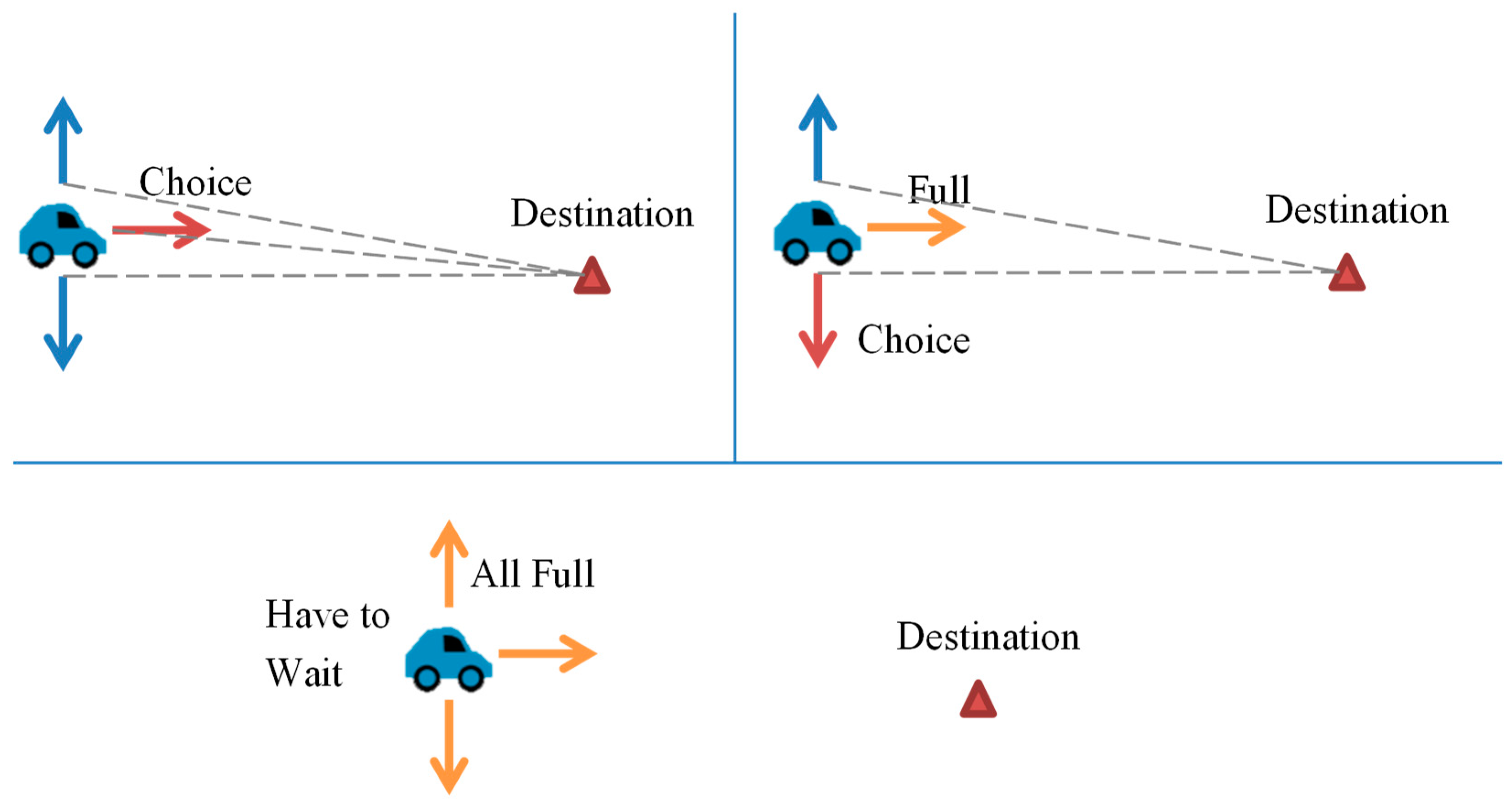
3.2. Agent Behavior in Regular Driving Pattern
3.3. Scenario Design
4. Results
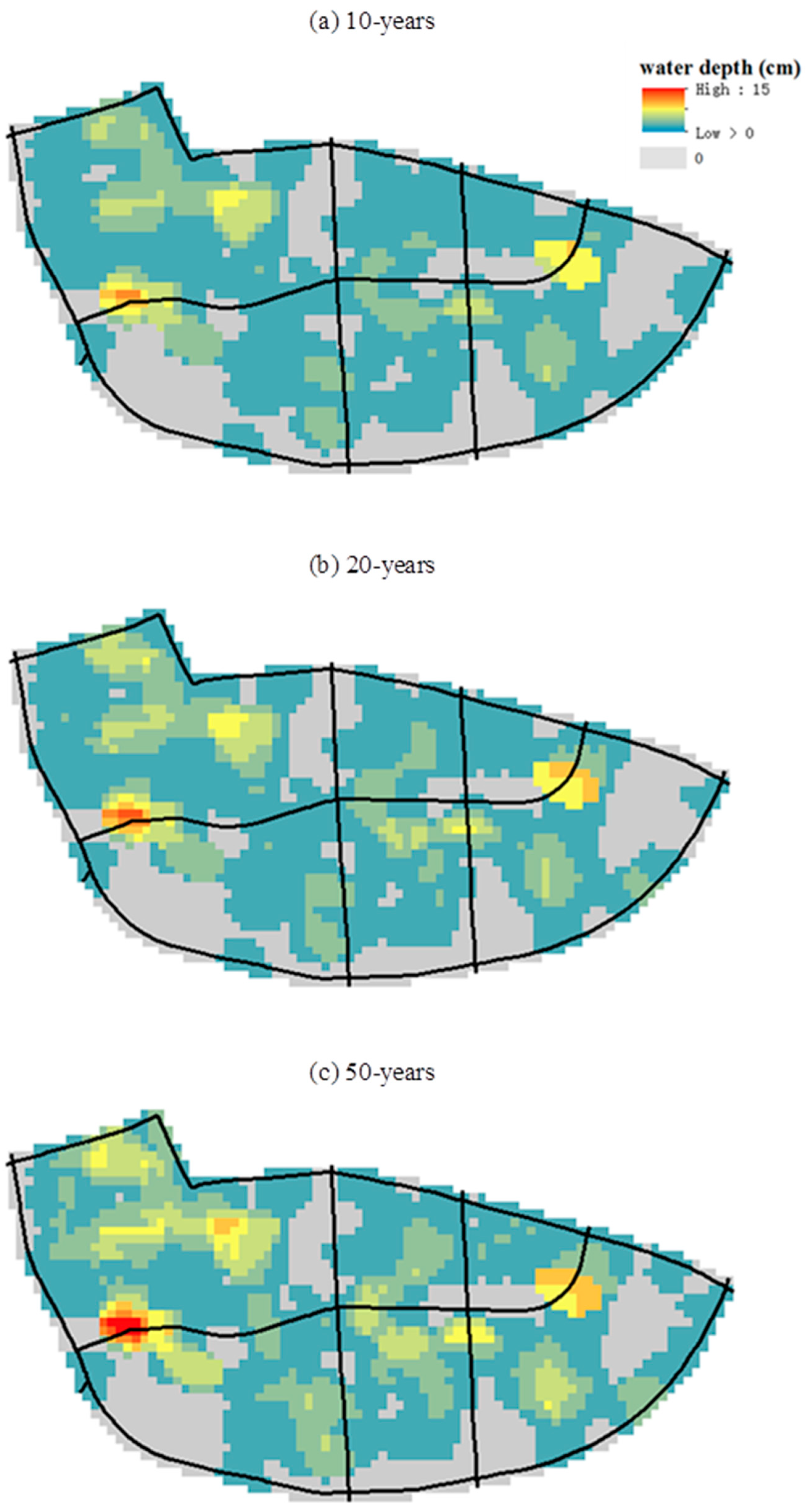
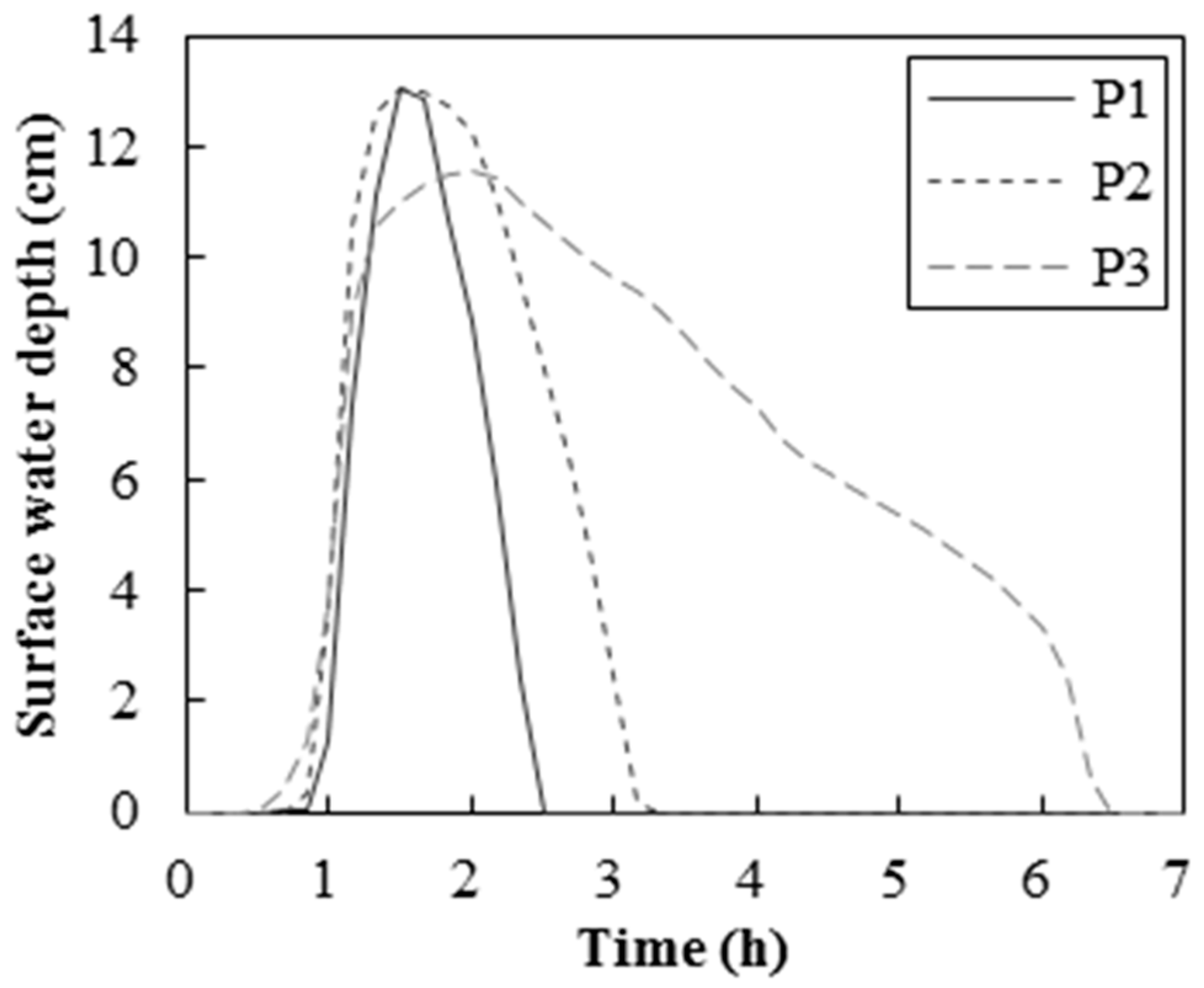
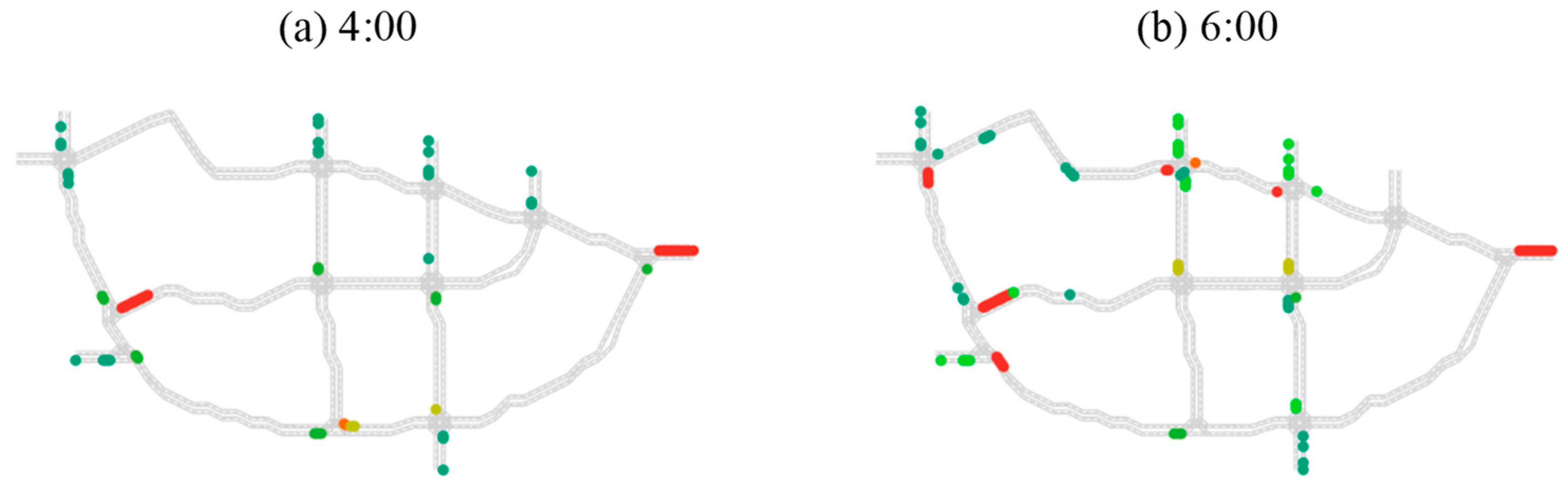
4.1. Results of Flooding Simulation
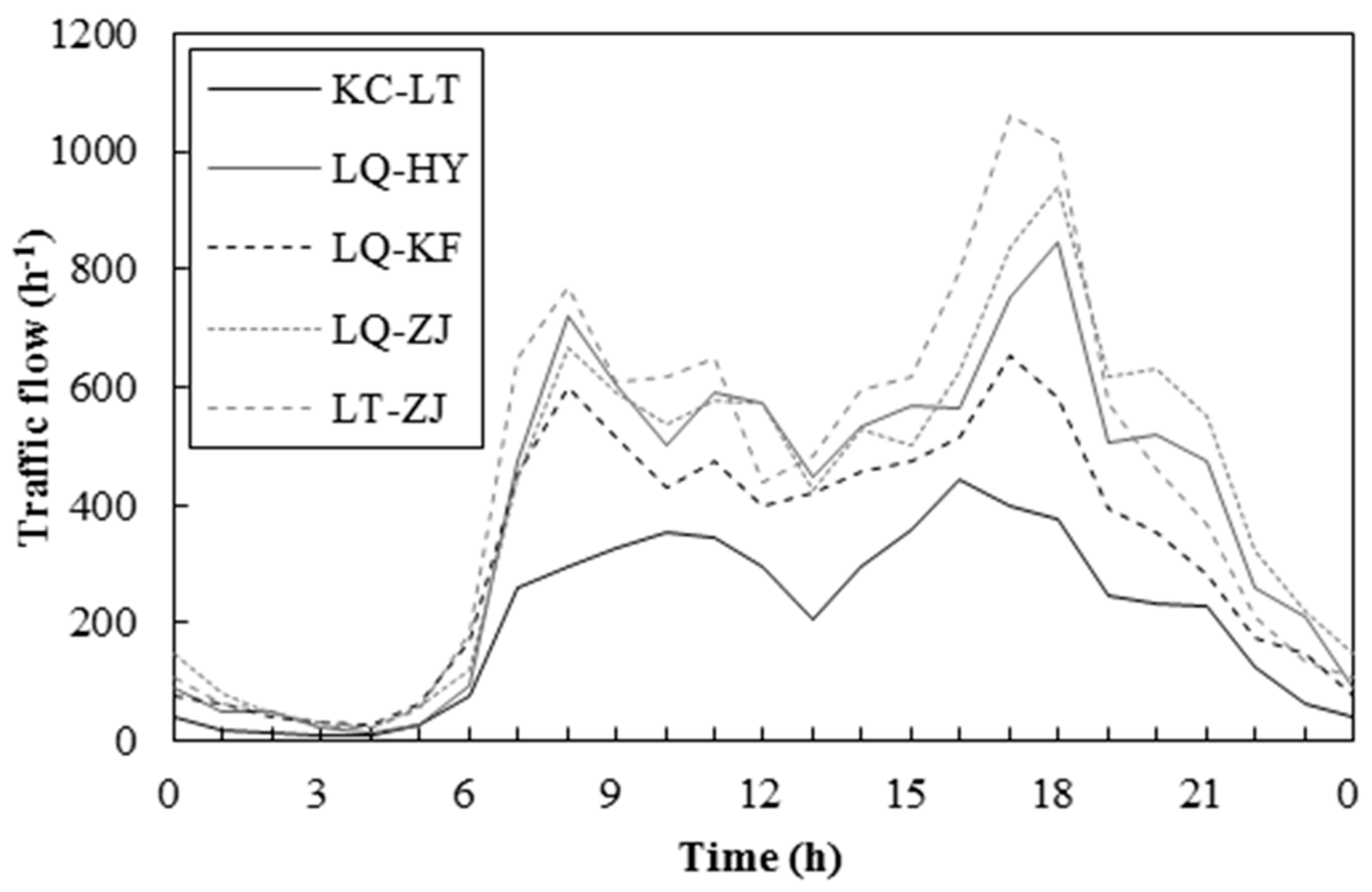
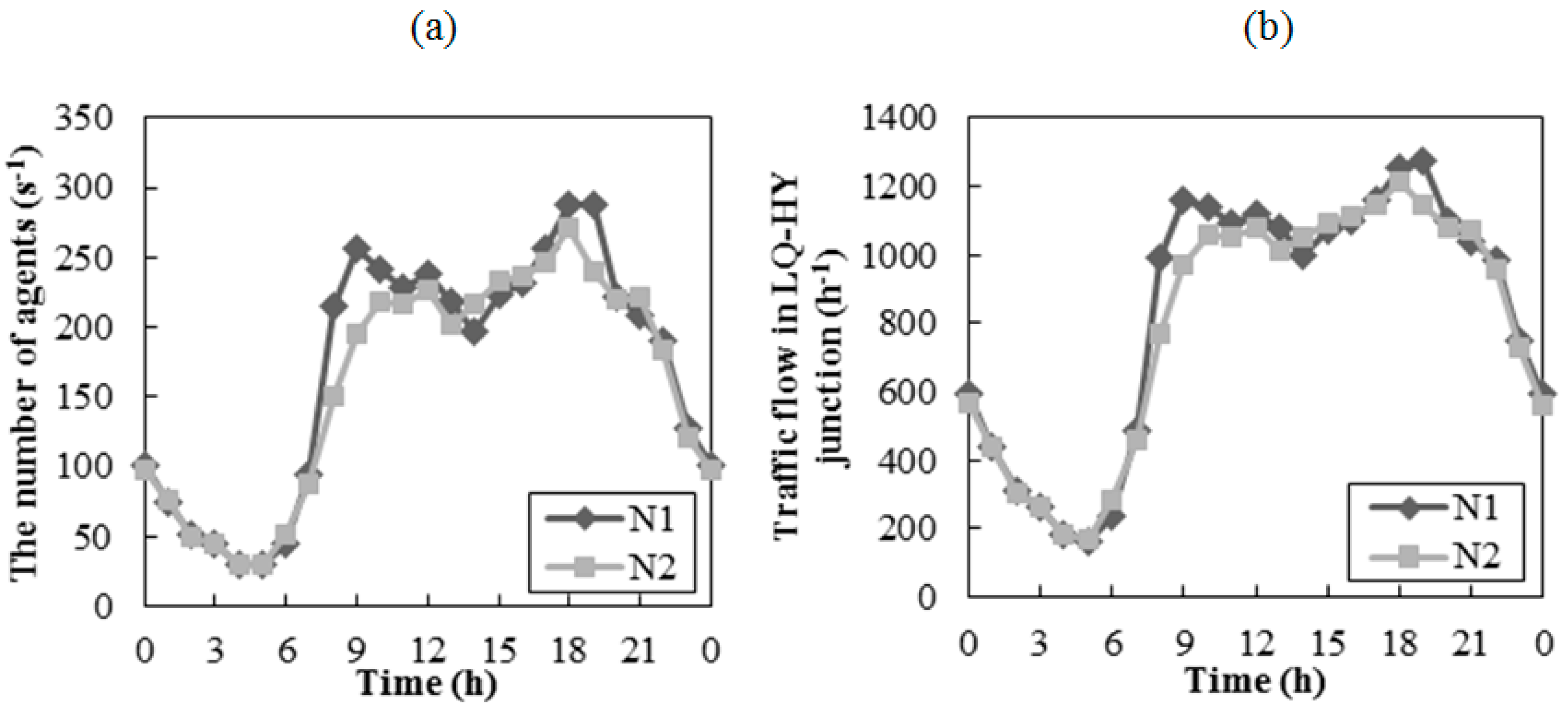
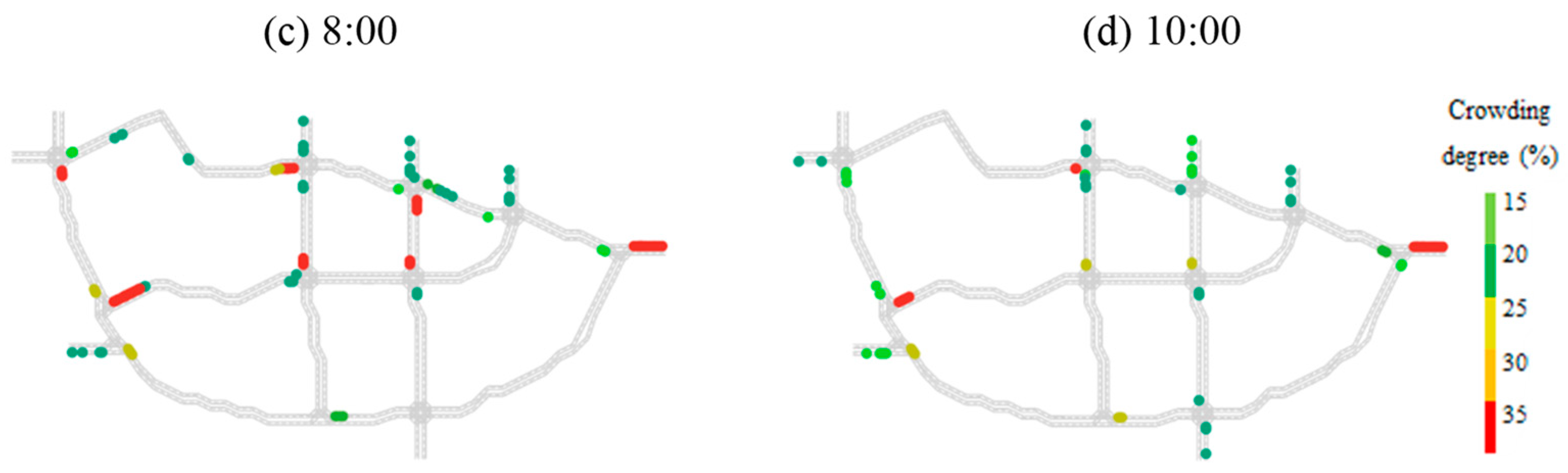
4.2. Results of Traffic Simulation
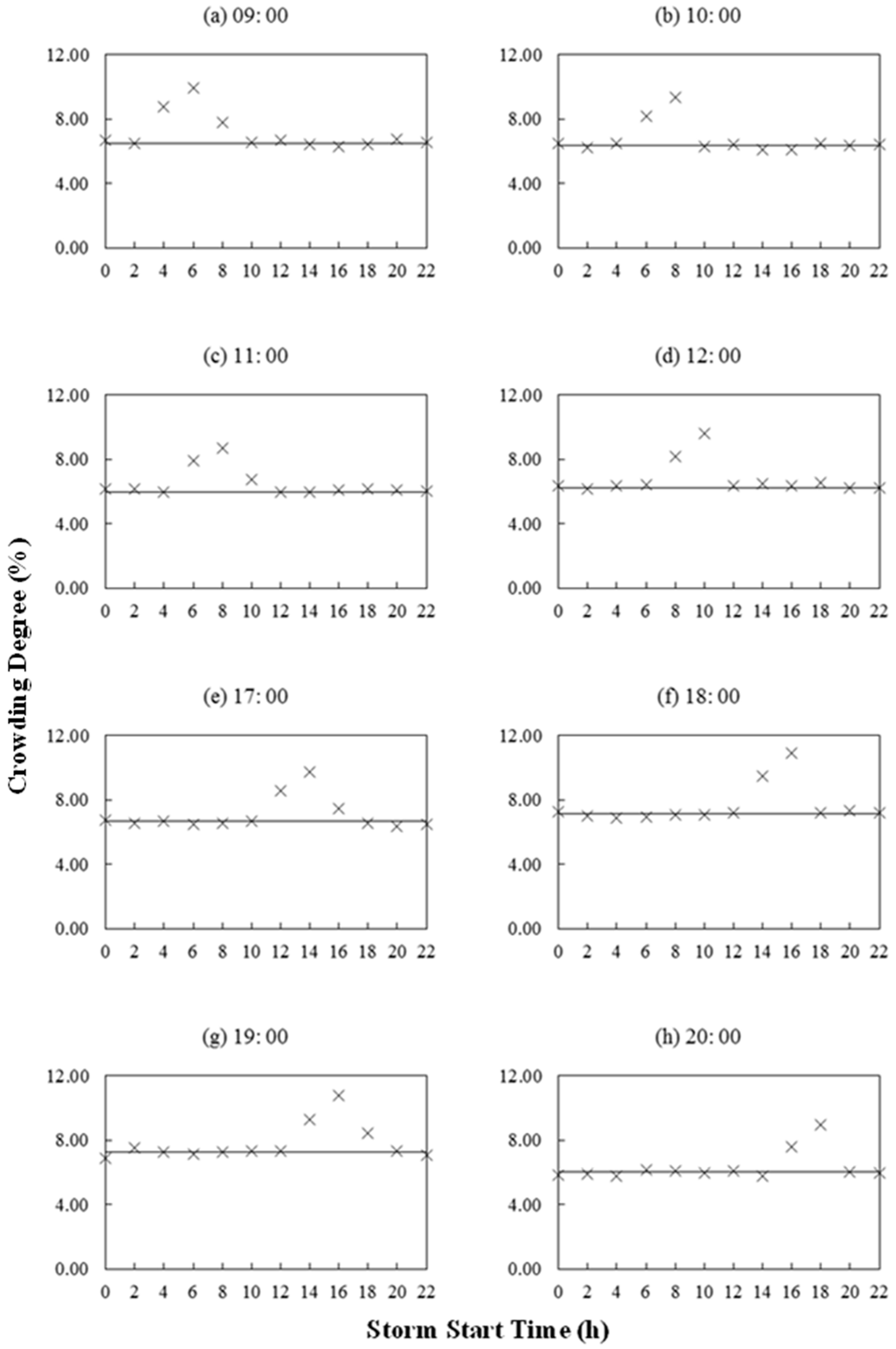
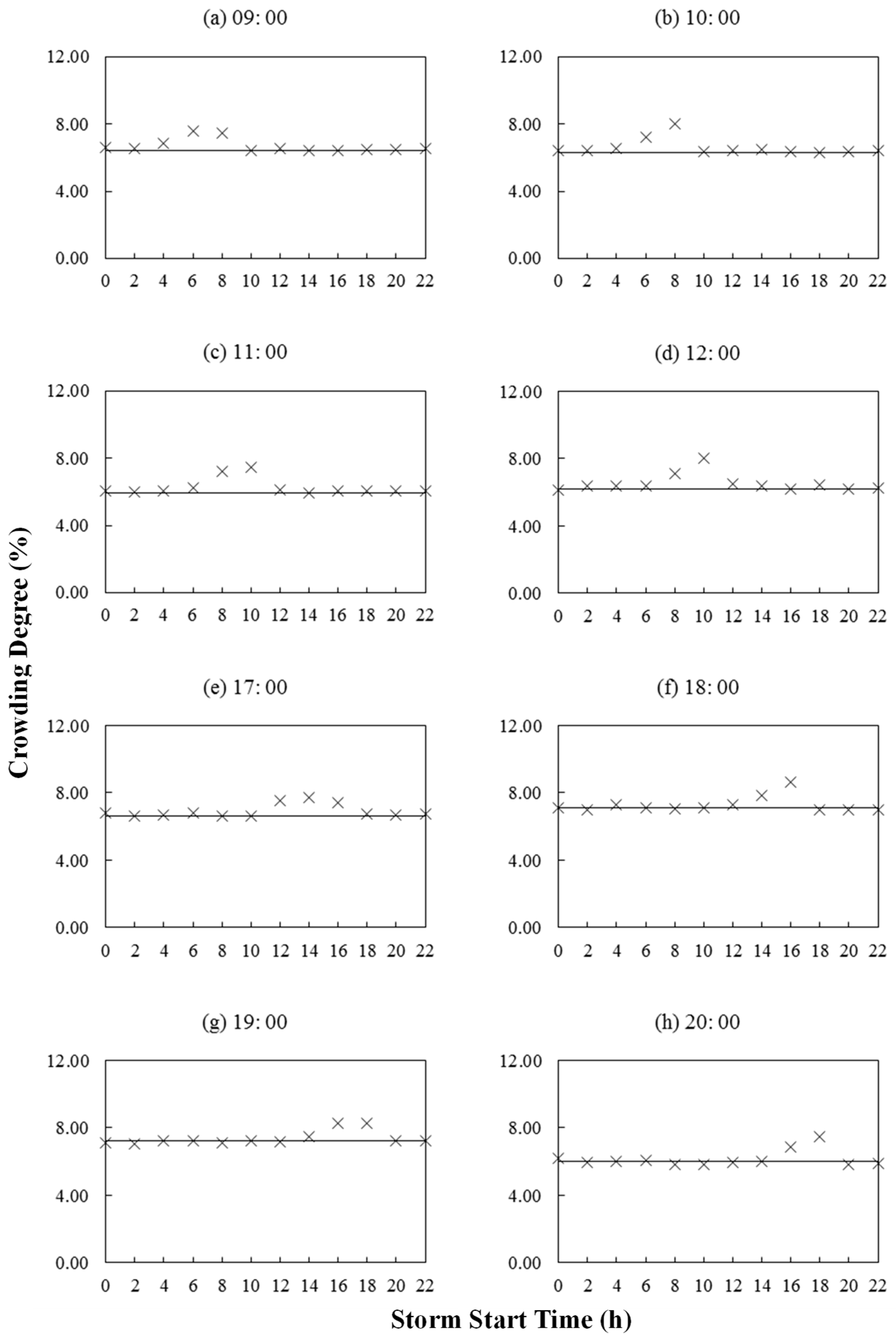
4.3. Crowding Degree under Different Storm Start Times
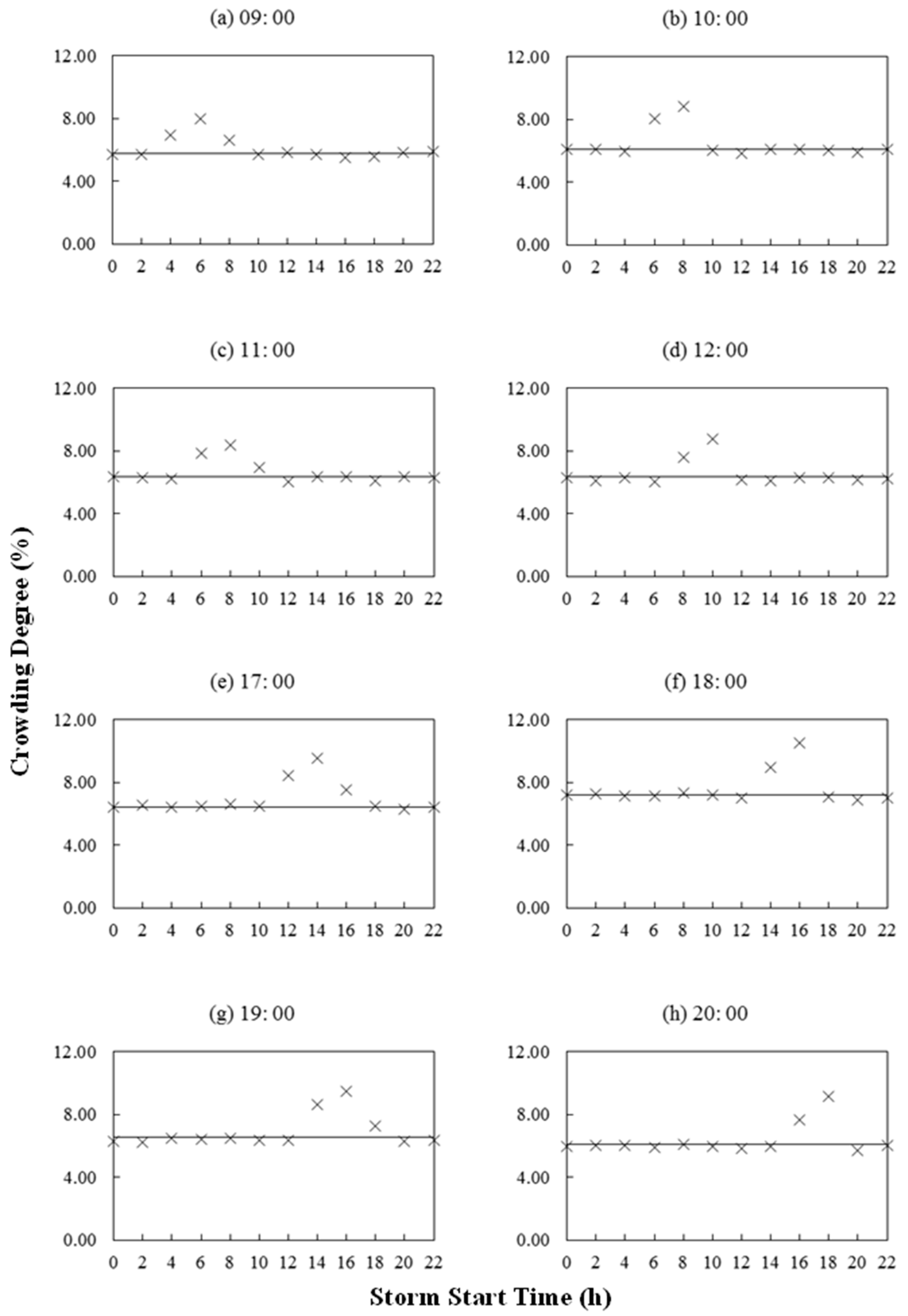
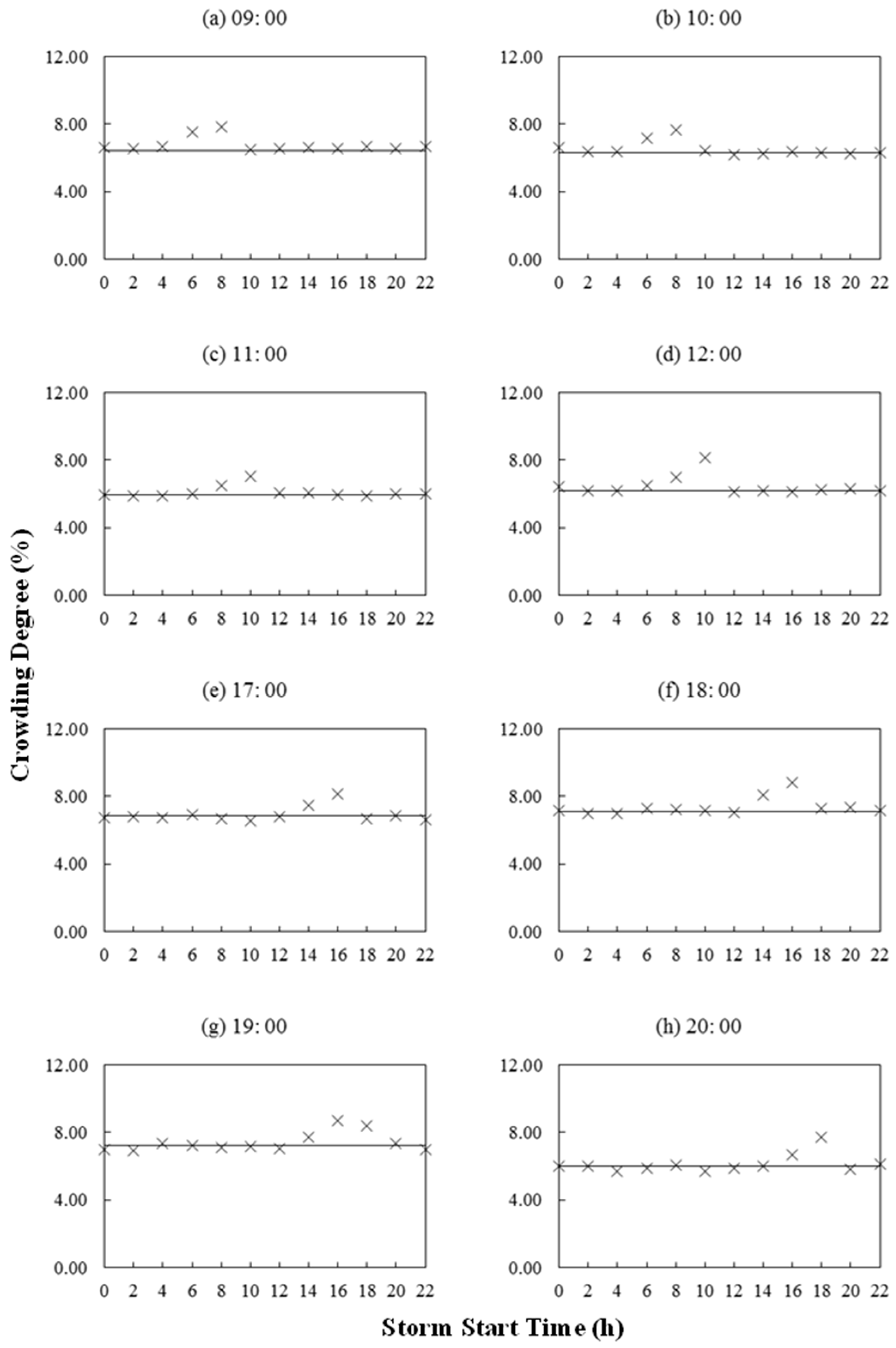
4.4. Crowding Degree under Different Rainfall Intensity
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Tang, T.Q.; Caccetta, L.; Wu, Y.H.; Huang, H.J.; Yang, X.B. A macro model for traffic flow on road networks with varying road conditions. J. Adv. Transp. 2014, 48, 304–317. [Google Scholar] [CrossRef]
- Greenshields, B.D. A study of traffic capacity. Highw. Res. Board Proc. 1935, 14, 448–477. [Google Scholar]
- Sugihakim, R.; Alatas, H. Application of a Boltzmann-entropy-like concept in an agent-based multilane traffic model. Phys. Lett. A 2016, 380, 147–155. [Google Scholar] [CrossRef]
- Manley, E.; Cheng, T.; Penn, A.; Emmonds, A. A framework for simulating large-scale complex urban traffic dynamics through hybrid agent-based modelling. Comput. Environ. Urban Syst. 2014, 44, 27–36. [Google Scholar] [CrossRef]
- Maroto, J.; Delso, E.; Felez, J.; Cabanellas, J.M. Real-Time Traffic Simulation with a Microscopic Model. IEEE Trans. Intell. Transp. Syst. 2006, 7, 513–527. [Google Scholar] [CrossRef]
- Newell, G.F. A simplified car-following theory: A lower order model. Transp. Res. Part B 2002, 36, 195–205. [Google Scholar] [CrossRef]
- Ward, J.A. Car-following models: Fifty years of linear stability analysis—A mathematical perspective. Transp. Plan. Technol. 2011, 34, 3–18. [Google Scholar]
- Yu, Y.; Kamel, A.E.; Gong, G.; Li, F. Multi-agent based modeling and simulation of microscopic traffic in virtual reality system. Simul. Model. Pract. Theory 2014, 45, 62–79. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Palma, A.D.; Kanaroglou, P. Dynamic Model of Peak Period Traffic Congestion with Elastic Arrival Rates. Transp. Sci. 1986, 20, 164–181. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Maksimović, C.; Ivetić, M.; Savić, D. SIPSON—Simulation of interaction between pipe flow and surface overland flow in networks. Water Sci. Technol. 2005, 52, 275–283. [Google Scholar] [PubMed]
- Leandro, J. Advanced Modelling of Flooding in Urban Areas: Integrated 1D/1D and 1D/2D Models; University of Exeter: Exeter, UK, 2008. [Google Scholar]
- DHI. MIKE-STORM. 2007. Available online: http://www.dhigroup.com/ (accessed on 16 September 2017).
- DHI. MIKE-21. 2007. Available online: http://www.dhigroup.com/ (accessed on 16 September 2017).
- Carr, R.S.; Smith, G.P. Linking of 2D and Pipe hydraulic models at fine spatial scales. Water Pract. Technol. 2007, 2. [Google Scholar] [CrossRef]
- Chen, S.H.; Djordjević, S.; Leandro, J.; Savić, D. The Urban Inundation Model with Bidirectional Flow Interaction between 2D Overland Surface and 1D Sewer Networks. 2007. Available online: http://hdl.handle.net/10871/16020 (accessed on 6 October 2017).
- Spry, R.; Zhang, S. Modelling of Drainage Systems and Overland Flowpaths at Catchment Scales. In Book of Proceedings: 7th International Conference on Urban Drainage Modelling and the 4th International Conference on Water Sensitive Urban Design; Monash University: Melbourne, Australia, 2006. [Google Scholar]
- Ata, R. Telemac2d User Manual, version 7.2. 2017. Available online: http://wiki.opentelemac.org/ (accessed on 29 September 2017).
- Cools, M.; Moons, E.; Wets, G. Assessing the Impact of Weather on Traffic Intensity. Weather Clim. Soc. 2008, 2, 60–68. [Google Scholar] [CrossRef]
- Lin, Q.; Nixon, W.A. Effects of Adverse Weather on Traffic Crashes: Systematic Review and Meta-Analysis. Transp. Res. Record J. Transp. Res. Board 2008, 2055, 139–146. [Google Scholar]
- Goodwin, L.C. Weather Impacts on Arterial Traffic Flow; Road Weather Management Program: Washington, DC, USA, 2002.
- Billot, R.; Faouzi, N.E.E.; Vuyst, F.D. Multilevel Assessment of the Impact of Rain on Drivers’ Behavior. Transp. Res. Record J. Transp. Res. Board 2009, 2107, 134–142. [Google Scholar] [CrossRef]
- Su, B.; Huang, H.; Li, Y. Integrated simulation method for waterlogging and traffic congestion under urban rainstorms. Nat. Hazards 2016, 81, 23–40. [Google Scholar] [CrossRef]
- Leandro, J.; Martins, R. A methodology for linking 2D overland flow models with the sewer network model SWMM 5.1 based on dynamic link libraries. Water Sci. Technol. 2016, 73, 3017–3026. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.S.; Leandro, J.; Djordjeviä, S. Modelling sewer discharge via displacement of manhole covers during flood events using 1D/2D SIPSON/P-DWave dual drainage simulations. Urban Water J. 2015, 13, 830–840. [Google Scholar] [CrossRef]
- Rossman, L.E. SWMM 5.0 Manual; EPA/600/R-05/040; CHI Press: Cincinnati, OH, USA, 2008. [Google Scholar]
- Fernandes, E.H.; Dyer, K.R.; Niencheski, L.F.H. Calibration and Validation of the TELEMAC-2D Model to the Patos Lagoon (Brazil). J. Coast. Res. 2001, 34, 470–488. [Google Scholar]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47, 1837–1840. [Google Scholar] [CrossRef]
- Wilensky, U.; Stroup, W. Netlogo User Manual; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1999. [Google Scholar]
- Nasello, C.; Tucciarelli, T. Dual Multilevel Urban Drainage Model. J. Hydraul. Eng. 2005, 131, 748–754. [Google Scholar] [CrossRef]
- Reuschel, A. Vehicle movements in a platoon. Oesterreichisches Ingenieur-Archir 1950, 4, 193–215. [Google Scholar]
- Chandler, R.E.; Herman, R.; Montroll, E.W. Traffic Dynamics: Studies in Car Following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef]
- Kometani, E.; Sasaki, T. Dynamic Behaviour of Traffic with a Nonlinear Spacing-Speed Relationship; Elsevier Publishing Co.: Amsterdam, The Netherlands, 1959. [Google Scholar]
- Krauß, S. Microscopic Modeling of Traffic Flow: Investigation of Collision Free Vehicle Dynamics; University of Cologne: Cologne, Germany, 1998. [Google Scholar]
- Chowdhury, D.; Santen, L.; Schadschneider, A. Statistical physics of vehicular traffic and some related systems. Phys. Rep. 2000, 329, 199–329. [Google Scholar] [CrossRef]
- Oluwaseyi, O.S.; Adebola, O.; Edwin, K.A.; Okoko, E.E.; Stephen, M. Examination of On-Street Parking and Traffic Congestion Problems in Lokoja. J. Rheumatol. 2014, 27, 1336–1342. [Google Scholar]
- Cen, G.; Shen, J.; Fan, R. Research on Rainfall Pattern of Urban Design Storm. Adv. Water Sci. 1998, 9, 41–46. [Google Scholar]
| Attribute | Water Depth (cm) | |||
|---|---|---|---|---|
| 0 | 10 | 20 | 30 | |
| Male, Age < 35 | 50.9 | 38.4 | 27.6 | 16.9 |
| Male, Age ≥ 35 | 49.8 | 37.1 | 26.0 | 14.9 |
| Female, Age < 35 | 50.8 | 37.5 | 26.0 | 14.4 |
| Female, Age ≥ 35 | 49.8 | 36.1 | 24.3 | 12.5 |
| Scenarios | Rainfall Return Periods | Weekdays or Weekends |
|---|---|---|
| RA1 | 10 years | Weekdays |
| RA2 | 10 years | Weekends |
| RB1 | 20 years | Weekdays |
| RB2 | 20 years | Weekends |
| RC1 | 50 years | Weekdays |
| RC2 | 50 years | Weekends |
| N1 | No rain | Weekdays |
| N2 | No rain | Weekends |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Dai, Q.; Deng, Y.; Zhang, A.; Zhang, Y.; Zhang, S. Indirect Damage of Urban Flooding: Investigation of Flood-Induced Traffic Congestion Using Dynamic Modeling. Water 2018, 10, 622. https://doi.org/10.3390/w10050622
Zhu J, Dai Q, Deng Y, Zhang A, Zhang Y, Zhang S. Indirect Damage of Urban Flooding: Investigation of Flood-Induced Traffic Congestion Using Dynamic Modeling. Water. 2018; 10(5):622. https://doi.org/10.3390/w10050622
Chicago/Turabian StyleZhu, Jingxuan, Qiang Dai, Yinghui Deng, Aorui Zhang, Yingzhe Zhang, and Shuliang Zhang. 2018. "Indirect Damage of Urban Flooding: Investigation of Flood-Induced Traffic Congestion Using Dynamic Modeling" Water 10, no. 5: 622. https://doi.org/10.3390/w10050622
APA StyleZhu, J., Dai, Q., Deng, Y., Zhang, A., Zhang, Y., & Zhang, S. (2018). Indirect Damage of Urban Flooding: Investigation of Flood-Induced Traffic Congestion Using Dynamic Modeling. Water, 10(5), 622. https://doi.org/10.3390/w10050622





