Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption
Abstract
:1. Introduction
2. Materials and Methods
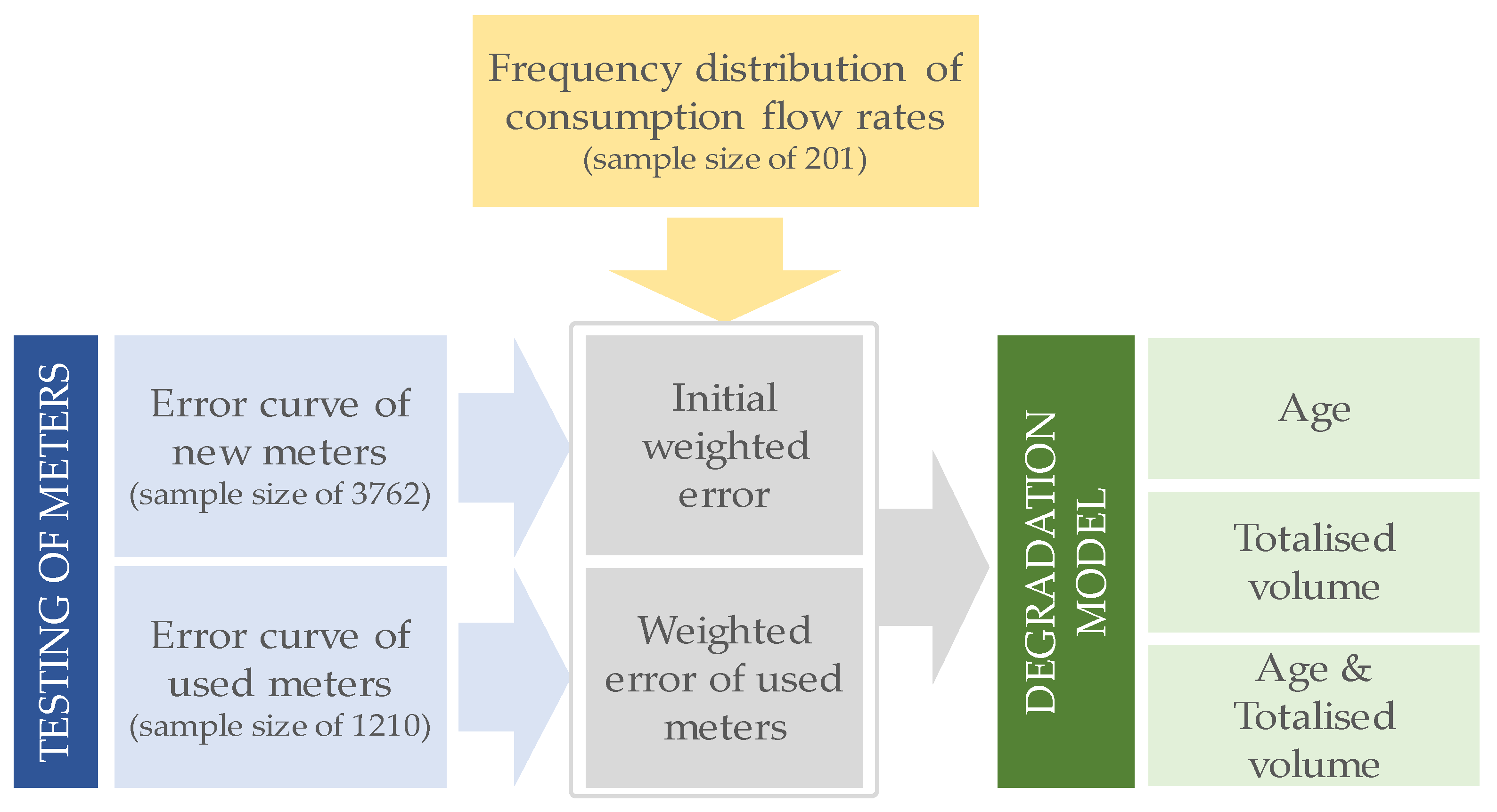
2.1. General Approach
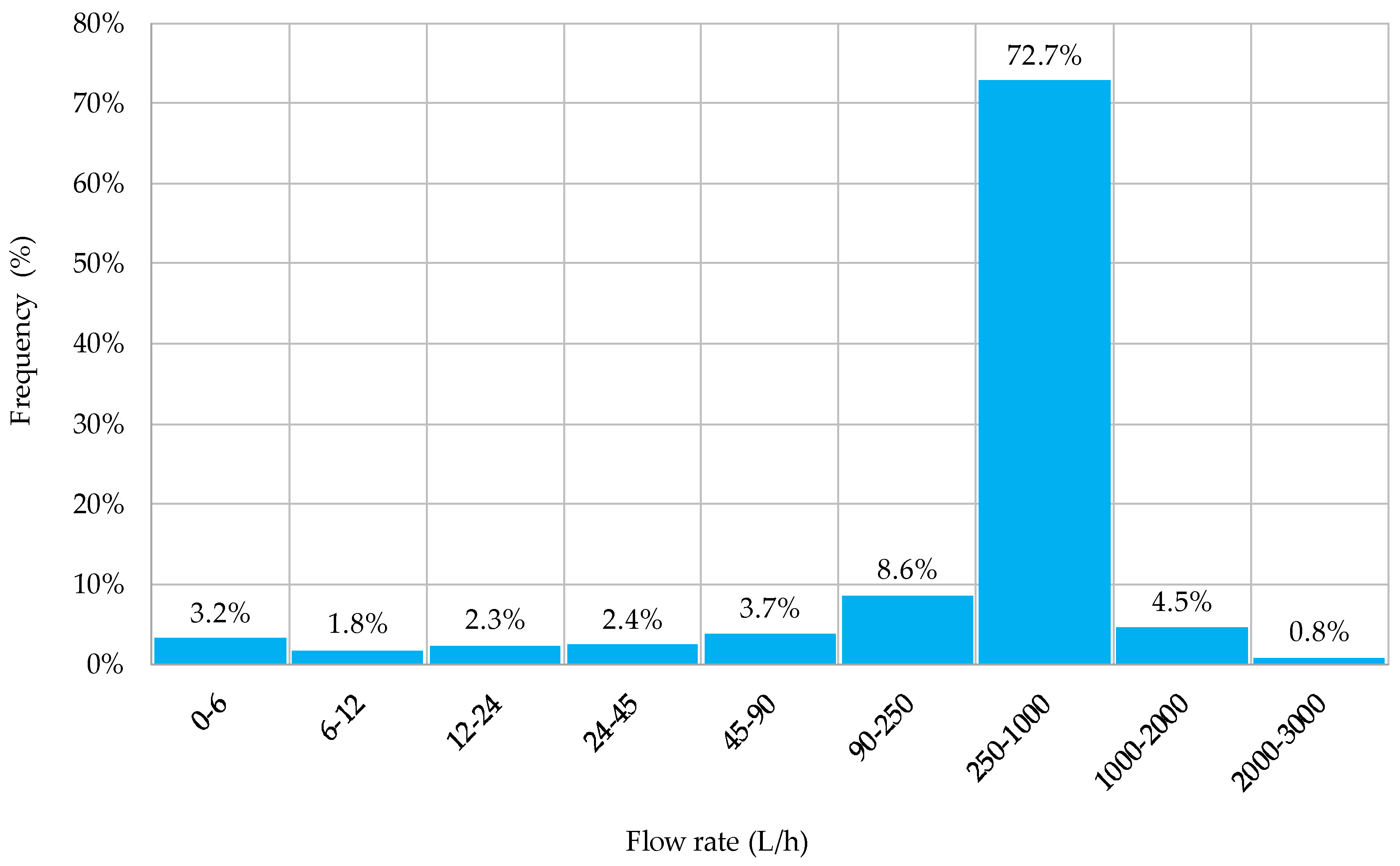
2.2. Water Consumption Flow Rates of Domestic Users
2.3. Testing Equipment and Procedures
2.4. Water Meter Sample Description
3. Results and Discussion
3.1. Error Curves
3.1.1. Error Curves of New Meters
3.1.2. Error Curves of Ageing Meters
3.2. Weighted Error of New Meters
3.3. Degradation Rate of the Weighted Error
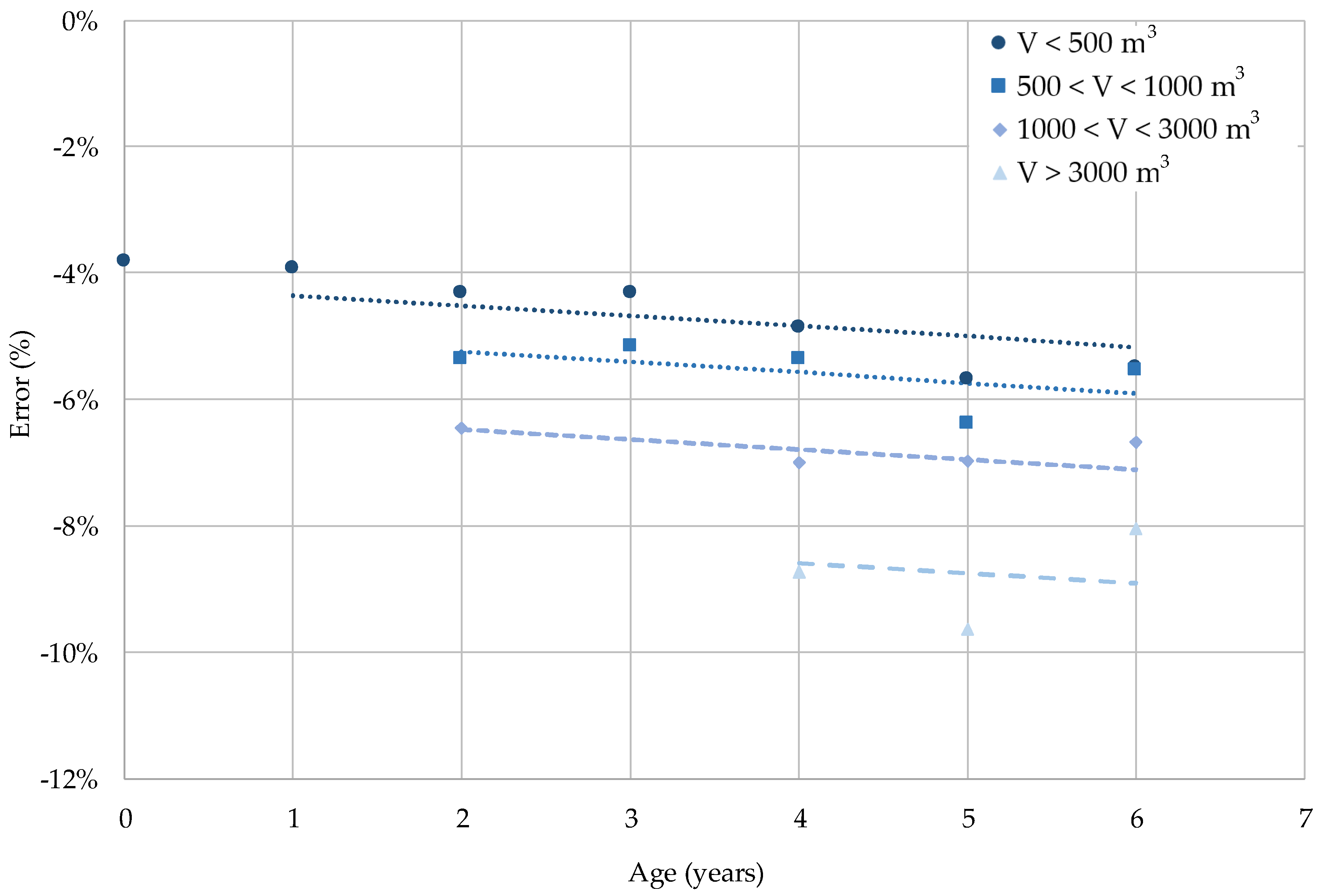
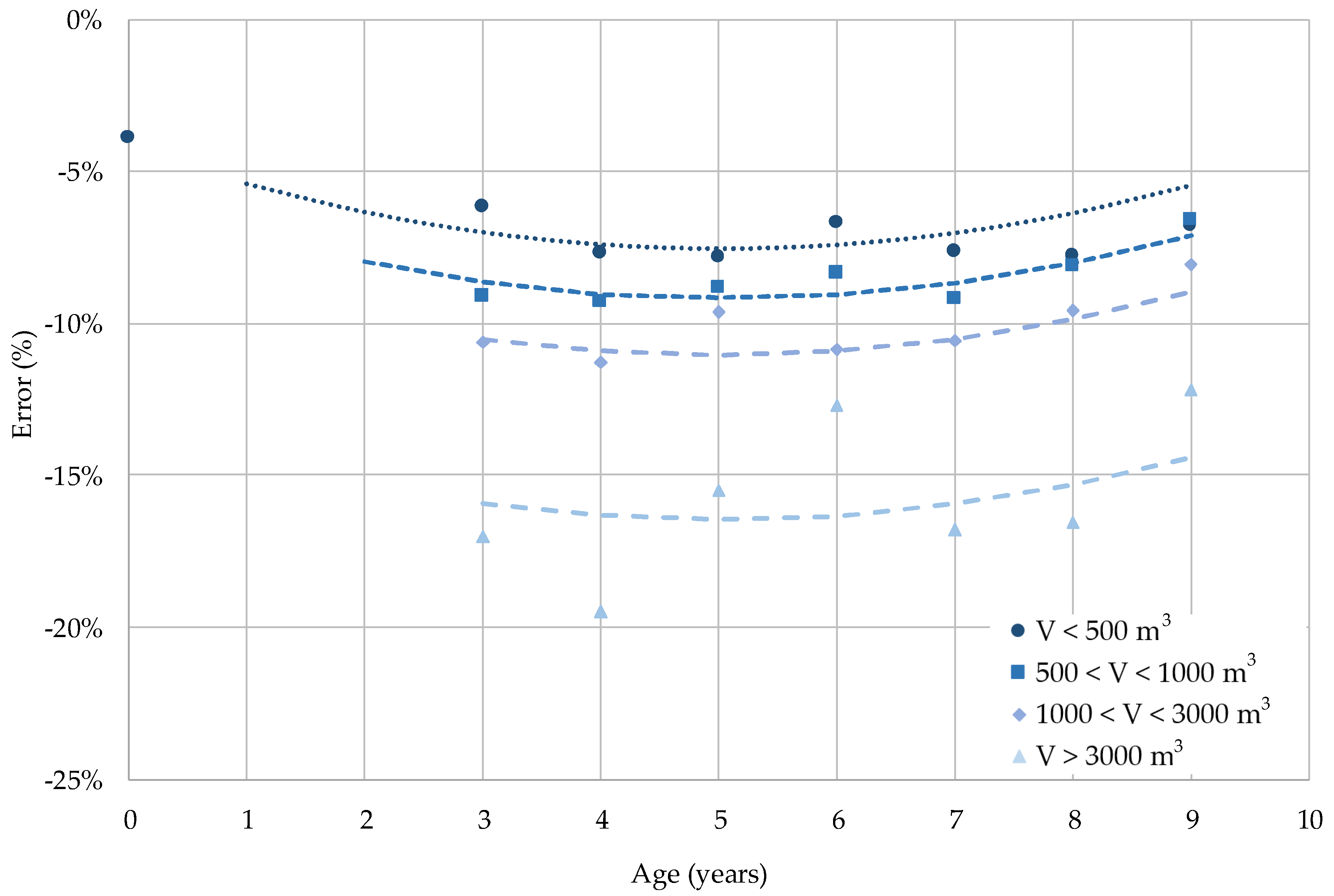
3.3.1. Degradation Rate with Age
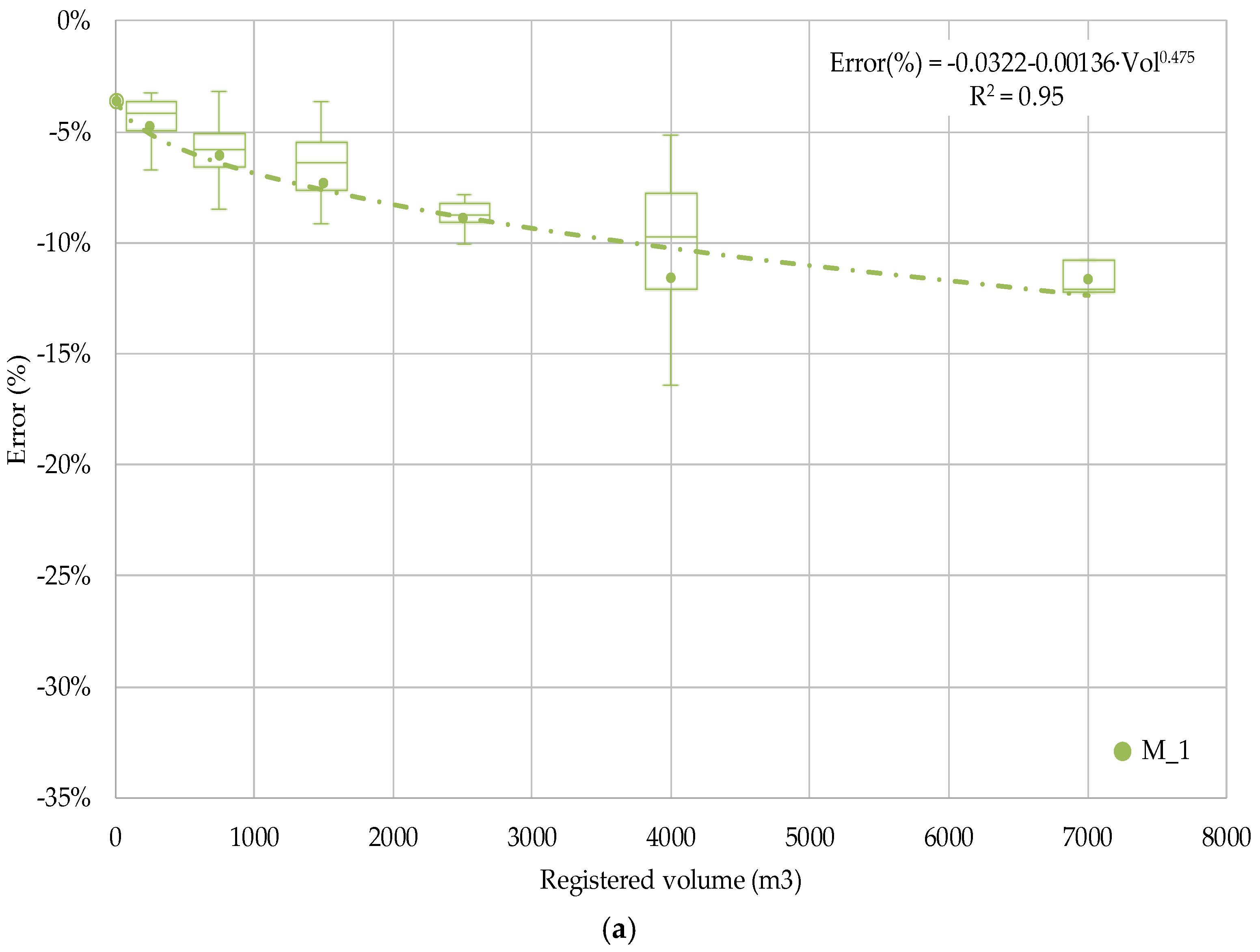
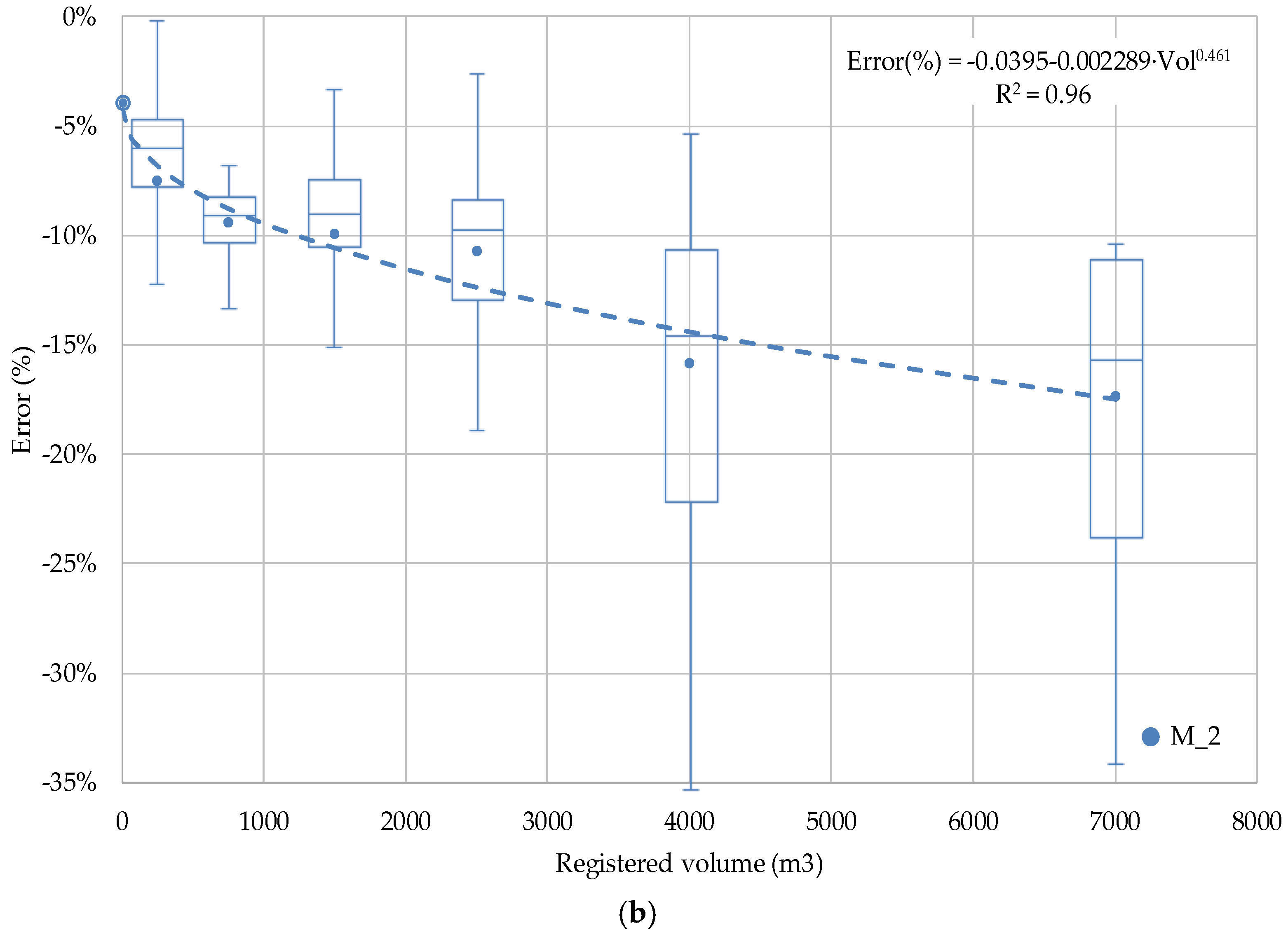
3.3.2. Degradation Rate with Totalised Volume
3.3.3. Degradation Rate with Age and Totalised Volume
3.3.4. Mathematical Degradation Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lambert, A.O. International report: Water losses management and techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar]
- International Organization for Standardization (ISO). ISO 4064-1:2014—Water Meters for Cold Potable Water and Hot Water—Part 1: Metrological and Technical Requirements; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- International Organization for Standardization (ISO). ISO 4064-3:2014—Water Meters for Cold Potable Water and Hot Water—Part 3: Test Report Format; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Mbabazi, D.; Banadda, N.; Kiggundu, N.; Mutikanga, H.; Babu, M. Determination of domestic water meter accuracy degradation rates in Uganda. J. Water Supply Res. Technol. 2015, 64, 486–492. [Google Scholar] [CrossRef]
- Mutikanga, H.; Sharma, S.; Vairavamoorthy, K. Investigating water meter performance in developing countries: A case study of Kampala, Uganda. Water SA 2011, 37, 567–574. [Google Scholar] [CrossRef]
- Fontanazza, C.M.; Freni, G.; la Loggia, G.; Notaro, V.; Puleo, V. A composite indicator for water meter replacement in an urban distribution network. Urban Water J. 2012, 9, 419–428. [Google Scholar] [CrossRef]
- Fontanazza, C.M.; Notaro, V.; Puleo, V.; Freni, G. The apparent losses due to metering errors: A proactive approach to predict losses and schedule maintenance. Urban Water J. 2015, 12, 229–239. [Google Scholar] [CrossRef]
- Mutikanga, H.E.; Sharma, S.; Vairavamoorthy, K. Water loss management in developing countries: Challenges and prospects. Am. Water Works Assoc. J. 2009, 101, 57–68. [Google Scholar] [CrossRef]
- Mutikanga, H.E.; Sharma, S.K.; Vairavamoorthy, K. Assessment of apparent losses in urban water systems. Water Environ. J. 2011, 25, 327–335. [Google Scholar] [CrossRef]
- Díaz, I.; Flores, J. Precisión de la Medida de los Consumos Individuales de Agua en la Comunidad de Madrid; Canal de Isabel II: Madrid, Spain, 2010; ISBN 978-8-49-364453-6. [Google Scholar]
- Larraona, G.S.; Rivas, A.; Ramos, J.C. Computational modeling and simulation of a single-jet water meter. J. Fluids Eng. 2008, 130, 051102. [Google Scholar] [CrossRef]
- Zhen, W.; Tao, Z. Computational study of the tangential type turbine flowmeter. Flow Meas. Instrum. 2008, 19, 233–239. [Google Scholar] [CrossRef]
- Rizzo, A.; Cilia, J. Quantifying Meter Under-Registration Caused by the Ball Valves of Roof Tanks (for Indirect Plumbing Systems). In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005; pp. 1–12. [Google Scholar]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; La Loggia, G.; Notaro, V.; Puleo, V. A mathematical model to evaluate apparent losses due to meter under-registration in intermittent water distribution networks. Water Sci. Technol. Water Supply 2013, 13, 914–923. [Google Scholar] [CrossRef]
- Criminisi, A.; Fontanazza, C.M.; Freni, G.; La Loggia, G. Evaluation of the apparent losses caused by water meter under-registration in intermittent water supply. Water Sci. Technol. 2009, 60, 2373–2382. [Google Scholar] [CrossRef] [PubMed]
- Arregui, F.J.; Cabrera, E.J.; Cobacho, R. Integrated Water Meter Management; IWA Publishing: London, UK, 2006. [Google Scholar]
- Bowen, P.T.; Harp, J.F.; Entwistle, J.M., Jr.; Shoeleh, M. Evaluating Residential Water Meter Performance; Prepared for AWWA Research Foundation—Version details—Trove; AWWA Research Foundation and American Water Works Association: Denver, CO, USA, 1991.
- Richards, G.L.; Johnson, M.C.; Barfuss, S.L. Apparent losses caused by water meter inaccuracies at ultralow flows. J. Am. Water Works Assoc. 2010, 102, 123–132. [Google Scholar] [CrossRef]
- Stoker, D.M.; Barfuss, S.L.; Johnson, M.C. Flow measurement accuracies of in-service residential water meters. J. Am. Water Works Assoc. 2012, 104, 33. [Google Scholar] [CrossRef]
- Pasanisi, A. Aide à la Décision Dans la Gestion des Parcs de Compteurs d’eau Potable. Ph.D. Thesis, ENGREF (AgroParisTech), Paris, France, 2004. [Google Scholar]
- Shields, D.J.; Barfuss, S.L.; Johnson, M.C. Revenue recovery through meter replacement. J. Am. Water Works Assoc. 2012, 104, 69–70. [Google Scholar] [CrossRef]
- Arregui, F.J.; Cobacho, R.; Cabrera, E., Jr.; Espert, V. A graphical method to calculate the optimum replacement period of water meters. J. Water Resour. Plan. Manag. 2011, 137, 143–146. [Google Scholar] [CrossRef]
- Yee, M.D. Economic analysis for replacing residential meters. Am. Water Works Assoc. J. 1999, 91, 72–77. [Google Scholar] [CrossRef]
- Davis, S. Residential Water Meter Replacement Economics. In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005; pp. 1–10. [Google Scholar]
- Allender, H. Determining the economical optimum life of residential water meters. Water Eng. Manag. 1996, 143, 20–24. [Google Scholar]
- Gavara, F. Estudio del Comportamiento Metrológico de los Contadores en Abastecimientos de Agua. Optimización de su Gestión para la Reducción de las Pérdidas Comerciales. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2015. [Google Scholar]
- Arregui, F.J. Meter Error Calculator. Available online: http://personales.upv.es/farregui/ (accessed on 21 March 2018).
- Hill, C.; Davis, S.E. Economics of Domestic Residential Water Meter Replacement Based on Cumulative Volume. In Proceedings of the AWWA Annual Conference, San Francisco, CA, USA, 12–16 June 2005. [Google Scholar]
- Bowen, P.T.; Association, A.W.W.; Foundation, A.R. Residential Water Use Patterns; The Foundation and American Water Works Association: Denver, CO, USA, 1993. [Google Scholar]
- Deoreo, W.B.; Mayer, P.W.; Dziegielewski, B.; Kiefer, J.C. Residential End Uses of Water, Version 2 (4309B); The Water Research Foundation: Denver, CO, USA, 2016. [Google Scholar]
- Beal, C.; Stewart, R.A. South East Queensland Residential End Use Study: Final Report. Urban Water Security Research Alliance Technical Report No. 47, City East, Australia. 2011. Available online: http://www.urbanwateralliance.org.au/publications/UWSRA-tr47.pdf (accessed on 7 May 2018).
- Arregui, F.J.; Cabrera, E.; Cobacho, R.; García-Serra, J. Reducing Apparent Losses Caused by Meters Inaccuracies. Technology 2006, 1, wpt2006093. [Google Scholar] [CrossRef]
- Spitzer, D.W. Flow Measurement: Practical Guides for Measurement and Control; The Instrumentation, Systems, and Automation Society (ISA): Research Triangle Park, NC, USA, 2001. [Google Scholar]
- Paton, R. Calibration and Standards in Flow. In Handbook of Measuring System Design; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- ISO. ISO 4064-2:2014—Water Meters for Cold Potable Water and Hot Water—Part 2: Test Methods; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Arregui, F.J.; Martinez, B.; Soriano, J.; Parra, J.C. Tools for Improving Decision Making in Water Meter Management. In Proceedings of the 5th IWA Water Loss Reduction Specialist Conference, Cape Town, South Africa, 26–30 April 2009; pp. 225–232. [Google Scholar]
- Barfuss, S.L. Flow Meter Accuracy. In Proceedings of the American Council for an Energy-Efficient Economy (ACEEE), Berkeley, CA, USA, 10–12 May 2011. [Google Scholar]
- Barfuss, S.L.; Johnson, M.C.; Neilsen, M.A. Accuracy of In-Service Water Meters at Low and High Flow Rates; Water Research Foundation: Denver, CO, USA, 2011. [Google Scholar]
- Sumrak, M.L.; Johnson, M.C.; Barfuss, S.L. Comparing Low Flow Accuracy of Mechanical and Electronic Meters. J. Am. Water Works Assoc. 2016, 108, E327–E334. [Google Scholar] [CrossRef]
- ISO 4064-1:1993—Measurement of Water Flow in Closed Conduits—Meters for Cold Potable Water—Part 1: Specifications. Available online: https://www.iso.org/standard/9772.html (accessed on 20 March 2018).
- Arregui, F.J.; Palau, C.V.; Gascón, L.; Peris, O. Evaluating domestic water meter accuracy. A case study. Pumps Electromech. Devices Syst. Appl. Urban Water Manag. 2003, 1, 343. [Google Scholar]
- Diaz, I.; Flores, J. Accurate Assessment of under Metering in MADRID Water Supply. In Proceedings of the 5th IWA Specialist Conference on Efficient Use and Management of Urban Water (Efficient 2009), Sydney, Australia, 25–28 October 2009. [Google Scholar]
- Male, J.W.; Noss, R.R.; Moore, I.C. Identifying and Reducing Losses in Water Distribution Systems; Noyes Publications: Park Ridge, NJ, USA, 1985. [Google Scholar]
- Mukheibir, P.; Stewart, R.A.; Giurco, D.P.; Halloran, K.O. Understanding non-registration in domestic water meters: Implications for meter replacement strategies. Water J. 2012, 39, 95–100. [Google Scholar]
- Szilveszter, S.; Beltran, R.; Fuentes, A. Performance analysis of the domestic water meter park in water supply network of Ibarra, Ecuador. Urban Water J. 2017, 14, 85–96. [Google Scholar] [CrossRef]
- Arregui, F.J.; Cabrera, E.J.; Cobacho, R.; García-Serra, J. Key factors affecting water meter accuracy. In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005; pp. 1–10. [Google Scholar]

| Meter Type | Tech. | Class | Standard | Qpermanent (m3/h) | Length (mm) | Sample—New Meters | Sample—Used Meters |
|---|---|---|---|---|---|---|---|
| M_1 | Single-Jet | B | ISO4064:1993 | 1.5 | 115 | 1068 | 406 |
| M_2 | Single-Jet | B | ISO4064:1993 | 1.5 | 115 | 2694 | 804 |
| Meter | Sample Size | Qstart (L/h) | 15 L/h | 30 L/h | 60 L/h | 120 L/h | 600 L/h | 1500 L/h | 3000 L/h |
|---|---|---|---|---|---|---|---|---|---|
| M_1 | 1068 | 5.3 | −8.9 | 1.5 | 1.3 | 1.5 | 1.5 | 1.3 | −3.6 |
| M_2 | 2694 | 5.3 | −8.4 | 3.3 | 2.7 | 0.9 | 0.8 | 0.6 | 0.5 |
| ISO 4064 Error tolerance | N/A | ±5 | ±5 | ±2 | ±2 | ±2 | ±2 | ||
| Age (years) | Meters Tested | 15 L/h | 30 L/h | 60 L/h | 120 L/h | 750 L/h | 1500 L/h | 2750 L/h |
|---|---|---|---|---|---|---|---|---|
| 1–2 | 79 | −12.2 | 0.9 | 1.3 | 1.4 | 1.1 | 0.9 | 0.3 |
| 3–4 | 96 | −22.3 | −0.8 | 1.3 | 1.2 | 0.9 | 0.7 | 0.1 |
| 5–6 | 114 | −49.1 | −14.3 | −4.7 | −1.2 | −0.4 | 0.3 | −0.2 |
| >7 | 117 | −35.2 | −8.1 | −2.5 | −0.7 | −0.3 | −0.4 | −1.0 |
| Age (years) | Meters Tested | 15 L/h | 30 L/h | 60 L/h | 120 L/h | 750 L/h | 1500 L/h | 2750 L/h |
|---|---|---|---|---|---|---|---|---|
| 3 | 62 | −73.0 | −24.5 | −8.1 | −4.5 | −1.8 | −1.7 | −1.4 |
| 4 | 37 | −87.5 | −39.4 | −10.6 | −4.3 | −1.7 | −1.5 | −1.2 |
| 5 | 161 | −53.0 | −22.0 | −8.8 | −4.7 | −2.3 | −2.1 | −1.4 |
| 6 | 16 | −68.9 | −16.3 | −4.6 | −3.1 | −1.7 | −1.2 | −6.4 |
| 7 | 133 | −53.4 | −17.8 | −8.0 | −6.0 | −3.8 | −3.4 | −5.4 |
| 8–9 | 162 | −61.2 | −20.8 | −9.0 | −5.5 | −2.7 | −2.3 | −6.2 |
| >10 | 233 | −55.7 | −14.6 | −5.4 | −3.8 | −2.1 | −4.0 | −7.4 |
| Total. Volume (m3) | Meters Tested | 15 L/h | 30 L/h | 60 L/h | 120 L/h | 750 L/h | 1500 L/h | 2750 L/h |
|---|---|---|---|---|---|---|---|---|
| 0–500 | 206 | −19.3 | −0.5 | 0.7 | 1.3 | 0.8 | 0.7 | 0.1 |
| 500–1000 | 89 | −30.6 | −5.4 | −0.7 | 0.5 | 0.4 | 0.1 | −0.4 |
| 1000–2000 | 67 | −40.8 | −10.2 | −3.3 | −0.5 | 0.1 | −0.2 | −0.7 |
| 2000–3000 | 23 | −69.9 | −14.7 | −2.5 | −0.9 | −0.3 | −0.4 | −0.8 |
| 3000–5000 | 14 | −87.7 | −44.7 | −19.0 | −15.2 | −7.7 | 0.2 | −1.0 |
| >5000 | 7 | −77.1 | −42.8 | −21.3 | −5.9 | −1.3 | −1.4 | −1.4 |
| Total. Volume (m3) | Meters Tested | 15 L/h | 30 L/h | 60 L/h | 120 L/h | 750 L/h | 1500 L/h | 2750 L/h |
|---|---|---|---|---|---|---|---|---|
| 0–500 | 201 | −35.8 | −11.4 | −4.6 | −2.6 | 0.3 | 0.4 | −0.7 |
| 500–1000 | 190 | −50.8 | −10.9 | −4.1 | −2.5 | −1.6 | −1.2 | −1.2 |
| 1000–2000 | 262 | −64.3 | −15.9 | −4.0 | −2.5 | −1.4 | −2.2 | −3.9 |
| 2000–3000 | 106 | −82.8 | −32.1 | −10.4 | −4.5 | −1.7 | −2.9 | −8.0 |
| 3000–5000 | 35 | −94.4 | −65.8 | −26.9 | −12.6 | −3.9 | −3.7 | −20.5 |
| >5000 | 10 | −97.6 | −62.7 | −29.4 | −15.0 | −4.5 | −11.8 | −21.4 |
| Parameter | Meter M_1 | Meter M_2 |
|---|---|---|
| E0 | −3.49 | −3.91 |
| A | −0.152 | −1.313 |
| B | −0.00149 | 0.131 |
| C | −0.0174 | −0.00291 |
| D | 0.657 | 0.959 |
| Model | Meter M_1 Totalised Volume | Meter M_2 Totalised Volume | ||||
|---|---|---|---|---|---|---|
| 900 m3 | 1500 m3 | 4500 m3 | 900 m3 | 1500 m3 | 4500 m3 | |
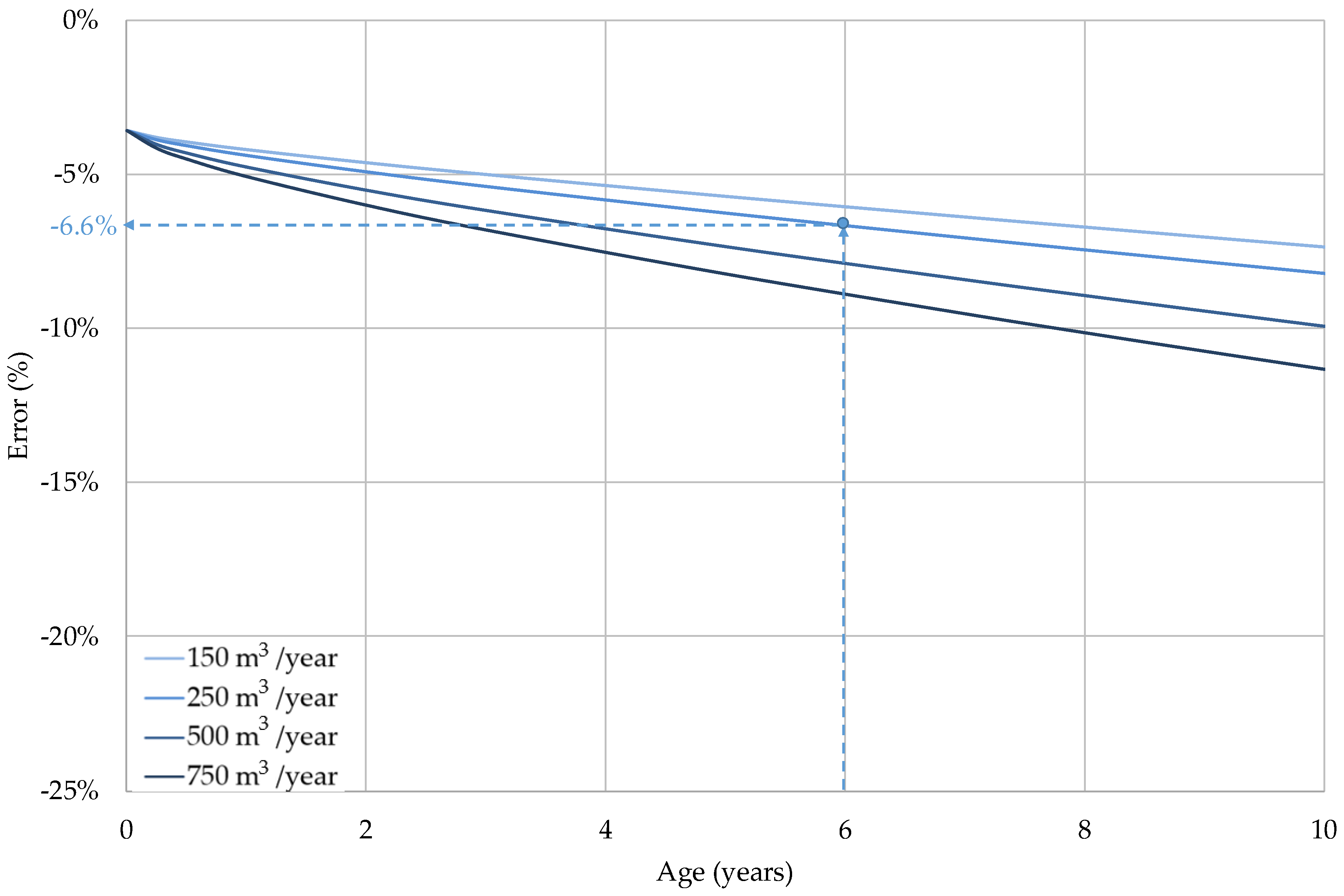
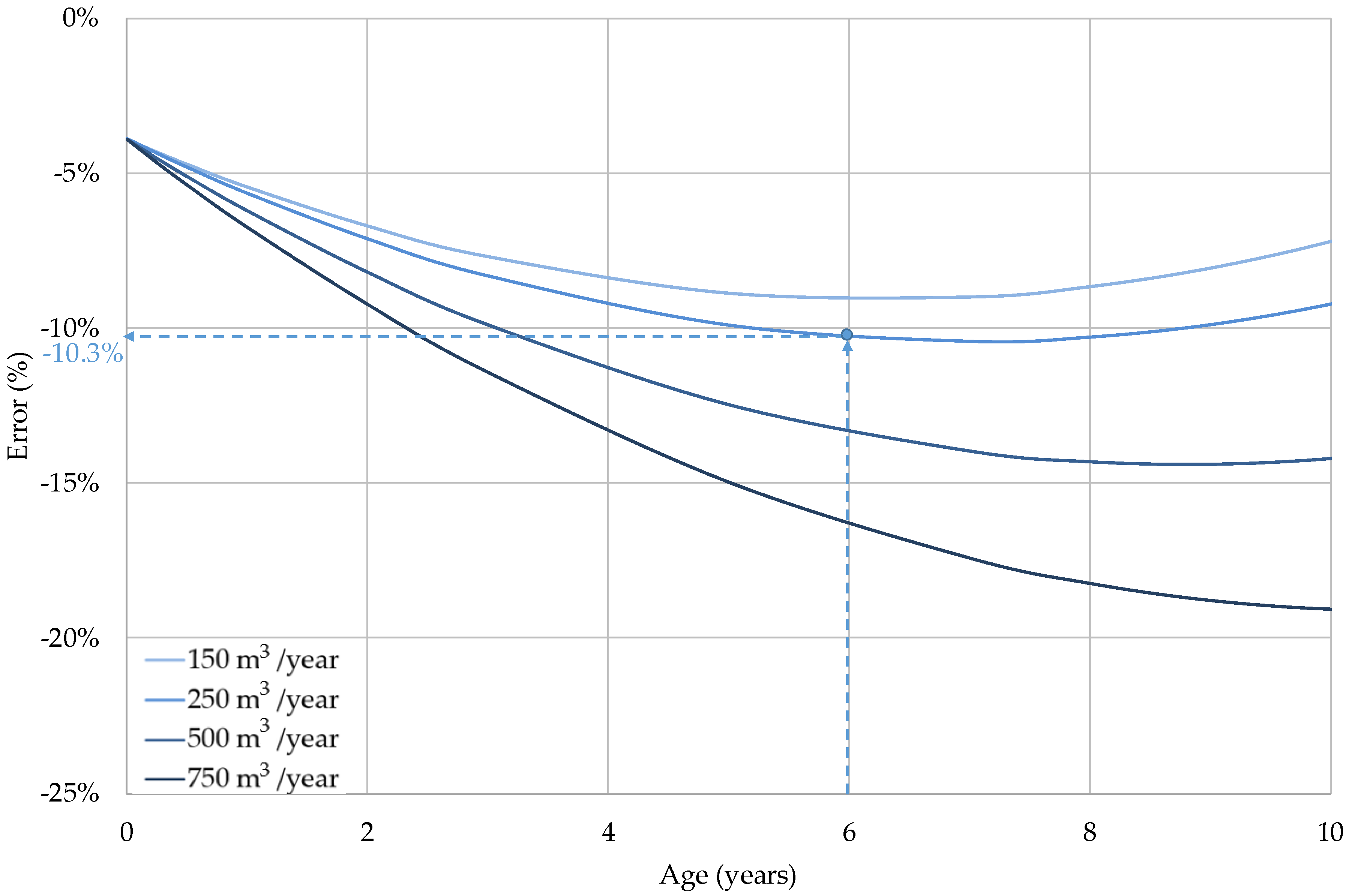
| Age | −6.4% | −6.4% | −6.4% | −9.3% | −9.3% | −9.3% |
| Totalised volume | −6.7% | −7.6% | −10.6% | −9.2% | −10.6% | −15.0% |
| Age & Totalised volume | −6.0% | −6.6% | −8.6% | −9.0% | −10.3% | −16.3% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arregui, F.J.; Gavara, F.J.; Soriano, J.; Pastor-Jabaloyes, L. Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption. Water 2018, 10, 612. https://doi.org/10.3390/w10050612
Arregui FJ, Gavara FJ, Soriano J, Pastor-Jabaloyes L. Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption. Water. 2018; 10(5):612. https://doi.org/10.3390/w10050612
Chicago/Turabian StyleArregui, Francisco J., Francesc J. Gavara, Javier Soriano, and Laura Pastor-Jabaloyes. 2018. "Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption" Water 10, no. 5: 612. https://doi.org/10.3390/w10050612
APA StyleArregui, F. J., Gavara, F. J., Soriano, J., & Pastor-Jabaloyes, L. (2018). Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption. Water, 10(5), 612. https://doi.org/10.3390/w10050612






