Assessing Long-Term Hydrological Impact of Climate Change Using an Ensemble Approach and Comparison with Global Gridded Model-A Case Study on Goodwater Creek Experimental Watershed
Abstract
1. Introduction
2. Materials and Methods
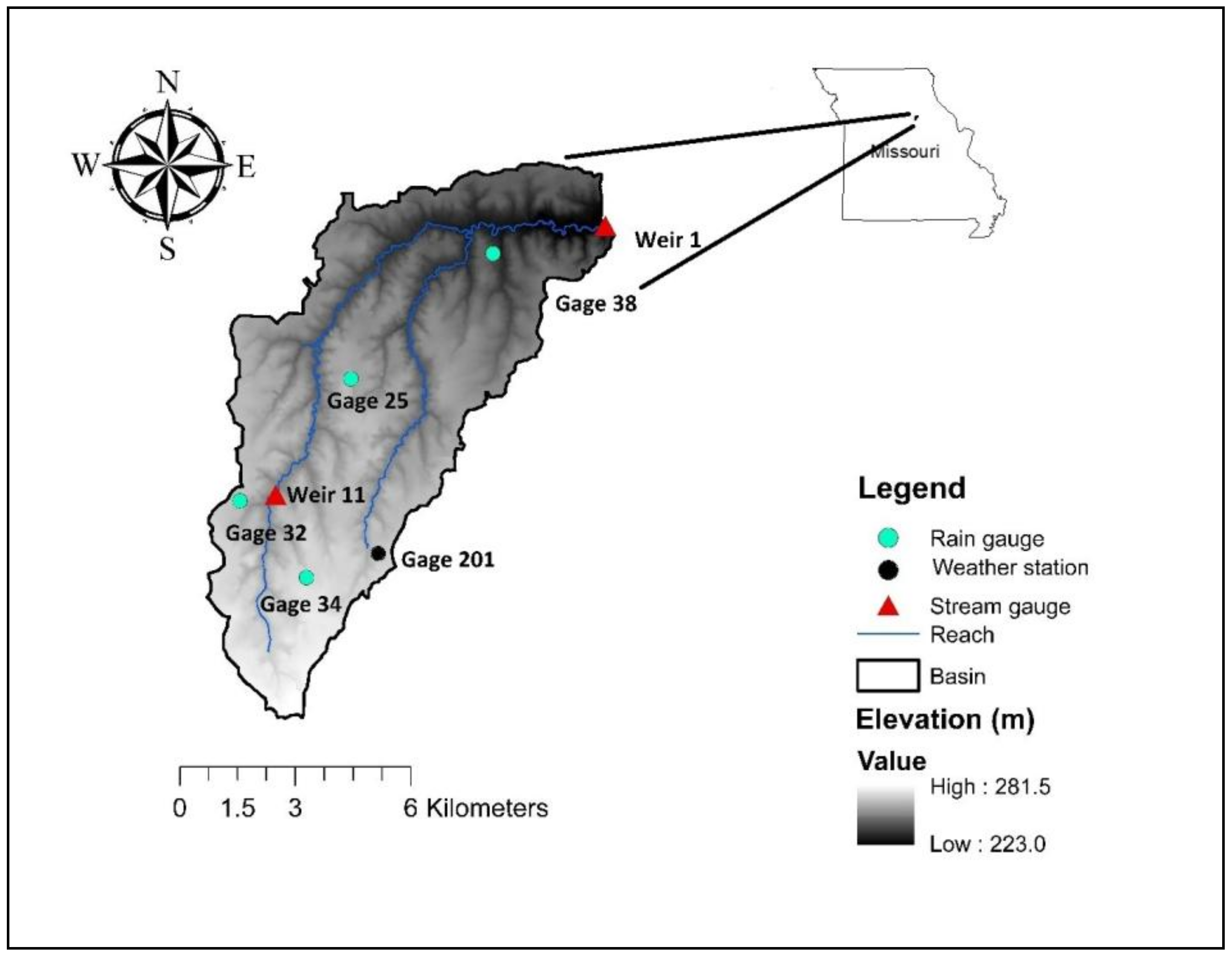
2.1. Watershed Description and Data Sources
2.2. Description of SWAT Model and Model Setup for GCEW
2.3. LPJmL and JeDi Model Overview
2.4. SWAT Model Calibration, Validation and Evaluation Criteria
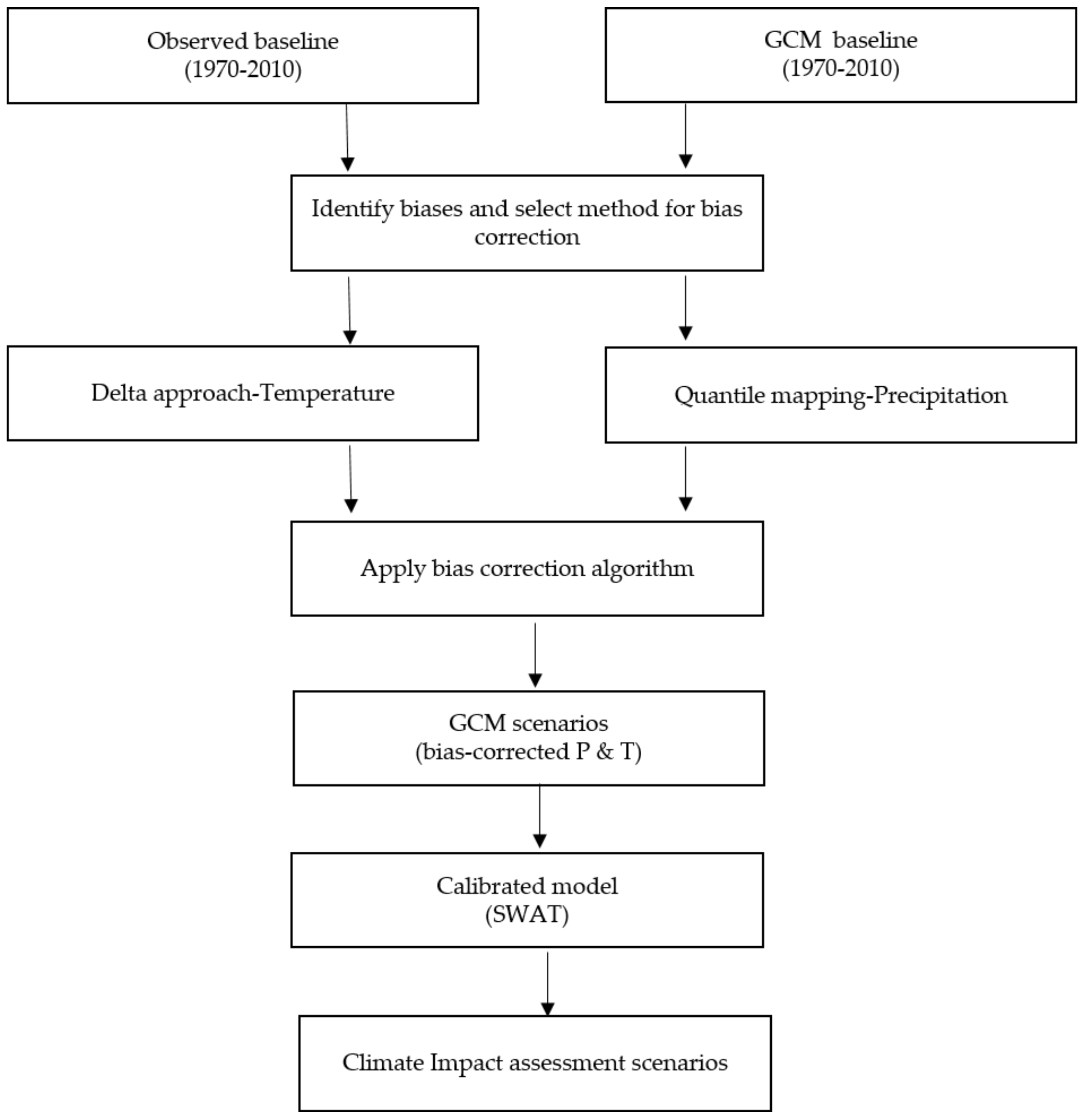
2.5. Climate Data and Bias Correction Methods
2.5.1. Statistical Downscaling: Temperature-Delta Method
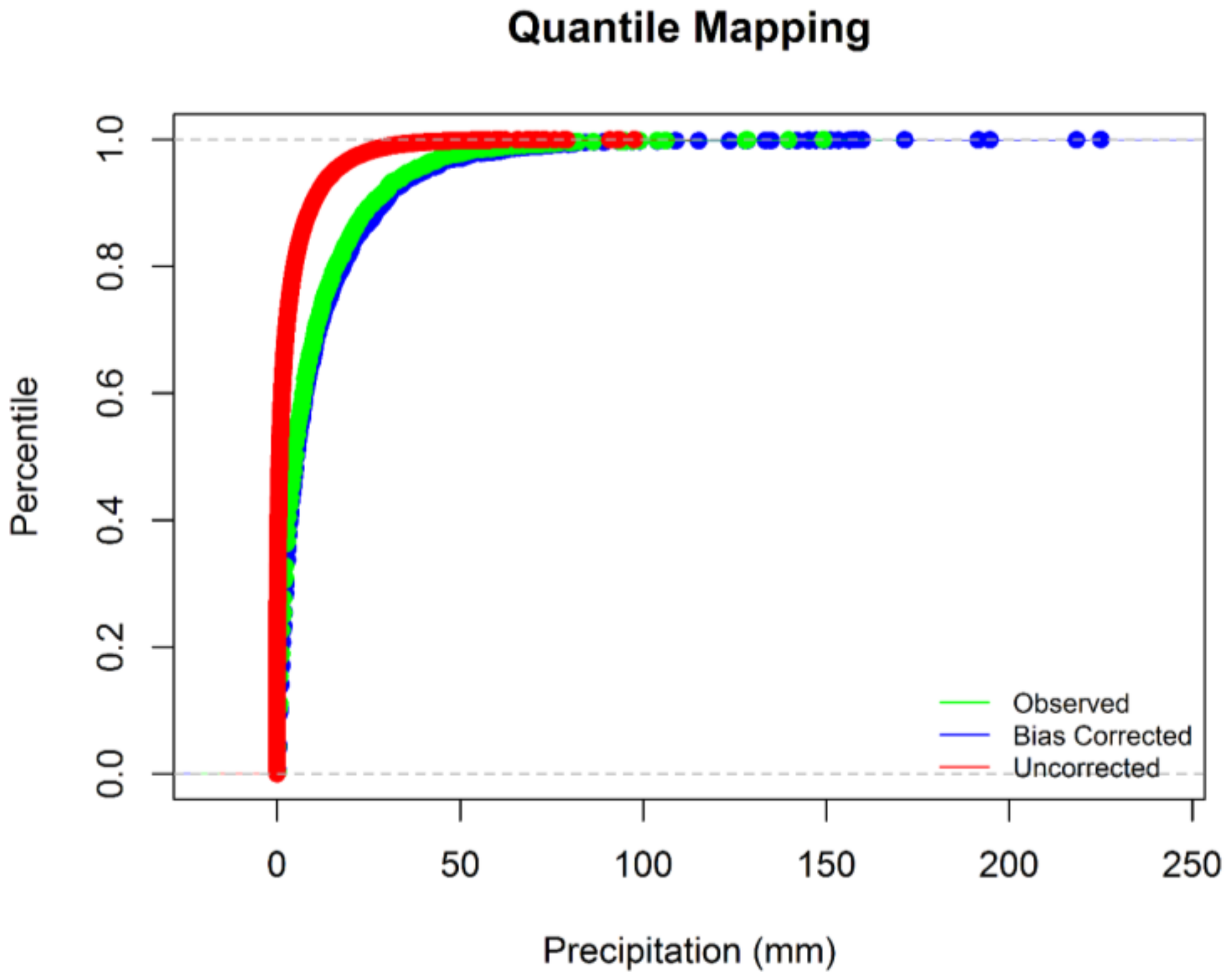
2.5.2. Statistical Downscaling: Precipitation-Quantile Mapping
2.6. Simulation Scenarios. Impacts of Climate Change on Water Yield, Evapotranspiration, and Surface Runoff
3. Results and Discussion
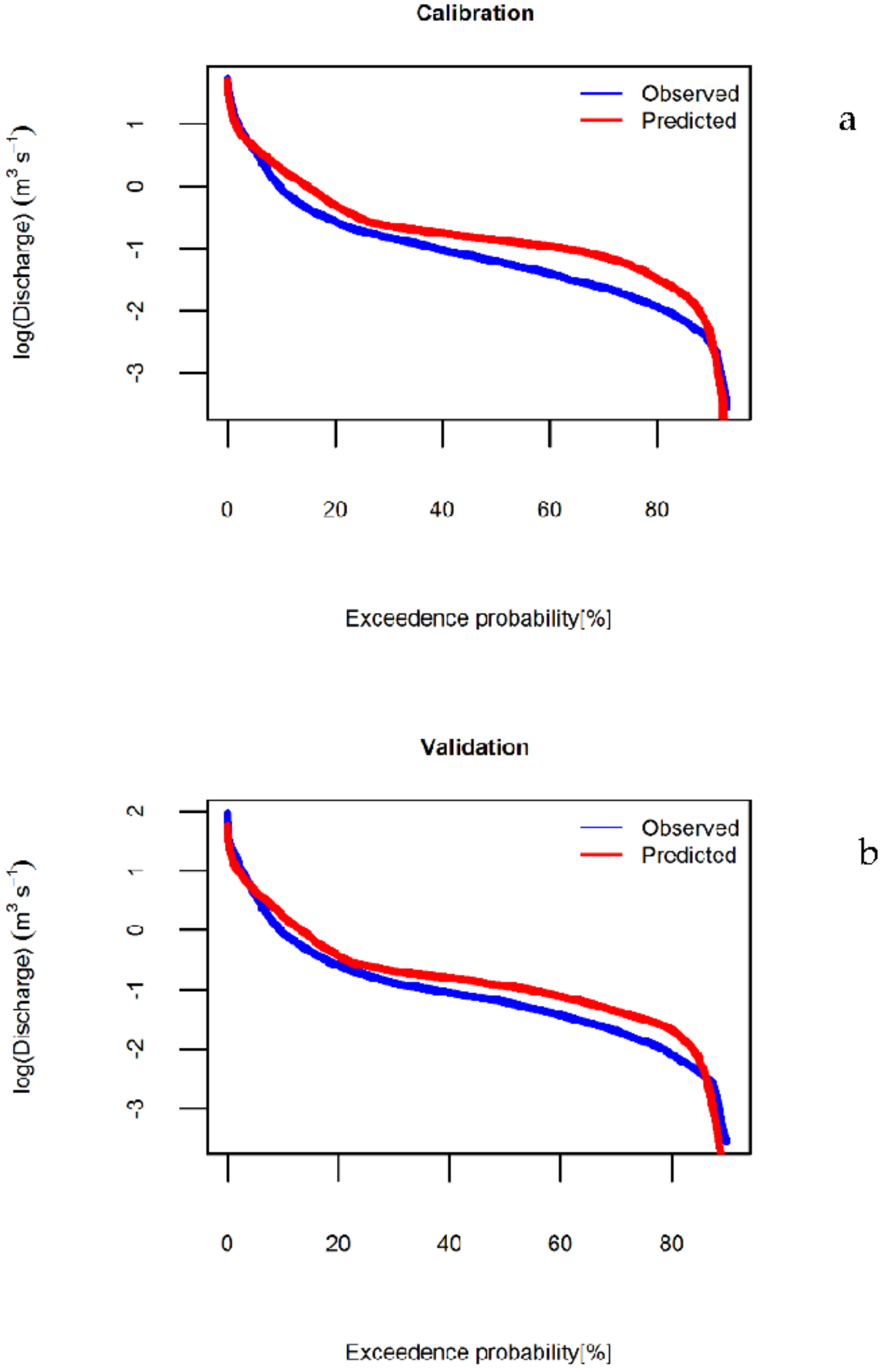
3.1. Model Calibration and Validation
3.2. Downscaled GCM Projection
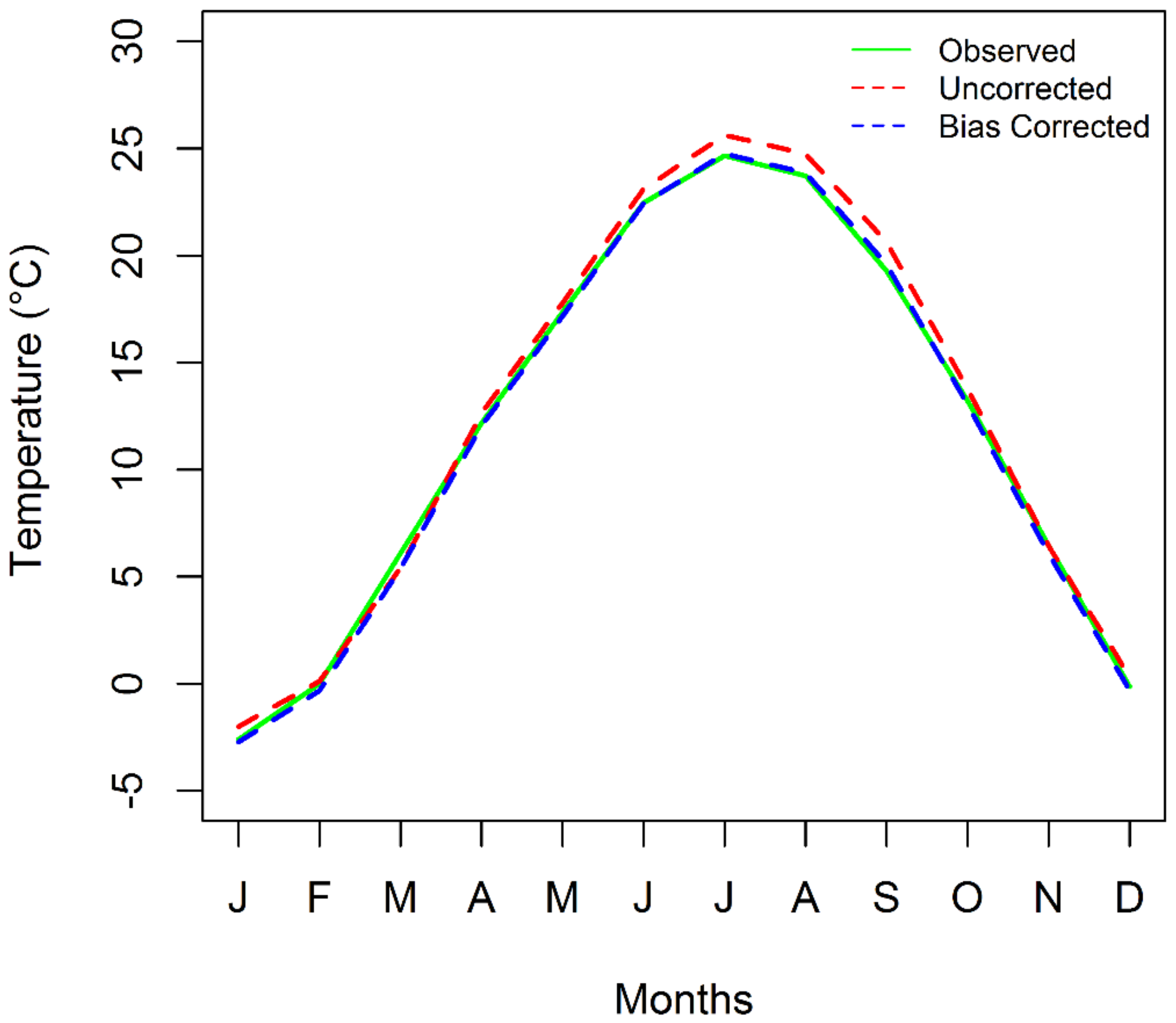
3.2.1. Temperature
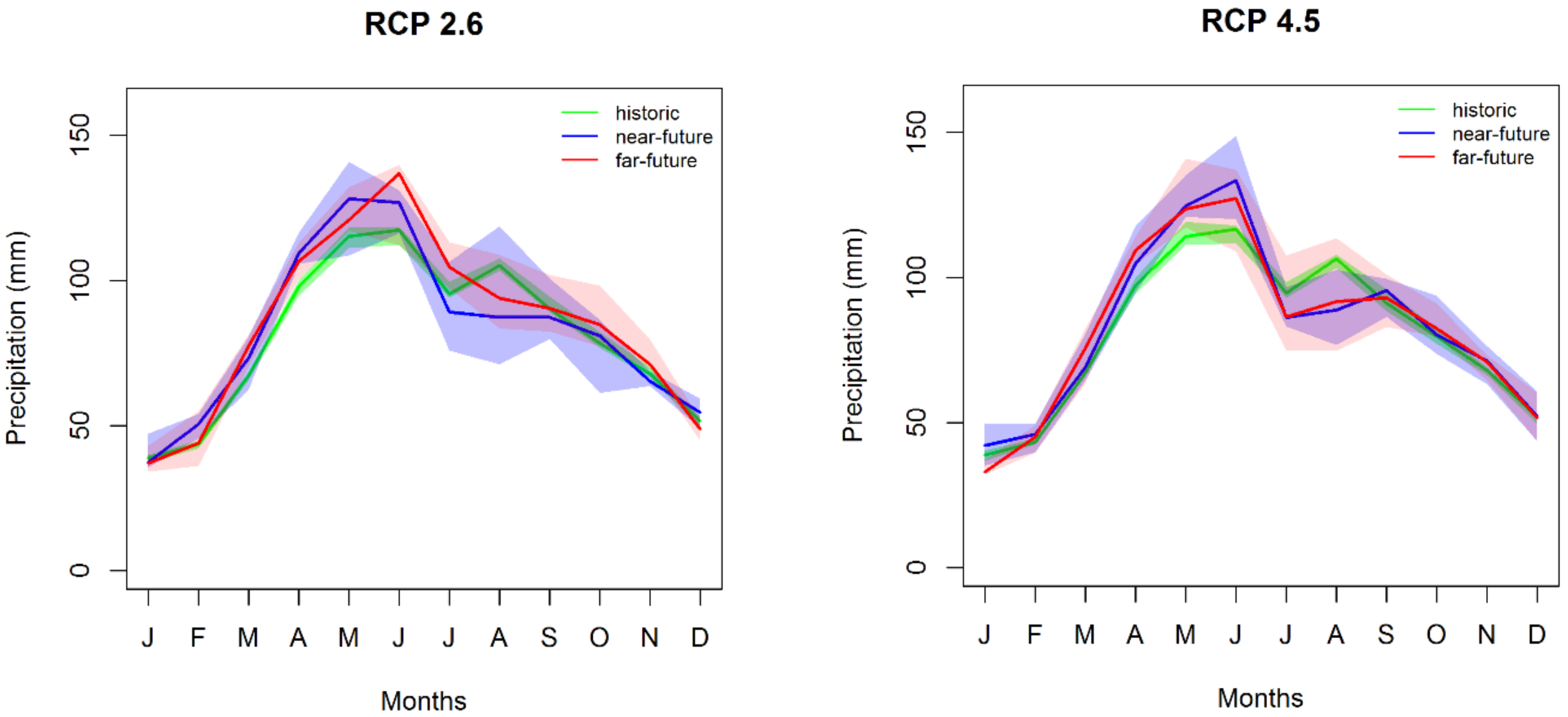
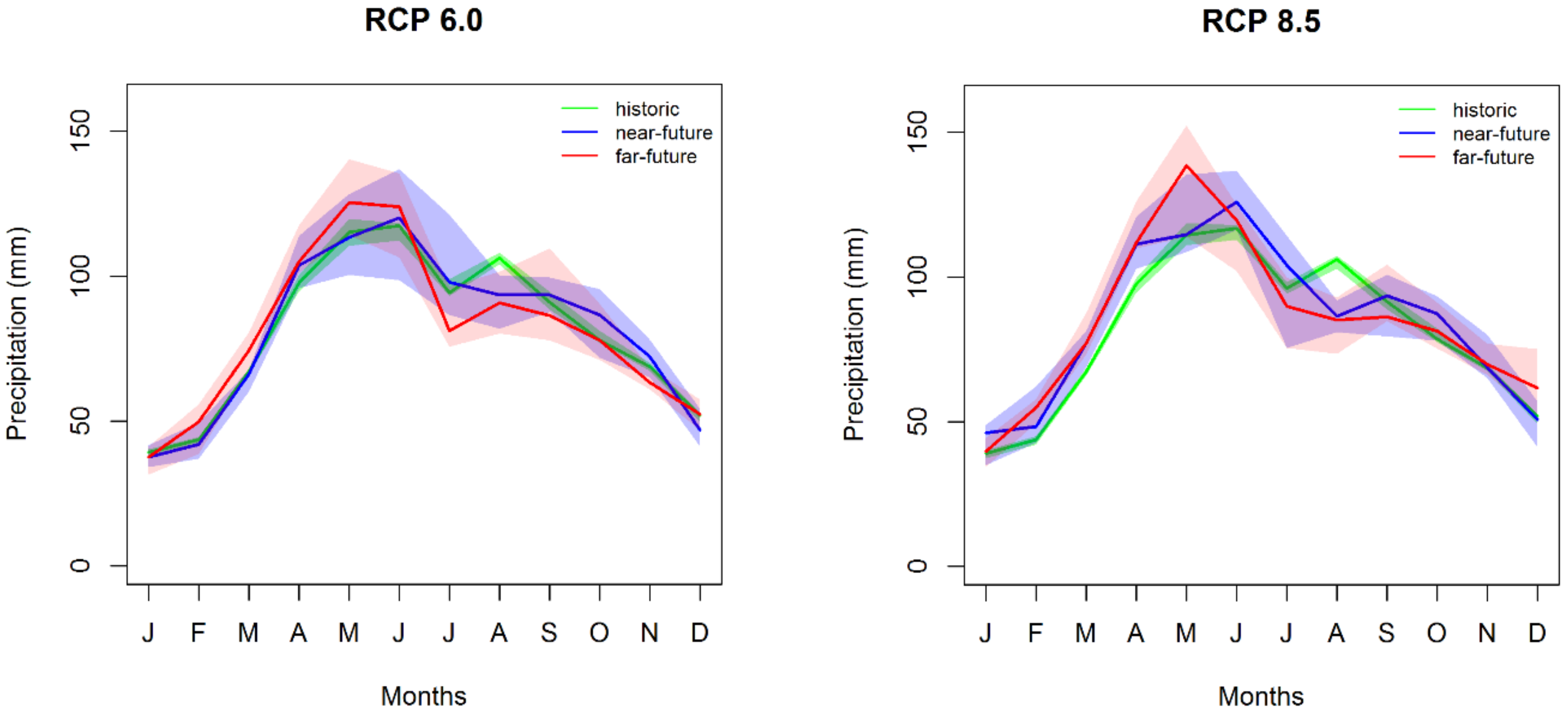
3.2.2. Precipitation
3.3. Climate Change Impact on Hydrological Output
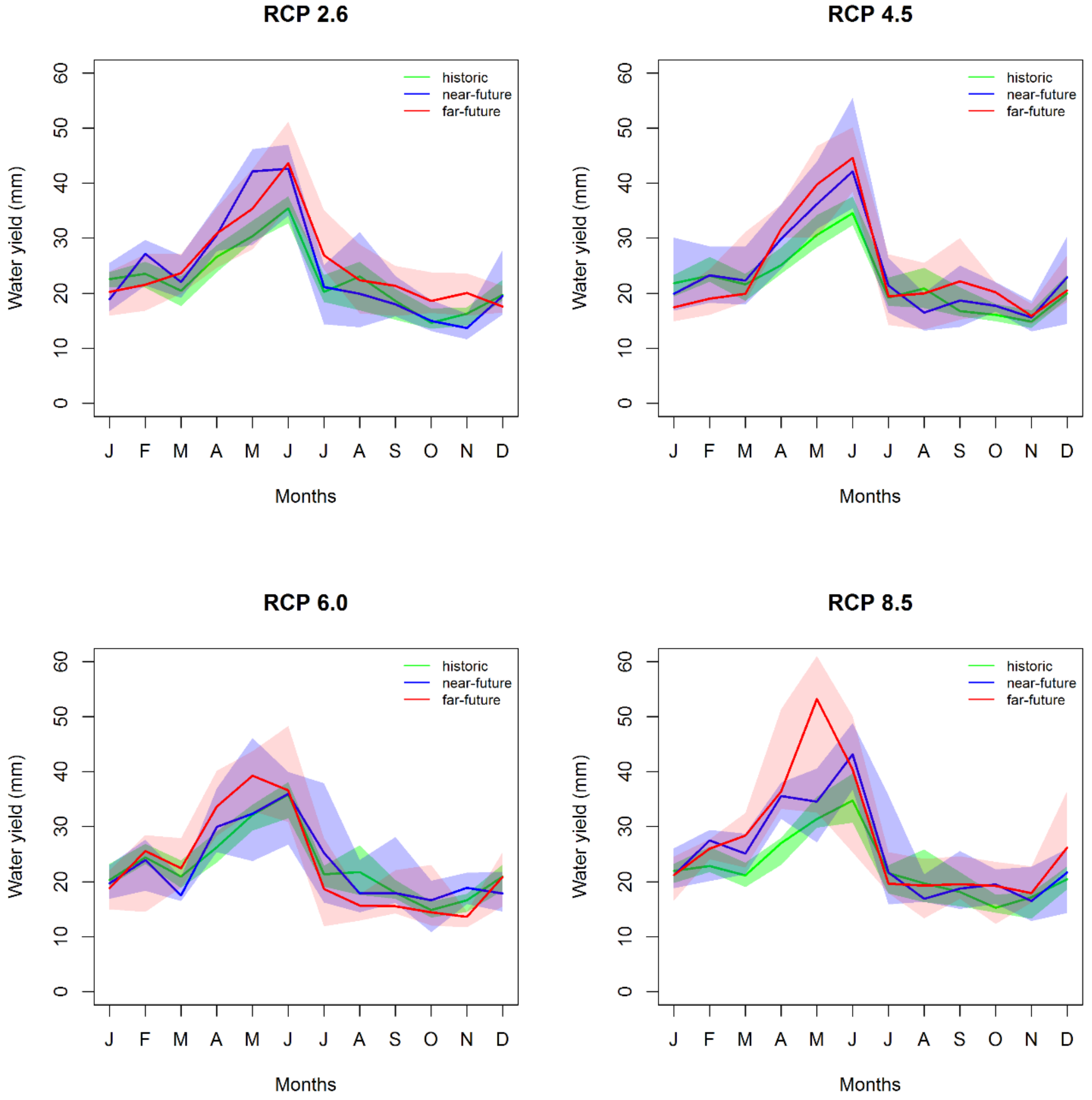
3.3.1. Water Yield
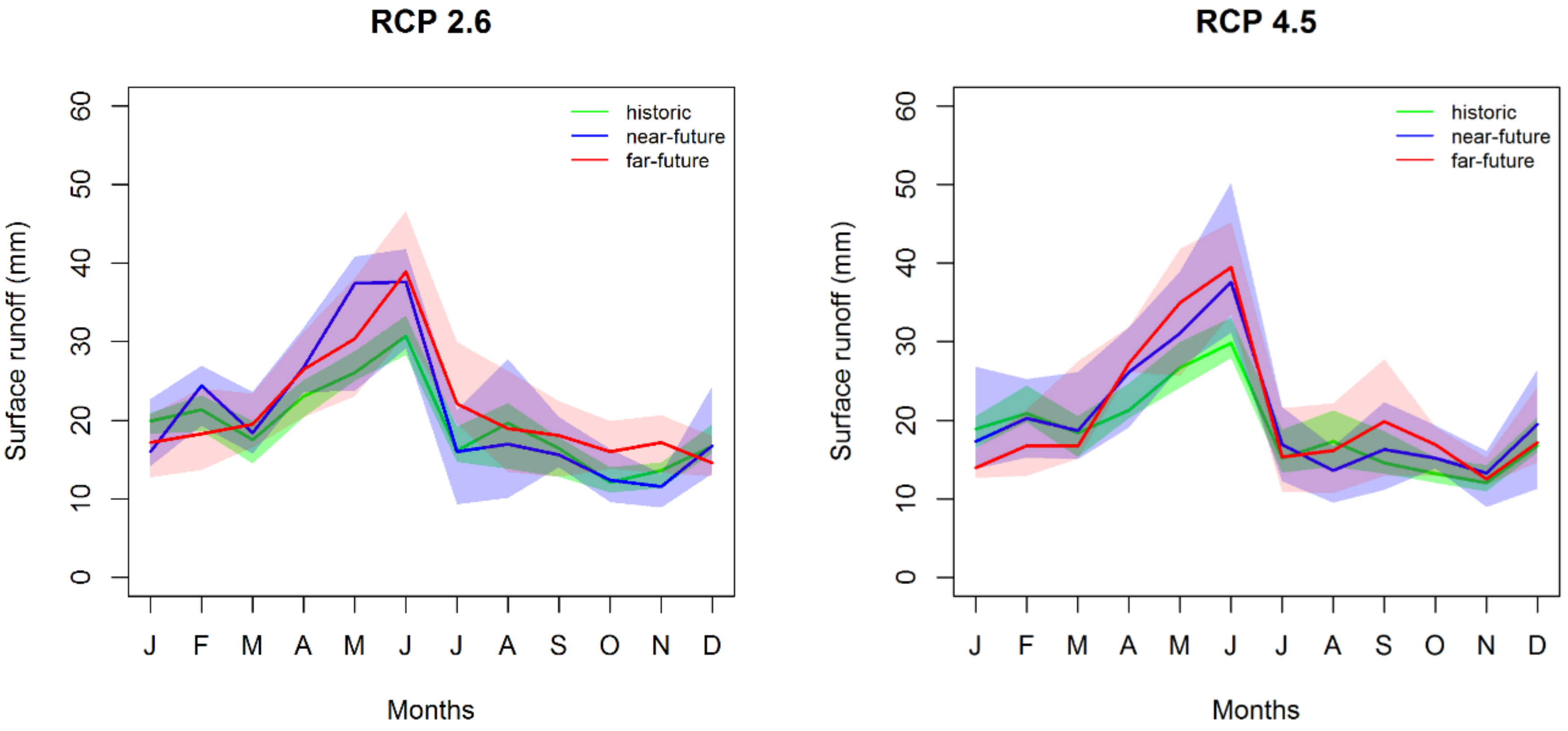
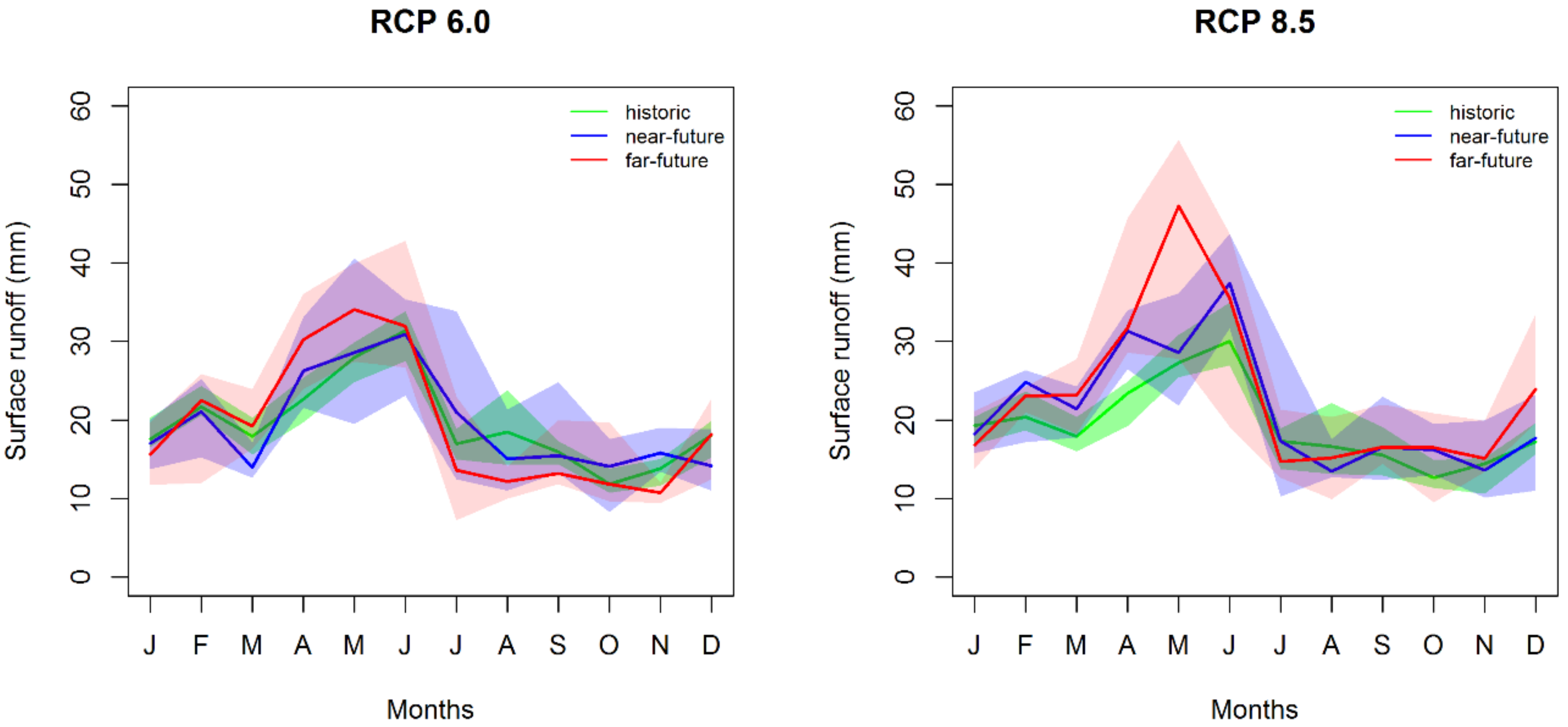
3.3.2. Surface Runoff
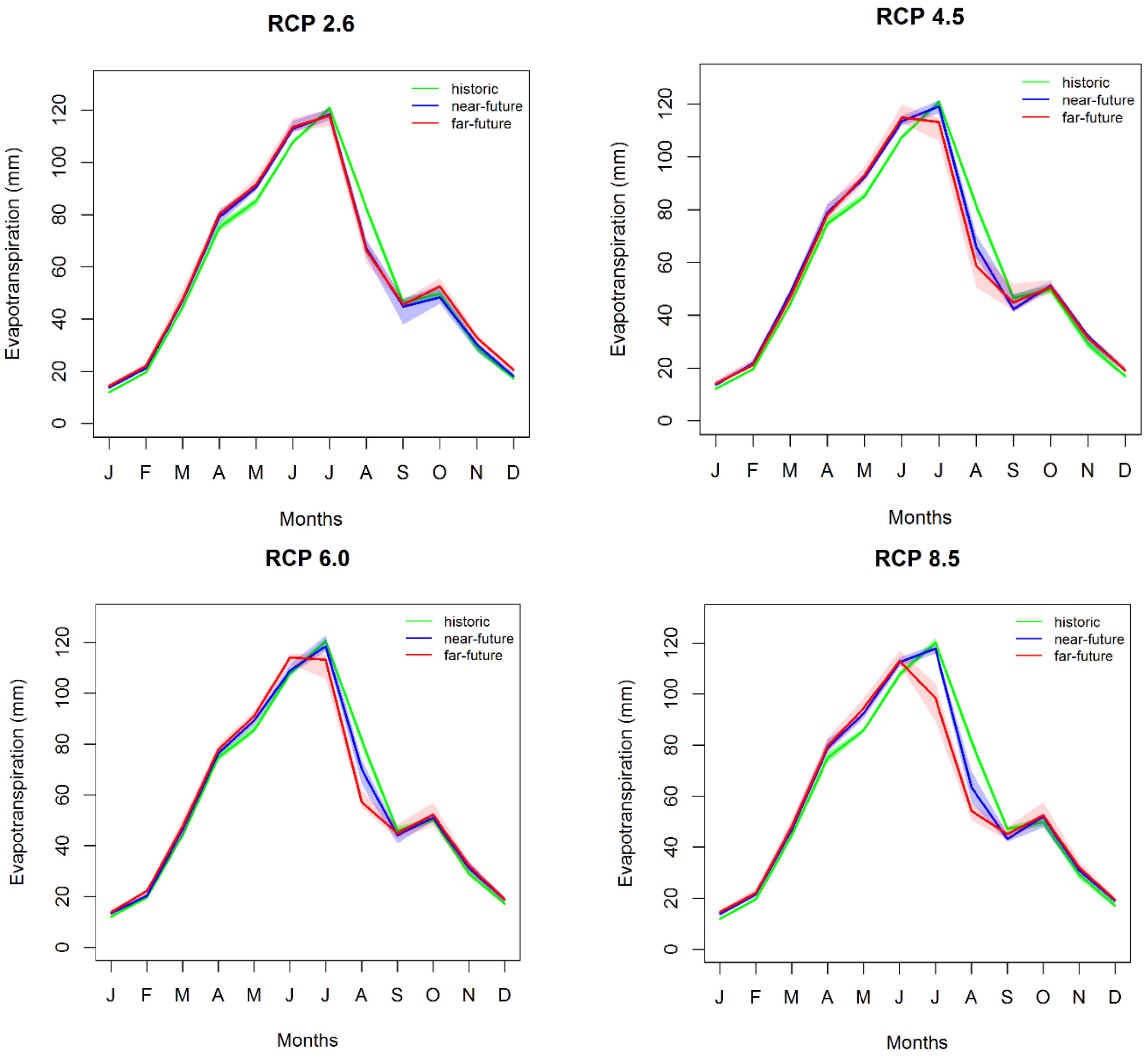
3.3.3. Evapotranspiration
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Wit, M.; Stankiewicz, J. Changes in Surface Water Supply across Africa with Predicted Climate Change. Science 2006, 311, 1917–1921. [Google Scholar] [CrossRef] [PubMed]
- Schewe, J.; Heinke, J.; Gerten, D.; Haddeland, I.; Arnell, N.W.; Clark, D.B.; Dankers, R.; Eisner, S.; Fekete, B.M.; Colón-González, F.J. Multimodel Assessment of Water Scarcity under Climate Change. Proc. Natl. Acad. Sci. USA 2014, 111, 3245–3250. [Google Scholar] [CrossRef] [PubMed]
- Gregory, R.D.; Willis, S.G.; Jiguet, F.; Voříšek, P.; Klvaňová, A.; Strien, A.V.; Huntley, B.; Collingham, Y.C.; Couvet, D.; Green, R.E. An Indicator of the Impact of Climatic Change on European Bird Populations. PLoS ONE 2009, 4, e4678. [Google Scholar] [CrossRef] [PubMed]
- Moritz, C.; Agudo, R. The future of species under climate change: Resilience or decline? Science 2013, 341, 504–508. [Google Scholar] [CrossRef] [PubMed]
- Bellard, C.; Bertelsmeier, C.; Leadley, P.; Thuiller, W.; Courchamp, F. Impacts of climate change on the future of biodiversity. Ecol. Lett. 2012, 15, 365–377. [Google Scholar] [CrossRef] [PubMed]
- Walther, G.-R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.-M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological Responses to Recent Climate Change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Schlenker, W.; Hanemann, W.M.; Fisher, A.C. The Impact of Global Warming on US Agriculture: An Econometric Analysis of Optimal Growing Conditions. Rev. Econ. Stat. 2006, 88, 113–125. [Google Scholar]
- Cubasch, U.; Wuebbles, D.; Chen, D.; Facchini, M.C.; Frame, D.; Mahowald, N.; Winther, J.G. Introduction: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Pachauri, R.K.; Allen, M.; Barros, V.; Broome, J.; Cramer, W.; Christ, R.; Church, J.; Clarke, L.; Dahe, Q.; Dasgupta, P. Climate Change 2014: Synthesis Report: Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y. The Impacts of Climate Change on Water Resources and Agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Kucharik, C.J.; Serbin, S.P. Impacts of Recent Climate Change on Wisconsin Corn and Soybean Yield Trends. Environ. Res. Lett. 2008, 3, 034003. [Google Scholar] [CrossRef]
- Le, P.V.; Kumar, P.; Drewry, D.T. Implications for the Hydrologic Cycle Under Climate Change due to the Expansion of Bioenergy Crops in the Midwestern United States. Proc. Natl. Acad. Sci. USA 2011, 108, 15085–15090. [Google Scholar] [CrossRef] [PubMed]
- Intergovernmental Panel on Climate Change (IPCC). What Is a GCM? Available online: http://www.ipcc-data.org/guidelines/pages/gcm_guide.html (accessed on 11 September 2017).
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Schneider, S.H. Introduction to climate modeling. In Coupled Climate System Modeling; Trenberth, K.E., Ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Peel, M.C.; Srikanthan, R.; McMahon, T.A.; Karoly, D.J. Uncertainty in runoff based on Global Climate Model precipitation and temperature data & ndash; Part 2: Estimation and uncertainty of annual runoff and reservoir yield. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 4579–4638. [Google Scholar]
- Qiao, L.; Pan, Z.; Herrmann, R.B.; Hong, Y. Hydrological Variability and Uncertainty of Lower Missouri River Basin Under Changing Climate. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 246–260. [Google Scholar] [CrossRef]
- Fowler, H.; Blenkinsop, S.; Tebaldi, C. Linking Climate Change Modelling to Impacts Studies: Recent Advances in Downscaling Techniques for Hydrological Modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Haasnoot, M.; van Deursen, W.P.A.; Guillaume, J.H.A.; Kwakkel, J.H.; van Beek, E.; Middelkoop, H. Fit For Purpose? Building and Evaluating a Fast, Integrated Model for Exploring Water Policy Pathways. Environ. Model. Softw. 2014, 60, 99–120. [Google Scholar] [CrossRef]
- Jha, M.; Gassman, P.; Panagopoulos, Y. Regional Changes in Nitrate Loadings in the Upper Mississippi River Basin under Predicted Mid-century Climate. Reg. Environ. Chang. 2015, 15, 449–460. [Google Scholar] [CrossRef]
- Panagopoulos, Y.; Gassman, P.; Arritt, R.; Herzmann, D.; Campbell, T.; Jha, M.; Kling, C.; Srinivasan, R.; White, M.; Arnold, J. Surface Water Quality and Cropping Systems Sustainability Under a Changing Climate in the Upper Mississippi River Basin. J. Soil Water Conserv. 2014, 69, 483–494. [Google Scholar] [CrossRef]
- Ouyang, F.; Zhu, Y.; Fu, G.; Lü, H.; Zhang, A.; Yu, Z.; Chen, X. Impacts of Climate Change Under CMIP5 RCP Scenarios on Streamflow in the Huangnizhuang Catchment. Stoch. Environ. Res. Risk Assess. 2015, 29, 1781–1795. [Google Scholar] [CrossRef]
- Ficklin, D.; Stewart, I.; Maurer, E. Effects of Projected Climate Change on the Hydrology in the Mono Lake Basin, California. Clim. Chang. 2013, 116, 111–131. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Stewart, I.T.; Maurer, E.P. Climate Change Impacts on Streamflow and Subbasin-Scale Hydrology in the Upper Colorado River Basin. PLoS ONE 2013, 8, e71297. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, I.N.; Bomblies, A.; Wemple, B.C. The Use of CMIP5 Data to Simulate Climate Change Impacts on Flow Regime within the Lake Champlain Basin. J. Hydrol. Reg. Stud. 2015, 3, 160–186. [Google Scholar] [CrossRef]
- Stone, M.C.; Hotchkiss, R.H.; Mearns, L.O. Water Yield Responses to High and Low Spatial Resolution Climate Change Scenarios in the Missouri River Basin. Geophys. Res. Lett. 2003, 30, 1186. [Google Scholar] [CrossRef]
- Jha, M.; Pan, Z.; Takle, E.S.; Gu, R. Impacts of Climate Change on Streamflow in the Upper Mississippi River Basin: A Regional Climate Model Perspective. J. Geophys. Res. Atmos. 2004, 109, 09105. [Google Scholar] [CrossRef]
- Choi, W.; Pan, F.; Wu, C. Impacts of climate change and urban growth on the streamflow of the Milwaukee River (Wisconsin, USA). Reg. Environ. Chang. 2017, 17, 889–899. [Google Scholar] [CrossRef]
- Tavakoli, M.; De Smedt, F. Impact of climate change on streamflow and soil moisture in the Vermilion Basin, Illinois. J. Hydrol. Eng. 2011, 17, 1059–1070. [Google Scholar] [CrossRef]
- Jha, M.K.; Gassman, P.W. Changes in hydrology and streamflow as predicted by a modelling experiment forced with climate models. Hydrol. Process. 2014, 28, 2772–2781. [Google Scholar] [CrossRef]
- Ahmadi, M.; Records, R.; Arabi, M. Impact of Climate Change on Diffuse Pollutant Fluxes at the Watershed Scale. Hydrol. Process. 2014, 28, 1962–1972. [Google Scholar] [CrossRef]
- Al-Mukhtar, M.; Dunger, V.; Merkel, B. Assessing the Impacts of Climate Change on Hydrology of the Upper Reach of the Spree River: Germany. Water Resour. Manag. 2014, 28, 2731–2749. [Google Scholar] [CrossRef]
- Ye, L.; Grimm, N. Modelling Potential Impacts of Climate Change on Water and Nitrate Export from a Mid-sized, Semiarid Watershed in the US Southwest. Clim. Chang. 2013, 120, 419–431. [Google Scholar] [CrossRef]
- Seaber, P.R.; Kapinos, F.P.; Knapp, G.L. Hydrologic Unit Maps; USGPO: Washington, DC, USA, 1987. [Google Scholar]
- Liang, X. A Two-Layer Variable Infiltration Capacity Land Surface Representation for General Circulation Models; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Williams, J.R.; Izaurralde, R.C. The APEX model. In Watershed Models; Singh, V.P., Frevert, D.K., Eds.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Freeze, R.A.; Harlan, R. Blueprint for a Physically-based, Digitally-simulated Hydrologic Response Model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Clark, M.P.; Bierkens, M.F.P.; Samaniego, L.; Woods, R.A.; Uijenhoet, R.; Bennet, K.E.; Pauwels, V.R.N.; Cai, X.; Wood, A.W.; Peters-Lidard, C.D. The Evolution of Process-based Hydrologic Models: Historical Challenges and the Collective Quest for Physical Realism. Hydrol. Earth Syst. Sci. Discuss. 2017, 2017, 1–14. [Google Scholar]
- Sadler, E.J.; Lerch, R.N.; Kitchen, N.R.; Anderson, S.H.; Baffaut, C.; Sudduth, K.A.; Prato, A.A.; Kremer, R.J.; Vories, E.D.; Myers, D.B. Long-term Agroecosystem Research in the Central Mississippi River Basin: Introduction, Establishment, and Overview. J. Environ. Qual. 2015, 44, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development; Wiley Online Library: Hoboken, NJ, USA, 1998. [Google Scholar]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the Swat Model on a Large Rwer Basin with Point and Nonpoint Sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation: Version 2009; USDA Agricultural Research Service and Texas A&M Blackland Research Center: Temple, TX, USA, 2011. [Google Scholar]
- Baffaut, C.; John Sadler, E.; Ghidey, F.; Anderson, S.H. Long-term Agroecosystem Research in the Central Mississippi River Basin: SWAT Simulation of Flow and Water Quality in the Goodwater Creek Experimental Watershed. J. Environ. Qual. 2015, 44, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Udawatta, R.P.; Motavalli, P.P.; Garrett, H.E. Phosphorus Loss and Runoff Characteristics in Three Adjacent Agricultural Watersheds with Claypan Soils. J. Environ. Qual. 2004, 33, 1709–1719. [Google Scholar] [CrossRef] [PubMed]
- Jung, W.; Kitchen, N.; Sudduth, K.; Anderson, S. Spatial Characteristics of Claypan Soil Properties in an Agricultural Field. Soil Sci. Soc. Am. J. 2006, 70, 1387–1397. [Google Scholar] [CrossRef]
- Sadler, E.J.; Sudduth, K.A.; Drummond, S.T.; Vories, E.D.; Guinan, P.E. Long-term Agroecosystem Research in the Central Mississippi River Basin: Goodwater Creek Experimental Watershed Weather Data. J. Environ. Qual. 2015, 44, 13–17. [Google Scholar] [CrossRef] [PubMed]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A trend-preserving bias correction–the ISI-MIP approach. Earth Syst. Dyn. 2013, 4, 219–236. [Google Scholar] [CrossRef]
- Warszawski, L.; Frieler, K.; Huber, V.; Serdeczny, O.; Piontek, F.; Schewe, J. Research Design of the Intersectoral Impact Model Intercomparison Project (ISI-MIP). Proc. Natl. Acad. Sci. USA 2014, 111, 3228–3232. [Google Scholar] [CrossRef] [PubMed]
- Baffaut, C.; Sadler, E.J.; Ghidey, F. Long-term Agroecosystem Research in the Central Mississippi River Basin: Goodwater Creek experimental Watershed Flow Data. J. Environ. Qual. 2015, 44, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Missouri Spatial Data Information Services (MSDIS), 2016. Available online: http://msdis.missouri.edu/data/dem/ (accessed on 25 April 2018).
- Soil Survey Geographic Data (SSURGO), 2016. Available online: http://websoilsurvey.sc.egov.usda.gov/App/WebSoilSurvey.aspx (accessed on 25 April 2018).
- National Agricultural Statistics Service (NASS) Cropland Data Layer (CDL), 2010. Available online: http://nassgeodata.gmu.edu/CropScape/ (accessed on 25 April 2018).
- Bondeau, A.; Smith, P.C.; Zaehle, S.; Schaphoff, S.; Lucht, W.; Cramer, W.; Gerten, D.; Lotze-Campen, H.; Müller, C.; Reichstein, M. Modelling the Role of Agriculture for the 20th Century Global Terrestrial Carbon Balance. Glob. Chang. Biol. 2007, 13, 679–706. [Google Scholar] [CrossRef]
- Pavlick, R.; Drewry, D.T.; Bohn, K.; Reu, B.; Kleidon, A. The Jena Diversity-Dynamic Global Vegetation Model (JeDi-DGVM): A Diverse Approach to Representing Terrestrial Biogeography and Biogeochemistry based on Plant functional Trade-offs. Biogeosciences 2013, 10, 4137–4177. [Google Scholar] [CrossRef]
- Nachtergaele, F.; van Velthuizen, H.; Verelst, L.; Batjes, N.; Dijkshoorn, J.; van Engelen, V.; Fischer, G.; Jones, A.; Montanarella, L.; Petri, M. Harmonized World Soil Database; ISRIC: Wageningen, The Netherlands, 2009. [Google Scholar]
- Klein Goldewijk, K. A Historical Land Use Data Set for the Holocene, HYDE 3.2; EGU General Assembly Conference Abstracts: Vienna, Austria, 2016; p. 1574. [Google Scholar]
- Diimenil, M.E.; Giorgetta, M.; Schlese, U.; Schullzweida, U. The Atmospheric General Circulation Model ECHAM-4: Model Description and Simulation of Present-Day Climate; MPI Report 218; Max Planck Institut Meteorologie: Hamburg, Germany, 1996. [Google Scholar]
- The Inter-Sectoral Impact Model Intercomparision Project (ISI-MIP) Data Repository, 2014. Available online: https://esg.pik-potsdam.de/search/isimip-ft/ (accessed on 25 April 2018).
- Abbaspour, K.; Vejdani, M.; Haghighat, S. SWAT-CUP Calibration and Uncertainty Programs for SWAT. In MODSIM 2007 International Congress on Modelling and Simulation; Modelling and Simulation Society of Australia and New Zealand: Canberra, Australia, 2007. [Google Scholar]
- Neitsch, S.; Arnold, J.; Kiniry, J.E.A.; Srinivasan, R.; Williams, J. Soil and Water Assessment Tool User’s Manual Version 2000; GSWRL Report 202; Grassland, Soil & Water Research Laboratory: Temple, TX, USA, 2002. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Maurer, E.P.; Brekke, L.; Pruitt, T.; Duffy, P.B. Fine-resolution Climate Projections Enhance Regional Climate Change Impact Studies. Eos Trans. Am. Geophys. Union 2007, 88, 504. [Google Scholar] [CrossRef]
- Bias Corrected Constructed Analog (BCCA) Downscaled Data, 2014. Available online: http://gdo-dcp.ucllnl.org/downscaled_cmip_projections/ (accessed on 25 April 2018).
- Wu, T.; Song, L.; Li, W.; Wang, Z.; Zhang, H.; Xin, X.; Zhang, Y.; Zhang, L.; Li, J.; Wu, F.; et al. An Overview of BCC Climate System Model Development and Application for Climate Change Studies. Acta Meteorol. Sin. 2014, 28, 34–56. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Dunne, J.P.; John, J.G.; Adcroft, A.J.; Griffies, S.M.; Hallberg, R.W.; Shevliakova, E.; Stouffer, R.J.; Cooke, W.; Dunne, K.A.; Harrison, M.J. GFDL’s ESM2 Global Coupled Climate-carbon Earth System Models. Part I: Physical Formulation and Baseline Simulation Characteristics. J. Clim. 2012, 25, 6646–6665. [Google Scholar] [CrossRef]
- Dunne, J.P.; John, J.G.; Shevliakova, E.; Stouffer, R.J.; Krasting, J.P.; Malyshev, S.L.; Milly, P.; Sentman, L.T.; Adcroft, A.J.; Cooke, W. GFDL’s ESM2 Global Coupled Climate–Carbon Earth System Models. Part II: Carbon System Formulation and Baseline Simulation Characteristics. J. Clim. 2013, 26, 2247–2267. [Google Scholar] [CrossRef]
- Watanabe, S.; Hajima, T.; Sudo, K.; Nagashima, T.; Takcmura, T.; Okajima, H.; Nozawa, T.; Kawase, H.; Abe, M.; Yokohata, T. MIROC-ESM 2010: Model Description and Basic Results of CMIP5-20c3m experiments. Geosci. Model Dev. 2011, 4, 845–872. [Google Scholar] [CrossRef]
- Watanabe, M.; Suzuki, T.; O’ishi, R.; Komuro, Y.; Watanabe, S.; Emori, S.; Takemura, T.; Chikira, M.; Ogura, T.; Sekiguchi, M. Improved Climate Simulation by MIROC5: Mean States, Variability, and Climate Sensitivity. J. Clim. 2010, 23, 6312–6335. [Google Scholar] [CrossRef]
- Yukimoto, S.; Adachi, Y.; Hosaka, M.; Sakami, T.; Yoshimura, H.; Hirabara, M.; Tanaka, T.Y.; Shindo, E.; Tsujino, H.; Deushi, M. A New Global Climate Model of the Meteorological Research Institute: MRI-CGCM3-Model Description and Basic Performance. J. Meteorol. Soc. Jpn. 2012, 90, 23–64. [Google Scholar] [CrossRef]
- Bentsen, M.; Bethke, I.; Debernard, J.; Iversen, T.; Kirkevåg, A.; Seland, Ø.; Drange, H.; Roelandt, C.; Seierstad, I.; Hoose, C. The Norwegian Earth System Model, NorESM1-M-Part 1: Description and Basic Evaluation. Geosci. Model Dev. Discuss. 2012, 5, 2843–2931. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Deursen, W.V. Estimates of Future Discharges of the River Rhine using Two Scenario Methodologies: Direct Versus Delta Approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and Dynamical Downscaling of the Seine Basin Climate for Hydro-Meteorological Studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Johnson, F.; Sharma, A. Accounting for Interannual Variability: A Comparison of Options for Water Resources Climate Change Impact Assessments. Water Resour. Res. 2011, 47, 04508. [Google Scholar] [CrossRef]
- Block, P.J.; Souza Filho, F.A.; Sun, L.; Kwon, H.H. A Streamflow Forecasting Framework using Multiple Climate and Hydrological Models; Wiley Online Library: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ines, A.V.; Hansen, J.W. Bias Correction of Daily GCM Rainfall for Crop Simulation Studies. Agric. For. Meteorol. 2006, 138, 44–53. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias Correction of Monthly Precipitation and Temperature Fields from Intergovernmental Panel on Climate Change AR4 Models using Equidistant Quantile Matching. J. Geophys. Res. Atmos. 2010, 115, 1984–2012. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Dettinger, M.D.; Cayan, D.R. Downscaling with Constructed Analogues: Daily Precipitation and Temperature Fields Over the United States; California Energy Commission: Sacramento, CA, USA, 2008. [Google Scholar]
- Grillakis, M.G.; Koutroulis, A.G.; Tsanis, I.K. Multisegment Statistical Bias Correction of Daily GCM Precipitation Output. J. Geophys. Res. Atmos. 2013, 118, 3150–3162. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Leuprecht, A. Empirical-statistical Downscaling and Error Correction of Daily Precipitation from Regional Climate Models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Perez, J.; Menendez, M.; Mendez, F.; Losada, I. Evaluating the Performance of CMIP3 and CMIP5 Global Climate Models over the North-east Atlantic Region. Clim. Dyn. 2014, 43, 2663–2680. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Santer, B.D.; Gleckler, P.J. Selecting Global Climate Models for Rgional Climate Change Studies. Proc. Natl. Acad. Sci. USA 2009, 106, 8441–8446. [Google Scholar] [CrossRef] [PubMed]
- Peters, G.P.; Andrew, R.M.; Boden, T.; Canadell, J.G.; Ciais, P.; Le Quéré, C.; Marland, G.; Raupach, M.R.; Wilson, C. The Challenge to Keep Global Warming Below 2 °C. Nat. Clim. Chang. 2013, 3, 4–6. [Google Scholar] [CrossRef]
- Chiyuan, M.; Qingyun, D.; Qiaohong, S.; Yong, H.; Dongxian, K.; Tiantian, Y.; Aizhong, Y.; Zhenhua, D.; Wei, G. Assessment of CMIP5 Climate Models and Projected Temperature Changes over Northern Eurasia. Environ. Res. Lett. 2014, 9, 055007. [Google Scholar]
- Terink, W.; Hurkmans, R.T.W.L.; Torfs, P.J.J.F.; Uijlenhoet, R. Evaluation of a Bias Correction Method Applied to Downscaled Precipitation and Temperature Reanalysis Data for the Rhine Basin. Hydrol. Earth Syst. Sci. 2010, 14, 687–703. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, J.; Powell, A., Jr. Discrepancies of Surface Temperature Trends in the CMIP5 Simulations and Observations on the Global and Regional Scales. Clim. Past Discuss. 2013, 9, 6161–6178. [Google Scholar] [CrossRef]
- Kim, H.M.; Webster, P.J.; Curry, J.A. Evaluation of Short-term Climate Change Prediction in Multi-model CMIP5 Decadal Hindcasts. Geophys. Res. Lett. 2012, 39, 10701. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.; Raper, S.; Riahi, K. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 2011, 109, 213. [Google Scholar] [CrossRef]
- Van Vuuren, D.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.; Kram, T.; Krey, V.; Lamarque, J.-F.; et al. The Representative Concentration Pathways: An Overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Feng, Z.; Leung, L.R.; Hagos, S.; Houze, R.A.; Burleyson, C.D.; Balaguru, K. More frequent intense and long-lived storms dominate the springtime trend in central US rainfall. Nat. Commun. 2016, 7, 13429. [Google Scholar] [CrossRef] [PubMed]
- Risbey, J.S.; Entekhabi, D. Observed Sacramento Basin Streamflow Response to Precipitation and Temperature Changes and its Relevance to Climate Impact Studies. J. Hydrol. 1996, 184, 209–223. [Google Scholar] [CrossRef]
- Yang, D.; Herath, S.; Musiake, K. Spatial resolution sensitivity of catchment geomorphologic properties and the effect on hydrological simulation. Hydrol. Process. 2001, 15, 2085–2099. [Google Scholar] [CrossRef]
- Warszawski, L.; Frieler, K.; Huber, V.; Piontek, F.; Serdeczny, O.; Schewe, J. The Inter-sectoral Impact Model Intercomparison Project (ISI–MIP): Project Framework. Proc. Natl. Acad. Sci. USA 2014, 111, 3228–3232. [Google Scholar] [CrossRef] [PubMed]
- Suleiman, A.A.; Hoogenboom, G. Comparison of Priestley-Taylor and FAO-56 Penman-Monteith for Daily Reference Evapotranspiration Estimation in Georgia. J. Irrig. Drain. Eng. 2007, 133, 175–182. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Luedeling, E.; Zhang, M. Climate Change Sensitivity Assessment of a Highly Agricultural Watershed using SWAT. J. Hydrol. 2009, 374, 16–29. [Google Scholar] [CrossRef]

| Land Use | Area (ha) | %Watershed Area |
|---|---|---|
| Corn | 1702.6 | 23.1 |
| Forest | 444.5 | 6.0 |
| Hay | 540.7 | 7.3 |
| Pasture | 1049.5 | 14.3 |
| Soybean | 3052.1 | 41.4 |
| Switchgrass | 73.5 | 1.0 |
| Urban | 501.5 | 6.9 |
| Model | CMIP5 Climate Modeling Group | Model ID | Reference |
|---|---|---|---|
| 1 | Beijing Climate Center, China Meteorological Administration | bcc-csm1-1 | [65] |
| 2 | National Center for Atmospheric Research | ccsm4.1 | [66] |
| 3 | National Center for Atmospheric Research | ccsm4.2 | [66] |
| 4 | NOAA Geophysical Fluid Dynamics Laboratory | gfdl-esm2g | [67] |
| 5 | NOAA Geophysical Fluid Dynamics Laboratory | gfdl-esm2m | [68] |
| 6 | Institut Pierre-Simon Laplace | ipsl-cm5a-lr | [68] |
| 7 | Institut Pierre-Simon Laplace | ipsl-cm5a-mr | [68] |
| 8 | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies | miroc-esm | [69] |
| 9 | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies | miroc-esm-chem | [69] |
| 10 | Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology | miroc5 | [70] |
| 11 | Meteorological Research Institute | mri-cgcm3 | [71] |
| 12 | Norwegian Climate centre | noresm1-m | [72] |
| Scenarios | 2016–2045 | 2046–2075 |
|---|---|---|
| CO2 Concentration in Part per Million (ppm) | ||
| RCP 2.6 | 428 | 440 |
| RCP 4.5 | 437 | 507 |
| RCP 6.0 | 431 | 515 |
| RCP 8.5 | 454 | 611 |
| Parameter | Definition | Default Value | Adjusted Value |
|---|---|---|---|
| ESCO | Soil evaporation compensation factor | 0.95 | 0.88 |
| GWQMN | Shallow aquifer depth of water required for return | 0 | 55 |
| flow to occur (mm) | |||
| GW_DELAY | Groundwater delay time (days) | 31 | 55 |
| SOL_AWC | Available water capacity of the soil layer (mm H2O/mm soil) | - | 0.04 † |
| CH_N | Manning’s “n” value for the main channel | 0.014 | 0.019 |
| CH_K | Effective hydraulic conductivity in main channel | 0 | 0.08 |
| Alluvium (mm/hr.) | |||
| SMTMP | Snow melt temperature (°C) | 0.5 | −2.5 |
| SMFMN | Snow melt min rate (mm H2O/°C-day) | 4.5 | 1.5 |
| EVRCH | Reach evaporation adjustment factor | 1 | 0.5 |
| MSK_X | Weighting factor that controls the relative importance | 0.2 | 0.1 |
| of inflow and outflow in determining the storage in the reach | |||
| MSK_CO2 | Calibration coefficient used to control impact of the | 0.25 | 3.5 |
| storage time constant for low flow upon the time constant value calculated for the reach | |||
| ALPHA_BF | Baseflow alpha factor (1/days) | 0.0048 | 0.1 |
| SHALLST | Initial depth of water in the shallow aquifer (mm) | 1000 | 600 |
| Water Yield (% Change over the Baseline) | ||||||||
|---|---|---|---|---|---|---|---|---|
| RCP 2.6 | RCP 4.5 | RCP 6.0 | RCP 8.5 | |||||
| Near Future | Far Future | Near Future | Far Future | Near Future | Far Future | Near Future | Far Future | |
| Median | 9.9 | 12.0 | 10.4 | 6.2 | 5.4 | −1.0 | 19.0 | 29.4 |
| 1st Quartile | 5.6 | 8.4 | 2.4 | 0.1 | −2.9 | −2.7 | 7.7 | 19.9 |
| 3rd Quartile | 11.1 | 19.2 | 11.6 | 28.3 | 8.9 | 16.3 | 23.1 | 31.4 |
| Surface Runoff | ||||||||
| Median | 10.1 | 12.2 | 9.7 | 7.2 | 5.9 | −0.9 | 20.9 | 29.9 |
| 1st Quartile | 6.6 | 10.0 | 3.6 | 1.6 | −3.0 | −3.0 | 7.8 | 20.0 |
| 3rd Quartile | 12.4 | 20.0 | 11.3 | 28.1 | 8.2 | 17.6 | 24.4 | 31.0 |
| Evapotranspiration | ||||||||
| Median | 0.1 | 3.1 | 1.6 | 0.1 | 0.8 | −0.3 | 2.1 | −2.1 |
| 1st Quartile | −1.1 | 1.9 | 1.8 | −0.8 | −0.7 | −2.5 | 0.4 | −1.4 |
| 3rd Quartile | 1.0 | 2.2 | 0.1 | 1.3 | 0.5 | 0.7 | 0.4 | −2.4 |
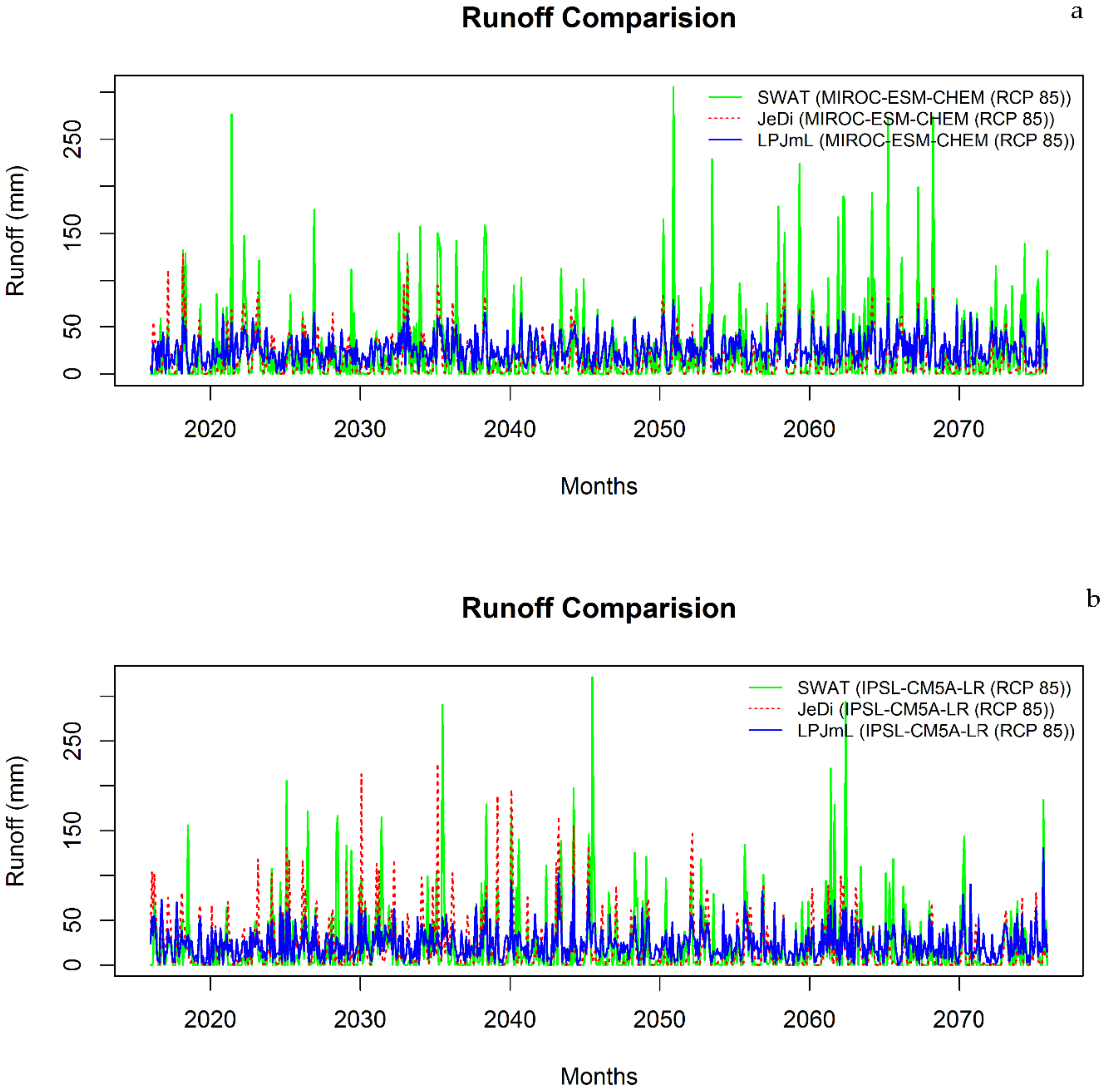
| GCM | Runoff (mm)-SWAT | Runoff (mm)-LPJmL | Runoff (mm)-JeDi-DVGM | |||
|---|---|---|---|---|---|---|
| Period | NF | FF | NF | FF | NF | FF |
| ipsl-cm5a-lr | 24.4 aA | 20 cC | 23.9 a | 23.3 d | 26.5 A | 15.5 D |
| miroc-esm-chem | 20.7 aA | 26.4 cC | 24 a | 26.8 c | 18.4 B | 14.8 D |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gautam, S.; Costello, C.; Baffaut, C.; Thompson, A.; Svoma, B.M.; Phung, Q.A.; Sadler, E.J. Assessing Long-Term Hydrological Impact of Climate Change Using an Ensemble Approach and Comparison with Global Gridded Model-A Case Study on Goodwater Creek Experimental Watershed. Water 2018, 10, 564. https://doi.org/10.3390/w10050564
Gautam S, Costello C, Baffaut C, Thompson A, Svoma BM, Phung QA, Sadler EJ. Assessing Long-Term Hydrological Impact of Climate Change Using an Ensemble Approach and Comparison with Global Gridded Model-A Case Study on Goodwater Creek Experimental Watershed. Water. 2018; 10(5):564. https://doi.org/10.3390/w10050564
Chicago/Turabian StyleGautam, Sagar, Christine Costello, Claire Baffaut, Allen Thompson, Bohumil M. Svoma, Quang A. Phung, and Edward J. Sadler. 2018. "Assessing Long-Term Hydrological Impact of Climate Change Using an Ensemble Approach and Comparison with Global Gridded Model-A Case Study on Goodwater Creek Experimental Watershed" Water 10, no. 5: 564. https://doi.org/10.3390/w10050564
APA StyleGautam, S., Costello, C., Baffaut, C., Thompson, A., Svoma, B. M., Phung, Q. A., & Sadler, E. J. (2018). Assessing Long-Term Hydrological Impact of Climate Change Using an Ensemble Approach and Comparison with Global Gridded Model-A Case Study on Goodwater Creek Experimental Watershed. Water, 10(5), 564. https://doi.org/10.3390/w10050564






