1. Introduction
Design flood estimation is often required by engineers, hydrologists, and agriculturalists for the design of hydraulic structures, such as dams, bridges, or culverts. The choice of design flood values has a great impact not only on the investment and benefit of the project, but also on the safety of the infrastructures [
1,
2,
3,
4].
When sufficiently long observed flow records (the annual maximum peak discharge or flood volume series) at the interest site are available, the design flood values are generally estimated from flood frequency analysis. The main modeling problem in flood frequency analysis is the selection of a probability distribution for flood magnitudes coupled with the choice of parameter estimation procedures [
5]. Probability distributions provide the essential basic formulae to model a flood quantile in terms of its exceedance probability. Once a distribution is selected, the next step is to estimate its parameters. Different probability distributions are proposed and used depending on, among others, the climatic and the geographical characteristics of the study region. In the United States, the log-Pearson type III (LP3) distribution is recommended as the candidate distribution for defining the annual maximum flood series, and the method of moments is used to determine the statistical parameters [
6]. The Pearson type III (P3) distribution and curve fitting procedure are recommended by the Ministry of Water Resources of China as a standard procedure for flood frequency analysis [
3]. The Generalized Logistic (GL) distribution is found to be more suitable for United Kingdom (UK) flood data [
7]. The L-moments approach is preferred for parameter estimation because of its robust properties in the presence of usually small or large values (outliers) and is recommended by many authors. However, this conventional flood frequency analysis method is mainly concentrated on the analysis of annual maximum flood series in the natural condition.
In recent decades, many reservoirs have been built in river basins for flood prevention, hydropower generation, and water supply to meet the need of world population growth and rapid social economy development [
2,
8,
9]. Reservoirs cause important changes in the river regime downstream by altering the spatial and temporal distribution of the river flow [
10]. During the flood season, a reservoir stores flood runoff and it then releases downstream to the channel over a longer period of time. This operation reduces the peak discharge of inflow, resulting in lower water-surface elevation and less damage [
11]. In this case, the observed flood records at the downstream site are no longer natural due to the operation of upstream reservoirs. Correspondingly, the discharge magnitude-frequency curve (or design flood values) in the natural condition can not represent the real flood regime and characteristic under the long-term condition [
12,
13]. Therefore, the operation rules of the upstream reservoirs should be involved in the estimation of the downstream design floods. Unfortunately, few research works considering this impact could be found in the reference literature.
Under the influence of upstream reservoirs, the inflow contributing watersheds to downstream site consists of various sub-basins (including reservoir sites and interval basins) and the inflow of reservoirs has been transformed into outflow by man-made operation rules. This situation makes the determination of design flood values at the downstream site very complex and difficult. The impact of reservoirs operation on the downstream design floods depends on (1) the characteristics of the reservoirs, e.g., capacity and operation rules, for that the reservoir capacity limits the amount of runoff that can be collected and held for release at a non-damaging rate, and the operation rules determine the manner of release; (2) the proportion of reservoir inflow to flood that occurred at the downstream site. The proportion of reservoir site governs the amount of runoff that the reservoir can control, since a reservoir will store only inflow from the upstream area [
11]. In general, the bigger the proportion of upstream reservoir basin, the larger the impact of reservoir on design floods at downstream.
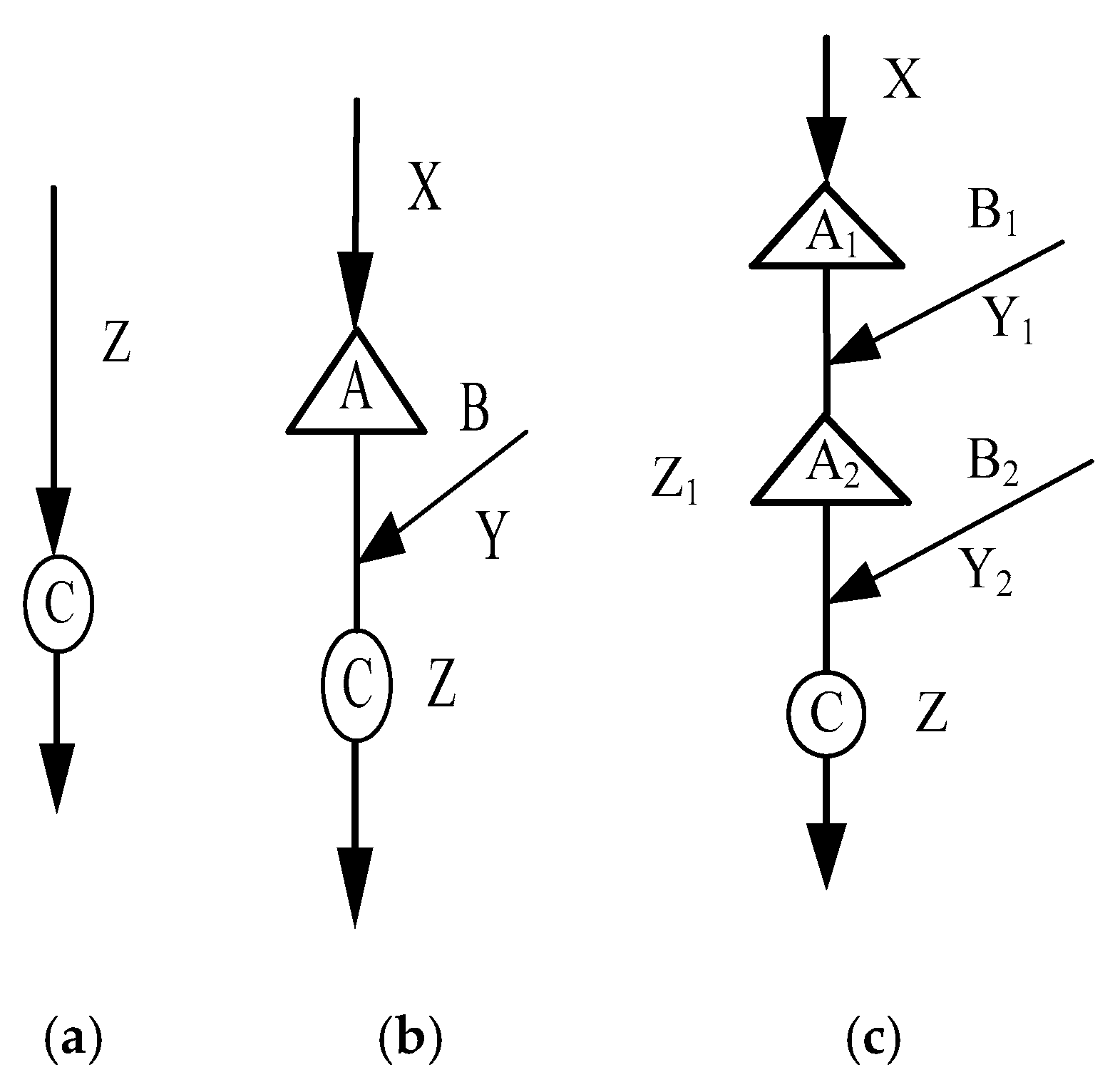
Conventionally, the general framework of flood regional composition is used to determine the design flood values at downstream site of reservoirs. This general framework includes two steps [
13]. First, it is assumed that there are no reservoirs exist and various sub-basins are in the natural condition. A design flood event with probability
p is selected from the natural flood magnitude-frequency curve at downstream site. It requires searching for appropriate combinations of floods that occurred at various sub-basins in the natural condition. The corresponding natural design flood hydrograph at various sub-basins are derived by using the same flood amplification ratio of their respective typical flood hydrograph [
14,
15]. Then, the design flood at the downstream site under the influence of upstream reservoir can be obtained through flood routing by incorporating operation rules. The influenced design flood is assigned the same probability
p as that of the natural condition.
When the characteristics of the reservoir are determined, the most important issue is to find an appropriate combination of floods that occurred at various sub-basins [
16]. It can be easily seen that the number of possible flood regional combination is countless. But, these infinite combinations are generally not equivalent from a practical point of view. Indeed, different combination can result in different design flood values at downstream site under the influence of upstream reservoirs. Moreover, the combinations differ also in terms of their probability of occurrence, which is measured by the joint probability density function. Therefore, how to select appropriate combinations (i.e., flood regional composition method) is extremely important. In practice, several combinations, such as the most likely, the worst, and the best combinations, should be selected to evaluate the impact of upstream reservoirs on design flood at downstream site [
17].
The Equivalent Frequency Regional Composition (EFRC) method has been recommended by the Ministry of Water Resources of China [
3]. However, the EFRC method deems perfect correlation between peak floods that occurred at one sub-basin and downstream site, which implicitly assumes that the rainfall and the hydrologic surface process are uniformly distributed for all of the sub-basins. In real case, there are different correlations (or dependence) between the sub-basins due to spatial and temporal variation of rainfall and land surface process. It therefore often makes the design flood fails to meet the flood prevention standard at the downstream site since the resulting design flood value is neither the most likely nor the worst composition. Furthermore, the currently used EFRC method can only be applied step by step to complex cascade reservoirs, which is not only difficult to implement, but is also subjective to some degree [
3,
13]. Flood regional composition is the stochastic combinations of flood variables (peak or volume) at different sub-basins, and the scientific way to analyse this problem is based on the joint distribution of these related variables. In recent years, much progress has been made in the method of joint probability distribution simulation, including the successful application of copula functions in hydrology. Copulas have been introduced in hydrology by De Michele and Salvadori in 2003 [
18]. The first multivariate frequency analysis and return period calculation, multivariate design, multivariate hazard scenarios, and corresponding failure probabilities were given by Salvadori and De Michele [
19], Salvadori et al. [
20,
21]. There are manifold advantages in using copulas to model joint distributions: they give (a) flexibility in choosing arbitrary marginal distribution and structure of dependence; (b) easier extension to more than two variables; and, (c) separate analysis of marginal distribution and dependence structure [
12,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33]. Therefore, the copula function can offer an effective tool to search for appropriate flood regional compositions.
This study aims to improve the flood regional composition method for design flood estimation of cascade reservoirs. The structure of the paper is as follows.
Section 2 outlines the general framework of the flood regional composition and briefly introduces the currently used EFRC method.
Section 3 presents the methodology of two flood regional composition methods, i.e., the Conditional Expectation Regional Composition (CERC) method and the Most Likely Regional Composition (MLRC) method based on the copula function.
Section 4 reports a case study of the Shuibuya-Geheyan-Gaobazhou cascade reservoirs that were located at the Qingjiang River, which is a tributary of Yangtze River in China using the two proposed methods and compared with the EFRC method.
Section 5 contains some discussions.
Section 6 summarizes the conclusions.
3. Flood Regional Composition Methods Based on Copulas
In order to overcome the drawbacks of the EFRC method, two flood regional composition methods that can suit for arbitrary (perfect or not perfect) correlation are proposed both for single reservoir and cascade reservoirs that are based on copulas. The concept and procedure of the methods are described in following.
3.1. Joint Distribution Based on Copulas
Multivariate distribution construction using copulas was developed by Sklar [
34]. Every joint distribution can be written in terms of a copula and its univariate marginal distributions. Copula is a function that connects multivariate probability distribution to its one-dimensional marginal distributions [
35]. Let
Fxi(
xi) (
i = 1, 2, …,
n) be the marginal cumulative distribution functions (CDFs) of
Xi, the objective is to determine the multivariate distribution, which is denoted as
Hx1,x2,…,xn(
x1,
x2,
…,
xn) or simply
H. Thus, the multivariate probability distribution
H is expressed in terms of its margins and the associated dependence function, which is known as Sklar’s theorem:
where
C is copula and uniquely determined whenever
Fxi(
xi) are continuous, and captures the essential features of the dependence among the random variables.
Different families of copulas have been proposed and described by Nelsen [
35]. The Archimedean family is selected in our study because it can be easily constructed and applied to whether the correlation among the hydrological variables is positive or negative [
20,
28,
29]. A large variety of copulas belong to this family. Four one-parameter Archimedean copulas, including the Gumbel-Hougaard (GH), Ali-Mikhai-Haq, Frank, and Cook-Johnson copulas, have been applied in frequency analysis by many authors [
12,
23,
24,
25,
26].
Among the four Archimedean copulas, the GH copula functions are the most widely used to construct the joint distribution of flood peak flows or flood volumes. The two-dimensional GH copula function is defined as [
23]:
where
C(
u,
v) is the two-dimensional copula function;
u and
v represent the marginal distribution functions; and,
θ is the dependence parameter of copula, which can be estimated by Equation (9):
where
is the Kendall’s tau correlation coefficient. It is assumed that for a random sample of bivariate observations (
x1,
y1), (
x2,
y2), …, (
xN,
yN), the Kendall’s tau
can be computed as [
23]:
where
N is the number of observations; sign = 1 if (
xi −
xj) (
yi −
yj) > 0; sign = −1, if (
xi −
xj) (
yi −
yj) < 0;
i, j = 1, 2, …,
N.
The three-dimensional asymmetric GH copula function is defined as [
26]:
where
C(
u,
v,
w) is the three-dimensional copula function;
u,
v, and
w represent the marginal distribution functions, respectively;
θ1 and
θ2 are the dependence parameters of copula, which can be estimated by the maximum likelihood method [
36].
The Cramer-von Mises test is used to measure the goodness of fit of the copula distribution [
37,
38]. The approximate
p-value is computed by [
39]
where
T and
Tb denote the test statistic and the bootstrapped test statistic, respectively.
N is the number of bootstrap iterations.
3.2. Conditional Expectation Regional Composition (CERC) Method
The corresponding flood volume
Y at the interval basin B is not unique given the flood volume of reservoir A site
X = x. The occurrence probability of the case
Y ≤
y varies with
x, and the conditional CDF of
Y can be expressed as
where
FY|X(
y|
x) is the conditional CDF of
Y given
X =
x, and
P is the non-exceedance probability.
Given
, the conditional expected value of
Y is given by Equation (14):
where
fY|X(
y|
x) is the conditional density function,
fY|X(
y|
x)
= d[
FY|X(
y|
x)]/
dy.
The CDFs of
X and
Y are
FX(
x) and
FY(
y), respectively. Let
U = FX(
x) and
V = FY(
y). Then,
U and
V are uniformly distributed random variables; and,
u denotes a specific value of
U, and
v denotes a specific value of
V. Using the copula function, the joint CDF
F(
x,y) can be expressed as
F(
x,y)
= C(
FX(
x),
FY(
y))
= C(
u,
v) [
35].
The conditional CDF
FY|X(
y|
x) and PDF
fY|X(
y|
x) can be expressed by Equations (15) and (16) using copula function, respectively.
where
is the density function of
, and
;
is the PDF of
Y.
Thus, Equation (14) can be rewritten as
Changing the integral variable from
y to
v, with the corresponding integral interval from (
) to [0, 1], the Equation (17) can be expressed as
where
is the inverse function of CDF
.
If
can satisfy the water balance Equation (19), then [
,
] is the CERC for single reservoir system.
For cascade reservoirs, let X, Y1, and Y2 be random variables with marginal CDFs, , , and , corresponding PDFs, , , and . and are the two-dimensional copula functions with PDFs and . and are the inverse functions of CDF and , respectively.
Given
,
and
are the conditional expected values of
Y1 and
Y2, respectively, which also can be calculated taking Equation (18) for reference. If
can satisfy the water balance Equation (20), then the [
,
,
] is the CERC for cascade reservoirs system.
3.3. Most Likely Regional Composition (MLRC) Method
As discussed above, all the possible flood regional compositions differ in terms of their probability of occurrence, which can be measured by the value of joint PDF of random variables
X and
Y, i.e.,
f(
x,
y), as follows [
35]:
where
fx(
x) is the PDF of
X.
The combination (
x,
y) is more likely to occur when the value of density function
f(
x,
y) is increased [
20]. In order to search for the MLRC, the
f(
x,
y) is maximized by subjecting water balance constraint in Equation (1) for given
Z =
zp. Substituting
y =
zp −
x to Equation (21), then it leads to
In China,
X and
Y are usually considered to follow the P3 distributions [
3]. The density functions of the P3 distribution and copula functions are continuous and unimodal [
33,
40]. Therefore, the joint probability density function
f(
x, zp −
x) must be continuous and unimodal. In this case, the first order derivative equals to zero will reach the maximum value, and the following equation should be satisfied
After simplification, Equation (23) leads to
where
,
,
;
and
are the corresponding derived functions of PDFs.
The corresponding marginal PDFs of
X and
Y can be expressed as [
3,
41]:
where
,
,
and
,
,
are the shape, scale, and location parameters of P3 distributions for
X and
Y, respectively;
is the gamma function.
Then,
and
can be represented as:
Then, Equation (24) can be rewritten as
The dichotomy method can be used to solve nonlinear Equation (31), and the MLRC for single reservoir system (x, zp − x) will be obtained.
For cascade reservoir, the joint PDF of random variables
X,
Y1, and
Y2 can be expressed, as follows [
42,
43]:
where
is the PDF of
C(
u,
v,
w), and
=
.
For given
Z =
zp, the
f(
x,
y1,
y2) is maximized subjected to water balance constraint in Equation (2). Substituting
y2 =
zp −
x −
y1 to Equation (32) leads to
Similarly, the first order derivative
f(
x,
y1,
zp −
x −
y1) that is equal to zero will reach the maximum value, and the following equation should be satisfied
After simplification, Equation (34) lead to
where
,
,
and
;
,
and
are the corresponding derived function of the PDFs.
If
X,
Y1, and
Y2 all follow the P3 distributions, taking Equations (25) to (30) for reference, then Equation (35) can also be rewritten as
where
,
,
;
,
,
and
,
,
are the three (shape, scale and location) parameters of P3 distributions for
X,
Y1, and
Y2, respectively. The Newton iteration method is used to solve nonlinear Equation (36), and the MLRC for cascade reservoirs system (
x,
y1,
zp, x,
y1) will be obtained.
4. Case Study
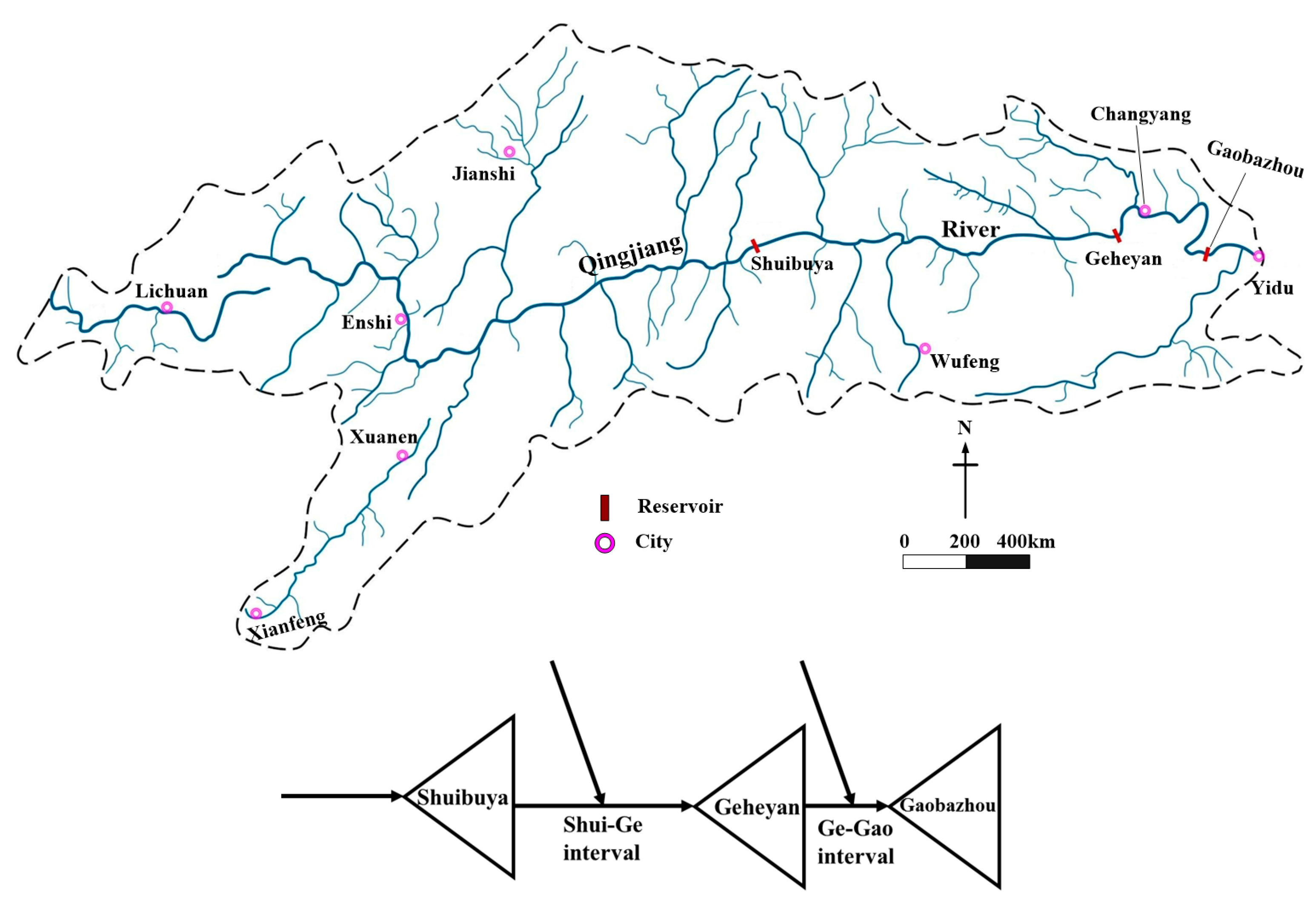
To exemplify the proposed methods, the Qingjiang cascade reservoirs in China are selected. As shown in
Figure 2, the Qingjiang River is one of the main tributaries of Yangtze River with a basin area of 17,000 km
2. The mean annual rainfall, runoff depth, and annual average discharge are approximately 1460 mm, 876 mm, and 423 m
3/s, respectively. The total length of the mainstream is 423 km with a hydraulic drop of 1430 m.
Along the Qingjiang River, a three-step cascade (Shuibuya, Geheyan, and Gaobazhou) reservoir has been constructed from upstream to downstream. The characteristic parameter values of these three reservoirs are given in
Table 1. The areas of the two interval basins, one is between Shuibuya and Geheyan reservoirs (Shui-Ge interval basin), and the other is between Geheyan and Gaobazhou reservoirs (Ge-Gao interval basin), are 3570 km
2 and 1220 km
2, respectively. In this case study, design floods of the Gaobazhou reservoir site are estimated under the impact of Geheyan reservoir and Shuibuya-Geheyan cascade reservoirs operation, respectively; and, the results are compared with those of the natural condition to quantitatively evaluate the impact of upstream reservoirs.
4.1. Natural River Flow Discharge Data Series
A common problem in the statistical analysis of river flow discharges is that watershed changes have occurred during the period of record so that values reflect a nonstationary condition. If the changes are mainly due to the construction of reservoirs, it is possible to adjust flow at a downstream gauge to natural condition by routing reservoir holdouts (increments of stored water) to the hydrologic gauge station adding the routed discharge to the observed discharge. The water balance equation is used to restore natural flow [
11], i.e., the stored water flow discharge of the reservoir is
where
V(
t) and
V(
t, 1) are reservoir storages at the end of interval
t and
t − 1, respectively (m
3); Δ
t is the length of time interval (s); and,
QS is the stored water flow discharge (m
3/s).
The natural river flow discharge at gauge station is
in which
where
QN and
QO are the natural and observed river flow discharges at gauge station, respectively (m
3/s);
QR is the reservoir stored water flow routed to the gauge station by the Muskingum method (m
3/s);
C1,
C2,and
C3 are routing coefficients that are defined in terms of Δ
t, K (storage-time constant), and
x (weighting factor), and they can be estimated by the Least Square method. In this study,
K and
x are eaual to 2 h and 0.45, respectively.
The Shuibuya, Geheyan, and Gaobazhou cascade reservoirs have been built in the year of 2008, 1994, and 2001, respectively. There are three hydrologic gauge stations at these dam sites before the construction of reservoir, where the river flow discharge are observed. Therefore, the natural river flow discharge data series (from 1965 to 2010 with 3 h time interval) are restored and obtained by the above method.
There is no flow gauge station in the interval areas and the lateral flow is estimated by water balance equation and the Muskingum routing method. Taking the Shui-Ge inter-basin as an example, the lateral flow
Qsg is estimated by
where
Qs and
Qg are the natural river flows of Shuibuya and Geheyan dam sites, respectively.
Qs~g represents the natural river flow discharge at the Shuibuya dam site that was routed to the Geheyan dam site by the Muskingum routing method [
44,
45].
The procedure introduced above is a standard procedure used in China for restoring river flow discharge data influenced by upstream reservoir. The data used in this study were provided by the Bureau of Hydrology of Yangtze River Water Resources Commission. They are reliable and have been widely used in the planning, design, operation, and management of water resources in the Qingjiang River basin.
4.2. Operation Rules of Shuibuya and Geheyan Reservoirs
As shown in
Table 1, the flood limited water level (FLWL) of the Shuibuya and Geheyan reservoirs during flood season are 391.8 m and 192.2 m (a.m.s.l.), respectively. The flood control operation rules of Shuibuya reservoir are described, as follows [
46,
47]:
- (1)
If the inflow discharge is less than or equal to the design peak flow with probability 5% (the return period is 20 years), then the reservoir water level is controlled within 397 m (a.m.s.l.);
- (2)
If the inflow discharge is greater than the design peak discharge with a probability of 5% (the return period is 20 years), but less than the spillway capacity, then the reservoir outflow equals to the inflow; otherwise, the reservoir outflow equals to the spillway capacity.
The flood control operation rules of Geheyan reservoir are described as follows [
46,
47].
- (1)
If the inflow discharge is less than or equal to 11,000 m3/s, then the outflow of reservoir equals to the inflow;
- (2)
If the inflow discharge is larger than 11,000 m3/s and reservoir water level is less than 200.0 m (a.m.s.l.), then the outflow of reservoir is controlled within 11,000 m3/s;
- (3)
When the reservoir water level has reached 200.0 m (a.m.s.l.), if the inflow discharge is less than or equal to 13,000 m3/s, then the outflow of reservoir is equal to the inflow; if the inflow discharge is larger than 13,000 m3/s and the reservoir water level is less than 203.0 m (a.m.s.l.), then the outflow of reservoir is controlled within 13,000 m3/s; and,
- (4)
When the reservoir water level has reached 203.0 m (a.m.s.l.), if the inflow discharge is larger than 13,000 m3/s and less than the spillway capacity, then the outflow of reservoir is equal to the inflow; otherwise, the outflow of the reservoir is equal to the spillway capacity.
4.3. Estimation of Marginal Distributions
According to the regulation characteristics of Shuibuya-Geheyan cascade reservoirs, three-day natural flood volumes (
W3) at Shuibuya, Geheyan, and Gaobazhou reservoir sites, Shui-Ge and Ge-Gao inter-basins, and natural peak flow (
Qm) at Gaobazhou reservoir site are all i.i.d. random variables and are assumed to follow P3 distributions. The parameters of these six P3 distributions are estimated by the curve-fitting method [
3], and the results are listed in
Table 2. A Chi-Square Goodness-of-fit test is performed to test the assumption,
H0, that the flood magnitudes follow the P3 distribution.
Table 2 shows that the assumption could not be rejected at the 5% significance level.
4.4. Determinations of Joint Distributions
To study the impact of the Geheyan reservoir, both the CERC method and MLRC method need the (a) bivariate distribution of W3 at Geheyan reservoir site and Ge-Gao inter-basin. To study the impact of Shuibuya-Geheyan cascade reservoirs, CERC method needs (b) bivariate distributions of W3 at Shuibuya reservoir site and Shui-Ge inter-basin, and (c) bivariate distributions of W3 at the Shuibuya reservoir site and Ge-Gao inter-basin. While MLRC method needs, the (d) trivariate distribution of W3 at the Shuibuya reservoir site, Shui-G and Ge-Gao inter-basins. In this case study, these four (one for single reservoir and three for cascade reservoirs) joint distributions are used and are constructed using the GH copula functions, respectively.
Dependence parameters of the four joint distributions are estimated using Equation (9) or maximum likelihood method that is based on the observed data from 1965 to 2010 and the results are listed in
Table 3. The Cramer-von Mises test is used to measure the goodness of fit of the copula distribution. The
p-values of the four joint distributions are calculated and also listed in
Table 3. It is illustrated from
Table 3 that the assumption that variables (a) (b) (c), and (d) follow GH copula function cannot be rejected at 5% significance level with
p-values that are all larger than 0.05.
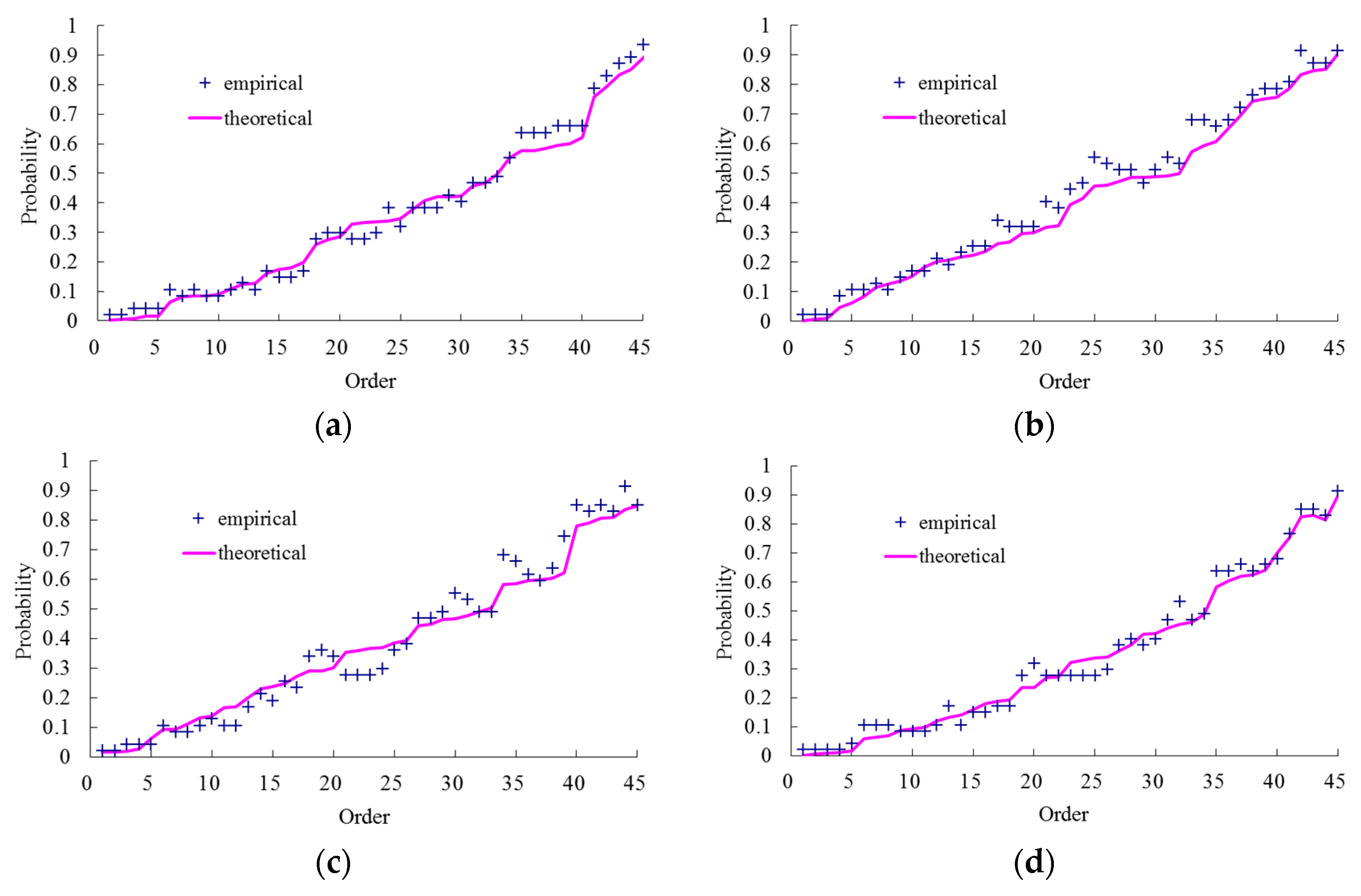
In flood frequency analysis, the Pearson type III distribution and the curve fitting method have been recommended by the Ministry of Water Resources, China [
3]. Here, we plot empirical and theoretical joint CDFs to test the fitting ability. A two-dimensional table is constructed in which the variables
X and
Y are arranged in ascending order. The empirical joint CDF (
Pei) can be computed by the Gringorten plotting-position formula [
23]:
where
Lm,n is the number of occurrences of the combinations of
xi and
yi.
Likewise, a three-dimensional table also can be constructed in which the variables
X,
Y and
Z are arranged in ascending order. The empirical joint CDF also can be computed by the Gringorten plotting-position formula [
25]:
where
Tm,n,r is the number of occurrences of the combinations of
xi,
yj, and
zk.
The empirical joint CDFs calculated by Equations (41) and (42) and theoretical values for four joint CDFs that are mentioned above are plotted in
Figure 3, which show an overall satisfactory agreement of between the empirical and theoretical joint CDFs.
4.5. The Impact of Geheyan Reservoir Operation
The EFRC, CERC, and MLRC methods for single reservoir were used to analyse flood regional composition of Geheyan reservoir site and Ge-Gao interval basin.
(1) EFRC method
It is assumed that the equivalent frequency floods occur at the Gaobazhou reservoir site and the Geheyan reservoir site, while the corresponding flood occurs at the Ge-Gao interval basin.
(2) CERC method
A given flood occurs at Geheyan reservoir site, while the conditional expected value occurs at Ge-Gao interval basin, and then the conditional expected composition can be determined by the trial and error method.
(3) MLRC method
The maximum value of joint PDF is taken as the objective to determine the most likely composition from the perspective of occurrence probability.
Flood regional compositions of design flood volume at the Gaobazhou reservoir site are calculated based on the three methods mentioned above. Therefore, the three-day flood volume proportions of Geheyan reservoir site and Ge-Gao interval basin are calculated, and the results are listed in
Table 4.
It is shown in
Table 4 that the proportions of the Ge-Gao interval basin are constant (8.3%) with different design frequencies at the Gaobazhou reservoir site by the EFRC method. The MLRC method exhibits that when flood with return period exceeding 20 years occurs at Gaobazhou reservoir site, the proportions of Geheyan reservoir site range from 89.0% to 89.9%, which is smaller than its proportion of area (92.2%); the proportions of the Ge-Gao inter-basin range from 10.1% to 11.0%, which is larger than its proportion of area (7.8%); it is also shown that the flood volume at the Gaobazhou reservoir site is largely dependent on the flood volume at the Geheyan reservoir site, and the proportion of the Geheyan reservoir site decreases gradually as design flood magnitude at the Gaobazhou reservoir site increases. Generally speaking, the bigger the flood proportion of the Geheyan reservoir site, the larger the impact on design floods at Gaobazhou the reservoir site.
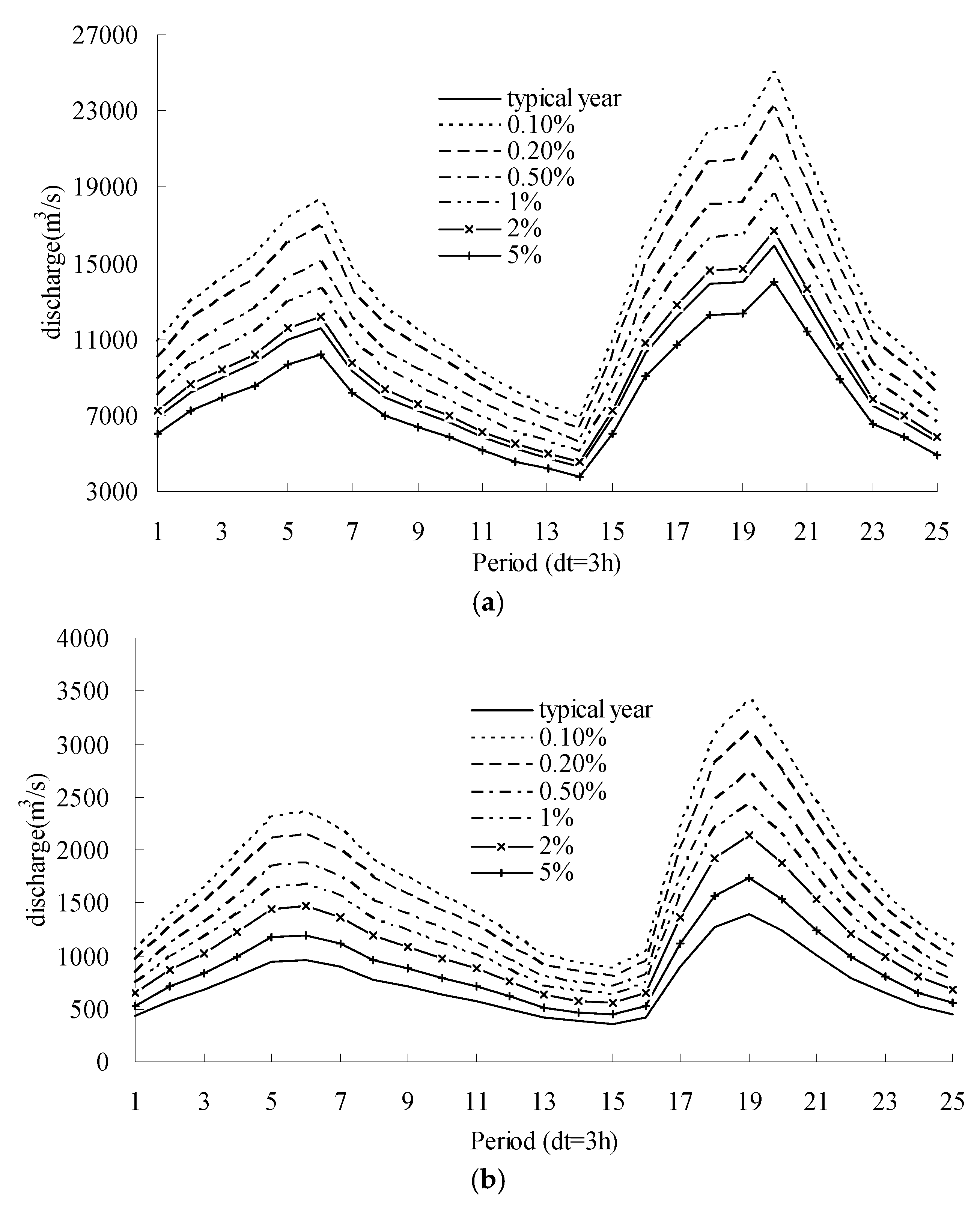
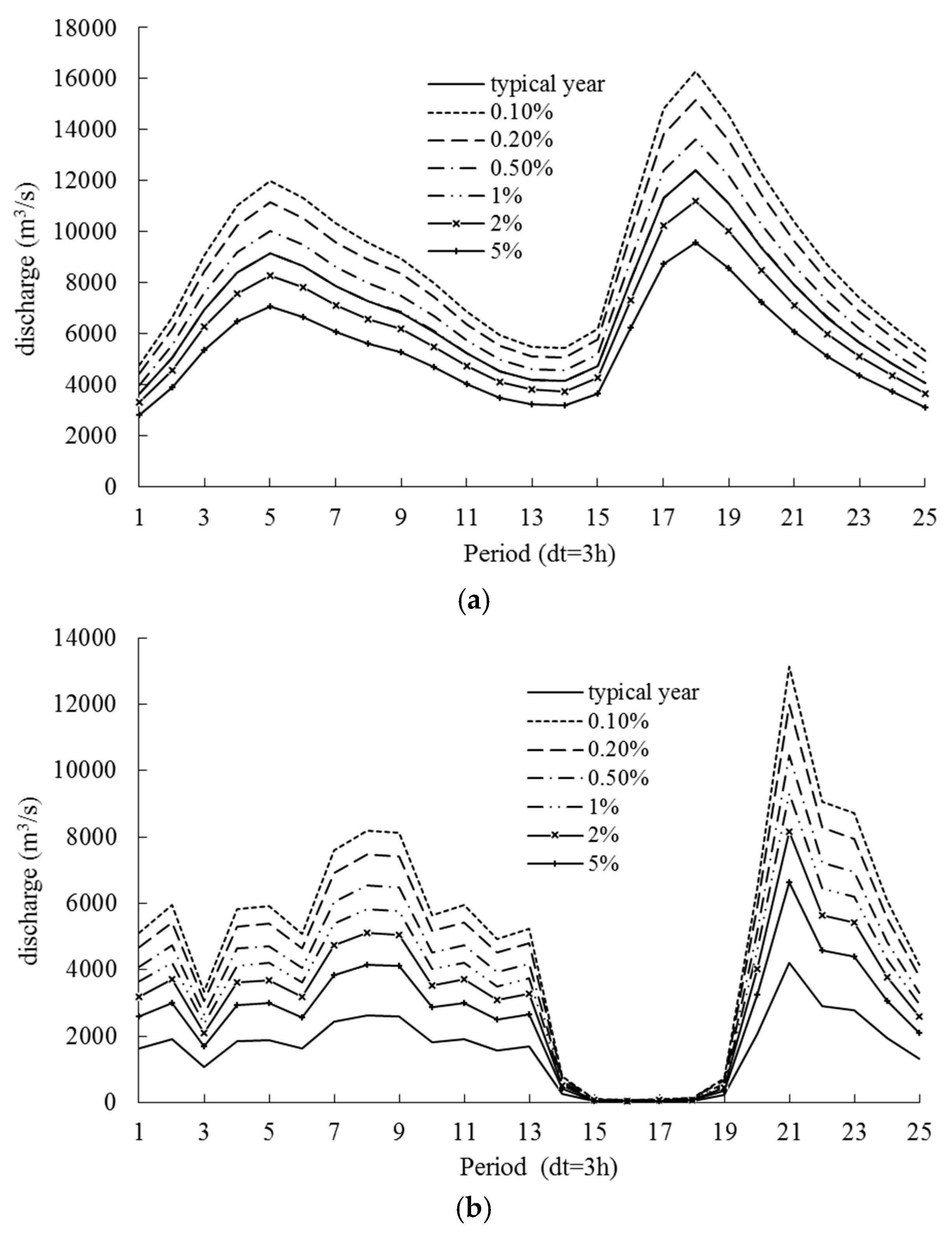
Maximum three-day flood hydrographs in 1997 are selected as the typical floods. The corresponding flood hydrographs with different design frequencies for these three methods at the Geheyan reservoir site and Ge-Gao interval basin are obtained by the same flood amplification ratio [
14,
15]. Taking the most likely method as an example, the results are plotted in
Figure 4.
For each method, the two design flood hydrographs at the Geheyan reservoir site and Ge-Gao inter-basin are routed through the Geheyan reservoir by taking into account of its operation rules (see
Figure 4). The peak discharges at the Gaobazhou reservoir site with different return periods by these three methods under the impact of upstream Geheyan reservoir operation are summarized in
Table 5, in which the Reduction Rate (RR) calculated by the following equation:
where
QN represents the peak discharge under natural condition;
QE is the peak discharge estimated by one of these methods (i.e., EFRC, CFRC, and MLRC) under the impact of upstream reservoir operation.
As shown in
Table 5, all of the design peak discharges at the Gaobazhou reservoir site have been reduced due to the impact of Geheyan reservoir operation, e.g., for 100-year design values, the reduction ranges from 5360 m
3/s to 5900 m
3/s. In general, the differences among the methods are not large. For return periods between 20 and 1000 years, the maximum variation of reduction rate among these three methods is about 3.3%. However, the design values of EFRC method are systematically smaller than those of the two methods based on copulas and thus yield an underestimation, which may lead to an increased risk in the hydrological design.
The CFRC and MLRC methods can better capture the spatial correlation of floods that occurred at the Geheyan reservoir site and the Ge-Gao inter-basin. Thus, these two methods with stronger statistical basis are found more reasonable to estimate design floods under the influence of Geheyan reservoir operation.
4.6. Impact of Shuibuya-Geheyan Cascade Reservoirs Operation
Similarly, these three methods were used to analyse flood regional compositions of the Shuibuya reservoir site, Shui-Ge and Ge-Gao inter-basins.
(1) EFRC method
It is assumed that the equivalent frequency floods occur at the Gaobazhou reservoir site and the Geheyan reservoir site, the corresponding flood occurs at Ge-Gao inter-basin; while the equivalent frequency floods also occur at Shuibuya reservoir site and Geheyan reservoir site, and the corresponding flood occurs at Shui-Ge inter-basin.
(2) CERC method
A given flood occurs at Shuibuya reservoir site, while the conditional expected values occur at the Shui-Ge and Ge-Gao inter-basins, respectively. Then, the conditional expected composition can also be determined by the trial and error method.
(3) MLRC method
The maximum value of joint PDF is taken as the objective to determine the most likely composition from the perspective of probability occurrence.
Flood regional compositions of design flood volume at the Gaobazhou reservoir site are calculated based on these three methods mentioned above. Therefore, the three-day flood volume proportions of Shuibuya reservoir site, Shui-Ge and Ge-Gao inter-basins are calculated and the results are listed in
Table 6.
It is seen from
Table 6 that the proportions of Ge-Gao inter-basin are constant (8.3%) with different design frequencies at the Gaobazhou reservoir site by the EFRC method. This consequence occurs because of the unreasonable assumption in the traditional EFRC method. The control area of Ge-Gao interval basin is 1220 km
2, constituting 7.8% of the control area of the Gaobazhou reservoir. In addition, the design floods of the Geheyan and Gaobazhou reservoirs are both based on the Changyang hydrological gauge station. The P3 parameters for annual maximum W
3 series for Geheyan and Gaobazhou reservoir are quite similar with scale and shape parameters almost equal to each other (
Table 2). Therefore, their design floods almost change by ratio and the proportions of Ge-Gao interval basin are approximately constant (8.3%) and independent of the design frequency under the equivalent frequency assumption. Results of the MLRC method exhibit that when flood with return period exceeding 20 years at Gaobazhou reservoir site occurs, the proportions of Shuibuya reservoir site range from 57.4% to 61.1%, which is smaller than its proportion of area (69.4%); the proportions of Shui-Ge inter-basin range from 29.2% to 31.8%, which is larger than its proportion of area (22.8%); the proportions of Ge-Gao inter-basin range from 9.7% to 10.8%, which is larger than its proportion of area (7.8%). It is also shown that the floods at the Gaobazhou reservoir site are mainly dependent on the floods at Shuibuya reservoir site, and the proportion of the Shuibuya reservoir site decreases gradually with the increase of the design flood magnitude at the Gaobazhou reservoir site.
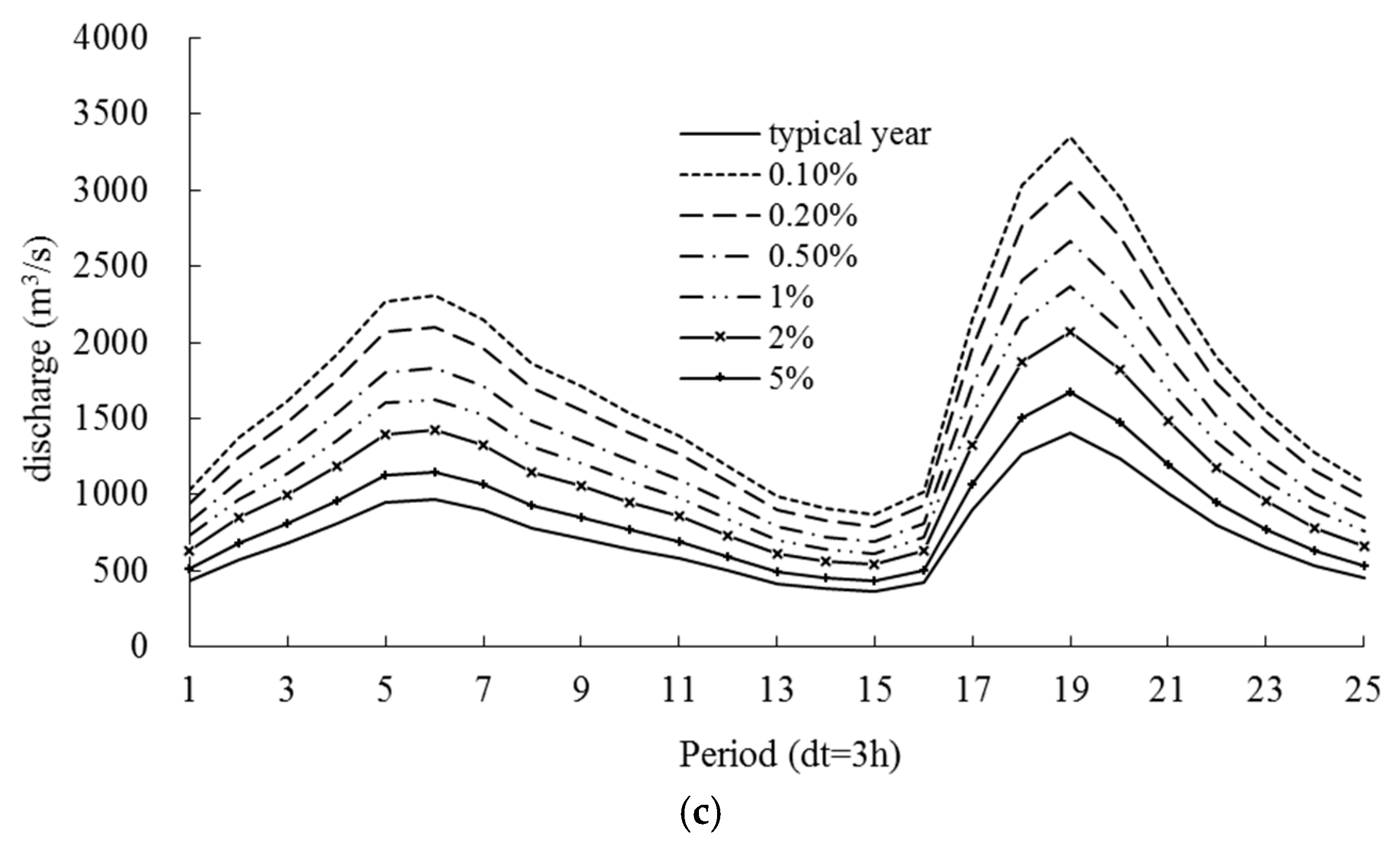
Maximum three-day flood hydrographs in 1997 are selected as the typical floods. The corresponding flood hydrographs with different design frequencies for the three methods at the Shuibuya reservoir site, Shui-Ge and Ge-Gao inter-basins are obtained by the same flood amplification ratio. Taking the MLRC method as an example, the results are plotted in
Figure 5.
For each method, the three design flood hydrographs at the Shuibuya reservoir site, Shui-Ge and Ge-Gao inter-basins are routed through the Shuibuya-Geheyan cascade reservoirs by taking into account of their respective operation rules (see
Figure 5). The flow hydrographs at Gaobazhou reservoir site are derived and the peak discharges under the influence of Shuibuya-Geheyan cascade reservoirs operation are obtained.
Peak flows at Gaobazhou reservoir site with different return periods in the natural condition and that estimated by three methods under the influence of Shuibuya-Geheyan cascade reservoirs are summarized in
Table 7. The reduction rate (RR), defined by Equation (46), and is also shown in
Table 7.
The results in the
Table 7 also imply that all of the design peak discharges at the Gaobazhou reservoir site have been reduced due to the impact of the upstream Shuibuya-Geheyan cascade reservoirs operation, e.g., for 100-year design peak flow, the reduction ranges from 6710 m
3/s to 6920 m
3/s. For return periods between 20- and 1000-year, the maximum variation of reduction rate among these three methods is about 3.0%.
It is found that the design values of EFRC method are smaller than those of the two methods that are based on copulas for return periods of 1000-, 500-, 100-, and 50-year, while greater for return periods of 200- and 20-year. It is suggested that the traditional EFRC method which assumes that the floods occurred at Gaobazhou reservoir site, Geheyan reservoir site and Shuibuya reservoir site are perfectly correlated may lead to an under- or overestimation of the risk in hydrological design. The CERC and MLRC methods have considered the actual spatial correlation of floods occurred at the Shuibuya reservoir site, Shui-Ge and Ge-Gao inter-basins. These two methods with a stronger statistical basis are also more reasonable than the EFRC method for estimating design floods under the impact of the Shuibuya-Geheyan cascade reservoirs operation.
5. Discussion
The design flood estimation results at the Gaobazhou reservoir site under the impact of Geheyan reservoir and Shuibuya-Geheyan cascade reservoirs were analyzed using three different methods. The findings and their implications are discussed, as follows.
The currently used EFRC method that assumes the perfect correlation (i.e., correlation coefficient is equal to 1) between peak floods occurred at one sub-basin and downstream site does not always conform to the actual situation. To overcome this drawback of the EFRC method, the CERC and MLRC methods that loose the assumption of perfect correlation are proposed. Compared with the EFRC method, the CERC and MLRC methods only add correlation coefficients (or parameters) of flood volumes between sub-basins. These parameters can be easily estimated by the available methods [
23,
28,
35]. The proposed methods are found to be more flexible in hydrological design compared with EFRC method.
Although no huge differences can be shown from the results estimated by EFRC, CERC, and MLRC methods in this case study, it should be noted that the Qingjiang basin belongs to a middle sized basin that the equivalent frequency flood at each sub-basin is likely to occur with downstream site.
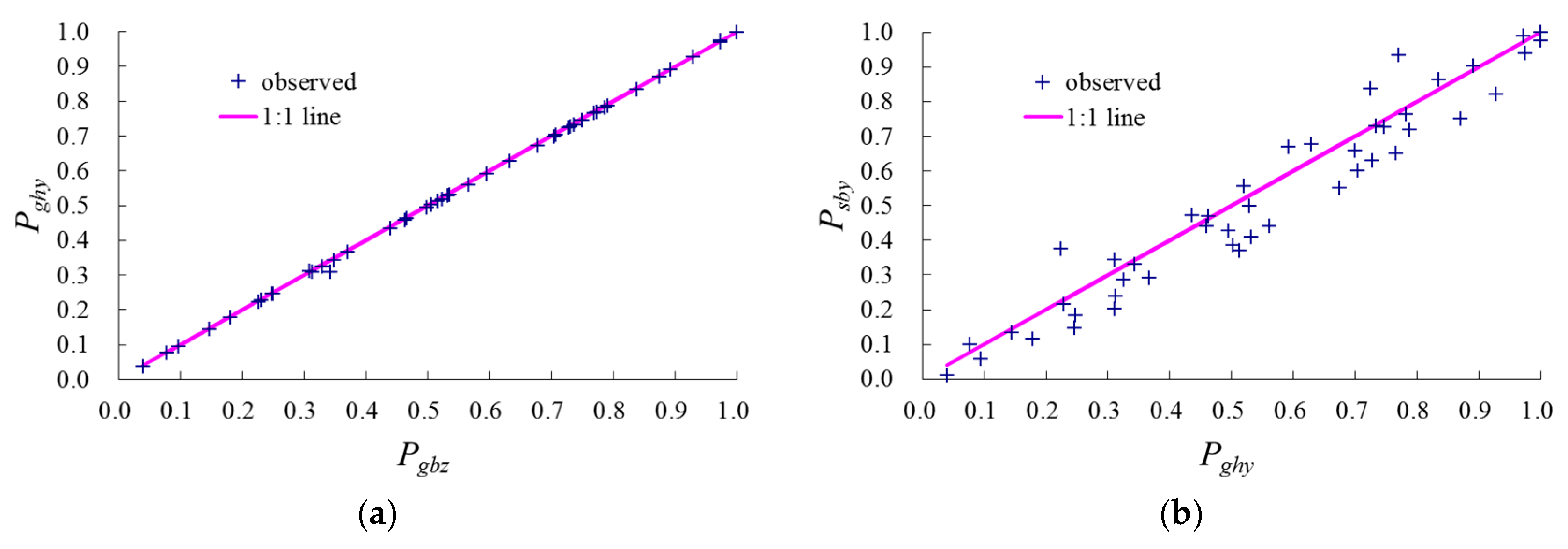
Figure 6 shows that differences between Ge-Gao and Shui-Ge inter-basins, on which
Psby,
Pghy, and
Pgbz represent the exceedance probability of 3-day flood volume for Shuibuya, Geheyan and Gaobazhou reservoir sites, respectively. The straight lines show the conditions when exceedance probability of three-day flood volume for Geheyan and Gaobazhou, Shuibuya and Geheyan are identical, respectively. It is seen that the equivalent frequency floods at Geheyan and Gaobazhou reservoir sites are more likely to occur in comparing with the Shuibuya and Geheyan reservoir sites. This difference is due to that the area proportion of Ge-Gao inter-basin (7.8%) is smaller than that of Shui-Ge inter-basin (24.7%). The difference of results for these methods will be increased as the proportion of the inter-basin area increases.
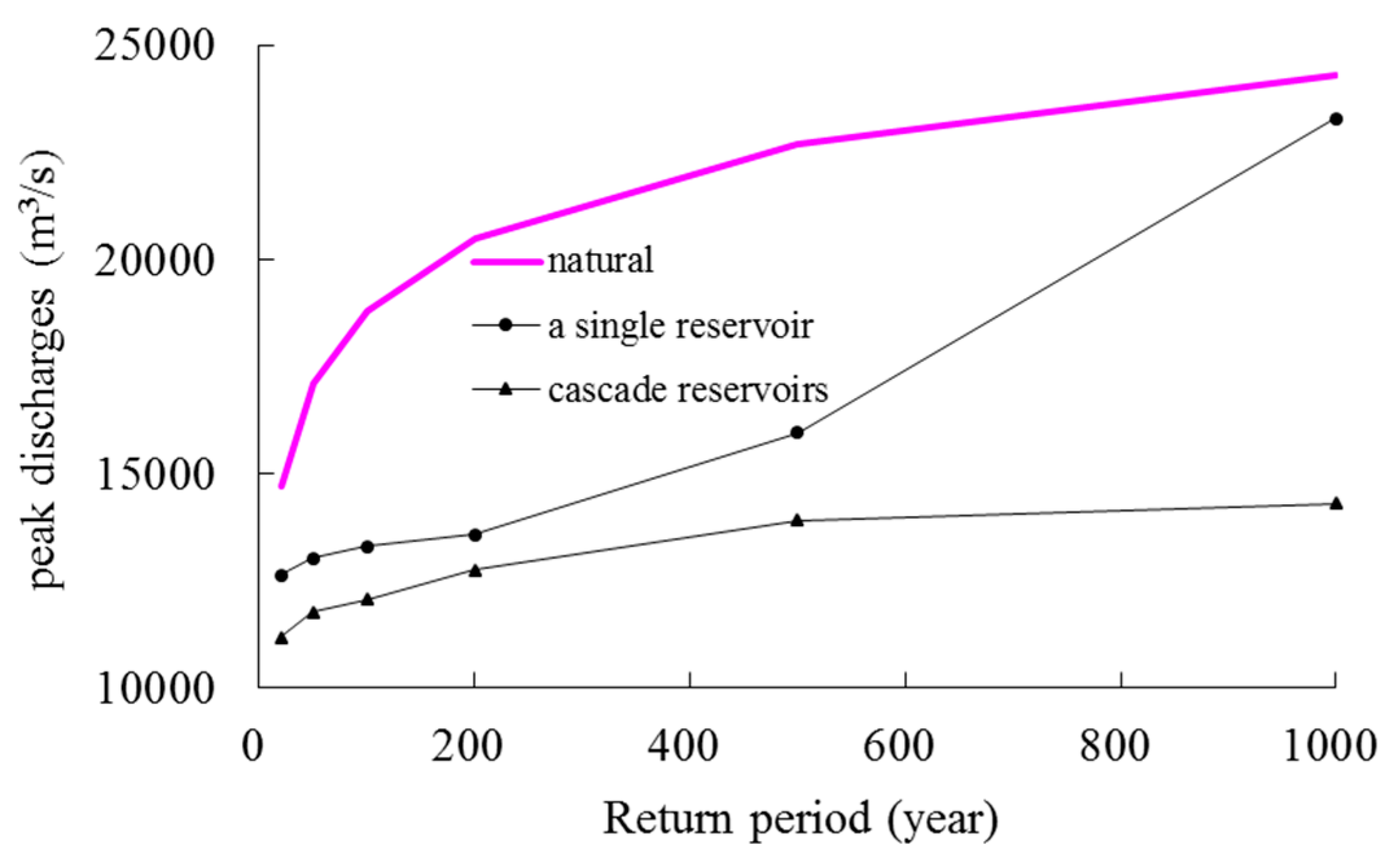
Design floods at the downstream site have been reduced by the regulation of upstream reservoirs as shown in
Figure 7. The peak discharges that were estimated at the downstream site involving the joint operation of the cascade reservoirs are reduced much more significantly than those of single reservoir being taken into consideration. For example, 100-year design peak flow (average of three methods) at the Gaobazhou reservoir site is cut by about 35% for cascade reservoirs.
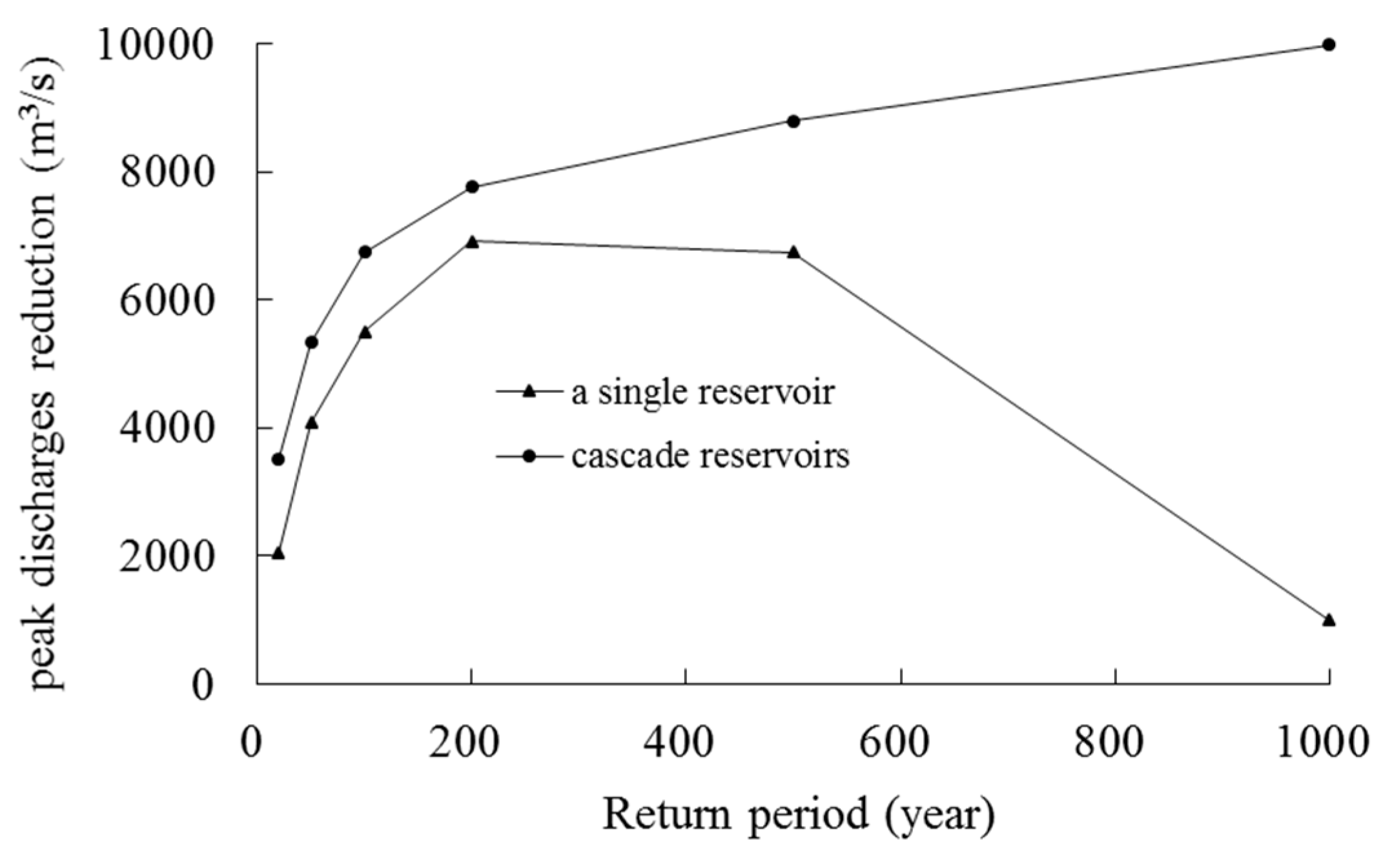
The cutting patterns of estimated peak discharges (average of three methods) at the Gaobazhou reservoir site are different for single and cascade reservoirs. As shown in
Figure 8, with the increase of design flood magnitude at the Gaobazhou reservoir site, the reduction curve increases firstly and it then decreases for single reservoir case, and the peak discharge reductions are 2140 m
3/s, 7060 m
3/s, and 1070 m
3/s corresponding with return periods of 20-year, 200-year, and 1000-year, respectively. While the reduction curve increases continuously for the cascade reservoirs and the peak discharge reductions are 3580 m
3/s, 7820 m
3/s, and 9980 m
3/s corresponding with 20-, 200-, and 1000-year return periods, respectively.