Flow Velocity Effects on Fe(III) Clogging during Managed Aquifer Recharge Using Urban Storm Water
Abstract
:1. Introduction
- chemical, including precipitation of elements (such as iron or aluminum), aquifer matrix dissolution, and temperature;
- physical, including suspended solids, interstitial fines migration, unintentional fracturing of the aquifer, and formation damage that occurs during bore construction;
- mechanical, including entrained air/gas binding;
- biological, including algae growth, and the presence of iron or sulfate reducing bacteria.
2. Materials and Methods
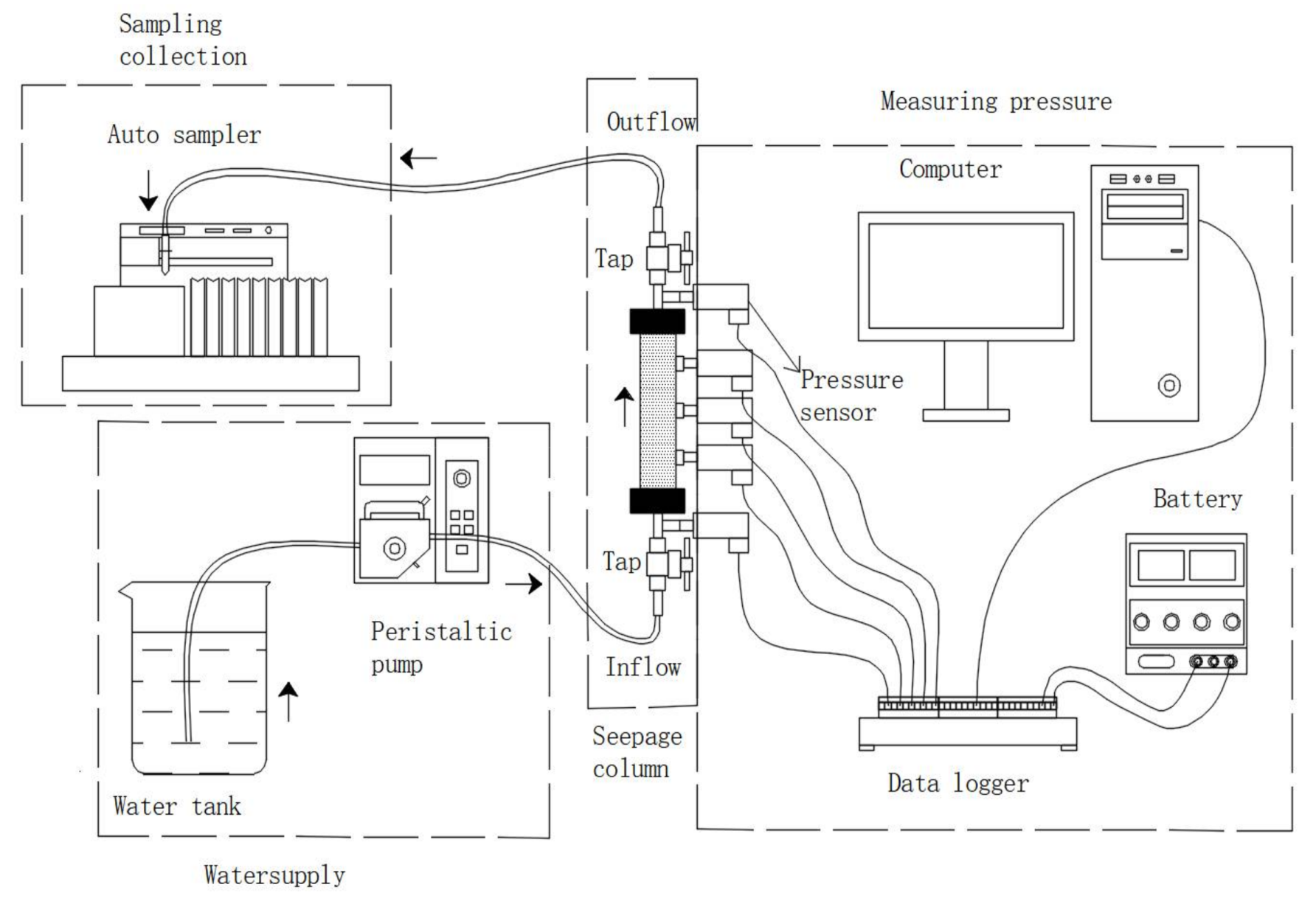
2.1. Experimental Apparatus
2.2. Column Hydraulic Properties
2.3. Analytical Measurements
2.4. Column Dismantling
3. Results and Discussion
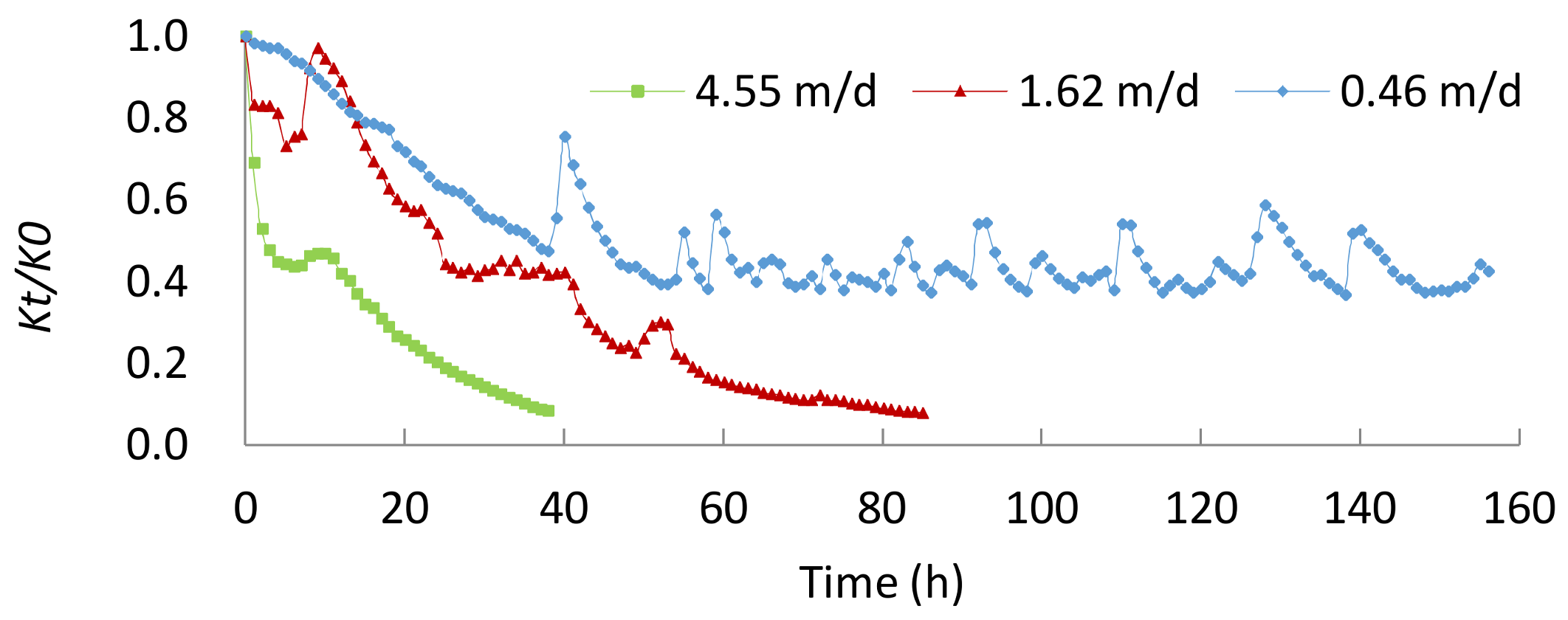
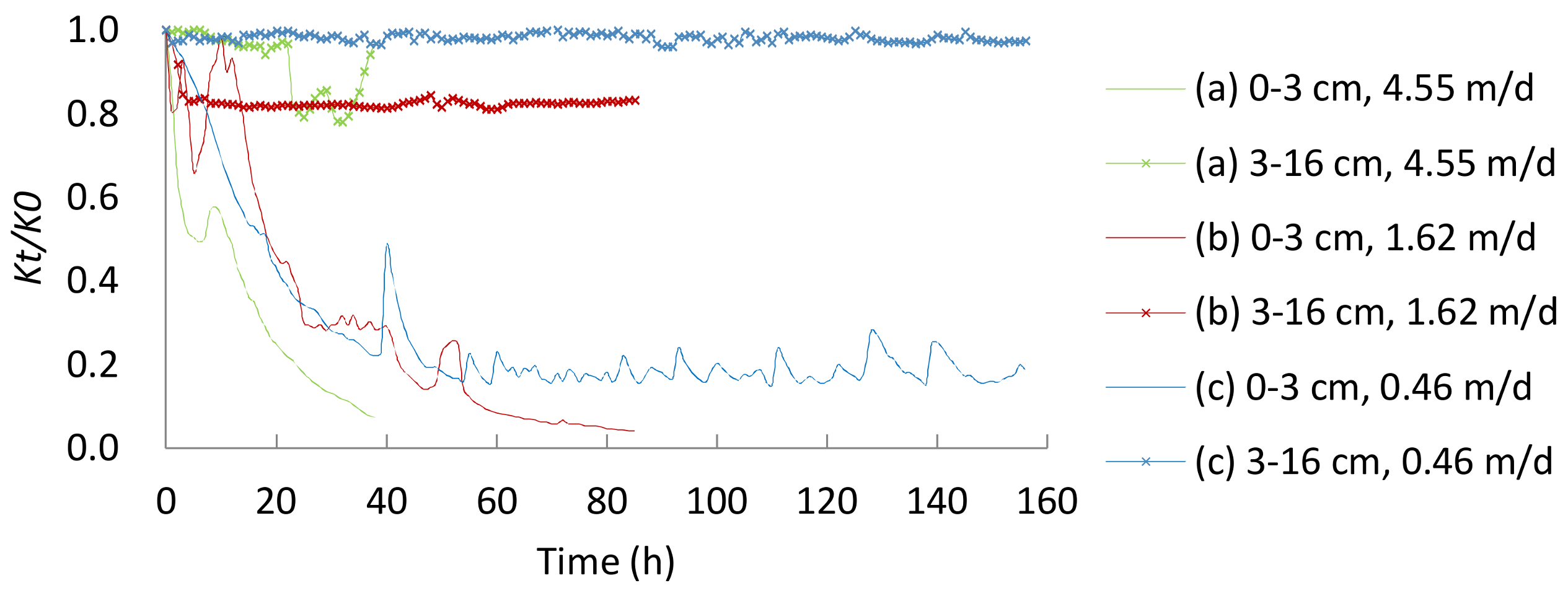
3.1. Hydraulic Conductivity Changes
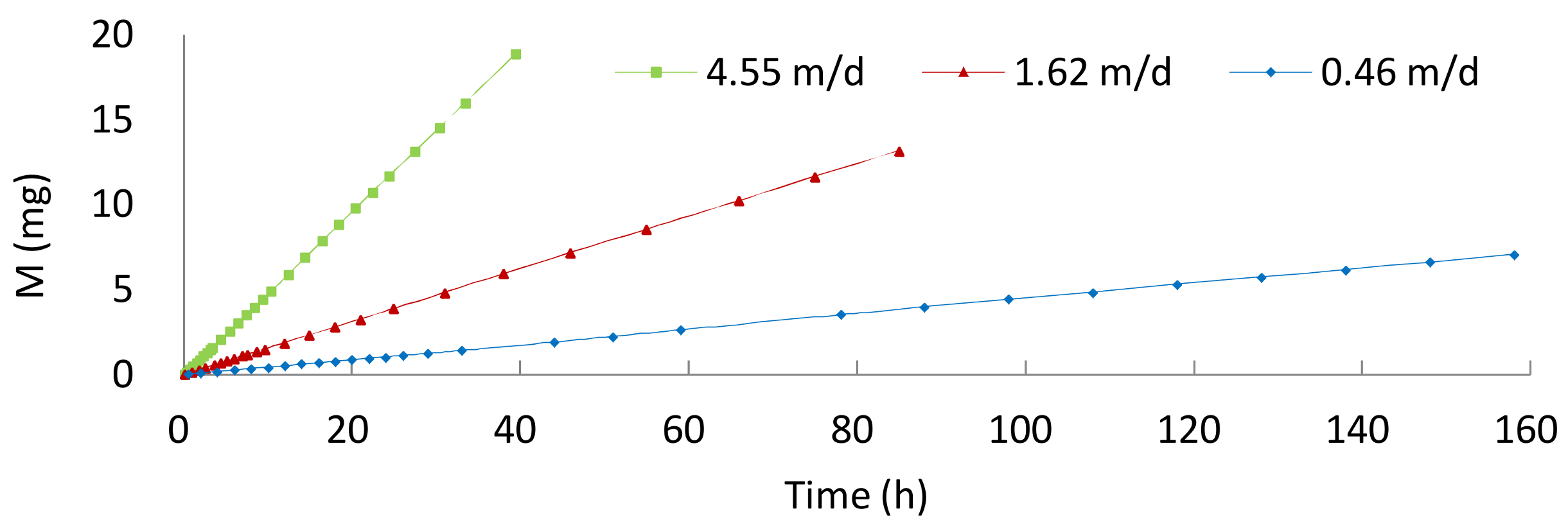
3.2. Mass Deposition
3.3. Fe(III) Clogging Mechanism
4. Conclusions
- (1)
- The form of Fe(III) in recharge water was Fe(OH)3 particles, which occupied the pore spaces of the inlet surface, leading to porous clogging. The main mechanism for the porous matrix intercept of Fe(OH)3 colloidal particles was surface filtration.
- (2)
- Deposition rates and porous media clogging depend on flow velocity. Increased flow velocity caused increased deposition and reduced hydraulic conductivity, i.e., increased clogging.
- (3)
- Physicochemical mechanisms, particularly orthokinetic flocculation, had severely affected by flow velocity. Higher velocities could promote Fe(OH)3 particle flocculent precipitation, increasing Fe(III) deposition mass, and hence decreasing hydraulic conductivity.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rinckpfeiffer, S.; Ragusa, S.; Sztajnbok, P.; Vandevelde, T. Interrelationships between biological, chemical, and physical processes as an analog to clogging in aquifer storage and recovery (ASR) wells. Water Res. 2000, 34, 2110–2118. [Google Scholar] [CrossRef]
- Stephens, D.B.; Miller, M.; Moore, S.J.; Umstot, T.; Salvato, D.J. Decentralized Groundwater Recharge Systems Using Roofwater and Storm-water Runoff. J. Am. Water Resour. Assoc. 2012, 48, 134–144. [Google Scholar] [CrossRef]
- Beganskas, S.; Fisher, A.T. Coupling distributed storm-water collection and managed aquifer recharge: Field application and implications. J. Environ. Manag. 2017, 200, 366–379. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Du, X.; Yang, Y.; Ye, X. Surface clogging process modeling of suspended solids during urban storm-water aquifer recharge. J. Environ. Sci. 2012, 24, 1418–1424. [Google Scholar] [CrossRef]
- Martin, R. (Ed.) Clogging Issues Associated with Managed Aquifer Recharge Methods; IAH Commission on Managing Aquifer Recharge: Adelaide, Australia, 2013. [Google Scholar]
- Dillon, P.J.; Hickinbotham, M.R.; Pavelic, P. Review of International Experience in Injecting Water into Aquifers for Storage and Reuse; National Conference Publication (Institution of Engineers, Australia): Barton, Australia, 1994; pp. 13–14, 16–19. [Google Scholar]
- Mcdowell-Boyer, L.M.; Hunt, J.R.; Nicholas, S. Particle Transport through Porous Media. Water Resour. Res. 1986, 22, 1901–1921. [Google Scholar] [CrossRef]
- Houben, G.J. Iron oxide incrustations in wells. Part 1: Genesis, mineralogy and geochemistry. Appl. Geochem. 2003, 18, 927–939. [Google Scholar] [CrossRef]
- Bugan, R.D.H.; Jovanovic, N.; Israel, S.; Tredoux, G.; Genthe, B.; Steyn, M.; Allpass, D.; Bishop, R.; Marinus, V. Four decades of water recycling in Atlantis (Western Cape, South Africa): Past, present and future. Water SA 2016, 42, 577–594. [Google Scholar] [CrossRef]
- Houben, G.J.; Weihe, U. Spatial distribution of incrustations around a water well after 38 years of use. Groundwater 2010, 48, 53–58. [Google Scholar] [CrossRef]
- Houben, G.J. The influence of well hydraulics on the spatial distribution of well incrustations. Groundwater 2006, 44, 668–675. [Google Scholar] [CrossRef] [PubMed]
- Tredoux, G.; Genthe, B.; Steyn, M.; Engelbrecht, J.F.P.; Wilsenach, J.; Jovanovic, N. An assessment of the Atlantis artificial recharge water supply scheme (Western Cape, South Africa). WIT Trans. Ecol. Environ. 2009, 127, 403–413. [Google Scholar]
- Voudouris, K. Artificial Recharge via Boreholes Using Treated Wastewater: Possibilities and Prospects. Water 2011, 3, 964–975. [Google Scholar] [CrossRef]
- Li, L.; Steefel, C.I.; Kowalsky, M.B.; Englert, A.; Hubbard, S.S. Effects of physical and geochemical heterogeneities on mineral transformation and biomass accumulation during biostimulation experiments at Rifle, Colorado. J. Contam. Hydrol. 2010, 112, 45–63. [Google Scholar] [CrossRef] [PubMed]
- Faber, S.; Al-Maktoumi, A.; Kacimov, A.; Al-Busaidi, H.; Al-Ismaily, S.; Al-Belushi, M. Migration and deposition of fine particles in a porous filter and alluvial deposit: Laboratory experiments. Arabian J. Geosci. 2016, 9, 293. [Google Scholar] [CrossRef]
- Mays, D.C.; Hunt, J.R. Hydrodynamic Aspects of Particle Clogging in Porous Media. Environ. Sci. Technol. 2005, 39, 577–584. [Google Scholar] [CrossRef] [PubMed]
- Mesticou, Z.; Kacem, M.; Dubujet, P. Coupling Effects of Flow Velocity and Ionic Strength on the Clogging of a Saturated Porous Medium. Transp. Porous Media 2016, 112, 265–282. [Google Scholar] [CrossRef]
- Thompson, A.R.; Stotler, R.L.; Macpherson, G.L.; Liu, G. Laboratory Study of Low-Flow Rates on Clogging Processes for Application to Small-Diameter Injection Wells. Water Resour. Manag. 2015, 29, 5171–5184. [Google Scholar] [CrossRef]
- Hutchinson, A.S. Estimation and Quantification of Injection Well Clogging, Tucson, Arizona. Master’s Thesis, University of Arizona, Tucson, AZ, USA, 1993. [Google Scholar]
- Du, X.; Wang, Z.; Ye, X. Potential Clogging and Dissolution Effects During Artificial Recharge of Groundwater Using Potable Water. Water Resour. Manag. 2013, 27, 3573–3583. [Google Scholar] [CrossRef]
- Kandra, H.; Mccarthy, D.; Deletic, A. Assessment of the Impact of Stormwater Characteristics on Clogging in Stormwater Filters. Water Resour. Manag. 2014, 29, 1031–1048. [Google Scholar] [CrossRef]
- Pedretti, D.; Barahona-Palomo, M.; Bolster, D.; Fernàndez-Garcia, D.; Sanchez-Vila, X.; Tartakovsky, D.M. Probabilistic analysis of maintenance and operation of artificial recharge ponds. Adv. Water Resour. 2012, 36, 23–35. [Google Scholar] [CrossRef]
- Nan, T.; Shao, J.; Cui, Y. Column test-based features analysis of clogging in artificial recharge of groundwater in Beijing. J. Groundw. Sci. Eng. 2016, 4, 88–95. [Google Scholar]
- Eliassen, R. An Experimental and Theoretical Investigation of the Clogging of a Rapid Sand Filter. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1935. [Google Scholar]
- Bennacer, L.; Ahfir, N.D.; Alem, A.; Wang, H. Coupled Effects of Ionic Strength, Particle Size, and Flow Velocity on Transport and Deposition of Suspended Particles in Saturated Porous Media. Transp. Porous Media 2017, 118, 251–269. [Google Scholar] [CrossRef]
- Kappler, A.; Straub, K.L. Geomicrobiological cycling of iron. Rev. Mineral. Geochem. 2005, 59, 85–108. [Google Scholar] [CrossRef]
- Zhu, Z. Theory on Orthokinetic Flocculation of Cohesive Sediment: A Review. J. Geosci. Environ. Prot. 2014, 2, 13–23. [Google Scholar] [CrossRef]
- Serra, T.; Colomer, J.; Logan, B.E. Efficiency of different shear devices on flocculation. Water Res. 2008, 42, 1113–1121. [Google Scholar] [CrossRef] [PubMed]
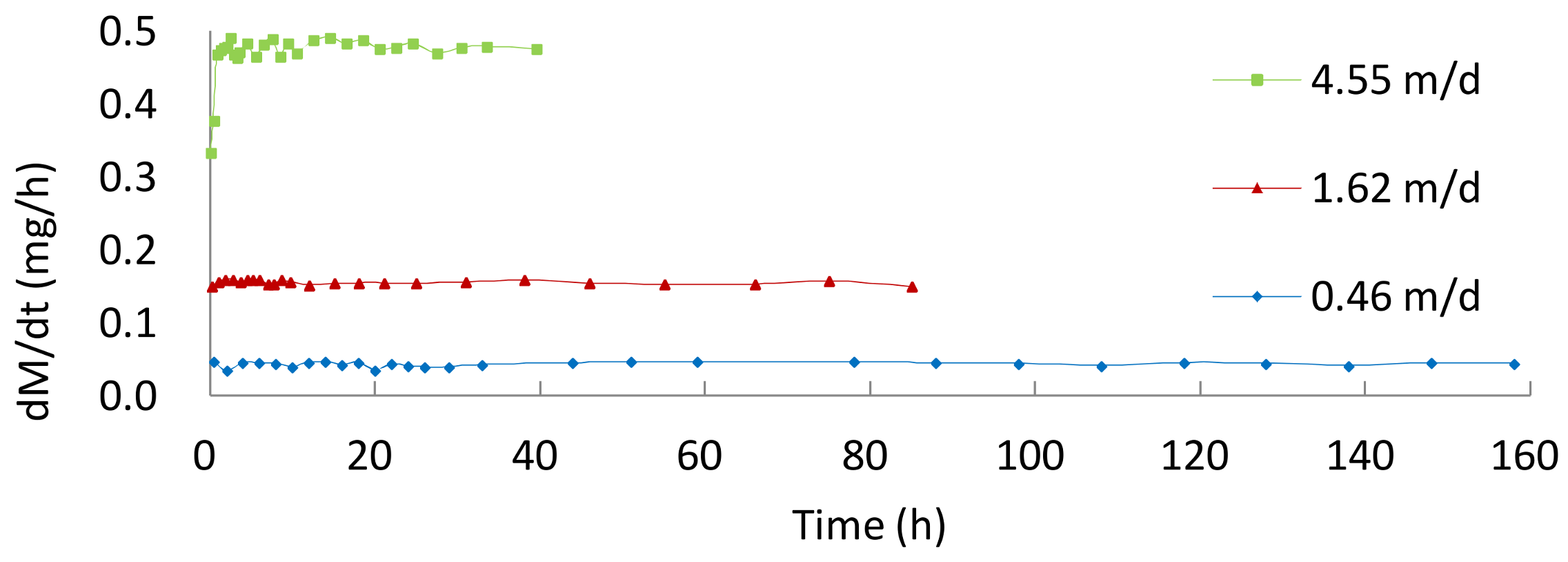
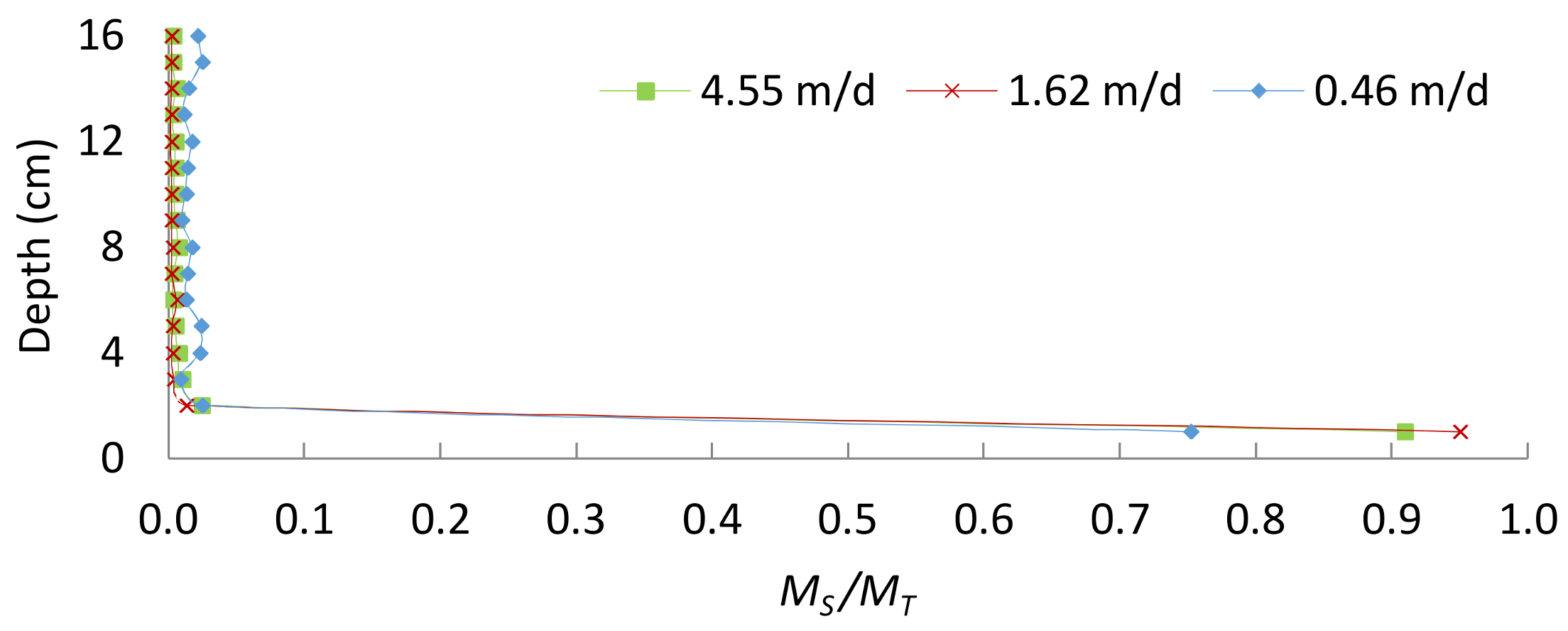
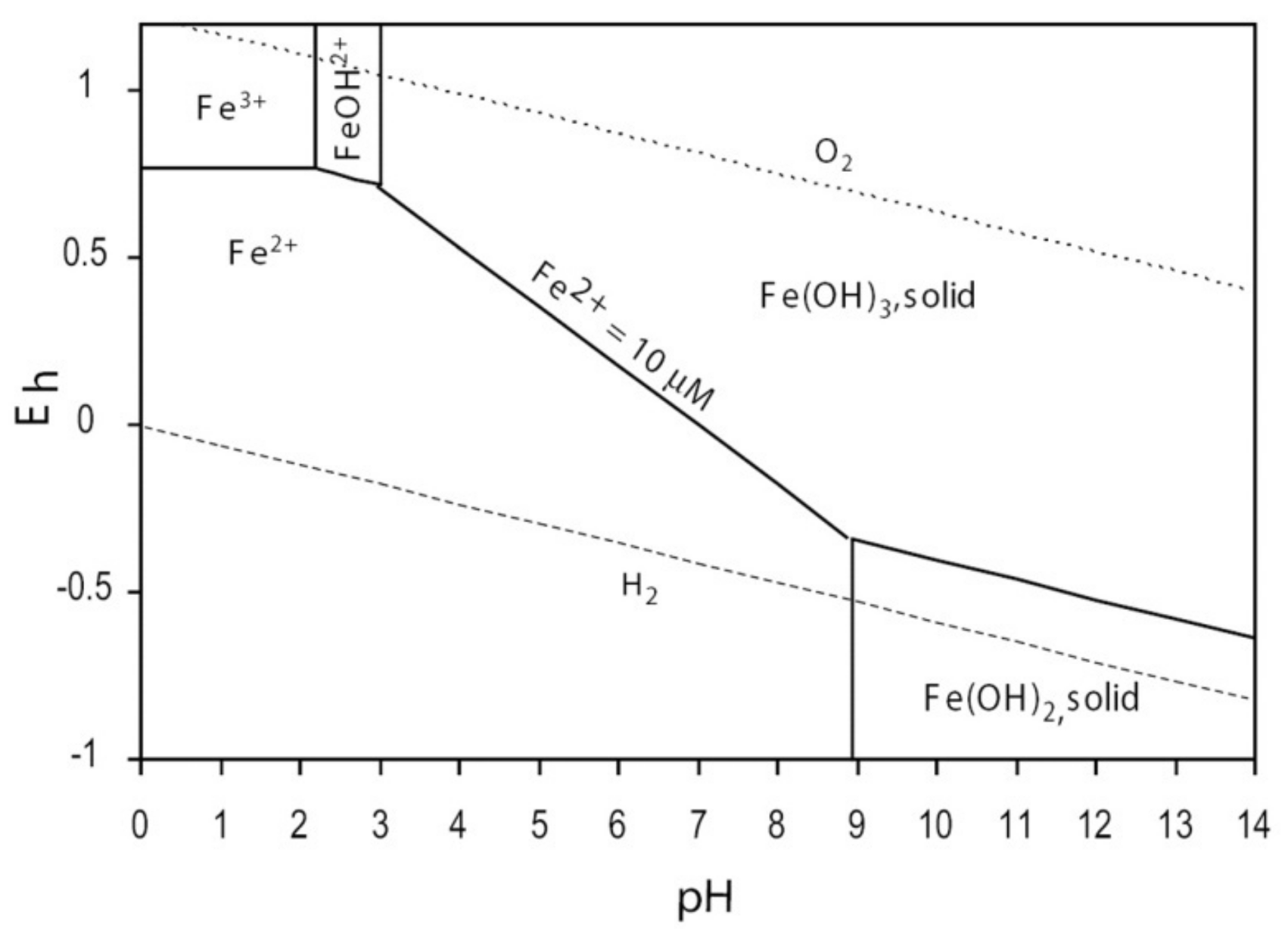
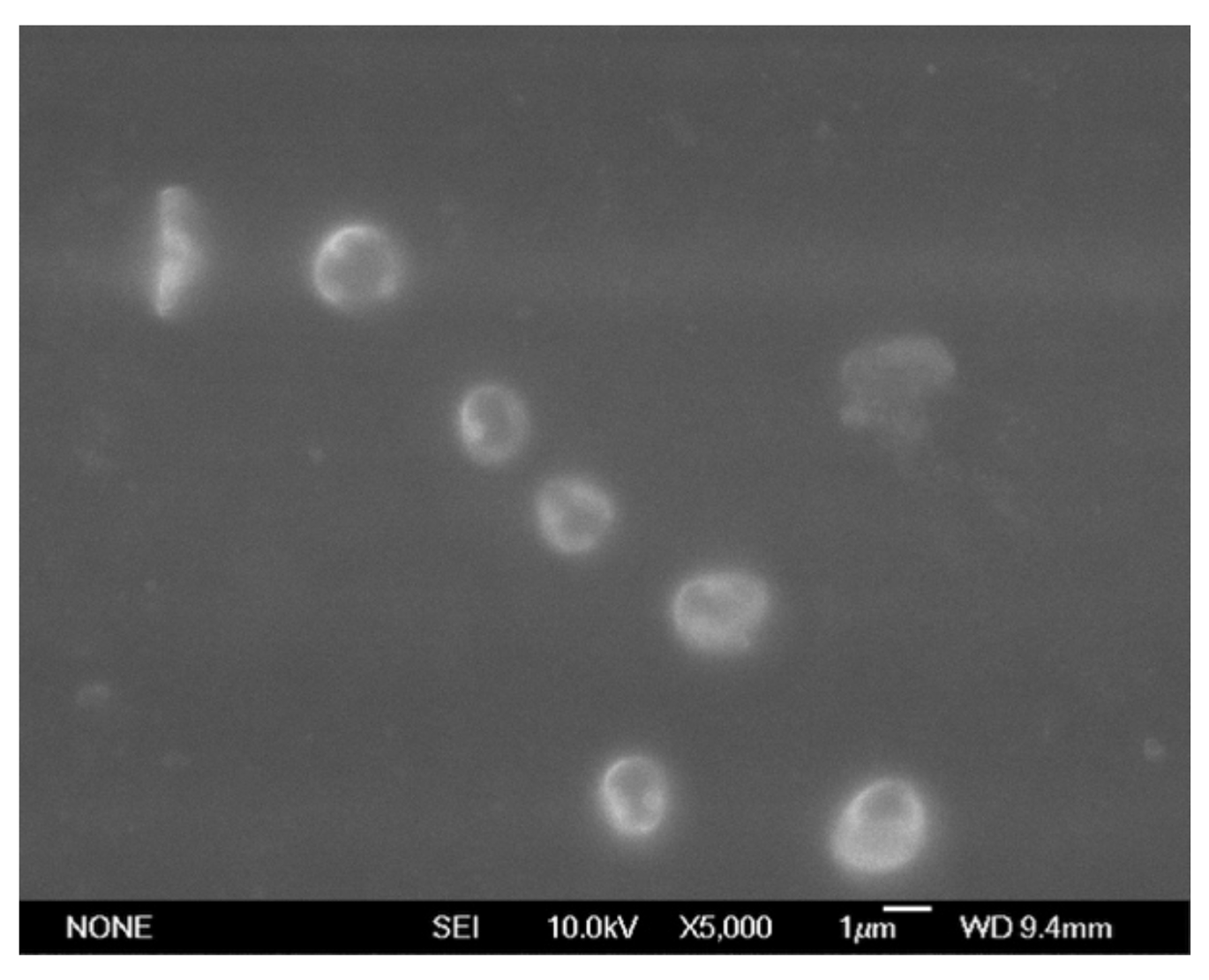


| Flow Velocity | 4.55 m/d | 1.62 m/d | 0.46 m/d |
|---|---|---|---|
| MA(mg) | 19.54 | 13.77 | 7.67 |
| Mc (mg) | 18.86 | 13.17 | 7.07 |
| MT (mg) | 18.13 | 12.98 | 6.99 |
| σ | 0.04 | 0.01 | 0.01 |
| MT/MA | 0.93 | 0.94 | 0.91 |
| 0–1 cm VM | 0.91 | 0.95 | 0.75 |
| 1–16 cm VM | 0.09 | 0.05 | 0.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Zhang, H.; Ye, X.; Lu, Y. Flow Velocity Effects on Fe(III) Clogging during Managed Aquifer Recharge Using Urban Storm Water. Water 2018, 10, 358. https://doi.org/10.3390/w10040358
Du X, Zhang H, Ye X, Lu Y. Flow Velocity Effects on Fe(III) Clogging during Managed Aquifer Recharge Using Urban Storm Water. Water. 2018; 10(4):358. https://doi.org/10.3390/w10040358
Chicago/Turabian StyleDu, Xinqiang, Hexuan Zhang, Xueyan Ye, and Ying Lu. 2018. "Flow Velocity Effects on Fe(III) Clogging during Managed Aquifer Recharge Using Urban Storm Water" Water 10, no. 4: 358. https://doi.org/10.3390/w10040358
APA StyleDu, X., Zhang, H., Ye, X., & Lu, Y. (2018). Flow Velocity Effects on Fe(III) Clogging during Managed Aquifer Recharge Using Urban Storm Water. Water, 10(4), 358. https://doi.org/10.3390/w10040358







