Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Stochastic Modeling of Monthly Precipitation
2.3. Standardized Precipitation Index
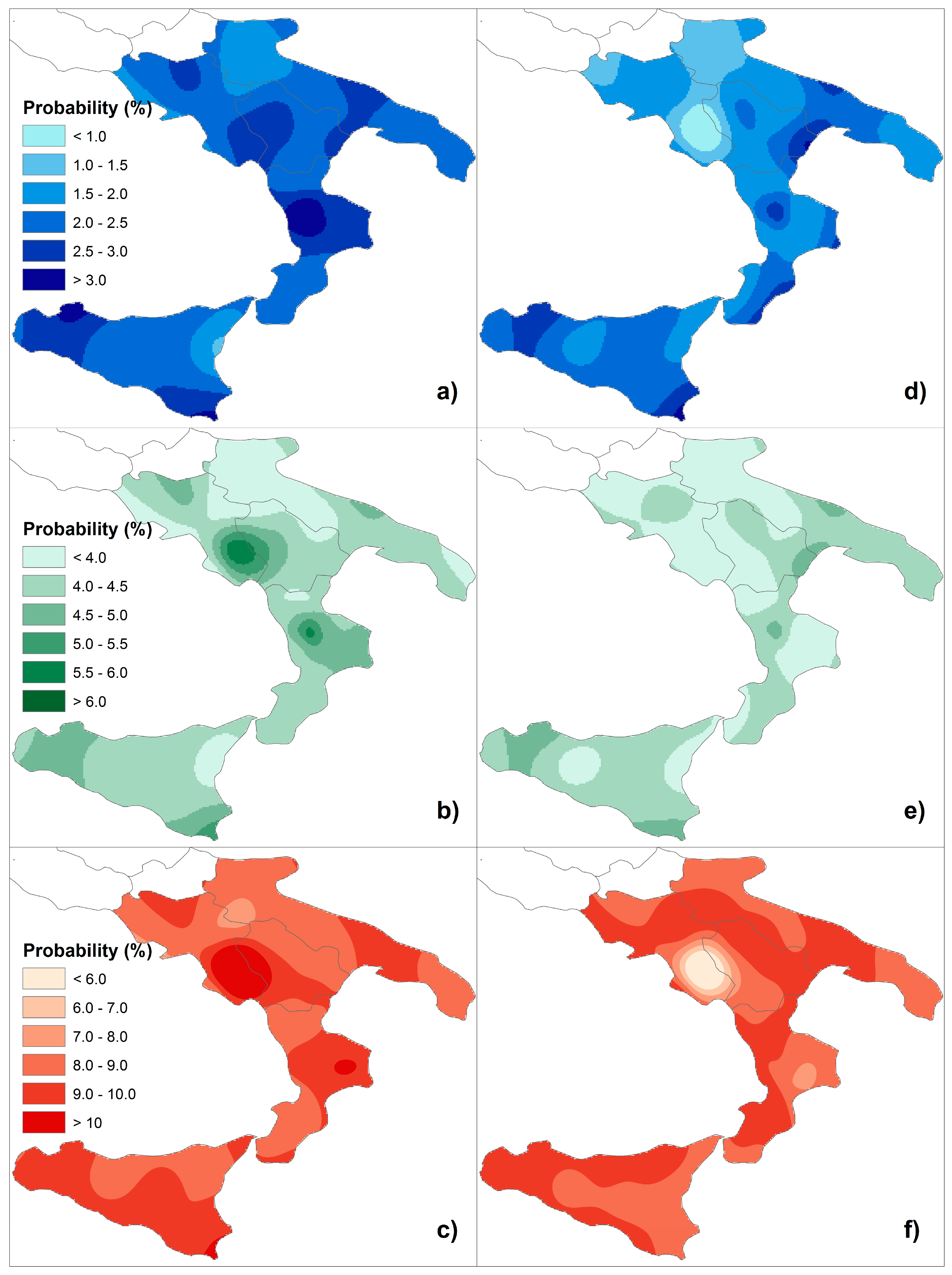
3. Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Estrela, T.; Vargas, E. Drought management plans in the European Union. Water Resour. Manag. 2010, 26, 1537–1553. [Google Scholar] [CrossRef]
- Willems, P.; Arnbjerg-Nielsen, K.; Olsson, J.; Nguyen, V.T.V. Climate change impact assessment on urban rainfall extremes and urban drainage: Methods and shortcomings. Atmos. Res. 2012, 103, 106–118. [Google Scholar] [CrossRef]
- Kreibich, H.; Di Baldassarre, G.; Vorogushyn, S.; Aerts, J.C.; Apel, H.; Aronica, G.T.; Arnbjerg-Nielsen, K.; Bouwer, L.M.; Bubeck, P.; Caloiero, T.; et al. Adaptation to flood risk: Results of international paired flood event studies. Earth’s Future 2017, 5, 953–965. [Google Scholar] [CrossRef]
- Flannigan, M.D.; Amiro, B.D.; Logan, K.A.; Stocks, B.J.; Wotton, B.M. Forest fires and climate change in the 21st century. Mitig. Adapt. Strateg. Glob. Chang. 2006, 11, 847–859. [Google Scholar] [CrossRef]
- Lionello, P.; Abrantes, F.; Gacic, M.; Planton, S.; Trigo, R.; Ulbrich, U. The climate of the Mediterranean region: Research progress and climate change impacts. Reg. Environ. Chang. 2014, 14, 1679–1684. [Google Scholar] [CrossRef]
- Li, Y.; Ye, W.; Wang, M.; Yan, X. Climate change and drought: A risk assessment of crop-yield impacts. Clim. Res. 2009, 39, 31–46. [Google Scholar] [CrossRef]
- Yevjevich, V.; Da Cunha, L.; Vlachos, E. Coping with Droughts; Water Resources Publications: Littleton, CO, USA, 1983. [Google Scholar]
- Zaidman, M.D.; Rees, H.G.; Young, A.R. Spatio-temporal development of streamflow droughts in north-west Europe. Hydrol. Earth Syst. Sci. 2012, 5, 733–751. [Google Scholar] [CrossRef]
- Lloyd-Huhes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Fink, A.H.; Brücher, T.; Krüger, A.; Leckebush, G.C.; Pinto, J.G.; Ulbrich, U. The 2003 European summer heatwaves and drought-synoptic diagnosis and impacts. Weather 2004, 59, 209–216. [Google Scholar] [CrossRef]
- Hannaford, J.; Lloyd-Hughes, B.; Keef, C.; Parry, S.; Prudhomme, C. Examining the large-scale spatial coherence of European drought using regional indicators of precipitation and streamflow deficit. Hydrol. Processes 2011, 25, 1146–1162. [Google Scholar] [CrossRef]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation, A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012. [Google Scholar]
- IPCC. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Philandras, C.M.; Nastos, P.T.; Kapsomenakis, J.; Douvis, K.C.; Tselioudis, G.; Zerefos, C.S. Long term precipitation trends and variability within the Mediterranean region. Nat. Hazards Earth Syst. Sci. 2011, 11, 3235–3250. [Google Scholar] [CrossRef]
- Kelley, C.P.; Ting, M.; Seager, R.; Kushnir, Y. Mediterranean precipitation climatology, seasonal cycle, and trend as simulated by CMIP5. Geophys. Res. Lett. 2012, 39, L21703. [Google Scholar] [CrossRef]
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Precipitation variability and change in the Calabria region (Italy) from a high resolution daily dataset. Int. J. Climatol. 2012, 32, 57–73. [Google Scholar] [CrossRef]
- Caloiero, T.; Buttafuoco, G.; Coscarelli, R.; Ferrari, E. Spatial and temporal characterization of climate at regional scale using homogeneous monthly precipitation and air temperature data: An application in Calabria (Southern Italy). Hydrol. Res. 2015, 46, 629–646. [Google Scholar] [CrossRef]
- De Luis, M.; Raventos, J.; Gonzalez-Hidalgo, J.C.; Sanchez, J.R.; Cortina, J. Spatial analysis of rainfall trends in the region of Valencia (East of Spain). Int. J. Climatol. 2000, 20, 1451–1469. [Google Scholar] [CrossRef]
- Falloon, P.D.; Betts, R.A. The impact of climate change on global river flow in HadGEM1 simulations. Atmos. Sci. Lett. 2006, 7, 62–68. [Google Scholar] [CrossRef]
- Peterson, T.C.; Heim, R.R.; Hirsch, R.; Kaiser, D.P.; Brooks, H.; Diffenbaugh, N.S.; Dole, R.M.; Giovannettone, J.P.; Guirguis, K.; Karl, T.R.; et al. Monitoring and understanding changes in heat waves, cold waves, floods, and droughts in the United States: State of knowledge. Bull. Am. Meteorol. Soc. 2013, 94, 821–834. [Google Scholar] [CrossRef]
- Montanarella, L. Trends in land degradation in Europe. In Climate and Land Degradation; Sivakumar, M.V.K., Ndegwa, N., Eds.; Springer: Heidelberg, Germany, 2007; pp. 83–104. [Google Scholar]
- Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T.; Kaspar, F. Estimating the impact of global change on flood and drought risks in Europe: A continental, integrated analysis. Clim. Chang. 2006, 75, 273–299. [Google Scholar] [CrossRef]
- Minetti, J.L.; Vargas, W.M.; Poblete, A.G.; de la Zerda, L.R.; Acuña, L.R. Regional droughts in southern South America. Theor. Appl. Climatol. 2010, 102, 403–415. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q.; Oglesby, R.J. Influence of Atlantic sea surface temperatures on persistent drought in North America. Clim. Dynam. 2011, 37, 569–586. [Google Scholar] [CrossRef]
- Fang, K.; Gou, X.; Chen, F.; Davi, N.; Liu, C. Spatiotemporal drought variability for central and eastern Asia over the past seven centuries derived from tree-ring based reconstructions. Quat. Int. 2013, 283, 107–116. [Google Scholar] [CrossRef]
- Hua, T.; Wang, X.M.; Zhang, C.X.; Lang, L.L. Temporal and spatial variations in the Palmer Drought Severity Index over the past four centuries in arid, semiarid, and semihumid East Asia. Chin. Sci. Bull. 2013, 58, 4143–4152. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Analysis of Dry Spells in Southern Italy (Calabria). Water 2015, 7, 3009–3023. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. A stochastic model for the analysis of the temporal change of dry spells. Stoch. Environ. Res. Risk. Assess. 2015, 29, 143–155. [Google Scholar] [CrossRef]
- Sirangelo, B.; Caloiero, T.; Coscarelli, R.; Ferrari, E. Stochastic analysis of long dry spells in Calabria (Southern Italy). Theor. Appl. Climatol. 2015, 127, 711–724. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Hayes, M.J.; Svodoba, M.D. Drought monitoring and assessment in the US. In Drought and Drought Mitigation in Europe; Voght, J.V., Somma, F., Eds.; Kluwers: Dordrecht, The Netherlands, 2000; pp. 149–160. [Google Scholar]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. Drought monitoring with multiple time scales. In Proceedings of the 9th Conference on Applied Climatology, Dallas, TX, USA, 15–20 January 1995; pp. 233–236. [Google Scholar]
- Dubrovsky, M.; Svoboda, M.D.; Trnka, M.; Hayes, M.J.; Wilhite, D.A.; Zalud, Z.; Hlavinka, P. Application of relative drought indices in assessing climate-change impacts on drought conditions in Czechia. Theor. Appl. Climatol. 2009, 96, 155–171. [Google Scholar] [CrossRef]
- Zhai, L.; Feng, Q. Spatial and temporal pattern of precipitation and drought in Gansu Province Northwest China. Nat. Hazards 2009, 49, 1–24. [Google Scholar] [CrossRef]
- Xingcai, L.; Zongxue, X.U.; Bo, L. Spatio-temporal characteristics of Standardized Precipitation Index in the Taihu Basin during 1951–2000. Wuhan Univ. J. Nat. Sci. 2009, 14, 518–524. [Google Scholar]
- Logan, K.E.; Brunsell, N.A.; Jones, A.R.; Feddema, J.J. Assessing spatiotemporal variability of drought in the US central plains. J. Arid Environ. 2010, 74, 247–255. [Google Scholar] [CrossRef]
- Manatsa, D.; Mukwada, G.; Siziba, E.; Chinyanganya, T. Analysis of multidimensional aspects of agricultural droughts in Zimbabwe using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2010, 102, 287–305. [Google Scholar] [CrossRef]
- Sönmez, F.K.; Kömüscü, A.Ü.; Erkan, A.; Turgu, E. An analysis of spatial and temporal dimension of drought vulnerability in Turkey using the Standardized Precipitation Index. Nat. Hazards 2005, 35, 243–264. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Differences in spatial patterns of drought on different time sales: An analysis of the Iberian Peninsula. Water Resour. Manag. 2006, 20, 37–60. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V.D. Spatial and temporal analysis of drought in Greece using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F. Spatio-temporal variability of precipitation temperature and agricultural drought indices in Central Italy. Agric. For. Meteorol. 2011, 151, 301–313. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Bordi, I.; Cancelliere, A.; Rossi, G.; Sutera, A. Spatial variability of drought: An analysis of SPI in Sicily. Water Resour. Manag. 2003, 17, 273–296. [Google Scholar] [CrossRef]
- Mendicino, G.; Senatore, A.; Versace, P. A Groundwater Resource Index (GRI) for drought monitoring and forecasting in a Mediterranean climate. J. Hydrol. 2008, 357, 282–302. [Google Scholar] [CrossRef]
- Capra, A.; Consoli, S.; Scicolone, B. Long-term climatic variability in Calabria and effects on drought and agrometeorological parameters. Water Resour. Manag. 2013, 27, 601–617. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T. Drought events at different timescales in southern Italy (Calabria). J. Maps 2014, 10, 529–537. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Analyses of Drought Events in Calabria (Southern Italy) Using Standardized Precipitation Index. Water Resour. Manag. 2015, 29, 557–573. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. An Analysis of the Occurrence Probabilities of Wet and Dry Periods through a Stochastic Monthly Rainfall Model. Water 2016, 8, 39. [Google Scholar] [CrossRef]
- Capra, A.; Scicolone, B. Spatiotemporal variability of drought on a short–medium time scale in the Calabria Region (Southern Italy). Theor. Appl. Climatol. 2012, 3, 471–488. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The effect of the length of record on the standardized precipitation index calculation. Int. J. Climatol. 2005, 25, 505–520. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Belyaev, K.; Sergey, K.; Gulev, S.; Koltermann, P. Changes in the duration of European wet and dry spells during the last 60 years. J. Clim. 2013, 26, 2022–2047. [Google Scholar] [CrossRef]
- Wilks, D.S.; Wilby, R.L. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Hayhoe, H.N. Improvements of stochastic weather data generators for diverse climates. Clim. Res. 2000, 14, 75–87. [Google Scholar] [CrossRef]
- Liu, J.; Williams, J.R.; Wang, X.; Yang, H. Using MODAWEC to generate daily weather data for the EPIC model. Environ. Model. Softw. 2009, 24, 655–664. [Google Scholar] [CrossRef]
- Richardson, C.W. Stochastic simulation of daily precipitation temperature and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Sharma, A.; Lall, U. A nonparametric approach for daily rainfall simulation. Math. Comput. Simulat. 1999, 48, 361–371. [Google Scholar] [CrossRef]
- Srikanthan, R.; McMahon, T.A. Stochastic Generation of Rainfall and Evaporation Data; Technical Report 84; Australian Water Resources Council, Department of Resources and Energy: Canberra, Australia, 1985.
- Srikanthan, R.; Harrold, T.I.; Sharma, A.; McMahon, T.A. Comparison of two approaches for generation of daily rainfall data. Stoch. Environ. Res. Risk. Assess. 2005, 19, 215–226. [Google Scholar] [CrossRef]
- Wan, H.; Zhang, X.; Barrow, E.M. Stochastic modelling of daily precipitation for Canada. Atmos. Ocean 2005, 43, 23–32. [Google Scholar] [CrossRef]
- Woolhiser, D.A. Modelling daily precipitation—Progress and problems. In Statistics in the Environmental and Earth Sciences; Walden, A.T., Guttorp, P., Eds.; Edward Arnold: London, UK, 1992; pp. 71–89. [Google Scholar]
- Zheng, X.; Katz, R.W. Mixture model of generalized chain-dependent processes and its application to simulation of interannual variability of daily rainfall. J. Hydrol. 2008, 349, 191–199. [Google Scholar] [CrossRef]
- Srikanthan, R.; McMahon, T.A. Stochastic generation of annual monthly and daily climate data: A review. Hydrol. Earth Syst. Sci. 2001, 5, 653–670. [Google Scholar] [CrossRef]
- Yang, P.; Ling, T. Comparison of Bootstrapping and Markov Chain Monte Carlo for Copula Analysis of Hydrological Droughts. In Proceedings of the American Geophysical Union Fall Meeting 2015, San Francisco, CA, USA, 14–18 December 2015. Abstract ID: H12F-07. [Google Scholar]
- Montaseri, M.; Amirataee, B. Comprehensive stochastic assessment of meteorological drought indices. Int. J. Climatol. 2017, 37, 998–1013. [Google Scholar] [CrossRef]
- Longobardi, A.; Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial and temporal distribution of precipitation in a Mediterranean area (Southern Italy). Environ. Earth Sci. 2016, 75, 189. [Google Scholar] [CrossRef]
- Priestly, M.B. Spectral Analysis and Time Series; Academic Press: London, UK, 1994. [Google Scholar]
- Anderson, R.L. Distribution of serial correlation coefficient. Ann. Math. Stat. 1942, 13, 1–13. [Google Scholar] [CrossRef]
- Haan, C.T. Statistical Methods in Hydrology; Iowa State University Press: Ames, IA, USA, 1997. [Google Scholar]
- Edwards, D.; McKee, T. Characteristics of 20th century drought in the United States at multiple scale. In Atmospheric Science Paper 634; Department of Atmospheric Science, Colorado State University: Fort Collins, CO, USA, 1997. [Google Scholar]
- Angelidis, P.; Maris, F.; Kotsovinos, N.; Hrissanthou, V. Computation of drought index SPI with Alternative Distribution Functions. Water Resour. Manag. 2012, 26, 2453–2473. [Google Scholar] [CrossRef]
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications, INC: New York, NY, USA, 1970. [Google Scholar]
- Giordano, R.; Preziosi, E.; Romano, E. Integration of local and scientific knowledge to support drought impact monitoring: Some hints from an Italian case study. Nat. Hazards 2013, 69, 523–544. [Google Scholar] [CrossRef]
- Wu, J.; He, B.; Lu, A.; Zhou, L.; Liu, M.; Zhao, L. Quantitative assessment and spatial characteristics analysis of agricultural drought vulnerability in China. Nat. Hazards 2011, 56, 785–801. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Mancini, M. Trend detection of annual and seasonal rainfall in Calabria (Southern Italy). Int. J. Climatol. 2011, 31, 44–56. [Google Scholar] [CrossRef]
- Caloiero, T.; Callegari, G.; Cantasano, N.; Coletta, V.; Pellicone, G.; Veltri, A. Bioclimatic analysis in a region of southern Italy (Calabria). Plant Biosyst. 2015, 150, 1282–1295. [Google Scholar] [CrossRef]
- Pellicone, G.; Caloiero, T.; Coletta, V.; Veltri, A. Phytoclimatic map of Calabria (Southern Italy). J. Maps 2014, 10, 109–113. [Google Scholar] [CrossRef]





| ID Code | Rain Gauge | Region | Longitude | Latitude | No. of Years of Observation |
|---|---|---|---|---|---|
| 1 | Benevento (Genio Civile) | Campania | 14.769 | 41.117 | 72 |
| 2 | Bisaccia | Campania | 15.380 | 41.008 | 82 |
| 3 | Casalvelino | Campania | 15.102 | 40.184 | 76 |
| 4 | Caserta (Genio Civile) | Campania | 14.319 | 41.067 | 81 |
| 5 | Nusco | Campania | 15.088 | 40.886 | 84 |
| 6 | S. Angelo a Fasanella | Campania | 15.336 | 40.451 | 80 |
| 7 | Salerno (Genio Civile) | Campania | 14.736 | 40.667 | 79 |
| 8 | Cersosimo | Basilicata | 16.348 | 40.051 | 65 |
| 9 | Grassano | Basilicata | 16.270 | 40.632 | 61 |
| 10 | Lagopesole | Basilicata | 15.737 | 40.804 | 83 |
| 11 | Maratea | Basilicata | 15.717 | 39.984 | 62 |
| 12 | Pisticci | Basilicata | 16.735 | 40.295 | 67 |
| 13 | Vaglio di Lucania | Basilicata | 15.916 | 40.667 | 68 |
| 14 | Altamura | Apulia | 16.554 | 40.824 | 86 |
| 15 | Bari (Osservatorio) | Apulia | 16.873 | 41.118 | 86 |
| 16 | Biccari | Apulia | 15.191 | 41.393 | 84 |
| 17 | Brindisi | Apulia | 17.938 | 40.629 | 86 |
| 18 | Cerignola | Apulia | 15.906 | 41.264 | 85 |
| 19 | San Marco in Lamis | Apulia | 15.637 | 41.711 | 87 |
| 20 | Santa Maria di Leuca | Apulia | 18.356 | 39.800 | 85 |
| 21 | Taranto | Apulia | 17.251 | 40.465 | 86 |
| 22 | Vieste | Apulia | 16.176 | 41.881 | 86 |
| 23 | Campotenese | Calabria | 16.068 | 39.873 | 79 |
| 24 | Capo Spartivento | Calabria | 16.056 | 37.927 | 68 |
| 25 | Cassano allo Ionio | Calabria | 16.319 | 39.783 | 74 |
| 26 | Cecita | Calabria | 16.538 | 39.400 | 70 |
| 27 | Cittanova | Calabria | 16.078 | 38.352 | 77 |
| 28 | Cosenza | Calabria | 16.265 | 39.287 | 79 |
| 29 | Filadelfia | Calabria | 16.293 | 38.787 | 76 |
| 30 | Isola di Capo Rizzuto | Calabria | 17.094 | 38.961 | 67 |
| 31 | Joppolo | Calabria | 15.905 | 38.592 | 68 |
| 32 | San Pietro in Guarano | Calabria | 16.314 | 39.346 | 72 |
| 33 | Scilla | Calabria | 15.720 | 38.252 | 64 |
| 34 | Tiriolo | Calabria | 16.510 | 38.940 | 58 |
| 35 | Acireale | Sicily | 15.159 | 37.599 | 85 |
| 36 | Castelbuono | Sicily | 14.079 | 37.929 | 81 |
| 37 | Castronuovo di Sicilia | Sicily | 13.599 | 37.679 | 82 |
| 38 | Chiaramonte Gulfi | Sicily | 14.699 | 37.029 | 86 |
| 39 | Floresta | Sicily | 14.909 | 37.979 | 85 |
| 40 | Leonforte | Sicily | 14.379 | 37.629 | 81 |
| 41 | Noto | Sicily | 15.059 | 36.879 | 82 |
| 42 | Palermo Oss. Astronomico | Sicily | 13.349 | 38.099 | 61 |
| 43 | Palma di Montechiaro | Sicily | 13.759 | 37.199 | 81 |
| 44 | San Saba | Sicily | 15.499 | 38.279 | 69 |
| 45 | Sciacca | Sicily | 13.079 | 37.499 | 85 |
| 46 | Trapani | Sicily | 12.499 | 38.009 | 84 |
| SPI Value | Class | Probability (%) |
|---|---|---|
| SPI ≥ 2.0 | Extremely wet | 2.3 |
| 1.5 ≤ SPI < 2.0 | Severely wet | 4.4 |
| 1.0 ≤ SPI < 1.5 | Moderately wet | 9.2 |
| 0.0 ≤ SPI < 1.0 | Mildly wet | 34.1 |
| −1.0 ≤ SPI < 0.0 | Mild drought | 34.1 |
| −1.5 ≤ SPI < −1.0 | Moderate drought | 9.2 |
| −2.0 ≤ SPI < −1.5 | Severe drought | 4.4 |
| SPI < −2.0 | Extreme drought | 2.3 |
| ID Code | Rain Gauge | λ | p | ||
|---|---|---|---|---|---|
| 1 | Benevento (Genio Civile) | 0.436 | 2 | 1 | 1 |
| 2 | Bisaccia | 0.546 | 2 | 1 | 1 |
| 3 | Casalvelino | 0.490 | 2 | 3 | 0 |
| 4 | Caserta (Genio Civile) | 0.473 | 2 | 2 | 1 |
| 5 | Nusco | 0.510 | 2 | 2 | 1 |
| 6 | S.Angelo a Fasanella | 0.429 | 2 | 2 | 1 |
| 7 | Salerno (Genio Civile) | 0.433 | 2 | 2 | 0 |
| 8 | Cersosimo | 0.359 | 2 | 1 | 0 |
| 9 | Grassano | 0.429 | 2 | 2 | 1 |
| 10 | Lagopesole | 0.469 | 2 | 2 | 1 |
| 11 | Maratea | 0.461 | 2 | 2 | 0 |
| 12 | Pisticci | 0.352 | 2 | 1 | 1 |
| 13 | Vaglio Di Lucania | 0.444 | 2 | 3 | 0 |
| 14 | Altamura | 0.431 | 2 | 2 | 0 |
| 15 | Bari (Osservatorio) | 0.413 | 2 | 2 | 0 |
| 16 | Biccari | 0.488 | 2 | 2 | 1 |
| 17 | Brindisi | 0.393 | 2 | 2 | 0 |
| 18 | Cerignola | 0.407 | 2 | 1 | 1 |
| 19 | San Marco in Lamis | 0.431 | 2 | 2 | 0 |
| 20 | Santa Maria di Leuca | 0.383 | 2 | 3 | 1 |
| 21 | Taranto | 0.374 | 2 | 2 | 1 |
| 22 | Vieste | 0.392 | 2 | 1 | 1 |
| 23 | Campotenese | 0.466 | 2 | 2 | 1 |
| 24 | Capo Spartivento | 0.338 | 3 | 2 | 0 |
| 25 | Cassano allo Ionio | 0.473 | 2 | 2 | 0 |
| 26 | Cecita | 0.442 | 2 | 2 | 1 |
| 27 | Cittanova | 0.401 | 2 | 1 | 1 |
| 28 | Cosenza | 0.477 | 2 | 2 | 1 |
| 29 | Filadelfia | 0.477 | 2 | 3 | 1 |
| 30 | Isola di Capo Rizzuto | 0.315 | 2 | 3 | 1 |
| 31 | Joppolo | 0.498 | 2 | 1 | 0 |
| 32 | San Pietro in Guarano | 0.513 | 2 | 2 | 1 |
| 33 | Scilla | 0.484 | 2 | 1 | 1 |
| 34 | Tiriolo | 0.405 | 2 | 2 | 1 |
| 35 | Acireale | 0.299 | 2 | 1 | 0 |
| 36 | Castelbuono | 0.390 | 3 | 2 | 0 |
| 37 | Castronuovo Di Sicilia | 0.389 | 2 | 1 | 0 |
| 38 | Chiaramonte Gulfi | 0.371 | 2 | 1 | 1 |
| 39 | Floresta | 0.378 | 3 | 2 | 0 |
| 40 | Leonforte | 0.363 | 2 | 1 | 1 |
| 41 | Noto | 0.320 | 2 | 1 | 1 |
| 42 | Palermo Oss. Astronomico | 0.431 | 3 | 2 | 0 |
| 43 | Palma di Montechiaro | 0.333 | 2 | 3 | 0 |
| 44 | San Saba | 0.381 | 2 | 2 | 1 |
| 45 | Sciacca | 0.331 | 2 | 1 | 1 |
| 46 | Trapani | 0.408 | 3 | 2 | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caloiero, T.; Sirangelo, B.; Coscarelli, R.; Ferrari, E. Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series. Water 2018, 10, 336. https://doi.org/10.3390/w10030336
Caloiero T, Sirangelo B, Coscarelli R, Ferrari E. Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series. Water. 2018; 10(3):336. https://doi.org/10.3390/w10030336
Chicago/Turabian StyleCaloiero, Tommaso, Beniamino Sirangelo, Roberto Coscarelli, and Ennio Ferrari. 2018. "Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series" Water 10, no. 3: 336. https://doi.org/10.3390/w10030336
APA StyleCaloiero, T., Sirangelo, B., Coscarelli, R., & Ferrari, E. (2018). Occurrence Probabilities of Wet and Dry Periods in Southern Italy through the SPI Evaluated on Synthetic Monthly Precipitation Series. Water, 10(3), 336. https://doi.org/10.3390/w10030336





