A Thermodynamical Approach for Evaluating Energy Consumption of the Nanofiltration-Crystallization Process on Selective Separation of Chloride and Sulfate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermodynamical Approach for Membrane Process
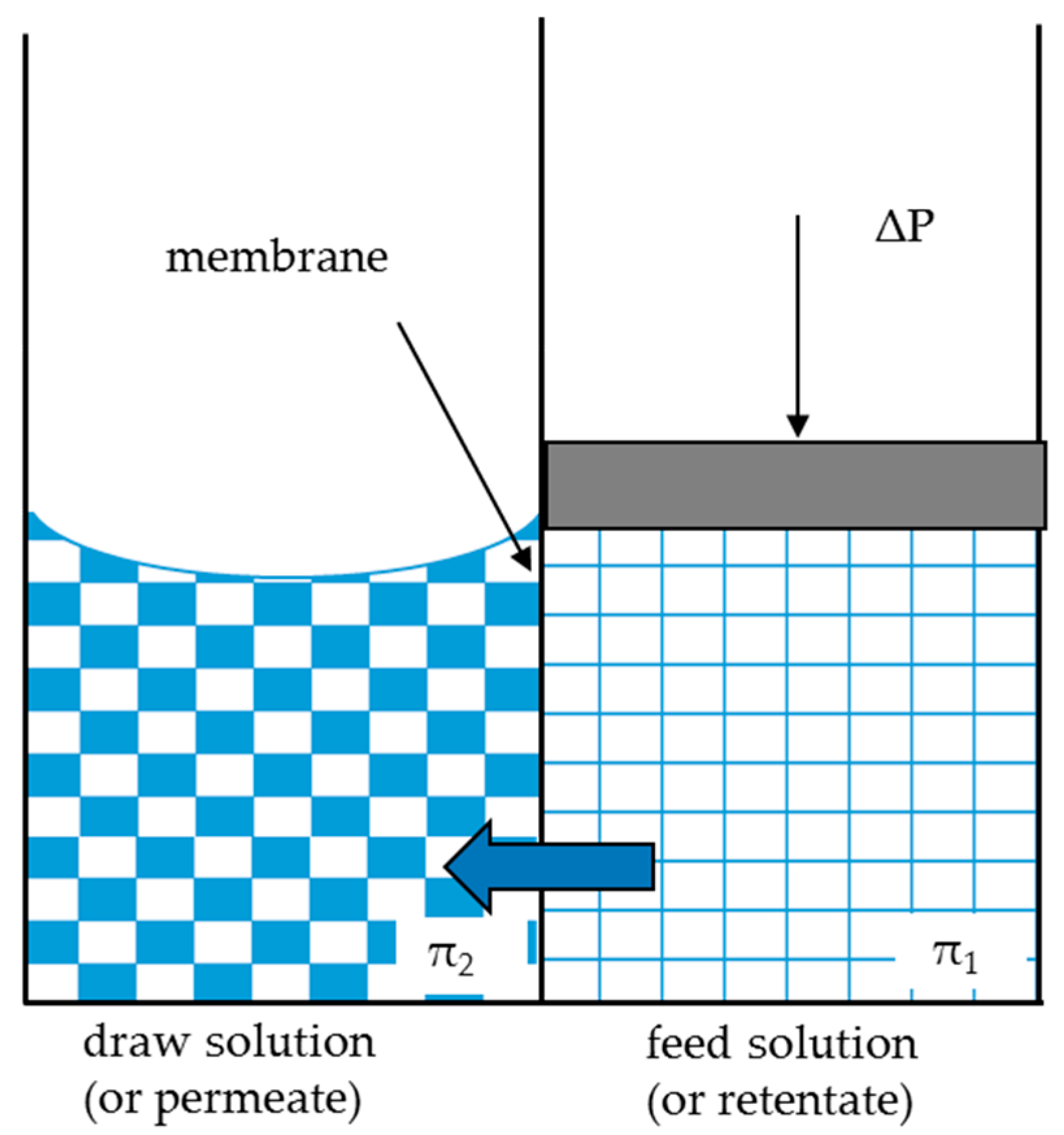
2.1.1. FO Unit Model
2.1.2. NF Unit Model
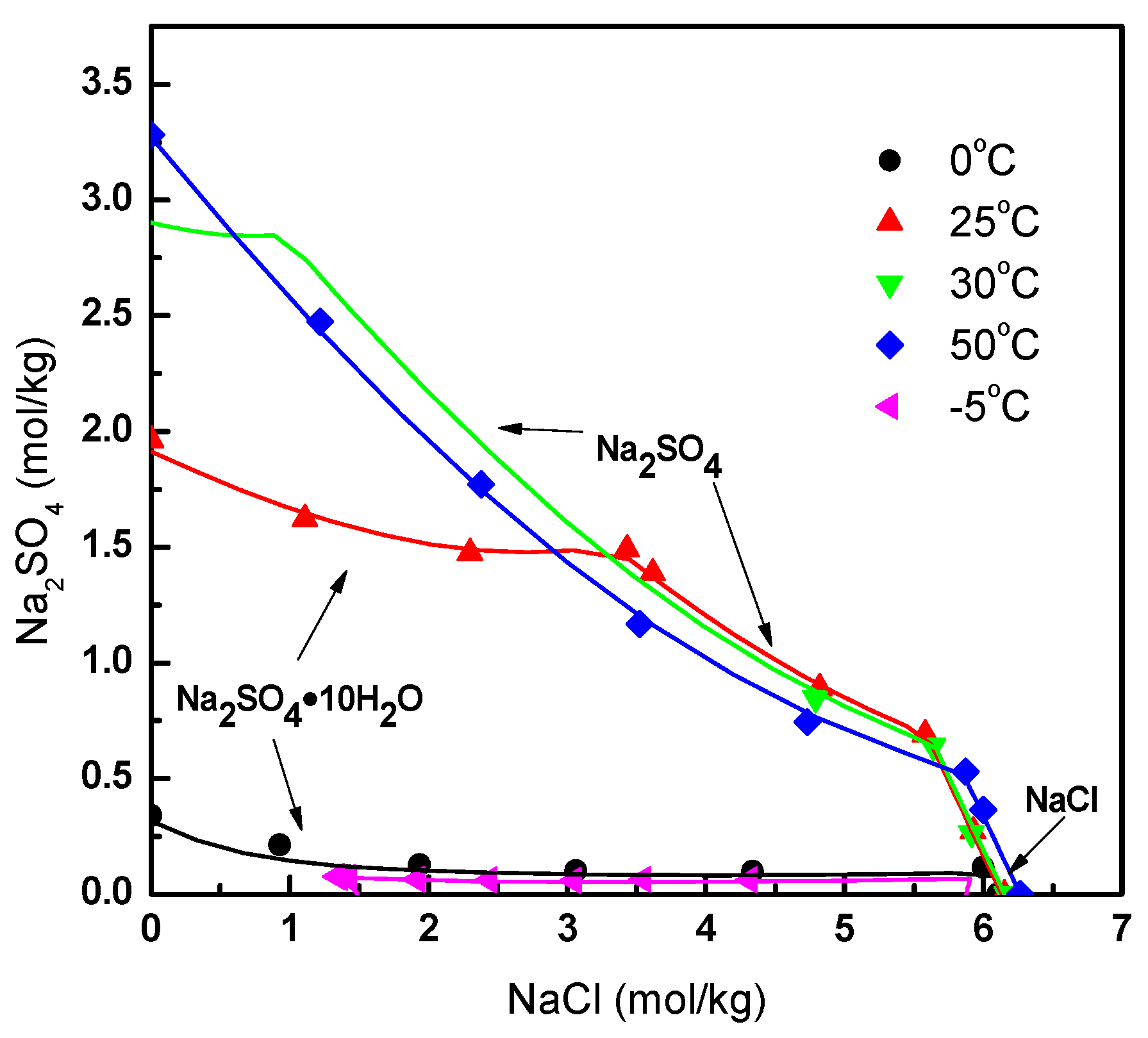
2.2. Thermodynamic Model
2.3. Process Design
3. Results
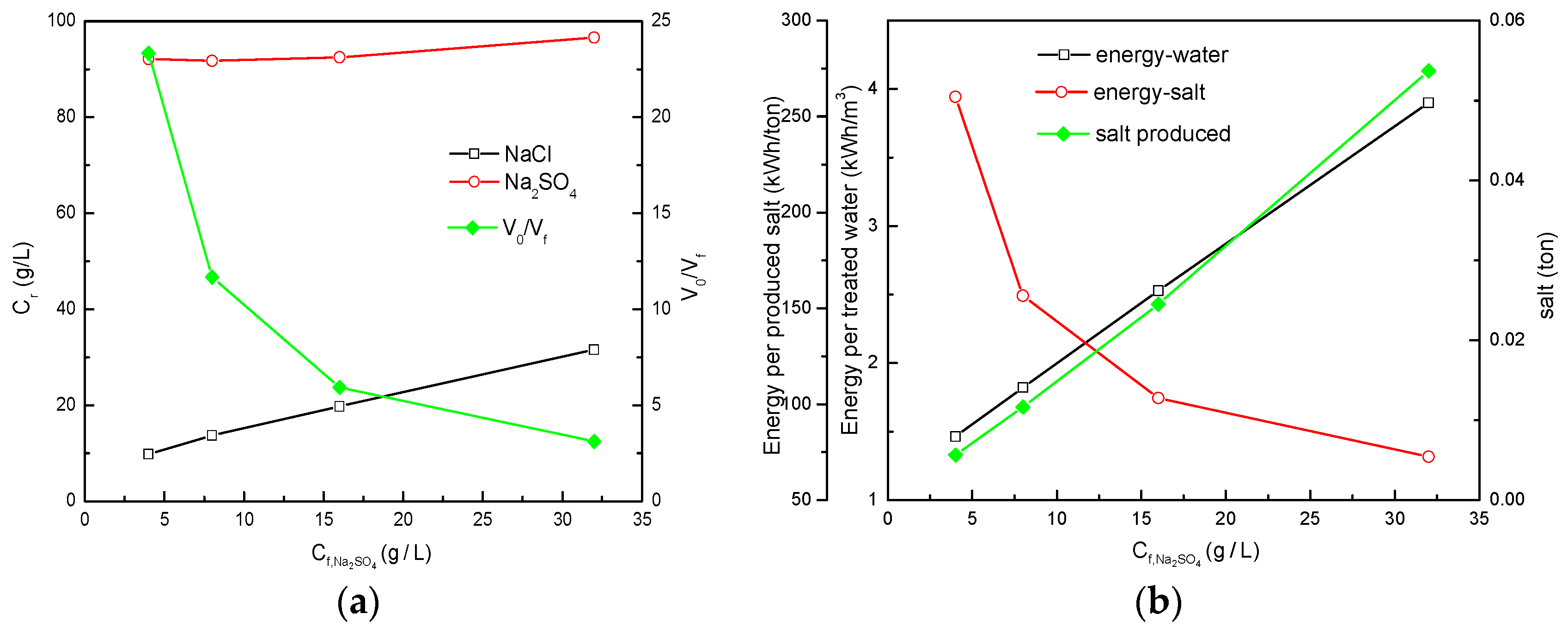
3.1. Effect of the Feed Concentration on NF-Cryst Process
3.1.1. NF-Cryst Process Configuration Results under Different Total Salt Concentrations
3.1.2. NF-Cryst Simulation Results under Different /
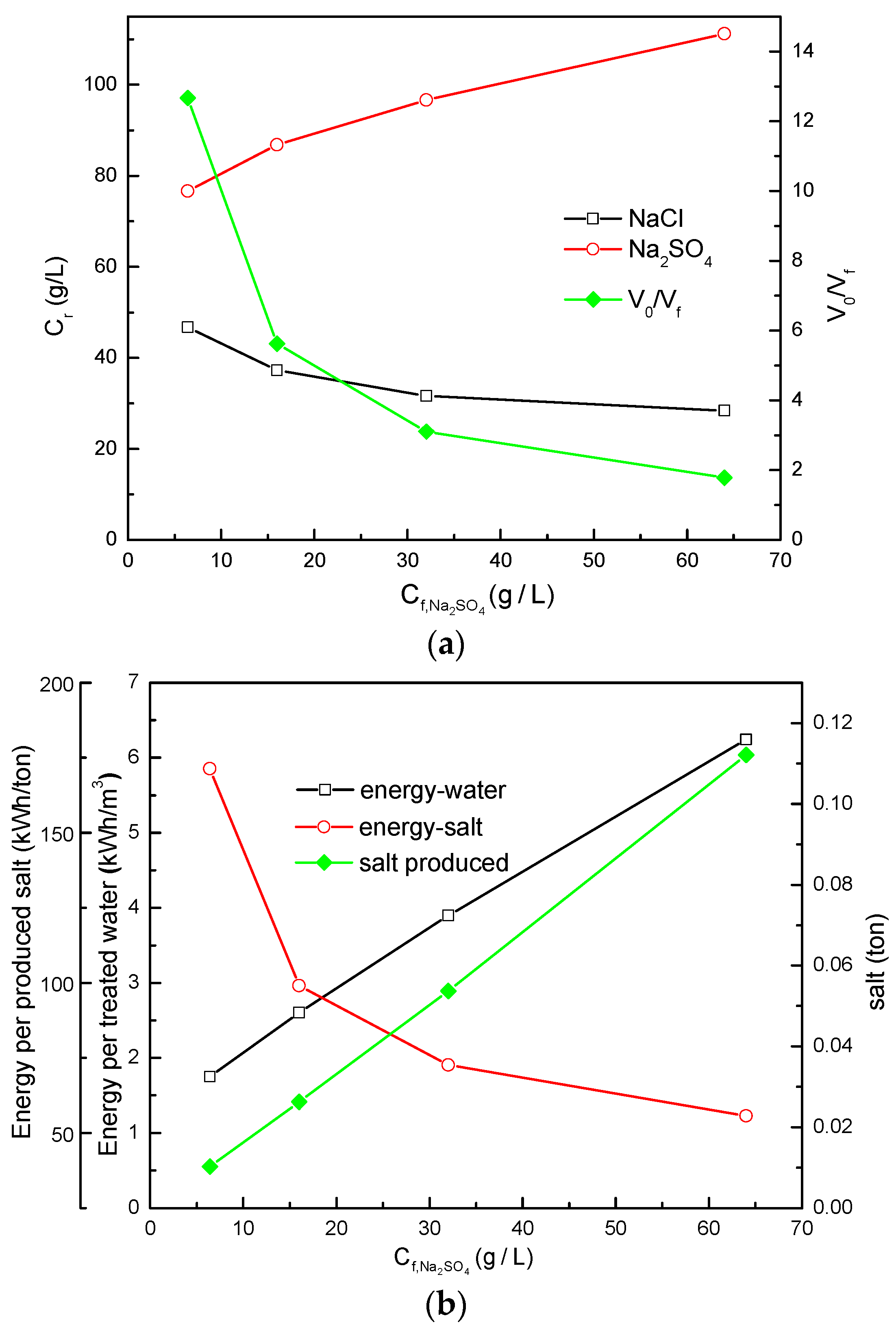
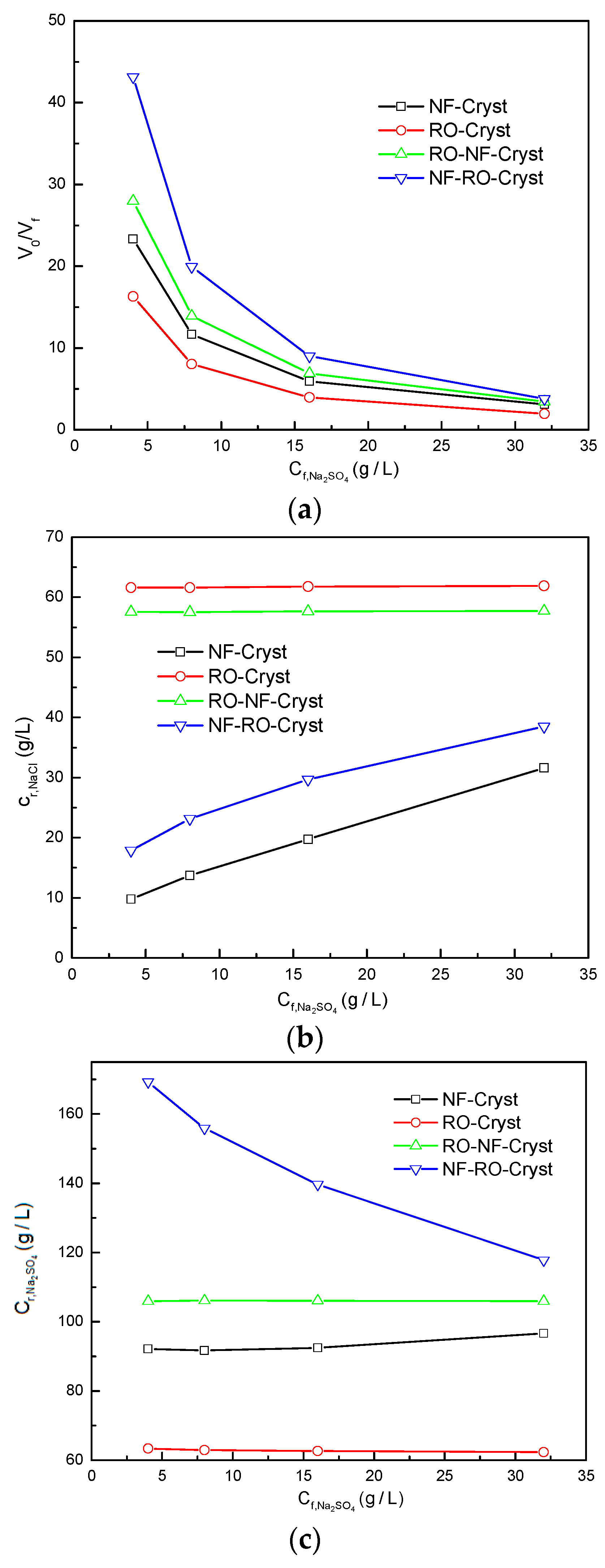
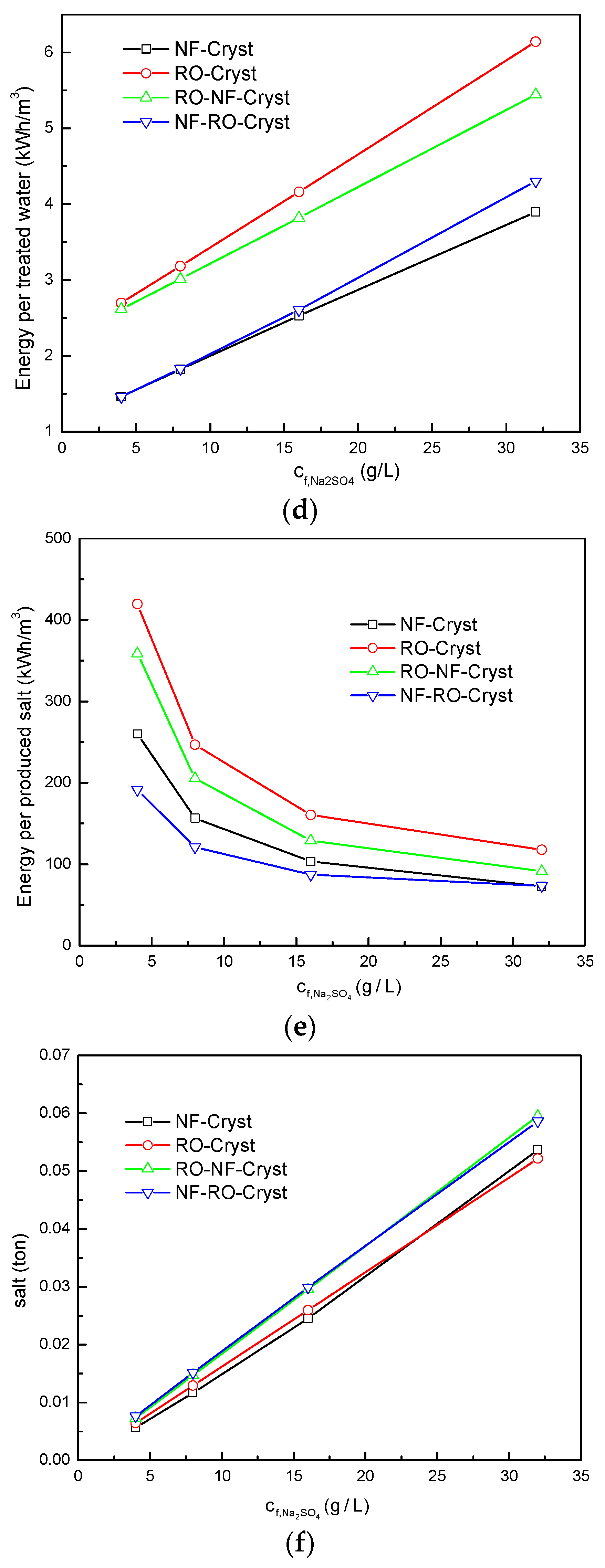
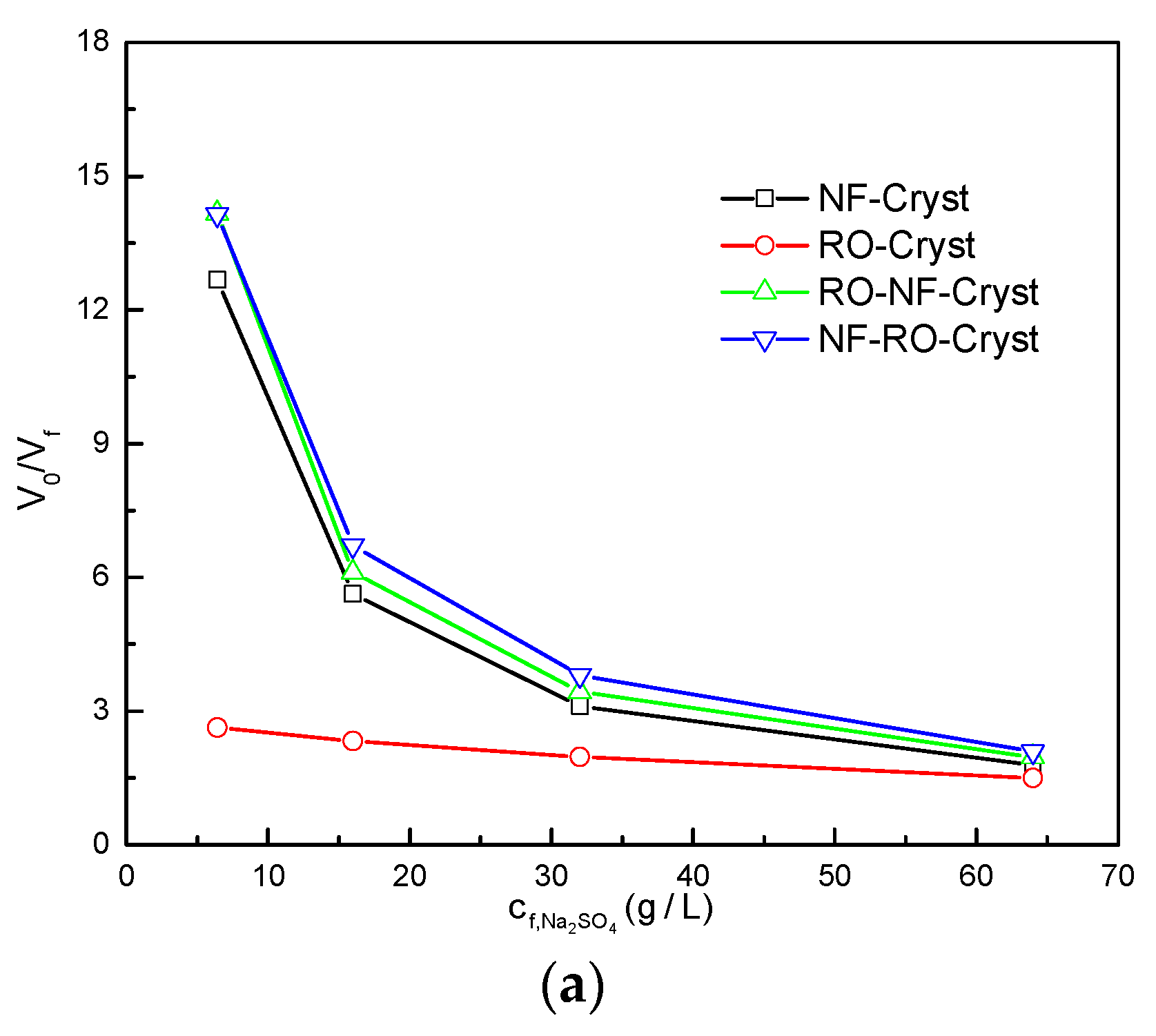
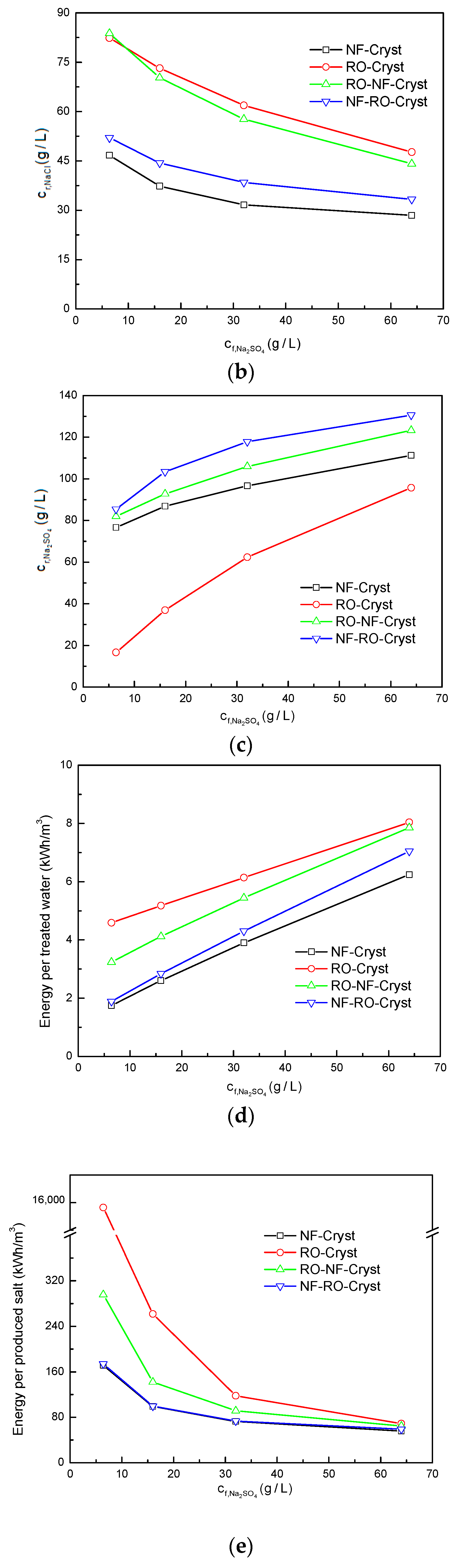
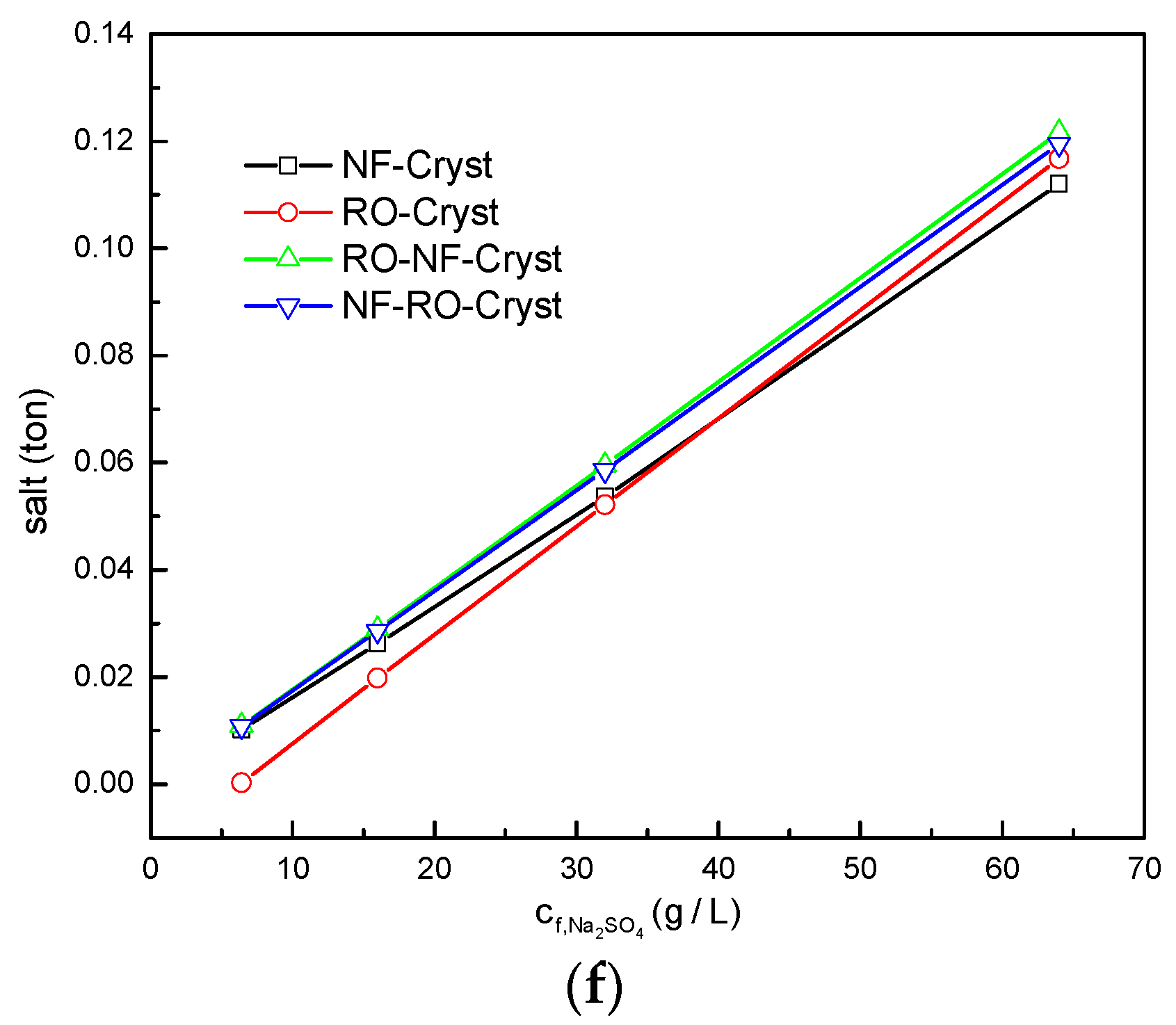
3.2. Comparison between Different Process Configurations
3.2.1. Comparison of Simulation Results under Different Total Salt Concentrations
3.2.2. Comparison of Simulation Results under Different /
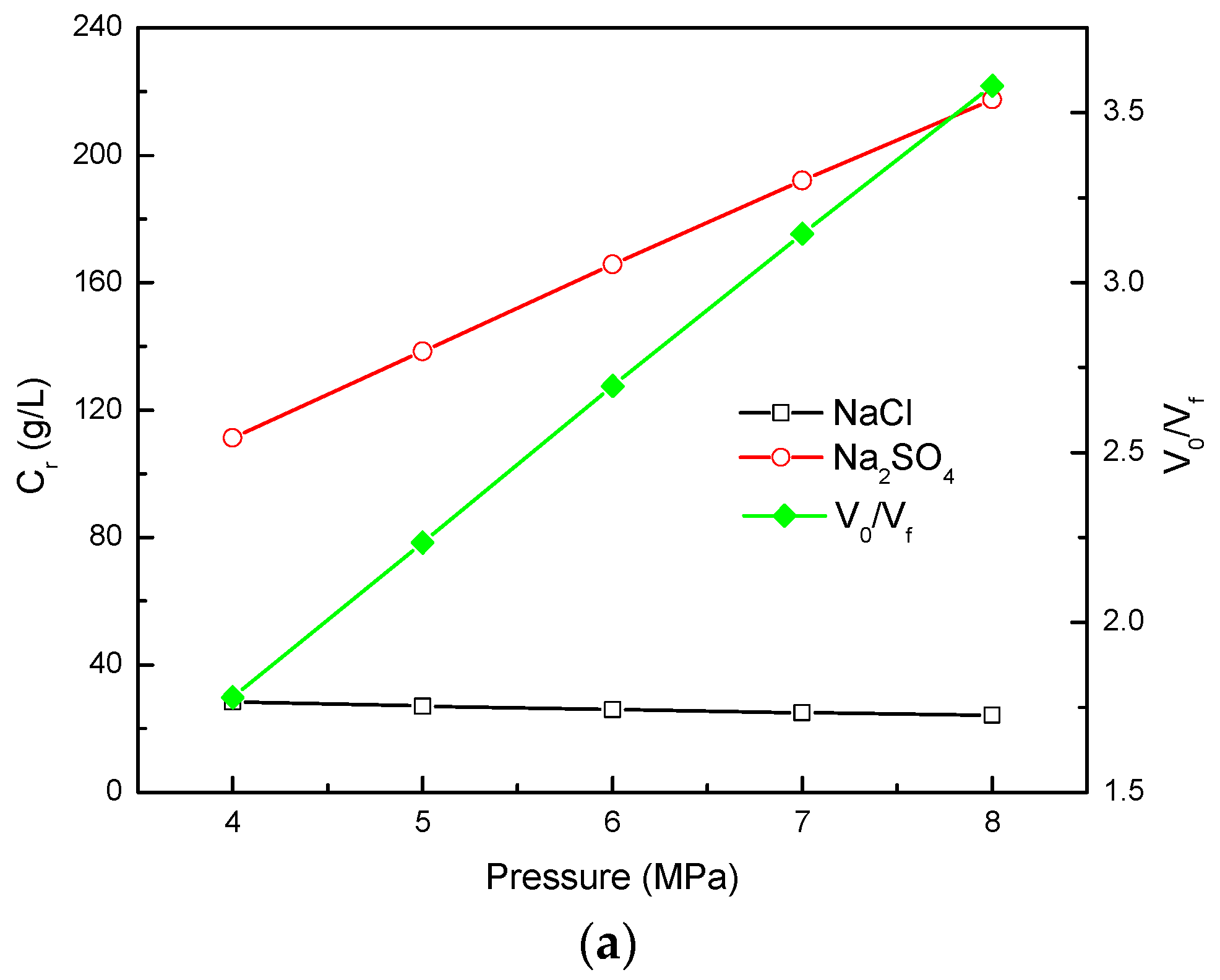
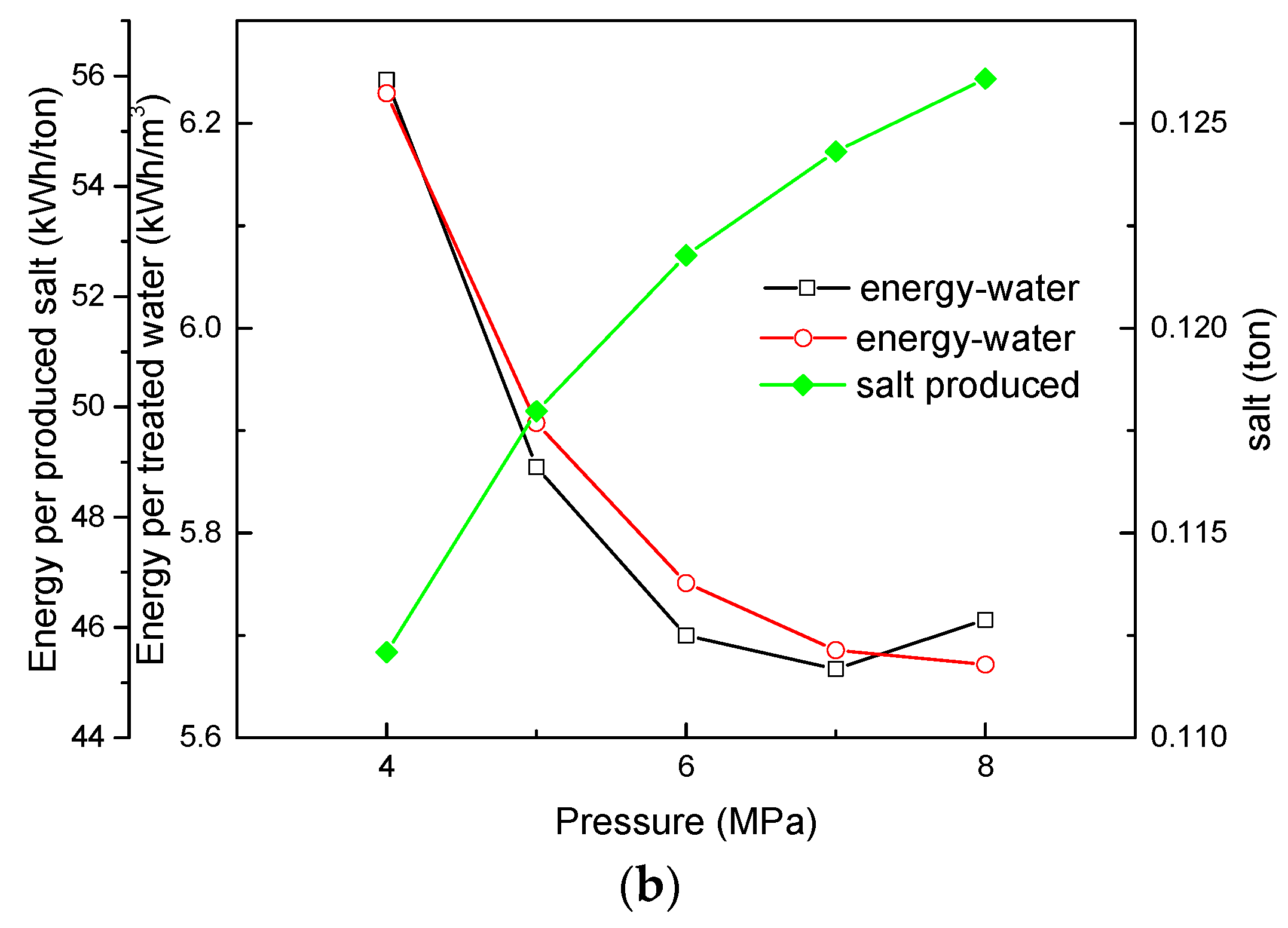
3.3. Effect of NF Operating Pressure
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Glossary of Terms
| Term | Definition |
| Cl− rejection | |
| SO42− rejection | |
| concentration of NaCl in the feed | |
| / | concentration ratio of NaCl over Na2SO4 in the feed |
| V0/Vf | concentration multiple |
| Ewater | energy consumption per cubic meter of treated water (kWh/m3) |
| Esalt | energy consumption per ton of salt production (kWh/ton) |
| Subscripts | Definition |
| f | feed |
| p | permeate |
| r | retentate |
References
- Lefebvre, O.; Moletta, R. Treatment of organic pollution in industrial saline wastewater: A literature review. Water Res. 2006, 40, 3671–3682. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Xu, F.; Li, X.; Li, Q.; Cao, B. Research on Treatment of High Salinity Wastewater. Environ. Sci. Manag. 2014, 39, 72–75. [Google Scholar]
- Hajbi, F.; Hammi, H.; M’nif, A. Reuse of RO Desalination Plant Reject Brine. J. Phase Equilib. Diffus. 2010, 31, 341–347. [Google Scholar] [CrossRef]
- Gao, S. Study on the Comprehensive Utilization of High Salinity Wastewater. Master’s Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Rodriguez-DeLaNuez, F.; Franquiz-Suarez, N.; Esther Santiago, D.; Miguel Veza, J.; Jaime Sadhwani, J. Reuse and minimization of desalination brines: A review of alternatives. Desalination Water Treat. 2012, 39, 137–148. [Google Scholar] [CrossRef]
- Garcia-Aleman, J.; Dickson, J.M. Mathematical modeling of nanofiltration membranes with mixed electrolyte solutions. J. Membr. Sci. 2004, 235, 1–13. [Google Scholar] [CrossRef]
- Cavaco Morão, A.I.; Szymczyk, A.; Fievet, P.; Brites Alves, A.M. Modelling the separation by nanofiltration of a multi-ionic solution relevant to an industrial process. J. Membr. Sci. 2008, 322, 320–330. [Google Scholar] [CrossRef]
- Mohammad, A.W.; Teow, Y.H.; Ang, W.L.; Chung, Y.T.; Oatley-Radcliffe, D.L.; Hilal, N. Nanofiltration membranes review: Recent advances and future prospects. Desalination 2015, 356, 226–254. [Google Scholar] [CrossRef]
- Wang, X.; Shang, W.; Wang, D.; Wu, L.; Tu, C. Characterization and applications of nanofiltration membranes: State of the art. Desalination 2009, 236, 316–326. [Google Scholar] [CrossRef]
- Wang, X.L.; Tsuru, T.; Nakao, S.I.; Kimura, S. The electrostatic and steric-hindrance model for the transport of charged solutes through nanofiltration membranes. J. Membr. Sci. 1997, 135, 19–32. [Google Scholar] [CrossRef]
- Zhou, D.; Zhu, L.; Fu, Y.; Zhu, M.; Xue, L. Development of lower cost seawater desalination processes using nanofiltration technologies—A review. Desalination 2015, 376, 109–116. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Curcio, E.; Drioli, E. Process intensification in the textile industry: The role of membrane technology. J. Environ. Manag. 2004, 73, 267–274. [Google Scholar] [CrossRef] [PubMed]
- Van der Bruggen, B. Integrated Membrane Separation Processes for Recycling of Valuable Wastewater Streams: Nanofiltration, Membrane Distillation, and Membrane Crystallizers Revisited. Ind. Eng. Chem. Res. 2013, 52, 10335–10341. [Google Scholar] [CrossRef]
- Drioli, E.; Curcio, E.; Criscuoli, A.; Profio, G.D. Integrated system for recovery of CaCO3, NaCl and MgSO4·7H2O from nanofiltration retentate. J. Membr. Sci. 2004, 239, 27–38. [Google Scholar] [CrossRef]
- Curcio, E.; Ji, X.; Quazi, A.M.; Barghi, S.; Di Profio, G.; Fontananova, E.; Macleod, T.; Drioli, E. Hybrid nanofiltration–membrane crystallization system for the treatment of sulfate wastes. J. Membr. Sci. 2010, 360, 493–498. [Google Scholar] [CrossRef]
- Zhang, W.; Miao, M.; Pan, J.; Sotto, A.; Shen, J.; Gao, C.; Van der Bruggen, B. Separation of divalent ions from seawater concentrate to enhance the purity of coarse salt by electrodialysis with monovalent-selective membranes. Desalination 2017, 411, 28–37. [Google Scholar] [CrossRef]
- Lidén, A.; Persson, K. Feasibility Study of Advanced NOM-Reduction by Hollow Fiber Ultrafiltration and Nanofiltration at a Swedish Surface Water Treatment Plant. Water 2016, 8, 150. [Google Scholar] [CrossRef]
- Keucken, A.; Wang, Y.; Tng, K.; Leslie, G.; Spanjer, T.; Köhler, S. Optimizing Hollow Fibre Nanofiltration for Organic Matter Rich Lake Water. Water 2016, 8, 430. [Google Scholar] [CrossRef]
- Uyanık, O.; Özkan, O.; Koyuncu, O. NF-RO Membrane Performance for Treating the Effluent of an Organized Industrial Zone Wastewater Treatment Plant: Effect of Different UF Types. Water 2017, 9, 506. [Google Scholar] [CrossRef]
- Zhu, A.; Christofides, P.D.; Cohen, Y. Effect of Thermodynamic Restriction on Energy Cost Optimization of RO Membrane Water Desalination. Ind. Eng. Chem. Res. 2009, 48, 6010–6021. [Google Scholar] [CrossRef]
- Chemical Process Optimization Software—Chemical Process Design. Available online: http://www.aspentech.com/products/engineering/aspen-plus/ (accessed on 10 November 2017).
- Chang, H.; Liau, J.; Ho, C.; Wang, W. Simulation of membrane distillation modules for desalination by developing user’s model on Aspen Plus platform. Desalination 2009, 249, 380–387. [Google Scholar] [CrossRef]
- Sharifian, S.; Harasek, M.; Haddadi, B. Simulation of Membrane Gas Separation Process Using Aspen Plus® V8.6. Chem. Prod. Process Model. 2016, 11. [Google Scholar] [CrossRef]
- Zeng, L.; Du, M.; Wang, X. A Thermodynamical Approach for Evaluating Energy Consumption of the Forward Osmosis Process Using Various Draw Solutes. Water 2017, 9, 189. [Google Scholar] [CrossRef]
- Ghizellaoui, S.; Chibani, A.; Ghizellaoui, S. Use of nanofiltration for partial softening of very hard water. Desalination 2005, 179, 315–322. [Google Scholar] [CrossRef]
- Schaep, J.; Van der Bruggen, B.; Uytterhoeven, S.; Croux, R.; Vandecasteele, C.; Wilms, D.; Van Houtte, E.; Vanlergberghe, F. Removal of hardness from groundwater by nanofiltration. Desalination 1998, 119, 295–301. [Google Scholar] [CrossRef]
- Pérez-González, A.; Ibáñez, R.; Gómez, P.; Urtiaga, A.M.; Ortiz, I.; Irabien, J.A. Nanofiltration separation of polyvalent and monovalent anions in desalination brines. J. Membr. Sci. 2015, 473, 16–27. [Google Scholar] [CrossRef]
- Yan, Z.Q.; Zeng, L.M.; Li, Q.; Liu, T.Y.; Matsuyama, H. Selective separation of chloride and sulfate by nanofiltration for high saline wastewater recycling. Sep. Purif. Technol. 2016, 166, 135–141. [Google Scholar] [CrossRef]
- Stephen, H.; Stephen, T. Binary Systems: Solubilities of Inorganic and Organic Compounds; Pergamon: Oxford, UK, 2013. [Google Scholar]
- Zhu, Z. Water and Salt System Phase Diagram and Its Application; Tianjin University Press: Tianjin, China, 2002. [Google Scholar]
- Wang, X.L.; Ding, N. Technology and Application of RO and NF; Chemical Industry Press: Beijing, China, 2005. [Google Scholar]
- Freeman, S.D.N.; Stocker, T.F. Comparison of two thin-film composite membranes: Low pressure FT-30 to very low pressure NF40HF. Desalination 1987, 62, 183–191. [Google Scholar] [CrossRef]
- GE Osmonics Membranes. Available online: http://www.lenntech.com/products/membrane/osmonics/osmonics.htm (accessed on 10 November 2017).

| (g·L−1) | (g·L−1) | ||
|---|---|---|---|
| 4 | 4 | 0.288 | 0.996 |
| 8 | 8 | 0.224 | 0.993 |
| 16 | 16 | 0.125 | 0.986 |
| 32 | 32 | 0.000 | 0.974 |
| 32 | 6.4 | 0.155 | 0.978 |
| 32 | 16 | 0.097 | 0.979 |
| 32 | 32 | 0.000 | 0.974 |
| 32 | 64 | −0.189 | 0.960 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, M.-y.; Zeng, L.-m.; Wang, X.-l. A Thermodynamical Approach for Evaluating Energy Consumption of the Nanofiltration-Crystallization Process on Selective Separation of Chloride and Sulfate. Water 2018, 10, 331. https://doi.org/10.3390/w10030331
Du M-y, Zeng L-m, Wang X-l. A Thermodynamical Approach for Evaluating Energy Consumption of the Nanofiltration-Crystallization Process on Selective Separation of Chloride and Sulfate. Water. 2018; 10(3):331. https://doi.org/10.3390/w10030331
Chicago/Turabian StyleDu, Ming-yuan, Lan-mu Zeng, and Xiao-lin Wang. 2018. "A Thermodynamical Approach for Evaluating Energy Consumption of the Nanofiltration-Crystallization Process on Selective Separation of Chloride and Sulfate" Water 10, no. 3: 331. https://doi.org/10.3390/w10030331
APA StyleDu, M.-y., Zeng, L.-m., & Wang, X.-l. (2018). A Thermodynamical Approach for Evaluating Energy Consumption of the Nanofiltration-Crystallization Process on Selective Separation of Chloride and Sulfate. Water, 10(3), 331. https://doi.org/10.3390/w10030331




