Dip Phenomenon in High-Curved Turbulent Flows and Application of Entropy Theory
Abstract
:1. Introduction
2. Materials and Methods
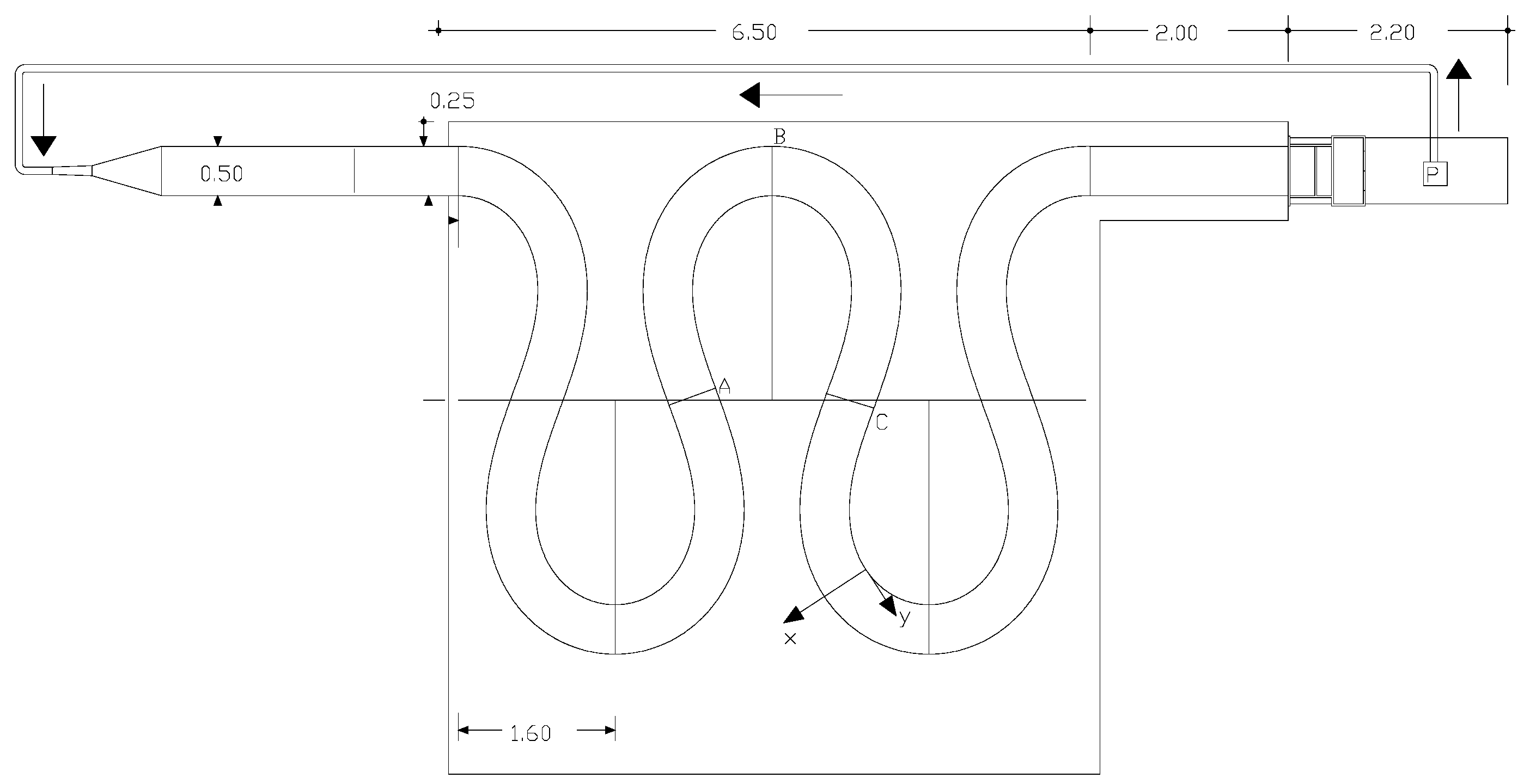
2.1. Experimental Dataset
2.2. Pertinent Aspects and Summary of Previous Results
- -
- Termini ([33]) conducted experiments under the hydraulic conditions that are considered in the present work in order to examine the effect of the continuously changing channel’s curvature on flow pattern. She verified that, because of the changing channel curvature, the flow accelerates near the outer bank from the beginning of the bend to the inflection section downstream and decelerates near the inner bank. The flow accelerated zone is more evident for B/h > 10 than for B/h < 10. Such a different behaviour is caused by the secondary circulation that develops more significantly in the case of B/h < 10 than in the case of B/h > 10, and that attenuates the effect of the convective acceleration close to the outer bank (see also in [31]).
- -
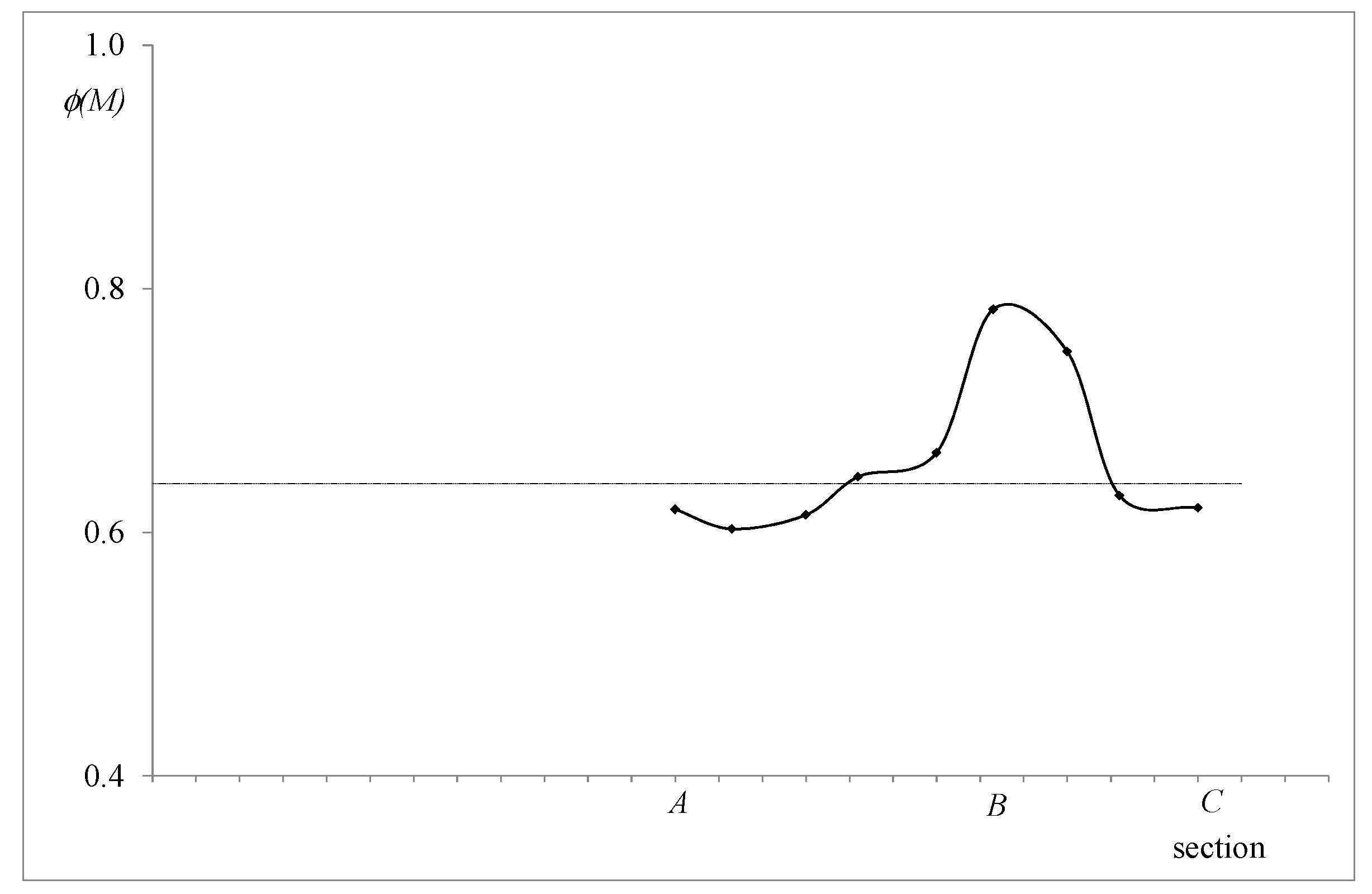
- Termini and Moramarco ([29]) investigated the effect of the downstream variation of the channel’s curvature on the applicability of the linear entropic relationship between the maximum velocity, umax, and the mean flow velocity, um, through a dimensionless parameter Φ(M). As result, they observed that the ratio um/umax, and thus the value of the parameter Φ(M), varies along the bend. In particular, Termini and Moramarco ([29]) demonstrated that, in contrast to what observed in straight channels ([28]) where Φ(M) assumed a value that was almost constant and on average equal to 0.65, along the meandering bend the parameter Φ(M) increases passing from the inflection section to the apex section and decreases from the apex section to the inflection section downstream, assuming a value of around 0.8 close to the apex section and of around 0.6 at the inflection section. This behavior can be observed from Figure 2, where the values of the parameter Φ(M), as obtained by Termini and Moramarco ([29]), along the bend are reported.
3. Results
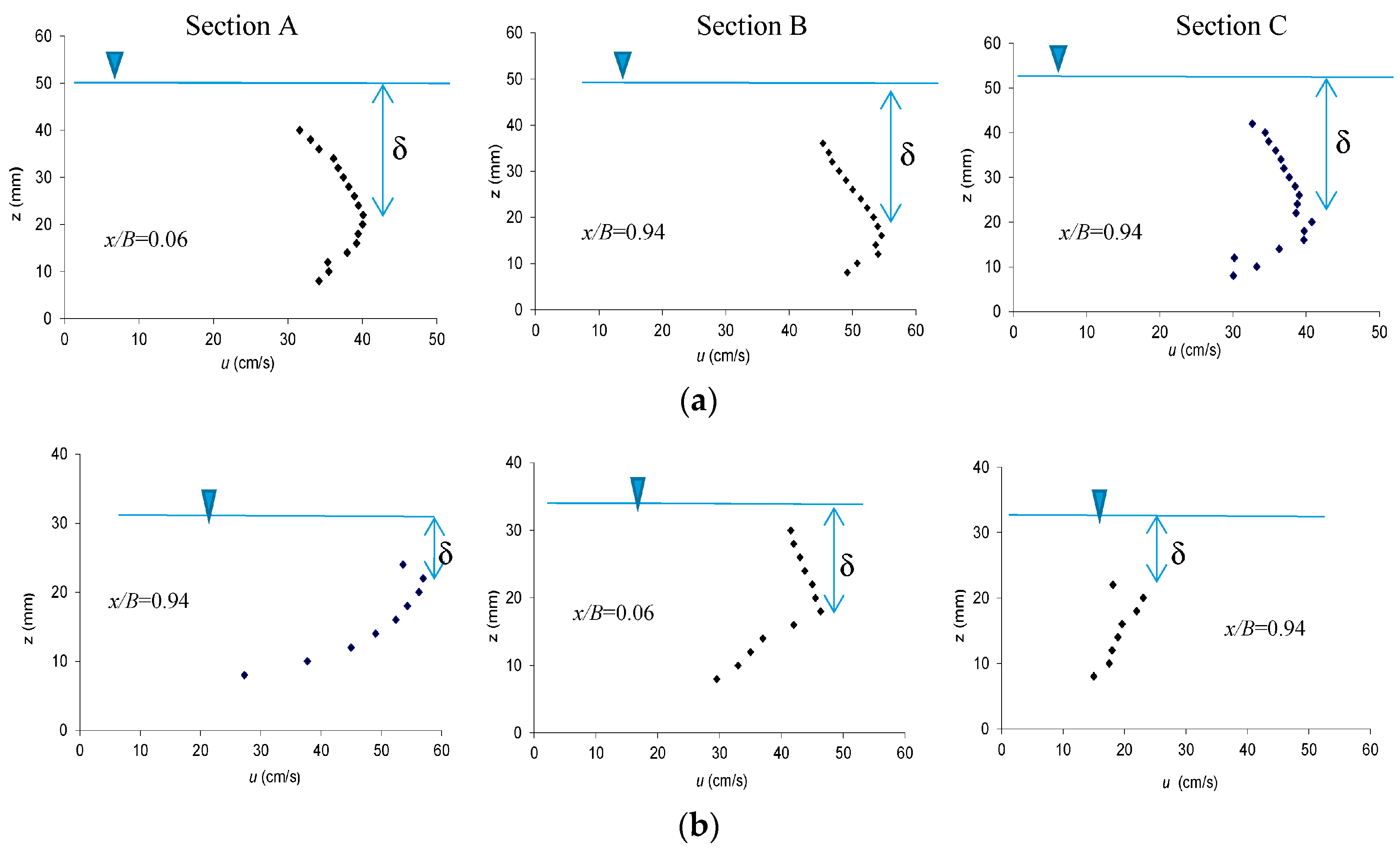
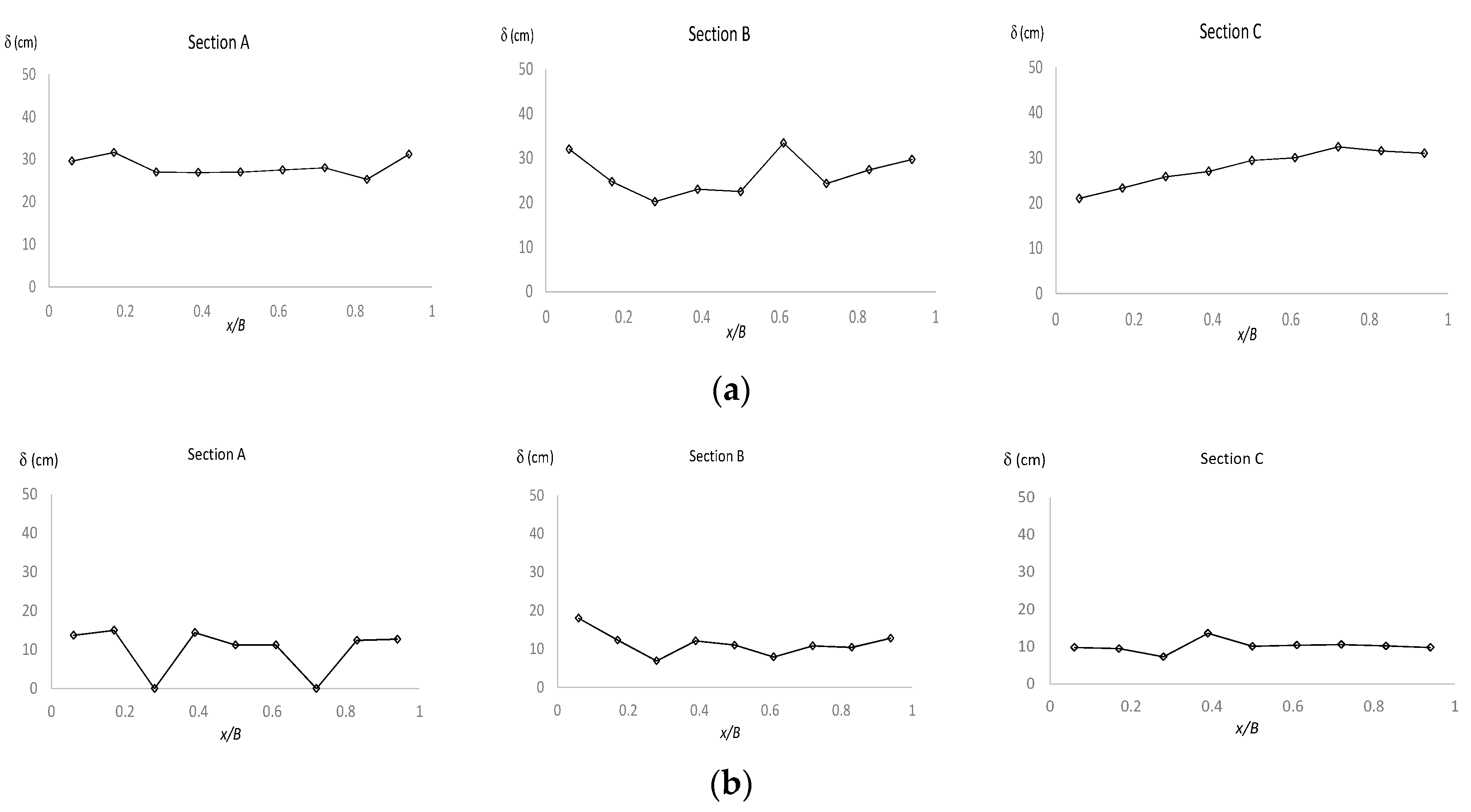
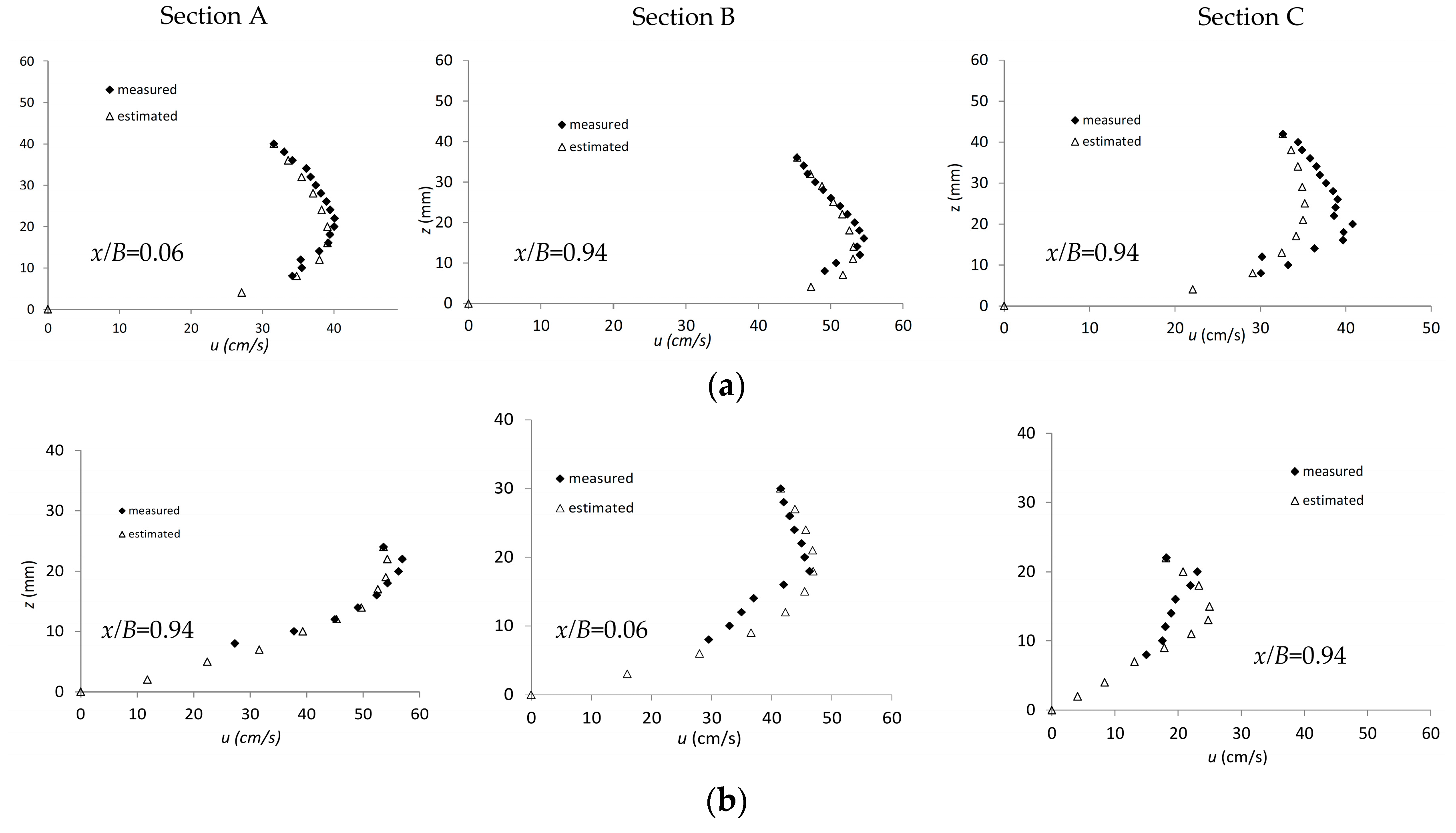
3.1. Measured Velocity Profiles and Effect of the Aspect Ratio on the Velocity-Dip
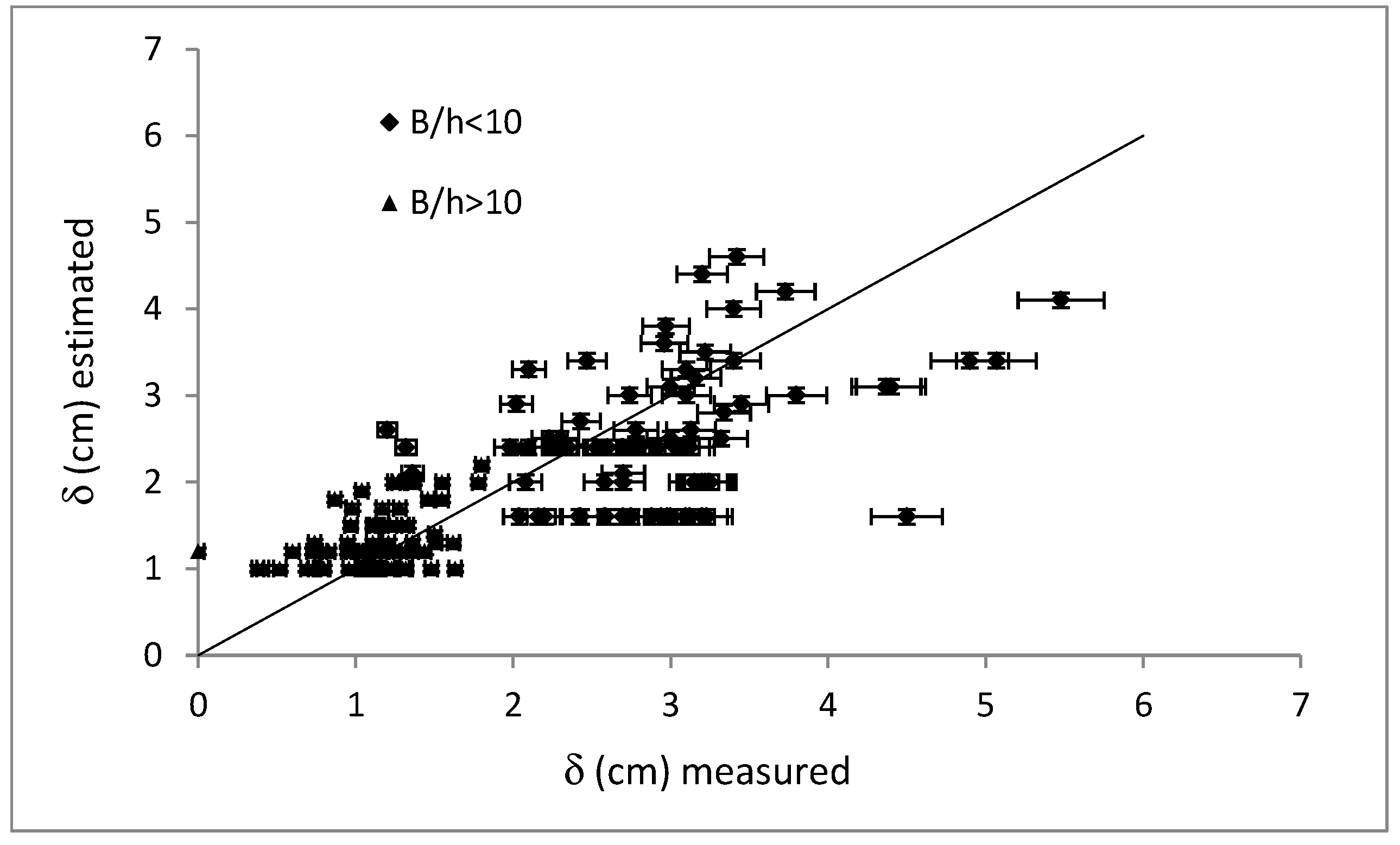
3.2. Application of the Entropic Model to Estimate the Velocity-Dip Phenomenon
4. Discussion and Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Song, T.; Graf, W.H. Velocity and turbulence distribution in unsteady open-channel flows. J. Hydraul. Eng. 1996, 122, 141–154. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; Balkema, A.A., Ed.; CRC Press: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Coles, D. The low of the wake in the turbulent boundary layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef]
- Finley, P.J.; Phoe, K.C.; Poh, C.J. Velocity measurements in a thin turbulent water layer. La Houille Blanche 1966, 6, 713–721. [Google Scholar] [CrossRef]
- Kironoto, B.A.; Graf, W.H. Turbulence Characteristic in Rough Uniform Open-Channel Flow; Laboratoire de Researches Hydrauliques, Ecole Polytechnique Federale: Lausanne, Switzerland, 1994. [Google Scholar]
- Guo, J.; Julien, P.Y. Application of the modified log-wake law in open-channels. J. Appl. Fluid Mech. 2008, 1, 17–23. [Google Scholar]
- Cioffi, F.; Gallerano, F. Velocity and concentration profiles in a channel with movable end erodible bed. J. Hydraul. Res. 1991, 29, 387–401. [Google Scholar] [CrossRef]
- Da Silva, M.F.; Kanani, A. A study of large-scale horizontal; in alluvial streams with a view towards its morphological consequences. In Free Surface Flows and Transport Processes, GeoPlanet: Earth and Planetary Sciences; Springer: Berlin, Germany, 2018; pp. 1–25. [Google Scholar]
- Najafabadi, E.F.; Afzalimehr, H.; Rowinski, P.M. Flow structure through a fluvial pool-riffle sequence—Case study. J. Hydro-Environ. Res. 2018, 19, 1–15. [Google Scholar] [CrossRef]
- Flores, O.; Riley, J.J.; Horner-Devine, A.R. On the dynamics of turbulence near a free surface. J. Fluid Mech. 2017, 821, 248–265. [Google Scholar] [CrossRef]
- Troiani, G.; Cioffi, F.; Casciola, C. Free surface-vorticity interactions in an open channel flow. J. Hydraul. Eng. 2004, 130, 313–323. [Google Scholar] [CrossRef]
- Steffler, P.M.; Rajaratnam, N.; Peterson, A.W. LDA measurements in open channel flow. J. Hydraul. Eng. ASCE 1985, 111, 119–130. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open channel flow measurements with a laser Doppler anemometer. J. Hydraul. Eng. ASCE 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Greco, M.; Moramarco, T. Influence of bed roughness and cross section geometry on medium and maximum velocity ratio in open-channel flow. J. Hydraul. Eng. ASCE 2016, 142, 06015015. [Google Scholar] [CrossRef]
- Sarma, K.V.N.; Lakshminarayana, P.; Lakshmana Rao, N.S. Velocity distribution in smooth rectangular open channel. J. Hydraul. Eng. ASCE 1983, 109, 270–289. [Google Scholar] [CrossRef]
- Yang, S.Q.; Tan, S.K.; Lim, S.Y. Velocity distribution and dip phenomenon in smooth uniform open channel flow. J. Hydraul. Eng. ASCE 2004, 130, 1179–1186. [Google Scholar] [CrossRef]
- Yan, J.; Tang, H.; Xiao, Y.; Li, K.; Tian, Z. Experimental study on influence of boundary on location of maximum velocity in open channel flows. Water Sci. Eng. 2011, 4, 185–191. [Google Scholar]
- Bonakdari, H.; Larrarte, F.; Lassabatere, L.; Joannis, C. Turbulent velocity profile in fully-developed open channel flows. Environ. Fluid Mech. 2008, 8, 1–17. [Google Scholar] [CrossRef]
- Absi, R. An ordinary differential equation for velocity distribution and dip-phenomenon in open channel flows. J. Hydraul. Res. 2011, 49, 82–89. [Google Scholar] [CrossRef]
- Kundu, S. Prediction of velocity-dip-position over the entire cross section of open channel flows using entropy theory. Environ. Earth 2017, 76, 363. [Google Scholar] [CrossRef]
- Stearns, E.P. A reason why the maximum velocity of water flowing in open channels is below the surface. Trans. ASCE 1983, 7, 331–338. [Google Scholar]
- Cardoso, A.H.; Graf, W.H.; Gust, G. Uniform flow in a smooth open channel. J. Hydraul. Res. 1989, 27, 603–616. [Google Scholar] [CrossRef]
- Yang, S.Q.; Lee, J.W. Reynolds shear stress distributions in a gradually varied flow. J. Hydraul. Res. 2007, 45, 462–471. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Tarpanelli, A. From Surface Flow Velocity Measurements to Discharge Assessment by the Entropy Theory. Water 2017, 9, 120. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of Entropy Concept in open-channel flow study. J. Hydraul. Eng. ASCE 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Xia, R. Relation between mean and maximum velocities in a natural river. J. Hydraul. Eng. ASCE 1997, 123, 720–723. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channel based on Chiu’s velocity distribution equation. J. Hydraul. Eng. ASCE 2004, 9, 42–50. [Google Scholar] [CrossRef]
- Moramarco, T.; Termini, D. Entropic approach to estimate the mean flow velocity:experimental investigation in laboratory flumes. Environ. Fluid Mech. 2015, 15, 1163–1179. [Google Scholar] [CrossRef]
- Termini, D.; Moramarco, T. Application of entropic approach to estimate the mean flow velocity and Manning roughness coefficient in a high-curvature flume. Hydrol. Res. Dec. 2016, 2016. [Google Scholar] [CrossRef]
- Blanckaert, K.; Graf, W.H. Momentum transport in sharp open-channel bends. J. Hydraul. Eng. ASCE 2004, 130, 186–198. [Google Scholar] [CrossRef]
- Termini, D.; Piraino, M. Experimental analysis of cross-sectional flow motion in a large amplitude meandering bend. Earth Surf. Process. Landf. 2011, 36, 244–256. [Google Scholar] [CrossRef]
- Termini, D. Momentum transport and bed shear stress distribution in a meandering bend: Experimental analysis in a laboratory flume. Adv. Water Resour. 2015. [Google Scholar] [CrossRef]
- Termini, D. Experimental observations of Flow and Bed processes in a Large-amplitude Meandering Flume. J. Hydraul. Eng. ASCE 2009, 135, 575–587. [Google Scholar] [CrossRef]
- Yalin, M.S. River Mechanics; Pregamon Press: London, UK, 1992. [Google Scholar]
- Hooke, R.L. Distribution of sediment transport and shear stress in a meander bend. J. Geol. 1975, 83, 543–565. [Google Scholar] [CrossRef]
- Whiting, P.J.; Dietrich, W.E. Experimental Studies of Bed Topography and Flow Patterns in Large-Amplitude Meanders, 1. Observations. Water Resour. Res. 1993, 29, 3605–3614. [Google Scholar] [CrossRef]
- Da Silva, A.M.F.; El-Tahawy, T.; Tape, W.D. Variations of flow pattern with sinuosity in sine-generated meandering streams. J. Hydraul. Eng. ASCE 2006, 132, 1003–1014. [Google Scholar] [CrossRef]
- Herschy, R.W. Streamflow Measurement; Elsevier: London, UK, 1985. [Google Scholar]
| δav (%) = 53 | |||||||||
| B/h < 10 | x/B | ||||||||
| Section | 0.06 | 0.17 | 0.28 | 0.39 | 0.5 | 0.61 | 0.72 | 0.83 | 0.94 |
| A | 57.36 | 61.24 | 52.94 | 52.85 | 52.94 | 53.40 | 53.85 | 47.47 | 56.52 |
| B | 53.33 | 43.56 | 35.94 | 43.40 | 44.55 | 58.19 | 52.48 | 60.35 | 64.99 |
| C | 39.62 | 47.26 | 51.81 | 52.94 | 57.20 | 57.69 | 61.83 | 61.17 | 60.78 |
| δav (%) = 34 | |||||||||
| B/h > 10 | x/B | ||||||||
| Section | 0.06 | 0.17 | 0.28 | 0.39 | 0.5 | 0.61 | 0.72 | 0.83 | 0.94 |
| A | 43.22 | 48.39 | 0.00 | 47.37 | 35.90 | 35.90 | 0.00 | 38.27 | 36.60 |
| B | 50.00 | 35.86 | 20.97 | 37.69 | 35.48 | 26.42 | 37.50 | 36.62 | 44.44 |
| C | 32.89 | 32.20 | 24.91 | 40.48 | 33.55 | 34.21 | 34.64 | 33.77 | 32.89 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Termini, D.; Moramarco, T. Dip Phenomenon in High-Curved Turbulent Flows and Application of Entropy Theory. Water 2018, 10, 306. https://doi.org/10.3390/w10030306
Termini D, Moramarco T. Dip Phenomenon in High-Curved Turbulent Flows and Application of Entropy Theory. Water. 2018; 10(3):306. https://doi.org/10.3390/w10030306
Chicago/Turabian StyleTermini, Donatella, and Tommaso Moramarco. 2018. "Dip Phenomenon in High-Curved Turbulent Flows and Application of Entropy Theory" Water 10, no. 3: 306. https://doi.org/10.3390/w10030306
APA StyleTermini, D., & Moramarco, T. (2018). Dip Phenomenon in High-Curved Turbulent Flows and Application of Entropy Theory. Water, 10(3), 306. https://doi.org/10.3390/w10030306






