Abstract
Turbulence measurement of a dense jet perpendicularly issued into a crossflow is investigated experimentally. The flow-velocity components were extensively measured with a high frequency Acoustic Doppler Velocimeter (ADV) system, whereas, a Micro Scale Conductivity Temperature instrument was used to measure the jet salinity. Special attention is given to understand the jet flow-structures in the flow symmetry plane. The flow velocity-fields, the jet trajectory, the turbulence intensities, the turbulent kinetic energy, the turbulent length scales, and the dispersion coefficients have been analyzed. The flow velocity-fields show that the dense jet is characterized by two distinct regions: an ascending region, of jet-like mixing, and a descending region of plume-like mixing. In this study, a new scaling approach of the jet trajectories, based on the jet characteristic length scales, is proposed, leading to an empirical closed-form expression to predict the jet trajectory. The turbulence analysis shows that the jet is accompanied by high levels of flow-turbulence intensities and large kinetic energy production. The results of the turbulent length scales indicate that the ambient flow-field, without jet effect, is an isotropic process. However, in the jet flow-field, a significant spatial-variation of the turbulent length scales was observed, indicating an anisotropic process. The trends of the dispersion coefficients follow those of the turbulent length scales. In comparison with the ambient flow, the jet flow-field shows a decrease of the longitudinal dispersion coefficient and an increase of the vertical one, leading to the increase of the jet width.
1. Introduction
The mixing of discharged fluids with a surrounding natural fluid is of primary concern for a wide range of engineering and environmental applications, i.e., the discharge of wastewater in receiving natural water bodies, the ascending motions of thermals in the atmosphere, the dynamic of volcanic eruption columns, the fuel injection in combustion chambers, the engineering propulsion systems, the propagation of smoke in free or enclosed spaces [1]. Brine discharge from desalination plants, as an example, is the concern of many countries around the world. Many nations, having very scarce water resources or suffer water shortages, are being forced to develop alternative sources derived from seawater desalination to meet the demand for freshwater. The brine is typically discharged into a receiving water body (coastal water, ocean, river, lake) as a turbulent jet (Figure 1) [2], reflecting a number of complex hydrodynamic phenomena and affecting the ecosystem services. Discharge systems need to be well designed to achieve a rapid mixing of the discharged brine, reducing environmental impacts. Therefore, a good knowledge of the interaction between a discharge system (e.g., dense jet) and a receiving water environment is required to promote best environmental management practices.
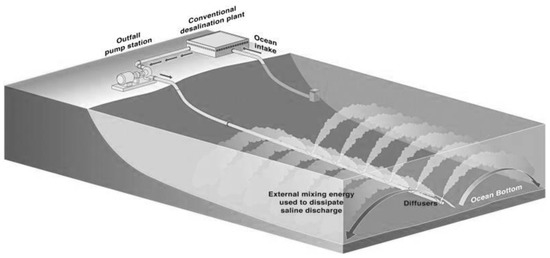
Figure 1.
Schema of a brine discharge system at a desalination plant [2].
The effluent jet properties are usually different than the environmental water properties, i.e., the temperature, the density, the salinity, the chemical composition, the buoyancy-induced rise or fall of the discharged flow. Since all components of aquatic ecosystems are very sensitive to any water quality changes, a rapid and maximum dilution of the jet discharge within the ambient flow is a key solution to keep the ecosystem healthy and sustainable. Mixing of turbulent jets within surrounding environment was the topic of numerous experimental, analytical and numerical studies [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].
Using a three-dimensional laser-induced fluorescence (3DLIF), Gungor and Roberts [19] carried out a series of laboratory experiments on the dilution of vertical dense jets in a flowing current. The investigators observed that the jet reveals very complex flows, spatially varying and depend on the current speeds urF, where ur is the ratio of ambient to jet velocity and F is the jet densimetric Froude number. These complex phenomena make the jet difficult to numerically manage. Thanks to the extensive jet-concentration measurements, the authors obtained a detailed three-dimensional picture of the jet structure within the surrounding environmental flow. They indicated that, at low speeds (urF < 0.5), the jet descending flow is strongly asymmetric and of complex hydrodynamic structure, experiencing a sharp curvature at its terminal rise height. At urF = 0.9, a slight asymmetry occurs in the ascending region, whereas, an almost vertical symmetry of the jet was observed in the descending region. Recently, Ben Meftah et al. [18], analyzing the same data of the present study but focusing on the vortical structure of the jet, definitely confirmed the formation of counter-rotating vortex pair (CRVP) through both the ascending and descending jet regions, a topic of conjecture in many previous studies without any experimental demonstration.
Both studies of Gungor and Roberts [19] and Ben Meftah et al. [18] indicated that, at high speeds (urF > 2), the jet undergoes rapid dispersion in the receiving water body by the effect of the ambient flow-turbulence. This significantly reduces the negative-buoyancy effect of the jet, leading to the disappearance of the descending region. At urF > 2, the dense jet almost behaves as a momentum jet discharged into a crossflow [5,14,20,21].
Analysis of vortex system of turbulent jets, issuing into a crossflow [5,6,22,23,24,25], suggested that the CRVP increase entrainment of the crossflow into the jet, leading to better jet mixing. Kaminski et al. [26] depicted that, at small scale, the agents of entrainment are turbulent eddies, which form a mixing layer between the jet and its surrounding flow. The diffusion/mixing processes strongly depend on the strain rates and/or scalar dissipation rates. Danckwerts [27] indicated that the mixing process is a breaking-up of a clump of fluid from large scales to smaller scales, leading to differences in scalar concentration values. The author pointed out that the mixing degree in flow fields can be mainly expressed by two statistically-defined quantities: a scale and an intensity of segregation. In the case of turbulent flows, the scale and intensity of segregation are analogous to the turbulent length-/time-scale and the turbulence intensity, respectively. The determination of such scales requires adequate measurements/simulations of the flow turbulence. Recently, Galeazzo et al. [28] have focused on the study of turbulent mixing within a jet in crossflow, comparing experimental results with those of numerical simulations. The authors used a combination between planar particle image velocimetry and laser induced fluorescence to measure the turbulent velocity and concentration flow fields. The comparison of their experimental results with simulated results, using RANS and LES, showed that the mean jet velocity field was well described, however, the turbulent quantities, such as the Reynolds stresses and the predicted turbulent mixing, were not in good agreement with the experiments.
Due to the complexity of turbulent jet flow structure and its challenging numerical simulation, in the present study, we will experimentally try to examine some turbulence characteristic parameters of a dense round jet vertically discharged into a flowing current. The flow velocity-fields, the jet trajectory, the turbulence intensity, the turbulent kinetic energy, the turbulent length-scales, and the dispersion coefficients will be specifically analyzed. These parameters are very helpful for validation and calibration of numerical models of dense jets.
2. Theoretical Analysis
An inclined dense jet discharged into a flowing current [19,29,30] can almost be characterized by two distinct phases: (i) a rapid ascent phase; and (ii) a gradually descent phase [18]. During the ascent phase, the jet behaves as a momentum pure jet discharged into a crossflow. With a small value of ur, the jet is only weakly affected near the exit, penetrating uprightly into the crossflow before bending over. During the descent phase, the jet changes to a kind of negatively buoyant jet/plume; its velocity significantly reduces, the downward buoyant forces cause the discharge to gradually fall back and its trajectory impacts the bottom at a downstream distance xi. Near the bottom, the discharge laterally spreads in all directions, forming a bottom layer of spreading density current of thickness zL.
Figure 2 shows a definition sketch of a typical dense jet discharged normally to a main shallow flow of depth H. The jet consists of a vertical (of an angle relative to the horizontal θ = 90°) round nozzle, of a diameter D and a port height z0, which releases effluent of an initial density ρ0 into a channel crossflow of fluid density ρa, with ρa < ρ0. The jet discharges at an initial velocity U0 in a uniform channel/ambient flow of mean velocity Ua. The effluent consists of saltwater solution of initial conductivity c0 and that of the ambient flow is ca, ca < c0. Figure 2 also shows the jet trajectory. In Figure 2, zt indicates the maximum rise height of the jet trajectory occurred at the downstream distance xt. All the basic symbols and the system of coordinates are clearly indicated in Figure 2.
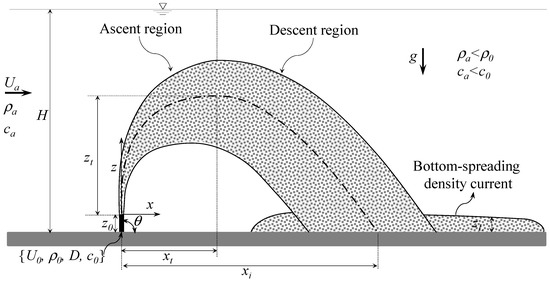
Figure 2.
Definition sketch of the vertical dense jet in shallow water. The jet trajectory (jet axis or centerline) is indicated by the dashed-dot curve.
The exact equations describing a negative buoyant jet flow are generally the unsteady Navier-Stokes and the concentration equations. Direct numerical resolution of turbulent jet flow, at the small-scale motions, remains a challenge for engineers and scientists. The statistical approach, however, is more feasible, averaging the motion equations over time. The continuity equation is:
The momentum equations are:
The time-averaged concentration equation, neglecting the molecular diffusion against the turbulent diffusion, is:
where ρ is the fluid density, Ui (=U, V, W) are the mean velocity components in the xi (=x, y, z) directions, in which x, y and z are the streamwise, the spanwise and the vertical directions, respectively, t is the time, μ is the dynamic viscosity, τij = −ρUi’U’j is the time-averaged stress of u’iu’j(t) over the length of the time series, p is the fluid pressure, g’ = [(ρ0 − ρ)/ρ]g is the reduced gravity, g is the gravity acceleration, C is the mean fluid concentration, U’C’ is the time-averaged concentration transport by turbulent velocity fluctuations u’ic(t) over the length of the time series and Ki (=Kx, Ky, Kz) is the dispersion coefficient in the xi (=x, y, z) directions, respectively. The instantaneous velocity and concentration are defined as ui(t) = Ui + ui’(t) and c(t) = C + c’(t), where ui = (u, v, w) in the x, y and z directions, respectively, and ui’ = (u’, v’, w’) is its fluctuation, while c’ is the concentration fluctuation. The second member of the left-hand side of Equation (3) describe the advection of the solute in the three directions. The dispersion coefficient in the right-hand side of Equation (3) aggregate all the turbulent diffusion in the three directions.
At high Reynolds numbers, the turbulence is assumed to be at equilibrium, i.e., the production term is of order of the dissipation term. The turbulent kinetic energy of velocity fluctuations cascades from large to small scales of motion. In the analysis of the flow-dispersion interaction, the turbulent kinetic energy (TKE) is important in determining the turbulent dispersion coefficient and thus the mass transport [31]. At equilibrium, the transport equation of the turbulent kinetic energy is expressed as:
where k = 1/2Ui’Ui’ is the time-averaged turbulent kinetic energy of 1/2ui’ui’(t) over the length of the time series, Ui’P’ is the time-averaged pressure diffusion of ui’p’(t), Ui’k’ is the time-averaged turbulent transport of 1/2ui’ui’ui’(t) and Di is the turbulent diffusion coefficient.
The dispersion coefficients, Ki, and the turbulent diffusion coefficients, Di, are strongly flow dependent, varying with the flow field, especially in the case of a dense jet discharged into a flowing current. These coefficients are properties of the flow. Therefore, the obvious question that arises for any numerical simulation of the dense jet is: what are the values of these coefficients in any particular situation and positions within the jet/ambient flows and how do they depend on the measured mean properties of the flow.
Since the dimensions of Di must be length squared per time, lending to a product of a velocity scale and a length scale, a physical meaningful expression of Di can be obtained as:
where Li is a characteristic eddy length scale and (k)1/2 is a turbulent velocity scale.
Analogous to the expression of D in Equation (5), it is also possible to assume that the net dispersion coefficients of Equation (3) could be proportional to:
On another hand, by assuming that the Boussinesq approximation is valid and the flow is fully turbulent, the initial properties of an inclined dense jet discharged into a cross-flow is characterized by its discharge volume flux Q0, its momentum flux M0 and its buoyancy flux B0, defined as:
where A0 = πD2/4 is the jet source area. These fluxes can be combined with the ambient velocity, Ua, to provide some relevant length scales, such as:
Briefly, lM is the jet-to-plume length and measures the relative importance of the initial momentum flux against the buoyancy flux, differentiating the region of jet-like mixing dominance from the region of buoyancy dominance (for z/Lm << 1, as an example, the initial momentum effect will be dominant over the bouncy effec), lm is the jet-to-crossflow length scale and measures the relative importance of the initial excess momentum flux to the ambient flow-velocity (for z/lm << 1, the jet velocity is so much higher than the ambient velocity and then a momentum jet will be vertically grown within the ambient flow), and lQ is the discharge length scale and indicates the distance over which the volume flux of the entrained ambient fluid becomes approximately equal to the initial volume flux (for z/lQ < 10, the jet diameter will have a direct effect on the flow characteristics) [19,32].
Defining a velocity scale [19] as:
For vertical jets (θ is invariant) discharged in large channels (with no effect of side walls on the jet), any dimensionless jet property Φ can be expressed as:
The ratio lM/lQ in Equation (10) is proportional to the jet densimetric Froude Number F as:
According to Gungor and Roberts [19], the dynamical effect of the ambient current is mainly determined by the ratio of the ambient velocity to the characteristic velocity Ua/Uc, which is also equal to lM/lm. For round jet nozzle this ratio can be expressed as:
Equations (10)–(12) clearly indicate that all the dependent geometric scales of the flow, such as xt, xi, zt can therefore be written as:
taking into account that lM is proportional to DF.
Gungor and Roberts [19] and Roberts and Toms [33] observed that, for lQ << lM (F >> 1), the dynamic effect of the source volume flux becomes negligible, and then F does not appear as an individual variable. After these assumptions Equation (13) becomes:
3. Experimental Method
Experiments were carried out in a closed circuit flume, specifically designed for the study of buoyant jets, at the Coastal Engineering Laboratory (LIC) of the Department of Civil, Environmental, Land, Building Engineering, and Chemistry of the Polytechnic University of Bari (Italy). The system consists of a rectangular channel made of glass, 15 m long, 4 m wide and 0.4 m deep (Figure 3). The fresh water at ambient temperature is supplied from a downstream big metallic tank, by means a centrifugal electro-pump to an upstream steel tank. The upstream tank is equipped with a side-channel spillway with adjustable height in order to maintain constant flow-head condition. The overflowing water reaches again the downstream tank. The pumped and overflowed flow rates are measured by means two electromagnetic flow meters, mounted on the channel system. To create a smooth flow transition, damping inlet turbulence, from the upstream tank to the flume, a set of stilling grids were installed in the outlet of the upstream tank.
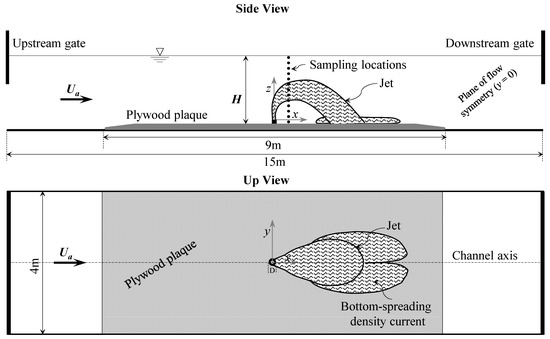
Figure 3.
General sketch of the laboratory flume with the jet flow. For the sake of simplicity, only one vertical profile is qualitatively presented to show the sampling locations, the same sampling locations are repeated at different downstream locations x/D along the plane of flow symmetry.
The second part of the laboratory model consists of a dense jet hydraulic system. To mix tap/fresh water with salt (NaCl), a large cylindrical storage tank made by fiberglass, of maximum volume 6 m3, is used. The tank is equipped with four compressed air jets, installed on two levels at opposite positions, to mix the salt with the fresh water. The saltwater is pumped through a pipeline to the jet nozzle. This pipeline is equipped with a regulating valve and a magnetic flow meter to provide a well-defined flow discharge. The jet nozzle is of diameter D = 10 mm, vertically mounted in the flume center at a port height z0 = 10 mm above the flume bottom.
In order to elucidate the three-dimensional characteristics of the vertical dense jet, both the velocity and the salinity flow fields were measured at several sampling locations along the plane of flow symmetry (y = 0) and at different cross-sections downstream the jet source (x = 0). Since the grid spacing of samples is O (1 cm), the measuring instruments are attached to a semi-automatic cross-beam to accurately move and align the different probes at each sampling location. The salinity field was measured by means of a Micro Scale Conductivity Temperature Instrument (MSCTI) by Precision Measurement Engineering (PME), designed to measure the temperature and electrical conductivity of water solutions and moving fluids, containing conductive ions. Before starting acquiring data, the probe could be calibrated using a salt solution, of known salinity, prepared in laboratory. At each measurement location, 1000 acquisitions of the water conductivity were carried out at 20 Hz. The velocity data were collected using a 3-D Acoustic Doppler Velocimeter (ADV)-Vectrino system, developed by Nortek, for 60 s at a sampling rate of 150 Hz. The sampling volume of the ADV was located 5 cm below the transmitter probe. The Vectrino was used with a velocity range equal to ±0.30 m/s, a measured velocity accuracy of ±0.5%, a sampling volume of vertical extent of 7 mm. For high-resolution measurements, the manufacturer recommends a 15 db signal-to-noise ratio (SNR) and a correlation coefficient larger than 70%. The acquired data were filtered based on the Tukey’s method and the bad samples (SNR < 15 db and correlation coefficient < 70%) were also removed. Additional details concerning the channel setup and the ADV operations can be found elsewhere in [34,35,36,37,38].
The initial experimental conditions and some parameters of the performed experimental runs are reported in Table 1, where T is the water temperature. In addition to the experimental data of the present study, in Table 1, the data obtained by Gungor and Roberts [19] for ten other different configurations, of various values of urF, are also illustrated.

Table 1.
Initial experimental conditions and parameters of the investigated runs.
4. Results and Discussion
4.1. Jet Velocity Fields
Since turbulence is the most important mechanism that leads to substantial mixing of the jet within the surrounding environment, dense measurements, in high frequency, of the ambient/jet flow velocity-field were carried out. Figure 4 and Figure 5, as an example, show the vertical profiles of the flow velocity at different downstream locations, x/D, away from the jet source. The profiles refer to runs R1 and R2 and represent the streamwise time-averaged velocity component, U, and the vertical time-averaged velocity component, W, both normalized by Ua. All of them were obtained in the plane of flow symmetry (y = 0). On Figure 4 and Figure 5, the jet axis positions, location of maximum jet velocity (velocity resultant of U and W), are indicated by horizontal arrows. Note that, due to the flow symmetry, the spainwise velocity, V, is theoretically expected to be null and therefore it has not any physical significance in this plane.
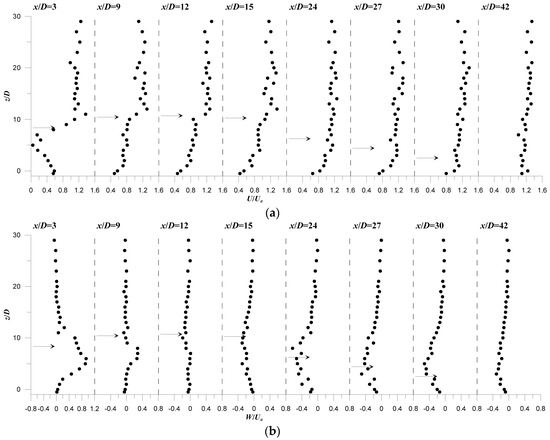
Figure 4.
Normalized velocity profiles in the plane of flow symmetry (y = 0) of run R1 at ur = 0.131 and urF = 1.006: (a) U/Ua; (b) W/Ua. The horizontal arrow on the profiles indicate the position of the jet axis.
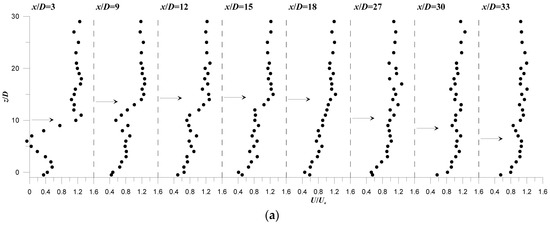
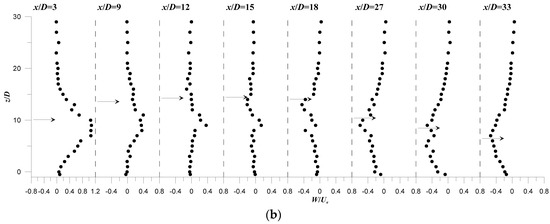
Figure 5.
Normalized velocity profiles in the plane of flow symmetry (y = 0) of run R2 at ur = 0.109 and urF = 1.071: (a) U/Ua; (b) W/Ua.
The trend of the jet axis, shown by the arrows on Figure 4 and Figure 5, clearly indicates that the jet initially penetrates upward within the ambient current, attains a terminal rise height at the downstream distance xt (Figure 2) and then it inclines downward, showing two distinct characteristic regions: an ascending region followed by a descending one [18]. Figure 4a and Figure 5a show that the trend of the vertical profile of U/Ua gradually changes with the increase of x/D. In the ascending region (x/D < 12 and 15, respectively for R1 and R2), the U/Ua-profiles show two characteristic maxima: an absolute maximum, located within the jet flow-field slightly above the jet axis, and a local maximum, appeared in the jet wake-like region.
This finding is in good agreement with results obtained by Ben Meftah et al. [14] and Sherif and Pletcher [39] for momentum jets in crossflow. This suggests that, in the ascending region, the jet is primarily driven by momentum flux, behaving like a vertical non-buoyant jet in crossflow [5,14,39]. The velocity profiles in Figure 4a and Figure 5a show that the absolute maximum of U/Ua, in the jet flow-field, always appears slightly above the jet axis. The magnitudes of both maxima gradually decrease as x/D increases, as clearly shown by the profiles of run R2. In the wake region, close to the jet source, the jet velocity U/Ua experiences very small and negative values. At x/D = 3, as an example, U/Ua ≈ 0.05 and −0.1 with R1 and R2, respectively. This confirms the wake vortices formation at the inner part of the jet, as also mentioned in the previous study by Fric and Roshko [40]. For all the profiles at any position x/D, U/Ua shows an almost constant value of order 1.2Ua, over the flow depth starting from the jet outer-boundary up to the free-surface flow. These results are in complete agreement with those obtained by Ben Meftah et al. [14] and Sherif and Pletcher [39], reflecting simply the vertical distribution of U/Ua in the ambient current without the jet effects. In the descending region, the two velocity-maxima are less pronounced, and the U/Ua-profiles, at x/D > 30, resemble a classical vertical profile of mean velocity in an open channel flow.
Unlike the streamwise velocity component, the W/Ua-profiles are differently developed over the flow depth. They always experience a single peak below the jet axis. In the ascending region, W/Ua shows positive values which gradually decrease as going further away from the jet source, similar to what happens with momentum jets in crossflows [14,39]. At the downstream distance xt (Figure 2), where the jet flow practically becomes horizontal, W/Ua significantly reduces. In the descending region, W/Ua shows negative values, indicating that the jet bends downward.
The jet trajectory is one of the most important parameter characterizing a jet discharged into a crossflow. It principally reflects the ability of the jet to penetrate within the ambient flow, revealing its spreading/mixing process. Despite the numerous previous studies conducted on turbulent jets, there is no recognized closed-form expression of the jet trajectory. Indeed, it was always observed some scatters between the different proposed scaled jet trajectories. According to Hasselbrink and Mungal [20], this scattering is partly due to the definitions of the jet trajectory and partly from opinions on the best form of the correlating equation. In the present study, the jet trajectory is defined as the curve formed by the locus of maximum velocity at the different downstream positions x/D, along the plane of flow symmetry, which is usually known as the jet axis, or the locus of the maximum concentration along the same plane, usually known as the jet centerline.
For momentum jets, Margason [41], as an example, reviewing several correlations of jet-trajectory coordinates, concluded that much of the revised data could be collapsed well by normalizing the jet-trajectory coordinates x and z with the ratio D/ur, leading to a simple power-law in the form of urz/D = α(urx/D)β, where α and β are coefficient determined experimentally.
Figure 6 shows the jet trajectories of runs R1 to R5 scaled with D/ur and plotted in log-log scales. It is important to note here that these trajectories refer to the jet axis, as above defined. In addition to the data of the present study, the jet centerlines (as above defined) obtained by Gungor and Roberts [19] for a dense jet of five different values of urF are also plotted. On Figure 6 we also plot some predicted and experimental trajectories obtained in previous studies [41,42,43] for momentum jets.
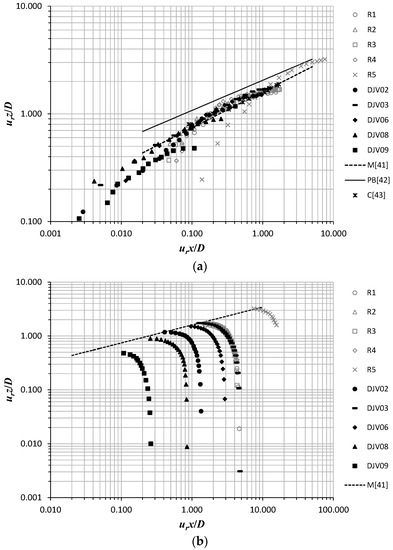
Figure 6.
Normalized jet trajectory: (a) ascending region; (b) descending region. R1 to R5 represent the jet axis of the present study, DJV02 to DJV09 are the jet centerlines of Gungor and Roberts [19], M [41] is a similar power-law of momentum jet trajectory proposed by Margason [41], PB [42] is a similar power-law of momentum jet trajectory proposed by Pratte and Baines [42], and C [43] are experimental data of momentum jet trajectory obtained by Chochua et al. [43].
In the ascending region, as shown in Figure 6a, the dense jet trajectories of the present study and those of Gungor and Roberts [19] almost exhibit the same power-law exponent. The data of the different trajectories tend to collapse onto a single curve, following the data of Margason [41], Pratte and Baines [42], and Chochua et al. [43]. The almost similarity between the different jet trajectories in Figure 6a clearly indicates that the dense jet in the ascending region behaves as a momentum jet, and therefore its trajectory seems to be predictable by a simple power-law as proposed by Margason [41].
Figure 6b shows the normalized jet trajectories in the descending region. It can be clearly seen the significant gap between the different trajectories. In the descending region, the scaling of the jet trajectory by D/ur does not show similarity between the different runs. On the other hand, the examination of Figure 6b, indicates that the trajectories are not randomly scattered between them, but they show a kind of systematic gaps. The jet trajectories show a “manure fork-shape” of inclined “root”, following the power-law (dashed line on the figure) proposed by Margason [41], and parallel “tines”, as shown by the different trajectories. The distance between the “tines” seems proportional to urF. When urF increases, the jet trajectory linearly translates (along almost the dashed line on the figure) to the right. For comparable values of urF, such as the case in runs R1 to R4 of the present study and in run DJV03 of Gungor and Roberts [19] (Table 1), the jet trajectories collapse onto an almost single curve. The absence of similarity between the jet trajectories at different values of urF is related to the choice of the scaling mode, where the scaling with D/ur is not appropriate to represent all the trajectories by a typical profile.
Figure 6b also indicates that the maximum rise height (ending and beginning of the ascending and descending regions, respectively) of the jet trajectories appeared at different longitudinal and vertical coordinates. This points out that, despite the collapse of the jet trajectories in Figure 6a onto an almost single curve, the scaled profiles in the ascending region, really, suffer an incomplete similarity. Therefore, the application of a power-law as proposed by Margason [41] can simply predict the tendency of the jet trajectory in the ascending region, but not the exact profile. The incomplete similarity between the jet trajectories, following the scaling mode proposed for momentum jets, makes us think of another compatible scaling rule. In a recent study, Gungor and Roberts [19] suggested that, based on dimensional analysis of the initial characteristic physical properties of a dense jet, the jet trajectory coordinates could be scaled by DF. Nevertheless, the authors observed that the scaling of the jet trajectories by DF leads to one “universal” trajectory for only experiments that have the same values of urF, as also observed in Figure 6b scaling the jet trajectory by D/ur. Once again, it can be noted that the scaling of the jet trajectories by DF is also not appropriate to represent the trajectories of different urF-values by a typical profile.
At urF < 2, it was observed that the dense jet is characterized by an ascending and a descending regions [14,19] and its trajectory is fundamentally described by three characteristic length scales (Figure 2) xi, xt and zt (Table 1). In the present study, we will try to rescale the jet trajectory as z/zt vs. x/xt, in the ascending region, and z/zt vs. [1 + (x − xt)/(xi − xt)], in the descending region. Figure 7a illustrates both the rescaled jet axis, for all the experimental runs illustrated in Table 1 of the present study (except that of run R5 at urF > 2, where the jet undergoes rapid dispersion by the effect of the ambient flow-turbulence), and the jet centerline for runs R1 and R2. The results of the present study are also compared to the centerline trajectories obtained by Gungor and Roberts [19]. Figure 7a clearly shows that all the jet trajectories (axis and centerline), of the present study and those of Gungor and Roberts [19], perfectly collapse onto a single profile. In the ascending region, at x/xt < 0.03, it can be noted a slight data scattering, due to the effect of the potential core region of the jet. The rescaling of the jet trajectories by xt, xi and zt leads to a typical trajectory for all experiments with complete independence of urF (ranging almost between 0.2 and 1.1 in the present study). This typical trajectory is predictable by the following proposed closed-form expression:
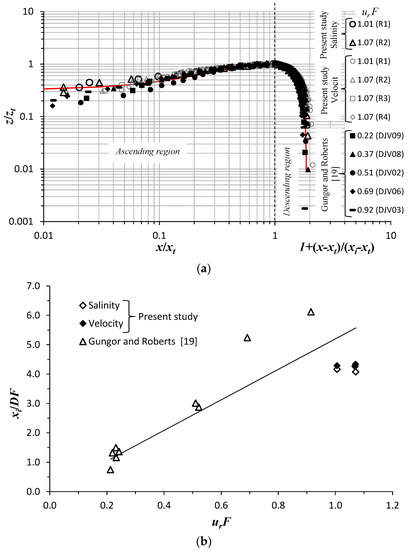
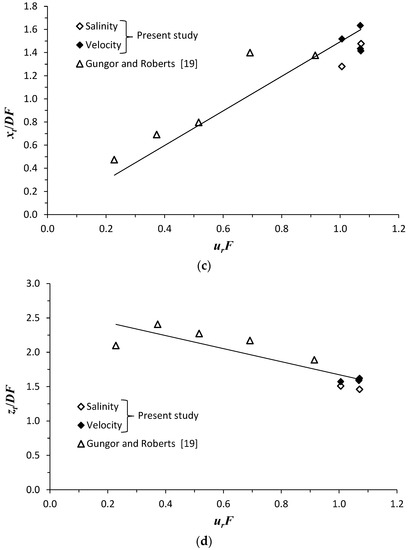
Figure 7.
Jet trajectory analysis: (a) scaling of jet trajectories based on the characteristic length scales xi, xt and zt. The solid red curve represents the solution of Equation (15); (b) xi/DF versus urF; (c) xt/DF versus urF; (d) zt/DF versus urF. The solid regression lines on (b–d) refer to the data of jet concentration of the present study and that of Gungor and Roberts [19].
In order to make Equation (15) easily practicable, expressions of xi, xt and zt can be found, based on the dimensional analysis as depicted in Equation (14). Figure 7b–d show, respectively, the normalized jet characteristic lengths xi/DF, xt/DF and zt/DF plotted versus urF. Based on the experimental data of the present study and that of Gungor and Roberts [19], xi, xt and zt, for the jet centerline, can be approximately predicted by the following semi-empirical equations:
For the jet axis, it is suggested the use of Equations (16)–(18), keeping almost the same value of xt and increasing that of xi and of zt by almost 8%, since the jet axis appears slightly above the jet centerline.
The advantage of the proposed scaling approach, represented by Equations (15)–(18), is its simplicity. It is relatively easy to predict the trajectory of any dense jet vertically discharged into a flowing current, of urF ranging almost between 0.2 and 1.1. This approach can be extended with vertical dense jets of urF < 2 and for inclined dense jets, which is the subject of a future study. Indeed, such approach is very useful to many engineering and environmental applications such as the brine discharge from desalination plants or dense wastewater discharge.
4.2. Turbulence Intensity Associated with the Jet Flow-Field
This section focuses on the analysis of the jet flow-field-turbulence intensities. The turbulence intensity is defined as the ratio of the standard deviation of the flow velocity fluctuation to the ambient mean velocity Ua. Hereafter, we indicate by U’/Ua, V’/Ua and W’/Ua, the streamwise, the spanwise and the vertical flow turbulence intensities, where U’, V’ and W’ are the standard deviation of the streamwise, the spanwise and the vertical flow velocity component fluctuations, respectively.
Figure 8 and Figure 9, as an example, illustrate the vertical profiles of U’/Ua and W’/Ua, at different downstream positions x/D of runs R1 and R2. The data refer to the plane of flow symmetry (y = 0). Due to the flow symmetry, the spanwise velocity is theoretically expected to be null and therefore V’ has not any physical significance in this plane. U’/Ua shows the largest values in the ascending region. In this region, U’/Ua almost shows an absolute peak near the jet axis. In general, according to previous studies, this peak is a distinct off-axis peak, where the turbulence undergoes a slight decrease at the jet axis. This behavior is less pronounced with the current profiles because the vertical profiles are not perfectly orthogonal to the jet axis. Figure 8a and Figure 9a show that U’/Ua significantly increases in the jet flow-field as compared to that in the ambient flow-field (upper part of profiles). Moreover, it can be noted that U’/Ua gradually decays as x/D increases. It shows a maximum value equal to 0.83, 0.93, 1.05 and 1.17 at x/D = 3, and 0.45, 0.47, 0.49 and 0.61at x/D = 12, for runs R1 to R4, respectively. These values clearly indicate that U’/Ua increases as ur decreases. In the descending region, U’/Ua continues to decrease monotonically. Far from jet source, at x/D > 27, U’/Ua shows values comparable to those of the ambient flow-field.
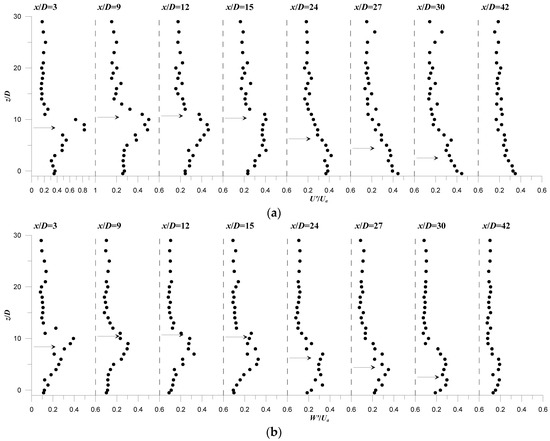
Figure 8.
Vertical profiles of the flow turbulence intensity at different downstream positions x/D along the plane of flow symmetry (y = 0) of run R1: (a) U’/Ua; (b) W’/Ua. The horizontal arrow on the profiles indicate the position of the jet axis.
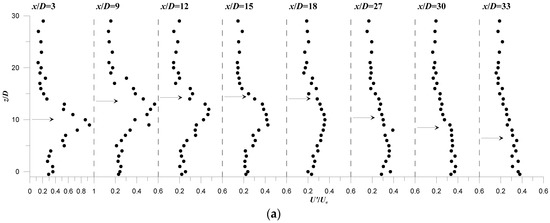
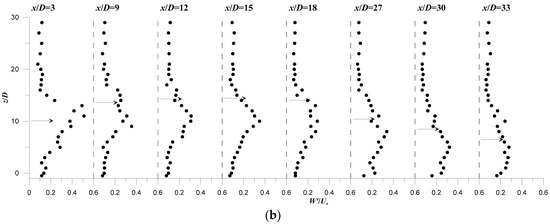
Figure 9.
Vertical profiles of the flow turbulence intensity at different downstream positions x/D along the plane of flow symmetry (y = 0) of run R2: (a) U’/Ua; (b) W’/Ua.
Figure 8b and Figure 9b show that the highest values of W’/Ua take place in the jet flow-field. W’/Ua also shows an absolute peak below the jet axis. In the ascending region, W’/Ua decreases as x/D increases, attains minimum values at the maximum rise height position, as shown at x/D = 9 and 12, and then starts to slightly increase in the descending region with the increase of x/D. Outside the jet flow-field, independently of x/D, W’/Ua for both runs R1 and R2 shows almost constant values of O(0.10) over the flow depth.
In order to get more information on the jet-turbulence-intensity behavior, an analysis of the maximum-turbulence-intensity decay/rise as a function of the downstream distance from the jet exit is examined for runs R1 to R4. Figure 10a,b show, respectively, a plot of U’m/Ua and W’m/Ua against x/xt, where the subscribed m indicates the maximum value of U’/Ua and W’/Ua on the vertical profiles of Figure 8 and Figure 9. Figure 10a shows that, for all runs, U’m/Ua continuously decays as a function of x/xt, regardless its appearance in the ascending (x ≤ xt) or in the descending regions (x ≥ xt). Figure 10a indicates that U’m/Ua decays more rapidly in the ascending region than in the descending region. As going further downstream, the decrease-rate of U’m/Ua as a function of x/xt significantly reduces.
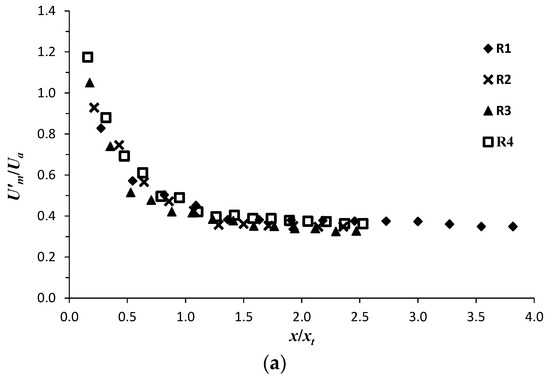
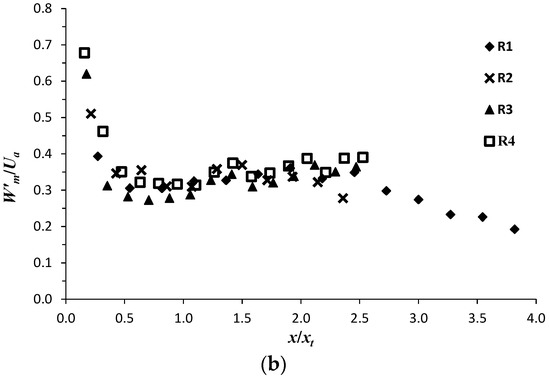
Figure 10.
Decay/rise of the maximum turbulence intensity as a function of the downstream position x/xt: (a) U’m/Ua; (b) W’m/Ua.
In the ascending region, W’m/Ua behaves in a similar way as U’m/Ua. It strongly decays in the ascending region, attaining a minim value at x = xt (Figure 2). In the descending region, however, W’m/Ua shows a gradual increase as x/xt increases and then starts to decrease again, as clearly shown with R1 for x/xt > 2.5. The decay and rise of W’m/Ua are related to the vertical-velocity behavior, which shows a decrease of its magnitude along the ascending region as x/D increases, attains almost null values at xt and then starts to increase along the descending region, as above discussed (Figure 4 and Figure 5).
Figure 11 displays, as an example, the vertical profiles of the time-averaged turbulent kinetic energy, k, normalized by Ua2, at different downstream positions x/D from the jet exit. The data refer to runs R1 and R2. Figure 11 clearly highlights a significant increase of k/Ua2 within the jet flow-field. Outside the jet flow-field, k/Ua2 experiences almost constant values over the ambient flow-depth. It is of O(0.02) above the jet outer-boundary, and O(0.04) below the jet inner-boundary. Figure 11 indicates that the largest values of k/Ua2 take place below the jet axis, as indicated by the horizontal arrows on the figure. This indicates that the jet wake-region is a location of maximum turbulent energy production.
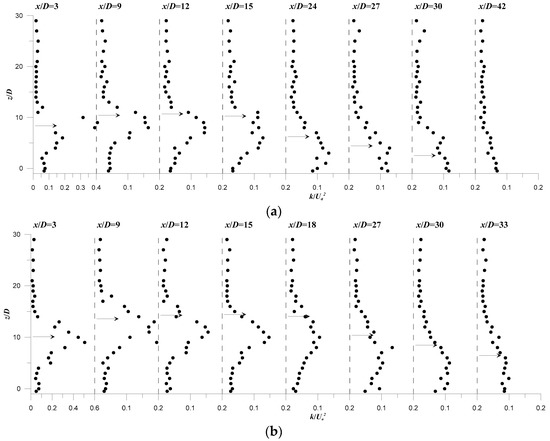
Figure 11.
Vertical profiles of the normalized time-averaged turbulent kinetic energy at different downstream positions x/D: (a) run R1; (b) run R2. The horizontal arrows on the profiles indicate the position of the jet axis.
The examination of Figure 11 also reveals that the production of turbulent kinetic energy is locally variable with jet flow-field. k/Ua2 monotonically decreases as x/D increases, reaching values comparable to those obtained in the ambient flow at considerable downstream positions x/D, as shown on Figure 11a at x/D = 42. In Figure 12 we plot the maximum values of k/Ua2 versus x/xt for runs R1 to R4. Figure 12 shows that km/Ua2 strongly reduces along the ascending region as x/xt increases. It is reduced by up to 65% at x = xt as compared to its value at x/xt = 0.16. In the descending region, km/Ua2 shows a very slight increase until x/xt = 2.5, and then returns to decrease again, but very gradually.
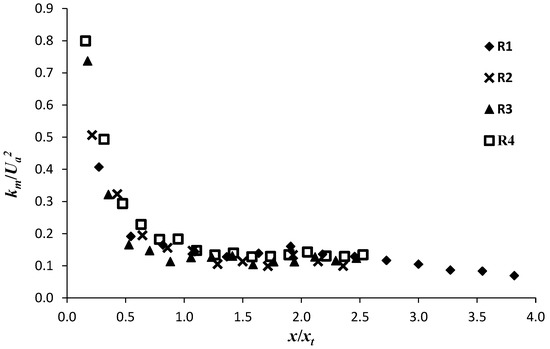
Figure 12.
Decay of the maximum turbulent kinetic energy k/Ua2 as a function of x/xt.
4.3. Turbulent Length Scales and Dispersion Coefficients
Determination of the largest scales in a turbulent flow is of crucial importance for experimental and numerical investigations, defining suitable domain-dimensions (area or volume) for computation. As above shown in Equations (5) and (6), both the turbulent diffusion and net dispersion coefficients, are proportional to a characteristic eddy length-scale of the turbulent flow. In the present study, the characteristic eddy length-scale Li is simply calculated as the integral time scale Ti times the local time-averaged velocity Ui, where Ti is computed integrating the autocorrelation of the measured instantaneous flow velocities.
Figure 13 and Figure 14 illustrate the vertical profiles of the integral length-scales Lx and Lz, normalized by the jet diameter D, at different downstream position x/D. The data always refer to run R1 and R2, respectively. The profiles are presented in semi-logarithmic plot for a better visualization of the data. The most important observation from Figure 13 and Figure 14 is the significant spatial-variation of Lx and Lz in the jet flow-field, which is more pronounced in the ascending region. In the ambient flow-region, above the jet outer-boundary or at x/D = 42 (with small jet effect) in R1, Lx and Lz are nearly constant over the flow depth. They are, respectively, equal to almost 10D, a value of order the channel flow depth H, and 0.5D. This seems reasonable for the ambient flow where the vertical-velocity component is very small as compared with the streamwise component.
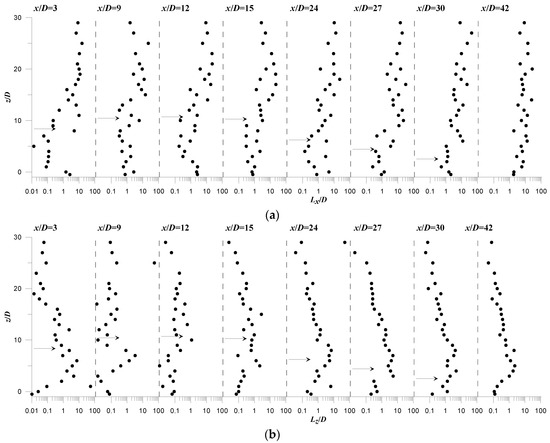
Figure 13.
Vertical profiles of the normalized turbulent length scales at different downstream positions x/D at the plane of flow symmetry (y = 0) of run R1: (a) Lx/D; (b) Lz/D. The horizontal arrow on the profiles indicate the position of the jet axis.
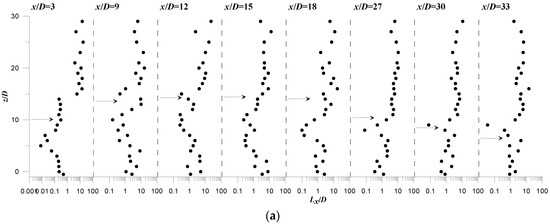
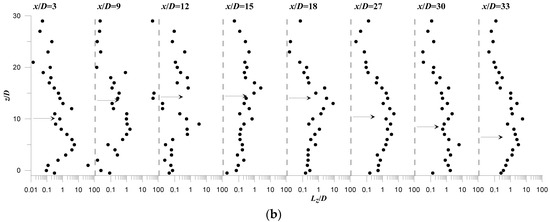
Figure 14.
Vertical profiles of the normalized turbulent length scales at different downstream positions x/D at the plane of flow symmetry (y = 0) of run R2: (a) Lx/D; (b) Lz/D.
In the jet flow-field, Lx decrease as compared to that obtained in the ambient flow-field. Lx shows a typical trend over the flow depth, as represented by the profile at x/D = 9 for both runs R1 and R2. This profile shows that Lx reduces from a values of O(10D), above the jet outer-boundary, to a value of O(D) in the jet upper-region, increases at the jet axis and then again decreases to a scale of O(D) in the wake-like region. Figure 13 and Figure 14 indicate that the jet wake region is the location of minimum Lx-scales. As x/D increases, the typical trend of Lx gradually changes and disappears at large values of x/D, resembling a profile in the ambient flow-field. Figure 13 and Figure 14 indicate that Lz behaves contrary to Lx. It increases in the jet upper-region, attaining values of order 3 to 5D, decreases at the jet axis and then significantly increases in the wake-like region, as clearly shown in Figure 14b at x/D = 3 to 12.
Figure 15 and Figure 16 depict the vertical profiles of k½Lx/UaD and k½Lx/UaD, order of magnitude of the normalized dispersion coefficients Kx and Kz, at different downstream position x/D, for runs R1 and R2. According to previous studies [31,44], the net dispersion coefficient can be generally determined as Ki = αk½Li, where the scale factor α will differ between the vertical and horizontal diffusion and differ from a location to another within the jet flow-field. Following Nepf [44], the scale factor is of O(1). Figure 15 and Figure 16 show that Kx and Kz roughly behave like Lx and Lz, respectively. These observation support the assumption that turbulent diffusion is proportional to the turbulent eddies length-scales. The change in eddy scales controls the turbulent diffusion, such that the longitudinal dispersion Kx is reduced in the jet flow-field, despite the fact that the turbulence intensity is increased, as shown in Figure 8, Figure 9 and Figure 11a. This finding is in good agreement with that observed by Nepf [44] for turbulent flow dispersion in vegetated channel. The decrease of the longitudinal dispersion Kx, as compared to that of the ambient flow-field, is somewhat recovered by an increase of the vertical dispersion Kz, increasing the jet width, and consequently the transversal dispersion Ky could be also increased. As a conclusion, the results of the present study demonstrate that the turbulent dispersion of the jet flow is an anisotropic process. It is strongly influenced by the jet hydrodynamic structure itself. In the jet flow-field, the longitudinal dispersion Kx decreases enough as compared to that in the ambient flow-field, promoting an increase of the vertical dispersion Kz, and consequently an increase of the jet width occurs.


Figure 15.
Trend of the turbulent dispersion coefficient Kx and Kz at different downstream positions x/D at the plane of flow symmetry (y = 0) of run R1: (a) kx ~ k½Lx/UaD; (b) kz ~ k½Lz/UaD. The horizontal arrow on the profiles indicate the position of the jet axis.
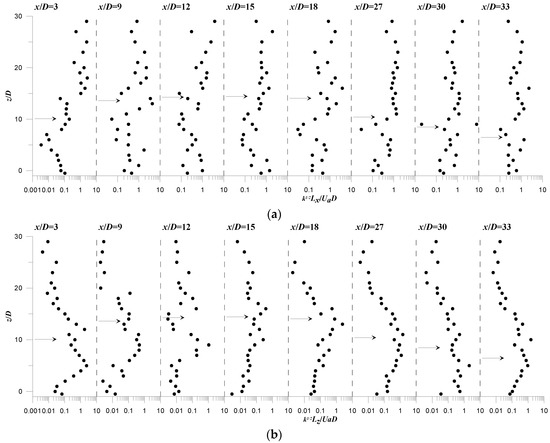
Figure 16.
Trend of the turbulent dispersion coefficient Kx and Kz at different downstream positions x/D at the plane of flow symmetry (y = 0) of run R2: (a) kx ~ k½Lx/UaD; (b) kz ~ k½Lz/UaD.
5. Conclusions
With population growth, urbanization, and industrial expansion the quantity of waste/brackish water discharge into natural water bodies in continuously increasing. In coastal environments, as an example, the brine of desalination plants is usually discharged as a turbulent jet flow, producing complex hydrodynamic phenomena within the surrounding ambient and affecting the ecosystem. Discharge systems need to be well designed to reduce their environmental impact. Therefore, a good knowledge of the interaction between effluent discharge and surrounding flow-field is required to promote best environmental management practices. This manuscript focuses on the analysis of flow turbulence structures that develop when a dense round jet, consisting of a saltwater solution, is injected perpendicularly into a flowing current of fresh water.
At urF < 2, the measured flow velocity fields show that the dense jet is characterized by two distinct regions: a rapidly ascending region and a gradually descending region. In the ascending region, the buoyancy effect is dominated by the jet momentum flux and the mixing is jet-like, analogously to momentum jets. In the descending region, the jet flow is buoyancy-driven and the mixing is plume-like.
In this study, a new scaling approach of the jet trajectories, based on the jet characteristic length scales xi, xt and zt (Figure 2), is proposed. This new rescaling rule enables all the trajectories to collapse onto a typical profile, independent of the current speed parameter urF, leading to an empirical closed-form expression as depicted in Equation (15). By proposing empirical expressions of xi, xt and zt, the new scaling approach become very practical and easily applicable to predict the trajectory of any dense jet, of urF ranging between 0.2 and 1.1, vertically discharged into a flowing current.
The detailed turbulence data reported in this study indicate that the strength of both the streamwise and the vertical turbulence intensities significantly increases in the jet flow-field as compared to the ambient flow-field. The largest values of the turbulence intensities consistently occur in the ascending region. The experimental results also reveal that the turbulence intensities increase with the decrease of ur-ratio. The streamwise turbulence intensity shows a rapid decay along the ascending region and very gradually decay in the descending region. The vertical turbulence intensity, however, rapidly decays in the ascending region, attains a minimum value at x = xt, gradually rises in the beginning of the descending region and then undergoes again a decay as going further downstream. The time-averaged turbulent kinetic energy also shows a significant increase in the jet flow-field. The maximum production of turbulent kinetic energy takes place in the jet wake-region.
The distribution, in the plane of flow symmetry, of the longitudinal and vertical integral length scales, respectively, indicates that the ambient flow-field is isotropic process. In the jet flow-field, the turbulent lengths scales show a significant spatial-variation, indicating an anisotropic process. The trends of the turbulent dispersion coefficients Kx and Kz follow those of the turbulent length scales Lx and Lz, respectively. The change in eddy scales controls the turbulent diffusion of the jet flow. In comparison with the ambient flow-field, Kx shows an enough reduction in the jet flow-field, however, an increase of the vertical dispersion Kz occurs, leading to the increase of the jet width.
Acknowledgments
The experiments were carried out at the Coastal Engineering Laboratory of the Department of Civil, Environmental, Land, Building Engineering, and Chemistry of the Polytechnic University of Bari, Italy.
Author Contributions
Mouldi Ben Meftah performed the experiments, analyzed the data and wrote the paper; Michele Mossa contributed suggestions and reviewed the manuscript.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Van Reeuwijk, M.; Salizzoni, P.; Hunt, G.R.; Craske, J. Turbulent transport and entrainment in jets and plumes: A DNS study. Phys. Rev. Fluids 2016, 1, 074301. [Google Scholar] [CrossRef]
- Voutchkov, N. Overview of seawater concentrate disposal alternatives. Desalination 2011, 273, 205–219. [Google Scholar] [CrossRef]
- McDougall, T.J. Negatively buoyant vertical jets. Tellus 1981, 33, 313–320. [Google Scholar] [CrossRef]
- Rathgeber, D.E.; Becker, H.A. Mixing between a round jet and a transverse turbulent pipe flow. Can. J. Chem. Eng. 1983, 61, 148–157. [Google Scholar] [CrossRef]
- Andreopoulos, J.; Rodi, W. Experimental investigation of jets in a crossflow. J. Fluid Mech. 1984, 138, 93–127. [Google Scholar] [CrossRef]
- Broadwell, J.E.; Breidenthal, R.E. Structure and mixing of a transverse jet in incompressible flow. J. Fluid Mech. 1984, 148, 405–412. [Google Scholar] [CrossRef]
- Gu, R.; Stefan, H.G. Stratification dynamics in wastewater stabilization ponds. Water Res. 1995, 29, 1909–1923. [Google Scholar] [CrossRef]
- Huq, P.; Dhanak, M.R. The bifurcation of circular jets in crossflow. Phys. Fluids 1996, 8, 754. [Google Scholar] [CrossRef][Green Version]
- Cotel, A.J.; Breidenthal, R.E. Jet detrainment at a stratified interface. J. Geophys. Res. Atmos. 1997, 102, 23813–23818. [Google Scholar] [CrossRef]
- Jirka, G.H. Improved Discharge Configurations for brine effluents from desalination plants. J. Hydraul. Eng. 2008, 134, 116–120. [Google Scholar] [CrossRef]
- Marugán-Cruz, C.; Rodríguez-Rodríguez, J.; Martínez-Bazán, C. Negatively buoyant starting jets. Phys. Fluids 2009, 21, 117101. [Google Scholar] [CrossRef]
- Roberts, D.A.; Johnston, E.L.; Knott, N.A. Impacts of desalination plant discharges on the marine environment: A critical review of published studies. Water Res. 2010, 44, 5117–5128. [Google Scholar] [CrossRef] [PubMed]
- Bashitialshaaer, R. An experimental study to improve the design of brine discharge from desalination plants. Am. J. Environ. Prot. 2013, 2, 176–182. [Google Scholar] [CrossRef][Green Version]
- Ben Meftah, M.; De Serio, F.; Malcangio, D.; Mossa, M.; Petrillo, A.F. Experimental study of a vertical jet in a vegetated crossflow. J. Environ. Manag. 2015, 164, 19–31. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.; Jia, L.; Zhang, J.; Shu, Z.; Mi, J. On the flow structure of an inclined jet in crossflow at low velocity ratios. Int. J. Heat Fluid Flow 2016, 58, 11–18. [Google Scholar] [CrossRef]
- Nada, S.A.; Fouda, A.; Elattar, H.F. Parametric study of flow field and mixing characteristics of outwardly injected jets into a crossflow in a cylindrical chamber. Int. J. Therm. Sci. 2016, 102, 185–201. [Google Scholar] [CrossRef]
- Mossa, M.; Ben Meftah, M.; De Serio, F.; Nepf, H.M. How vegetation in flows modifies the turbulent mixing and spreading of jets. Sci. Rep. 2017, 7, 6587. [Google Scholar] [CrossRef] [PubMed]
- Ben Meftah, M.; Malcangio, D.; De Serio, F.; Mossa, M. Vertical dense jet in flowing current. Environ. Fluid Mech. 2018, 18, 75–96. [Google Scholar] [CrossRef]
- Gungor, E.; Roberts, P.J.W. Experimental studies on vertical dense jets in a flowing current. J. Hydraul. Eng. 2009, 135, 935–948. [Google Scholar] [CrossRef]
- Hasselbrink, E.F.; Mungal, M.G. Transverse jets and jet flames. Part 1. Scaling laws for strong transverse jets. J. Fluid Mech. 2001, 443, 1–25. [Google Scholar] [CrossRef]
- Hasselbrink, E.F.; Mungal, M.G. Transverse jets and jet flames. Part 2. Velocity and OH field imaging. J. Fluid Mech. 2001, 443, 27–68. [Google Scholar] [CrossRef]
- Fearn, R.; Weston, R.P. Vorticity associated with a jet in a cross flow. AIAA J. 1974, 12, 1666–1671. [Google Scholar] [CrossRef]
- Cortelezzi, L.; Karagozian, A.R. On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 2001, 446, 347–373. [Google Scholar] [CrossRef]
- Marzouk, Y.M.; Ghoniem, A.F. Vorticity structure and evolution in a transverse jet. J. Fluid Mech. 2007, 575, 267–305. [Google Scholar] [CrossRef]
- Karagozian, A.R. Transverse jets and their control. Prog. Energy Combust. Sci. 2010, 36, 531–553. [Google Scholar] [CrossRef]
- Kaminski, E.; Tait, S.; Carazzo, G. Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 2005, 526, 361–376. [Google Scholar] [CrossRef]
- Danckwerts, P.V. The definition and measurement of some characteristics of mixtures. Appl. Sci. Res. 1952, A3, 279–296. [Google Scholar] [CrossRef]
- Galeazzo, F.C.C.; Donnert, G.; Habisreuther, P.; Zarzalis, N.; Valdes, R.J.; Krebs, W. Measurement and Simulation of Turbulent Mixing in a Jet in Crossflow. J. Eng. Gas Turbines Power 2011, 133, 061504. [Google Scholar] [CrossRef]
- Cipollina, A.; BonFigurelio, A.; Micale, G.; Brucato, A. Dense jet modelling applied to the design of dense effluent diffusers. Desalination 2004, 167, 459–468. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Dense Jet Discharges in shallow water. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- De Serio, F.; Ben Meftah, M.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2017. [Google Scholar] [CrossRef]
- Abessi, O.; Saeedi, M.; Davidson, M.; Zaker, N.H. Flow Classification of Negatively Buoyant Surface Discharge in an Ambient Current. J. Coast. Res. 2012, 278, 148–155. [Google Scholar] [CrossRef]
- Roberts, P.J.W.; Toms, G. Inclined Dense Jets in Flowing Current. J. Hydraul. Eng. 1987, 113, 323–340. [Google Scholar] [CrossRef]
- Ben Meftah, M.; De Serio, F.; Mossa, M.; Pollio, A. Experimental study of recirculating flows generated by lateral shock waves in very large channels. Environ. Fluid Mech. 2008, 8, 215–238. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M.; Pollio, A. Considerations on shock wave/boundary layer interaction in undular hydraulic jumps in horizontal channels with a very high aspect ratio. Eur. J. Mech. B Fluids 2010, 29, 415–429. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. A modified log-law of flow velocity distribution in partly obstructed open channels. Environ. Fluid Mech. 2016, 16, 453–479. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 2013, 25, 045102. [Google Scholar] [CrossRef]
- Ben Meftah, M.; De Serio, F.; Mossa, M. Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 2014, 26, 065102. [Google Scholar] [CrossRef]
- Sherif, S.A.; Pletcher, R.H. Measurements of the flow and turbulence characteristics of round jets in crossflow. J. Fluids Eng. 1989, 111, 165–171. [Google Scholar] [CrossRef]
- Fric, T.F.; Roshko, A. Vortical structure in the wake of a transverse jet. J. Fluid Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef]
- Margason, R.J. The Path of a Jet Directed at Large Angles to a Subsonic Stream; N.A.S.A., TN.D. 4919; Langley Research Center: Hampton, VA, USA, 1968. [Google Scholar]
- Pratte, B.D.; Baines, W.D. Profiles of the round turbulent jet in a crossflow. J. Hydraul. Eng. Div. ASCE 1967, 92, 53–64. [Google Scholar]
- Chochua, G.; Shyy, W.; Thakur, S. A computational and experimental investigation of turbulent jet and crossflow interaction. Numer. Heat Transf. Part A Appl. 2000, 38, 557–572. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).