Abstract
The jet test device has been predominantly used for in situ critical shear stress (τc) and erodibility coefficient (kd) measurements of cohesive streambanks/beds using three analytical procedures: the Blaisdell method (BM), the iterative approach (IP), and the scour depth approach (SDP). Existing studies have reported that τc and kd estimates can be influenced by the computational procedure, time intervals for scour-hole depth measurements, and the pressure head selection. This study compared estimates of τc and kd among the three computational procedures using single and multiple pressure settings (SPS, MPS). A new method is introduced applying incrementally increasing pressure heads, hypothesizing depth-averaged erodibility parameters would be generated that better represent bank and fluvial erosion. Estimates of τc applying the MPS-BM procedure were greater by 17% to 100% compared with SPS-BM procedures and kd estimates were lower with less variability (σ = 3.54) compared with other procedures from 126 jet tests among 21 Tennessee stream sites. This finding supports the hypothesis of increasing τc and decreasing kd with greater soil depths into the bank, suggesting the MPS-BM procedure can improve the estimation of τc and kd using the mini-jet test device. Overall, this study demonstrates the need to standardize field and computational procedures.
1. Introduction
Concept development of a jet device for estimating erosion rates for cohesive soils was first introduced by Dunn [1], where critical shear stress (τc) and the erodibility coefficient (kd) are measured and used in the excess shear stress equation. The excess shear stress equation is expressed as: , where . is the erosion rate (cm·s−1), kd (cm3·N−1·s−1), τc (Pa), τb is the hydraulic boundary shear stress (Pa), and m is an empirical exponent [2,3,4,5]. In the 1990s, researchers with the US Department of Agriculture further developed the jet device consisting of a large submergence tank (test chamber) 30.0 cm in diameter and height [3,6,7]. They provided operational guidance for the in situ field data collection, in which depths of the scour hole formed by the impinging jet are measured over time. Commonly referred to as the “original” jet tester, it has been the dominant measurement tool for estimating in situ erodibility of cohesive streambank soils [6,7]. In the 2010s, the mini-jet test device was developed and first used by Simon et al. [8], where its submergence tank is 101.6 mm in diameter and 7.0 cm in height. Due to its smaller size, light weight, and the ease of field operation, the mini-jet device is more applicable for in situ testing on bed and bank surfaces. Al-Madhhachi et al. [9] compared results from the original and mini-jet devices and found that kd values were not significantly different, whereas τc values were consistently lower from the mini-jet compared with the original jet tester.
Mini-jet operational guidance was provided by Al-Madhhachi et al. [9] where a constant pressure head setting with a pre-defined time interval were specified to measure the depth of the developing scour hole independent of soil type. However, their study noted that selection of the pressure head setting for a specific field test appeared to be dependent on soil type and the experience of the jet operator. Using the mini-jet device, Khanal et al. [10] recently investigated the influence of data collection time intervals and test termination times on erosion parameter estimations. They also suggested that an interactive effect of pressure head setting relative to the data collection intervals and length of the test may have influence on τc and kd estimations for different natural sediment types. It was hypothesized that inappropriate test selection of the pressure head setting could affect the τc and kd estimations significantly. Khanal et al. [10] identified the importance of the measurement time interval and pressure head selection; however, they did not report on the potential effect of changing soil properties with depth on τc and kd estimations. Differences in soil properties from the streambank surface inward into the bank material (subsurface) have the potential to influence the rate of scour hole development by the impinging jet. Therefore, critical research is needed to better understand how device operational procedures and streambank soil properties jointly affect the computation of erodibility parameters, and how operational procedures can be improved.
Many environmental factors affect streambank soil erodibility. It is well known that physical and geochemical properties of cohesive soils can affect erodibility, including bulk density, water content, dispersion ratio, percent clay and clay activity, plasticity index, organic matter content, pore water pH, and sodium adsorption ratio [2,11,12,13,14,15,16]. In general, cohesive soil properties consisting of clay, sand, silt, and gravel can be highly variable in natural riverine environments as a function of long-term geomorphic processes [17,18,19]. Mahalder et al. [16] found varying relationships to controlling erodibility parameters among different physiographic regions in Tennessee. Daly et al. [20] characterized variability of erodibility parameters within an Oklahoma watershed. At the local streambank scale, erodibility parameters varied among different surfaces vertically from the top of bank to the toe where an increase in bulk density and water content was observed, and thus, an increase in τc apparently associated with soil consolidation [21,22,23,24,25,26,27,28,29]. Soil bulk density appears to also increase at a point on the bank inward from the surface into the bank due to subaerial processes, the wetting and drying action in association with seasonal climate variations, where erosion rates reduce consequently inward from the bank surface [18,24,30]. It is thought that any in situ soil test on the thin surficial layers will therefore substantially influence estimation of erodibility parameters compared with the deeper bank soil layers. Several studies reported that τc of the upper surface (about 0–3 cm) is 3 to 5 times lower compared to underneath soil layers in both laboratory remolded and undisturbed soil samples [18,24,26]. The importance of bank point-scale variability is that it can affect the time-dependent measurements of scour hole depths during the jet device operation, particularly for the first few readings of a given test.
In order to improve operational procedures, the possible influence of soil property changes with depth of scour-hole development must be recognized, in addition to how data from the test measurements are used to compute τc and kd parameters. The computational procedure developed for the original jet device per Hanson and Cook [6] used the Blaisdell method (BM). More recent computational procedures have included the iterative principle (IP) described by Simon et al. [8] and the scour depth principle (SDP) described by Daly et al. [31]. Inconsistencies in τc and kd estimations have been reported using the same measured test data from the mini jet device [10,32,33]. Results from several studies have shown that the BM solution technique generally under-predicted τc compared with the IP and SDP methods [8,20,31,32]. A limited number of study results using the IP and SDP solution methods showed very high kd values corresponding to both higher and lower τc values. In addition to the solution technique, inconsistencies in τc and kd estimations are likely due to interdependent factors of soil property changes, and highly complex hydrodynamics and turbulence in the device test chamber as the scour hole shape develops [32,34,35,36]. Karamigolbaghi et al. [32] suggested that the head loss coefficient in the Blaisdell equation should be modified (BMM), accounting for jet confinement in the mini-jet device test chamber and its effect on scour hole development. Field observations reveal that depending on the soil type, soil physical conditions and resistance properties, and the jet characteristics, scour hole shape and formation alter with time and applied fluid forces. Similar observations were also reported by other studies [36,37,38,39,40]. These findings suggest that advances in the operational procedures for jet test devices need greater consideration of in situ soil properties, selection of appropriate test pressure head settings and measurement time intervals, and the computational methods for τc and kd estimation.
The objectives of this study were to: (1) investigate the influence of device pressure head selection on τc estimates leading to development of an alternative field procedure using multiple pressure settings during a test, (2) compare differences in τc and kd estimations from three computational procedures, the BM, IP, and SDP for single pressure (SPS) and multiple pressure (MPS) field procedures, and (3) qualitatively describe differences in scour hole development and morphology per varying soil types and the resulting patterns for τc and kd versus jet device pressure setting. The rationale for investigating the influence of pressure setting is that it is hypothesized that jet procedures with a single pressure head may lead to erodibility parameter estimates heavily influenced by the surficial soil layer. Theoretically, scour hole depth changes over time during a jet test vary with soil cohesion, bulk density and/or other soil conditions, and those rate and field measurement differences ultimately influence estimations of τc and kd per computational method selected. If τc and kd parameters derived by the jet test device using a single pressure setting reflect the erodibility of surficial bank surface to a greater extent, when used in the excess shear equation they may over-predict streambank erosion rates. This research uniquely applies a multiple-pressure setting procedure to improve the mini-jet test device’s field data collection and computational procedures for greater consistency in τc and kd estimations. Among research and practitioner river engineers there is a general understanding that erodibility measurements need to follow a standard procedure, and this study supports that effort.
2. Background for Jet Test Data Analysis
Estimating τc and kd from jet device test data has used the following computational procedures: BM [6,7], IP [8], and SDP [31]. These procedures are based on the theoretical understanding that shear stress can be computed from dispersion principles by a submerged fluid jet projected normal to an erodible surface developing a scour hole. Background on the computational procedures relevant to this study is described in this section. Hanson and Cook [6] developed an analytical procedure to calculate the erosion index parameter from jet test data based on jet diffusion principles developed by Stein and Nett [41]. This method was developed for the original submerged jet tester; however, the governing principles are consistent for both the original and mini-jet devices. The major assumption considered for this device was that the rate of scour depth or erosion rate (dJ/dt) is a function of maximum stress at boundary. Therefore, the jet erosion rate equation was organized as [6,7]:
where J is the scour depth (cm); Jp is the potential core length from jet origin (cm); kd is the erodibility coefficient (cm3·N−1·s−1); τ0 is the applied bottom shear stress (Pa); and τc is the critical shear stress (Pa).
Based on soil type and conditions, the initial erosion rate may be substantial approaching zero asymptotically for the jet device [41]. The depth at which the applied shear stress on the soil surface does not produce any erosion (dJ/dt = 0) is termed as the equilibrium scour depth (Je) and the shear stress to that depth is termed as τc.
where is the maximum shear stress due to the jet velocity at the nozzle (Pa); Cf = 0.00416 is the friction coefficient; is water density (kg·m−3); is the velocity of jet at orifice (cm·s−1); C is discharge coefficient; h is the applied head (cm) or pressure head; ; d0 is the nozzle diameter (cm); and Cd = 6.3 is the diffusion constant. Writing a dimensionless form, Equations (1) and (2) were formed as follows [6]:
where ; and . The dimensional time (T*) was also expressed as:
where t is the time of data measurement during the test; and is the reference time. Integrating Equation (3), the following form was developed [6]:
Using Equations (3) to (5), τc and kd can be calculated using an Excel™ spreadsheet. However, Blaisdell et al. [42] showed that the time required to attain Je is excessively high, hence, the calculation of τc becomes impractical for efficient field testing. Therefore, they proposed a technique to calculate Je by fitting scour depth data versus time as a hyperbolic function. The general form as proposed by Blaisdell et al. [42] of the equation was:
The coefficients A and fo can be determined using spreadsheet solver by fitting the scour depth data based on the plotting of f versus x, consequently, Je was calculated .
The IP and SDP approaches for estimating τc and kd are variations of the BM [20]. In the IP approach, initially τc and kd values are estimated from the Blaisdell solution based on T* and J* values. The erodibility parameters are then simultaneously solved in an iterative manner. The ultimate goal for this iterative solution method is to minimize the root-mean-square error between the measured and predicted time, where an upper bound of τc is included to prevent the solution from exceeding the equilibrium scour depth. In the IP, τc is a function of shear stress at the jet nozzle and maximum observed scour depth during jet test. Daly et al. [31] developed another spreadsheet routine that also solved for τc and kd iteratively, which is known as the SDP method. In this method, observed scour depth data from the jet test are fitted to the predicted scour depth data using the excess shear stress equation using initial guessed values of τc and kd. In this simultaneous solution method, by minimizing the sum of squared errors between measured and predicted scour depth data from the excess shear stress equation, final τc and kd values are estimated. Results of these recently developed solution techniques suggest a better fit with the measured scour depth data, though the reported kd values were found to be much higher and unrealistic in some cases.
3. Materials and Methods
3.1. Study Design
In order to meet the study objectives, two separate field operations were conducted for this study using the mini-jet test device. In the first field operation, the MPS approach was used at 21 sites across Tennessee from July 2014 through August 2015. The rationale for site selection was to obtain data across multiple physiographic regions [16], in which geographical details of these study sites are described below in Section 3.2. The second operation consisted of collecting scour hole depth measurements for a single pressure setting (SPS), and at the same site location collecting scour hole depth measurements using an alternative MPS approach. This comparative field operation was conducted during July 2017 on Gist Creek, Sevier County, Tennessee to provide sufficient justification for the MPS approach (Objective 1). Both field datasets applied the BM, IP, and SDP computational procedures in order to assess any differences between them (Objective 2). The Gist Creek dataset was collected after the main study which included the 21 statewide field sites to provide greater justification for applying the MPS procedure to improve the consistency of measured erodibility parameters. Field data collection and computational methods are described below in Section 3.3.
3.2. Study Area
The Gist Creek study site is located in the Ridge and Valley Physiographic Province in eastern Tennessee (Figure 1). Gist Creek is a third order stream with a bank full width of 20 m. Five test locations including the upper and lower bank positions were investigated (designated as Loca.-I, -II, -III, -IV, and -V), totaling 10 tests per SPS and MPS field procedures.

Figure 1.
Study site locations using the mini-jet test device in Tennessee, where Gist Creek is shown as a black square and the sites used for the multiple-pressure test among the different physiographic provinces [43] are shown as green circles.
The field operation that used the MPS procedure for 21 sites was conducted across the state of Tennessee in four physiographic provinces: Valley and Ridge, Central Basin, West Highland Rim, and Coastal Plain, each with diverse geological settings with different dominant soil properties that govern estimates for the erodibility parameters [16]. Among these regions, five stream sites were located in the Valley and Ridge Physiographic Province, three sites in the West Highland Rim and the Central Basin, and 13 sites in the West Tennessee Plain and West Tennessee Uplands, sub-regions of the Coastal Plain physiographic province (Figure 1). The majority of the sites were from the western part of Tennessee, which has predominantly cohesive (silt/clay) type materials. Mahalder et al. [16] have described the soil properties of each site in detail.
3.3. Field Data Collection and Computational Procedures
In general, site preparation for all mini-jet test locations consisted of taking care to maintain the ambient moisture content by avoiding days with rainfall. Test locations were visually selected so that soil was homogenous in character, and free from pebbles or rocks, vegetation, and root systems. Each test location was cleaned very gently using a shovel prior to conducting a test, and the bottom ring of the jet device was inserted into the soil using uniform pressure on the top of the bottom ring to minimize disturbances at the soil surface. After completing each test, two core samples near the test location were collected using a cylindrical coring device, which were analyzed in the University of Tennessee’ Geotechnical Laboratory for bulk density, water content, and unconfined compressive strength (UCS). Approximately 1.4 kg of soil was also collected from the inside of the jet’s bottom ring at each test location to measure selected physiochemical soil properties. Collectively, soil samples represented a wide variation in moisture content and bulk density associated with the diverse geological settings.
The jet operation procedure using the SPS follows the guidelines outlined by Hanson and Cook [7] and Al-Madhhachi et al. [9] with a slight modification, where scour-hole depth readings were measured at one-minute intervals. A centrifugal pump powered by a 2000-W portable generator provided water flow from the nearby stream through the jet device, and a constant pressure head was regulated by a ball valve and monitored by an inline pressure gage. The terminal test time was 46 min for a set pressure for the SPS method. These data were then used to estimate τc and kd by three computational methods: BM, SDP, and IP (Table 1).

Table 1.
Procedural summaries for field data collection and computation for erodibility parameters using the mini-jet device.
The jet operation procedure using the MPS generally followed the field guidance by Hanson and Cook [7] and Al-Madhhachi et al. [9]; however, in the MPS procedure five different pressure settings were applied, starting from a lower to a higher pressure at each testing location. Selected pressures were adjusted based on testing location, soil type and condition, and test erosion rates. The applied pressure ranged from 4.14 kPa to 44.12 kPa. In some testing locations, the initial pressure was set as high as 27.58 kPa because lower pressure settings did not produce a scour hole due to the resistant soil erosion properties. For each pressure head setting, the test duration at each location was about 12–20 min, where three different time intervals were selected during the tests for the scour-hole depth measurements. The different time intervals during a MPS test were: (i) 30-s intervals for the first two readings, (ii) one-minute time intervals for 2–6 min, and (iii) two-minute time intervals for depth measurements until test termination. The applied pressure head was then increased to the next pressure increment after 12 min if the measured scour-hole depth difference between two consecutive readings was not more than one millimeter. If the difference between two consecutive scour-hole depth readings was greater than one millimeter, the test was continued for the next two-minute interval. These procedures were repeated for each incremental increased pressure head settings at the same test location. The total run time for a test at each location (applying all the five pressure heads) was about 60–100 min, depending on the progression of the scour depth. MPS mini-jet testing was conducted at upper, middle, and lower bank positions where possible for the 21 sites across Tennessee. These data were then used to estimate τc and kd by three computational methods: BM, SDP, and IP (Table 1).
The SPS procedure was exclusively used at the Gist Creek study site where the MPS procedure was concurrently conducted for a method comparison (Objective 1). For accomplishing this objective, ten tests were conducted, five per upper and lower bank locations (Table 2). For each of the upper bank test locations, five different pressures heads were applied they were: 11.72 kPa, 16.55 kPa, 20.68 kPa, 27.58 kPa, and 33.09 kPa. For the lower bank the selected pressures heads were: 13.79 kPa, 20.68 kPa, 27.58 kPa, 33.78 kPa, and 41.37 kPa. These pressure heads were also used incrementally for the MPS method by following similar procedures as discussed in the previous paragraph.

Table 2.
Mini-jet test conditions comparing single pressure setting (SPS) and multiple pressure settings (MPS) field data procedures at the Gist Creek study site, including soil properties among the five test locations per upper and lower bank areas.
In the MPS procedure, τc and kd values were calculated individually for each pressure head setting and corresponding scour depth values. As summarized in Table 1, these data were used to estimate the erodibility parameters by the three computational methods: BM, SDP, and IP. Estimates for τc and kd using the BM was completed using a spreadsheet routine developed at the USDA National Sedimentation Laboratory. This spreadsheet routine was based on Hanson and Cook [6,7]. Erodibility parameters from the other two computational methods (SDP and IP) were also calculated using another spreadsheet provided per Daly et al. [31]. Therefore, using the MPS data and different computational procedures, τc and kd values were estimated and are denoted as: MPS-BM, MPS-SDP, and MPS-IP.
Per test pressure setting and associated individual computations of τc and kd, the erodibility parameters were plotted on normal graph paper. By doing so, three patterns were observed from these plots. Using selected data from the 21 stream sites across Tennessee, those patterns are demonstrated in Figure 2. The three distinct patterns were: (i) a concave-down shape (76 observations), (ii) a nearly linear pattern (20 observations), and (iii) scattered points (30 observations) using the MPS-BM method. For the concave-down shape, the critical shear stress (τc) was calculated by drawing an asymptotic line on the concave-down shaped curve (Figure 2a), and average values were taken for the scattered patterns. For the linearly increasing pattern, the maximum value was read from the plot as the τc value. The majority of the tests demonstrated the concave-down shape. Similar procedures were followed for kd value calculations. It is interesting to note that using MPS-SDP and MPS-IP methods, similar patterns were also observed. Though Figure 2 was provided in this paper only to demonstrate the computational procedures using MPS field collected data, these patterns appear to reflect a test response to the different soil properties. These patterns will be discussed further to supplement field observations related to dissimilarities in scour-hole development per different soil types (Objective 3). It is important to note that these plots in Figure 2 do not represent the same jet test data, rather the shapes are representative of different jet tests for the purpose of depicting the observed unique patterns.

Figure 2.
Response patterns of critical shear stress (τc) and erodibility coefficient (kd) to jet-test device pressure head setting. Data represented are identified for τc: (a) concave-down shape, (b) linear, (c) e scattered points and for kd: (d) concave-up shape, (e) linear, and (f) scattered points.
4. Results and Discussion
4.1. Comparison of SPS and MPS Methods for Estimating Critical Shear Stress
Test locations on Gist Creek and jet device pressure settings for SPS and MPS methods are summarized in Table 2. Soil properties were generally consistent among the five test locations but differed between the upper and lower bank areas (Table 2). The soil of the upper bank was predominantly found as semi-cohesive with the D50 value ranging between 75 µm to 95 µm with clay content 15%, and the PI value was about 5%. Lower bank soil was found as cohesive, the D50 value was between 33 µm to 40 µm, clay content was 25%, and the PI value was 10%. Bulk density averaged 1.78 g·cm−3 for the upper bank and 1.91 g·cm−3 for the lower bank.
Using the SPS method, selection of pressure head influenced τc estimates for different computational procedures for both lower and upper bank areas (Figure 3). BM results also found that estimated τc values were significantly different from the SDP and IP methods over the range of applied test pressures for the lower bank (p = 0.008), and upper bank (p < 0.001). Lower banks soils were more cohesive with higher bulk densities than the upper bank locations, and as expected, τc was greater. Regardless of soil type, τc values were considerably higher at lower pressure heads. The computational method appears to have a greater effect on τc estimates than individually per method, where for τc on the lower bank area the SDP procedure was substantially greater than the BM and IP procedures. However, for the upper bank soils, τc estimates were in similar ranges for the SDP and IP procedures.

Figure 3.
Using the SPS method, estimates of critical shear stress (τc) with different pressure heads are shown for the: (a) lower bank and (b) upper bank, based on the following computational procedures: BM = Blaisdell method, IP = iterative principle, SDP = scour depth principle, and BMM = modified Blaisdell method.
Karamigolbaghi et al. [32] reported that jet confinement could influence the jet test results and proposed a new value for the coefficient of Cf*Cd2 as 0.39 instead of 0.16, which is also introduced in the jet test data analyses equations. Using this new coefficient, test data were also analyzed and termed as modified Blaisdell method (BMM). In Figure 3, the BMM was compared with the three methods (BM, SDP, and IP), which applied the original coefficient value of 0.16. The τc estimates for BM and BMM procedures were similar among the pressure settings for the lower bank locations, which were more cohesive soils compared with the upper bank locations (Figure 3). Among the upper bank locations, τc estimates using the BMM procedure were considerably higher than the BM procedure at the lower pressures (less than about 17 kPa). This result suggests pressure head setting and jet hydraulics affect τc estimates to a greater extent, especially at lower pressure settings.
Using the MPS methods at the same Gist Creek test locations, τc values were generally more consistent among the five locations using the MPS-BM procedures (σ = 0.36 and 1.17 for lower and upper bank, respectively) compared with the MPS-SDP (σ = 0.91, and 5.51 for lower and upper bank, respectively) and MPS-IP (σ = 1.16, and 3.32 for lower and upper bank, respectively) procedures (Figure 4). Differences in estimated τc values between the lower and upper banks align with other studies [21,22,23]. Relationships between τc and corresponding pressure heads resulted in concave-down patterns (as demonstrated in Figure 2a) regardless of computational procedures. These findings also suggest that the τc of the upper soil surface in both laboratory remolded and undisturbed soil samples could be lower compared to soil underneath the surface layer [18,24,26]. Therefore, using the SPS method, estimated τc and kd values likely represent that of the surficial soil layer, whereas the MPS method estimated τc and kd values represent depth-averaged parameters for the bank soil.

Figure 4.
Based on the MPS method at the Gist Creek study site, critical shear stress (τc) estimates for the: (a) lower bank and (b) upper bank among the five test locations (Loca-1, -II, -III, -IV, and -V) and shown for the MPS-BM, MPS-IP, and MPS-SDP computational procedures.
Estimates for τc using the BM and BMM procedures were also compared with the MPS-BM procedure (Figure 5). From these results, it was identified that pressure head selection could significantly influence τc estimates regardless of the analysis method. However, τc estimates using the MPS-BM procedure were generally more consistent among the five test locations, for both the upper and lower banks. This supports the hypothesis that pressure head selection could significantly affect the τc estimation using the jet device, as was also observed by Khanal et al. [10].

Figure 5.
Estimates of critical shear stress (τc) at the five Gist Creek test locations for the: (a) lower bank and (b) upper bank area (Loca. -I, -II, - III, -IV, and -V). Computational methods: BM, BMM, and MPS-BM were compared.
The influence of the termination time interval on τc and kd estimations was investigated among the Gist Creek mini-jet test locations. Results from the data analyses found that if the test was terminated after 12–26 min, where the difference between two consecutive scour depth readings was less than 1 mm, estimated τc and kd values were similar with values from the full-length test. Therefore, in the new jet test operational protocol (MPS), a time interval of 12–20 min was selected for an applied pressure head by observing the difference between two consecutive scour depth readings at the end of any test. As noted earlier, subaerial processes appear to decrease bulk density at the bank surface compared to soil into the bank. In the operational protocol for the original jet tester as outlined by Hanson and Cook [7] and Al-Madhhachi et al. [9], scour hole depth measurements are recorded at five-minute intervals. Using the MPS method developed for this study, it was observed that if we arbitrarily change the initial six readings inside the first five-minute time interval compared to the published interval for scour depth readings, τc and kd varied significantly. Results from this study indicate the initial and termination time intervals can substantially influence τc and kd estimates. Similar observations were also reported by Khanal et al. [10] but greater details are provided in this study.
4.2. Comparison of MPS Method and Computational Procedures for Erodibility Parameters
Potential differences in τc and kd estimations from the newly developed MPS method were compared with the SPS method among the three computational procedures BM, IP, and SDP (Objective 2). Because no field tests were conducted using the SPS method among the 21 Tennessee sites, to compute τc and kd values per the SPS method scour depth readings corresponding to the first selected pressure head at each jet test were used and identified as: SPS-BM, SPS-IP, and SPS-SDP (Table 3).

Table 3.
Statistical summary of erodibility parameters computed using different computational methods: SPS-BM, MPS-BM, SPS-SDP, MPS-SDP, SPS-IP, and MPS-IP (as defined in Table 1).
Among the 21 stream sites (126 jet tests), soil textures varied but generally were predominantly silty-loam and silty-clay-loam (Figure 1). Atterberg limit tests indicated the presence of cohesiveness in the soil samples since the PI values were between ~3 and 21. The LL and PL values were between 24% and 43%, and 17% and 31%, respectively. Some of the soil samples had a low PI (3.4–7.5), even though the material met the criteria for cohesive soils (minimum clay content of 5–10% by weight) as defined by Raudkivi [45] and Mitchell and Soga [46]. Bulk density of the tested soils was between 1.52 g·cm−3 and 2.12 g·cm−3, and the D50 value was between 3.7 µm and 40 µm. Soil cohesion ranged from 8.55 kPa to 107.90 kPa. Details of other physical and geochemical properties of these soil samples were summarized in Mahalder et al. [16]. The relationship between τc and kd from the MPS-BM for the jet device dataset among the 21 Tennessee sites showed an inverse power relationship (Figure 6). The linear relationship between τc and kd is consistent with others [4,8,14], however the MPS result in this study scales higher for the erodibility parameters.
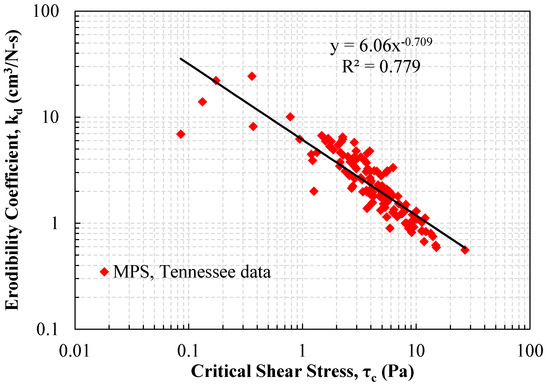
Figure 6.
Relationship between critical shear stress (τc) and erodibility coefficient (kd) using the MPS method data from this study.
Mean τc using the MPS-BM method was 5.13 Pa, over twice the mean of 2.48 Pa from the SPS-BM method (Table 3, Figure 7a). Estimates of τc between the MPS-BM and SPS-BM methods were statistically different (p < 0.001, Mann-Whitney U test, SPSS- v.23.0). Mean kd was 3.26 cm3·N−1·s−1 using the MPS-BM method and 3.84 cm3·N−1·s−1 from the SPS-BM method (Figure 7b); they were not significantly different (p = 0.116). Similarly, τc estimates from the MPS-BM procedure also compared with the SPS-SDP and SPS-IP procedures (Figure 7a). The mean τc values using the MPS-BM method was found to be 5.13 Pa, and for the SPS-SDP and SPS-IP the mean values were found to be 6.88 Pa and 7.07 Pa, respectively. The median τc using the MPS-BM method was statistically different from both the SPS-SDP and SPS-IP procedures (p < 0.001). Estimated kd values were significantly less for both the MPS-BM and SPS-BM procedures compared with the SPS-SDP and SPS-IP procedures (Table 3; Figure 7b). This result identified a major anomaly using these solution approaches where kd values increased with increasing τc values, and was similarly reported by Karamigolbaghi et al. [32]. It is important to note that a wide range (about 1 to 3 orders of magnitude difference) in the estimated τc and kd values were observed among this dataset using different computational procedures.
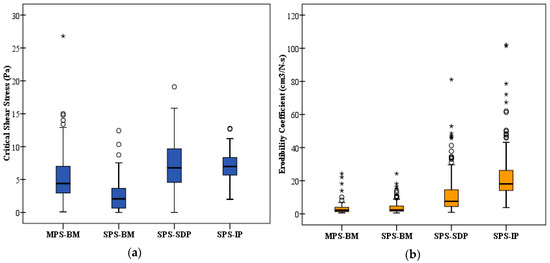
Figure 7.
(a) Critical shear stress, and (b) erodibility coefficient using the field methods and computation procedures: MPS-BM, SPS-BM, SPS-SDP, and SPS-IP (as defined in Table 1).
Erodibility parameters estimated from the 126 jet test dataset using the MPS-BM, MPS-SDP, MPS-IP procedures were also compared (Figure 8). The mean τc values were 8.51 Pa and 8.12 Pa, and mean kd values were 9.44 cm3·N−1·s−1 and 24.27 cm3·N−1·s−1 for MPS-SDP and MPS-IP procedures, respectively. The erodibility parameters (τc and kd) from the MPS-BM procedures were statistically different from the estimates using the MPS-SDP and MPS-IP procedures (p < 0.001, Mann-Whitney U test, SPSS v.23.0). Overall, τc and kd values were greater for both the MPS-SDP and MPS-IP procedures compared with SPS-SDP and SPS-IP. As defined in Figure 2, more discrete relationships between τc and the corresponding pressure heads were observed with MPS-SDP (58 observations) and MPS-IP (42 observations) procedures. Also, based on field observations, discrete relationships between τc and pressure head from the MPS method appeared to be dependent on the soil’s physical properties. Therefore, these relationships for MPS-SDP and MPS-IP procedures deviated from the hypothesis that τc increases with soil depth.
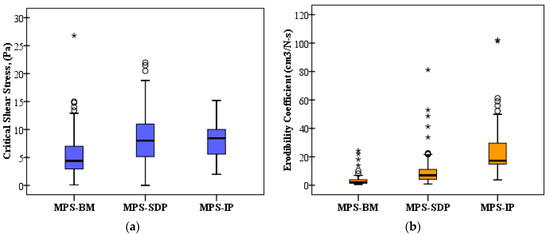
Figure 8.
A comparison of (a) critical shear stress and (b) erodibility coefficient using the MPS method for the computational procedures: MPS-BM, MPS-SDP, and MPS-IP (as defined in Table 1).
Pairwise differences for τc estimates between the MPS-BM and the other computational procedures were above and below a zero difference, though the median differences for these comparisons were negative except for the SPS-BM procedure (Figure 9a). The pairwise difference of τc between the MPS-BM and SPS-BM procedures was positive with a range between 0.0 and 14.32 Pa, which indicates the MPS-BM procedure predicted 17% to 100% higher τc values compared with the SPS-BM procedure. Of the 126 field tests only 29 resulted in positive τc pairwise differences between MPS-BM and SPS-SDP, and SPS-IP procedures. When comparing the pairwise differences for τc between MPS-BM and MPS-SDP, and MPS-IP procedures, only 13 and 18 observations were positive. The greater τc values for the MPS method apparently accounts for the increased cohesive properties of soil as the scour hole develops during the field test.
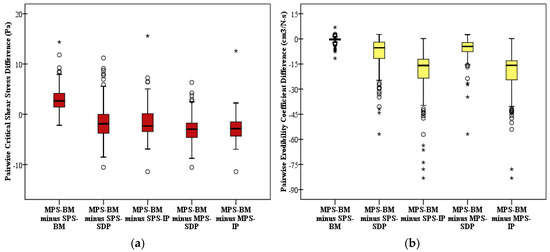
Figure 9.
Pairwise differences between different solution techniques for: (a) critical shear stress (τc), and (b) erodibility coefficient (kd) estimations between: MPS-BM and SPS-BM; MPS-BM and SPS-SDP; MPS-BM and SPS-IP; MPS-BM and MPS-SDP; and MPS-BM and MPS-IP procedures.
Pairwise differences for kd between MPS-BM and SPS-SDP, SPS-IP, MPS-SDP, and MPS-IP procedures were generally negative (Figure 9b). Therefore, both the SDP and IP procedures (using both the SPS and MPS methods) predicted much higher kd values compared with the MPS-BM procedure. In general, these variations among all the procedures demonstrate how both field protocols and computational procedures greatly influence in situ τc and kd values. Using the published datasets from the Daly et al. [20,31] studies, a slight increase in τc values were associated with significantly higher kd values (Figure 10). Therefore, significantly higher erosion rates are expected using the linear erosion model with the SPS-SDP and SPS-IP computational results. Karamigolbaghi et al. [32] showed that the SPS-SDP and SPS-IP procedures predicted physically unrealistic erosion rates (negative erosion rate) using the Hanson and Cook [7] data. Likewise, the MPS-SDP and MPS-IP procedures did not physically improve the uncertainty associated with these two methods. Furthermore, this study found inconsistent kd values using the SPS-SDP and SPS-IP procedures, which was also reported in previous studies [10,20,31].
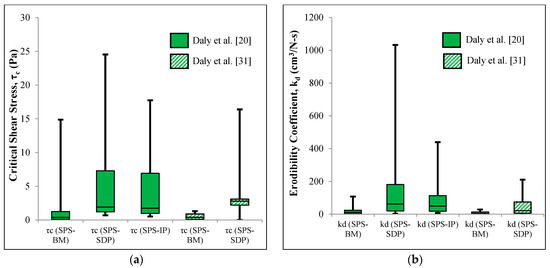
Figure 10.
Comparison of (a) critical shear stress (τc) and (b) erodibility coefficient (kd) using the SPS-BM, SPS-SDP and SPS-IP methods based on data from Daly et al. [20,31].
Daly et al. [22] suggested that a reduction factor (α) in the excess shear stress equation to estimate erosion parameters using the SPS-SDP and SPS-IP computational procedures, could alleviate the problem to some extent, expressed as follows in Equation (10):
However, the acceptability of these two computational procedures may be limited if a reduction factor is required for erosion prediction, because it is understood that the reduction factor is site specific and also dependent on the expertise of the person who is operating the jet device in different regions and soil properties. Thus, further research is needed to address this issue using these two methods.
4.3. Qualitative Observations in Scour-Hole Development and Morphology
Based on field observations, development and morphology of a scour hole subjected to jet hydraulic forces were dependent on several soil properties, which affected depth measurements over prescribed test time intervals. It has been demonstrated in this study how the time interval of scour-hole depth measurements, and the use of different computation procedures influence the estimation of the τc and kd parameters [10,21,31]. Thus, computed values of τc and kd are interdependent on soil properties, scour hole morphological development and depth measurements over time, and computational procedure using the depth measurements. As observed from this study, it was found that comparatively dry and loose soils (with higher D50) resulted in discrete patterns between pressure head settings and erodibility parameters (Figure 2c,f). By observing the position of the tested soil on the creek, it appeared that the soil formation age and cohesion had a substantial effect on the concave and linear increasing patterns (Figure 2a,b,d,e). It was also observed that a wider and shallower scour hole (Figure 11a) was observed for the concave and linear increasing patterns and a narrower deep scour hole (Figure 11b) was observed for the discrete pattern (Figure 2c,f). Nonlinear patterns appeared to occur as the scour depth increased with time and higher applied shear stress from increased device pressure (Figure 2a,d).

Figure 11.
Photos of scour hole formation in different soil physical conditions (a) wide and shallower, and (b) narrow and deeper.
Khanal et al. [10] attempted to correlate erodibility parameters with applied pressure heads, though no specific patterns were reported in their study conducted on laboratory remolded soils and a limited number of tests utilizing only three pressure heads per test. The use of laboratory remolded soils limits the range of τc and kd estimates that can be obtained for multiple pressure settings which generated different response patterns based on soil conditions (as observed in Figure 2). In addition, remolded soils add to uncertainty in parameter estimation associated with whether adequate time for consolidation has occurred, which over time may affect soil cohesion. Khanal et al. [10] did observe that the initial time interval and the termination time interval significantly influenced the estimates for erodibility parameters based on soil properties. In this study, it was found that a change in an initial few scour depth data points (4–5 data points) significantly affected the computed erodibility parameter values. This observation suggests estimation of erodibility parameters with the jet device using a single pressure setting can be greatly influenced by soil properties at the test surface. Because the bulk density and cohesion of the soil strata generally increases with depth into the streambank, applying multiple pressure settings with the jet device can alleviate some of these issues with over-predicting τc and kd for streambanks with cohesive soil. In addition, for the dataset applied in this study, it appears that estimates of τc and kd using the MPS-BM procedure were comparatively more consistent with the SPS-SDP, MPS-SDP, SPS-IP and MPS-IP procedures.
5. Conclusions
This study investigated the effect of different pressure settings on the mini-jet device using three published computational procedures (BM, SDP, and IP) for estimating the τc and kd erodibility parameters, in which a unique MPS procedure was developed and tested. The effect of time interval selection for scour-hole depth measurements during an in situ test was also examined for the different field and computational procedures. The experimental study was based on the hypothesis that streambank soil cohesion and bulk density increases from the near surface into the bank, differing due to subaerial processes and other environmental factors, therefore τc and kd are affected as the jet device forms the scour hole at a test location. It was also hypothesized by incrementally increasing device pressure settings during the test that it would compensate for the assumed change in soil properties as the scour hole develops. Collectively from 21 streambank sites across different Tennessee physiographic regions (a dataset of 126 jet tests), τc estimates applying the MPS-BM procedure were 17–100% greater than those applying the SPS-BM procedure, though the SPS-SDP, SPS-IP, MPS-SDP, and MPS-IP procedures generally estimated higher values. With kd estimates, MPS-BM showed lower values and less variation (σ = 3.54) in the dataset compared with the SPS-BM, SPS-SDP, SPS-IP, MPS-SDP, and MPS-IP procedures. These findings support the hypothesis of increasing τc and decreasing erodibility as the soil depth increases for cohesive soils, whereas the SPS-SDP, MPS-SDP, SPS-IP, and MPS-IP procedures estimated results contradicted the hypothesis. The MPS-BM procedure generated more consistent results for τc and kd estimates (smaller ranges for the same applied dataset) compared with the SPS methods and the three computational procedures (BM, SDP, and IP).
It appears that the MPS field methodology provides an alternative to the reduction factor (α) suggested by others to be incorporated in the excess shear stress equation to address the over-prediction of soil erosion on streambanks when τc and kd estimates are used from the SPS method. The advantage of using the MPS is that τc and kd estimates are determined in situ whereas α requires a known relationship as a function of soil properties. It was shown in this study, that relationships between applied device pressure, and τc and kd estimates were dependent on soil properties at the test location, which in turn affected the developmental morphology of the scour hole. Distinct patterns from these relationships were observed with different soil properties where it appears that with greater cohesion a concave-down to linear patterns were prominent in contrast to scattered patterns for less cohesive soils. This finding also suggests that the MPS method produces more consistent τc and kd estimates with more diverse soil properties.
Overall, it appears that the MPS method, in which incrementally increasing device pressure settings are applied for estimating τc and kd values, may better reflect fluvial erosion processes along a streambank/bed during a flood event. Consequently, average erodibility parameter values are represented rather than that of the surficial soil layer. The BM computational procedure appeared to generate more consistent estimates of τc and kd compared with the SDP and IP procedures, therefore the best results appear to be the MPS-BM procedure. More consistent procedures for estimating the erodibility parameters are a benefit to stream restoration practitioners improving on project designs that incorporate bank protection structures. Findings from this study suggest further research is needed to demonstrate its implications for improving the prediction of streambank erosion, in addition to an important and essential goal to standardize both field and computation methodologies.
Acknowledgments
This work was funded by Grant No. RES #2013-36 from the Tennessee Department of Transportation (TDOT). The authors would also like to thank Nancy Roberts for training and equipment support in the use of the Geotechnical Laboratory, Department of Civil and Environmental Engineering, the University of Tennessee, Knoxville. The authors would also like to thank Rob Thomas of USDA for sharing spreadsheets to analyze the jet-test device field data. Student field assistance was provided by Jordan Hicks and Zachariah Seiden.
Author Contributions
Badal Mahalder, the senior author generated the manuscript as part of his PhD dissertation, and co-authors John Schwartz, Angel Palomino, and Jon Zirkle supervised his research, in addition to direct text contributions to his study’s manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Dunn, I.S. Tractive Resistance of Cohesive Channels. J. Soil Mech. Found. 1959, 85, 1–24. [Google Scholar]
- Arulanandan, K.; Gillogley, E.; Tully, R. Development of a Quantitative Method to Predict Critical Shear Stress and Rate of Erosion of Natural Undisturbed Cohesive Soils; Waterways Experiment Station Technical Report, GL-80-5; USACE: Vicksburg, MS, USA, 1980. [Google Scholar]
- Hanson, G.J. Surface Erodibility of Earthen Channels at High Stresses. Part I-Open Channel Testing. Trans. ASAE 1990, 33, 127–131. [Google Scholar] [CrossRef]
- Hanson, G.J.; Simon, A. Erodibility of Cohesive Streambeds in the Loess Area of the Midwestern USA. Hydrol. Process 2001, 15, 23–28. [Google Scholar] [CrossRef]
- Sanford, L.P.; Maa, J.P.Y. A Unified Erosion Formulation for Fine Sediments. Mar. Geol. 2001, 179, 9–23. [Google Scholar] [CrossRef]
- Hanson, G.J.; Cook, K.R. Development of Excess Shear Stress Parameters for Circular Jet Testing. In ASAE Paper No. 97-2227; ASABE: St. Joseph, MI, USA, 1997. [Google Scholar]
- Hanson, G.J.; Cook, K.R. Apparatus, Test Procedures, and Analytical Methods to Measure Soil Erodibility in-situ. Appl. Eng. Agric. 2004, 20, 455–462. [Google Scholar] [CrossRef]
- Simon, A.; Thomas, R.E.; Klimetz, L. Comparison and Experiences with Field Techniques to Measure Critical Shear Stress and Erodibility of Cohesive Deposits. In Proceedings of the 2nd Joint Federal Interagency Conference on Sedimentation and Hydrologic Modeling, Las Vegas, NV, USA, 27 June–1 July 2010. [Google Scholar]
- Al-Madhhachi, A.T.; Hanson, G.J.; Fox, G.A.; Tyagi, A.K.; Bulut, R. Measuring Soil Erodibility Using a Laboratory “mini” JET. Trans. ASABE 2013, 56, 901–910. [Google Scholar]
- Khanal, A.; Fox, G.A.; Al-Madhhachi, A.T. Variability of Erodibility Parameters from Laboratory mini Jet Erosion Tests. J. Hydrol. Eng. 2016, 21. [Google Scholar] [CrossRef]
- Briaud, J.; Ting, F.; Chen, H.C.; Gudavilli, R.; Kwak, K.; Philogene, B.; Han, S.; Perugu, S.; Wei, G.; Nurtjahyo, P.; et al. SRICOS: Prediction of Scour Rate at Bridge Piers; Report 2937-1; Texas Transportation Institute, The Texas A&M University: College Station, TX, USA, 2001. [Google Scholar]
- Julian, J.; Torres, R. Hydraulic Erosion of Cohesive Riverbanks. Geomorphology 2006, 76, 193–206. [Google Scholar] [CrossRef]
- Wynn, T.M.; Mostaghimi, S. The Effects of Vegetation and Soil Type on Streambank Erosion, Southwestern Virginia, USA. J. Am. Water Resour. Assoc. AWARA 2006, 42, 69–82. [Google Scholar] [CrossRef]
- Thoman, R.W.; Nieggoda, S.L. Determining Erodibility, Critical Shear Stress, and Allowable Discharge Estimates for Cohesive Channels; Case Study in the Powder River Basin of Wyoming. J. Hydraul. Eng. 2008, 134, 1677–1687. [Google Scholar] [CrossRef]
- Grabowski, R.C.; Droppo, I.G.; Wharton, G. Erodibility of Cohesive Sediment: The Importance of Sediment Properties. Earth Sci. Rev. 2011, 105, 101–120. [Google Scholar] [CrossRef]
- Mahalder, B.; Schwartz, J.S.; Palomino, A.M.; Zirkle, J. Relationships between physical-geochemical soil properties and erodibility of streambanks among different physiographic provinces of Tennessee, USA. Earth Surf. Process. Landf. 2017. [Google Scholar] [CrossRef]
- Lick, W.; McNeil, J.; Xu, Y.J.; Taylor, C. Measurements of the Resuspension and Erosion of Sediments in Rivers; Department of Mechanical and Environmental Engineering, University of California: Santa Barbara, CA, USA, 1994. [Google Scholar]
- Zreik, D.A.; Krishnappan, B.G.; Germaine, J.T.; Madsen, O.S.; Ladd, C.C. Erosional and Mechanical Strengths of Deposited Cohesive Sediments. J. Hydraul. Eng. 1998, 124, 1076–1085. [Google Scholar] [CrossRef]
- Midgley, T.L.; Fox, G.A.; Wilson, G.V.; Heeren, D.M.; Langendoen, E.; Simon, A. Streambank Erosion and Instability Induced by Seepage: In-situ Constant-head Experiments. J. Hydrol. Eng. 2013, 18, 1200–1210. [Google Scholar] [CrossRef]
- Daly, E.R.; Fox, G.A.; Enlow, H.K.; Storm, D.E.; Hunt, S.L. Site-scale Variability of Streambank Fluvial Erodibility Parameters as Measured with a Jet Erosion Test. J. Hydrol. Process. 2015, 29, 5451–5464. [Google Scholar] [CrossRef]
- Sutarto, T.; Papanicolaou, T.A.N.; Wilson, C.G.; Langendoen, E.J. Stability Analysis of Semicohesive Streambanks with CONCEPTS: Coupling Field and Laboratory Investigations to Quantify the Onset of Fluvial Erosion and Mass Failure. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Daly, E.R.; Miller, R.B.; Fox, G.A. Modelling Streambank Erosion and Failure along Protected and Unprotected Composite Streambanks. Adv. Water Resour. 2015, 81, 114–127. [Google Scholar] [CrossRef]
- Daly, E.R.; Fox, G.A.; Fox, A.K. Correlating Site-scale Erodibility Parameters from Jet Erosion Tests to Soil Physical Properties. Trans. ASABE 2016, 59, 115–128. [Google Scholar] [CrossRef]
- McNeil, J.; Taylor, C.; Lick, W. Measurements of Erosion of Undisturbed Bottom Sediments with Depth. J. Hydraul. Eng. 1996, 122, 316–324. [Google Scholar] [CrossRef]
- Taylor, C.; Lick, W. Erosion Properties of Great Lakes Sediments; Department of Mechanical and Environmental Engineering, University of California: Santa Barbara, CA, USA, 1996. [Google Scholar]
- Jepsen, R.; Roberts, J.; Lick, W. Effects of Bulk Density on Sediment Erosion Rates. Water Air Soil Pollut. 1997, 99, 21–31. [Google Scholar] [CrossRef]
- Roberts, J.; Jepsen, R.; Gotthard, D.; Lick, W. Effects of Particle Size and Bulk Density on Erosion of Quartz Particles. J. Hydraul. Eng. 1998, 124, 1261–1267. [Google Scholar] [CrossRef]
- Perkins, R.G.; Honeywill, C.; Consalvey, M.; Austin, H.A.; Tolhurst, T.J.; Paterson, D.M. Changes in Microphytobenthic Chlorophyll a and EPS Resulting from Sediment Compaction Due to de-watering: Opposing Patterns in Concentration and Content. Cont. Shelf Res. 2003, 23, 575–586. [Google Scholar] [CrossRef]
- Perkins, R.G.; Sun, H.; Watson, J.; Player, M.A.; Paterson, D.M. In-line Laser Holography and Video Analysis of Eroded Flocs from Engineered and Estuarine Sediments. Environ. Sci. Technol. 2004, 38, 4640–4648. [Google Scholar] [CrossRef] [PubMed]
- Lick, W.; McNeil, J. Effects of Sediment Bulk Properties on Erosion Rates. Sci. Total Environ. 2001, 266, 41–48. [Google Scholar] [CrossRef]
- Daly, E.R.; Fox, G.A.; Al-Madhhachi, A.T.; Miller, R.B. A Scour Depth Approach for Deriving Erodibility Parameters from Jet Erosion Tests. Trans. ASABE 2013, 56, 1343–1351. [Google Scholar] [CrossRef]
- Karamigolbaghi, M.; Ghaneeizad, S.M.; Atkinson, J.F.; Bennett, S.J.; Wells, R.R. Critical Assessment of Jet Erosion Test Methodologies for Cohesive soil and Sediment. Geomorphology 2017, 295, 529–536. [Google Scholar] [CrossRef]
- Mahalder, B.; Schwartz, J.S.; Papanicolaou, A.N.T.; Palomino, A.M.; Zirkle, J. Comparison of erodibility parameters for cohesive streambank soils between an in-situ jet test device and laboratory conduit flume. J. Hydraul. Eng. 2018. (submitted). [Google Scholar]
- Craft, T.; Graham, L.; Launder, B. Impinging Jet Studies for Turbulence Model Assessment—II. An Examination of the Performance of Four Turbulence Models. Int. J. Heat Mass Transf. 1993, 36, 2685–2697. [Google Scholar] [CrossRef]
- Gibson, M.M.; Launder, B.E. Ground Effects on Pressure Fluctuations in the Atmospheric Boundary Layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Mercier, F.; Bonelli, S.; Pinettes, P.; Golay, F.; Anselmet, F.; Philippe, P. Comparison of CFD simulations with experimental Jet Erosion Tests results. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Clark, L.A.; Wynn, T.M. Methods for Determining Streambank Critical Shear Stress and Soil Erodibility: Implications for Erosion Rate Predictions. Trans. ASABE 2007, 50, 95–106. [Google Scholar] [CrossRef]
- Bonelli, S.; Brivois, O. The Scaling Law in the Hole Erosion Test with a Constant Pressure Drop. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1573–1595. [Google Scholar] [CrossRef]
- Bonelli, S.; Golay, F.; Mercier, F. On the Modelling of Interface Erosion; Erosion of Geomaterials; Wiley/ISTE: Hoboken, NJ, USA, 2012; Chapter 6; pp. 187–222. [Google Scholar]
- Golay, F.; Lachouette, D.; Bonelli, S.; Seppecher, P. Numerical Modelling of Interfacial Soil Erosion with Viscous Incompressible Flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 383–391. [Google Scholar] [CrossRef]
- Stein, O.R.; Nett, D.D. Impinging jet calibration of excess shear sediment detachment parameters. Trans. ASAE 1997, 40, 1573–1580. [Google Scholar] [CrossRef]
- Blaisdell, F.W.; Clayton, L.A.; Hebaus, C.G. Ultimate Dimension of Local Scour. J. Hydraul. Div. 1981, 107, 327–337. [Google Scholar]
- Miller, R.A. The Geologic History of Tennessee; Tennessee Division of Geology: Nashville, TN, USA, 1974; Volume 74. [Google Scholar]
- Hanson, G.J.; Robinson, K.M.; Cook, K.R. Scour below an overfall: Part II. Prediction. Trans. ASAE 2002, 45, 957–964. [Google Scholar] [CrossRef]
- Raudkivi, A.J. Loose Boundary Hydraulics, 3rd ed.; Pergamon Press: New York, NY, USA, 1990. [Google Scholar]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).