1. Introduction
Multi-reservoir systems operation is one of the classical issues of water resources management that has attracted the attention of researchers starting more than half a century ago (see for instance, [
1,
2,
3]). The problem is relevant around the world for its political, economic, and social implications, but is complex for at least two orders of reasons. On the one side, the multiplicity of stakeholders and goals that are normally involved in large multi-reservoir systems (see, for instance, [
4]) prevents a complete and shared formulation of the problem and often makes the collection and proper use of all the relevant information quite hard. On the other side, because of the difficulty of devising a computationally efficient and tractable mathematical method to deal with the uncertainty of future events, and specifically of future inflow and water uses.
Bellman SDP would in principle be the correct approach to solve this optimal control problem, and indeed has been the most widely used (e.g., [
5,
6,
7,
8,
9,
10,
11,
12]), but it suffers the well-known problem of the curse of dimensionality, i.e., the computational effort increases exponentially with the complexity of the considered system (i.e., number of reservoirs), and thus becomes rapidly intractable. In order to overcome the limitation of SDP, many techniques have been developed. They can be grouped considering whether they deal explicitly or implicitly with the stochasticity of inflows [
13,
14]. Explicit stochastic optimization (ESO) [
4,
15] utilizes the probability density functions (PDF) of the inflows. On the other hand, implicit stochastic optimization (ISO) [
16,
17] uses observed or synthetic inflow scenarios. For its computational advantages, ISO has become widely used in reservoir management studies (e.g., [
13]). Two different paths can be followed to derive optimal operating rules adopting an ISO framework: direct policy search [
18,
19], where a management rule, that optimizes the system objective(s), is selected within a predetermined class of functions; and fitting methods [
14], where a deterministic open-loop problem is first optimized with historical or synthetic hydrology, and then operating rules are selected to closely match the previous results. In both cases, the critical points are the choice of a sufficiently flexible class of possible management rules and, jointly, the amount of information (i.e., the arguments of the management rule) that must be available, at each time step, to the reservoir manager to determine the release.
The structure of the class of functions to be used also depends on other aspects: the presence of a single decision maker for the entire multi-reservoir system (or a cooperative situation) or separate managers for each reservoir; the presence of only one main management objective (water supply, hydropower production, ...) or multiple objectives; requirements of simplicity, reliability and so on.
In this work, the optimal control problem is solved applying an ISO framework and a fitting method. The unknown optimal closed-loop policy is assumed to belong to the very general class of NNs, trained using open-loop control sequences deterministically optimized for many synthetic scenarios. Even when such a very general structure for the operating rules is adopted, the problem of defining their architecture and specifically the input arguments to feed them in real time operation still remains.
This method was mainly used in the literature for single reservoirs [
20,
21,
22] or considering only a particular network structure (e.g., cascade reservoirs [
17]) and objective such as hydropower production [
23,
24,
25], water supply [
26,
27], flood control [
28,
29], water quality [
30]. Furthermore, many authors identified control rules to take the decision on the release considering only the storage of the reservoirs (e.g., [
31,
32]). Sometimes however, we can sample and estimate also other variables (e.g., inflows, evaporation, ...) which can be included as input of the operating rule [
4,
16,
21,
33]. The purpose of the current paper is to extend such previous works to address a situation of a complex multi-reservoir network with a combination of both series and parallel structures. In addition, we show how explicitly quantify the importance of sharing information between the reservoirs, considering as input of the control law of each of them not only the variables related to its catchment, but also the information of the other reservoirs which compose the network.
When a complex multi-reservoir system is considered, the ISO approach becomes more and more effective considering a longer inflow dataset, since this increases the probability of exploring a wider subset of the system state. For instance, the dataset we used for the current study is composed by 10,000 years of synthetic data, sampled with a monthly time step [
34].
Indeed, the Nile system case selected to test the approach is one of the most studied [
35,
36,
37,
38,
39,
40] and is definitely interesting under many perspectives: It is still widely discussed for its physical extension, socio-economic relevance and political implications [
41,
42,
43,
44,
45,
46].
The rest of this paper is structured as follows.
Section 2 shows tools and methods which are used for the optimal policy identification.
Section 3 briefly describes the main characteristics of the physical system and explains how the method has been adapted to this specific case. Results and performances obtained are reported and discussed in
Section 4, while the in last section some conclusions are drawn.
2. Methods
2.1. Problem Definition
Assuming a common (set of) objective(s)
J for the whole reservoir system, the optimal control rules correspond to the solution of the following problem:
where
t is the time step,
the
n-dimensional vectors of storages,
of water demands,
of inflows;
n being the number of reservoirs (catchments) in the considered area. The notation
indicates the entire trajectory of a generic variable
v from time 0 to the end of the management horizon
H, which, if the problem is assumed to be periodic with period T (typically, one year), corresponds to
. The solution of this functional problem are the operating rules
where
, represents the information on the system available at time
t.
This means that the optimal control problem, which in principle requires to find the best policy in the space of all functions from to , is reduced to a mathematical programming problem fixing the structure of the unknown policy and searching for its best parameterization.
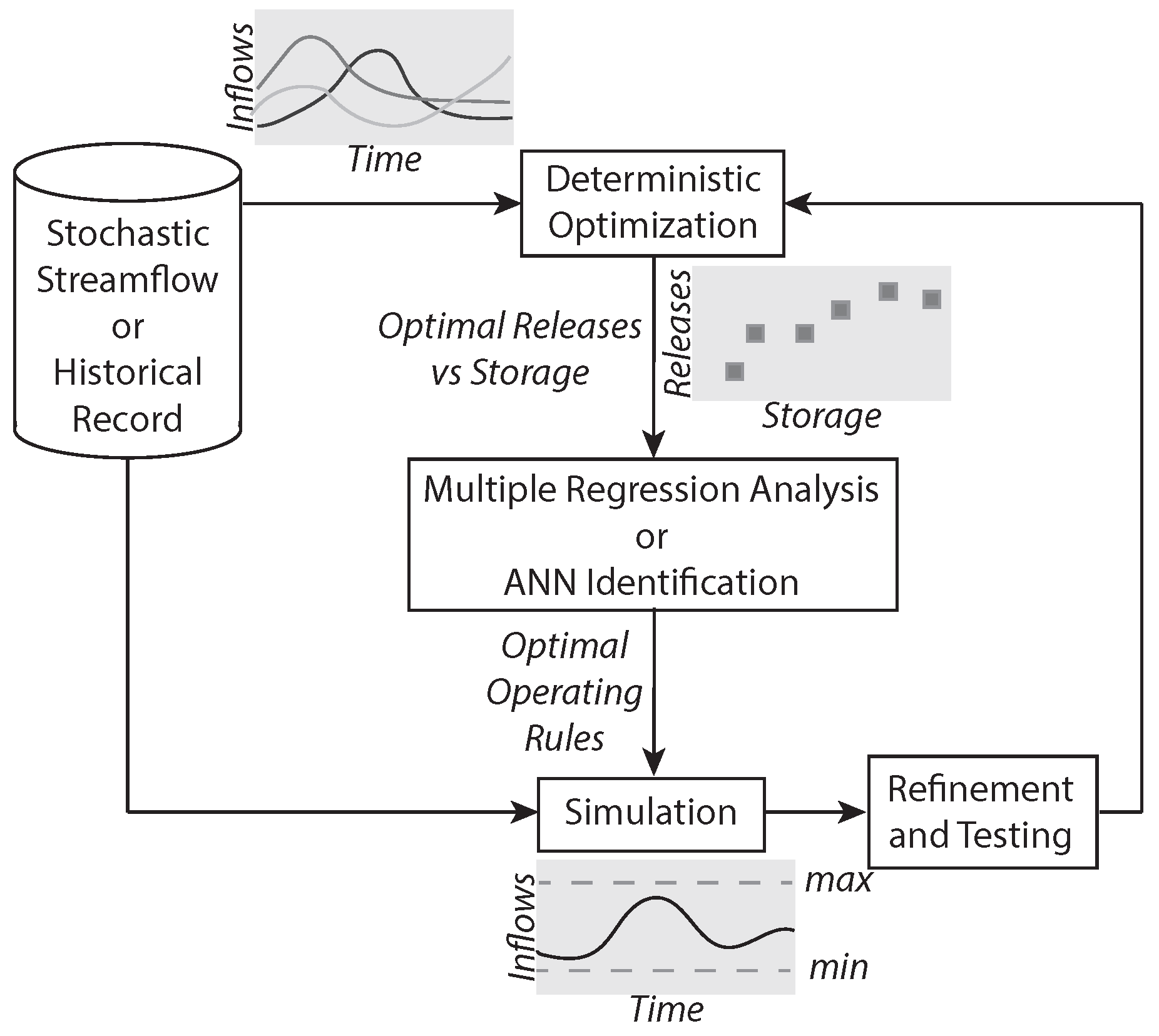
The ISO procedure adopted in order to solve the problem (Equations (1–5)) is schematically represented in
Figure 1.
It requires to consider many different scenarios, which represents how uncertainty is taken into account. It is basically composed by three steps:
Deterministic solution of many different open loop-problems each corresponding to one of the scenarios;
Fitting of a suffcienctly general class of functions to reproduce as much as possible the behaviour of the open-loop solution;
Testing of the identified rules with different scenarios on the complete system by new simulations.
One possibility is to use only historical data: in this way we can be sure that they perfectly represent the actual inflow process. Unfortunately, a robust identification of a policy requires a large number of samples, and it is nearly impossible to find such a long data series. It is thus necessary to make use of synthetic data, artificially generated starting from the statistical properties of the recorded input series. This approach allows to consider also events which have such a low probability that they never occurred in the past and even extremely severe episodes, that completely differ from the current inflow process (e.g., new regimes due to climate change), can be included to train the system to correctly react even in these extreme cases.
2.2. Deterministic Open-Loop Problem
If we assume to know in advance the values of the future inflows and, more in general, of the future disturbances, we are in fact dealing with a deterministic problem and it is sufficient to search for an open-loop sequence of control variables
. This means we determine the optimal releases for each reservoir and each time step, for all the management horizon, by solving the following problem:
The problem can be solved with one of the many algorithms for non-linear optimization (see, for instance [
31,
47,
48]). In the following case study, we selected a genetic approach, since genetic algorithms (GA):
Allow solving fairly quickly nonlinear problems with lots of dimensions. They are faster than methods that discretize the decisions space and perform an exhaustive search;
Guarantee a better performance than other random optimization methods, requiring an acceptable increasing of the computational effort;
Behave better than gradient-based methods when the objective function has lots of local optima.
GAs have some disadvantages too: they may become expensive from a computational point of view and the performance obtained is highly dependent on the initial population and the value assigned to the algorithm parameters such as the probability of crossover and mutation, and the fraction of individuals that are guaranteed to survive to the next generation (elite). Finding the best parametrization for a heuristic is not easy and, given the strong random component, even if it would be possible, it is not guaranteed that the setting obtained considering a scenario will work equally well for a different set of input data. In order to take into account these facts, each optimization is usually solved using different combinations of the parameters (i.e., crossover, mutation and elite fraction) which model the generation of the new population, performing a sensitivity analysis that also includes the population size.
2.3. Policy Identification
Solving problem (Equations (6–10)), we obtain the sequence of optimal releases at each time step corresponding to the inflow scenario under consideration. If we collect these sequences of optimal decisions, together with the information
relative to the conditions of the system at time step
t, we have a dataset which contains (possible) inputs and outputs of the control laws. For this purpose the dataset constituted by pairs
should be split into a subset for the control laws identification (say,
) and another for the analysis of the performances of the identified policies (
). Assuming that the control laws belong to the class
, we solve the problem:
where
is a suitable definition of the distance between the operating rule output and target
. The solution of problem (Equation (
11)) is the operating rule
.
As said previously, the variable
represents the information available at time
t, when the reservoir manager has to take the decisions on the release. It is possible to identify two main features of this information: the first is the type of variables describing the current hydrologic condition of the catchment, the second is about their spatial distribution, namely if they concern other catchments in the system, beside that under consideration. We can, for instance, assume that this information is full, if we have access to all the variables of the related catchment (storages, water demands, inflows, evaporation, ...), or incomplete if we know only the reservoir storages and the water demands. From a spatial point of view, the inputs of the control law of a certain reservoir can be the information relative to the whole system (centralized information) (see e.g., [
32,
49,
50]) or to the single reservoir (decentralized information).
Since it is not easy to define a priori a rule class which satisfactory captures the relationship between available information and releases, especially when data on the actual system management are missing, the use of extremely flexible models is recommended. In particular, we considered NNs which are known to be universal approximators under rather general conditions and for this reason have been widely used in environmental systems modeling [
51,
52,
53]. However, when selecting this very general class of rules, several specific details have to be fixed, besides the type and number of input variables: the number and cardinality of the hidden layer(s), the mathematical formulation and cardinality of the output layer, the activation functions of all neurons. For instance, one may develop a single NN for the entire system, thus using an output layer with as many neurons as the releases to be computed, or separate NNs for each reservoir with a single output. As to the activation functions, possible choices are:
sigmodal functions, for which the universal approximation theorem was first proved [
54,
55];
radial basis functions, since it has been recently empirically proved that they can be more appropriate in some contexts similar to the one considered here [
19].
For NNs identification, the dataset composed of samples has to be further split into the training set, validation set, and testing set. In order to find the most appropriate model complexity, the number of hidden layer neurons has to be varied across a suitable range, making some repetitions for each value and selecting the networks which has the best performance on the testing set. The neural control law can finally be identified using a supervised learning approach (e.g., Levenberg-Marquardt algorithm).
2.4. Rule Testing
The output of the identification step is a fully operational management rule, i.e., a relation that, given the hydrologic conditions of the catchment(s) at each time step, computes the consequent release(s) from the reservoir(s). Such rules can be analysed in different ways. For instance, one may check their shape in relation to one or more input variables. A classical requirement is that, with other hydrologic variables in average conditions, the rules are non-decreasing with respect to reservoir storage. The most common way to analyse these results is to simulate again the behavior of the system using the identified rules as they would operate in real time with new inflow scenarios (not used in the identification step) and check the overall performances. Such performances will obviously be different for different scenarios and thus a set of meaningful statistical indicators must be defined (e.g., average values, extremes with a 1% probability of occurrences, number of days above or below a given threshold, ...).
3. Case Study Description
3.1. The Nile River basin
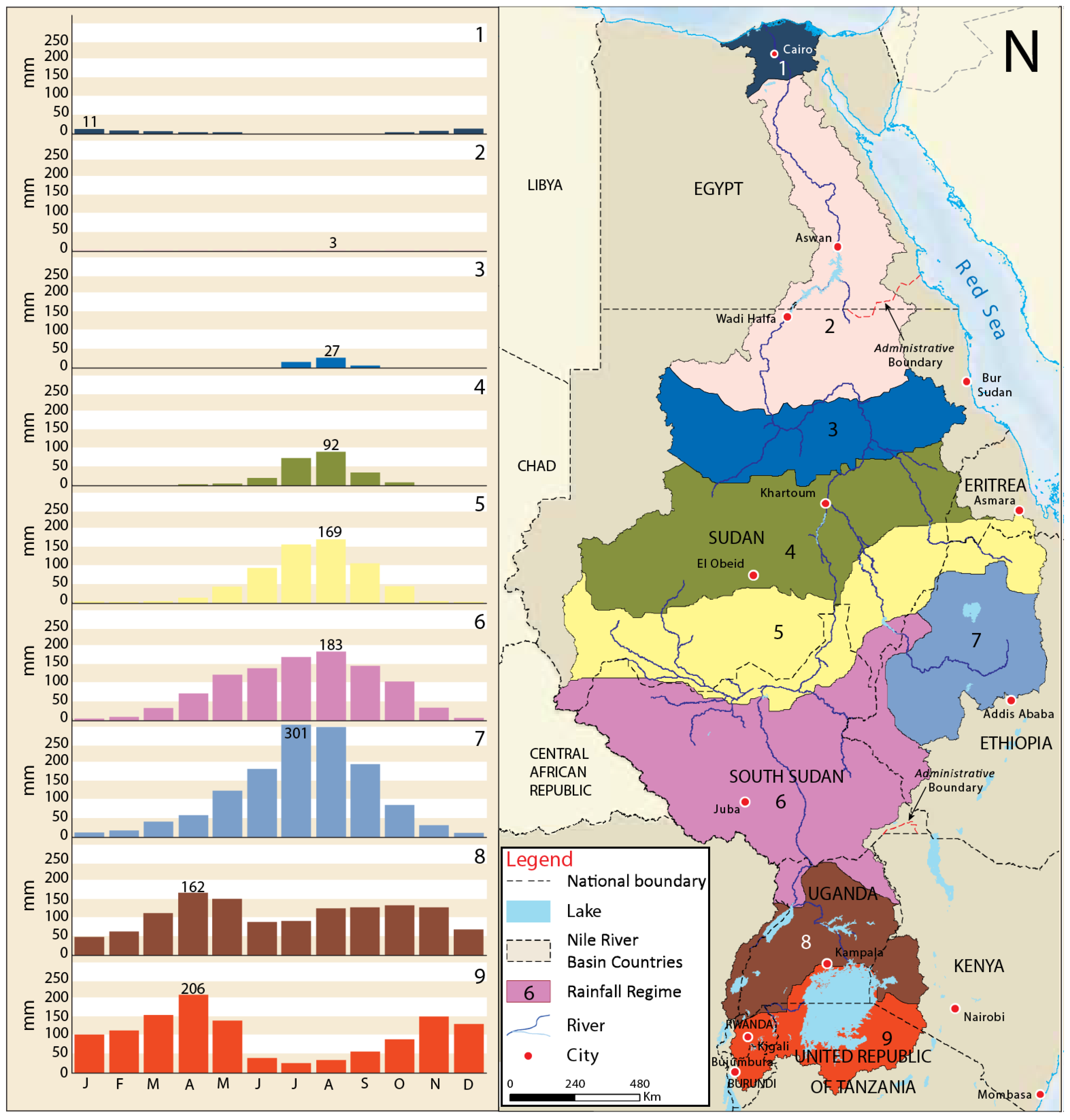
The Nile River, with an estimated length of over
km, is the longest river flowing in Africa and one of the longest on Earth. It is fed by two main river systems: the White Nile, with its sources on the Equatorial Lake Plateau and the Blue Nile, with its sources in the Ethiopian highlands. It crosses regions with very different climates and rainfall regimes, as shown in
Figure 2.
The Nile River is a key element for the development of the riparian countries and for the political relations in the region. Nowadays Egypt continues to be the primary user of Nile water, even if it is the most downstream country of the basin. This means that the water availability in Egypt is strongly dependent on the behaviors and on the strategies of the upstream countries, also because of the rainfall scarcity typical of the desert areas (see
Figure 2).
In the past, the political instability and poverty in the other nine riparian countries has limited their ability to negotiate a different water allocation [
58].
Many projects have been developed in recent years by the upstream countries (e.g., the Merowe Dam in Sudan, the Tekeze Dam and the Grand Ethiopian Renaissance Dam in Ethiopia). The development of these infrastructures will certainly modify the flow regime and possibly reduce the water volume available in Egypt, and thus the competition among the riparian countries for the water use will probably increase. For this and other reasons, water resources management is a fundamental topic in the region, which can affect also other aspects of the relationship between the governments and could also lead to critical situations in the future, as it happened in the past.
3.2. Model Formulation
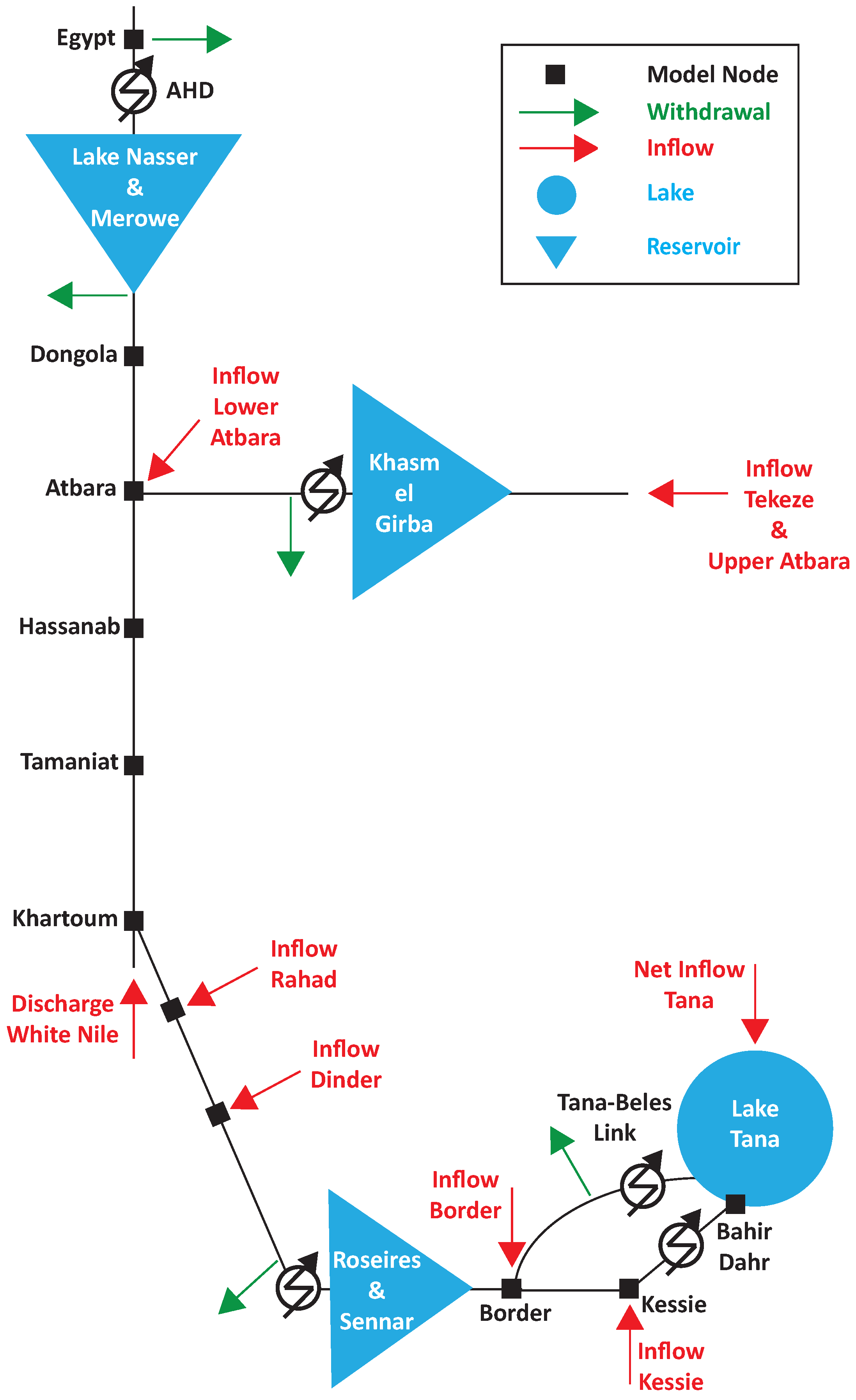
For the purpose of this work, we consider the following components: natural lakes, artificial reservoirs, hydrological network, hydroelectric power plants, and agricultural districts. All these factors have a key role in determining the overall state of the system and they are typically included in models describing the phenomena which characterize the hydrology of an anthropized catchment when observed on such a large scale. The time step used in the formulation is one month, as in all the previous studies on the Nile. The schematic representation of the considered system can be seen in
Figure 3.
3.2.1. System Variables
The Nile basin size makes it impossible to consider every single element of the system. For this reason, we modeled only the elements that are more relevant under a management prospective. All the considered system variables, which may represent states, input, or output, are presented in the following. The reader can refer to
Figure 3 to have a better understanding of what they represent. In particular, we consider the White Nile flow joining the main river in Khartoum as an external input. Indeed, it has an almost constant flow rate and represents only a minor portion of the overall water budget of the system.
(1) State Variables
The state vector
is composed by four elements representing the storage of the reservoirs at time
t:
where
and
are the storage of Lake Tana and Khasm el Girba, respectively.
represent the storage of the equivalent reservoir which models together Roseires and Sennar, on the Blue Nile. The same goes for Lake Nasser, the reservoir behind Aswan High Dam, and Merowe, modeled with the state variable
.
(3) Decision Variables
The decision variables, which are the argument of the optimization process and represents the decisions on the release from each reservoir:
(4) Internal Variables
There are finally other variables, such as the discharge in a point of the network, that do not fall into any of these categories. They are partial results of the calculation, which could be useful in order to have a feeling of what is happening in the system. Some internal variables which had been computed for further examinations are:
the natural outflow from Lake Tana at Bahir Dahr, ;
the discharges downstream of Border, , and Dongola, , which are the inflows to Roseires reservoir and Lake Nasser;
others discharges at some significant points of the network such as Tamaniat () and Hassanab () on the Main Nile, the discharge of the Blue Nile at Khartoum () and of the river Atbara just before the junction with the Main Nile ();
the hydraulic head of the power plants, computed as the difference, if positive, between the water level and the tailwater: , , , and .
3.2.2. Operating Objectives
Again abstracting from the complexity of the actual system, we assume that the purpose of the optimization process is to address the objectives of just two different groups of stakeholders: hydroelectric energy producers and farmers; and to determine a satisfactory final compromise solution.
We thus assume that hydropower and agricultural production are the only relevant (or at least the most important) objectives of the entire system. This means that we imagine that the different countries cooperate to optimize these objectives, even if this does not mean that they share all the information. This does not reflect the real situation of the system, but may provide a useful reference for future agreements.
(1) Hydropower Production
The hydropower production
in the generic interval
, is equal to the energy produced [GWh] by a certain power plant
i in that time period and can be obtained with the following expressions:
where:
is the overall efficiency of the power plant;
is the specific weight of water, equal to ;
is the hydraulic head, expressed in m;
the fourth factor represents the flow rate that will be used for power production, expressed in , computed as the minimum between the release from the reservoir and the maximum flow that can go through the turbines ();
is a coefficient of dimensional conversion, which contains the duration of the time step, 1 month, and whose value is in order to obtain an energy value expressed in .
is the sum of the energy produced in the five considered power plants.
(2) Water Supply to Agricultural Districts
Agricultural districts are characterized by a “cost” variable expressing the water deficits, in
, obtained as the difference, if positive, between the water demand and the water supply. The monthly deficits of the
i-th district can thus be computed as follows:
is the sum of all the water deficits relative to the agricultural districts.
(3) Objective Space Definition
Starting from the two groups of Equations (
12) and (
13) representing the objectives, it is possible to compute the two statistics
and
. The first is the yearly average of the energy production of all the power plants of the system. The second is the yearly average of the total water deficit. The two values are normalized for convenience to the range
(0 coincides with the best value of the objective and 1 with the worst) using the theoretical bounds of the feasible range of
and
.
3.2.3. Constraints
The equations which constitute the constraints of the model represent the dynamic of the considered system. The Nile hydrological simulation model used here is mainly based on SIMMODEL [
34] and Nile decision support tool (Nile-DST) [
59], with some adjustments that will be discussed below. As already mentioned, many hydrological studies and models have been developed for the Nile basin, but their differences do not appear to be relevant for the current study.
(1) White Nile
In this work, the reservoirs in the White Nile catchment are not modeled and its flow in Khartoum is taken as an external input: this could seem to be an excessive coarse approximation, given the extension of the sub-basin concerned. It is, however, important to underline that the presence of the Sudd swamps in fact disconnects the upstream and downstream subcatchments. The flow rate of the river at Mongalla (upstream from the swamps) has an average of 1048
. After this node, the flow enters the Sudd region, where more than half of the Nile’s water is lost, due to evaporation and transpiration. The average flow rate of the White Nile at the tails of the swamps is almost constant throughout the year and averages 510
, contributing about thirty percent of the total flow of the Nile River as shown in
Figure 4.
Hence, modeling the dynamic of White Nile system is not so important in order to understand the reservoirs dynamics in the rest of the system.
(2) Blue Nile
The Blue Nile, known also as Abbay, originates from Lake Tana. For the modeling of this regulated lake a traditional water balance equation is used:
where
is the storage at time
t,
the net inflow (actual inflow minus evaporation and seepage),
the natural outflow of the lake at Bahir Dahr exit and
the regulated release to the Tana-Beles link, an artificial channel that connects Lake Tana and Beles River, creating a consistent hydraulic head used for power generation and providing the water required for the agricultural district. The natural outflow is directed to the Blue Nile falls, 30 km downstream from Bahir Dahr, where a weir diverts some of the released water to Chara-Chara to be used for power generation at Tis Abay I and Tis Abay II plants (total installed capacity of 85 MW). In order to complete the description of this component of the system, the relationship between storage, level and surface are needed. The function used is that identified by [
63], which expresses level and area as a third degree polynomial function of the storage.
The discharge at Border,
, is computed applying the balance equation to the reach which starts from Lake Tana exit:
Roseires and Sennar reservoirs are considered as a single equivalent reservoir whose storage is the sum of the two. The inflow into Roseires (
) is a linear function of the Blue Nile discharge at Border and the reservoir is modeled with the mass balance Equation (
16),
being the function linking the surface to the storage. These functions are normally obtained by interpolation of digital elevation model (DEM) values and are available for all the reservoirs in the system.
According to Nile-DST, the flow motion in the reach from Sennar to Khartoum is considered as a rigid translation with a distributed loss. The loss coefficient is a constant value: 1% for every 100 river kilometers [
59] traveled along the 370 km reach. Dinder and Rahad rivers flow into the Blue Nile at 110 and 170 km downstream from Sennar, respectively.
(3) Atbara
The hydrographic basin upstream from Khasm el Girba Dam is composed by two different rivers: Upper Atbara and Tekeze, that join just before the reservoir. Tekeze is the main stream and upper Atbara a small tributary. We simply considered the inflow to Khasm el Girba reservoir () as the sum of the two flows.
The model of Khasm el Girba reservoir is similar to those of Lake Tana and Roseires. Once the withdrawal of the agricultural district has been subtracted, the flow released from Khasm el Girba continues along lower Atbara course until the city of Atbara, where there is the Main Nile junction.
(4) Main Nile
The Main Nile, also known as Desert Nile or Cataract Nile, is the reach that starts from Khartoum and goes downstream till the Mediterranean Sea. In this work, only the part from Khartoum to Aswan High Dam has been considered: Egypt is taken into account only for its water demand, because the existing downstream barrages (e.g., Assiut and Delta barrages) are mainly used to divert water to agricultural districts and because of their small dimensions have a very limited importance in a model with a monthly time step. The water motions along the Main Nile cannot be modeled as a rigid instantaneous translation, because of the length of the reach between Khartoum and Aswan (1847 km). We thus used the linear autoregressive model identified in [
34]. Lake Nasser and Merowe are considered as a unique equivalent reservoir, which is modeled again with the mass balance equation [
35].
3.3. Deterministic Open-Loop Problem
For the Nile system described above, a 10,000 year synthetic series of the inputs has been computed in [
34,
59,
64]. Such a large set of inflows covers a wide set of different conditions thus guaranteeing that even very critical cases are examined. In principle, it is possible to formulate a single problem which performs the optimization for the 7500 years reserved for identification. This means we should consider an extremely large number of decision variables (
months for each reservoir, making a total of 360,000 variables), which in fact makes it impossible to obtain a satisfactory suboptimal solution. In order to reduce such a problem, we use a shorter time horizon and solve the problem many times. We thus reorganize the synthetic data into 1500 5-year scenarios, which means we repeat an optimization problem with 240 decision variables, 1500 times. Since the first and the last months of each scenarios are influenced by the initial conditions and the lack of penalty on the final state, the first and the last year of each scenario have not been considered in the following identification step. This strongly reduces the influence of the initial state and of the finite horizon and allows the determination of an efficient solution for a long term, potentially infinite, time horizon in the following step of the procedure.
As to the settings of the GA for solving all these deterministic problems, the decision space has been uniformly sampled generating the initial population with a Sobol sequence. The parameters of the algorithm (population size, crossover, mutation and elite probabilities) have been tuned defining for each of them a reasonable range and testing all the possible combinations.
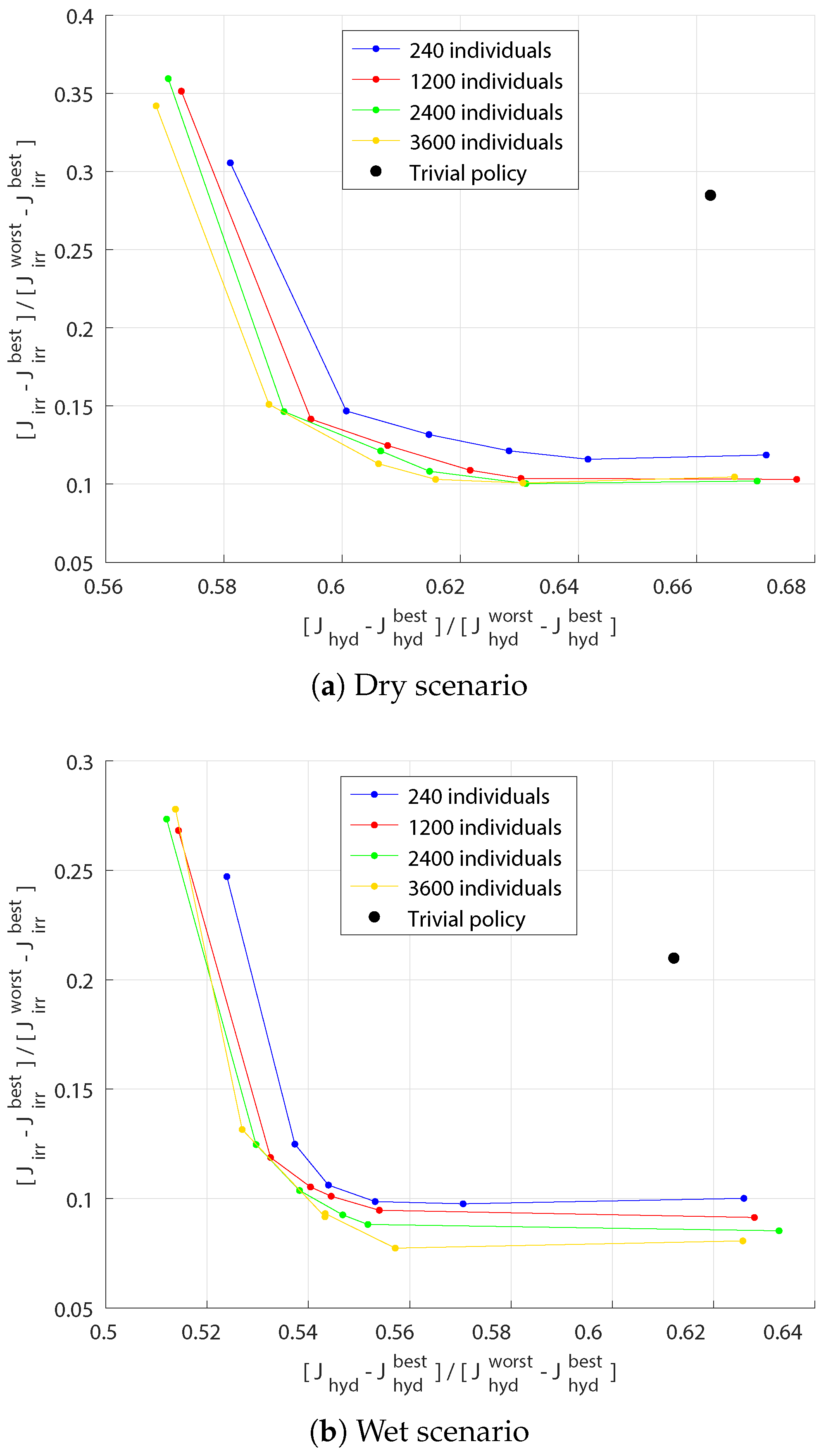
The two-objectives Pareto fronts obtained for some particularly dry and particularly wet scenarios, whose inflow values are summarized in
Table 1, can be seen in
Figure 5.
Historical policies cannot be used for comparison, since they are not even defined for the set of synthetic inflows used in this open-loop optimization. In order to have a control policy to compare with the solutions of the optimization, a trivial policy which consists of releasing at each time step the largest possible water volume was simulated. Its performances are also shown in
Figure 5.
The Pareto fronts obtained with a population of 240 individuals is definitively dominated, while the fronts obtained with other alternatives are quite close to one another, so we decided to use a population of 2400 individuals.
Once the selected Pareto front is computed, we have to define a single trade-off solution in order to obtain the corresponding operating rules (in principle, each point of the front corresponds to a set of different rules). The best approach for this, would be to directly interact with the actual stakeholders to determine how they weight the two objectives. Being this impossible (actual stakeholders do not share the objectives assumed in this study), we limited our search to the intermediate points of the front, since the extremes of the front practically take into account only one objective at a time, not representing a compromise between the stakeholders. All the considered fronts have nearly the same shape and the maximum curvature is where the hydropower and agricultural objectives are weighted and , respectively.
4. Results
4.1. Control Laws
A statistical analysis of the optimization results shows that the releases from Lake Tana into Tana-Beles link are not correlated with any other variables. In fact, the values of this flow obtained with the optimization, always remain in a very limited range: the optimized release is often equal to the pipes capacity (
) and even when this is not the case, the difference is usually negligible (see
Figure 6).
This means that it is not necessary to identify a control law for Lake Tana because it is sufficient to always release a flow equivalent to the maximum feasible value.
An in depth analysis shows that there is a physical reason behind this conclusion: the lake has a storage capacity of about 35 and an average depth of only 8 m. There are two orders of magnitude between the storage capacity and the maximum release plus the water level has a very limited variability and thus the hydraulic head is almost constant.
Considering Roseires, Khasm el Girba and Nasser reservoirs, the high rank correlation between the release and some of the variables composing the information vector, suggests that a trivial policy does not provide an acceptable performance and thus a rule which reproduces the relationship between inputs and optimal releases has to be identified.
The 54,000 samples
have been split into training (
of the whole dataset), validation (
) and testing set, composed of the remaining
. In order to find a suitable model complexity, the number of hidden layer neurons has been varied from 1 to 25, making 100 repetitions for each value and selecting the networks which provide the best performance on the testing set. Among the many possible training algorithm available, the neural operating rules have been identified using the Levenberg-Marquardt one, that has been widely used in hydrological problems [
65].
The number of hidden layer neurons selected is 5: for this value, the performance computed on the validation set reaches the optimum, suggesting that the identified network has a proper complexity. Note that, since thousands of samples are available for the identification, there are not remarkable differences between the performances obtained with training, validation and testing set.
As to the information vector used in the control laws, the four different cases specified in
Table 2, have been considered. They correspond to different sets of the input parameters listed in
Section 3.2.
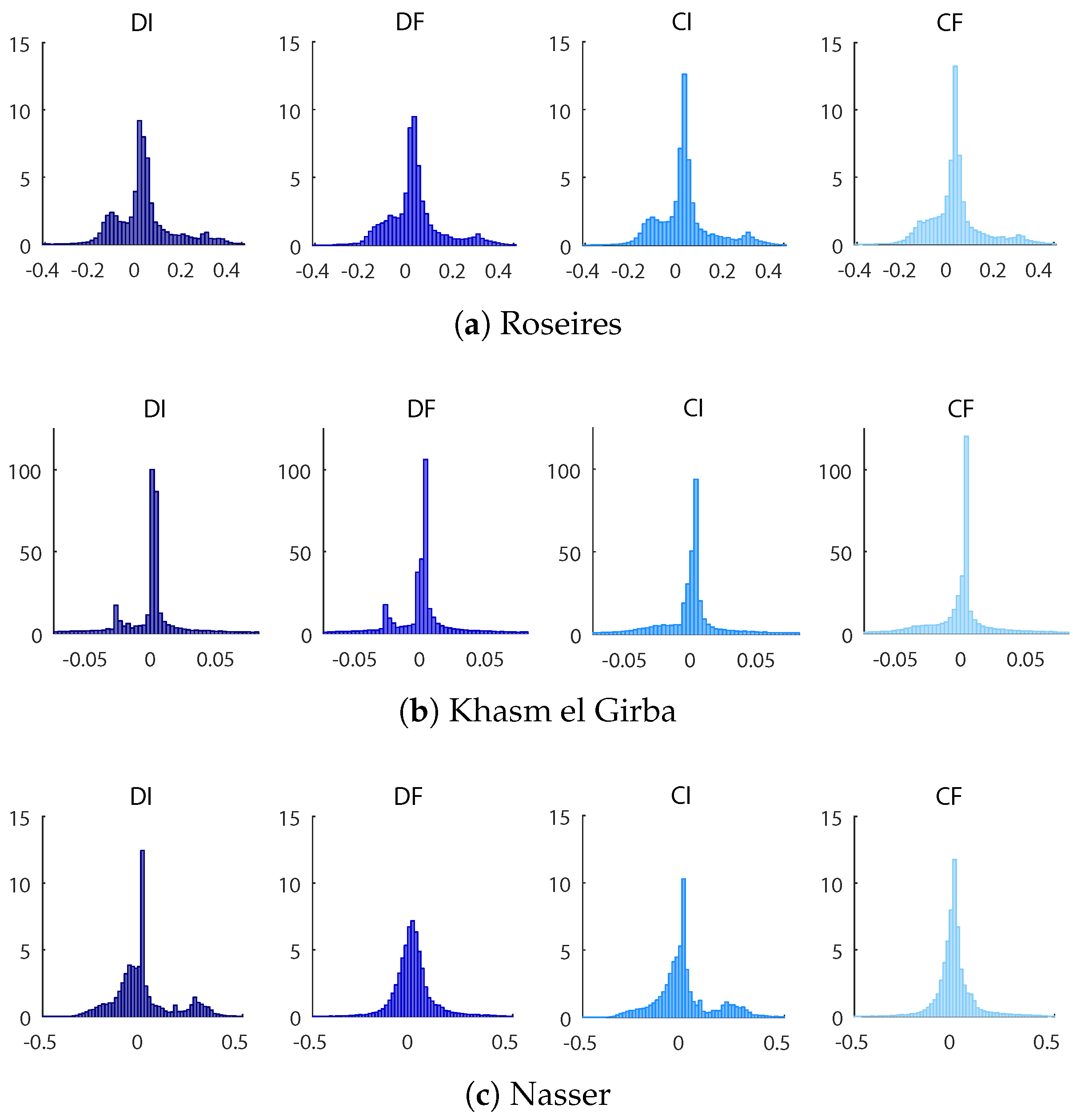
The worst fitting is always when a decentralized (D) and incomplete (I) information is considered. In order to decrease the gap between target and rules output, it is possible to work in two different directions: including information about the storage and water demand of the other reservoirs (centralized information C) or adding other variables providing a more detailed description of the considered reservoir and its hydrological basin (full hydrological information F). The case (CF), is the one which guarantees the most consistent fitting. A proof of this can be found in
Figure 7, in terms of residual distribution, and in
Table 3, considering the Pearson’s correlation coefficients.
Figure 7, in particular, shows the distributions of the differences between the optimal open-loop releases and those obtained with the NN control policy. It is evident that all the distributions have remarkable peaks in correspondence of a null error.
Table 3 can be useful in order to make a comparison between two different commonly used activation functions: sigmoid and radial basis. Other activation functions such as rectified linear units (ReLU) are indeed possible (see for instance, [
66]) and have been tested. However, as can be easily noted by the experiment results reported in the table in terms of correlation coefficients, it is clear that the two function shapes provide almost the same performance. This confirms what Hornik showed in 1991: it is not the specific choice of the activation function, but rather the multilayer feedforward architecture itself which gives neural networks the potential of being universal approximators [
67].
4.2. System Performances
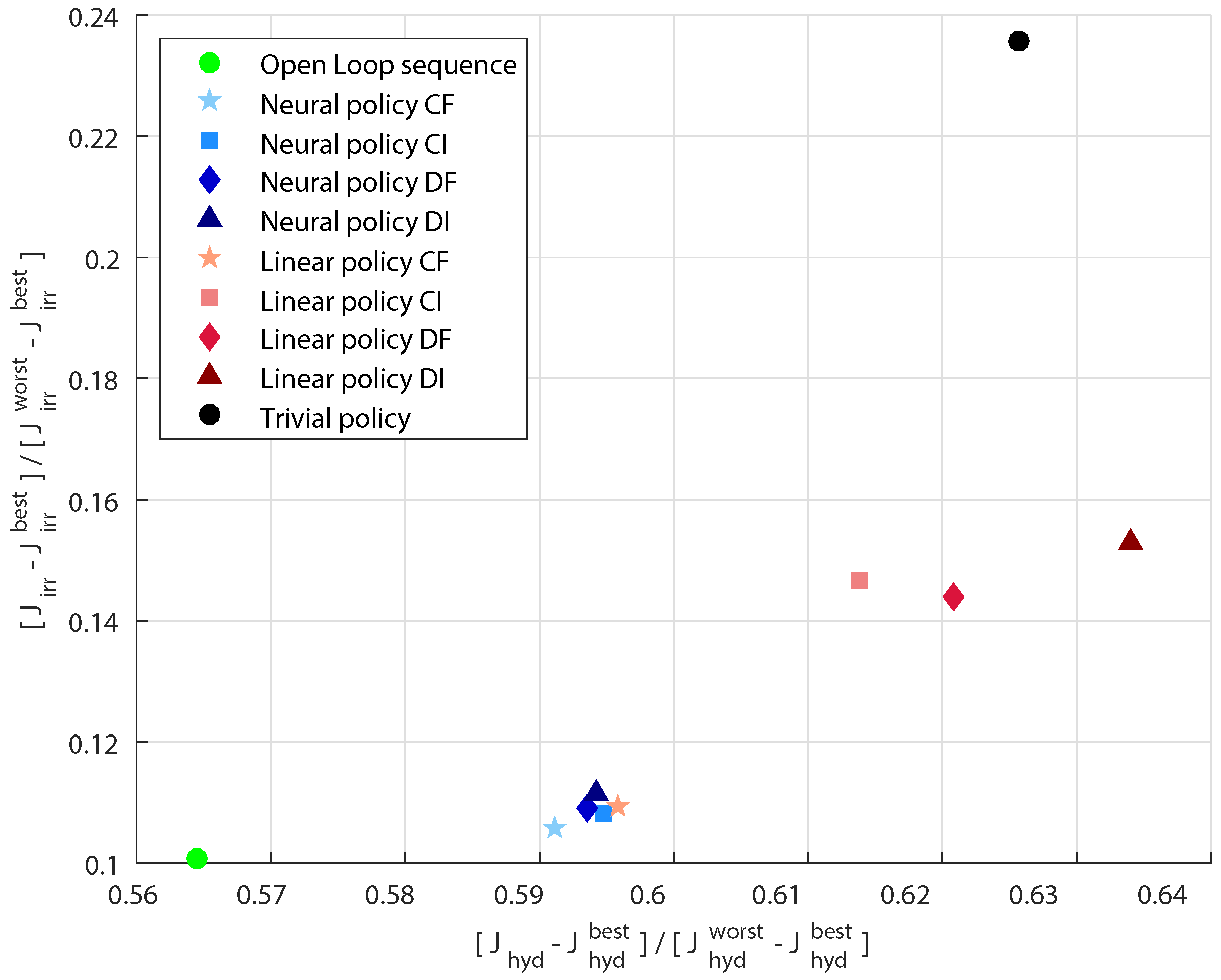
In order to evaluate the performance of the system when it is managed with the identified policies, we used 500 5-year synthetic scenarios ( of the whole dataset), that were not used for model identification. Since the historical policy is not available, we decided to compare the obtained solutions with some other control options:
a trivial policy, which releases the maximum feasible flow at each time step;
a closed-loop linear policy, which takes as input the same variables of the neural policy. Since we considered four different cases depending on the available information (DI, DF, CI, and CF), four different linear policies have been identified;
the open-loop control sequence computed with the GA. The performance obtained using this control sequence can be considered as a utopia point, in the sense that it is the target to which we wish to get close. This point represents the best performance which is possible to obtain when all the future inflows are deterministically known.
First of all, it can be noted that, as expected, there are neither solutions dominated by the trivial policy, nor solutions which over-perform the point obtained with the deterministic optimization. An interesting remark is relative to the comparison between linear and non-linear control laws: the neural policy always dominates the linear policy, when the same information is provided as input. On the other hand, adding further information (and thus more parameters), the performance of the linear policy become similar to that provided by the non-linear control. This fact suggests that when lots of information is available, there is no need of using a complex architecture for the policy. Conversely, when the amount of available information is limited, the neural policy is considerably better than the linear one. Hence, complex non-linear models, can be really important especially when sampling and/or estimating further variables is not possible or require a considerable effort.
It is also interesting to note, that, despite the quite different use of inflow information, the suggested neural policies achieves almost the same agricultural deficit and considerably improves the hydropower production with respect to other simpler management rules.
5. Concluding Remarks
This work implements and evaluates a method for multi-reservoir system operation. In particular, it shows how it is possible to identify a closed-loop control policy, following the ISO approach. It is important to underline that the identified policy can appropriately deal with problems affected by random disturbances, as it happens for the real world systems, and thus can be potentially used for practical applications. The performances obtained allow to draw some interesting conclusions.
First of all, it is demonstrated that the neural approach provides a better performance than the linear ones. This may sound obvious, but in practice it sometimes happens that linear models, which are easier to identify since it is possible to find exactly the best parametrization, over-perform more complex nonlinear models. The advantage of using a nonlinear architecture instead of a linear one is substantial when only a few variables are given as input to the control rule. On the other hand, if lots of information is available (and thus more parameters can be optimized), the distance between the solution provided by the two models becomes less significant. In this work, we assumed to exactly know the value of all the variables composing the information vector. In fact, this is not always the case: it is possible to have a precise measure for lots of variables (e.g., storages, water demands) but there could also be some information that cannot be easily sampled and thus has to be estimated. Considering these situations, it could be extremely useful to use a neural policy, since we can save lot of time and resources that would have been otherwise needed.
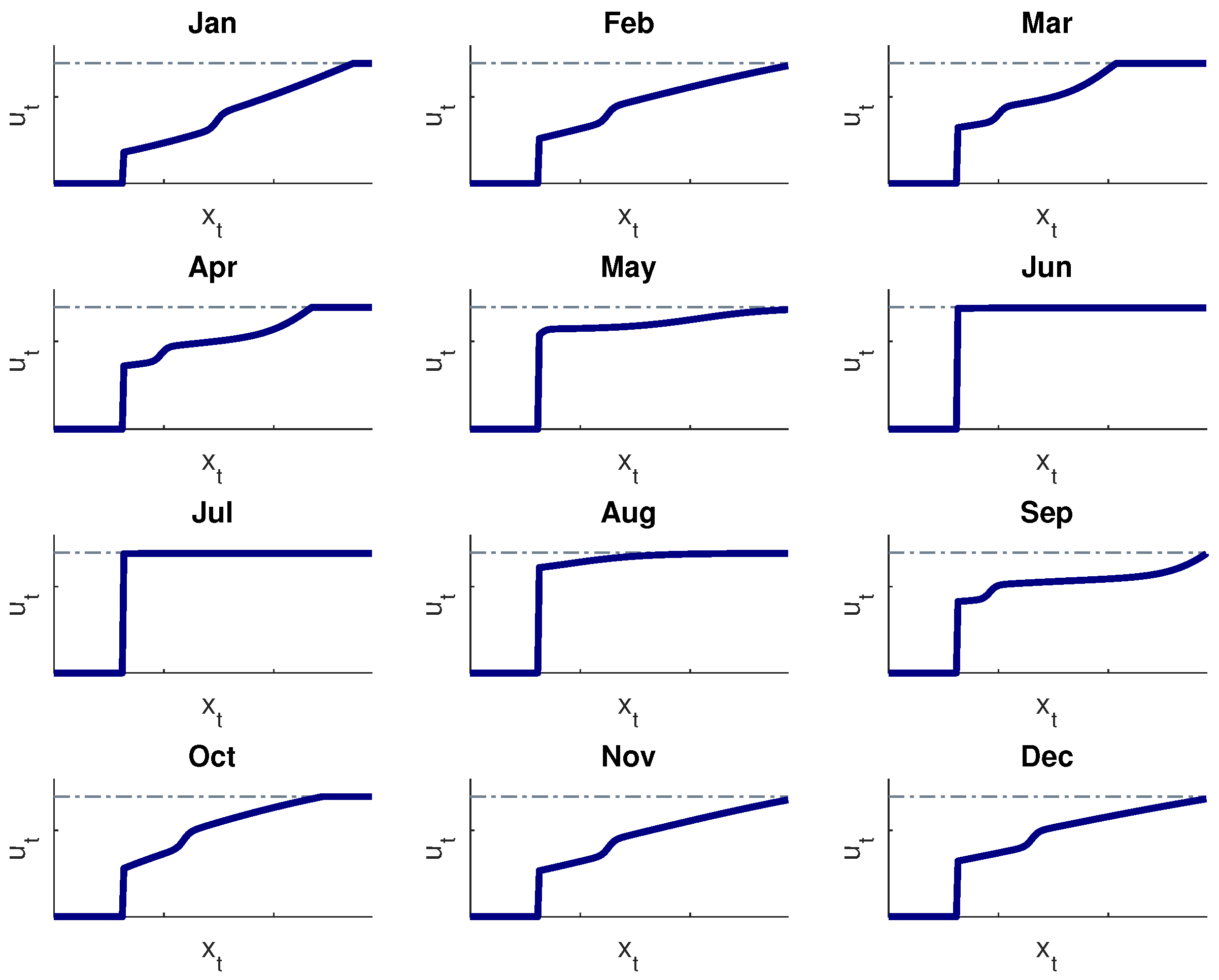
It is, however, well-known that NNs are not very popular in practice, since they often appear as a rather cryptic black-box. Once calibrated, they can easily be transformed (and probably they always should) into multi-dimensional response surfaces, showing the suggested release for each set of input values. Section of such surfaces (sometimes called profile plots) may for instance be used to examine how the manager should react to the variation of a single given variable.
Figure 9 illustrates the link between storage and release for Lake Nasser, in the different months. It is apparent that they can be interpreted as instances of a classical piece-wise linear decision rule.
The last aspect which has to be taken into account is relative to the approximations introduced in the procedure. The first refers to the fact that we are not able to provide a perfect description of the system. One can only define a model where a number of features of the real system are not considered, and try to consider only the elements which are necessary for the specific goals.
Indeed, in many cases there is a close connection between the degree of accuracy of the model and the complexity of the method used for its solution. The approach used in this work allows a better decoupling between the model of the physical system and the determination of the best control rules, since their identification simply requires a vector of hydrological variables and a vector of target releases. These can be produced in many different ways, including exploiting the answers of expert managers on how they would react in different circumstances.
Once we obtained a suitable model of the system, there are other two approximations which are more strictly related with the proposed procedure and with the identification of the policy. The open-loop control sequences we obtained using the GA are very likely to be suboptimal, since we are using a heuristic method to solve a non-linear programming problem. This means that even if we assume to be able to guarantee a perfect matching between information and decisions, the control laws we identify make reference to a somehow suboptimal set of decisions. On the other hand, even if we assume to have the optimal open-loop control sequence, we would not be able to identify a control law which provides the same perfect matching between information and decisions. Besides the obvious approximation of the procedure adopted for the calibration of the control rule parameters, there is an intrinsic difference between the open-loop and the closed-loop policies: the first has complete information about the future and can determine the release of every month in every specific year in the best way; the second is based on the current system state and can only assume an “average” future. This is why, the closed-loop rule is cyclostationary over the year and cannot but replicate the same decision year by year, if the basin condition are the same, independently from the possibly dry or wet future. It is thus theoretically impossible to completely fill the gap between the performances of an optimal open-loop management and a cyclostationary release rule. The two-steps rule identification method adopted in this work can be easily applied to other multi-reservoir systems, provided a sufficiently long sequence of inflows is available. While this is true for any regression method, the training of NNs is particularly demanding and, in practice, this would almost inevitably requires the development of a series of synthetic inflows. Another key characteristic of the method is that the NN rules are trained to replicate a specific optimal control sequence. This means that, when a multiplicity of objectives is present, a compromise solution must be defined early in the procedure. This is not always the case in practice, since reaching a compromise solution implies an active involvement of all stakeholders which may need the analysis of the performances of several plausible regulation policies. In the future, we plan to further compare the approach with other methods, such as direct policy search, and explore the possibility of better embedding multi-objective problems into it.