Effectiveness of a Natural Headwater Wetland for Reducing Agricultural Nitrogen Loads
Abstract
1. Introduction
2. Materials and Methods
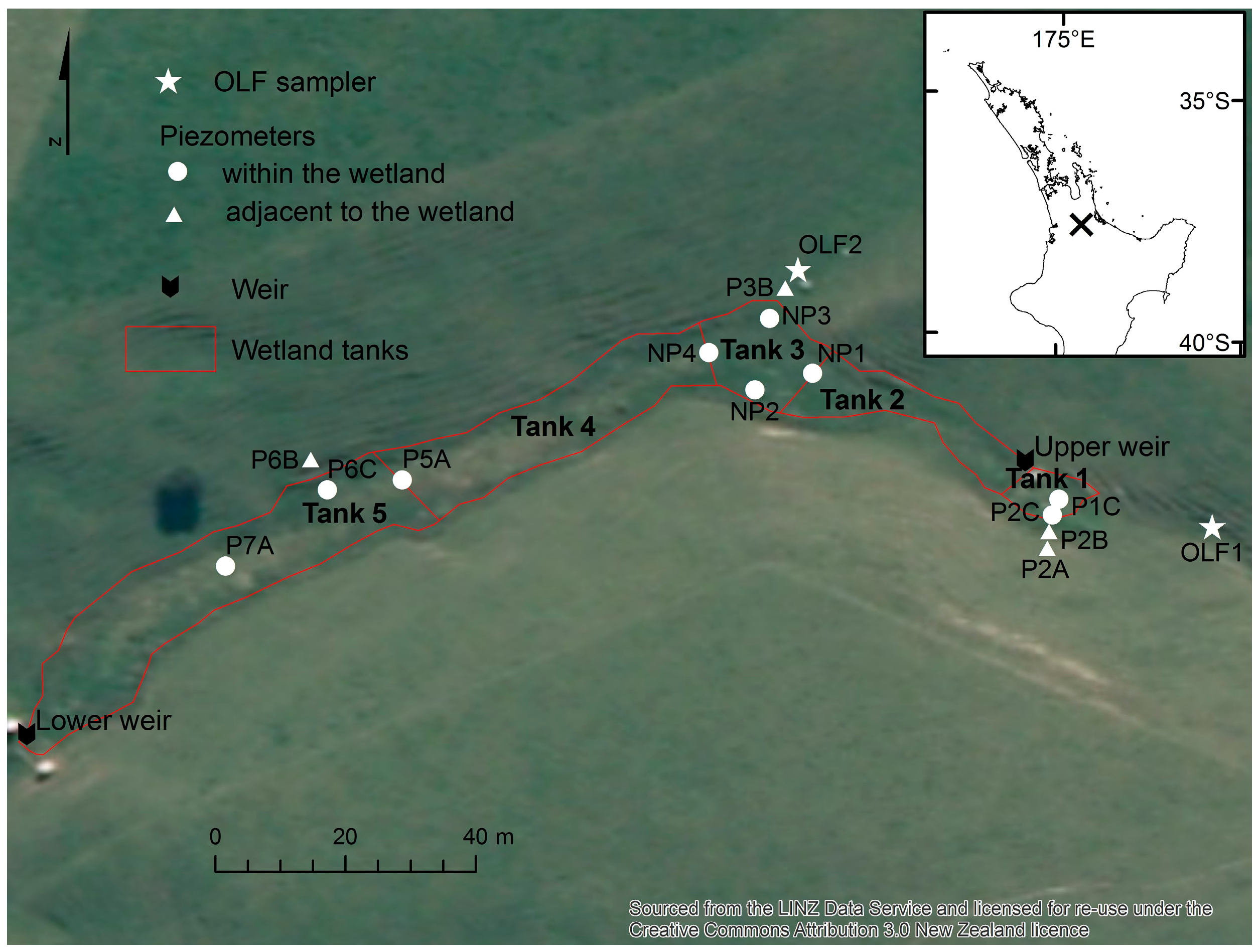
2.1. Study Site
2.2. Site Monitoring
2.3. Laboratory Analysis
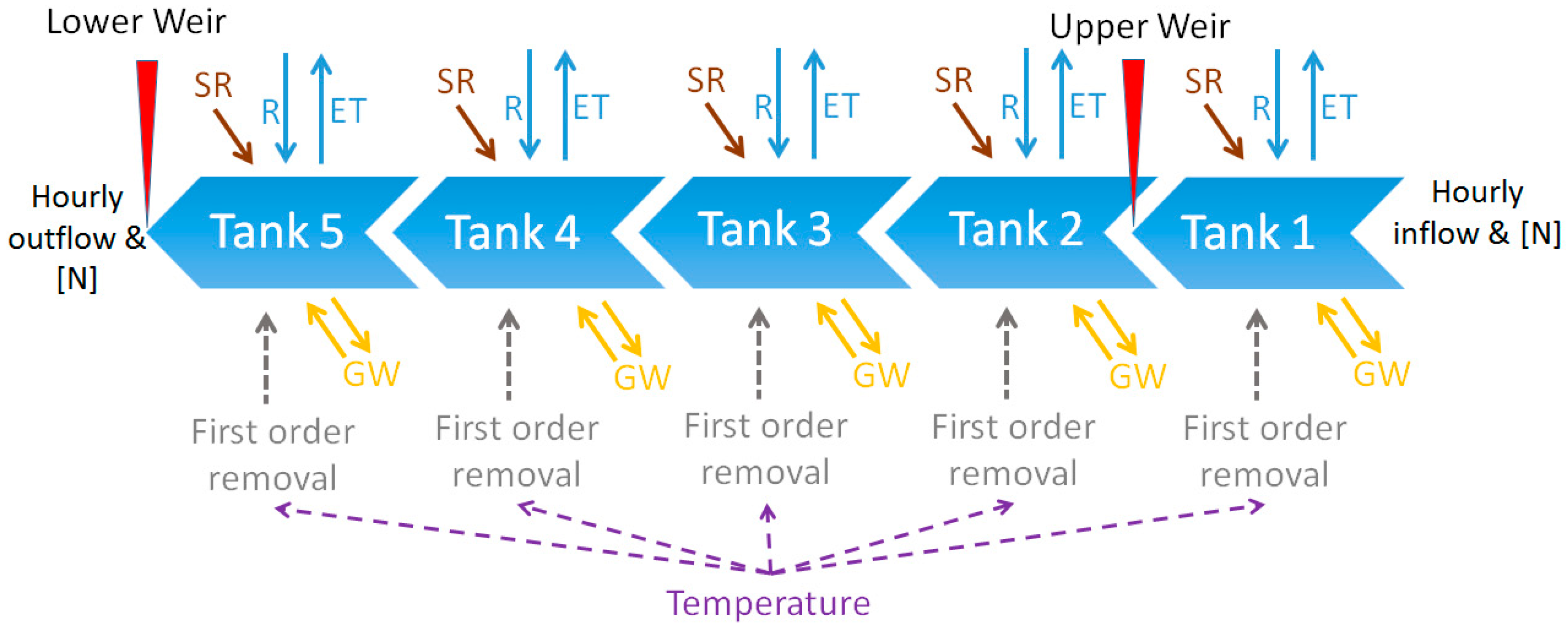
2.4. Modelling Nitrogen Removal
3. Results
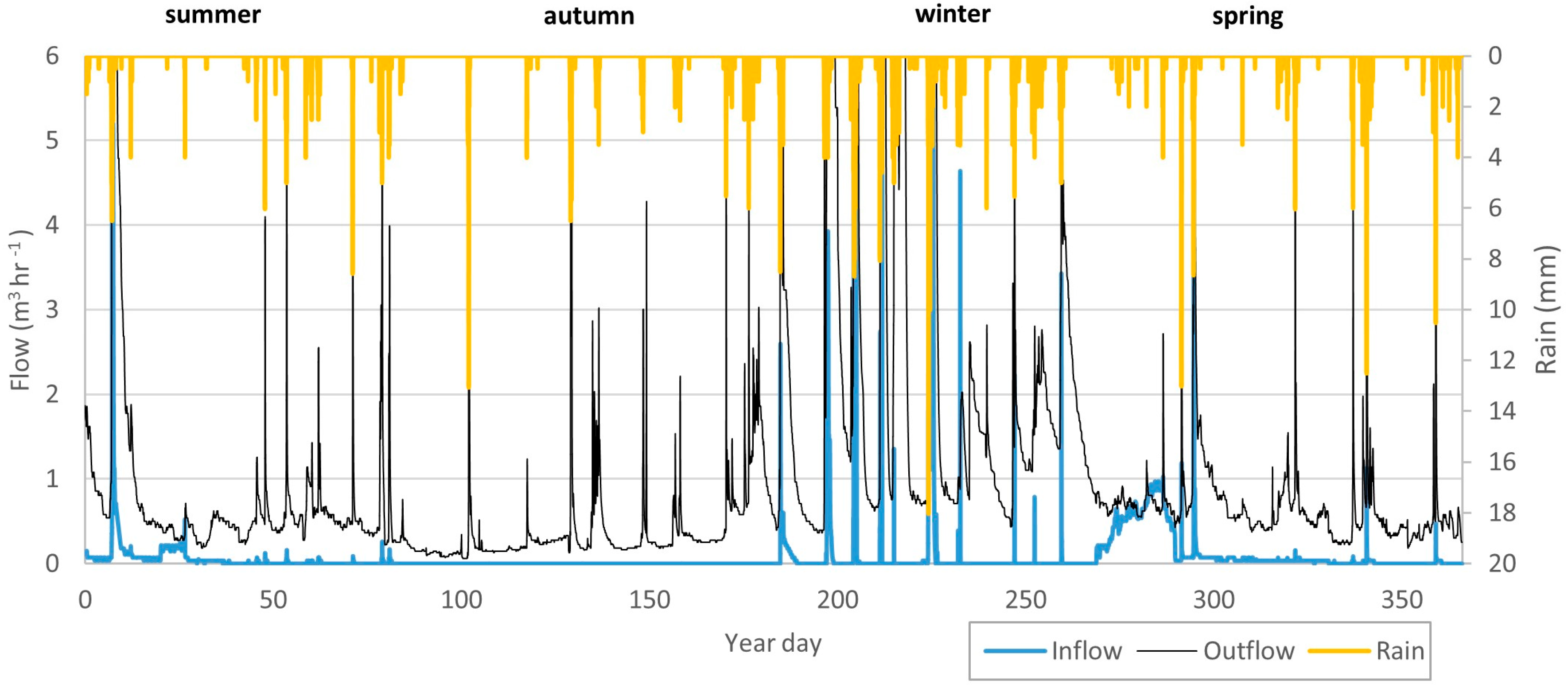
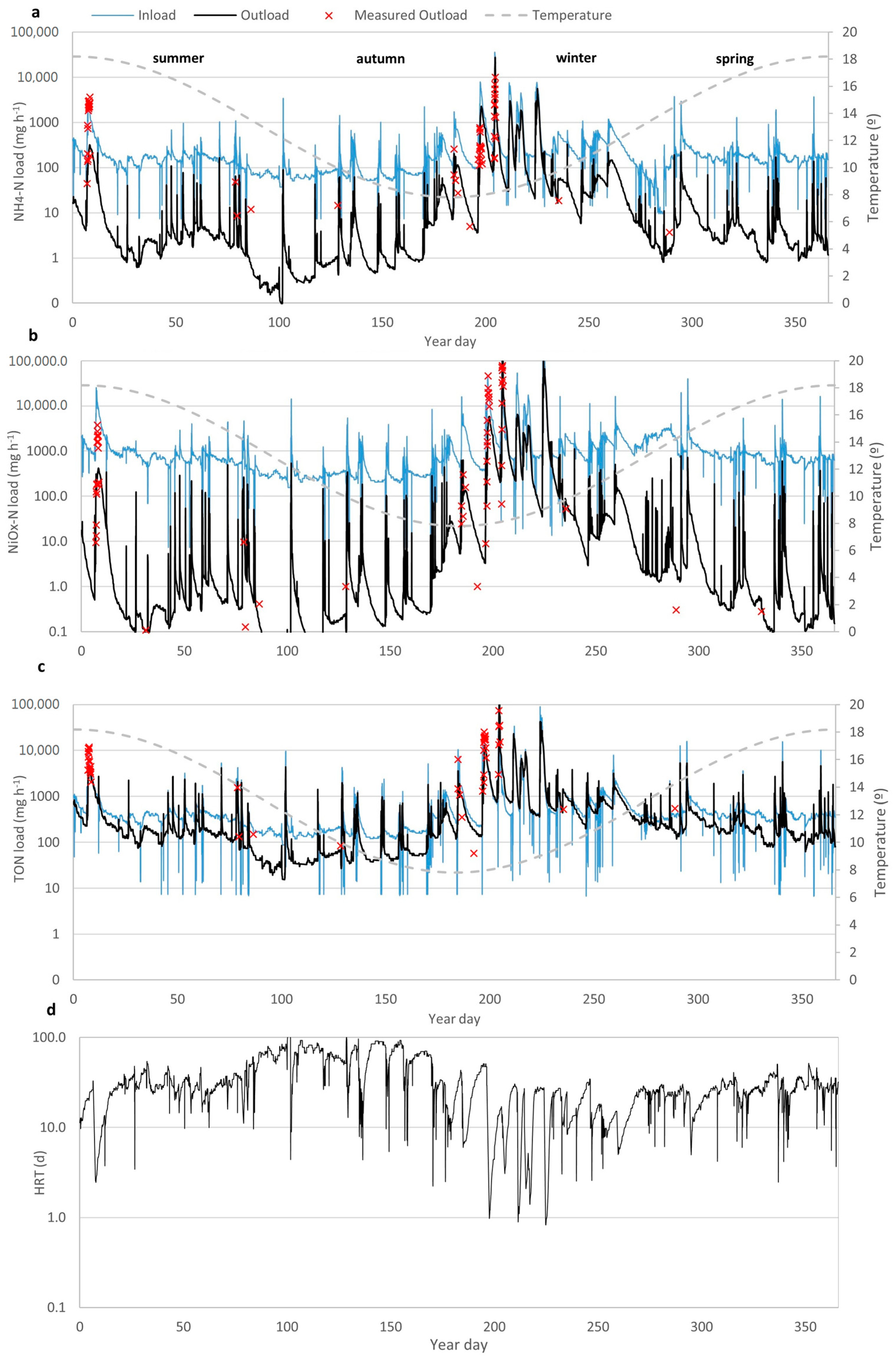
3.1. Hydrology of the Wetland
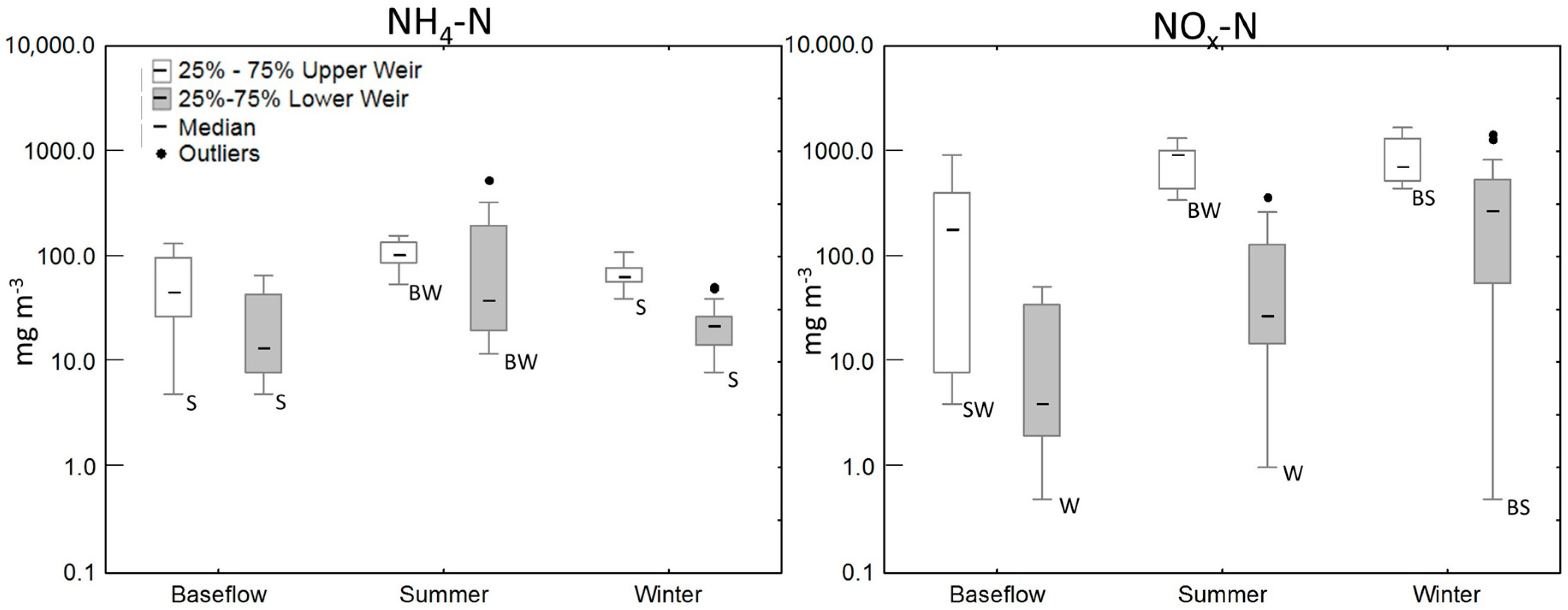
3.2. Water Quality of the Wetland
3.3. Modelling Wetland N Species Removal Efficiency
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Passeport, E.; Vidon, P.; Forshay, K.J.; Harris, L.; Kaushal, S.S.; Kellogg, D.Q.; Lazar, J.; Mayer, P.; Stander, E.K. Ecological Engineering Practices for the Reduction of Excess Nitrogen in Human-Influenced Landscapes: A Guide for Watershed Managers. Environ. Manag. 2013, 51, 392–413. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L.; Yang, Y.S. An approach to catchment-scale groundwater nitrate risk assessment from diffuse agricultural sources: A case study in the Upper Bann, Northern Ireland. Hydrol. Process. 2008, 22, 4274–4286. [Google Scholar] [CrossRef]
- Tanner, C.; Sukias, J. Multiyear nutrient removal performance of three constructed wetlands intercepting tile drain flows from grazed pastures. J. Environ. Qual. 2011, 40, 620–633. [Google Scholar] [CrossRef] [PubMed]
- Kadlec, R.H. Constructed marshes for nitrate removal. Crit. Rev. Environ. Sci. Technol. 2012, 42, 934–1005. [Google Scholar] [CrossRef]
- Baker, L.A. Design considerations and applications for wetland treatment of high-nitrate waters. Water Sci. Technol. 1998, 38, 389–395. [Google Scholar]
- Fisher, J.; Acreman, M.C. Wetland nutrient removal: A review of the Wetland nutrient removal: A review of the evidence. Hydrol. Earth Syst. Sci. Discuss. 2004, 8, 673–685. [Google Scholar] [CrossRef]
- Davidsson, T.E.; Stahl, M. The influence of organic carbon on nitrogen transformations in five wetland soils. Soil Sci. Soc. Am. J. 2000, 64, 1129–1136. [Google Scholar] [CrossRef]
- Matheson, F.E.; Nguyen, M.L.; Cooper, A.B.; Burt, T.P.; Bull, D.C. Fate of 15N-nitrate in unplanted, planted and harvested riparian wetland soil microcosms. Ecol. Eng. 2002, 19, 249–264. [Google Scholar] [CrossRef]
- Xu, J.H.; He, S.B.; Wu, S.Q.; Huang, J.C.; Zhou, W.L.; Chen, X.C. Effects of HRT and water temperature on nitrogen removal in autotrophic gravel filter. Chemosphere 2016, 147, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Ambus, P.; Christensen, S. Denitrification variability and control in a riparian fen irrigated with agricultural drainage water. Soil Biol. Biochem. 1993, 25, 915–923. [Google Scholar] [CrossRef]
- Bernal, B.; Anderson, C.J.; Mitsch, W.J. Nitrogen Dynamics in Two Created Riparian Wetlands over Space and Time. J. Hydrol. Eng. 2017, 22. [Google Scholar] [CrossRef]
- Zaman, M.; Nguyen, M.L.; Gold, A.J.; Groffman, P.M.; Kellogg, D.Q.; Wilcock, R.J. Nitrous oxide generation, denitrification, and nitrate removal in a seepage wetland intercepting surface and subsurface flows from a grazed dairy catchment. Aust. J. Soil Res. 2008, 46, 565–577. [Google Scholar] [CrossRef]
- Matthew, C.; Horne, D.J.; Baker, R.D. Nitrogen loss: An emerging issue for the ongoing evolution of New Zealand dairy farming systems. Nutr. Cycl. Agroecosyst. 2010, 88, 289–298. [Google Scholar] [CrossRef]
- Statistics New Zealand. Agriculture, Horticulture, and Forestry. 2016. Available online: http://www.stats.govt.nz/infoshare/ (accessed on 7 March 2017).
- Parfitt, R.L.; Stevenson, B.A.; Dymond, J.R.; Schipper, L.A.; Baisden, W.T.; Ballantine, D.J. Nitrogen inputs and outputs for New Zealand from 1990 to 2010 at national and regional scales. N. Z. J. Agric. Res. 2012, 55, 241–262. [Google Scholar] [CrossRef]
- Tanner, C.; Sukias, J.; Burger, D. Realising the value of remnant wetlands as farm attenuation assets. In Moving Farm Systems to Improved Nutrient Attenuation; Currie, L.D., Burkitt, L.L., Eds.; Occassional Report No. 28; Fertilizer and Lime Research Centre, Massey University: Palmerston North, New Zealand, 2015. [Google Scholar]
- Ausseil, A.G.E.; Dymond, J.R.; Shepherd, J.D. Rapid mapping and prioritisation of wetland sites in the Manawatu-Wanganui region, New Zealand. Environ. Manag. 2007, 39, 316–325. [Google Scholar] [CrossRef] [PubMed]
- Gluckman, P. New Zealand’s Fresh Waters: Values, State Trends and Human Impacts; Office of the Prime Minister’s Chief Science Advisor: Wellington, New Zealand, 2017; Available online: http://www.pmcsa.org.nz/wp-content/uploads/PMCSA-Freshwater-Report.pdf (accessed on 7 February 2018).
- Organization for Economic Cooperation and Development (OECD). Third Environmental Performance Review: New Zealand 2017; Organization for Economic Cooperation and Development (OECD): Paris, France, 2017. [Google Scholar]
- McKergow, L.A.; Rutherford, J.C.; Timpany, G.C. Livestock-Generated Nitrogen Exports from a Pastoral Wetland. J. Environ. Qual. 2012, 41, 1681–1689. [Google Scholar] [CrossRef] [PubMed]
- Peterson, B.J. Control of Nitrogen Export from Watersheds by Headwater Streams. Science 2001, 292, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Jordan, T.E.; Whigham, D.F.; Hofmockel, K.H.; Pittek, M.A. Nutrient and Sediment Removal by a Restored Wetland Receiving Agricultural Runoff. J. Environ. Qual. 2003, 32, 1534–1547. [Google Scholar] [CrossRef] [PubMed]
- Kovacic, D.A.; David, M.B.; Gentry, L.E.; Starks, K.M.; Cooke, R.A. Effectiveness of constructed wetlands in reducing nitrogen and phosphorus export from agricultural tile drainage. J. Environ. Qual. 2000, 29, 1262–1274. [Google Scholar] [CrossRef]
- Borin, M.; Tocchetto, D. Five year water and nitrogen balance for a constructed surface flow wetland treating agricultural drainage waters. Sci. Total Environ. 2007, 380, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Knox, A.K.; Dahlgren, R.A.; Tate, K.W.; Atwill, E.R. Efficacy of natural wetlands to retain nutrient, sediment and microbial pollutants. J. Environ. Qual. 2008, 37, 1837–1846. [Google Scholar] [CrossRef] [PubMed]
- O’Geen, A.T.; Budd, R.; Gan, J.; Maynard, J.J.; Parikh, S.J.; Dahlgren, R.A. Mitigating Nonpoint Source Pollution in Agriculture with Constructed and Restored Wetlands. In Advances in Agronomy; Academic Press: Cambridge, MA, USA, 2010; Volume 108, ISBN 9780123810311. [Google Scholar]
- Wilcock, R.J.; Monaghan, R.M.; Quinn, J.M.; Campbell, A.M.; Thorrold, B.S.; Duncan, M.J.; McGowan, A.W.; Betteridge, K. Land-use impacts and water quality targets in the intensive dairying catchment of the Toenepi Stream, New Zealand. N. Z. J. Mar. Freshw. Res. 2006, 40, 123–140. [Google Scholar] [CrossRef]
- Müller, K.; Srinivasan, M.S.; Trolove, M.; McDowell, R.W. Identifying and linking source areas of flow and P transport in dairy-grazed headwater catchments, North Island, New Zealand. Hydrol. Process. 2010, 24, 3689–3705. [Google Scholar] [CrossRef]
- Hughes, A.; Tanner, C.; McKergow, L.; Sukias, J. Unrestricted dairy cattle grazing of a pastoral headwater wetland and its effect on water quality. Agric. Water Manag. 2016, 165, 72–81. [Google Scholar] [CrossRef]
- Porteous, A.; Mullan, B. The 2012-13 Drought: An Assessment and Historical Perspective; MPI Technical Paper No: 2012/18; Prepared for the Ministry for Primary Industries; National Institute of Water and Atmospheric Research: Wellington, New Zealand, 2013. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998; p. 300. ISBN 9251042195. [Google Scholar]
- StatSoft Inc StatSoft. Available online: http://www.statsoft.com/ (accessed on 1 November 2017).
- Kadlec, R.H. Nitrate dynamics in event-driven wetlands. Ecol. Eng. 2010, 36, 503–516. [Google Scholar] [CrossRef]
- French, R.H. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Kadlec, R.H.; Wallace, S.D. Treatment Wetlands, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9781566705264. [Google Scholar]
- Wilcock, R.J.; Müller, K.; Van Assema, G.B.; Bellingham, M.A.; Ovenden, R. Attenuation of nitrogen, phosphorus and E. coli inputs from pasture runoff to surface waters by a farm wetland: The importance of wetland shape and residence time. Water Air Soil Pollut. 2012, 223, 499–509. [Google Scholar] [CrossRef]
- Wells, N.S.; Baisden, W.T.; Horton, T.; Clough, T.J. Spatial and temporal variations in nitrogen export from a New Zealand pastoral catchment revealed by stream water nitrate isotopic composition. Water Resour. Res. 2016, 52, 2840–2854. [Google Scholar] [CrossRef]
- Parfitt, R.L.; Baisden, W.T.; Schipper, L.A.; Mackay, A.D. Nitrogen inputs and outputs for new zealand at national and regional scales: Past, present and future scenarios. J. R. Soc. N. Z. 2008, 38, 71–87. [Google Scholar] [CrossRef]
- Tanner, C.; Kadlec, R.; Gibbs, M.; Sukias, J.; Nguyen, M. Nitrogen processing gradients in subsurface-flow treatment wetlands—Influence of wastewater characteristics. Ecol. Eng. 2002, 18, 499–520. [Google Scholar] [CrossRef]
- Zierholz, C.; Prosser, I.P.; Fogarty, P.J.; Rustomji, P. In-stream wetlands and their significance for channel filling and the catchment sediment budget, Jugiong Creek, New South Wales. Geomorphology 2001, 38, 221–235. [Google Scholar] [CrossRef]
- Ackerman, J.R.; Peterson, E.W.; Van der Hoven, S.; Perry, W.L. Quantifying nutrient removal from groundwater seepage out of constructed wetlands receiving treated wastewater effluent. Environ. Earth Sci. 2015, 74, 1633–1645. [Google Scholar] [CrossRef]
- Maxwell, E.; Peterson, E.W.; O’Reilly, C.M. Enhanced Nitrate Reduction within a Constructed Wetland System: Nitrate Removal within Groundwater Flow. Wetlands 2017, 37, 413–422. [Google Scholar] [CrossRef]
- Brauer, N.; Maynard, J.J.; Dahlgren, R.A.; O’Geen, A.T. Fate of nitrate in seepage from a restored wetland receiving agricultural tailwater. Ecol. Eng. 2015, 81, 207–217. [Google Scholar] [CrossRef]
- Rutherford, J.C.; Nguyen, M.L. Nitrate removal in riparian wetlands: Interactions between surface flow and soils. J. Environ. Qual. 2004, 33, 1133–1143. [Google Scholar] [CrossRef] [PubMed]
- Whitmire, S.L.; Hamilton, S.K. Rapid Removal of Nitrate and Sulfate in Freshwater Wetland Sediments. J. Environ. Qual. 2005, 34, 2062–2071. [Google Scholar] [CrossRef] [PubMed]
- Burns, D.A.; Nguyen, L. Nitrate movement and removal along a shallow groundwater flow path in a riparian wetland within a sheep-grazed pastoral catchment: Results of a tracer study. N. Z. J. Mar. Freshw. Res. 2002, 36, 371–385. [Google Scholar] [CrossRef][Green Version]
- Mulholland, P.J.; Valett, H.M.; Webster, J.R.; Thomas, S.A.; Cooper, L.W.; Hamilton, S.K.; Peterson, B.J. Stream denitrification and total nitrate uptake rates measured using a field 15N tracer addition approach. Limnol. Oceanogr. 2004, 49, 809–820. [Google Scholar] [CrossRef]
- Malhi, S.S.; McGill, W.B.; Nyborg, M. Nitrate losses in soils: Effect of temperature, moisture and substrate concentration. Soil Biol. Biochem. 1990, 22, 733–737. [Google Scholar] [CrossRef]
- Addy, K.; Gold, A.; Nowicki, B.; McKenna, J.; Stolt, M.; Groffman, P. Denitrification capacity in a subterranean estuary below a Rhode Island fringing salt marsh. Estuaries 2005, 28, 896–908. [Google Scholar] [CrossRef]
- Schaefer, S.C.; Alber, M. Temperature controls a latitudinal gradient in the proportion of watershed nitrogen exported to coastal ecosystems. Biogeochemistry 2007, 85, 333–346. [Google Scholar] [CrossRef]
- Holtan-Hartwig, L.; Dörsch, P.; Bakken, L.R. Low temperature control of soil denitrifying communities: Kinetics of N2O production and reduction. Soil Biol. Biochem. 2002, 34, 1797–1806. [Google Scholar] [CrossRef]
- Tanner, C.; Kadlec, R. Influence of hydrological regime on wetland attenuation of diffuse agricultural nitrate losses. Ecol. Eng. 2013, 56, 79–88. [Google Scholar] [CrossRef]
- Hernandez, M.E.; Mitsch, W.J. Denitrification in created riverine wetlands: Influence of hydrology and season. Ecol. Eng. 2007, 30, 78–88. [Google Scholar] [CrossRef]
- Yates, C.N.; Varickanickal, J.; Cousins, S.; Wootton, B. Testing the ability to enhance nitrogen removal at cold temperatures with C. aquatilis in a horizontal subsurface flow wetland system. Ecol. Eng. 2016, 94, 344–351. [Google Scholar] [CrossRef]
- Van Kessel, C.; Clough, T.; van Groenigen, J.W. Dissolved Organic Nitrogen: An Overlooked Pathway of Nitrogen Loss from Agricultural Systems? J. Environ. Qual. 2009, 38, 393–401. [Google Scholar] [CrossRef] [PubMed]
- Vogt, E.; Braban, C.F.; Dragosits, U.; Durand, P.; Sutton, M.A.; Theobald, M.R.; Rees, R.M.; McDonald, C.; Murray, S.; Billett, M.F. Catchment land use effects on fluxes and concentrations of organic and inorganic nitrogen in streams. Agric. Ecosyst. Environ. 2015, 199, 320–332. [Google Scholar] [CrossRef]
- Ghani, A.; Müller, K.; Dodd, M.; Mackay, A. Dissolved organic matter leaching in some contrasting New Zealand pasture soils. Eur. J. Soil Sci. 2010, 61, 525–538. [Google Scholar] [CrossRef]
- Pellerin, B.A.; Wollheim, W.M.; Hopkinson, C.S.; McDowell, W.H.; Williams, M.R.; Vörösmarty, C.J.; Daley, M.L. Role of wetlands and developed land use on dissolved organic nitrogen concentrations and DON/TDN in northeastern U.S. rivers and streams. Limnol. Oceanogr. 2004, 49, 910–918. [Google Scholar] [CrossRef]
- Seitzinger, S.P.; Sanders, R.W.; Styles, R. Bioavailability of DON from natural and anthropogenic sources to estuarine plankton. Limnol. Oceanogr. 2002, 47, 353–366. [Google Scholar] [CrossRef]
- Wymore, A.S.; Rodríguez-Cardona, B.; McDowell, W.H. Direct response of dissolved organic nitrogen to nitrate availability in headwater streams. Biogeochemistry 2015, 126, 1–10. [Google Scholar] [CrossRef]
- Lipson, D.; Näsholm, T. The unexpected versatility of plants: Organic nitrogen use and availability in terrestrial ecosystems. Oecologia 2001, 128, 305–316. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, S.C.; Scholefi, D.; Pain, B. Nitrogen cycling in grazing systems. In Nitrogen Fertilization in the Environment; Bacon, P.E., Ed.; Marcel Dekker: New York, NY, USA, 1995. [Google Scholar]
| Wetland Area (m2) | Apparent Catchment Area * (m2) | Over 15° Slope Areas Draining to the Wetland (m2) | |
|---|---|---|---|
| Tank 1 | 56 | 23,710 | 3613 |
| Tank 2 | 191 | 4408 | 803 |
| Tank 3 | 173 | 14,397 | 1686 |
| Tank 4 | 409 | 4697 | 1021 |
| Tank 5 | 637 | 4341 | 1096 |
| Total | 1467 | 51,553 | 8218 |
| k20 | C* (mg/m3) | θ | Reference | |
|---|---|---|---|---|
| NH4-N | 5–86 | 0 | 1.049 | Kadlec and Wallace [35] |
| NOx-N | 5–168 | 0 | 1.106 | Kadlec [4] |
| TON | 5–62 | 20 | 1.017 | Wilcock [36] |
| TN | 4–40 | 200 | 1.056 | Kadlec and Wallace [35] |
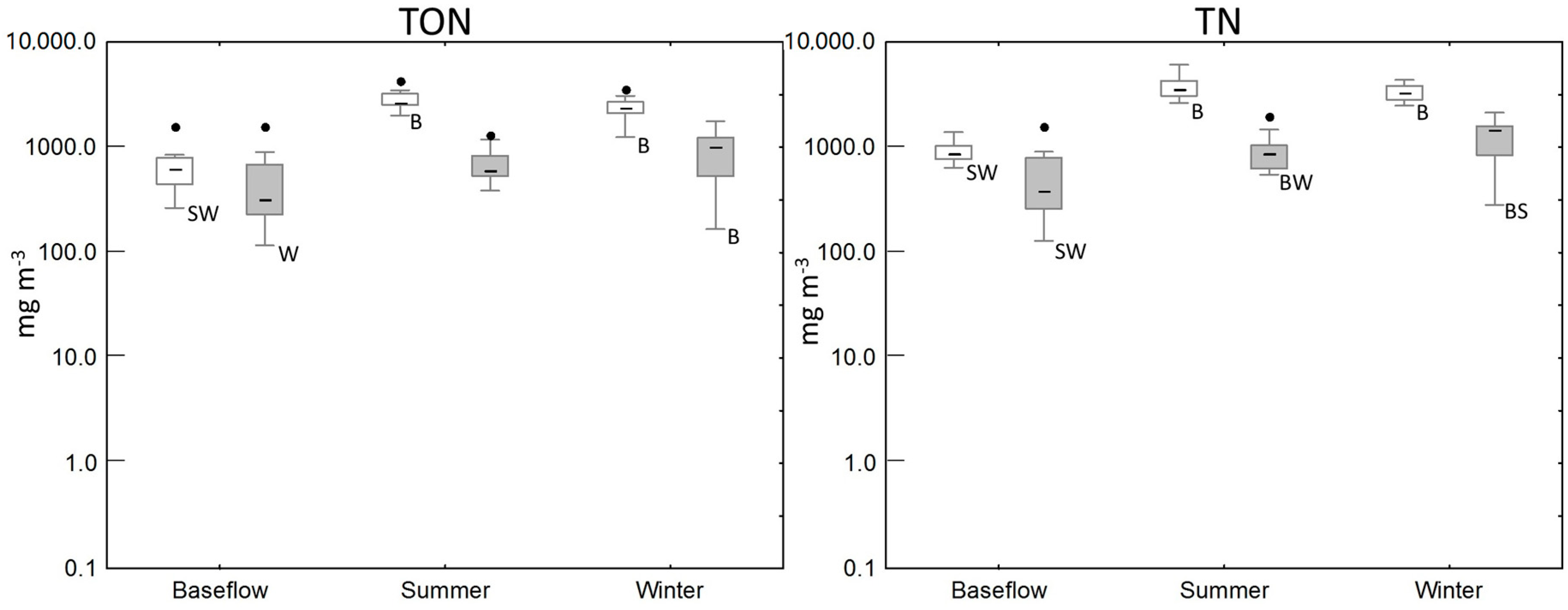
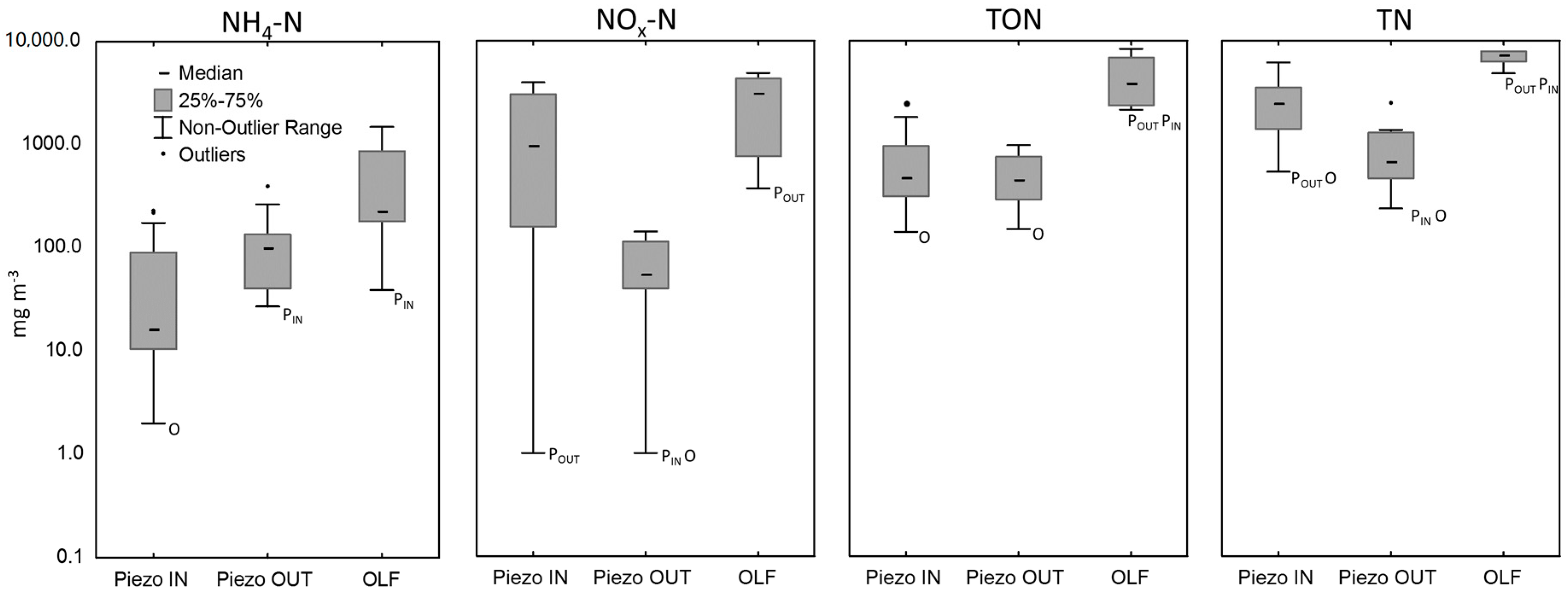
| Site | n | NH4-N (mg/m3) | NOx-N (mg/m3) | TON (mg/m3) | TN (mg/m3) |
|---|---|---|---|---|---|
| Piezometers adjacent to the wetland | 15 | 99 (27–389) | 55 (1–885) | 441 (148–3266) | 688 (235–3850) |
| Piezometers within the wetland | 44 | 17 (2–2440) | 956 (1–3930) | 461 (139–5927) | 2495 (533–10700) |
| Overland-flow (OLF) | 6 | 228 (39–1490) | 3165 (367–4860) | 3929 (2134–8352) | 7320 (4830–13,500) |
| Upper weir | |||||
| Baseflow | 11 | 46 (5–733) | 186 (4–923) | 628 (266–1591) | 880 (640–2510) |
| Summer/Autumn | 9 | 105 (55–487) | 934 (346–1330) | 2640 (2005–4263) | 3851 (2630–6080) |
| Winter/Spring | 36 | 65 (40–110) | 715 (447–1680) | 2383 (1247–3595) | 3245 (2490–4360) |
| Lower weir | |||||
| Baseflow | 15 | 14 (5–177) | 4 (1–52) | 322 (117–1594) | 381 (129–1600) |
| Summer/Autumn | 33 | 43 (12–537) | 28 (1–376) | 586 (387–4601) | 864 (550–4830) |
| Winter/Spring | 47 | 22 (8–67) | 280 (1–1450) | 1009 (167–1768) | 1490 (321–2130) |
| Variable | Baseflow | Summer Storms | Winter Storms | |||
|---|---|---|---|---|---|---|
| Z | p-Value | Z | p-Value | Z | p-Value | |
| NH4-N | 1.54 | 0.12 | 1.27 | 0.20 | 7.52 | 0.00 |
| NOx-N | 3.24 | 0.00 | 4.52 | 0.00 | 5.72 | 0.00 |
| TDN | 2.33 | 0.02 | 4.26 | 0.00 | 7.02 | 0.00 |
| TON | 1.57 | 0.12 | 4.28 | 0.00 | 7.32 | 0.00 |
| TN | 2.49 | 0.01 | 4.31 | 0.00 | 7.77 | 0.00 |
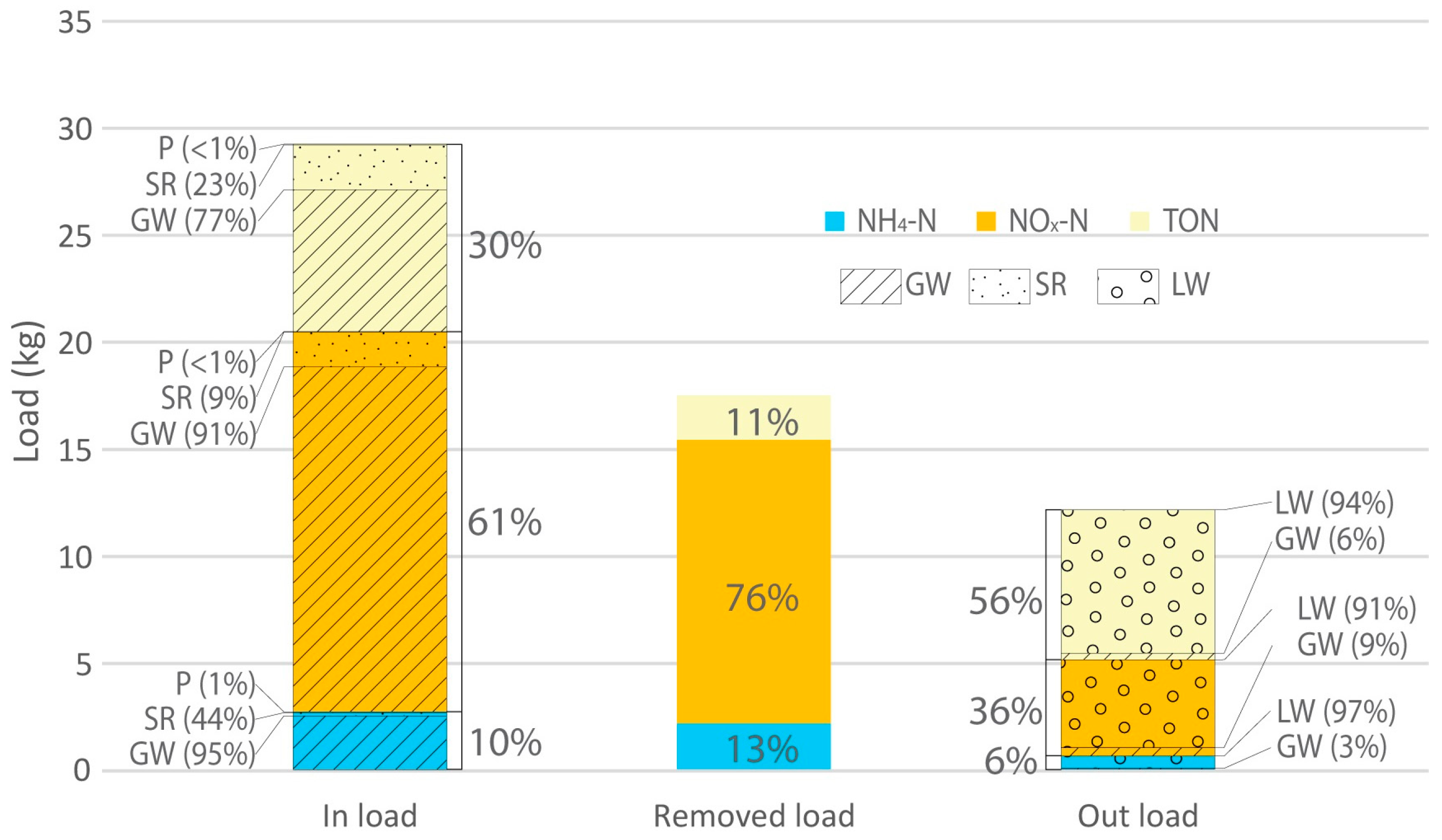
| Flow-Type | Daily Mass Loading Rate (mg/m2/day) | Daily Mass Removal Rate (mg/m2/day) | Performance (%) | |
|---|---|---|---|---|
| NH4-N | Winter/Spring storms | 49 | 21 | 44 |
| Summer/Autumn storms | 6 | 5 | 90 | |
| Baseflow | 4 | 1 | 78 | |
| All | 5 | 4 | 73 | |
| NO3-N | Winter/Spring storms | 730 | 492 | 67 |
| Summer/Autumn storms | 48 | 47 | 97 | |
| Baseflow | 21 | 16 | 80 | |
| All | 33 | 25 | 76 | |
| TON | Winter/Spring storms | 328 | 114 | 35 |
| Summer/Autumn storms | 38 | 17 | 44 | |
| Baseflow | 11 | 2.0 | 20 | |
| All | 16 | 4 | 26 | |
| TN | Winter/Spring storms | 1147 | 589 | 51 |
| Summer/Autumn storms | 95 | 71 | 75 | |
| Baseflow | 41 | 16 | 40 | |
| All | 60 | 35 | 57 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uuemaa, E.; Palliser, C.C.; Hughes, A.O.; Tanner, C.C. Effectiveness of a Natural Headwater Wetland for Reducing Agricultural Nitrogen Loads. Water 2018, 10, 287. https://doi.org/10.3390/w10030287
Uuemaa E, Palliser CC, Hughes AO, Tanner CC. Effectiveness of a Natural Headwater Wetland for Reducing Agricultural Nitrogen Loads. Water. 2018; 10(3):287. https://doi.org/10.3390/w10030287
Chicago/Turabian StyleUuemaa, Evelyn, Chris C. Palliser, Andrew O. Hughes, and Chris C. Tanner. 2018. "Effectiveness of a Natural Headwater Wetland for Reducing Agricultural Nitrogen Loads" Water 10, no. 3: 287. https://doi.org/10.3390/w10030287
APA StyleUuemaa, E., Palliser, C. C., Hughes, A. O., & Tanner, C. C. (2018). Effectiveness of a Natural Headwater Wetland for Reducing Agricultural Nitrogen Loads. Water, 10(3), 287. https://doi.org/10.3390/w10030287





