Uncertainty Analysis of a Two-Dimensional Hydraulic Model
Abstract
:1. Introduction
2. Methods
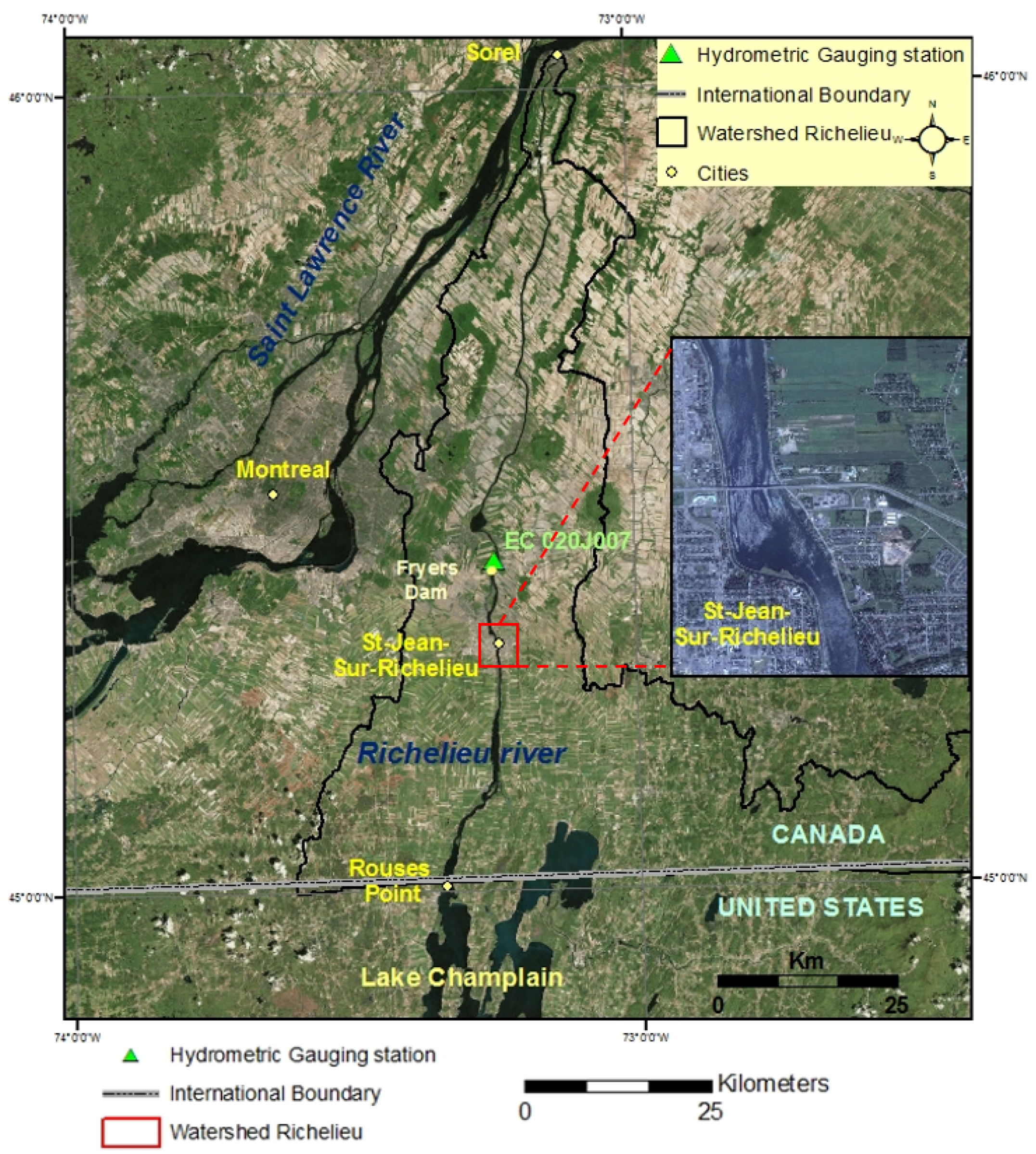
2.1. Study Area
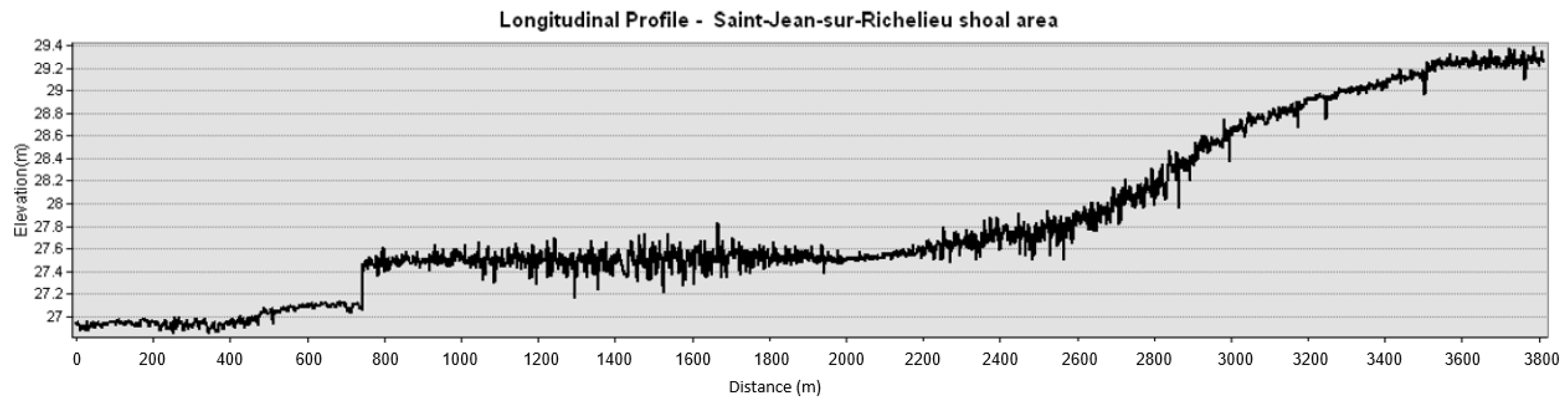
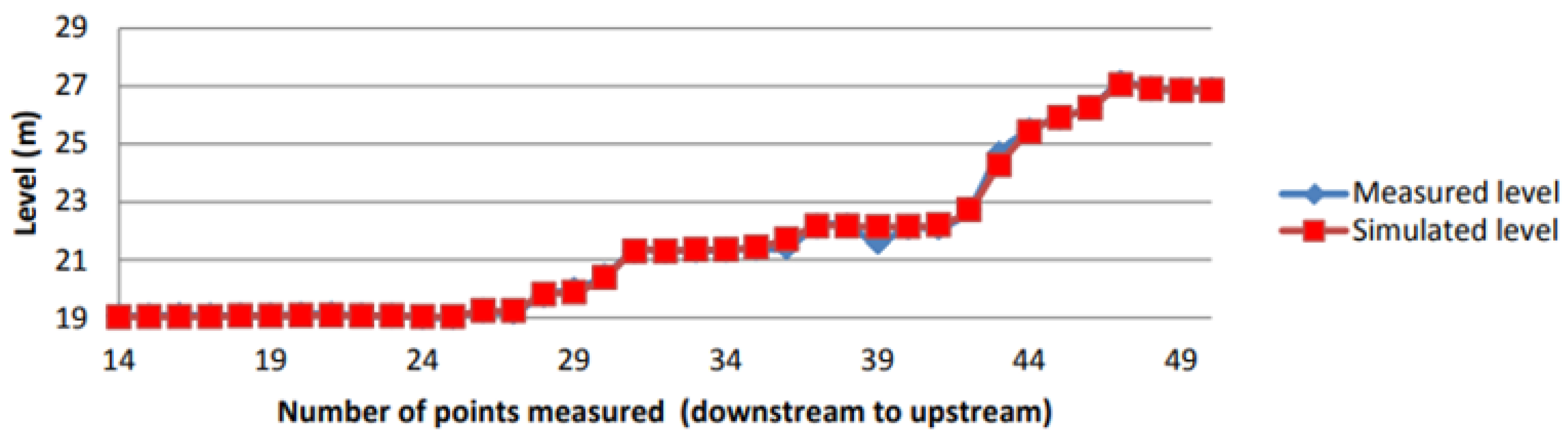
2.2. Hydraulic Model of the Richelieu River
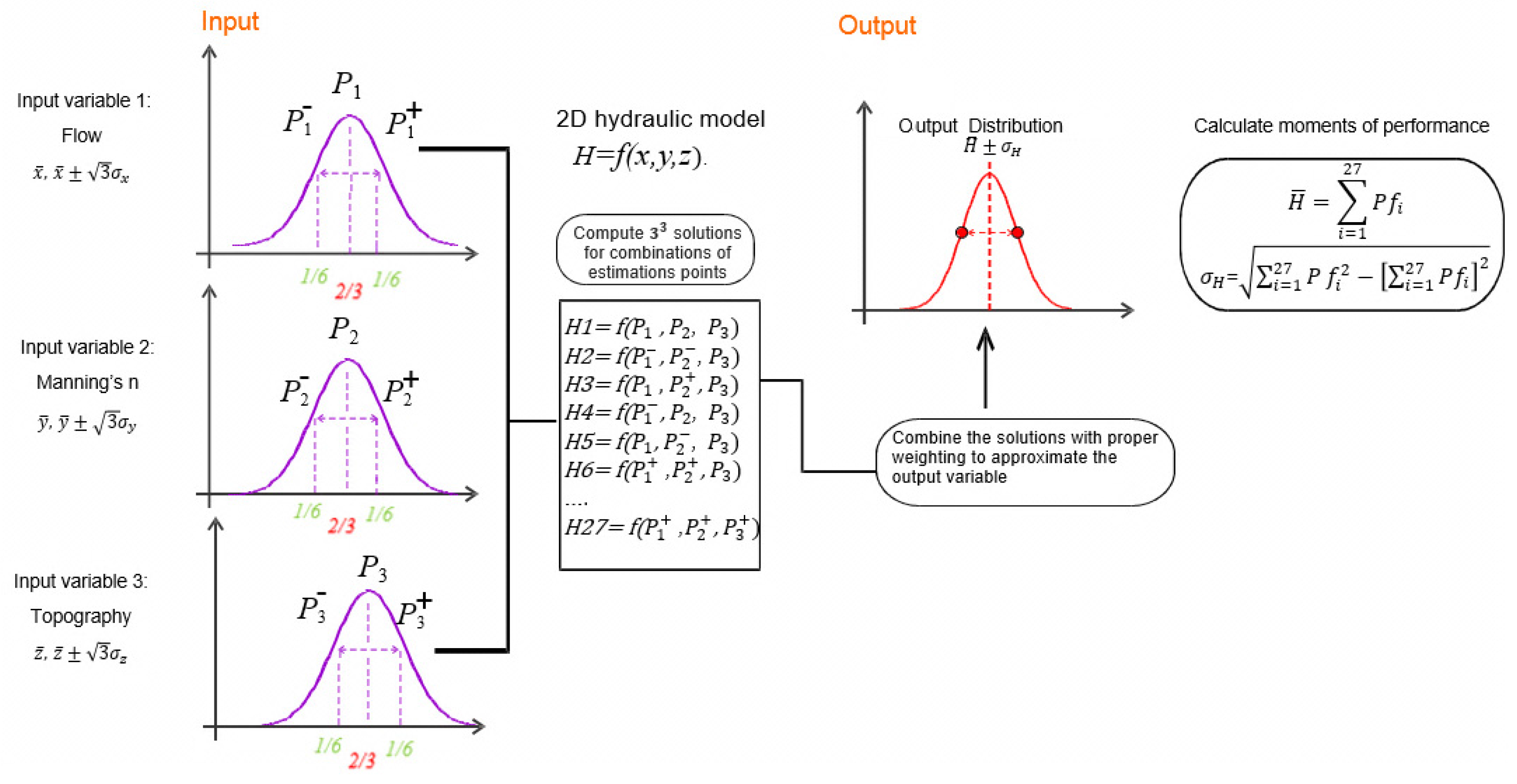
2.3. Point Estimate Method
3. Quantification of Uncertainty
3.1. Flow Rate
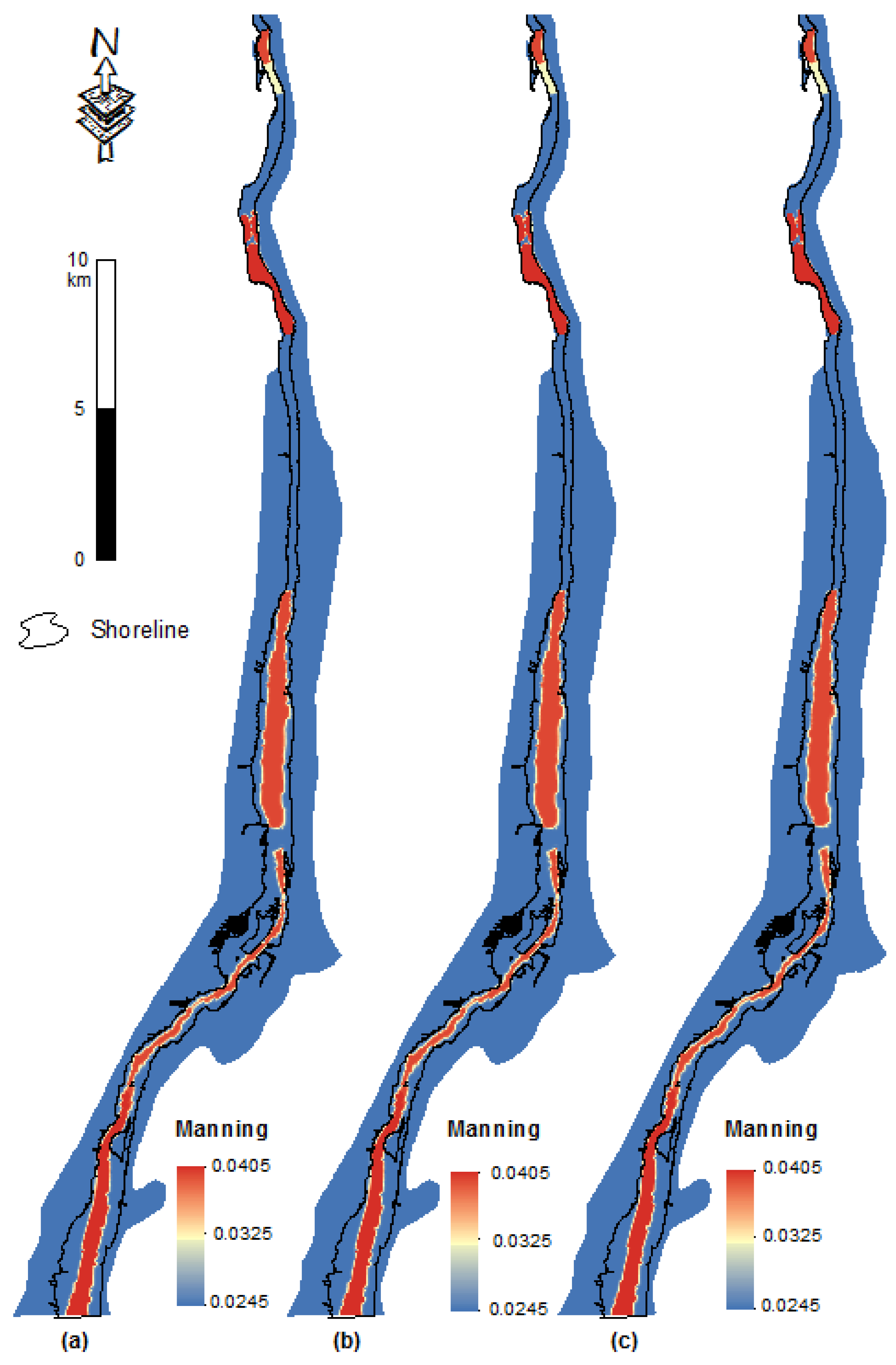
3.2. Manning’s n Coefficient
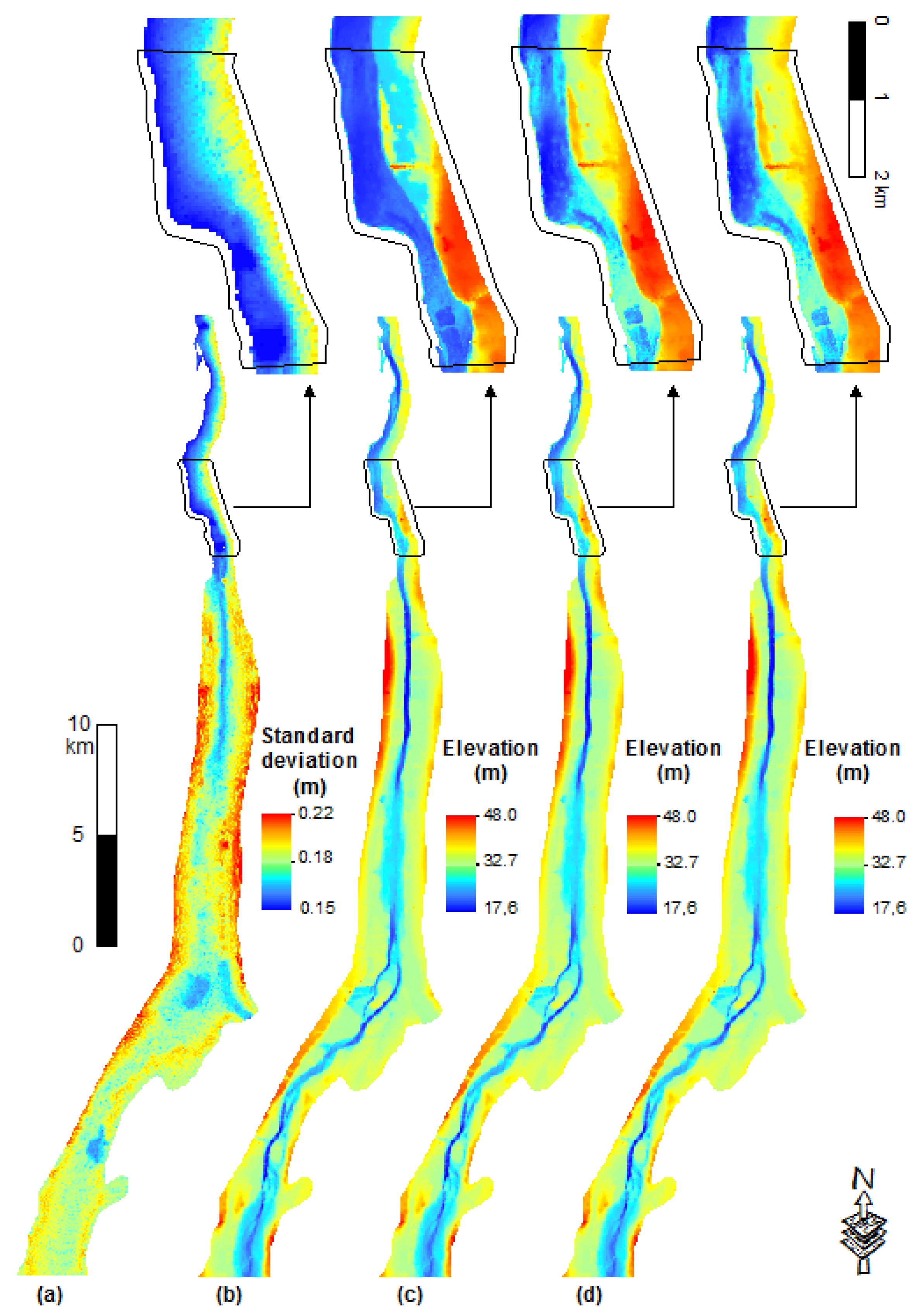
3.3. Topography
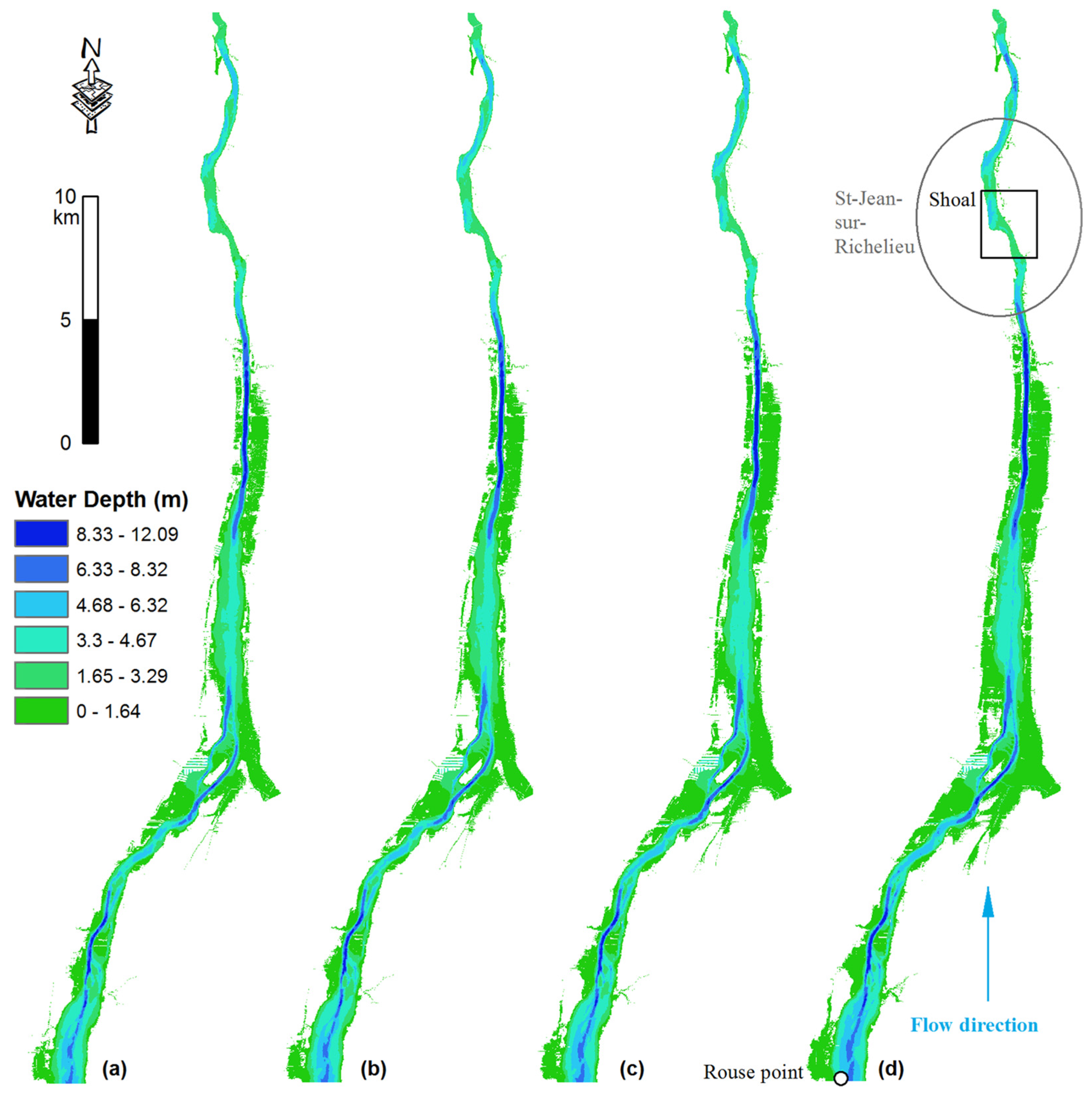
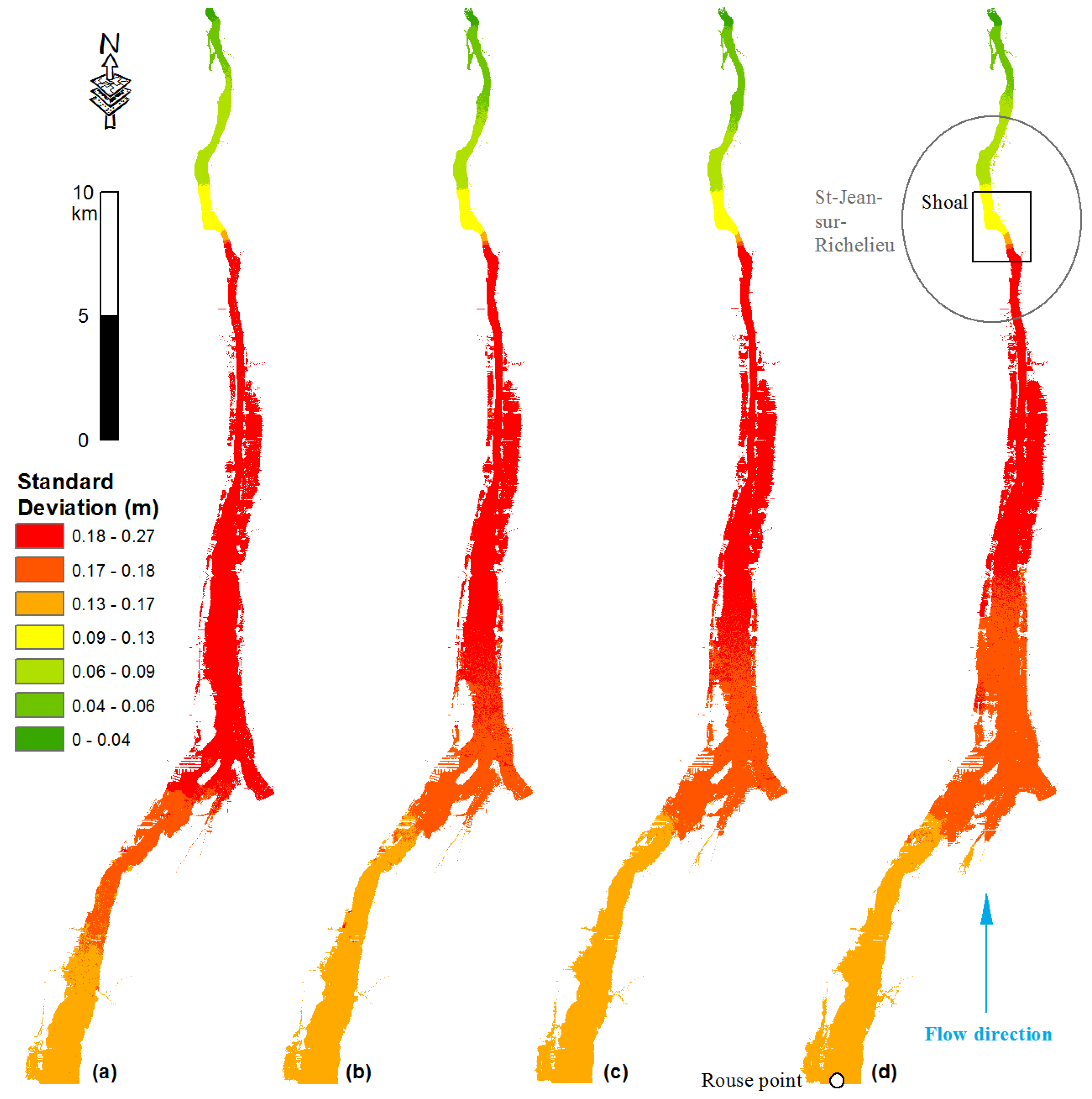
4. Uncertainty in the Model Output
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bates, P.D.; Pappenberger, F.; Romanowicz, R.J. Uncertainty in flood inundation modelling. In Applied Uncertainty Analysis for Flood Risk Management; Beven, K., Hall, J., Eds.; Imperial College Press: Singapore, 2014; pp. 232–269. [Google Scholar]
- Aronica, G.; Franza, F.; Bates, P.; Neal, J. Probabilistic evaluation of flood hazard in urban areas using monte carlo simulation. Hydrol. Processes 2012, 26, 3962–3972. [Google Scholar] [CrossRef]
- Fewtrell, T.; Bates, P.D.; Horritt, M.; Hunter, N. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Processes 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Uusitalo, L.; Lehikoinen, A.; Helle, I.; Myrberg, K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environ. Model. Softw. 2015, 63, 24–31. [Google Scholar] [CrossRef]
- Apel, H.; Aronica, G.; Kreibich, H.; Thieken, A. Flood risk analyses—How detailed do we need to be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- Aronica, G.; Hankin, B.; Beven, K. Uncertainty and equifinality in calibrating distributed roughness coefficients in a flood propagation model with limited data. Adv. Water Resour. 1998, 22, 349–365. [Google Scholar] [CrossRef]
- Hall, J.; Tarantola, S.; Bates, P.; Horritt, M. Distributed sensitivity analysis of flood inundation model calibration. J. Hydraul. Eng. 2005, 131, 117–126. [Google Scholar] [CrossRef]
- Horritt, M. Stochastic modelling of 1-d shallow water flows over uncertain topography. J. Comput. Phys. 2002, 180, 327–338. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in hec-ras using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Cimorelli, L.; Cozzolino, L.; Della Morte, R.; Pianese, D. An improved numerical scheme for the approximate solution of the parabolic wave model. J. Hydroinform. 2013, 15, 913–925. [Google Scholar] [CrossRef]
- Cimorelli, L.; Cozzolino, L.; Della Morte, R.; Pianese, D. Analytical solutions of the linearized parabolic wave accounting for downstream boundary condition and uniform lateral inflows. Adv. Water Resour. 2014, 63, 57–76. [Google Scholar] [CrossRef]
- Cimorelli, L.; Cozzolino, L.; Della Morte, R.; Pianese, D.; Singh, V.P. A new frequency domain analytical solution of a cascade of diffusive channels for flood routing. Water Resour. Res. 2015, 51, 2393–2411. [Google Scholar] [CrossRef]
- Cozzolino, L.; Cimorelli, L.; Covelli, C.; Della Morte, R.; Pianese, D. Boundary conditions in finite volume schemes for the solution of shallow-water equations: The non-submerged broad-crested weir. J. Hydroinform. 2014, 16, 1235–1249. [Google Scholar] [CrossRef]
- Cozzolino, L.; Cimorelli, L.; Covelli, C.; Morte, R.D.; Pianese, D. Novel numerical approach for 1d variable density shallow flows over uneven rigid and erodible beds. J. Hydraul. Eng. 2013, 140, 254–268. [Google Scholar] [CrossRef]
- Cozzolino, L.; Della Morte, R.; Cimorelli, L.; Covelli, C.; Pianese, D. A broad-crested weir boundary condition in finite volume shallow-water numerical models. Procedia Eng. 2014, 70, 353–362. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Lamb, R.; Blazkova, S.D. Uncertainty in flood frequency analysis. In Applied Uncertainty Analysis for Flood Risk Management; Imperial College Press: London, UK, 2014; pp. 153–197. [Google Scholar]
- Nachtnebel, H.-P.; Faber, R. Assessment and management of flood risks in austria. Struct. Infrastruct. Eng. 2009, 5, 333–339. [Google Scholar] [CrossRef]
- Di Baldassarre, G. Floods in a Changing Climate: Inundation Modelling; Cambridge University Press: Cambridge, UK, 2012; Volume 3. [Google Scholar]
- Stedinger, J.; Vogel, R.; Foufoula-Georgiou, E. Frequency Analysis of Extreme Events. In Handbook of Hydrology; Chapter 18; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Effects of Rating-Curve Uncertainty on the Calibration of Numerical Hydraulic Models; First IAHR European Congress: Edinburgo, UK, 2010. [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Aronica, G.; Beven, K. Bayesian updating of flood inundation likelihoods conditioned on flood extent data. Hydrol. Processes 2004, 18, 3347–3370. [Google Scholar] [CrossRef]
- Noack, M.; Yoeruek, A. Uncertainty in hydrodynamic-numerical modelling of flood areas. Hydrol. Wasserbewirtschaftung 2008, 52, 173–178. [Google Scholar]
- Hunter, N.; Bates, P.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S. Benchmarking 2d hydraulic models for urban flood simulations. Proc. Inst. Civ. Eng.: Water Manag. 2008, 161, 13–30. [Google Scholar]
- Wohl, E.E. Uncertainty in flood estimates associated with roughness coefficient. J. Hydraul. Eng. 1998, 124, 219–223. [Google Scholar] [CrossRef]
- Johnson, P.A. Uncertainty of hydraulic parameters. J. Hydraul. Eng. 1996, 122, 112–114. [Google Scholar] [CrossRef]
- Cesare, M. First-order analysis of open-channel flow. J. Hydraul. Eng. 1991, 117, 242–247. [Google Scholar] [CrossRef]
- Horritt, M. A linearized approach to flow resistance uncertainty in a 2-d finite volume model of flood flow. J. Hydrol. 2006, 316, 13–27. [Google Scholar] [CrossRef]
- Mays, L.W.; Tung, Y.-K. Hydrosystems Engineering and Management; Water Resources Publication: Glasgow, UK, 2002. [Google Scholar]
- Burnham, M.W.; Davis, D.W. Accuracy of Computed Water Surface Profiles; Hydrologic Engineering Center: Davis, CA, USA, 1986. [Google Scholar]
- Huang, Y.; Qin, X. Uncertainty analysis for flood inundation modelling with a random floodplain roughness field. Environ. Syst. Res. 2014, 3, 1. [Google Scholar] [CrossRef]
- Altarejos-García, L.; Escuder-Bueno, I.; Serrano-Lombillo, A.; de Membrillera-Ortuño, M.G. Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis. Struct. Saf. 2012, 36, 1–13. [Google Scholar] [CrossRef]
- Merwade, V.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in flood inundation mapping: Current issues and future directions. J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef]
- Hardy, R.; Bates, P.; Anderson, M. The importance of spatial resolution in hydraulic models for floodplain environments. J. Hydrol. 1999, 216, 124–136. [Google Scholar] [CrossRef]
- Monte, B.E.O.; Costa, D.D.; Chaves, M.B.; Magalhães, L.D.O.; Uvo, C.B. Hydrological and hydraulic modelling applied to the mapping of flood-prone areas. RBRH 2016, 21, 152–167. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Abdullah, A.; Vojinovic, Z.; Price, R.; Aziz, N. Improved methodology for processing raw lidar data to support urban flood modelling–accounting for elevated roads and bridges. J. Hydroinform. 2012, 14, 253–269. [Google Scholar] [CrossRef]
- Mercer, B. Dems created from airborne ifsar—An update. In Proceedings of the ISPRS Congress International Archives of Photogrammetry and Remote Sensing, Istanbul, Turkey, 12–23 July 2004. [Google Scholar]
- Goncalves, J.; Oliveira, A. Accuracy analysis of dems derived from aster imagery. Int. Arch. Photogramm. Remote Sens. 2004, 35, 168–172. [Google Scholar]
- Kornus, W.; Alamús, R.; Ruiz, A.; Talaya, J. Assessment of dem accuracy derived from spot-5 high resolution stereoscopic imagery. Int. Arch. Photogramm. Remote Sens. 2004, 35, 445–453. [Google Scholar]
- Liu, D.; Matthies, H. Uncertainty quantification with spectral approximations of a flood model. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2010; p. 012208. [Google Scholar]
- Alho, P.; Hyyppä, H.; Hyyppä, J. Consequence of dtm precision for flood hazard mapping: A case study in sw finland. Nordic J. Surv. Real Estate Res. 2009, 6, 21–39. [Google Scholar]
- Savage, J.T.S.; Bates, P.; Freer, J.; Neal, J.; Aronica, G. When does spatial resolution become spurious in probabilistic flood inundation predictions? Hydrol. Processes 2016, 30, 2014–2032. [Google Scholar] [CrossRef]
- Vojinovic, Z.; Seyoum, S.; Mwalwaka, J.; Price, R. Effects of model schematisation, geometry and parameter values on urban flood modelling. Water Sci. Technol. 2011, 63, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Vojinovic, Z.; Tutulic, D. On the use of 1d and coupled 1d-2d modelling approaches for assessment of flood damage in urban areas. Urban Water J. 2009, 6, 183–199. [Google Scholar] [CrossRef]
- Pappenberger, F.; Iorgulescu, I.; Beven, K.J. Sensitivity analysis based on regional splits and regression trees (sars-rt). Environ. Model. Softw. 2006, 21, 976–990. [Google Scholar] [CrossRef]
- Parodi, U.; Ferraris, L. Influence of stage discharge relationship on the annual maximum discharge statistics. Nat. Hazards 2004, 31, 603–611. [Google Scholar] [CrossRef]
- Montanari, A. What do we mean by ‘uncertainty’? The need for a consistent wording about uncertainty assessment in hydrology. Hydrol. Processes 2007, 21, 841–845. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Maskey, M.; Shrestha, D.L. Instance-based learning compared to other data-driven methods in hydrological forecasting. Hydrol. Processes 2008, 22, 275–287. [Google Scholar] [CrossRef]
- Tung, Y.-K. Uncertainty and reliability analysis in water resources engineering. J. Contemp. Water Res. Educ. 2011, 103, 13–21. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Processes 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. A limits of acceptability approach to model evaluation and uncertainty estimation in flood frequency estimation by continuous simulation: Skalka catchment, czech republic. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V.; Sorooshian, S.; Bastidas, L.A.; Shuttleworth, W.J. Constraining land surface and atmospheric parameters of a locally coupled model using observational data. J. Hydrometeorol. 2005, 6, 156–172. [Google Scholar] [CrossRef]
- Melching, C. An improved first-order reliability approach for assessing uncertainties in hydrologic modeling. J. Hydrol. 1992, 132, 157–177. [Google Scholar] [CrossRef]
- Kuczera, G.; Parent, E. Monte carlo assessment of parameter uncertainty in conceptual catchment models: The metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef]
- Maskey, S.; Guinot, V.; Price, R.K. Treatment of precipitation uncertainty in rainfall-runoff modelling: A fuzzy set approach. Adv. Water Resour. 2004, 27, 889–898. [Google Scholar] [CrossRef]
- Romanowicz, R.; Beven, K. Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J. Ignorance is bliss: Or seven reasons not to use uncertainty analysis. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P. How much physical complexity is needed to model flood inundation? Hydrol. Processes 2012, 26, 2264–2282. [Google Scholar] [CrossRef]
- Aronica, G.; Bates, P.; Horritt, M. Assessing the uncertainty in distributed model predictions using observed binary pattern information within glue. Hydrol. Processes 2002, 16, 2001–2016. [Google Scholar] [CrossRef]
- Van der Sluijs, J.P. Uncertainty and precaution in environmental management: Insights from the upem conference. Environ. Model. Softw. 2007, 22, 590–598. [Google Scholar] [CrossRef]
- Riboust, P.; Brissette, F. Climate change impacts and uncertainties on spring flooding of lake champlain and the richelieu river. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 776–793. [Google Scholar] [CrossRef]
- Secretan, Y. H2D2 Software. 2013. Available online: http://www.gre-ehn.ete.inrs.ca/H2D2 (accessed on 22 April 2014).
- Heniche, M.; Secretan, Y.; Boudreau, P.; Leclerc, M. A two-dimensional finite element drying-wetting shallow water model for rivers and estuaries. Adv. Water Resour. 2000, 23, 359–372. [Google Scholar] [CrossRef]
- Dhatt, G.; Touzot, G.; Lefrançois, E. Méthode des Éléments Finis; Hermès Lavoisier: Paris, France, 2005. [Google Scholar]
- Secretan, Y.; Matte, P. H2d2: Développement de Stratégies de Résolutions Non-Stationnaires et Non-Linéaires; Institut national de la recherche scientifique (INRS): Québec, Canada, 2010. [Google Scholar]
- Da Silva Holanda, P.; Blanco, C.J.C.; Mesquita, A.L.A.; Junior, A.C.P.B.; de Figueiredo, N.M.; Macêdo, E.N.; Secretan, Y. Assessment of hydrokinetic energy resources downstream of hydropower plants. Renew. Energy 2017, 101, 1203–1214. [Google Scholar] [CrossRef]
- Holanda, P.D.S.; Blanco, C.J.C.; Cruz, D.O.D.A.; Lopes, D.F.; Barp, A.R.B.; Secretan, Y. Hydrodynamic modeling and morphological analysis of lake gua preta: One of the water sources of belém-pa-brazil. J. Braz. Soc. Mech. Sci. Eng. 2011, 33, 117–124. [Google Scholar] [CrossRef]
- Boudreau, P.; Cantin, J.-F.; Bouchard, A.; Champoux, O.; Fortin, P.; Fiset, J.-M.; Fortin, N.; Thérien, J.; Morin, Groupe de travail technique international du lac Champlain et de la rivière Richelieu. Création d’un Modèle Hydraulique 2d de la Rivière Richelieu Entre Rouses Point et sorel (tâche 2-3); Environnement Canada: Gatineau, QC, Canada, 2015.
- Rosenblueth, E. Point estimates for probability moments. Proc. Natl. Acad. Sci. USA 1975, 72, 3812–3814. [Google Scholar] [CrossRef] [PubMed]
- Che-Hao, C.; Yeou-Koung, T.; Jinn-Chuang, Y. Evaluation of probability point estimate methods. Appl. Math. Model. 1995, 19, 95–105. [Google Scholar] [CrossRef]
- Harr, M.E. Probabilistic estimates for multivariate analyses. Appl. Math. Model. 1989, 13, 313–318. [Google Scholar] [CrossRef]
- Christian, J.T.; Baecher, G.B. Point-estimate method as numerical quadrature. J. Geotech. Geoenviron. Eng. 1999, 125, 779–786. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Tata McGraw-Hill Education: New York, NY, USA, 1988. [Google Scholar]
- Pukelsheim, F. The three sigma rule. Am. Stat. 1994, 48, 88–91. [Google Scholar]

| Preprocessing | Processing | Postprocessing |
|---|---|---|
| PEM approach sampling | H2D2 model | Propagation of uncertainty |
 | ||
| Number of Node (N) | Coordinate | Weights |
|---|---|---|
| 0 | 0 | 1 |
| 1 | −1,1 | |
| 2 |
| Case | Topography | Manning’s | Flow Rate | Weight |
|---|---|---|---|---|
| Case H1 | Min | Min | Min | |
| Case H2 | Min | Min | Mean | |
| Case H3 | Min | Min | Max | |
| Case H4 | Min | Mean | Min | |
| Case H5 | Min | Mean | Mean | |
| Case H6 | Min | Mean | Max | |
| Case H7 | Min | Max | Min | |
| Case H8 | Min | Max | Mean | |
| Case H9 | Min | Max | Max | |
| Case H10 | Mean | Min | Min | |
| Case H11 | Mean | Min | Mean | |
| Case H12 | Mean | Min | Max | |
| Case H13 | Mean | Mean | Min | |
| Case H14 | Mean | Mean | Mean | |
| Case H15 | Mean | Mean | Max | |
| Case H16 | Mean | Max | Min | |
| Case H17 | Mean | Max | Mean | |
| Case H18 | Mean | Max | Max | |
| Case H19 | Max | Min | Min | |
| Case H20 | Max | Min | Mean | |
| Case H21 | Max | Min | Max | |
| Case H22 | Max | Mean | Min | |
| Case H23 | Max | Mean | Mean | |
| Case H24 | Max | Mean | Max | |
| Case H25 | Max | Max | Min | |
| Case H26 | Max | Max | Mean | |
| Case H27 | Max | Max | Max |
| 759 | 39.4 | 690.75 | 827.24 |
| 824 | 36 | 761.64 | 886.35 |
| 936 | 33.7 | 877.62 | 994.37 |
| 1113 | 39.4 | 1044.75 | 1181.24 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oubennaceur, K.; Chokmani, K.; Nastev, M.; Tanguy, M.; Raymond, S. Uncertainty Analysis of a Two-Dimensional Hydraulic Model. Water 2018, 10, 272. https://doi.org/10.3390/w10030272
Oubennaceur K, Chokmani K, Nastev M, Tanguy M, Raymond S. Uncertainty Analysis of a Two-Dimensional Hydraulic Model. Water. 2018; 10(3):272. https://doi.org/10.3390/w10030272
Chicago/Turabian StyleOubennaceur, Khalid, Karem Chokmani, Miroslav Nastev, Marion Tanguy, and Sebastien Raymond. 2018. "Uncertainty Analysis of a Two-Dimensional Hydraulic Model" Water 10, no. 3: 272. https://doi.org/10.3390/w10030272
APA StyleOubennaceur, K., Chokmani, K., Nastev, M., Tanguy, M., & Raymond, S. (2018). Uncertainty Analysis of a Two-Dimensional Hydraulic Model. Water, 10(3), 272. https://doi.org/10.3390/w10030272







