Improving Stochastic Modelling of Daily Rainfall Using the ENSO Index: Model Development and Application in Chile
Abstract
1. Introduction
2. Materials and Methods
2.1. Meteorological Stations and Climatic Data
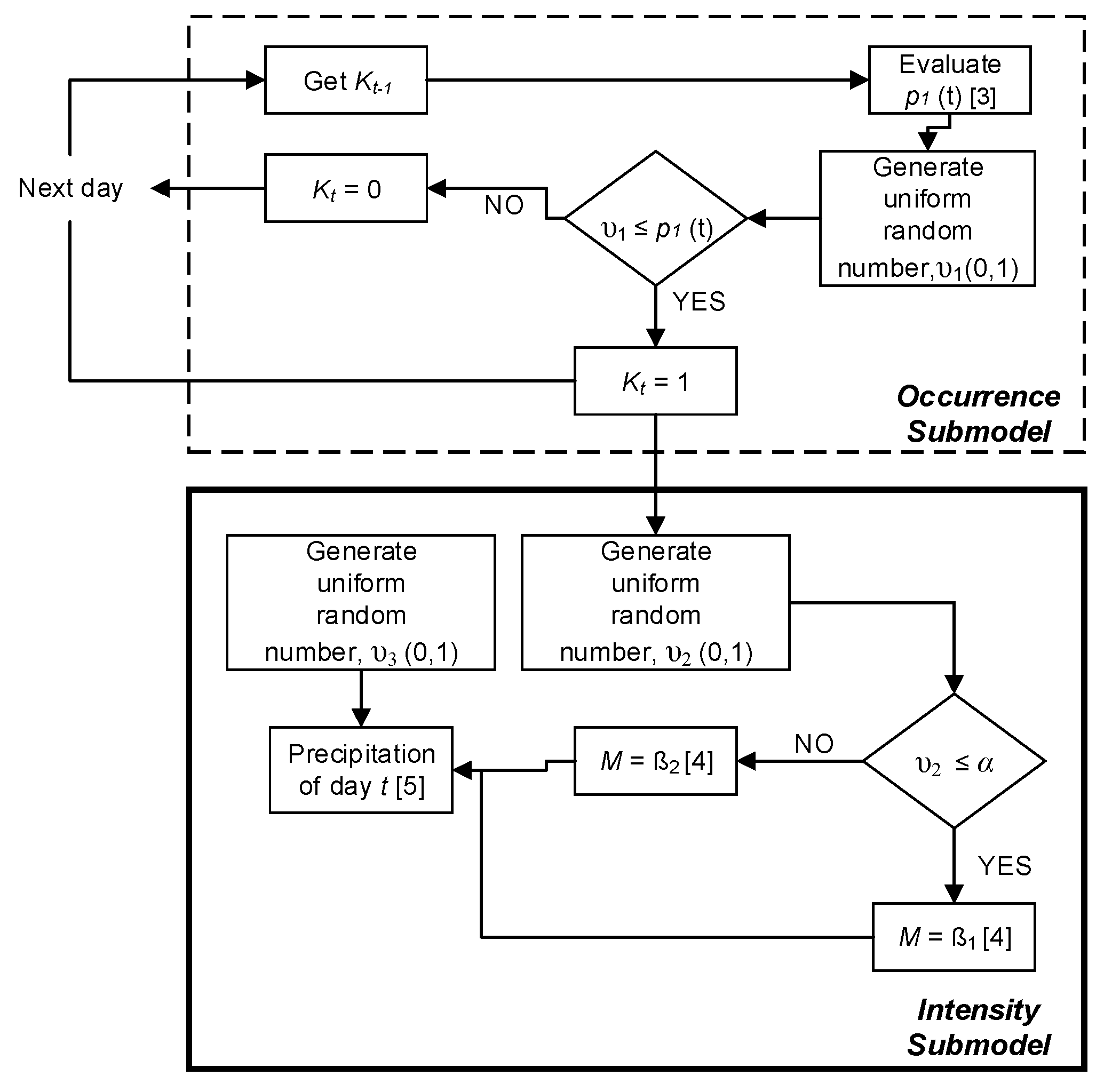
2.2. Precipitation Occurrence Submodel
2.3. Precipitation Intensity Submodel
3. Results
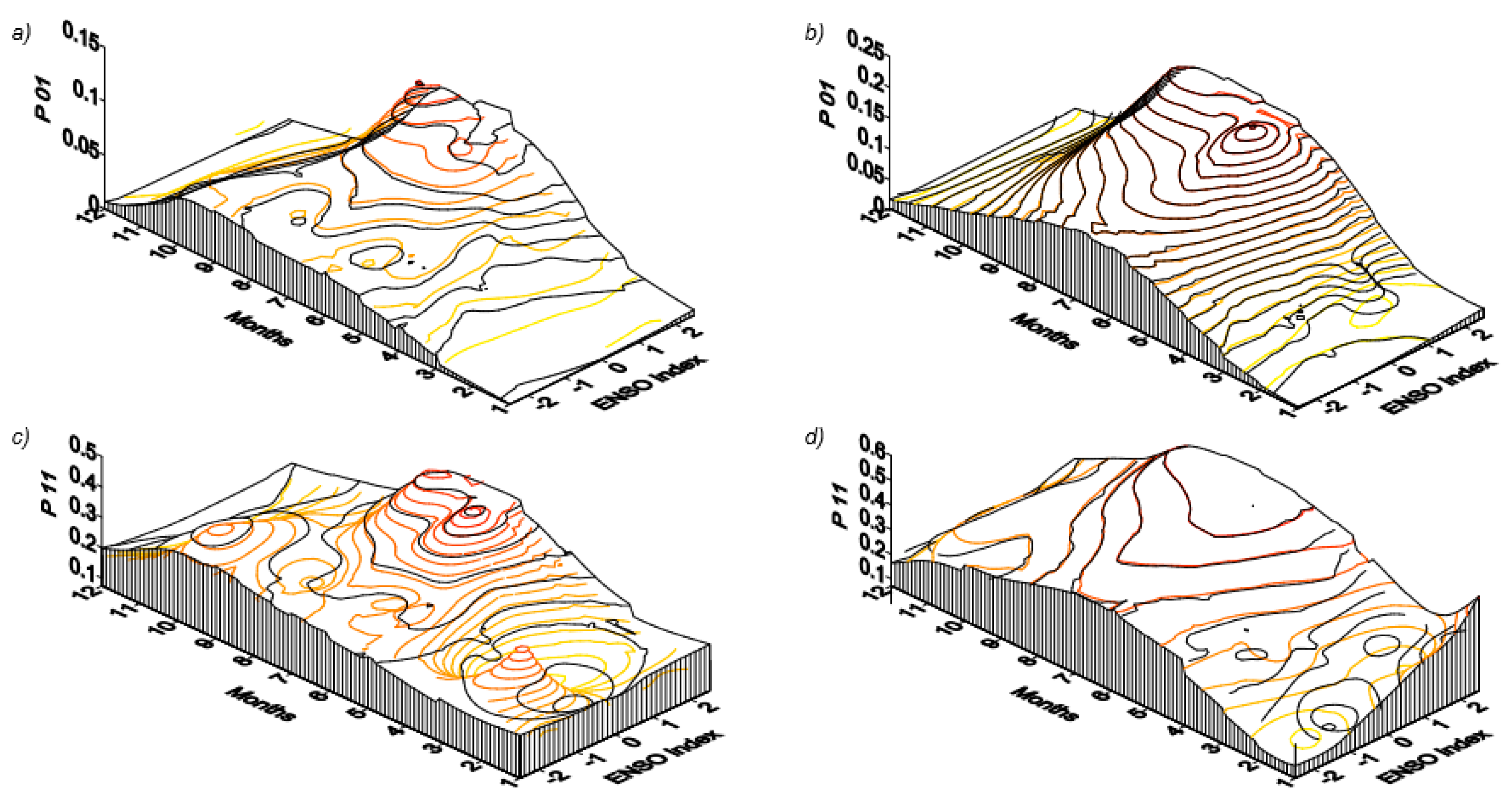
3.1. Precipitation Occurrence
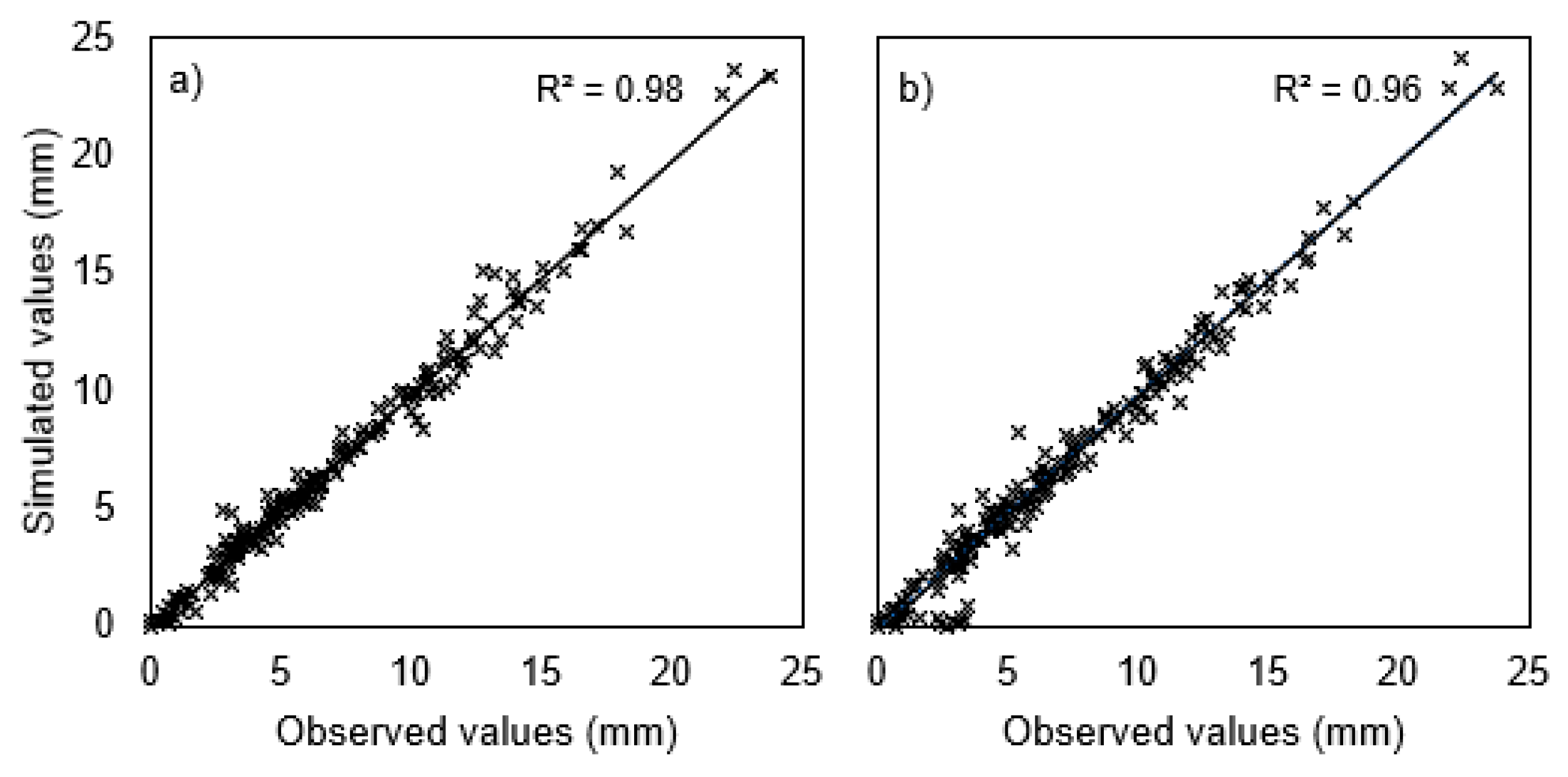
3.2. Precipitation Intensity
3.2.1. Annual Precipitation
3.2.2. Monthly Precipitation
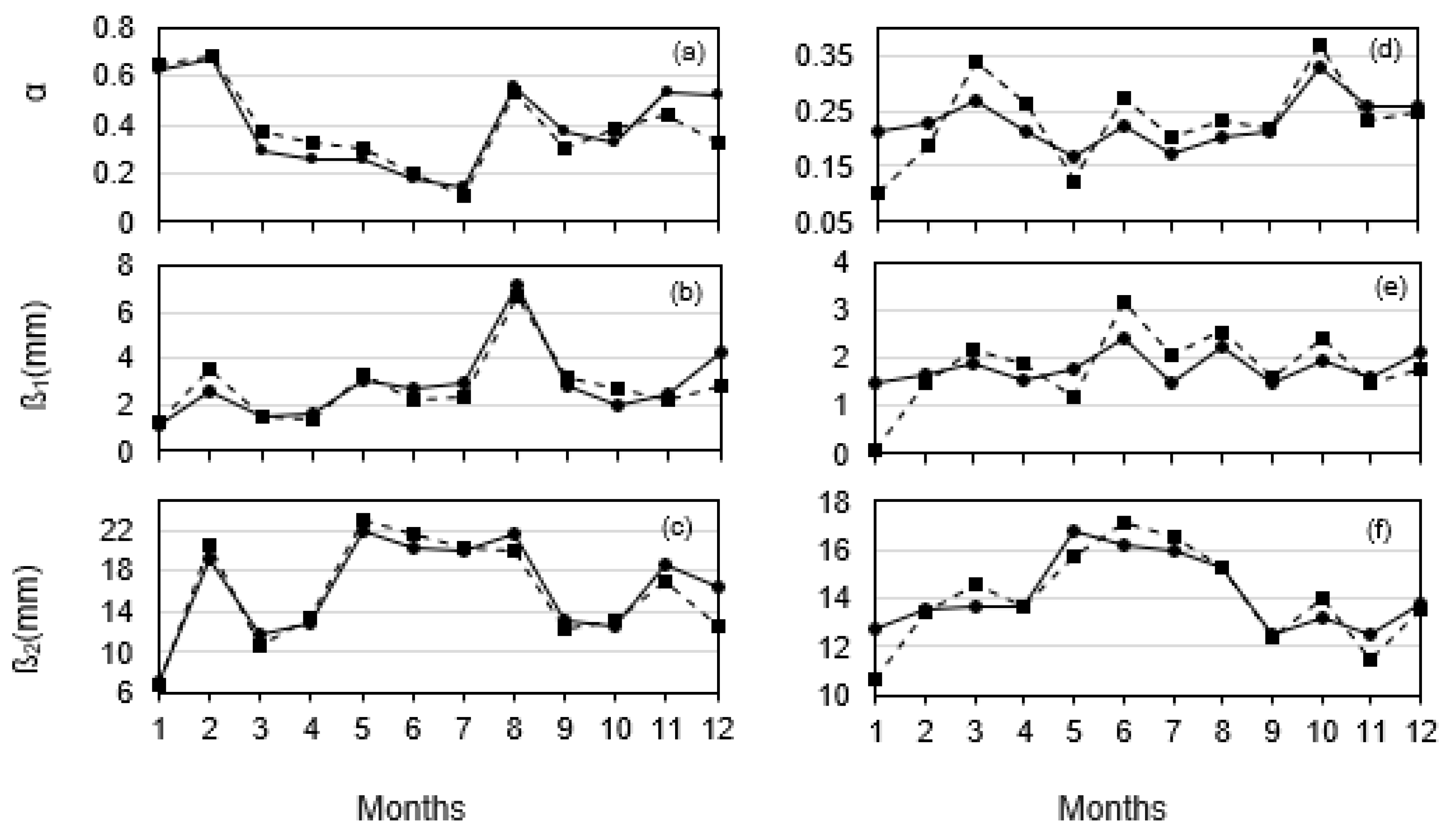
3.2.3. Mixed Exponential Distribution Parameters
3.2.4. Interannual Variability
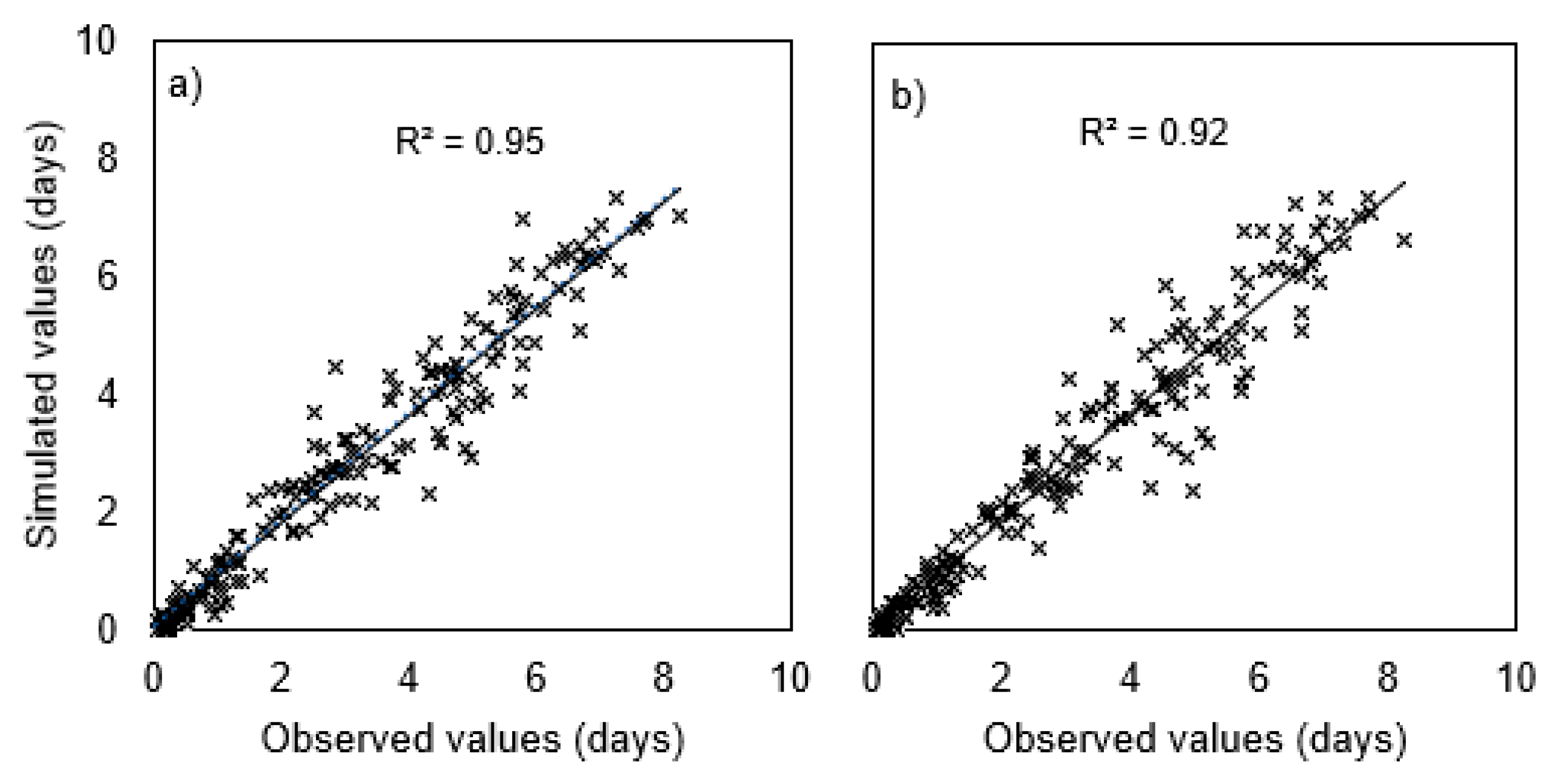
3.2.5. Wet and Dry Spell Durations
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| WGs | Weather Generators |
| WGEN | Weather Generate by Richardson and Wright |
| GLM | Generalized Lineal Model |
| ENSO index | Monthly Sea Surface Temperature Anomalies of the Region 3.4 of El Niño-Southern Oscillation |
| CLIGEN | CLImate GENerator |
References
- Richardson, C.W.; Wright, D.A. WGEN: A Model for Generating Daily Weather Variables; U.S. Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1984.
- Ebrahimpour, M.; Ghahreman, N.; Orang, M. Assessment of climate change impacts on reference evapotranspiration and simulation of daily weather data using SIMETAW. J. Irrig. Drain. Eng. 2013, 140, 04013012. [Google Scholar] [CrossRef]
- Graae, B.J.; De Frenne, P.; Kolb, A.; Brunet, J.; Chabrerie, O.; Verheyen, K.; Pepin, N.; Heinken, T.; Zobel, M.; Shevtsova, A. On the use of weather data in ecological studies along altitudinal and latitudinal gradients. Oikos 2012, 121, 3–19. [Google Scholar] [CrossRef]
- Gleason, M.L.; Duttweiler, K.B.; Batzer, J.C.; Taylor, S.E.; Sentelhas, P.C.; Monteiro, J.E.B.A.; Gillespie, T.J. Obtaining weather data for input to crop disease-warning systems: Leaf wetness duration as a case study. Sci. Agric. 2008, 65, 76–87. [Google Scholar] [CrossRef]
- Strandman, H.; Väisänen, H.; Kellomäki, S. A procedure for generating synthetic weather records in conjunction of climatic scenario for modelling of ecological impacts of changing climate in boreal conditions. Ecol. Model. 1993, 70, 195–220. [Google Scholar] [CrossRef]
- Wilks, D.S.; Wilby, R.L. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Richardson, C.W. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Sharpley, A.N.; Williams, J.R. EPIC-Erosin/Productivity Impact Calculator: 1. Model Documentation; USDA: Washington, DC, USA, 1990.
- Nicks, A.D.; Lane, L.J.; Gander, G.A. Weather Generator. In USDA-Water Erosion Prediction Project: Hillslope Profile Model Documentation; Report; NSERL: West Lafayette, IN, USA, 1995. [Google Scholar]
- Lobo, G.P.; Frankenberger, J.R.; Flanagan, D.C.; Bonilla, C.A. Evaluation and improvement of the CLIGEN model for storm and rainfall erosivity generation in Central Chile. Catena 2015, 127, 206–213. [Google Scholar] [CrossRef]
- Racsko, P.; Szeidl, L.; Semenov, M. A serial approach to local stochastic weather models. Ecol. Model. 1991, 57, 27–41. [Google Scholar] [CrossRef]
- Semenov, M.A.; Barrow, E.M. Use of a stochastic weather generator in the development of climate change scenarios. Clim. Chang. 1997, 35, 397–414. [Google Scholar] [CrossRef]
- Semenov, M.A.; Barrow, E.M. LARS-WG: A Stochastic Weather Generator for Use in Climate Impact Studies. 2002. Available online: http://resources.rothamsted.ac.uk/sites/default/files/groups/mas-models/download/LARS-WG-Manual.pdf (accessed on 1 February 2018).
- McKague, K.; Rudra, R.; Ogilvie, J. CLIMGEN-A Convenient Weather Generation tool for Canadian Climate Stations. In Proceedings of the Meeting of the CSAE/SCGR Canadian Society for Engineering in Agricultural Food and Biological Systems, Montreal, QC, Canada, 6–9 July 2003; pp. 6–9. [Google Scholar]
- Chen, J.; Brissette, F.P.; Leconte, R. A daily stochastic weather generator for preserving low-frequency of climate variability. J. Hydrol. 2010, 388, 480–490. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. WeaGETS—A Matlab-based daily scale weather generator for generating precipitation and temperature. Procedia Environ. Sci. 2012, 13, 2222–2235. [Google Scholar] [CrossRef]
- Dubrovský, M.; Buchtele, J.; Žalud, Z. High-frequency and low-frequency variability in stochastic daily weather generator and its effect on agricultural and hydrologic modelling. Clim. Chang. 2004, 63, 145–179. [Google Scholar] [CrossRef]
- Wetterhall, F.; Bárdossy, A.; Chen, D.; Halldin, S.; Xu, C. Statistical downscaling of daily precipitation over Sweden using GCM output. Theor. Appl. Climatol. 2009, 96, 95. [Google Scholar] [CrossRef]
- Bardossy, A.; Plate, E.J. Space-time model for daily rainfall using atmospheric circulation patterns. Water Resour. Res. 1992, 28, 1247–1259. [Google Scholar] [CrossRef]
- Pickering, N.B.; Hansen, J.W.; Jones, J.W.; Wells, C.M.; Chan, V.K.; Godwin, D.C. WeatherMan: A utility for managing and generating daily weather data. Agron. J. 1994, 86, 332–337. [Google Scholar] [CrossRef]
- Jones, P.G.; Thornton, P.K. MarkSim: Software to generate daily weather data for Latin America and Africa. Agron. J. 2000, 92, 445–453. [Google Scholar] [CrossRef]
- Qian, B.; Gameda, S.; Hayhoe, H.; De Jong, R.; Bootsma, A. Comparison of LARS-WG and AAFC-WG stochastic weather generators for diverse Canadian climates. Clim. Res. 2004, 26, 175–191. [Google Scholar] [CrossRef]
- Qian, B.; Gameda, S.; Hayhoe, H. Performance of stochastic weather generators LARS-WG and AAFC-WG for reproducing daily extremes of diverse Canadian climates. Clim. Res. 2008, 37, 17–33. [Google Scholar] [CrossRef]
- Mavromatis, T.; Hansen, J.W. Interannual variability characteristics and simulated crop response of four stochastic weather generators. Agric. For. Meteorol. 2001, 109, 283–296. [Google Scholar] [CrossRef]
- Gaur, A.; Simonovic, S.P. Towards reducing climate change impact assessment process uncertainty. Environ. Process. 2015, 2, 275–290. [Google Scholar] [CrossRef]
- King, L.M.; McLeod, A.I.; Simonovic, S.P. Simulation of historical temperatures using a multi-site, multivariate block resampling algorithm with perturbation. Hydrol. Process. 2014, 28, 905–912. [Google Scholar] [CrossRef]
- King, L.M.; McLeod, A.I.; Simonovic, S.P. Improved weather generator algorithm for multisite simulation of precipitation and temperature. J. Am. Water Resour. Assoc. 2015, 51, 1305–1320. [Google Scholar] [CrossRef]
- Jones, P.D.; Kilsby, C.G.; Harpham, C.; Glenis, V.; Burton, A. UK Climate Projections Science Report: Projections of Future Daily Climate for the UK from the Weather Generator; University of Newcastle: Newcastle, UK, 2009. [Google Scholar]
- Christierson, B.V.; Vidal, J.-P.; Wade, S.D. Using UKCP09 probabilistic climate information for UK water resource planning. J. Hydrol. 2012, 424, 48–67. [Google Scholar] [CrossRef]
- Wan, H.; Zhang, X.; Barrow, E.M. Stochastic modelling of daily precipitation for Canada. Atmos. Ocean 2005, 43, 23–32. [Google Scholar] [CrossRef]
- Taulis, M.E.; Milke, M.W. Estimation of WGEN weather generation parameters in arid climates. Ecol. Model. 2005, 184, 177–191. [Google Scholar] [CrossRef]
- Wilks, D.S. Extending logistic regression to provide full-probability-distribution MOS forecasts. Meteorol. Appl. 2009, 16, 361–368. [Google Scholar] [CrossRef]
- Stern, R.D.; Coe, R. A model fitting analysis of daily rainfall data. J. R. Stat. Soc. Ser. A Gen. 1984, 147, 1–34. [Google Scholar] [CrossRef]
- Yang, C.; Chandler, R.E.; Isham, V.S.; Wheater, H.S. Spatial-temporal rainfall simulation using generalized linear models. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Chandler, R.E. On the use of generalized linear models for interpreting climate variability. Environmetrics 2005, 16, 699–715. [Google Scholar] [CrossRef]
- Verdin, A.; Rajagopalan, B.; Kleiber, W.; Katz, R.W. Coupled stochastic weather generation using spatial and generalized linear models. Stoch. Environ. Res. Risk Assess. 2015, 29, 347–356. [Google Scholar] [CrossRef]
- Furrer, E.M.; Katz, R.W. Improving the simulation of extreme precipitation events by stochastic weather generators. Water Resour. Res. 2008, 44, 76. [Google Scholar] [CrossRef]
- Kim, Y.; Katz, R.W.; Rajagopalan, B.; Podestá, G.P.; Furrer, E.M. Reducing overdispersion in stochastic weather generators using a generalized linear modeling approach. Clim. Res. 2012, 53, 13–24. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B. Overdispersion phenomenon in stochastic modeling of precipitation. J. Clim. 1998, 11, 591–601. [Google Scholar] [CrossRef]
- Walker, G.T. Correlations in seasonal variations of weather. I. A further study of world weather. Mem. Indian Meteorol. Dep. 1924, 24, 275–332. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. Quantifying southern oscillation-precipitation relationships. J. Clim. 1996, 9, 1043–1059. [Google Scholar] [CrossRef]
- Kane, R.P. Rainfall extremes in some selected parts of Central and South America: ENSO and other relationships reexamined. Int. J. Climatol. 1999, 19, 423–455. [Google Scholar] [CrossRef]
- Meza, F.J. Recent trends and ENSO influence on droughts in Northern Chile: An application of the Standardized Precipitation Evapotranspiration Index. Weather Clim. Extremes 2013, 1, 51–58. [Google Scholar] [CrossRef]
- Montecinos, A.; Aceituno, P. Seasonality of the ENSO-related rainfall variability in central Chile and associated circulation anomalies. J. Clim. 2003, 16, 281–296. [Google Scholar] [CrossRef]
- Aceituno, P.; Fuenzalida, H.; Rosenblüth, B. Climate along the extratropical west coast of South America. In Earth Systems Responses Global Change; Mooney, H.A., Fuentes, E.R., Kronb, B.I., Eds.; Academic Press: San Diego, CA, USA, 1993; pp. 61–69. [Google Scholar]
- Quintana, J.; Aceituno, P. Trends and interdecadal variability of rainfall in Chile. In Proceedings of the 8 ICSHMO, Foz do Iguacu, Brazil, 24–28 April 2006; pp. 24–28. [Google Scholar]
- Masiokas, M.H.; Villalba, R.; Luckman, B.H.; Le Quesne, C.; Aravena, J.C. Snowpack variations in the central Andes of Argentina and Chile, 1951–2005: Large-scale atmospheric influences and implications for water resources in the region. J. Clim. 2006, 19, 6334–6352. [Google Scholar] [CrossRef]
- Sánchez, A.; Morales, R. Las Regiones de Chile: Espacio Físico y Humano-Económico; Editorial Universitaria: Santiago, Chile, 1993. [Google Scholar]
- National Oceanic and Atmospheric Administration. Available online: http://www.esrl.noaa.gov/psd/data/climateindices/list/ (accessed on 24 January 2017).
- Furrer, E.M.; Katz, R.W. Generalized linear modeling approach to stochastic weather generators. Clim. Res. 2007, 34, 129–144. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100, ISBN 0-12-385022-3. [Google Scholar]
- Akaike, H. Factor analysis and AIC. Psychometrika 1987, 52, 317–332. [Google Scholar] [CrossRef]
- Heidke, P. Berechnung des Erfolges und der Güte der Windstärkevorhersagen im Sturmwarnungsdienst. Geogr. Ann. 1926, 8, 301–349. [Google Scholar]
- Breinl, K.; Di Baldassarre, G.; Lopez, M.G.; Hagenlocher, M.; Vico, G.; Rutgersson, A. Can weather generation capture precipitation patterns across different climates, spatial scales and under data scarcity? Sci. Rep. 2017, 7, 5449. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Brissette, F.; Chen, J. Finding the most appropriate precipitation probability distribution for stochastic weather generation and hydrological modelling in Nordic watersheds. Hydrol. Process. 2013, 27, 3718–3729. [Google Scholar] [CrossRef]
- Wilks, D.S. Multisite generalization of a daily stochastic precipitation generation model. J. Hydrol. 1998, 210, 178–191. [Google Scholar] [CrossRef]
- Wilby, R.L.; Conway, D.; Jones, P.D. Prospects for downscaling seasonal precipitation variability using conditioned weather generator parameters. Hydrol. Process. 2002, 16, 1215–1234. [Google Scholar] [CrossRef]
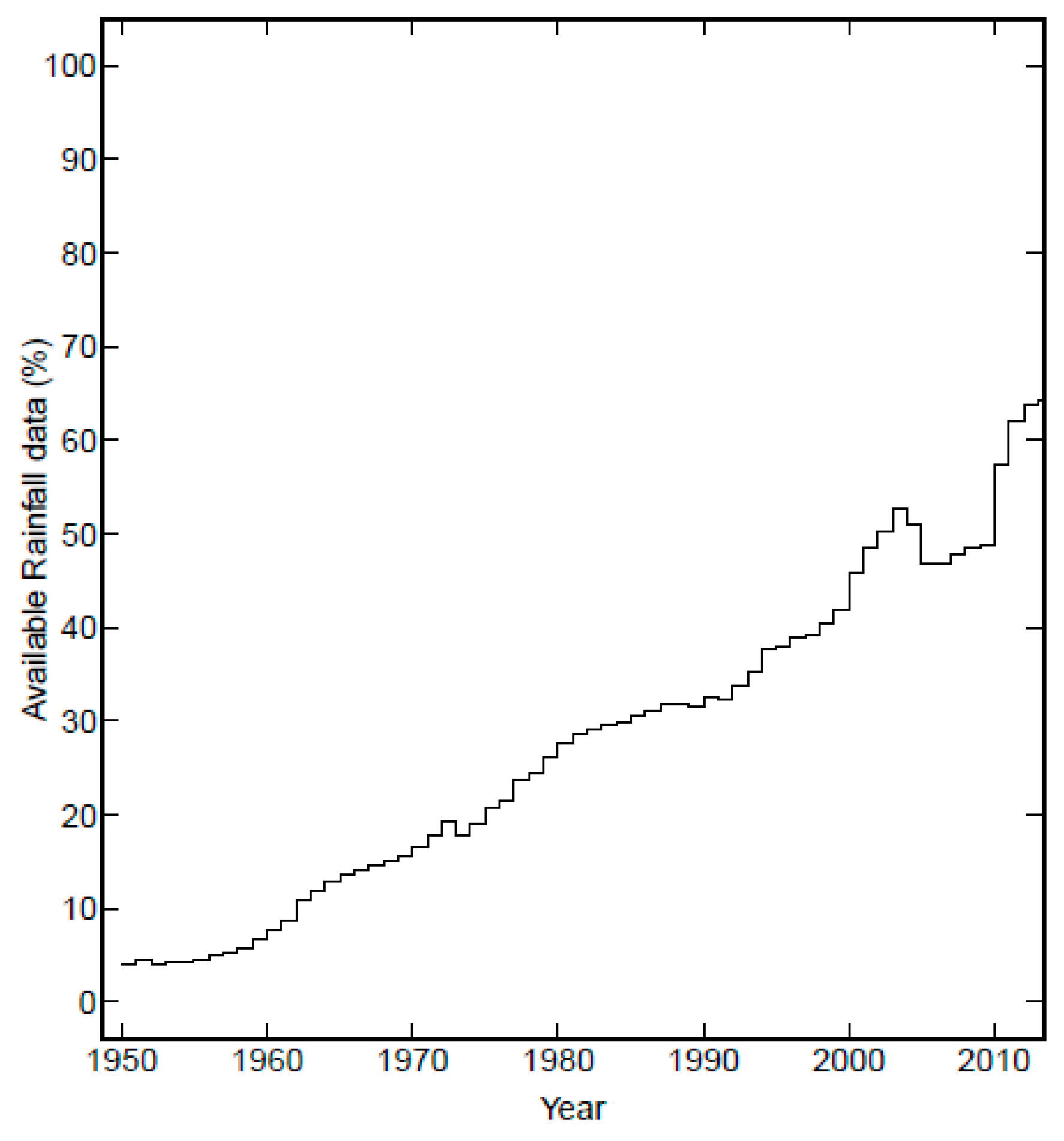
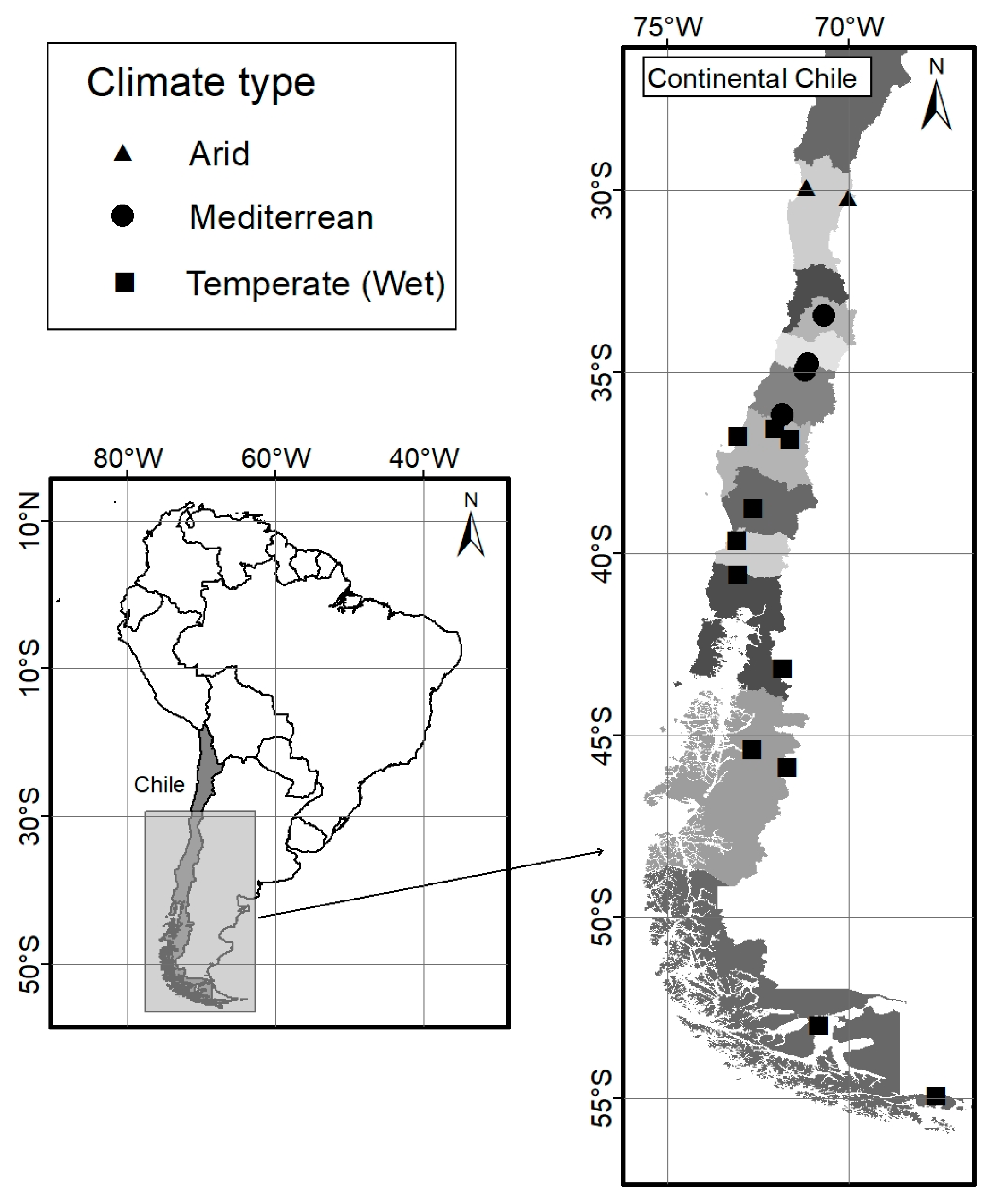
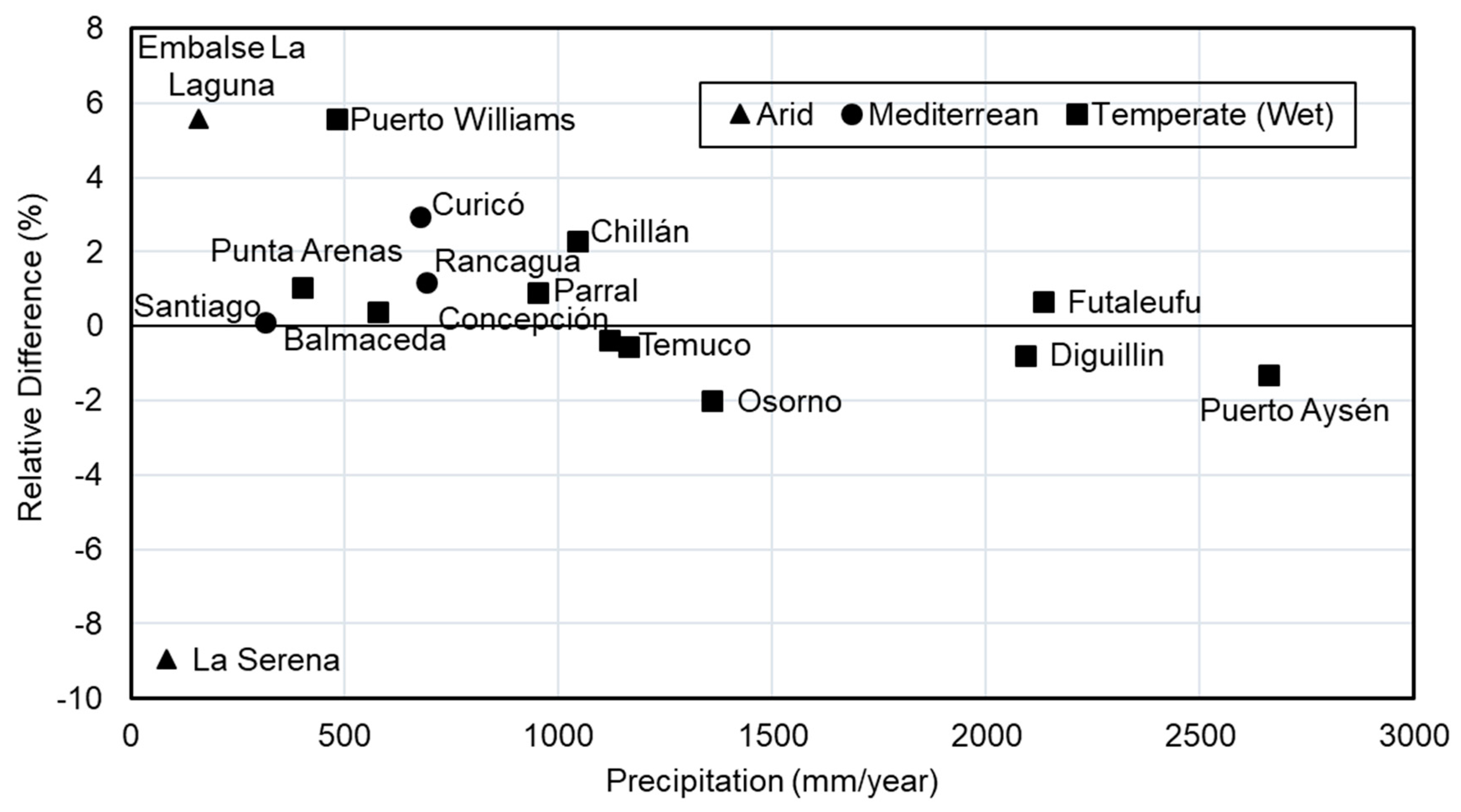
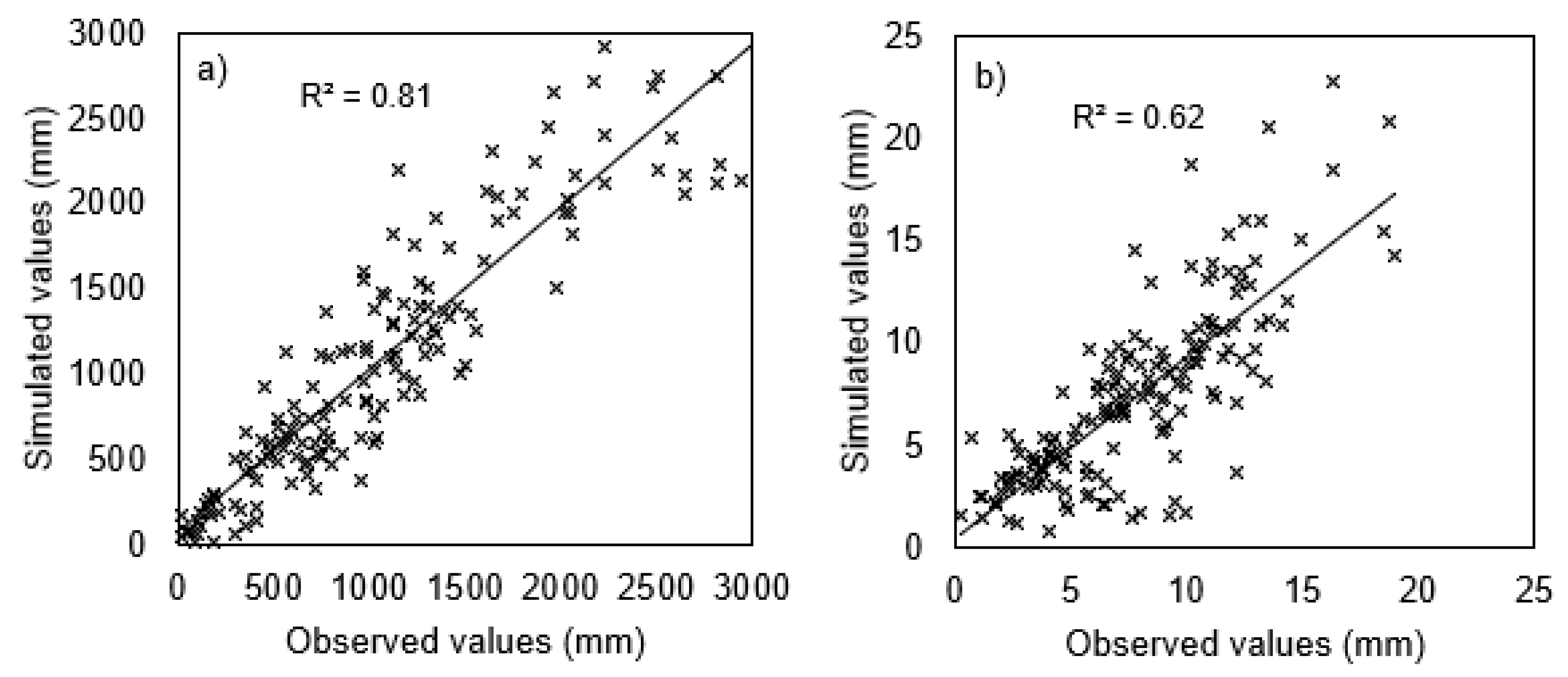
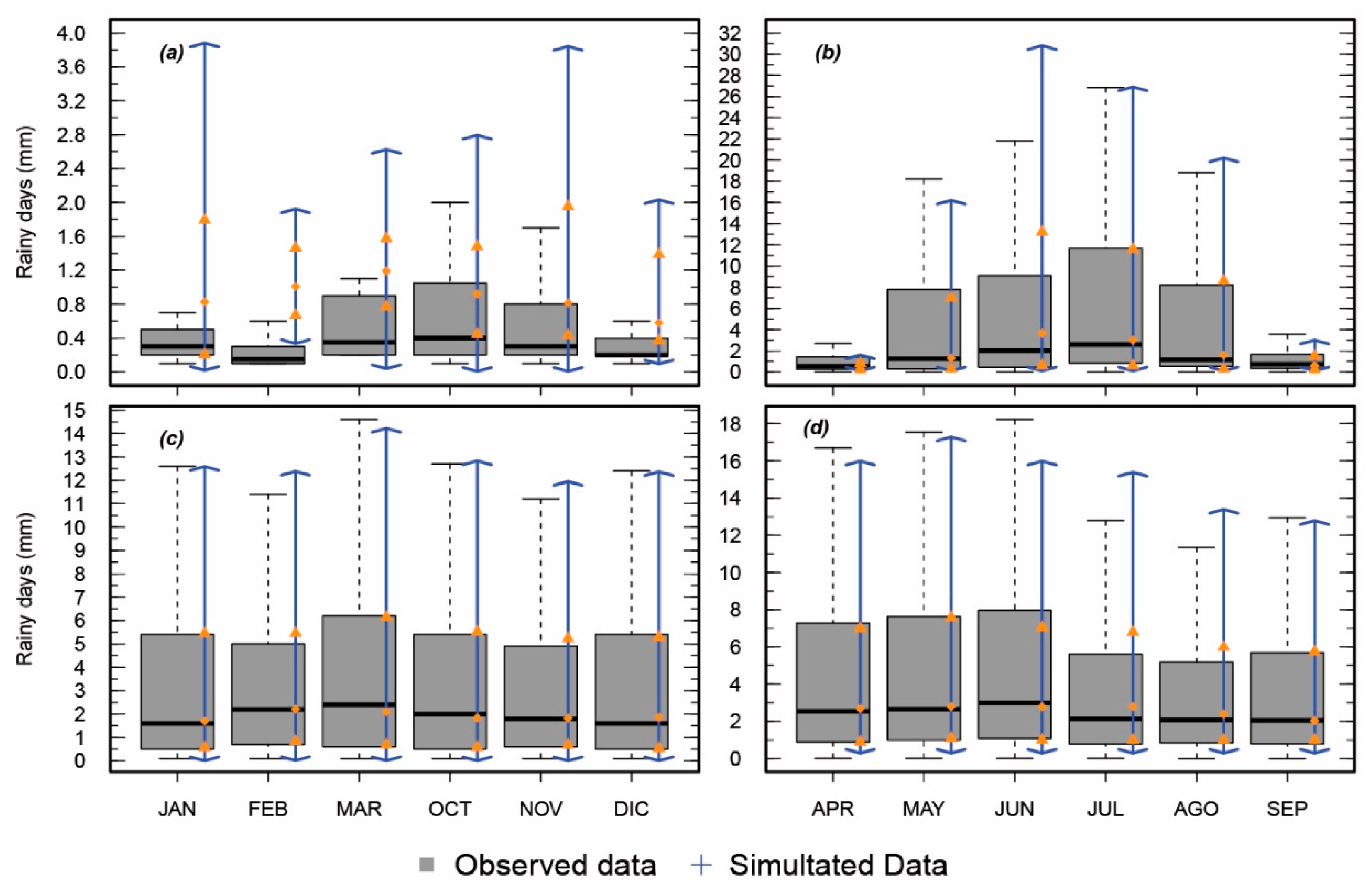
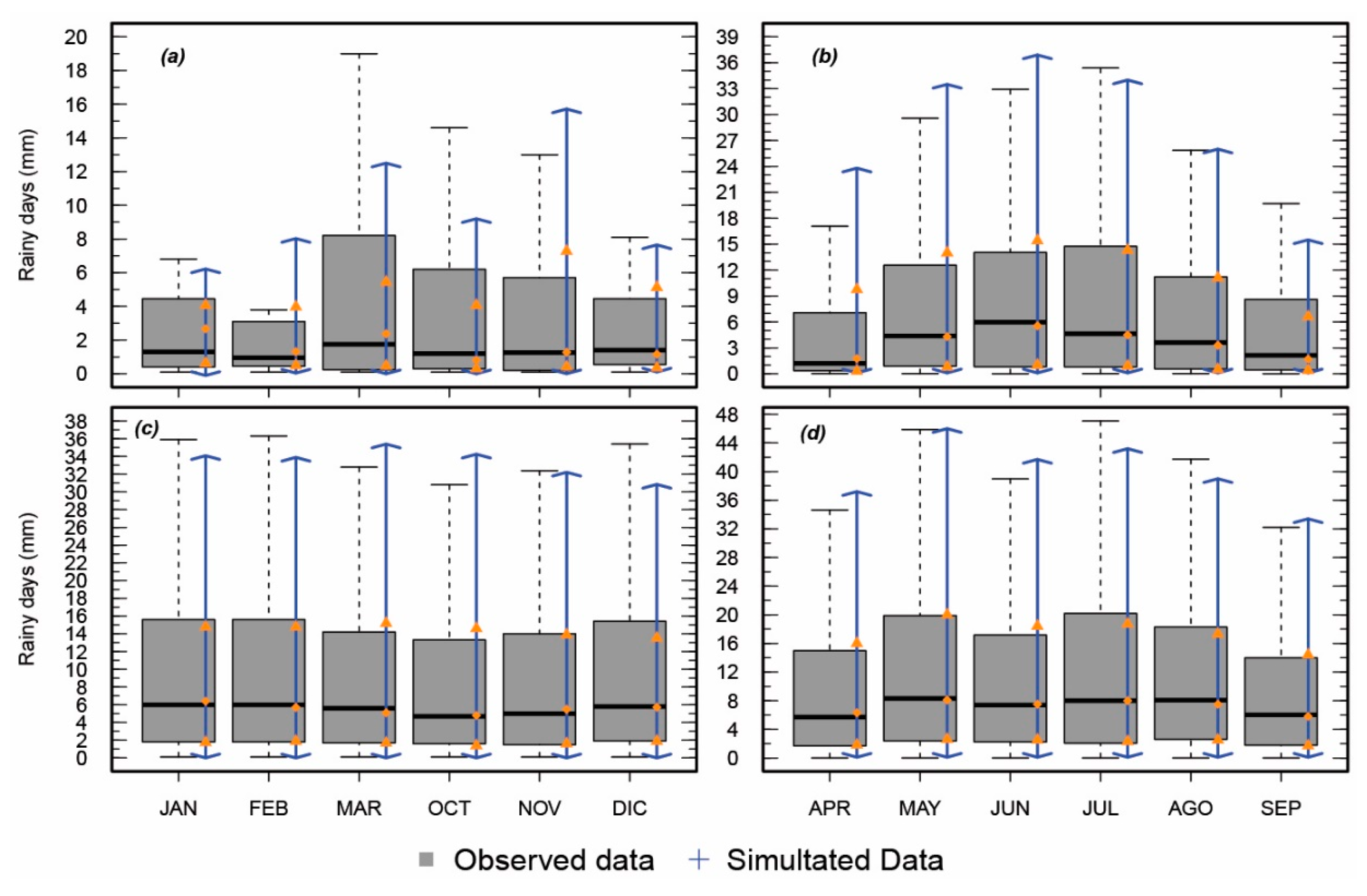

| Station Name | Climate | Latitude (° South) | Longitude (° West) | Elevation (m a.s.l.) | Begginning | End | % Missing Data | Average Annual Precipitation (mm) |
|---|---|---|---|---|---|---|---|---|
| La Serena | Arid | 29°55′ | 71°12′ | 142 | 01/01/1950 | 31/12/2013 | 3.6 | 84.3 |
| Embalse La Laguna | Arid | 30°12′ | 70°02′ | 3160 | 01/01/1964 | 31/12/2013 | 0.7 | 159.7 |
| Santiago | Mediterrean | 33°27′ | 70°40′ | 527 | 01/01/1950 | 31/12/2013 | 0 | 314.1 |
| Rancagua | Mediterrean | 34°46′ | 71°07′ | 239 | 01/09/1971 | 31/12/2013 | 1.5 | 691.7 |
| Curicó | Mediterrean | 34°58′ | 71°13′ | 225 | 01/01/1950 | 31/12/2013 | 10.4 | 675,5 |
| Parral | Temperate | 36°11′ | 71°49′ | 175 | 01/02/1993 | 31/12/2013 | 0 | 952.2 |
| Diguillin | Temperate | 36°52′ | 71°38′ | 670 | 01/05/1959 | 31/12/2013 | 0.8 | 2091.5 |
| Chillán | Temperate | 36°35′ | 72°02′ | 151 | 01/01/1950 | 31/12/2013 | 12.6 | 1044.0 |
| Concepción | Temperate | 36°46′ | 73°03′ | 12 | 01/01/1950 | 31/12/2013 | 0 | 1119.5 |
| Temuco | Temperate | 38°46′ | 72°38′ | 92 | 01/01/1950 | 31/12/2013 | 13.0 | 1163.4 |
| Futaleufu | Temperate | 43°11′ | 71°51′ | 350 | 01/01/1960 | 31/12/2013 | 2.7 | 2133.8 |
| Osorno | Temperate | 40°36′ | 73°03′ | 61 | 01/01/1950 | 31/12/2013 | 10.8 | 1358.1 |
| Balmaceda | Temperate | 45°54′ | 71°41′ | 520 | 01/01/1958 | 31/12/2013 | 0 | 576.3 |
| Puerto Aysén | Temperate | 45°24′ | 72°42′ | 10 | 01/01/1950 | 31/12/2013 | 7.9 | 2661.6 |
| Punta Arenas | Temperate | 53°00′ | 70°50′ | 39 | 01/01/1950 | 31/12/2013 | 3.2 | 399.7 |
| Puerto Williams | Temperate | 54°55′ | 67°37′ | 30 | 01/01/1950 | 31/12/2013 | 19.9 | 480.8 |
| Valdivia | Temperate | 39°39′ | 73°04′ | 18 | 01/01/1950 | 31/12/2013 | 3.7 | 1836.2 |
| Station Name | GLM Parameters | Goodness of Fit with ENSO Index | Goodness of Fit without ENSO Index | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | AIC | R2 | RMSE | AIC | ||||
| La Serena | −2.80 | 1.81 | 0.40 | 0.70 | 0.10 | 890.90 | 0.51 | 0.70 | 966.91 |
| Embalse La Laguna | −3.11 | 2.45 | 0.40 | 0.62 | 0.61 | 645.22 | 0.43 | 2.31 | 670.46 |
| Santiago | −1.83 | 1.64 | 0.10 | 0.56 | 0.94 | 1800.51 | 0.33 | 3.10 | 2100.67 |
| Rancagua | −1.71 | 1.72 | 0.10 | 0.76 | 0.91 | 1277.10 | 0.52 | 4.58 | 1877.21 |
| Curicó | −1.43 | 1.43 | 0.20 | 0.48 | 0.70 | 1744.11 | 0.34 | 0.91 | 1750.84 |
| Parral | −1.15 | 1.32 | 0.05 | 0.67 | 0.97 | 1863.85 | 0.53 | 1.19 | 1975.91 |
| Diguillin | −1.03 | 1.51 | 0.08 | 0.42 | 1.15 | 2044.91 | 0.47 | 1 | 2043.22 |
| Chillán | −1.10 | 1.42 | 0.10 | 0.53 | 1 | 2060.73 | 0.53 | 1 | 2061.11 |
| Concepción | −0.92 | 1.51 | 0.01 | 0.33 | 1.10 | 2434.81 | 0.30 | 1.16 | 2436.80 |
| Temuco | −0.53 | 1.41 | −0.07 | 0.52 | 1.12 | 2119.91 | 0.41 | 1.17 | 2125.91 |
| Futaleufu | −0.45 | 1.43 | −0.09 | 0.22 | 1.18 | 1934.75 | 0.20 | 1.19 | 1934.69 |
| Osorno | −0.40 | 1.51 | −0.01 | 0.43 | 1.09 | 2112.81 | 0.43 | 1.11 | 2114.88 |
| Balmaceda | −0.81 | 1.15 | −0.01 | 0.52 | 1.32 | 2226.31 | 0.50 | 1.21 | 2228.39 |
| Puerto Aysén | 0.10 | 1.51 | −0.10 | 0.64 | 1.05 | 2058.81 | 0.62 | 1.06 | 2057.61 |
| Punta Arenas | −0.91 | 0.83 | 0.09 | 0.42 | 1.05 | 2315.61 | 0.40 | 1.10 | 2416.10 |
| Puerto Williams | −1.01 | 0.92 | −0.12 | 0.33 | 1 | 1900.11 | 0.21 | 1.12 | 1955.41 |
| Valdivia | −0.33 | 1.71 | −0.01 | 0.34 | 1.06 | 2146.54 | 0.32 | 1 | 2100.62 |
| Climate Type | Station Name | Observed | GLM with ENSO Index | HSS | GLM without ENSO Index | HSS | ||
|---|---|---|---|---|---|---|---|---|
| (0) | (1) | (0) | (1) | |||||
| Arid | La Serena | (0) | 3340 | 95 | 0.52 | 3303 | 132 | 0.01 |
| (1) | 100 | 118 | 208 | 10 | ||||
| Arid | Embalse La Laguna | (0) | 3320 | 119 | 0.46 | 3318 | 121 | 0.03 |
| (1) | 105 | 109 | 201 | 13 | ||||
| Mediterrean | Santiago | (0) | 3000 | 272 | 0.16 | 2956 | 316 | 0.04 |
| (1) | 290 | 90 | 330 | 50 | ||||
| Mediterrean | Rancagua | (0) | 2756 | 350 | 0.12 | 2744 | 367 | 0.10 |
| (1) | 421 | 120 | 423 | 118 | ||||
| Mediterrean | Curicó | (0) | 2621 | 430 | 0.13 | 2631 | 420 | 0.11 |
| (1) | 441 | 161 | 452 | 150 | ||||
| Temperate | Parral | (0) | 2306 | 573 | 0.12 | 2365 | 514 | 0.11 |
| (1) | 523 | 250 | 551 | 222 | ||||
| Temperate | Diguillin | (0) | 2212 | 586 | 0.12 | 2130 | 668 | 0.09 |
| (1) | 574 | 281 | 573 | 282 | ||||
| Temperate | Chillán | (0) | 2194 | 556 | 0.15 | 2183 | 567 | 0.13 |
| (1) | 590 | 312 | 599 | 303 | ||||
| Temperate | Concepción | (0) | 2054 | 638 | 0.13 | 1995 | 661 | 0.10 |
| (1) | 632 | 364 | 649 | 347 | ||||
| Temperate | Temuco | (0) | 1411 | 756 | 0.10 | 1403 | 773 | 0.09 |
| (1) | 821 | 655 | 818 | 658 | ||||
| Temperate | Futaleufu | (0) | 1100 | 849 | 0.09 | 1100 | 849 | 0.04 |
| (1) | 900 | 804 | 900 | 804 | ||||
| Temperate | Osorno | (0) | 1096 | 806 | 0.09 | 1133 | 769 | 0.08 |
| (1) | 859 | 891 | 902 | 848 | ||||
| Temperate | Balmaceda | (0) | 1640 | 777 | 0.05 | 1663 | 754 | 0.01 |
| (1) | 780 | 456 | 844 | 392 | ||||
| Temperate | Puerto Aysén | (0) | 1008 | 766 | 0.04 | 1025 | 709 | 0.02 |
| (1) | 1000 | 878 | 1090 | 828 | ||||
| Temperate | Punta Arenas | (0) | 1973 | 618 | 0.22 | 2004 | 73 | 0 |
| (1) | 1500 | 61 | 1516 | 59 | ||||
| Temperate | Puerto Williams | (0) | 1008 | 726 | 0.04 | 1025 | 709 | 0.02 |
| (1) | 1040 | 878 | 1090 | 828 | ||||
| Temperate | Valdivia | (0) | 898 | 629 | 0.09 | 898 | 629 | 0.07 |
| (1) | 1043 | 1082 | 1087 | 1038 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urdiales, D.; Meza, F.; Gironás, J.; Gilabert, H. Improving Stochastic Modelling of Daily Rainfall Using the ENSO Index: Model Development and Application in Chile. Water 2018, 10, 145. https://doi.org/10.3390/w10020145
Urdiales D, Meza F, Gironás J, Gilabert H. Improving Stochastic Modelling of Daily Rainfall Using the ENSO Index: Model Development and Application in Chile. Water. 2018; 10(2):145. https://doi.org/10.3390/w10020145
Chicago/Turabian StyleUrdiales, Diego, Francisco Meza, Jorge Gironás, and Horacio Gilabert. 2018. "Improving Stochastic Modelling of Daily Rainfall Using the ENSO Index: Model Development and Application in Chile" Water 10, no. 2: 145. https://doi.org/10.3390/w10020145
APA StyleUrdiales, D., Meza, F., Gironás, J., & Gilabert, H. (2018). Improving Stochastic Modelling of Daily Rainfall Using the ENSO Index: Model Development and Application in Chile. Water, 10(2), 145. https://doi.org/10.3390/w10020145






